Abstract
Aligning active units ranging from bacteria through animals to drones often are subject to moving in a random environment; however, its influence on the emerging flows is still far from fully explored. For obtaining further insight, we consider a simple model of active particles moving in the presence of randomly distributed obstacles, representing quenched noise in two dimensions. Here we show that our model leads to rich behaviours that are less straightforwardly accessible by experiments or analytic calculations but are likely to be inherent to the underlying kinetics. We find a series of symmetry-breaking states despite the applied disorder being isotropic. For increasing obstacle densities, the system changes its collective motion patterns from (i) directed flow (ii) through a mixed state of locally directed or locally rotating flow to (iii) a globally synchronised rotating state, thereby the system violating overall chiral symmetry. Phase (iii) crosses over to a state (iv) in which clusters of locally synchronised rotations are observed. We find that if both present, quenched rather than shot noise dominates the behaviours, a feature to be considered in future related works.
Similar content being viewed by others
Introduction
Systems made of many self-propelled units exhibit a broad range of fascinating collective motion patterns, the examples ranging from macromolecular level to groups of organisms1,2,3,4,5,6 and the observed behaviours are reminiscent of those in equilibrium many particle systems as well as are manifestations of further kinds of features. While a phase change from a disordered to an ordered state occurs both in equilibrium and far from equilibrium, a conspicuous, qualitatively different behaviour in systems of actively moving entities is the emergence of several kinds of rotational motions due to various origins. Systems in which units move along circular trajectories cover a wide range with complexity being manifested from molecular motors-driven biological macromolecules7,8, colonies of bacteria9,10, cells11,12,13,14, ants15, fish16 to even groups of people17. In these works, it was implied that the reason behind the rotating patterns of group motion was either global spatial confinement, adhesive forces between the particles or a violation of the left-right symmetry on the individual level. Examples of the latter kind of symmetry breaking include bending of a macromolecule8, chirality-broken swimming of sperm cells18 and spiral background director19. Even the flexible, fluctuating boundary of a droplet can result in a single drop-spanning vortex of active particles20.
An important paradigm of the widely observed systems of self-propelled entities is soft active matter3,21,22 consisting of particles interacting through alignment forces and being subject to fluctuations while moving at approximately the same speed. Experiments in which rotations have been observed allow the control of the conditions and have been carried out using macromolecule assays7,8, colonies of bacteria23,24,25,26 or, since the introduction of the elegant experiments first involving Quincke particles27, using small spherical beads. In the latter experiments, colloidal microrollers are propelled by an electric field27,28,29. In the subcritical version of the experiment, free-standing vortexes have recently been observed and modelled30 and finally, they have also been reported in a newer setup involving magnetic beads driven by an oscillating magnetic field31,32.
In the context of the above, it is natural to ask: what are the main factors leading to the rotational motion of active matter? In the above-referenced works, several origins of the rotation patterns during group motion have been demonstrated. (1) One quite general and obvious source of a single rotating pattern is spatial confinement. Under its presence, the only stationary solution for moving together is circling within the area. Confinement can be of various origins ranging from physical barriers to some specific reason for staying close to a region of preference due to, e.g., chemoattractants or at a potential roosting site. (2) Another important, although less common, mechanism of the rotation of a flock is a result of relatively strong adhesion among the units. If the members of a group are attracted to each other efficiently, they stay as close as if they were confined by a wall. This results in rotation if the velocity of the individuals is larger than the directional velocity of the centre of mass of the whole flock, which may be limited by various factors. (3) The next class of the origin of rotation is the breaking of the left-right or chiral symmetry on the individual level. Examples include a curved shape of a self-propelled macromolecule, chirality-broken swimming of sperm cells or spiral background directors as well as particles with magnetic charges. Any specific angular dependence, e.g., anisotropy, in the form of the interaction can also be a source of emerging rotations. (4) Finally, as it was demonstrated in ref. 33 rotating regions arranged as a vortex lattice can emerge at the dry-wet crossover region in a model of active nematics.
Until very recently, the perturbations considered have predominantly been assumed to be shot noise-like, i.e., being uncorrelated in both space and time. On the other hand, such units of active matter as macromolecules, bacteria, colloids, etc., are, in many cases moving in a disordered environment with inhomogeneities representing temporally and spatially correlated perturbations. If the random perturbation is present in the form of a time-independent array of obstacles, it is assumed to be analogous to quenched noise. Thus, we address the question: can isotropic quenched noise result in rotational patterns of motion?
Introducing randomly placed obstacles, i.e., quenched disorder into active matter systems, has a relatively short history. The first paper considering this sort of quenched noise was published by Chepizhko et. al.34 in a paper which demonstrated the interesting and paradoxical effect of the existence of an optimal level of noise resulting in the maximum amount of directed flow in the system. They also demonstrated that due to obstacles, particles can get trapped, resulting in genuine subdiffusion and isolated rotation35 and meandering of the particles. The effects of inhomogeneities in a medium were also investigated both theoretically and by carrying out simulations by using continuous quenched fields affecting the motion of aligning particles subject to rules implying anisotropy in the interactions36. Localisation of the particles was shown theoretically, and simulations indicated the appearance of particles getting trapped and moving along closed trajectories with neighbouring trajectories synchronising and merging in time.
Further work also showed that the particles can rotate around obstacles collectively in a region surrounding a given large obstacle37. It was also found that bands of co-moving particles can survive disorder if the interaction is topological type38 while swirling patterns were observed in simulations of two kinds of active particles in ref. 39. Rich—and relevant from the point of our paper—motion patterns were observed in the beautiful experiments on Quincke rollers moving among randomly placed obstacles28,29. Flocking in an inhomogeneous medium was studied in ref. 40 using a sophisticated continuum equation approach, and it was shown that under the assumptions they made, collective effects were more robust in such an active system than its equilibrium counterpart. On the other hand, randomly placed rotators were shown to destroy global flow beyond a critical density41 just as quenched disorder is capable of destroying quasi-long-range order in an active nematic42. An important class of related experiments involves the collective motion patterns of units of biological origin. Such experiments involving both living active units and quenched perturbations have mostly been carried out by introducing microscopic obstacles into colonies of swimming bacteria26,43, but these obstacles were arranged according to specific regular patterns. To the best of our knowledge, the papers by Nishiguchi et al.44 and Reinken et al.26, reporting on the collective motion patterns of swimming bacteria in the presence of obstacles arranged as the nodes of lattices (square, hexagonal and Kagome-like) are the only publications which present experimental evidence of local rotation of living active matter due to inhomogeneity. Although obstacles typically cause an overall slowdown of flocking velocity, the situation is more complex, and the possible range of phenomena has not been fully explored yet. For example, paradoxically—as was shown recently by Kamdar et al.45—obstacles can even result in enhanced mobility of bacteria when they move in a complex fluid containing colloidal particles.
In the above two paragraphs, we provided a selective account of systems made of both active particles and mostly static, small, passive objects that can be considered as being obstacles. However, rotational motion is so widespread in active matter systems that we briefly also overview those works which report on chiral motion patterns due to alternative causes. If an efficient adhesive force keeps the particles in a confined area, they are bound to end up rotating within that area in both two dimensions, as in ref. 46, and in three dimensions, as shown in the recent work by Susumu and Narya47. A larger class of systems with rotational patterns of motion is associated with anisotropic or chiral forces acting on the level of individual particles. Assuming that the particles on their own would move along circular trajectories, Levis et al.48 showed that in such systems, activity induces synchronisation that results in both mutual flocking and self-sorting of rotating regions in the system. In their paper48, it is also shown that synchronisation occurs and is enhanced by self-propelled motion even in cases when the natural periods of the individually rotating particles follow a time-independent distribution. Similar rotating clusters were obtained in the simulations of Ventejou et al.49 aimed at clarifying the susceptibility of orientationally ordered active matter to chirality disorder. Very recently, Tan et al. reported on a spectacular experiment on the synchronised rotation of aggregated starfish embryos50.
In this paper, we aim to investigate a simple model of dense active matter with disorder. Our goal is to uncover possible, not yet reported, types of collective motion patterns of active aligning particles in the presence of randomly distributed, static, particle-like obstacles. Among the numerous interesting questions related to such active matter systems, one can address the one which is concerned with the nature of the transitions between the observed patterns of motion. For example: Is it analogous to those taking place in equilibrium systems? Can it be interpreted in terms of order parameters changing abruptly if the transition is of first-order type or continuously as it happens in the case of second-order phase transitions? Or alternatively, the situation is more complex, and in the transitional region, new types of behaviours can be observed, as a recent theory by Fruchart et al. predicts51. Our system is made of two kinds of units interacting in an asymmetric or nonreciprocal manner because the moving ones are repelled by the obstacles, while the obstacles do not react to the moving ones. Thus, we may see a behaviour that is analogous to nonreciprocal phase transitions51 allowing an extended region of mixed moving phases including rotations. Such mixed moving phases, which are obviously nonexistent in equilibrium systems, were observed experimentally and interpreted by simulations52 of actomyosin motility assay.
Results
Model
Model and definitions
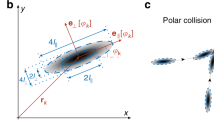
We model the dynamics of self-propelled particles interacting with each other and with randomly distributed obstacles in two dimensions. The main features of the related interactions are visualised in Fig. 1. Figure 1a depicts an overall view of the model. The active particles tend to align their direction of motion if they are within the alignment radius and are repelled by a distance-dependent force both by each other and by the obstacles. Motivations for considering soft repulsion have both computational and physical origins. Our model is intentionally simple but, at the same time, takes into account some realistic conditions. A repulsion force accounting for two independent forms of interactions is originating from and inspired by experiments. Our “hardcore” is not the abstract condition of zero potential outside the hardcore radius and an infinite potential inside it: instead, it is assumed to represent a strong repulsion exerted by two realistic bodies having an elastic type of repulsion, much like two microrollers or even two bacteria repel each other when pushed against each other. The softer, gradually decaying exponential term is assumed to represent forces arising due to the fact that longer-range interactions between entities moving in a medium are usually generated by various mechanisms, including pressure gradients in experiments on Quincke rollers27,30, screening of electric charges, gradients of chemoattractants, etc. On the computational side, pure hardcore may result in undesirable sudden jumps and require a qualitatively different algorithm from those used for continuously changing interaction potentials.
Green circles denote particles and black circles denote obstacles a overall view, b visualises particle–obstacle repulsion, c particle–particle alignment and d particle–particle repulsion. The repulsion terms correspond to a sum of hardcore and an exponentially decaying soft term. e illustrates the magnitude of repulsion.
Perhaps the most important feature of our approach is that it is fully isotropic; it has no anisotropy, chirality or attraction built into it in any way. The other important feature is the softness of the interaction force.
The model we are studying can be considered as made of two kinds of particles, A and B, one kind of them moving (A) while the other ones (B) are being fixed in space with the repulsion force acting between all of the particles being identical. Thus, particles B can “push” particles A away, but A cannot change the position of B particles, and in this way, the interactions are such that particles B represent quenched noise and, at the same time, the effects of repulsion are not reciprocal51. The position of each particle is updated at each time step as:
where xi and vi respectively denote the position and the velocity of the particle and dt = 1 is assumed in our simulations. Thus, the velocities of the particles are obtained from a combination of an alignment (\({{{{{{{{\bf{v}}}}}}}}}_{i}^{{{{{{{{\rm{align}}}}}}}}}\)) and a repulsion (\({{{{{{{{\bf{v}}}}}}}}}_{i}^{{{{{{{{\rm{rep}}}}}}}}}\)) term, which are calculated from the expressions given below.
The alignment term, in the spirit of ref. 53, has an alignment velocity magnitude valign and a unit vector ei pointing in the direction of θi:
with
where j runs over the indices of particles within the alignment radius of particle i including itself, see Fig. 1c. In Eq. (5) < θ(t) > i denotes the average direction of the particles being within the alignment radius ralign of particle i. η denotes the shot noise which is drawn from a uniform distribution in the interval \([-\frac{\eta }{2},\frac{\eta }{2}]\).
When defining the repulsion term, we implement rules in the spirit of simulations aiming at interpreting the collective motion of entities having a hardcore and an exponentially decaying soft repelling force (see, e.g., refs. 30,54). The particle–particle and obstacle–particle repulsion terms are given by:
here k runs over the particles and obstacles that are within the repulsion radius (rrep) of particle i excluding i. It is important to note here that the velocity and the force terms are used in our approach interchangeably since we consider—as it is common in active matter studies—the over-damped limit of the dynamics. The constant rrep is the repulsion coefficient which controls the magnitude of the interaction. The first term in the sum is the soft interaction where ri is the core radius of the particle and rk is the core of either the neighbouring particle or obstacle, both the ri and rk are usually equal to rrep. The second term in the sum models the hardcore short-range interactions where the particle–particle pair or particle–obstacle pair are touching, here the parameter \({c}_{{{{{{{{\rm{core}}}}}}}}}\) controls the relative strength of the interaction, and the g(x) function is 0 if ∣xi − xj∣ ≥ rk + ri and is equal to its argument otherwise as is illustrated in Fig. 1b, d, e. Lastly, the eki(t) term is the unit vector from particle k to particle i. Further, if the value of the repulsion term is less than 1/10 of \({c}_{{{{{{{{\rm{rep}}}}}}}}}\exp \frac{{r}_{i}+{r}_{k}}{A}\) we drop its effect. The value of parameter A controls this cut-off radius (rcut-off).
Model versus recent experiment
The above model, in spite of its simplicity, allows us to simulate a rich variety of possible behaviours in systems with active particles moving in a disordered environment. In order to demonstrate this feature of our model, we use as reference the very recent results of Chardac et al.29 on the states of active colloidal particles in chambers with randomly distributed obstacles. We find that our active particles exhibit very similar motion patterns to those observed experimentally for an appropriately selected set of parameters. If the densities of the moving particles and the obstacles, their respective sizes, as well as the magnitude of the alignment and repulsive forces are tuned to reflect those in the experiments, we observe an almost perfect matching of the experimental and simulational results. To support this statement, we display the two kinds of visual data in Fig. 2. In addition, we also visualised the similarity of the behaviours by comparing the corresponding videos: see the experimental video in ref. 29 and our Supplementary movie 1.
The model is compared with ref. 29. a, b show frames from the movies of the motion and c, d show the corresponding velocity fields, where (a) and (c) are from ref. 29 (reproduced with permission of the authors), and (b) and (d) were obtained during our simulations. In panel (b), the green dots are particles, and the black ones are obstacles. The blue and yellow circles in (c) and (d) denote topological defects in the velocity field. This comparison demonstrates that our model is able to reproduce the “meander” state of motion discovered experimentally by Chardac et al.29.
Definitions of the order parameters
To quantify the behaviour of our system, we have defined four order parameters: global flow, average direction, rotational ratio, and global rotation. These parameters are calculated from the data starting from a time point T0 rather than the initial frame to ensure that the simulation has reached a statistically stationary state.
The global flow order parameter is the displacement of the particles normalised by the displacement of the run without shot noise, quenched noise and repulsion with the same number of particles, size, and number of frames. Since we are using periodic boundary conditions in most of our simulations, taking the displacement by taking the difference between the initial and the final position would be misguiding, so we sum over the velocities for each agent throughout the analysing time interval and then calculate the displacement from that.
The calculation could be summarised as follows:
where \({{\Delta }}{{{{{{{{\bf{x}}}}}}}}}_{max}=\parallel \mathop{\sum }\nolimits_{{T}_{0}}^{T}{v}_{{{{{{{{\rm{align}}}}}}}}}dt\parallel\) is denoting the maximum displacement in a run without obstacles and repulsion; hence dividing by it will normalise the results. A value close to 1 corresponds to the particles having a relatively large displacement, while the value 0 means that there is no displacement on average. This latter case may occur if the density of the obstacles is so large that nearly all particles become trapped/blocked.
The average direction is calculated according to:
where \({\hat{{{{{{{{\bf{v}}}}}}}}}}_{i}(t)\) denotes the unit vector in the direction of the velocity of particle i at time t. This order parameter quantifies how similar the directions of the particles are. A value of 1 denotes a state where all the particles are moving in the same direction, while a value of 0 represents no average direction of the individual motion of the particles. In simple systems, the above two order parameters would be nearly the same; however, for complex motion patterns—see later—they can exhibit a characteristic deviation.
Throughout our paper, the notion “rotating particles” means particles circling around some spontaneously selected centre of motion. The order parameter for rotations is obtained as the ratio of rotating particles to all of the particles from the expression:
where Nrot denotes the number of particles that are rotating. Each particle is counted as rotating if its motion in more than 90% of the frames corresponds to a rotational motion. A particle is considered to be in a rotational motion trajectory in a time interval if it is going through a nearly circular path and it is coming back close to its initial position. The details about the algorithm are described in “Methods”, “Quantifying rotations”.
Lastly, global rotation is calculated as:
where NACW denotes the number of particles rotating anticlockwise, and NCW denotes the number of particles rotating clockwise. Here a value 1 corresponds to a situation in which all of the particles are rotating in the same direction, whereas 0 means that half of them are rotating CW (ACW) while the other half rotating ACW (CW), respectively or no particle is rotating at all. For more details, see the “Methods” section.
States/patterns of collective motion
Based on our order parameters, we define six different collective motion patterns/phases describing the various collective states of our system. These states are summarised in Fig. 3, and videos are available as Supplementary movies 2–8. In this section, we will go through their definition.
-
(a)
Directional motion (Fig. 3a) is associated with a behaviour when the agents have a well-defined common direction of motion, i.e., they are moving as a coherent flock. This state is represented by a well-defined, finite global flow and average direction, as well as close to zero rotational ratio and global rotation. Details of the particular threshold values between states are given in the “Motion states” part of the “Methods” section.
-
(b)
The labyrinth state (Fig. 3b) is a mixture of states being locally analogous to the directional or the rotational state. This state contains groups of particles having either directional or rotational motion for a time interval and then changing their motion state. This state has values in middle ranges for all of the order parameters.
-
(c)
Synchronised rotation (Fig. 3c) and (d) Rotation (Fig. 3d) are our rotational states. Both have small global flow, mid-range average direction and large rotational ratio. The difference between the two rotational states is that while in the synchronised rotation state, all of the particles are rotating in the same direction resulting in large global rotation, in the rotation state, there are two kinds of groups of particles rotating—in a locally synchronised manner—in opposite directions which leads to smaller global rotation values.
All of the figures are for boxes with sizes 60 x 60 and using periodic boundary conditions. The panels (a)–(d) were obtained by using the values of the default parameters specified in Table 1 by changing the number of obstacles only. Thus, the simulations were carried out for obstacle densities 0.005, 0.39, 0.45 and 0.66, respectively. As for panel (e), we used all of the same parameters as given in Table 1 except that we used particle density = 0.22 and obstacle density = 0.66, while panel (f) was obtained for ralign = 0.75, robstacle = 0.2, rparticle = 0.1, crep = 0.033, valign = 0.2 and obstacle density = 0.22. The motion patterns shown are: a Particles move as a directional flock. b A mixture state of coexisting rotational and directional groups of particles, where the spatial boundaries of the two mixture states and the velocity field are changing during the simulations. c Synchronised rotation state where all the particles are rotating in the same direction. d Particles rotating in both directions. e Random state of motion. No directionality, no rotation. f A mixture state between the rotational and directional behaviour. Here, in contrast to the labyrinth state, the velocity field is nearly constant. We also visualised these motion states in the movies included in the Supplementary information, see: Supplementary movies 2–8, showing frames at every fifth time step.
The above-mentioned four states shown in Fig. 3a–d are our main states since we can reach all of them only by changing a single parameter, the obstacle density. In addition, we can observe two additional states, which we call Random (Fig. 3e) and Meander (Fig. 3f). The random state is completely random, meaning the absence of both directionality or any sort of ordered rotation. Here the particles are going through a fully random motion. The meander state is very much like the meander state in ref. 29. This state is similar to the labyrinth state by being a mixture of the directional and the rotational states, but here the particles are not forming groups of the same behaviour. In addition, temporal analysis supports that the velocity field in the labyrinth state is dynamic, whereas the velocity field in the meander state is nearly static in analogy with the vortex glass state of ref. 29. Finally, we note that in order to obtain the full richness of the motion states we report on, it was necessary to include the soft part of the interaction: without it, no extended synchronised regions emerge in the simulations, see: Supplementary movie 9.
Simulations
Simulation results
Most of our simulations were carried out in a square box assuming periodic boundary conditions. In order to demonstrate the flexibility of our approach, we also considered the case of a circular box with a wall repelling the particles with a distance-dependent force corresponding Eq. (6). More detailed information about this is given in the “Methods”, “Boundary Conditions” part. The initial positions of the particles and the obstacles were drawn from a uniform distribution; thus, for each individual simulation, their centres were randomly distributed in the simulational area.
We explored a wide range of parameters in the simulations. On the other hand, to concentrate on the most interesting patterns, in the majority of the cases, we used a set of default values for almost all of the parameters while varying only the remaining few ones. We mostly concentrated on the effect of the obstacle density, which can be considered as the level of quenched noise. The default parameters we used are shown in Table 1. In the following, we summarise our main findings concerning the four relevant aspects of the motion patterns appearing in the simulations of our model.
Our main results about the possible complex collective motion patterns are visualised in Fig. 3 and by the corresponding movies in Supplementary movies 2–8. In order to simultaneously represent both the momentary direction of motion and the direction of rotation, we used an innovative colour coding scheme as shown on the right side in Fig. 3. Particles which do not rotate are indicated by green arrows, while those rotating clockwise or anticlockwise are shown using shades from blue to turquoise and red to yellow, respectively.
Motion states
An essential aspect of behavioural changes in systems consisting of many similar units is the nature of the level of order and the transitions between the various observed states or, as they are called, in-equilibrium systems: phases. Although our system is in a far-from-equilibrium regime, we also consider that phenomena occurring during flocking in most of the cases can be interpreted in terms of approaches common in equilibrium statistical mechanics, as has been discussed, for example, in refs. 1,2,3,4,55. This fact was our motivation for defining order parameters and displaying these parameters in Fig. 4—as a function of the obstacle density playing the role of the “control parameter” in our case. The changes in the three order parameters depicted in Fig. 4a and Average Direction in Fig. 4b indicate behaviours that are novel in several respects. The gradual decay of the global flow parameter is, on the one hand, familiar from earlier studies demonstrating that introducing randomness into flocking results in a decay of the level of coherence in the flocking state, as was shown for both the case of shot noise2 and quenched noise through obstacles, for models see, e.g., ref. 34 or ref. 56, and for the experiment in ref. 28 or ref. 29.
The figure is drawn for 160 simulations in 60 x 60 boxes with periodic boundary conditions and parameters being the same as in Table 1. The error bars denote the standard error of the averages. a The red dotted line indicates the order parameter of the directional motion. Directional motion seems to be the dominating/only pattern of motion till obstacle density 0.3. In the interval 0.3–0.45, the particles are in a mixed state which we associate with a labyrinth-like pattern. In parallel, the Rotational Ratio (solid green line) shows that till 0.3, there is no rotation, and then in 0.3–0.45, particles start to rotate until nearly all of them are rotating in obstacle densities more than 0.45. The Global Rotation (blue dashed line) increases to approximately 1 at 0.45 obstacle density and then beyond approximately 0.45 decreases. The initial increase shows the emergence of a synchronised rotation state, and the decrease shows the transition from synchronised rotation to the rotation where both directions exist but with synchronisation on a local scale only. b The initial decrease of the average direction shows the loss of directionality in the motion of the particles, while the relatively sudden increase at 0.45 is due to the emergence of synchronised rotation.
Long-range order
Although our simulations are for limited system sizes, the question of the existence of long-range order is, however, relevant even on mesoscopic scales, and the nature of the presence of an order within a state is very relevant. The question is about the persistence of a locally ordered state both in space and time. In other words: does the correlation function corresponding to the order we consider, i.e., the direction of rotation decay as a function of distance or time, or is it maintained along these two variables? Our answer is that for systems sizes up to 100 x 100 (over 10 thousand particles), we see rotational order being the same over time and space in a simulational area with periodic boundary conditions. This is perhaps best demonstrated by our Fig. 5. For a detailed description of the calculations used in this part, see “Methods”, “Radial rotational correlation”.
Visualising and quantifying the range of correlations in the rotational state of the individual active particles. Yellow to red colours indicate particles rotating anticlockwise, while light to blue colours correspond to clockwise rotations. Although the direction of the momentary velocities spreads over 360°, the direction of rotation is the same everywhere in panel (a), and it is in both directions in panel (c). Panels b and d display the level to which rotations are correlated. Values close to 1 (as in panel (b)) indicate that the probability that two particles being at a distance within 50 lattice units rotating in the same direction is close to one, i.e., the rotations are fully correlated over the region considered. The decaying feature of the rotational correlations in panel (d) is due to the fact that (1) there are both clockwise and anticlockwise extended regions in the system for this set of the parameter values as well as due to (2) taking a time average over the configurations in a long run of the corresponding simulations. The results are for 100 x 100 runs with parameters the same as in Table 1.
However, in our case, unlike many of the common systems, the order parameter vanishes in a way by displaying an unusual dependence of its derivative close to a transition region. Our data show that just before the global flow completely ceases, the slope of the order parameter is non-monotonic. Although, at first sight, this might be attributed to a finite size effect, a further inspection of Fig. 4 adds a twist to this deviation from a usually monotonic approach of the first derivative to zero. In fact, in the region of the obstacle density values between about ~0.3 and 0.45, as the global flow approaches zero, a simultaneous and very different kind of motion pattern appears, i.e., the global rotation order parameter starts to increase. According to our simulations which are shown for medium box sizes of 60 x 60, the motion state that emerges in this region is best described by particles rotating in confined areas “surrounded” by obstacles. The quote mark here stands for a specific aspect of a soft active matter system with obstacles: even if the obstacles are distributed completely randomly, the particles spontaneously respond to such an environment as if it had “cages” or “chambers” within which they move as if this sort of confinement was analogous to a well-defined geometrical area. The trapping of self-propelled particles in the presence of obstacles was first described and discussed by Chepizhko et al. in ref. 34 and ref. 56. However, it is important to point out here that synchronous rotation occurring all over the system—as it happens in our case—emerges mostly due to the soft nature of the interaction and the relatively large density of both the active particles and the obstacles.
Perhaps the most conspicuous aspect of this rotational state is that the direction of the rotation of the particles is synchronised over the whole system within a narrow region of the obstacle densities. Full synchronisation is also due to the softness and the relatively large densities of the active particles so that they can interact even if they are not within the same local cage but are moving in circles in neighbouring ones. This is a delicate state since both the alignment and the repulsion rules act against such a synchronisation because of the following reason: Particles rotating in the same direction and getting close to each other in neighbouring cages would move in the opposite direction, while this is disfavoured by the alignment rule. The system seems to self-organise into a delicate state in which the particles rotate in neighbouring cages in such a way that, most of the time, they are as much further away from those rotating in the neighbouring cages as possible. In this way, both the cages and the pattern of motion are selected in a self-organised manner so that the state is optimal from the point of minimising conflicting configurations. The process shows analogies with other systems in which self-propelled units self-organise into a state which is partially ordered; for example, particles driven in opposite directions along a channel tend to form two separate lanes minimising the number of collisions; see, for example, ref. 57. The transition from partial to full synchronisation occurs gradually, although the slope of the order parameter function is steep. However, due to the corresponding error bars, its increase is definitely different from vertical. Figure 4a also shows that beyond obstacle densities close to 0.45, the level of system-wide synchronisation gradually decreases, and a state made of groups or “patches” of particles rotating in the same direction within a group, but rotating in the same or oppositely directions in different groups, is increasingly taking place.
Phase transitions and phase diagrams
The observation of the above collective motion patterns or “phases” calls for exploring the parameter spaces for which they occur. Thus, next, we constructed the corresponding phase diagrams in which the regions characterised by a given phase are visualised using four colours, as displayed in Fig. 6. Constructing such diagrams needs a considerable amount of CPU/GPU time; this is the reason for some ruggedness in the plots. However, the main tendencies are well seen: the behaviour is considerably less sensitive to the level of shot noise than that of the obstacle density representing quenched noise (see Fig. 6a). The way a given motion state depends on the number density of the particles or on their alignment radius is similar (see Fig. 6b, c) since both increasing the number density of the particles or their alignment radius results in an effective increase of the regions covered by the total area within which the particles interact.
The results are shown for 60 x 60 box size and obtained for periodic boundary conditions. In each panel (a), (b), and (c), the parameters—except the parameter along the Y-axis—are the same as those in Table 1. Panel a indicates that obstacle density dominates shot noise since there is no relevant change in the behaviour over much of the region of the shot noise values. Panel b shows the trade between the particle and obstacle densities. It shows that a dense medium is needed to see synchronised rotation. Panel c resembles panel (b) since the alignment radius is related to an effective particle density.
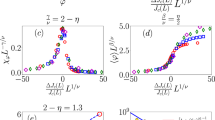
Both Figs. 4 and 6 suggest that examining the characteristic feature of the transition from the global flow to the global rotation states is of particular interest. Since the transition seems to be relatively sharp, we decided to test whether it is of first or second order. To obtain related information, we made use of two approaches (see Fig. 7): (1) plotting the distribution of the measured global rotation values averaged over many runs and (2) calculating the Binder cumulant58. In the case of a standard second-order phase transition, the histograms of the order parameter have a well-defined maximum, gradually moving from smaller to larger values of the position of the maximum as ordering takes place. In the case of a first-order transition, the behaviour is different, and the position of the maximum corresponding to small values of the order parameter moves from the left edge to its other peak for large order parameter values without a smooth shift from left to right. This happens as the histogram peak decreases for the small values and starts to increase for values close to 1 (see Fig. 7a, b), corresponding to the system assuming either a disordered or an almost fully ordered state. The Binder cumulant signals the order of the transition by either having no minimum for second-order transitions at all or having a sharp, well-defined minimum at the point of the control parameter at which a first-order transition takes place. Since both the histograms and the Binder cumulant are sensitive to fluctuations, we carried out the corresponding simulations for larger, i.e., 100 x box sizes.
Panels a and b denote the histograms of order parameters over 90 runs in a 100 x 100 box with parameters the same as in Table 1. Panels c and d show the Binder cumulant of each set of those runs. To calculate the error bars, we divided the 90 runs into six groups of randomly selected runs. Calculated the average Binder cumulant of each group as its value and then calculated the error using standard error. For further explanation and interpretation of the above complex dependencies, see the “Phase transitions and phase diagrams” section.
Thus, our Fig. 7c, d indicates a behaviour that is quite different from any related results reported earlier. We suggest that the unusual statistics of the Binder cumulant is likely to be a signature of the presence of a transition that does not fall into the category of either a second-order or a first-order transition. A further specific feature of the data plotted in Fig. 7 is that the anomalous behaviour of the Binder cumulant is more expressed for obstacle densities for which the two distinct peaks in the plot about the histograms do not show up yet (see also Supplementary Note 1 and Supplementary Fig. 1).
Since the behaviour of the Binder cumulant appeared to be very unusual, we decided to carry out several checks on its dependence on the density of obstacles. One test included the following procedure: we divided the 90 runs into six groups of randomly selected runs considering the averages obtained for the Binder cumulant in each group as independent measurements. Then, to obtain an estimate of the error bar of these averages, we took their standard deviation and divided it by the square root of 6. In the revised version of our paper, we include a slightly modified version of the Binder cumulant results by indicating the error bars obtained using the above procedure. We conclude that our values for the Binder cumulant, which seem to be fluctuating in the interval of obstacle densities between 0.34 and 0.4, can be well reproduced since the associated error bars are at least by a magnitude smaller than the values themselves.
An essential aspect of the kind of interpretation we use is the applicability of the observed behaviours to system sizes in the so-called thermodynamic limit, which is associated with systems sizes having linear extensions approaching infinity. Such sizes are not attainable in simulations, nor are reachable in the experiments on active matter. Thus, the range of the number of units we simulated is relevant from the point of experiments but is, obviously, far from the thermodynamic limit. Still, this size range is relevant, and perhaps this is why the class of systems belonging to this range was classified as being mesoscopic. Nevertheless, the behaviour of our system for much larger sizes is of interest, and it can be estimated by extrapolating the behaviour for increasing systems sizes.
Addressing in detail this important aspect of a model requires a large amount of extensive further calculations, which, in our case, may serve as a basis for a future study. In order to get some insight into whether the motion patterns or phases we observed would be present in a very large system, we carried out simulations for systems sizes with increasing linear size with L = 30, 60, 80, 120 and 140. We included a subset of the related preliminary results in the Supplementary information of our manuscript (see Supplementary Note 2 and Supplementary Fig. 2) which indicates that for the default parameter set we use, the globally synchronised state is likely to occur with a gradually decreasing probability of the runs as the system size is increasing, so it will be present on the mesoscopic scale. One of the reasons for this is the apparently unavoidable appearance of topological defects6 due to the fluctuating distribution of the obstacles. However, we would like to point out here that according to our results (see Supplementary movie 10), global synchronisation will occur for even larger systems than the largest ones we used for obtaining Figs. 4 and 7 if the alignment radius is increased to 2.5. The specific aspects of the behaviour for larger system sizes would go beyond the scope of this work but are expected to reveal further interesting details.
Wave propagation
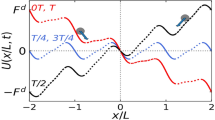
The final point we would like to present is concerned with the way a given direction of the rotating particles propagates in the simulation area. Figure 8 demonstrates this feature: as the number of time steps is increased, the borderline between regions of red colour corresponding to particles moving in a direction just above “horizontal” and yellow colour indicating particles moving in a direction just below “horizontal” has a tendency to proceed with a velocity depending in a complex way on the local distribution of the obstacles. We include this observation because of its similarity to propagating waves in an excitable medium (for a recent review, see ref. 59). The analogy is based on assuming that the momentary direction of motion corresponds to a given local state of the system and this state propagates across the system in a repeated manner. This similarity does not involve that the underlying fundamental rules would be analogous; in fact, they are quite different. The three major states of excitable media: excitable, excited and refractory, which are the major components producing waves in those systems, are not present in our system. We still thought of mentioning the similarity of the images as a function of time we obtain and those obtained for excitable media because one aspect of the two behaviours is common: there is a well-defined state propagating through the system. This state is a given direction of motion in our case and is one of the three basic states in the case of an excitable medium. In any case, there is an underlying cyclic process in both kinds of systems that can influence the behaviour in spatially neighbouring locations.
Snapshots from Supplementary movie 4 showing Synchronised Rotation. Here the word phase is used to denote the momentary angle of motion of the particles. At each iteration step, each particle transfers its phase to the neighbouring particles, which leads to a moving wave-like behaviour. The propagation of the phase wave is indicated by the advancing of the region with red colour, denoting angles close to but larger than 0 according to the colour code in Fig. 3.
Discussion
We have demonstrated above that the simple model we introduced in order to account for possible behaviours of dense active matter made of soft particles moving in a disordered medium may give rise to a rich and not yet observed set of collective motion states and the transitions between them. The most unexpected state we have found is made of particles exhibiting two types of synchronisation simultaneously. They rotate in the same direction locally, along nearly circular trajectories of average diameter, which is of the same order as their interactions radius, and, at the same time, they are all rotating in the same direction, either clockwise or anticlockwise at the distant points of the system as well. Our simulations show that the change of the collective motion pattern from a global directional flow to a state in which all particles are localised and rotate in a synchronous manner involves a complex phase in which two kinds of flows, directional and rotational, are both present.
Recently a few promising theories emerged that predict transitions, but these transitions involve a behaviour which cannot be classified into well-defined first or second-order transitions in equilibrium. It seems that phase transitions in active systems cannot be classified on the basis of the singularities of corresponding free energy. In fact, a recent theory on nonreciprocal phase transition predicts a very rich phase diagram with transitions between pure and mixed states51. We consider it as an open question whether an ensemble of self-propelled particles moving in a random environment made of particle-like obstacles can be interpreted as a system with nonreciprocal interactions. At least one of its aspects is reminiscent of nonreciprocity: if the repulsion forces are of the same form for both types of particles, then obstacles can push active particles, while the latter ones have no effect on the position of the pinned obstacles. Alternatively, using experimental and numerical simulation approaches, transitions between several new motion phases (e.g., involving topological defects) were observed with no well-defined singularities around the transition points (see e.g., refs. 6,33,36,52). We are discussing the above points in such detail because what we obtained from our mesoscopic scale simulations exhibits similar features: the transition from directional flow state to the state with virtually all particles rotating is not a simple only directional flow or only rotation, but there exists a mixed state (or states) between the two unique (either flow or rotation) states. Consequently, the methods used to decide the order of a transition in equilibrium do not result in a well-defined picture. In particular: the peaks in the histograms for the distribution of the order parameters are less pronounced than they would be for an equilibrium system, and second, the Binder cumulant (which was designed to detect a first-order phase transition in an equilibrium system) also displays anomalies.
The system size is another sensitive question here. We can numerically investigate systems up to a range of 10,000 to 20,000 particles because the memory constraints of the available GPU-s (Graphical Processing Units) make our algorithm efficient up to such system sizes. For these sizes, our results are robust and reproducible. This number of units is also common in most of the experiments, although some which involve molecular motors or a huge number of bacteria have a larger number of units but are still far from the 1023 particles commonly assumed in a standard statistical mechanics approach.
Together with the other outcomes of our simulations, our model has a specific aspect in the sense that it seems to couple a number of features typical for quite different alternative systems as follows: (1) it is constructed in the spirit of active matter systems or flocking, (2) it displays synchronised rotations occurring in models of synchronisation60 and in recent models, in ref. 61 and ref. 48, that couple swarming to rotations, (3) the nature of the transition between the global flow and global rotation states has similarities with coexisting phases found in nonreciprocal phase transitions (ref. 51) and (4) we observe the propagation of a state variable just like it happens in excitable media59. We can add two comments of general nature, which are indicated by our simulations: it seems that (at least for some parameter values) the system spontaneously self-organises into a stationary state in which the number of collisions is minimal and, since our approach allows to control the two kinds of noises independently, we conclude that it is likely that in active matter systems, the role of quenched noise dominates over shot noise type perturbations.
Methods
Simulations
To efficiently simulate a large number of particles, we used a GPU-Accelerated code which is based on CUDA Python. The results were obtained by using GEFORCE RTX 3060 and GEFORCE GTX 1070 GPU-s. At each time step, the velocity of each particle is calculated in parallel with other particles depending on the current positions and the directions of the particles and obstacles within its repulsion and alignment radius as given by equations (1)–(6). The order parameters were calculated by a combination of CPU and GPU computing to make the calculation more efficient in the steps where paralleling over the particles or time step would not shorten the computational time significantly.
Quantifying rotations
Quantifying the rotational behaviour is essential in our research. To obtain data for interpreting the rotational motion of particles and their full path with perfect accuracy one needs to store all the positions and the angles and then go through the data. Since this is computationally heavy, we made use of an approximate algorithm: we defined a trajectory as “rotation” if a particle completed a nearly circular path while its velocity vector was going through a full cycle. This corresponds to the following: for each particle and at each iteration, we calculated the rotation of the velocity vector as “rotation” at time t:
It is important to mention that our angles are stored in the [0, 2π] interval and we want to know the “direction” of the rotation. The issue with using the mentioned equation is that it will not give any information on the direction of the rotation and it will only give the angle difference. For example, if the θi(t) = 0 and \({\theta }_{i}(t+1)=\frac{\pi }{2}\) the code correctly calculates the size of rotation as π, but it will not understand whether the rotation was clockwise or anticlockwise. To handle this situation, we use the approximation that the velocity vectors cannot have a rotation more than π which is reasonable considering our default parameters given in Table 1. As a result of this approximation, the given example will be calculated as π radian rotation in an anticlockwise direction rather than \(\frac{3\pi }{2}\) in a clockwise direction. Using the same approximation, we also calculated the rotations close to the 0 or 2π point. For example, if \({\theta }_{i}(t)=\frac{5\pi }{3}\) and \({\theta }_{i}(t+1)=\frac{\pi }{3}\), we have a rotation of \(\frac{2\pi }{3}\) in the anticlockwise direction rather than \(\frac{4\pi }{3}\) in the clockwise direction.
After these calculations, we sum over the rotations and the displacement of the particle in a time interval until: First, the rotation sum reaches either −2 π or 2 π, and second, the displacement becomes smaller than a threshold value which is equal to the hardcore radius of particles (rparticle) in the current code. If both constraints are satisfied, we consider the particle to be rotating in that time interval, and the length of the time interval is counted as the period of the rotation. In addition, if the rotation sum is positive, it is counted to be a positive rotation or ACW, and if it is negative, it is a negative rotation or CW. The first constraint ensures that the path is nearly circular, and the combination of the two together ensures that the particles are coming back to their starting positions. Further, if it takes a particle longer than the maximum possible rotation time (MPRT) to satisfy both constraints, then the sums are made equal to zero, and we start over. This constraint is extremely important to make the model more accurate. Without this, the algorithm would not consider a motion to be rotational if a particle goes through a straight path and then starts rotating after a certain time point. By tuning the threshold and the MPRT value, the algorithm perfectly counts the rotational motions in our simulations since we are only interested in counting full cycles.
Motion states
Table 2 below depicts the threshold values of the order parameters used for defining the various motion states:
Boundary conditions
In circular box simulations, we simulate the wall as a chain of obstacles using Eq. (6) of the main text with small modifications:
where Rcirc is the radius of the circular box and ri(t) is the radial position vector.
Radial rotational correlation
The radial rotational correlation function (RRC) is calculated to quantify how much the direction of the rotation of each particle is correlated with its neighbours. The value is calculated as follows:
Here Si,r denotes the number of particles in closer than distance r to particle i which are rotating in the same direction. similarly Ni,r denotes the total number of particles in that radius. Hence, by averaging over all particles and time, RRC shows what ratio of particles at a certain radius are rotating in the same direction.
Data availability
The data are available from the corresponding author upon reasonable request.
Code availability
The main body of the code used in simulations is available at https://github.com/Danial-Vahabli/Vicsek_Model_with_Repulsion_Cuda. The full version of the code may be available from the corresponding author upon reasonable request.
References
Sumpter, D. J. T. Collective Animal Behavior. (Princeton University Press, 2010).
Vicsek, T. & Zafeiris, A. Collective motion. Phys. Rep. 517, 71–140 (2012).
Marchetti, M. C. et al. Hydrodynamics of soft active matter. Rev. Mod. Phys. 85, 1143–1189 (2013).
Cavagna, A. & Giardina, I. Bird flocks as condensed matter. Annu. Rev. Condens. Matter Phys.5, 183–207 (2014).
Alert, R., Casademunt, J. & Joanny, J.-F. Active turbulence. Annu. Rev. Condens. Matter Phys.13, 143–170 (2022).
Shankar, S., Souslov, A., Bowick, M. J., Marchetti, M. C. & Vitelli, V. Topological active matter. Nat. Rev. Phys. 4, 380–398 (2022).
Schaller, V., Weber, C., Semmrich, C., Frey, E. & Bausch, A. R. Polar patterns of driven filaments. Nature 467, 73–77 (2010).
Sumino, Y. et al. Large-scale vortex lattice emerging from collectively moving microtubules. Nature 483, 448–452 (2012).
Czirók, A., Ben-Jacob, E., Cohen, I. & Vicsek, T. Formation of complex bacterial colonies via self-generated vortices. Phys. Rev. E 54, 1791–1801 (1996).
Yamamoto, H. et al. Scattered migrating colony formation in the filamentous cyanobacterium, Pseudanabaena sp. NIES-4403. BMC Microbiol. 21, 227 (2021).
Méhes, E. & Vicsek, T. Collective motion of cells: from experiments to models. Integr. Biol. 6, 831–854 (2014).
Battersby, S. The cells that flock together. Proc. Natl Acad. Sci. USA 112, 7883–7885 (2015).
Be’er, A. & Ariel, G. A statistical physics view of swarming bacteria. Mov. Ecol. 7, 9 (2019).
Hong, X. et al. The lipogenic regulator SREBP2 induces transferrin in circulating melanoma cells and suppresses ferroptosis. Cancer Discov. 11, 678–695 (2021).
Couzin, I. D. & Franks, N. R. Self-organized lane formation and optimized traffic flow in army ants. Proc. Biol. Sci. 270, 139–146 (2003).
Calovi, D. S. et al. Swarming, schooling, milling: phase diagram of a data-driven fish school model. New J. Phys. 16, 015026 (2014).
Kolivand, H., Rahim, M. S., Sunar, M. S., Fata, A. Z. A. & Wren, C. An integration of enhanced social force and crowd control models for high-density crowd simulation. Neural Comput. Appl. 33, 6095–6117 (2021).
Riedel, I. H., Kruse, K. & Howard, J. A self-organized vortex array of hydrodynamically entrained sperm cells. Science 309, 300–303 (2005).
Koizumi, R. et al. Control of microswimmers by spiral nematic vortices: transition from individual to collective motion and contraction, expansion, and stable circulation of bacterial swirls. Phys. Rev. Res. 2, 033060 (2020).
Kokot, G., Faizi, H. A., Pradillo, G. E., Snezhko, A. & Vlahovska, P. M. Spontaneous self-propulsion and nonequilibrium shape fluctuations of a droplet enclosing active particles. Commun. Phys. 5, 91 (2022).
Toner, J., Tu, Y. & Ramaswamy, S. Hydrodynamics and phases of flocks. Ann. Phys. 318, 170–244 (2005).
Chaté, H. Dry aligning dilute active matter. Annu. Rev. Condens. Matter Phys. 11, 189–212 (2020).
Ben-Jacob, E., Cohen, I. & Levine, H. Cooperative self-organization of microorganisms. Adv. Phys. 49, 395–554 (2000).
Watanabe, K. et al. Dynamical properties of transient spatio-temporal patterns in bacterial colony of Proteus mirabilis. J. Phys. Soc. Japan 71, 650–656 (2002).
Wakita, J.-i, Tsukamoto, S., Yamamoto, K., Katori, M. & Yamada, Y. Phase diagram of collective motion of bacterial cells in a shallow circular pool. J. Phys. Soc. Japan 84, 124001 (2015).
Reinken, H. et al. Organizing bacterial vortex lattices by periodic obstacle arrays. Commun. Phys. 3, 76 (2020).
Bricard, A., Caussin, J.-B., Desreumaux, N., Dauchot, O. & Bartolo, D. Emergence of macroscopic directed motion in populations of motile colloids. Nature 503, 95–98 (2013).
Morin, A., Desreumaux, N., Caussin, J.-B. & Bartolo, D. Distortion and destruction of colloidal flocks in disordered environments. Nat. Phys. 13, 63–67 (2017).
Chardac, A., Shankar, S., Marchetti, M. C. & Bartolo, D. Emergence of dynamic vortex glasses in disordered polar active fluids. Proc. Natl Acad. Sci. USA 118, e2018218118 (2021).
Liu, Z. T. et al. Activity waves and freestanding vortices in populations of subcritical quincke rollers. Proc. Natl Acad. Sci. USA 118, e2104724118 (2021).
Kaiser, A., Snezhko, A. & Aranson, I. S. Flocking ferromagnetic colloids. Sci. Adv. 3, e1601469 (2017).
Han, K. et al. Emergence of self-organized multivortex states in flocks of active rollers. Proc. Natl Acad. Sci. USA 117, 9706–9711 (2020).
Doostmohammadi, A., Adamer, M. F., Thampi, S. P. & Yeomans, J. M. Stabilization of active matter by flow-vortex lattices and defect ordering. Nat. Commun. 7, 10557 (2016).
Chepizhko, O., Altmann, E. G. & Peruani, F. Optimal noise maximizes collective motion in heterogeneous media. Phys. Rev. Lett. 110, 238101 (2013).
Chepizhko, O. & Peruani, F. Diffusion, subdiffusion, and trapping of active particles in heterogeneous media. Phys. Rev. Lett. 111, 160604 (2013).
Peruani, F. & Aranson, I. S. Cold active motion: how time-independent disorder affects the motion of self-propelled agents. Phys. Rev. Lett. 120, 238101 (2018).
Mokhtari, Z., Aspelmeier, T. & Zippelius, A. Collective rotations of active particles interacting with obstacles. Europhys. Lett. 120, 14001 (2017).
Rahmani, P., Peruani, F. & Romanczuk, P. Topological flocking models in spatially heterogeneous environments. Commun. Phys. 4, 206 (2021).
Sampat, P. B. & Mishra, S. Polar swimmers induce several phases in active nematics. Phys. Rev. E 104, 024130 (2021).
Toner, J., Guttenberg, N. & Tu, Y. Swarming in the dirt: ordered flocks with quenched disorder. Phys. Rev. Lett. 121, 248002 (2018).
Das, R., Kumar, M. & Mishra, S. Polar flock in the presence of random quenched rotators. Phys. Rev. E 98, 060602 (2018).
Kumar, S. & Mishra, S. Active nematics with quenched disorder. Phys. Rev. E 102, 052609 (2020).
Galajda, P., Keymer, J., Chaikin, P. & Austin, R. A wall of funnels concentrates swimming bacteria. J. Bacteriol. 189, 8704–8707 (2007).
Nishiguchi, D., Aranson, I. S., Snezhko, A. & Sokolov, A. Engineering bacterial vortex lattice via direct laser lithography. Nat. Commun. 9, 4486 (2018).
Kamdar, S. et al. The colloidal nature of complex fluids enhances bacterial motility. Nature 603, 819–823 (2022).
Shimoyama, N., Sugawara, K., Mizuguchi, T., Hayakawa, Y. & Sano, M. Collective motion in a system of motile elements. Phys. Rev. Lett. 76, 3870–3873 (1996).
Ito, S. & Uchida, N. Emergence of a giant rotating cluster of fish in three dimensions by local interactions. J. Phys. Soc. Japan 91, 064806 (2022).
Levis, D., Pagonabarraga, I. & Liebchen, B. Activity induced synchronization: mutual flocking and chiral self-sorting. Phys. Rev. Res. 1, 023026 (2019).
Ventejou, B., Chaté, H., Montagne, R. & Shi, X.-q. Susceptibility of orientationally ordered active matter to chirality disorder. Phys. Rev. Lett. 127, 238001 (2021).
Tan, T. H. et al. Odd dynamics of living chiral crystals. Nature 607, 287–293 (2022).
Fruchart, M., Hanai, R., Littlewood, P. B. & Vitelli, V. Non-reciprocal phase transitions. Nature 592, 363–369 (2021).
Huber, L., Suzuki, R., Krüger, T., Frey, E. & Bausch, A. R. Emergence of coexisting ordered states in active matter systems. Science 361, 255–258 (2018).
Vicsek, T., Czirók, A., Ben-Jacob, E., Cohen, I. & Shochet, O. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 75, 1226–1229 (1995).
Helbing, D., Farkas, I. & Vicsek, T. Simulating dynamical features of escape panic. Nature 407, 487–490 (2000).
Baglietto, G. & Albano, E. V. Nature of the order-disorder transition in the Vicsek model for the collective motion of self-propelled particles. Phys. Rev. E 80, 050103 (2009).
Chepizhko, O. & Peruani, F. Active particles in heterogeneous media display new physics. Eur. Phys. J. Spec. Top. 224, 1287–1302 (2015).
Helbing, D. & Vicsek, T. Optimal self-organization. New J. Phys. 1, 13–13 (1999).
Binder, K. Finite size scaling analysis of Ising model block distribution functions. Zeitschrift für Physik B Condens. Matter 43, 119–140 (1981).
Zykov, V. S. & Bodenschatz, E. Wave propagation in inhomogeneous excitable media. Annu. Rev. Condens. Matter Phys. 9, 435–461 (2018).
Strogatz, S. H. From Kuramoto to Crawford: exploring the onset of synchronization in populations of coupled oscillators. Physica D 143, 1–20 (2000).
O’Keeffe, K. P., Hong, H. & Strogatz, S. H. Oscillators that sync and swarm. Nat. Commun. 8, 1504 (2017).
Acknowledgements
The authors thank S. H. Strogatz for illuminating suggestions and M. Nagy, F. Pakpour and L. L. Szánthó for useful discussions. This work was partly supported by the grant: (Hungarian) National Research, Development and Innovation Office grant No K128780. D.V. is grateful to the Erasmus+ Traineeship Programme of the European Commission for support.
Funding
Open access funding provided by Eӧtvӧs Loránd University.
Author information
Authors and Affiliations
Contributions
T.V. conceived the research. D.V. performed the calculations. Both authors discussed the results, drew conclusions and edited the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Demian Levis, Daiki Nishiguchi and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vahabli, D., Vicsek, T. Emergence of synchronised rotations in dense active matter with disorder. Commun Phys 6, 56 (2023). https://doi.org/10.1038/s42005-023-01173-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-023-01173-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.