Abstract
The discovery of superconductivity in hole-doped infinite layer nickelates, RNiO2 (R = Nd, Pr, La) has resulted in sustained interest in the field. A definitive picture of low-energy many-body states has not yet emerged. Here we provide insights into the low-energy physics, based on our embedded dynamical mean-field theory calculations, and propose a correlation (U)-temperature (T) phase diagram. The key features are a low-T Fermi liquid (FL) phase, a high-T Curie-Weiss regime, and an antiferromagnetic phase in a narrow U-T region. We associate the onset of the FL phase with partial screening of Ni-d moments; however, full screening occurs at lower temperatures. This may be related to insufficiency of conduction electrons to effectively screen the Ni-d moments, suggestive of Nozieres Exhaustion Principle. Our results suggest that RNiO2 are in the paramagnetic state, close to an antiferromagnetic dome, making magnetic fluctuations feasible. This may be consequential for superconductivity.
Similar content being viewed by others
Introduction
The quest for discovery of superconductivity at high temperatures has led to exploration of classes of materials other than the cuprates, resulting in exciting developments in superconductivity, and the unveiling of other novel properties of quantum materials. The recent observation of superconductivity in hole-doped infinite layer nickelates, RNiO2 (R = rare earth Nd, Pr, La)1,2,3 have generated tremendous interest in the field of condensed matter. Vigorous, innovative efforts in experiment and theory have been driven by the prospect of RNiO2 constituting another class of high TC superconductors, with the possibility of unconventional pairing. There is also the expectation that the infinite-layer nickelates, being iso-structural to the cuprates, may provide another perspective on understanding high TC superconductivity in the cuprates.
While magnetic excitations and damped spin waves have recently been observed in resonant inelastic x-ray scattering experiment in infinite layer NdNiO24, long-range magnetic order has not been observed so far. Earlier neutron scattering experiments5,6 on LaNiO2 and NdNiO2 did not find long-range magnetic order down to 5K and 1.7K, respectively. Likewise, a combination of μsr, magnetic susceptibility and specific heat measurement7 showed no long-range magnetic order down to 2K in polycrystalline LaNiO2. Spin susceptibility measurements on LaNiO25 showed weak temperature (T) dependence and pointed to two Curie–Weiss (CW) regimes, and recent experiment7 indicates deviation from Curie–Weiss behavior at high temperatures. Specific heat measurement7 on the same compound finds a linear-T behavior, suggestive of Fermi liquid behavior at low temperature.
To be able to arrive at an understanding of the mechanism of superconductivity, it is important to understand the electronic structure, nature and strength of correlations, and excitations in the normal state of the nickelates. Besides several model calculations8,9,10,11,12, there have been a number of first principle work, that generally fall into the categories of density functional theory (DFT and DFT + U)13,14,15,16,17 and dynamical mean-field theory (DMFT)18,19,20,21,22,23,24. There has also been work based on dynamical vertex approximation25. Since the nickelates are iso-electronic to the cuprates, there have been a number of useful efforts exploring the similarities and differences between the electronic structures of the two, namely, d8 vs. d9 electronic configuration of Ni; charge transfer energy, ϵd − ϵp, compared to that in the cuprates, and possibility of magnetic or insulating behavior in the nickelates.
It would be desirable to have a more definitive understanding of the low-energy many-body states of the nickelates, in particular, magnetic vs. paramagnetic, insulating vs. metallic or localized Ni-d moment vs. itinerant behavior, and if the physics is governed by single-orbital (as in the cuprates) or multi-orbital degrees of freedom. Likewise, a study that encompasses sufficiently wide ranges of temperature and correlation strength can shed light on the system behavior, phases and transitions between them.
To understand the nature of the many-body states of the RNiO2 class of materials at low, as well as, higher temperatures, we perform fully first principles DFT + embedded DMFT (eDMFT) calculations26,27,28,29 on LaNiO2 and NdNiO2. Our calculations in the paramagnetic and magnetic states constitute one of the very few fully-self-consistent eDMFT study in these systems and reveal a rich variety of physics. The physical picture that emerges is depicted in the correlation (U)–temperature (T) phase diagram (Fig. 1). Notable among several interesting features are a Fermi liquid (FL) phase at low temperature, a Curie–Weiss regime at high temperature, deviation from typical CW behavior at even higher temperatures, and an antiferromagnetic (AFM) phase straddling the FL and CW phases over a region of U and T. The onset of FL behavior is associated with partial screening of the Ni-d moment at some characteristic temperature; however, the temperature scale for full screening is determined to be lower. Our eDMFT calculations suggest that this may be due to insufficiency of electrons to screen the local moment, pushing the coherence scale to a lower temperature, which is often referred to as the Nozieres Exhaustion Principle (NEP)30,31, which we suggest plays a crucial role here.
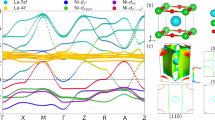
a shows the correlation-temperature (U–T) phase diagram where the boundaries of various electronic phases were determined from the fits of the calculated local magnetic susceptibility (χloc) for the nickel d electrons, and scattering rate (Σ) for the electrons in the nickel \({d}_{{x}^{2}-{y}^{2}}\) orbital. The susceptibility values and the corresponding error bars represent the mean and the standard deviation obtained from the last few converged iterations (usually 5) for each given calculation. The red (TCW) and green (T*) dashed lines denote the Curie–Weiss and Fermi liquid phase boundaries, respectively. The boundary (black dashed curve, TAFM) of the antiferromagnetic (AFM) phase was obtained by computing the temperature dependence of the magnetic order parameter, described in the text. The inset shows the U dependence of the local effective moment μeff, where the dashed line is a guide to the eye. b shows the low-temperature region of the U–T phase diagram, showing the regions of partially screened and fully screened (below TFLFS) Fermi liquid phases. c shows the temperature dependence of the calculated χloc for the Ni-d electrons for U = 7 eV and J = 1 eV. d, e show χloc with the focus on the low- and high- temperature ranges, respectively. The solid line represents the best fit with the Curie–Weiss–Wilson formula \({\chi }_{loc}=\frac{C{\mu }_{eff}^{2}}{(T+\sqrt{2}{T}^{* })}\) as explained in the text. From d, e, we observe that T* and TCW corresponds to the temperatures where χloc shows deviations from the Curie–Weiss behavior. f shows the temperature dependence of the calculated scattering rate (Σ) for the electrons in the Ni \({d}_{{x}^{2}-{y}^{2}}\) orbital, for the same value of U and J used for the susceptibility. g, h focus on the low-temperature region, where Σ is plotted vs. T and T2, respectively. The dashed line represents the best linear fit with the formula Σ = \(A({T}^{2}-{T}_{{{{{{{{\rm{FLFS}}}}}}}}}^{2})\), where A > 0. \({T}_{{{{{{{{\rm{CW}}}}}}}}}^{{\prime} }\), \({T}^{* {\prime} }\) and TFLFS are the temperatures at which Σ flattens at high-temperature, the system starts to show a Fermi liquid behavior (linear dependence of Σ on T2), and Σ goes to zero at low-temperature respectively. Note that \({T}^{* {\prime} }\) ≈ T*. The arrows show the position of various characteristic temperatures.
Results
Phase diagram
To construct the phase diagram, we perform calculations over a wide range of temperature (T ~ 50K–3500K) and correlation strength (U ~ 5–15 eV). In Fig. 1a, we show the overall U–T phase diagram and in Fig. 1b, only the low temperature part. The phase diagram is constructed based on our calculated local magnetic susceptibility, that provides information about the existence of local moment on the Ni ions (see Fig. 1c), and scattering rates, that give information about the electronic properties of a particular state—Fermi liquid vs. non-Fermi liquid; see Fig. 1f. As discussed later, these are supplemented by our study of density of states (DOS), orbitally projected spectral functions and hybridization, all as function of U and T.
The phase boundary between the FL and CW phases is shown by the green triangles. To establish this boundary, we fit the local magnetic susceptibility computed for various values of the correlation parameter U (for fixed exchange interaction J = 1 eV) to the Curie–Weiss–Wilson expression shown in the caption to Fig. 1. In Fig. 1c, we show a typical fit for the case of U = 7 eV. (Results and fits for several other values of U are presented in Supplementary Figs. 1 and 3 and Supplementary Note 1). Broadly, there are three regimes: the low-T regime where the magnetic susceptibility deviates from the Curie–Weiss susceptibility behavior, and at a lower temperature, approaches a constant. We denote this as the Fermi liquid regime. We call the intermediate regime, where the magnetic susceptibility can be fitted with a Curie–Weiss–Wilson formula (caption, Fig. 1), the Curie–Weiss I (CWI) regime. We note that the screening temperature obtained from Wilson formula, T*, is consistent with the temperature where the calculated magnetic susceptibility deviates from the CW behavior. At very high T, the local magnetic susceptibility deviates from the typical Curie–Weiss form; this is labeled Curie–Weiss II (CWII) regime. We denote the temperature that separates CWI and CWII regimes as TCW, shown as red squares in Fig. 1a. In Fig. 1c, the Fermi liquid regime is represented by the black symbols, CWI by the green ones and CWII by the red symbols.
To have a deeper understanding of the FL and CW phases, we studied the temperature-dependent scattering rates for d orbitals of the Ni ions; see Fig. 1f for U = 7 eV. (Results for other U’s are shown in Supplementary Figs. 2 and 3 and Supplementary Note 1). As in the case of magnetic susceptibility, the temperature-dependent scattering rate also shows three regimes: A low-T regime where the scattering rate is very small (zero within the error bar of the calculation); a second regime (still low-T) where the scattering rate has a T2 behavior, a feature of a Fermi liquid; a third regime at high-T where the scattering rate is large and tends toward a constant value. We call \({T}^{* {\prime} }\) the temperature below which the scattering rate has T2 behavior (see Fig. 1h) and we see that this temperature corresponds to the temperature T* below which the local susceptibility deviates from CWI behavior (see Fig. 1d). Thus the FL regime appears to be well established by both the scattering rate and the local magnetic susceptibility. We also observe that the temperature above \({T}^{* {\prime} }\), where the scattering rate tends to a constant value, is similar to TCW. In addition, the temperature, TFLFS, below which the scattering rate is practically zero (see Fig. 1g) corresponds to the temperature scale for a constant local magnetic susceptibility. These results can be interpreted in the following way: at very high temperatures, there is a local moment at the Ni sites due to the d electrons. With lowering of the temperature, these local moments start to get partly screened around T*, signaling the onset of FL behavior (green triangles in the phase diagram; see Fig. 1a, b). The moments, however, get fully screened only below TFLFS. This is denoted by blue stars in the phase diagram (Fig. 1a, b).
At high temperatures, T > TCW, the deviation from typical Curie–Weiss behavior is signaled by the scattering rate flattening toward a constant (Fig. 1f), and deviation of spin susceptibility from the CW behavior (Fig. 1e). This deviation could be due to a change in the local moment (resulting in slope different from that in CWI). We find that the constant moment in CWI regime switches to a temperature-dependent moment with TCW being the onset temperature (see Supplementary Fig. 4 and Supplementary Note 2).
As can be seen in Fig. 1a, b both the FL → CWI and the CWI → CWII crossover temperature scales decrease with increasing values of U, so that the FL regime is squeezed down as U is increased. From the plots of χ(T) and scattering rate Σ (Fig. 1c, f), it can also be seen that the scattering rate tracks the behavior of susceptibility. We have checked that in the FL regime, the imaginary part of the self-energy, ImΣ(iωn = 0) → 0 (as expected), while it is non-zero in the two CW regimes. The temperature dependence of our spin susceptibility has some commonality with susceptibility experiments5 that shows weak temperature dependence, and some evidence of flattening of a Curie–Weiss curve at lower temperatures. Also, the susceptibility was found to be significantly smaller than for a spin-1/2 paramagnet; the experimental data was shown not to fit to a S = 1/2 paramagnet, and indicated that effective spin of the system may be smaller than 1/2. Our calculations indicate that S ≤ 1/2 at low temperatures.
Spectral function, density of states, hybridization
To understand the electronic properties from a different perspective, we also computed the orbitally projected spectral function at various temperatures. Figure 2 shows the results for U = 7 eV. There is a clear consistency between the scattering rates and the spectral functions for the three regimes, FL, CWI and CWII. For example, the Ni-d states are coherent and situated around the Fermi level in the FL phase (see Fig. 2a) while they are very incoherent in the CWI and CWII phases (see Fig. 2b, c), as expected based on the scattering rates. At the higher temperatures (CWII regime), the spectral function is almost washed out, implying that there are no quasiparticles, just fluctuating local moments. In addition, if we zoom in around the Fermi level, we observe that the Ni-\({d}_{{x}^{2}-{y}^{2}}\) band progressively sharpens with lowering of T, and below TFLFS, becomes very sharp, i.e., highly coherent as expected due to the vanishing scattering rate; see Fig. 2d–i. It may be noted that the Ni-\({d}_{z^2}\) spectral function does not change much at all across the entire temperature range.
a–c show the temperature (T) dependence of the spectral function while the other panels show the temperature (T) dependence of the spectral function around the Fermi level for TFLFS < T < T* (d–f), and for T < TFLFS (g–i). In the last set of panels, we can see explicitly the high degree of coherence of the states at the Fermi level. The orbital character corresponding to {z2}, {x2–y2} and {xz, yz, xy} is given by red (R), green (G), and blue (B), respectively; any other color in the plots obtained from a RGB combination corresponds to orbital mixing of the {z2}, {x2–y2} and {xz, yz, xy}.
Since the spectral function shows the electronic states just along several paths in the Brillouin zone, we also plot in Fig. 3a the partial density of states (pDOS), for U = 7 eV at T = 150K for all the Ni-d, O-p, La-p and La-d orbitals, together with the hybridization corresponding to the Ni-d orbitals in Fig. 3b (Results for several other U’s and T’s are presented in Supplementary Figs. 5 and 6 in Supplementary Notes 3 and 4, respectively). The pDOS for the Ni-d orbitals show that the center of mass for the pDOS for Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital is around the Fermi level, while for the other d orbitals, the center of mass is at lower energies; thus these orbital make only a small contribution at the Fermi level. We find that the Ni-d states hybridize more with the O-p states and less with La-p or La-d states (see Supplementary Note 5 and accompanying Supplementary Fig. 7).
a shows the projected DOS for all the Ni-d orbitals, as well as the O-p, La-p and La-d orbitals. b shows the hybridization corresponding to the Ni-d orbitals. c, d show the temperature (T) dependence of the Ni-\({d}_{{x}^{2}-{y}^{2}}\) projected DOS and the corresponding hybridization, while e, f show the correlation (U) dependence of the same Ni-d projected DOS and the corresponding hybridization. The insets focus on the energy region around the Fermi level, which is marked by the zero on the energy axis.
Next, we consider the temperature dependence of the total and partial density of states. In Fig. 3c, d, we show the temperature dependence for the Ni-\({d}_{{x}^{2}-{y}^{2}}\) DOS, and its corresponding hybridization around the Fermi level. The other orbitals do not show a strong temperature dependence around the Fermi level (see Supplementary Note 6 and accompanying Supplementary Fig. 8). We observe that at low T, the \({d}_{{x}^{2}-{y}^{2}}\) pDOS has a peak structure just below the Fermi level; the peak structure decreases with increasing temperature, and eventually becomes rather flat. Similarly, at low T, the corresponding hybridization has a dip below Fermi level accompanied by a peak above; this feature become less pronounced with increasing temperature. The same type of behavior is seen at low temperature (shown for T = 150K) for other values of U; see Fig. 3e, f. With increasing U, the \({d}_{{x}^{2}-{y}^{2}}\) DOS peak around EF sharpens, and the hybridization with other orbitals decreases to some extent.
These feature of the \({d}_{{x}^{2}-{y}^{2}}\) pDOS and hybridization bear resemblance to results from calculations on a periodic Anderson model with an f and s electrons32. In that case, at T = 0K, the system shows a gap in the DOS at half filling for both s and f bands (with peaks in the DOS around the gap), accompanied by peak in hybridization within the gap. The gap in the DOS and the peak in the hybridization progressively disappear upon reducing the number of s-electrons. The f-electron pDOS shows an asymmetric peak shape around the Fermi level while the hybridization exhibits a dip followed by a peak, similar to an asymmetric sinusoidal curve (see Figs. 5 and 6 in the paper by Meyer and Nolting32). In addition, there are similarities between the high-T model calculations of aforementioned work and our eDMFT calculations; in both cases the impurity electron pDOS is flat around the Fermi energy. Reducing the number of s electrons results in an insufficient number of electrons to screen the f electrons; this was associated with Nozieres Exhaustion Principle30,31. Comparing the U dependence of our DOS and hybridization for the \({d}_{{x}^{2}-{y}^{2}}\) orbital (Fig. 3e, f), with that found in periodic Anderson model32 as function of decreasing s-electrons, we see a similar trend. This can be interpreted based on the local moment shown in the inset of our Fig. 1a. Since the total number of electrons in the system is conserved, increase of the local magnetic moment with increasing U means that the number of bath electrons that are left to screen the moment is decreasing.
To further explore screening of Ni-d electrons, besides LaNiO2, we also looked at the same properties for NdNiO2, see Fig. 4. The difference between LaNiO2 and NdNiO2 is that Nd has 3 f electrons. If we place the f electrons into the core in our calculations, we see that the temperature and correlation dependence of the DOS and hybridization are very similar to that of LaNiO2; see Fig. 4a–d, respectively. Since our results for LaNiO2, in some ways, resemble that of the periodic Anderson model (where NEP was suggested), we explored this aspect further in the case of NdNiO2. We can consider the f electrons as valence ones or in the core, as mimicking scenarios where we dope the system with holes or electrons (see Supplementary Note 7 and accompanying Supplementary Figs. 9 and 10). For example, if we start with the f electrons as valence electrons, when we put them into core, we can think of this system as a model system which is doped with holes. This is exactly the scenario in the periodic Anderson model32, when the number of s electrons is reduced while the number of f electrons in kept fixed. The DOS and hybridization in Fig. 4e, f have the same trends as the corresponding quantities in the periodic Anderson model calculation32. In addition, we looked at the T and U dependence of the non-correlated electrons and they have the same trends as the s electrons in the above-mentioned work (see our Fig. 5a–c).
a, b show the temperature (T) dependence of the Ni-\({d}_{{x}^{2}-{y}^{2}}\) projected DOS and the corresponding hybridization, while c, d show the correlation (U) dependence of the Ni-\({d}_{{x}^{2}-{y}^{2}}\) projected DOS and the corresponding hybridization. e, f show the “effects of doping” on the \({d}_{{x}^{2}-{y}^{2}}\) DOS and its corresponding hybridization, by placing the Nd-f electrons into valence or into the core. The insets focus on the energy region around the Fermi level, which is marked by the zero on the energy axis.
Nickel-d occupancy
To understand the increase of the local effective moment in the CW regime with increasing U, we also looked the Ni-d valence histogram, see Fig. 6. By studying the valence histogram we observe that the system is in a mixed d8–d9 configuration, with the d9 configuration being favored for small U and d8 for large U values.
There has been ongoing discussions/debate on the valence character of the Ni-d electron, in particular whether the character is more like Ni-d8 or Ni-d9. Based on our e-DMFT calculations, the occupancy of the Ni-d electrons, nd(U) changes from ~8.6e to ~8.35e as we go from U = 5 eV to U = 9 eV. The occupancies can be better understood on considering Fig. 6, which shows the probability of DMFT sampling of Ni-d superstates (configurations of microstates) for U = 5, 7 and 9 eV. Overall, we find higher probabilities for d9 vs. d8 configurations for U = 5 eV vs. U = 9 eV, thereby giving nd ~ 8.6 (closer to 9) for U = 5 eV, and nd ~ 8.35 (closer to 8) for U = 9 eV.
Magnetism
In addition to our paramagnetic (PM) calculations discussed above, we also carried out eDMFT calculations in the ferromagnetic (FM) and in-plane checkerboard antiferromagnetic (AFM) configurations for several values of U between 5 and 15 eV. The AFM structure is not stable for U ≤ 7 eV. For U > 7 eV, and up to 11 eV, it is stable in a certain range of temperatures shown in Fig. 1a, b (black dashed line) with ordered moment corresponding to ∣Sz∣ ~ 0.3, demonstrating a dome-like feature (see Supplementary Fig. 11 and Supplementary Note 8 for results supporting this). We note that the AFM state is only slightly lower in energy than the PM state, the energy difference ~5 meV, being within the DMFT error bar. The FM state is not stable for U = 5–12 eV, but may be stable for U ~ 13–15 eV. Our result, for U ≤ 7 eV, is consistent with neutron scattering experiment5,6, and μsr/magnetic susceptibility measurements7 that also do not find long-range magnetic order.
Effective mass and specific heat
Within DMFT, the quasiparticle renormalization factor, Z for the impurity orbitals can be obtained from the derivative of the imaginary part of the self-energy at the Fermi energy (ωn = 0). The corresponding effective mass m*/mDFT = 1/Z, Z being the quasiparticle renormalization. At T = 150 K (in the regime we have characterized as Fermi liquid), we find that for U = 5, 7, 9 eV, m*/mDFT for the \({d}_{{x}^{2}-{y}^{2}}\) orbital is 2.8, 4.3, 6.5 respectively, and for the \({d}_{z^2}\) orbital 1.3, 1.5, 1.7 respectively. This, together with our calculated DOS at EF, can be used to estimate the Ni-d electron contribution to the linear coefficient of the specific heat, given by: γ = const∑orbitalN(0)orbital/Zorbital mJ mol−1 K−2; where N(0)orbital is the density of states of an orbital at the Fermi energy, with units of 1/(eV/atom); Zorb is the renormalization factor of orbital being summed over; and the const = 2.349 results from unit conversion. The t2g orbitals are all occupied states and have no weight at the Fermi level. Hence, these do not enter into our estimate of γ. We estimate γ ~ 2.5, 3.0, 6.0 mJ mol−1 K−2 for U = 5, 7, 9 eV, respectively. Recent specific measurements7 on LaNiO2 find a linear-T behavior with a possible \({T}^{3}\ln T\) correction, reflecting Fermi liquid behavior at low temperature. The experimental γ ~ 4–5 mJ mol−1 K−2 are consistent with our estimates of γ. We note that our estimates are based solely on the contribution of the Ni-d orbitals and do not take into account O or La orbitals. Since the DOS of O-p and La-d orbitals at EF are very small, these would give negligible additional contribution (~0.1) to the total γ.
Discussions
Our first principle DFT + DMFT (eDMFT) calculation is one of the very few fully self-consistent DMFT calculations performed on the nickelate systems. Our approach differs in substantive ways from that of some of the other DMFT calculations, namely, (1) we do not employ Wannier projection, rather project on to quasi-atomic localized orbitals; (2) we use a large hybridization window of ±10 eV around the chemical potential; this eliminates the uncertainty from variously employed projection or downfolding procedures; (3) our calculations are fully charge-self-consistent in contrast with single-shot DMFT calculations that do not update the charge density in DFT part; (4) our use of exact double-counting scheme29 eliminates some double-counting issues and makes the Ni-d occupancy number more accurate.
There are important differences between our findings and those of some of the other DMFT work19,20 on LaNiO2 and NdNiO2. We do not find a stable AFM phase for U ≤ 7 eV; an AFM phase is found for U > 7 (up to U ~ 11 eV), but the energy difference between the AFM and the PM phase is found to lie within the error bar of our DMFT calculations. For NdNiO2, Karp et al.20 finds a stable AFM phase between U ~ 2.3 eV and U ~ 8 eV, with a crossover from AFM metal to AFM insulator between U ~ 5.7 and 8 eV. Also, in contradistinction with others, we do not find any insulating phase, even for large values of U up to 15 eV. Thus, we are at odds with Gu et al.19 that finds an insulating phase for U = 7 eV, and Karp et al.20 that obtains an insulating PM behavior in NdNiO2 for U > 7 eV. We note that these19,20 employ wannierization (to form a basis of maximally localized Wannier functions), perform DMFT calculations on downfolded model Hamiltonians, and are single-shot calculations (DFT charge not updated). Additionally, some of the calculations are on the Nd compound, though it has been pointed out that the Nd-f electrons may not play a crucial role in the nickelate properties; Gu et al.19 does not find much difference between the La and the Nd compound.
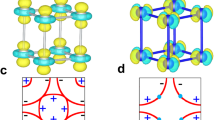
DFT and DFT + U studies15,24 find a second band, comprising of rare-earth 5d orbitals crossing the Fermi energy; a charge transfer energy appreciably larger than in the cuprates, and a antiferromagnetic state for certain values of U. While some of these aspects are also found in DMFT calculations18,19,20, there are differences between these and the DFT results. One variance pertain to the nature of a second band crossing the Fermi level ϵF. Karp et al.20, as well as fully-self-consistent DMFT21 and DFT + sicDMFT calculations18, find that the second band has mixed rare-earth (La or Nd)-\({d}_{z^2}\) and Ni-\({d}_{z^2}\) character at the Γ point and rare-earth Nd-dxz and Ni-dyz character at the A point; these form small electron pockets. These are at odds with Gu et al.19 that finds that the second band does not arise from hybridization with the rare-earth orbital, rather with interstitial s-electrons, mediated by O-p orbitals. DFT and some DMFT calculations18,21 find the Ni-3d-O-2p hybridization to be small, and others19 find this to be strong, though this may vary depending on the rare-earth in question21. As mentioned above in the “Spectral function, density of states, hybridization” sub-section in our “Results” section we find that the Ni-d states hybridize more with the O-p states and less with La-p or La-d states. Lechermann18, using fully self-consistent DFT + sicDMFT, finds an orbitally selective state with a Mott gap for \({d}_{{x}^{2}-{y}^{2}}\), and metallic \({d}_{z^2}\) for U ≥ 10 eV.
Our eDMFT calculations show that the coherence scale, i.e., the scale for full screening of the Ni-d moment, is pushed down to temperatures lower than expected. The progression from partial to full screening can be attributed to features in the temperature-dependent hybridization of the correlated Ni-\({d}_{{x}^{2}-{y}^{2}}\) electrons with the “bath”, i.e., the non-correlated electrons that include the rare-earth-d, O-p and other conduction electrons. More specifically, once the hybridization is allowed to be temperature-dependent and determined self-consistently, progressively decreasing the temperature causes hybridization to progressively decrease (and not increase in as in the Hubbard model, where hybridization is roughly proportional to the local Green’s function). This results in a protracted screening range (onset being our T*), and it takes much larger temperature interval to attain full screening and coherence. Physically, this may be a consequence of not having sufficient conduction electrons to screen all the local moments till a temperature much lower than T* is reached, when Kondo screening wins out and a Fermi liquid state is formed, i.e., our FLFS state below TFSFL. This points to a scenario in which Nozieres Exhaustion Principle30,31 is at play. We note that if there were sufficient conduction electrons to screen, then hybridization would not change much with temperature. (In the Hubbard model, it actually increases because the neighboring sites become coherent and allow the electrons to hop easier). Since the screening bath is provided by electrons in extended space (itinerant) orbitals, the system exhibits more similarity with Anderson lattice model than with Hubbard-type models. We note, however, that our system is one that is not in the extreme Kondo limit characterized by very small Kondo scale, rather, one in which the coherence scale is relatively large, \({{{{{{{\mathcal{O}}}}}}}}\)(100K); see Fig. 1.
At low energies, we do not find compelling evidence for the Hund’s metal scenario that has been proposed22 based on study of optical conductivity at intermediate energies. For a fixed U, we find weak dependence of the spectral function and spin susceptibility on the exchange interaction parameter, J, as it is varied from 1 to 0.1 eV; the variation with U is much larger (see Supplementary Note 9 and accompanying Supplementary Fig. 12 for details).
On the question of single-band vs. multi-band governing the physics of the nickelates, our work finds that in addition to the dominant \({d}_{{x}^{2}-{y}^{2}}\) band, the presence of a second band comprising of hybridized \({d}_{z^2}\) band around the Γ point. The second band contributes about 1/5 of the total Ni-d moment at low temperature (at 200 K). However, as our calculated temperature-dependent DOS, hybridization and spectral function show, the \({d}_{z^2}\) band does not show much temperature dependence. Thus, in our proposed picture, at higher temperatures, the physics would be governed by the single \({d}_{{x}^{2}-{y}^{2}}\) band.
The values of the Coulomb U in our calculations may appear larger than that typically used in different implementations of DFT + DMFT, as well as DFT + U. The fundamental reason, as previously discussed33 in the context of transition metal oxides, is the screening within the specific method itself. When one eliminates some degrees of freedom through downfolding, one ends up in a model that excludes certain screening channels, and hence the Coulomb interaction has to be reduced accordingly. In our approach, the system is not “downfolded” (to Wannier orbitals or models), and is much more localized in real space. Hence, more bands (which are allowed to hybridize with the localized correlated orbital) screen the correlated orbitals. This then requires larger screened Coulomb U.
Conclusion
In summary, based on fully self-consistent DFT + DMFT (eDMFT) calculations in the paramagnetic and magnetic states, we provide insights into the physics of the low-energy many-body states of the parent compounds of the infinite layer systems, and the associated correlation (U) and temperature (T) scales. The key features are a Fermi liquid phase at low temperature, a Curie–Weiss regime at high temperature, deviation from typical Curie–Weiss behavior at even higher temperature, and an antiferromagnetic phase over a narrow region of U and T. The onset of the Fermi liquid regime at a characteristic temperature T* is signaled by T2 quasiparticle scattering rate and deviation from Curie–Weiss behavior in local spin susceptibility. The Fermi liquid phase at low temperature is also consistent with recent specific heat measurement on LaNiO2 showing a linear-T behavior7. Based on calculated scattering rates, local spin susceptibility, and spectral function, we believe this to happen when the Ni-d moments start to undergo Kondo screening resulting in a Nozieres-type Fermi liquid. Interestingly, finer features are revealed upon closer analysis. Thus, the Ni-d moments get fully screened, and full coherence is achieved, only at a lower temperature, TFLFS, correlating with a constant spin susceptibility, a scattering rate that goes to zero, and an extremely sharp \({d}_{{x}^{2}-{y}^{2}}\) band feature near the Fermi level. The decreased coherence scale may be pointing to insufficiency of the bath electrons to effectively screen the Ni-d moments till a lower temperature is reached. This is indicative of the Nozieres Exhaustion Principle30,31 at play, as suggested in DMFT calculations in metallic Nickel34, and in calculations32 on periodic Anderson model. We note that there has been suggestion of a Kondo screening picture, as ours, of the ground state of the parent infinite layer nickelate, based on X-ray spectroscopy experiments35. We speculate that this picture of the screened Fermi liquid may have consequences for superconductivity in the doped compound. Based on the lack of experimental evidence for long-range magnetic order5,6,7, and the observation of magnetic excitations in NdNiO24, our calculations would place the RNiO2 materials close to the dome of anti-ferromagnetism in our phase diagram, thereby making antiferromagnetic fluctuations feasible. In particular, our study indicates that for LaNiO2, a non-magnetic state with nd closer to d9 (~8.6) can be achieved with U = 5–7 eV. Our constrained DMFT calculations gives U = 6.5 eV for LaNiO2, hereby providing an independent check on the range of values of U that we consider to be relevant here. Separating non-magnetic from magnetic behavior, U = 7 eV appears to be a “special point” in the phase diagram for LaNiO2. The same may be true for the Nd- or Pr-nickelate, with possibly different value of U as the characteristic scale for the onset of AFM. We do not find evidence for insulting behavior in LaNiO2 even for large values of U ~ 15 eV.
Methods
We employ DFT + embedded DMFT (eDMFT) method26,27,28,29 developed at Rutgers.
DFT
For obtaining the associated electronic band structure, using DFT, we performed the full-potential linearized augmented plane wave (FP-LAPW) method as implemented in the WIEN2k code36. The generalized gradient approximation Perdew-Burke-Ernzerhof (GGA-PBE) functional was used for the exchange and correlation potential. To obtain the self consistent charge density in each step we used the tetrahedron integration method with 1000 k-points in the full Brillouin zone (the density of states were computed using 30,000 k-points in the full Brillouin zone). During the self-consistency cycles, the energy and charge criteria were set to 0.00001 Ry and 0.00001 e−. Lattice parameters and the internal coordinates were kept fixed to the experimental values during the electronic structure calculations. The radius (R) of the muffin-tin (MT) spheres were taken to be 2.50, 2.00 and 1.72 Bohr for La, Ni and O respectively. RMT × K\({}_{\max }\) was set to 7, where K\({}_{\max }\) is the cutoff value of the modulus of the reciprocal lattice vectors and RMT is the smallest MT radius.
eDMFT
Our calculations are “fully self-consistent” between the DFT and DMFT parts, i.e., the charge is recalculated after a DMFT run and then iterated through the DFT and DMFT loops till charge convergence is achieved. We employ “exact double-counting”29, and use the “Full Coulomb” option (as opposed to “Ising”), i.e., the spin-rotation invariant form of the Coulomb repulsion of the Slater form28. We use a large hybridization window of ±10 eV. For the DMFT projectors, we choose quasi-atomic localized orbitals. The radial part is the solution of the Schroedinger equation in the muffin-tin sphere, with linearized energy at the Fermi level, and the angular dependence given by the spherical harmonics. In our projection technique, we only truncate the basis for the two-particle quantities, i.e., interaction and dynamic correlations are constrained to projection in real space around a given atom, while the large kinetic-part of the Hamiltonian is not approximated (or truncated) at all; all the degrees of freedom in this largest part of the Hamiltonian are treated by the complete basis. For the quantum impurity problem (Ni-d electron), we use a version of continuous time quantum Monte Carlo (CTQMC) impurity solver. For the room temperature Monte Carlo (MC) runs we employed at least 50 × 106 MC steps; the number of MC steps was increased with lowering the temperature (100 × 106 for 100 K) or decreased with increasing the temperature relative to the room temperature. We allowed the position of the chemical potential to vary during the self-consistent calculations The needed analytic continuation from imaginary to real frequency axis were done using the maximum entropy method. We take the well-known tetragonal crystal structure19 for RNiO2 with the rare earth element located at the center of the unit cell; the group symmetry being P4/mmm.
Data availability
The data that support the findings of this study are available from the corresponding author on reasonable request.
Code availability
The DFT calculations were performed using the proprietary code WIEN2k, and the open-source eDMFT code/impurity solver of K.H. at Rutgers University (http://hauleweb.rutgers.edu/tutorials/). K.H.’s eDMFT code is freely distributed for academic use under the Massachusetts Institute of Technology (MIT) License.
References
Li, D. et al. Superconductivity in an infinite-layer nickelate. Nature 572, 624–627 (2019).
Osada, M. et al. A superconducting praseodymium nickelate with infinite layer structure. Nano Lett. 20, 5735–5740 (2020).
Shengwei, Z. et al. Superconductivity in infinite-layer nickelate La1−xCaxNio2 thin films. Sci. Adv. 8, 9927 (2022).
Lu, H. et al. Magnetic excitations in infinite-layer nickelates. Science 373, 213–216 (2021).
Hayward, M., Green, M., Rosseinsky, M. & Sloan, J. Sodium hydride as a powerful reducing agent for topotactic oxide deintercalation: synthesis and characterization of the nickel(I) oxide LaNio2. J. Am. Chem. Soc. 121, 8843–8854 (1999).
Hayward, M. & Rosseinsky, M. Synthesis of the infinite layer Ni(I) phase NdNio2+x by low temperature reduction of NdNio3 with sodium hydride. Solid State Sci. 5, 839–850 (2003).
Ortiz, R. A. et al. Magnetic correlations in infinite-layer nickelates: an experimental and theoretical multimethod study. Phys. Rev. Res. 4, 023093 (2022).
Jiang, M., Berciu, M. & Sawatzky, G. A. Critical nature of the Ni spin state in doped NdNio2. Phys. Rev. Lett. 124, 207004 (2020).
Zhang, G.-M., Yang, Y.-f & Zhang, F.-C. Self-doped mott insulator for parent compounds of nickelate superconductors. Phys. Rev. B 101, 020501 (2020).
Hu, L.-H. & Wu, C. Two-band model for magnetism and superconductivity in nickelates. Phys. Rev. Res. 1, 032046 (2019).
Zhang, Y.-H. & Vishwanath, A. Type-II t − j model in superconducting nickelate Nd1−xSrxNio2. Phys. Rev. Res. 2, 023112 (2020).
Werner, P. & Hoshino, S. Nickelate superconductors: multiorbital nature and spin freezing. Phys. Rev. B 101, 041104 (2020).
Botana, A. S. & Norman, M. R. Similarities and differences between LaNio2 and CaCuO2 and implications for superconductivity. Phys. Rev. X 10, 011024 (2020).
Nomura, Y. et al. Formation of a two-dimensional single-component correlated electron system and band engineering in the nickelate superconductor NdNio2. Phys. Rev. B 100, 205138 (2019).
Been, E. et al. Electronic structure trends across the rare-earth series in superconducting infinite-layer nickelates. Phys. Rev. X 11, 011050 (2021).
Anisimov, V. I., Bukhvalov, D. & Rice, T. M. Electronic structure of possible nickelate analogs to the cuprates. Phys. Rev. B 59, 7901–7906 (1999).
Lee, K.-W. & Pickett, W. E. Infinite-layer LaNio2: Ni1+ is not Cu2+. Phys. Rev. B 70, 165109 (2004).
Lechermann, F. Late transition metal oxides with infinite-layer structure: nickelates versus cuprates. Phys. Rev. B 101, 081110 (2020).
Gu, Y., Zhu, S., Wang, X., Hu, J. & Chen, H. A substantial hybridization between correlated Ni-d orbital and itinerant electrons in infinite-layer nickelates. Commun. Phys. 3, 84 (2020).
Karp, J. et al. Many-body electronic structure of NdNio2 and CaCuO2. Phys. Rev. X 10, 021061 (2020).
Wang, Y., Kang, C.-J., Miao, H. & Kotliar, G. Hund’s metal physics: from SrNio2 to LaNio2. Phys. Rev. B 102, 161118 (2020).
Kang, C.-J. & Kotliar, G. Optical properties of the infinite-layer La1−xSrxNio2 and hidden Hund’s physics. Phys. Rev. Lett. 126, 127401 (2021).
Kitatani, M. et al. Nickelate superconductors—a renaissance of the one-band Hubbard model. npj Quantum Mater. 5, 59 (2020).
Leonov, I., Skornyakov, S. L. & Savrasov, S. Y. Lifshitz transition and frustration of magnetic moments in infinite-layer NdNio2 upon hole doping. Phys. Rev. B 101, 241108 (2020).
Held, K. et al. Phase diagram of nickelate superconductors calculated by dynamical vertex approximation. Front. Phys. 9, 1 (2022).
Georges, A., Kotliar, G., Krauth, W. & Rozenberg, M. J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 68, 13–125 (1996).
Kotliar, G. et al. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 78, 865–951 (2006).
Haule, K., Yee, C.-H. & Kim, K. Dynamical mean-field theory within the full-potential methods: electronic structure of CeIrIn5, CeCoIn5, and CeRhIn5. Phys. Rev. B 81, 195107 (2010).
Haule, K. Exact double counting in combining the dynamical mean field theory and the density functional theory. Phys. Rev. Lett. 115, 196403 (2015).
Nozieres, P. Impuretés magnétiques et effet kondo. Ann. Phys. Fr. 10, 19–35 (1985).
Nozieres, P. Some comments on Kondo lattices and the Mott transition. Eur. Phys. J. B 6, 447 (1998).
Meyer, D. & Nolting, W. Kondo screening and exhaustion in the periodic Anderson model. Phys. Rev. B 61, 13465–13472 (2000).
Haule, K., Birol, T. & Kotliar, G. Covalency in transition-metal oxides within all-electron dynamical mean-field theory. Phys. Rev. B 90, 075136 (2014).
Hausoel, A. et al. Local magnetic moments in iron and nickel at ambient and earth’s core conditions. Nat. Commun. 8, 16062 (2017).
Hepting, M. et al. Electronic structure of the parent compound of superconducting infinite-layer nickelates. Nat. Mater. 19, 381–385 (2020).
Blaha, P. et al. WIEN2k: an APW+lo program for calculating the properties of solids. J. Chem. Phys. 152, 074101 (2020).
Acknowledgements
G.L.P.’s and L.C.’s work were supported by a grant of the Romanian Ministry of Education and Research, CNCS–UEFISCDI, project number PN-III-P1-1.1-TE-2019-1767, within PNCDI III. K.H. was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, as a part of the Computational Materials Science Program, funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division. K.F.Q. acknowledges a QuantEmX grant from ICAM and the Gordon and Betty Moore Foundation, Grant GBMF5305, which partly funded this work.
Author information
Authors and Affiliations
Contributions
G.L.P. and K.F.Q. together conceived the problem. G.L.P. performed the calculations. G.L.P. and K.F.Q. processed and analyzed the data. L.C. contributed to the calculations of analytic continuation and scattering rates. G.L.P. and K.F.Q. wrote the first draft. G.L.P., K.F.Q. and K.H. discussed the results and physical interpretation, and arrived at the final version of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pascut, G.L., Cosovanu, L., Haule, K. et al. Correlation-temperature phase diagram of prototypical infinite layer rare earth nickelates. Commun Phys 6, 45 (2023). https://doi.org/10.1038/s42005-023-01163-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-023-01163-7
This article is cited by
-
Unconventional superconductivity without doping in infinite-layer nickelates under pressure
Nature Communications (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.