Abstract
Understanding the interplay between superconductivity and magnetism has been a longstanding challenge in condensed matter physics. Here we report high pressure studies on the C-type antiferromagnetic semiconductor EuTe2 up to 36.0 GPa. A structural transition from the I4/mcm to the C2/m space group is identified at ~16 GPa. Superconductivity is observed above ~5 GPa in both structures. In the low-pressure phase, magnetoresistance measurements reveal strong couplings between the local moments of Eu2+ and the conduction electrons of Te 5p orbits. The upper critical field of superconductivity is well above the Pauli limit. While EuTe2 becomes nonmagnetic in the high-pressure phase and the upper critical field drops below the Pauli limit. Our results demonstrate that the high upper critical field of EuTe2 in the low-pressure phase is due to the exchange field compensation effect of Eu2+ and the superconductivity in both structures may arise in the framework of the Bardeen-Cooper-Schrieffer theory.
Similar content being viewed by others
Introduction
Superconductivity in conventional Bardeen-Cooper-Schrieffer (BCS) superconductors arises from electron-lattice interaction without the involvement of magnetism1. Below the superconducting (SC) transition temperature, electrons form coherent spin singlet cooper pairs that can be suppressed by a Pauli-limited magnetic field. In contrast, one of the hallmarks of unconventional superconductivity is the interplay between magnetism and superconductivity. For example, superconductivity in copper oxide and iron-based high-temperature superconductors occurs near long-range magnetic order where the 3d electrons of the transition metals across the Fermi level contribute to both the magnetic correlations and superconductivity2,3,4,5,6. In some unconventional superconductors, electron pairing forms spin-singlet and the upper critical field needed to suppress superconductivity is also Pauli limited2,3,4,5,6. For unconventional superconductivity with an upper critical field exceeding the Pauli limit, such as recently discovered UTe27,8, electron pairing is believed to be spin triplets instead of singlets. In both spin-singlet and spin-triplet superconductors, magnetic fluctuations play an important role in the formation of cooper pairs as evidenced by the neutron spin resonance from inelastic neutron scattering spectra6,9.
Although the mechanism of superconductivity for conventional and unconventional superconductors may be fundamentally different, both superconductors can host magnetic local moments not directly associated with SC layers. For example, in a class of iron-based superconductors consisting of Eu2+, the 4f electrons with spin S = 7/2 could form an antiferromagnetic (AFM) or ferromagnetic sublattice coexisting and interacting with the magnetic sublattice of Fe10,11. However, the localized magnetism of Eu2+ does not interplay with the superconductivity seriously. For BCS superconductors such as RNi2B2C series (R = Y, Er, Ho, etc)9, the interplay between the magnetic order of the rare earth layers and superconductivity can dramatically affect the physical properties of the system including the upper critical field needed to suppress superconductivity.
Previously, our group reported an antiferromagnetically colossal magnetoresistance EuTe2 with a Néel temperature of TN = 11.4 K and a thermal-activation gap of 16.24 meV at atmospheric pressure12. The magnetic field drives polarization of the local moments of Eu2+ and results in the reconstruction of the Te 5p orbitals12,13. It is interesting to explore the pressure effect on the small gap colossal magnetoresistance compound and investigate the interplay of the Eu2+ local moments with itinerant electrons of Te. Based on previous studies on CrSiTe3, WTe2, EuIn2As2, and EuSn2As2, superconductivity may emerge and the valent state transition from Eu2+ to Eu3+ may occur for EuTe2 under pressure14,15,16,17. Very recently, a high-pressure study on EuTe2 up to 12.0 GPa indeed reveals superconductivity and suggests the SC pairing mechanism is exotic18.
Here, we present comprehensive experimental and theoretical investigations on EuTe2 under pressure up to 36.0 GPa. Neutron diffraction measurements demonstrate EuTe2 exhibits a C-type AFM order below TN. A pressure-induced structural transition at ~16 GPa is discovered. In the low-pressure (LP) phase, the C-type AFM transition temperature TN increases due to the enhancement of the magnetic exchange interactions of the compressed lattice. The thermal activation gap Ea is closed progressively, and superconductivity emerges above 5.0 GPa. The SC transition temperature Tcs spanning between 3~6 K in the pressure range of 5~27 GPa is irrespective of the structural transition and magnetism. While the upper critical field \({{\mu }_{0}H}_{{{{{{\rm{c}}}}}}2}\) for the superconductivity of the AFM LP phase is significantly larger than that of the superconductivity of the nonmagnetic high pressure (HP) phase. The \({{\mu }_{0}H}_{{{{{{\rm{c}}}}}}2}\) is affected by the microscopic spin texture of the Eu sublattice. The highest \({{\mu }_{0}H}_{{{{{{\rm{c}}}}}}2}\) is estimated to be 21.6 T for the spin-flipped state at 7.0 GPa. The ultra-high \({{\mu }_{0}H}_{{{{{{\rm{c}}}}}}2}\) could be understood by the compensation effect of the exchange field of Eu2+, the so-called Jaccarino and Peter mechanism19. Our results, therefore, establish the pressure-temperature phase diagram of EuTe2 and demonstrate the interesting interplay mechanism between Eu magnetic order, superconductivity, and pressure-induced structural lattice distortion.
Results
High-pressure structure
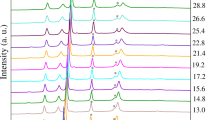
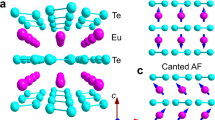
Figure 1 displays the in situ high-pressure synchrotron powder x-ray diffraction (XRD) patterns of EuTe2 up to 36.0 GPa at room temperature and the refined crystal structures below 15.9 GPa and above 17.9 GPa, defined as the LP phase and HP phase, respectively. The LP phase can be indexed by the tetragonal I4/mcm space group (No. 140), identical to the ambient pressure crystal structure. The divalent europium is coordinated by eight nearest-neighbor tellurium ions12. The edge-sharing octagonal units form the layers of the tetragonal crystal structure as shown in Fig. 1c.
a High-pressure XRD patterns of EuTe2 from 2.2 to 36.0 GPa with an x-ray wavelength of 0.6199 Å. The XRD patterns of the LP phase are in blue and that of the HP phase are in red. Tellurium undergoes two structural phase transitions within the measured pressure. The peaks from the Te impurity are marked by the triangles. b Crystal structures of the high pressure (HP) phase and (c) the low pressure (LP) phase of EuTe2.
In terms of the diffraction peaks changed under pressure, an obvious structural phase transition between 15.9 and 17.9 GPa could be identified. We conducted an extensive search on the HP structure of EuTe2 in the pressure range of \(0-25\) GPa via the CALYPSO method20,21,22. The monoclinic C2/m (No. 12) structure turns out to be a possible candidate for the HP phase at 17.9 GPa. Thus, we refined the experimental XRD pattern at 17.9 GPa by the Rietveld method through the TOPAS-Academic software23. The C2/m structure matches the XRD pattern of the HP phase well, as shown in Supplementary Fig. 1. Figure 1b shows the structure of the HP phase. The europium ions retain the eight-coordination but there is a significant deformation of the octagonal unit. This coordination unit exists in the compounds of Eu3S4 at atmospheric pressure, confirming that it is a stable coordination structure for europium chalcogenide24. Sulfur has a smaller ionic radius than tellurium, close to pressurized tellurium.
For the HP phase, slip occurs between the adjacent layers compared with the LP phase. As shown in Fig. 1b, c, the unit cell volume decreases sharply at the pressure-induced structural transition from 317.157(9) \({\mathring{\rm A} }^{3}\) at 15.9 GPa to 262.524(3) \({\mathring{\rm A} }^{3}\) at 17.9 GPa, which may be accompanied by the valent state transition from Eu2+ to nonmagnetic Eu3+. The diffraction peaks and structural transitions of Te impurity can be observed in Fig. 1a25,26. The refined XRD patterns and structural parameters for 9.7 and 17.9 GPa are shown in Supplementary Note 1.
High-pressure electrical and magnetic properties
To investigate the electrical properties of EuTe2 under pressure, we performed electrical transport measurements below 27.7 GPa. Figure 2a shows the temperature dependence of the resistance at various pressures, revealing semiconducting to metallic and SC transitions. Resistance as a function of pressure for selected temperatures is presented in Fig. 2b. The magnitude of the resistance decreases as pressure increases. The upturn in resistance at low pressure may be attributed to the scattering of conduction electrons by local moments of the Eu2+ ions. An abrupt drop in resistance appears between 14.7 and 16.2 GPa, consistent with the structural transition between 15.9 and 17.9 GPa. Thus, the structural transition pressure should occur at ~16.0 GPa. The resistance above ~50 K in Fig. 2a is fitted to the thermal activation-energy model \(\rho \left(T\right)={\rho }_{0}{{\exp }}({E}_{{{{{{\rm{a}}}}}}}/{k}_{{{{{{\rm{B}}}}}}}T)\), where \({\rho }_{0}\) is a prefactor, \({E}_{{{{{{\rm{a}}}}}}}\) is the thermal activation gap, and \({k}_{{{{{{\rm{B}}}}}}}\) is the Boltzmann constant. The gap of 16.24 meV for EuTe2 at ambient pressure is gradually closed by pressure, as shown in Fig. 2c and Supplementary Note 2. The evolution of the carriers against pressure at 10 K is also investigated by the Hall resistance measurements. The Hall coefficient remains positive, revealing that the majority of carriers are holes (Supplementary Note 3). The determined density of holes shows an abrupt enhancement across the structural transition similar to the observation in EuSn2As217.
a Temperature dependence of the resistance upon pressures up to 27.7 GPa. The Néel transition temperatures (TNs) are labeled on low-pressure curves. b Pressure dependence of the resistance at various temperatures up to 300 K shown on a logarithm scale. c Thermal-activation gaps (\({E}_{{{{{{\rm{a}}}}}}}\)s) derived from fittings of the resistance curves within the temperature range from 60 to 300 K using \(\rho \left(T\right)={\rho }_{0}{{\exp }}({E}_{{{{{{\rm{a}}}}}}}/{k}_{{{{{{\rm{B}}}}}}}T)\), where \({k}_{{{{{{\rm{B}}}}}}}\) is the Boltzmann constant. Different shapes of data points are measured on different samples. The black solid line is a guide to the eyes. The right axis represents the scale of carrier density. Error bars originating from the fitting process are smaller than the data points. d Integrals of magnetoresistance (MR) over the magnetic fields from −10 to 10 T as a function of pressure for selected temperatures. The dashed lines in (b–d) at 16.0 GPa mark the pressure of the structural transition.
To elucidate the magnetic state of the HP phase, we conducted systematic magnetoresistance (MR) measurements against temperature and pressure. At ambient pressure, EuTe2 shows colossal negative MR. Under pressure, the semiconducting gap is decreased, the resistance without a magnetic field becomes much smaller and the MR is suppressed accordingly (Supplementary Note 4). The integrated MRs (defined as \({{{{{\rm{MR}}}}}}=({\rho }_{{{{{{\rm{H}}}}}}}-{\rho }_{0})/{\rho }_{0}\times 100 \%\)) over the magnetic fields from −10 to 10 T as presented in Fig. 2d decrease as pressure and temperature, diminishing gradually above 16.2 GPa. The abrupt decrease in MR suggests that the HP phase is not magnetically ordered.
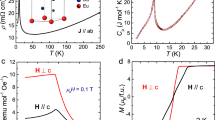
Figure 3 shows the resistance in a smaller temperature range as a colormap on a logarithm scale. The TN of the AFM transition and Tc of the SC transition under pressure could be identified from the resistance (Supplementary Note 5 and Note 6). Upon increasing pressure, the derived TNs increase from 11.4 K at ambient pressure to 16.7 K at 8.0 GPa. The superconductivity appears at 4.9 GPa with a Tc of 3.2 K, defined by the intersection of the tangent to the resistance curve during the transition process and the straight line of the normal state above the SC transition. The Tc reaches a maximum of 6.1 K at 7.0 GPa and decreases smoothly afterward across the structural transition, indicating that the AFM order and spin fluctuations of Eu2+ have not contributed to the cooper pairing mechanism directly.
The antiferromagnetic transition temperature TN and superconducting (SC) transition temperature Tc against pressure. The filled circles are calculated TNs. The color represents different resistance on a logarithm scale. Different shapes of data points are obtained from different measurements. The errors of the TNs are estimated from resistance measurements.
At ambient pressure and low temperature, the calculated energy difference between the A-type AFM and the C-type AFM is almost neglectable (about 1.5 meV per Eu)12. Neutron diffraction measurements were employed to distinguish the two magnetic structures. Although the neutron absorption from Eu atoms is serious, the magnetic reflections associated with the C-type AFM are observed unambiguously (Supplementary Note 7). To understand the underlying mechanism for the enhanced TN in compressed EuTe2, we investigate its exchange couplings based on the following spin model:
Considering the small gap of EuTe2, six nearest-neighbor (NN) Heisenberg exchange couplings are considered. In Eq. (1), A is the single-ion magnetic anisotropy parameter. For EuTe2 at ambient pressure, our density functional theory (DFT) calculations show that it exhibits a C-type AFM ground state with a small gap of 18 meV and out-of-plane magnetic easy axis, consistent with our neutron scattering measurements. Our Monte Carlo simulations reveal the TN is 13.17 K close to previous studies12. Under pressure, both the DFT calculations and Monte Carlo simulations indicate that the ground state is also the C-type AFM order. Four NN exchange couplings are strengthened obviously in regard to ferromagnetic (J < 0) or antiferromagnetic (J > 0) terms up to 11.8 GPa (Supplementary Table 2). This is understandable because the distances between the Eu2+ ions decrease under pressure. Correspondingly, the calculated TNs increase from 13.17 to 21.21 K at 11.8 GPa as shown in Fig. 3. For higher pressures near the structural transition, the Ruderman-Kittel-Kasuya-Yosida interaction may involve and lower the third and fourth NN exchange couplings, resulting in the decrease of the TN.
Spin state transitions and high upper critical field
Superconductivity emerges in both the LP and HP phases, which have distinct structures and magnetic ground states. To explore the role of the local moments of Eu2+ in superconductivity, we conducted resistance measurements at 7.0 and 18.0 GPa. Figure 4a, b shows the resistance as a function of the magnetic field and temperature at 7.0 GPa. A color map of the resistance is plotted in Fig. 4c. The C-type AFM structure of EuTe2 at ambient pressure undergoes a spin-flop transition at ~3.0 T and a spin-flip transition at ~8.0 T12. The magnetic fields for the spin-flop and spin-flip transitions below the TN of 15.6 K at 7.0 GPa are extracted from the resistance in Fig. 4a, yielding 5.5 T for the spin-flop and 12.5 T for the spin-flip transitions at 5 K (Supplementary Note 8). The increased magnetic fields compared with that at ambient pressure are proportional to the increase of TN. The SC transition temperatures Tcs at 7.0 GPa are determined from the resistance shown in Fig. 4b and displayed in Fig. 4c (Supplementary Note 9). We find the \({{\mu }_{0}H}_{{{{{{\rm{c}}}}}}2}-{T}_{{{{{{\rm{c}}}}}}}\) relation does not follow a simple Ginzburg-Landau (GL) formula, \({{\mu }_{0}H}_{{{{{{\rm{c}}}}}}2}(T)={\mu }_{0}{H}_{{{{{{\rm{c}}}}}}2}(0)[1-{(\frac{T}{{T}_{{{{{{\rm{c}}}}}}}})}^{2}]\). The experimentally determined Tcs against magnetic field could be separated into three segments, coincident with the AFM, spin flop, and spin flipped magnetic states. The \({\mu }_{0}{H}_{{{{{{\rm{c}}}}}}2}\)s for the spin flop and spin flipped states are well above the Pauli limit of \({\mu }_{0}{H}_{{{{{{\rm{c}}}}}}2}=1.84{\times T}_{{{{{{\rm{c}}}}}}}=11.2\) T, where Tc is 6.1 K at 7.0 GPa and zero field27. We compare the resistance under various magnetic fields at 18.0 GPa in Fig. 4d. The colormap of resistance suggests that the HP phase is nonmagnetic. The \({\mu }_{0}{H}_{{{{{{\rm{c}}}}}}2}\) can be described by a single GL formula with the \({T}_{{{{{{\rm{c}}}}}}}=5.5\) K and \({\mu }_{0}{H}_{{{{{{\rm{c}}}}}}2}=6.15\) T within the Pauli limit of 10.12 T.
a Magnetic field dependence of the resistance at 7.0 GPa and selected temperatures from 2.0 to 17.0 K. b Resistance from 2.0 to 30.0 K in different magnetic fields from 0 to 14.0 T measured every 0.5 T at 7.0 GPa. c A phase diagram with the antiferromagnetic order, spin flop, spin flip, and superconducting transitions. The solid lines are a guide for magnetic transitions. The dashed lines are the Ginzburg-Landau formula fittings to the segments of the superconducting transition temperatures. The color represents the magnitude of the resistance in (b) on a linear scale from 0.35 to 0.9 Ω. The magnetic fields of spin flop and spin-flip transitions are obtained from the magnetic field dependence of resistance in (a). d Phase diagram of the superconductivity against the magnetic field at 18.0 GPa. The inset is the resistance curves measured on selected magnetic fields. The color represents the magnitude of the resistance in the inset of (d) on a linear scale from 0.006 to 0.03 Ω. The dashed line is fitting to the Ginzburg-Landau formula.
Discussion
The superconductivity in EuTe2 arising from Te impurity can be excluded because of the high upper critical field28,29. In some compounds consisting of Te, the \({\mu }_{0}{H}_{{{{{{\rm{c}}}}}}2}\) could achieve the magnitude of several teslas, such as CrSiTe3, WTe2, HfTe5, Bi2Te3, and CsBi4Te6, where the normal states are not magnetically ordered14,15,30,31,32. The \({\mu }_{0}{H}_{{{{{{\rm{c}}}}}}2}\)s of these compounds are still below the Pauli limit. UTe2 superconducts below 1.6 K at ambient pressure with an ultra-high \({\mu }_{0}{H}_{{{{{{\rm{c}}}}}}2} \, > \, 45\) T33. The 5 f electrons of uranium cross the Fermi level and contribute to the magnetism and superconductivity directly, resulting in the heavy Fermi property and possible triplet pairing mechanism34,35.
Figure 5 shows the field dependence of Tcs in pressurized EuTe2. The \({\mu }_{0}{H}_{{{{{{\rm{c}}}}}}2}\)s are fitted for the experimentally determined AFM, spin flop, and spin flipped states to the GL formula, resulting in the upper critical fields of 10.1, 16.2, and 21.6 T, respectively. The Werthamer-Helfand-Hohenberg (WHH) formula of \({{\mu }_{0}H}_{{{{{{\rm{c}}}}}}2}\left(T\right)=-0.69\times d{H}_{{{{{{\rm{c}}}}}}2}/{dT}{{{{{{\rm{| }}}}}}}_{{T}_{{{{{{\rm{c}}}}}}}}\times {T}_{{{{{{\rm{c}}}}}}}\) is also adopted to estimate the upper critical fields for the three distinct magnetic states, resulting in \({{\mu }_{0}H}_{{{{{{\rm{c}}}}}}2}\)s of 10.7, 15.9, and 20.8 T, respectively36,37. The high \({\mu }_{0}{H}_{{{{{{\rm{c}}}}}}2}\)s for the spin flop and spin flipped states may be attributed to the compensation effect of the exchange field HJ produced by the local moments of Eu2+. We note for the spin-flipped state the direction of HJ is antiparallel to the direction of magnetic moments of Eu2+ on the Te sites. In this case, the net magnetic field HT acting on the conduction electrons is \({H}_{{{{{{\rm{T}}}}}}}={H}_{{{{{{\rm{c}}}}}}2}-|{H}_{{{{{{\rm{J}}}}}}}|\)38. As the Jaccarino-Peter mechanism, AFM spins do not contribute to the exchange field. The spin-flipped state with fully polarized moments of Eu2+ has the maximum HJ. If the sign of the coupling between the local spins and conduction electron spins is negative, the measured \({\mu }_{0}{H}_{{{{{{\rm{c}}}}}}2}\) should be larger than the Pauli limit19. As for Eu0.75Sn0.25Mo6S7.2S0.8, an applied magnetic field can progressively tune the compound from SC to normal, to SC again, and finally back to the normal state below 1 K39. To estimate the Pauli limit critical field Hp and HJ of Eu0.75Sn0.25Mo6S7.2S0.8 for the second SC phase with the lower and upper \({\mu }_{0}{H}_{{{{{{\rm{c}}}}}}2}\)s at 4 and 22 T, we have the constraints of: (i) 4 T\(-{\mu }_{0}{H}_{{{{{{\rm{J}}}}}}}=-{\mu }_{0}{H}_{{{{{{\rm{P}}}}}}}\), and (ii) 22 T\(-{\mu }_{0}{H}_{{{{{{\rm{J}}}}}}}={\mu }_{0}{H}_{{{{{{\rm{P}}}}}}}\). The \({\mu }_{0}{H}_{{{{{{\rm{J}}}}}}}\) and \({\mu }_{0}{H}_{{{{{{\rm{P}}}}}}}\) with values of 13 and 9 T could be derived, respectively. If we assume the HJ is comparable with that of EuTe2, the \({\mu }_{0}{H}_{{{{{{\rm{c}}}}}}2}\) for the spin flipped state in the LP phase of EuTe2 should be \(10.1+13\approx 23\) T, close to the fitted \({\mu }_{0}{H}_{{{{{{\rm{c}}}}}}2}\) of 21.6 T from the GL formula. Through DFT calculations, the localized Eu 4 f electrons reside ~1.25 eV below the Fermi level for the LP phase, while the Te 5p electrons crossing the Fermi level involve SC cooper pairing (Supplementary Note 10), consistent with the Jaccarino-Peter mechanism.
The circles are superconducting transition temperatures Tcs of EuTe2 determined from resistance at 7.0 GPa. The pink, yellow, and blue regions correspond to the antiferromagnetic order, spin flop, and spin flipped states. The black, orange, and blue dashed lines represent corresponding GL fittings. The Tcs, fitted \({\mu }_{0}{H}_{{{{{{\rm{c}}}}}}2}\)s using the GL formula, and the Werthamer-Helfand-Hohenberg formula for each magnetic state has been labeled.
In summary, we have studied the structural and electronic transport properties of EuTe2 under pressure. EuTe2 shows a SC transition above 5 GPa with a maximum Tc of 6.1 K at 7.0 GPa and a structural transition at 16 GPa. The transition temperature of the C-type AFM order is enhanced in compressed EuTe2 due to the increase of the magnetic exchange interactions. In the LP phase, superconductivity coexists with the AFM, spin flop, and spin flipped states. However, the electronic states of Eu2+ are well below the Fermi level and do not involve cooper pairing directly. The local moments of Eu2+ in the spin flop and spin flipped states produce an exchange field, compensating with the external field and resulting in an ultra-high upper critical field that is larger than the Pauli limit. The HP phase is nonmagnetic and the \({\mu }_{0}{H}_{{{{{{\rm{c}}}}}}2}-{T}_{{{{{{\rm{c}}}}}}}\) relation could be described by the GL formula with the \({\mu }_{0}{H}_{{{{{{\rm{c}}}}}}2}\) within the Pauli limit. Our results establish that EuTe2 is a pressure-induced superconductor with a high upper critical field which could be understood by the Jaccarino-Peter mechanism.
Methods
Single-crystal growth and neutron diffraction
Bulk single crystals of EuTe2 were grown by the self-flux method. Pure Eu and Te were combined in the molar ratio of 1:10 and sealed in an evacuated quartz ampoule. The ampoule was slowly heated to 850 °C in 100 h and held for 75 h, then slowly cooled to 450 °C in 300 h. The shiny black single crystals of EuTe2 were separated from the Te flux at 450 °C. The structure of EuTe2 was confirmed by single-crystal XRD.
The powder neutron diffraction experiments were carried out on the Xingzhi triple-axis spectrometer at the China Advanced Research Reactor40. Powder samples were stuck on an aluminum foil uniformly with a hydrogen-free glue to reduce the absorption of Eu, then sealed in a cylindrical vanadium container and loaded into a closed cycle refrigerator that regulates the sample temperature from 3.5 to 300 K. A neutron velocity selector was used upstream to cleanly remove higher order neutrons for the incident neutron energy fixed at 16 meV.
High-pressure XRD
The in situ high-pressure synchrotron powder XRD patterns of EuTe2 were collected at 300 K with an x-ray wavelength of 0.6199 Å on the Beijing Synchrotron Radiation Facility, Institute of High Energy Physics, Chinese Academy of Sciences. A symmetric diamond anvil cell with a pair of 300 μm diameter culets was used. A sample chamber with a diameter of 120 μm was drilled by laser in a pre-indented steel gasket. The EuTe2 single crystals were ground into fine powders and compressed into a pellet with an 80 μm diameter and 20 μm thickness. The pellet was loaded into the middle of the sample chamber and silicone oil was used as a pressure-transmitting medium. A ruby sphere was also loaded into the sample chamber and pressure was determined by measuring the shift of its fluorescence wavelength. The data were initially processed using Dioptas41 (with a CeO2 calibration) and the subsequent Rietveld refinements were managed using TOPAS-Academic42.
High-pressure magnetic and electrical property measurements
Magnetic and electrical measurements were taken on a physical property measurement system (PPMS, Quantum Design). High-pressure electrical transport measurements of EuTe2 single crystals were carried out using a miniature diamond anvil cell made from a Be–Cu alloy on a PPMS. Diamond anvils with a 400 μm culet were used, and the corresponding sample chamber (with a diameter of 150 μm) was made in an insulating gasket achieved by cubic boron nitride and epoxy mixture. NaCl powders were employed as the pressure-transmitting medium, providing a quasi-hydrostatic environment. The pressure was also calibrated by measuring the shift of the fluorescence wavelength of the ruby sphere, which was loaded in the sample chamber. The standard four-probe technique was adopted for these measurements.
Theoretical calculations
Our structure searching simulations are performed by the swarm-intelligence-based CALYPSO (Crystal structure AnaLYsis by Particle Swarm Optimization) method, which enables global minimization of energy surfaces by merging ab initio total-energy calculations22. The structure searching was carried out at pressures of 5, 15, and 25 GPa which covers the experimental pressure range. The simulation cell sizes of \(1{-}4\) formula units were set. The underlying ab initio structural relaxations were carried out using density functional theory within the Perdew–Burke–Ernzerhof exchange-correlation43 as implemented in the Vienna ab initio Simulation Package (VASP) code44,45.
DFT calculations are performed using the VASP at the level of the generalized gradient approximation43,46. We adopted the projector augmented wave pseudopotentials and a plane-wave cutoff energy of 500 eV44. The experimentally measured lattice constants are used in our calculations and the positions of all atoms are fully relaxed until the force on each atom is less than 0.01 eVÅ−1. We use U = 4.4 eV for Eu2+ ions because of the strong correlation among f electrons. The TN of the pressurized EuTe2 is obtained through parallel tempering Monte Carlo (MC) simulations47,48.
Data availability
The source data and related supporting information are available upon reasonable request from the corresponding author.
References
Bardeen, J., Cooper, L. & Schrieffer, J. Microscopic theory of superconductivity. Phys. Rev. 106, 162–164 (1957).
Si, Q., Yu, R. & Abrahams, E. High-temperature superconductivity in iron pnictides and chalcogenides. Nat. Rev. Mater. 1, 16017 (2016).
Scalapino, D. J. A common thread: The pairing interaction for unconventional superconductors. Rev. Mod. Phys. 84, 1383 (2012).
Fernandes, R. M. et al. Iron pnictides and chalcogenides: a new paradigm for superconductivity. Nature 601, 35–44 (2022).
Stewart, G. R. Unconventional superconductivity. Adv. Phys. 66, 75–196 (2017).
Dai, P. Antiferromagnetic order and spin dynamics in iron-based superconductors. Rev. Mod. Phys. 87, 855–896 (2015).
Ran, S. et al. Extreme magnetic field-boosted superconductivity. Nat. Phys. 15, 1250–1255 (2019).
Ran, S. et al. Nearly ferromagnetic spin-triplet superconductivity. Science (80-.) 365, 684–687 (2019).
Gammel, P. C. C. L., Bishop, D. J., Canfield, P. C., Gammel, P. L. & Bishop, D. J. New magnetic superconductors: a toy box for solid-state physicists. Phys. Today 51, 40–46 (1998).
Yu, J., Le, C., Li, Z. & Li, L. Coexistence of ferromagnetism, antiferromagnetism, and superconductivity in magnetically anisotropic (Eu,La)FeAs2. npj Quantum Mater. 6, 63 (2021).
Jin, W. T. et al. Phase diagram of Eu magnetic ordering in Sn-flux-grown Eu(Fe1−xCox)2As2 single crystals. Phys. Rev. B 94, 184513 (2016).
Yin, J. et al. Large negative magnetoresistance in the antiferromagnetic rare-earth dichalcogenide EuTe2. Phys. Rev. Mater. 4, 13405 (2020).
Yang, H. et al. Colossal angular magnetoresistance in the antiferromagnetic semiconductor EuTe2. Phys. Rev. B 104, 214419 (2021).
Pan, X. C. et al. Pressure-driven dome-shaped superconductivity and electronic structural evolution in tungsten ditelluride. Nat. Commun. 6, 7805 (2015).
Cai, W. et al. Pressure-induced superconductivity and structural transition in ferromagnetic CrSiTe3. Phys. Rev. B 102, 144525 (2020).
Yu, F. H. et al. Elevating the magnetic exchange coupling in the compressed antiferromagnetic axion insulator candidate EuIn2As2. Phys. Rev. B 102, 180404 (2020).
Sun, H. et al. Magnetism variation of the compressed antiferromagnetic topological insulator EuSn2As2. Sci. China Phys. Mech. Astron. 64, 118211 (2021).
Yang, P. T. et al. Pressured-induced superconducting phase with large upper critical field and concomitant enhancement of antiferromagnetic transition in EuTe2. Nat. Commun. 13, 2975 (2022).
Jaccarino, V. & Peter, M. Ultra-high-field superconductivity. Phys. Rev. Lett. 9, 290 (1962).
Wang, Y. et al. An effective structure prediction method for layered materials based on 2D particle swarm optimization algorithm. J. Chem. Phys. 137, 224108 (2012).
Wang, Y., Lv, J., Zhu, L. & Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B—Condens. Matter Mater. Phys. 82, 1–8 (2010).
Wang, Y., Lv, J., Zhu, L. & Ma, Y. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 183, 2063–2070 (2012).
Coelho, A. A. TOPAS and TOPAS-Academic: an optimization program integrating computer algebra and crystallographic objects written in C++. J. Appl. Crystallogr. 51, 210 (2018).
Ohara, H. et al. Charge ordering in Eu3S4 determined by the valence-difference contrast of synchrotron X-ray diffraction. Phys. B Condens. Matter 350, 353–365 (2004).
Sugimoto, T. et al. Bcc-fcc structure transition of Te. J. Phys. Conf. Ser. 500, 192018 (2014).
Jamieson, J. C. & Mcwhan, D. B. Crystal structure of tellurium at high pressures. Phys. Today 43, 1149 (2014).
Clogston, A. M. et al. Upper limit for the critical field in hard superconductors. Phys. Rev. Lett. 9, 266–267 (1962).
Akiba, K. et al. Magnetotransport properties of tellurium under extreme conditions. Phys. Rev. B 101, 245111 (2020).
Akahama, Y. et al. Pressure-Induced sperconductivity and phase transition. Solid State Communications 84, 803–806 (1992).
Qi, Y. et al. Pressure-driven superconductivity in the transition-metal pentatelluride HfTe5. Phys. Rev. B 94, 054517 (2016).
Zhang, J. L. et al. Pressure-induced superconductivity in topological parent compound Bi2Te3. Proc. Natl. Acad. Sci. USA 108, 24–28 (2011).
Malliakas, C. D., Chung, D. Y., Claus, H. & Kanatzidis, M. G. Superconductivity in the narrow-gap semiconductor CsBi4Te6. J. Am. Chem. Soc. 135, 14540 (2013).
Butch, N. P. et al. Expansion of the high field-boosted superconductivity in UTe2 under pressure. npj Quantum Mater. 6, 75 (2021).
Jiao, L. et al. Chiral superconductivity in heavy-fermion metal UTe2. Nature 579, 523 (2020).
Duan, C. et al. Resonance from antiferromagnetic spin fluctuations for superconductivity in UTe2. Nature 600, 636 (2021).
Li, Z. et al. Superconductivity above 200 K discovered in superhydrides of calcium. Nat. Commun. 13, 2863 (2022).
Werthamer, N. R., Helfand, E. & Hohenberg, P. C. Temperature and purity dependence of the superconducting critical field, Hc2. III. Electron spin and spin-orbit effects. Phys. Rev. 147, 295–302 (1966).
Brian Maple, M. Induction of superconductivity by applied magnetic fields. Nature 315, 95 (1985).
Meul, H. W. et al. Observation of magnetic-field-induced superconductivity. Phys. Rev. Lett. 53, 497 (1984).
Cheng, P. et al. Nuclear instruments and methods in physics research a design of the cold neutron triple-axis spectrometer at the China Advanced Research Reactor. Nucl. Inst. Methods Phys. Res. A 821, 17–22 (2016).
Prescher, C. & Prakapenka, V. B. DIOPTAS: a program for reduction of two- dimensional X-ray diffraction data and data exploration. High. Press. Res. 35, 223–230 (2015).
Coelho, A. A. Computer programs TOPAS and TOPAS-Academic: an optimization program integrating computer algebra and crystallographic objects written in C ++. J. Appl. Crystallogr. 51, 210 (2018).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Vargas-Hernández, R. A. Bayesian optimization for calibrating and selecting hybrid-density functional models. J. Phys. Chem. A 124, 4053–4061 (2020).
Lou, F. et al. PASP: Property analysis and simulation package for materials. J. Chem. Phys. 154, 114103 (2021).
Hukushima, K. & Nemoto, K. Exchange Monte Carlo method and application to spin glass simulations. J. Phys. Soc. Jpn. 65, 1604–1608 (1996).
Acknowledgements
This work at Sun Yat-Sen University was supported by the Guangdong Basic and Applied Basic Research Funds (Grant No. 2021B1515120015), National Natural Science Foundation of China (Grants No. 12174454, No. 12104518, No. 22090041, No. 92165204, No. 12074426, and No. 11227906), Guangzhou Basic and Applied Basic Research Funds (Grant No. 202201011123), Guangdong Provincial Key Laboratory of Magnetoelectric Physics and Devices (Grant No. 2022B1212010008), National Key Research and Development Program of China (Grant No. 2019YFA0705702), the Fundamental Research Funds for the Central Universities, Sun Yat-sen University (Grant No. 22QNTD3004) and the Research Funds of Renmin University of China (Grant No. 22XNKJ40). The work at Rice University is supported by the US Department of Energy, Basic Energy Sciences, under grant no. DE-SC0012311 and by the Robert A. Welch Foundation grant no. C-1839 (P.D.). We appreciate the support of BSRF, IHEP, CAS for high-pressure XRD measurements.
Author information
Authors and Affiliations
Contributions
M.W. and H.S. proposed and designed the research. H.S. carried out the high-pressure measurements and data analysis with the help of Y.H, C.H, N.L, M.H., L.L., H.L., Z.L., and M.L. Single crystals were synthesized by C.H. Theoretical calculations were carried out by L.Q., Y.Z., W.W., D.Y., and Y.H. Neutron diffraction measurements were conducted by P.C. with the support of H.Z., H.W., and L.H. M.W., H.S., and P.D. wrote the paper with input from all co-authors. M.W. oversaw the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sun, H., Qiu, L., Han, Y. et al. Exchange field enhanced upper critical field of the superconductivity in compressed antiferromagnetic EuTe2. Commun Phys 6, 40 (2023). https://doi.org/10.1038/s42005-023-01155-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-023-01155-7
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.