Abstract
Pores in nanoporous materials can be interconnected in different ways; preliminary evidence exists that connecting channels can affect the overall hydrophobicity of the material thus providing an additional parameter in designing applications that require controlled wetting properties. In this work, we show that the length of secondary channels is a key parameter to tune the overall hydrophobicity of the material: short secondary channels make the main pore effectively more hydrophilic than a simple cylindrical pore, while long secondary channels enhance its hydrophobicity, producing the macroscopic effect of superhydrophobic textures. This rich behavior is rooted in the spontaneous filling of the secondary channels, which is unexpected based on classical capillarity. This length-dependent filling is explained by the formation of hydrogen bonds bridging the main pores which becomes less frequent with longer channels. These findings could be useful for designing nanoporous materials with tailored wetting properties.
Similar content being viewed by others
Introduction
The intrusion and extrusion of non wetting liquids in nanoporous materials has been a topic of increasing interest in the last years, stimulated by the wealth of applications of Heterogeneous Lyophobic Systems (HLS), which can be used for energy storage or dissipation1,2,3 and for energy production via triboelectrification4,5. Car shock absorbers based on HLS have been developed and tested6,7, exploiting the hysteresis of the intrusion/extrusion process to dissipate mechanical vibrations. Engineering is not the only technological domain in which intrusion/extrusion has applications, others include liquid separation8,9, bioinspired nanochannels10,11,12, liquid chromatography13,14, and porosimetry15,16. Notwithstanding the broad range of applications of HLS, a quantitative understanding of how the intrusion or extrusion processes are related to the properties of the liquid and of the nanoporous material remains in many cases elusive.
Intrusion and extrusion pressures are the key parameters determining the application domain and conditions of HLS17. For example, systems with a large intrusion/extrusion pressure hysteresis, in which the intrusion pressure is much higher than the extrusion one, are suitable for energy absorption and damping. Systems with negligible hysteresis, on the contrary, are good for energy storage, to develop “mechanical batteries”. The absolute value of the intrusion and extrusion pressures is also relevant for applications, as it must match the values of the pressure at operative conditions. Within the framework of classical capillarity, the hydrophobicity and the diameter of the pore determine the intrusion pressure according to the macroscopic Kelvin–Laplace law18,19,20, hence, these are the only possible design parameters, limiting the flexibility in the design of new nanoporous materials. However, at the (sub)nanometer scale of meso and microporous materials, effects that are not considered in classical capillarity may become dominant11,21 (e.g., confinement of the liquid, line tension). Nanoscale effects are thus promising means to extend the limited number of design parameters for HLS.
Molecular Dynamics, by taking into account the discrete nature of the liquid and of the confining solid and thermal fluctuations, is the tool of choice to simulate nanoscale wetting processes. The intrusion and extrusion pressures have been found to be sensitive to changes in the speed of the process3, the temperature of the fluid22, its viscosity23, the size of the pores21,24, and the presence of dissolved species25,26,27,28. On the other hand, the effect of the topology and connectivity of the nanopores is also expected to play a key role in determining the intrusion/extrusion properties29. While it has been recently shown that the presence of secondary channels embedded in the main pore may increase the effective hydrophobicity of the pore30,31, the effect of secondary channels connecting the main pores can be very different due to the possibility of having fluid at both sides. Indeed, when comparing the intrusion and extrusion pressures of MFI and TON type zeolites, the importance of the connecting channels becomes apparent. The main pores of these zeolites are similar, but, in TON, they are independent while, in MFI, there are interconnecting secondary channels with 0.55 nm diameter and subnanometer lengths, similar to our system (Fig. 1). The reported intrusion/extrusion pressures differ by 100 MPa both in experiments and in simulations32,33, with MFI having the lower intrusion/extrusion pressure in agreement with the results shown below. The role of interconnecting secondary channels of different lengths is not well understood when discussing hierarchical materials, in particular mesoporous materials where the presence of interconnected channels increases their liquid retention34. The length of secondary channels can be controlled by fine-tuning of the manufacturing procedure for some hydrophobic materials, like the mesoporous silica SBA-1535, making it a relevant design parameter.
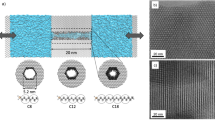
The system consists of two reservoirs of liquid water separated by a nanoporous slab with the main pores connecting them. Front and lateral views highlight the presence of orthogonal secondary channels connecting the main pores. The diameter of the main pores, D, is 1.54 nm. The secondary channels diameter, d, is 0.77 nm. The length of the main pores, Lmp, is 3.15 nm. The length of the secondary channels, Lsc, is varied in this study; in the illustrated example, Lsc = 1 nm. This figure was realized using Visual Molecular Dynamics (VMD)50, a molecular dynamics visualization tool.
In this work, we show by free-energy molecular dynamics that the characteristics of the secondary channels, namely their length, which was never been considered before, can dramatically change the wetting properties of the material. Our results demonstrate that the presence of secondary channels can facilitate the wetting of porous materials but does not guarantee it. More importantly, it suggests an effective design strategy for HLS, based on engineering the connectivity of the porous material.
Results
Molecular dynamics system
We consider the simple system of Fig. 1, consisting of a central pore surrounded by six identical pores, connected to the central one by secondary channels. This simple model is designed to investigate the general physical aspects of wetting of interconnected pores, including the intrusion/extrusion pressures. The central pore is connected to the identical lateral pores by 3 rings of secondary channels, distributed along the pore length. Each ring connects the central pore with the 6 lateral pores, resulting in a total of 18 secondary channels. The distance of the main pores is varied, making secondary porosity shallower or deeper, which allows to single out the effect of secondary pore length on the intrusion/extrusion cycle.
Despite its simplicity, this system is suitable to model real porous materials, such as the Cu2l MOF36. Indeed it has been shown21 that a simple cylindrical channel system reproduces the key features of MCM-41, a silica mesoporous material used in energy dissipation22,37. We used this particular arrangement for its resemblance to a hydrophobic zeolite of ITT type, ITQ-33 see29; however, in the following, we demonstrate that the wetting of these secondary channels does not depend on their specific arrangement and that it occurs for a range of lengths, radii, and surface chemistries (contact angles from 95∘ to 130∘) which are physically relevant (see Supplementary Notes 5–6).
Standard molecular dynamics falls short when used to simulate rare events38, as is the case of intrusion/extrusion of our nanoporous system39,40. We thus resorted to restrained molecular dynamics (RMD)41 to compute the free energy profile as a function of the filling of the central pore, while keeping the 6 lateral pores filled. Restrained molecular dynamics allowed us to effectively sample even those regions of phase space that would otherwise be inaccessible with standard molecular dynamics techniques, e.g., regions close to the free energy barrier that separates the wet and dry (meta)stable states that characterize this system. More details on RMD simulations are available in the methods section.
Channel length dependence of intrusion/extrusion characteristics
In Fig. 2, we report the free energy profile of our system as a function of the liquid filling. Regardless of the length of the secondary channels Lsc, our system presents one global and one local minimum of the free energy, corresponding to an empty and filled central pore, respectively. While it was expected that the wettability of the main pore depended on the number of secondary channels29,31, is was surprising to find it crucially depends also on Lsc. Taking the system without secondary porosity as a reference, in which the empty state is more stable than the filled one, one notices that for short secondary channels, Lsc = 0.2 nm, the free energy of the wet state is lower than the reference wet state, while for longer secondary channels the opposite is true. These results show that the length of the secondary porosity allows to tune the effective hydrophobicity of a porous system, making it effectively more hydrophilic or effectively more hydrophobic depending on the length of the secondary channels, a novel principle in the physics of confined liquids.
The free energy difference between the filled and empty states determines the thermodynamics stability of these states. However, Fig. 2 shows that a system prepared in the metastable state, the local minimum, must cross a free energy barrier in order to reach the stable state. This free energy barrier sets the timescale of the intrusion via an Arrhenius-like law11. This barrier depends on the pressure—with high pressures favouring intrusion and low ones extrusion. In previous works, it was assumed that a barrier of 10 kBT can be overcome in the typical duration of an experiment21; similarly, we estimate the intrusion and extrusion pressures from the free energy profiles at different pressures. This approach is computationally very expensive, thus, for the fundamental objectives of this work, we resort to an approximation that has been successfully applied in the literature21,39,42, adding to the original free-energy profile the term ΔpVv, where Vv is the volume of the vapor bubble, which linearly depends on the number of water molecules in the pore. The intrusion/extrusion pressure of the system is operationally defined as the pressure at which the free-energy profile presents an intrusion/extrusion barrier of 10 kBT, respectively, see Fig. 3a. Choosing different barriers is equivalent to allowing the system more time to relax toward its stable state, i.e., when comparing to an experimental pressure cycle, a different barrier corresponds to a different frequency of the cycle. We discuss the results when different barriers are considered in Supplementary Note 2.
a Free energy as a function of the normalized volume of the bubble in the main pore for different lengths of the secondary channels, Lsc, 0.2 nm (blue), 0.4 nm (orange), 0.6 nm (green), 1 nm (red), and 1.2 nm (pink); as a reference, we also report the case with no channels (purple) and the case in which the channels are kept forcefully empty (brown). The arbitrary constant of the free energy is set such that it is equal for all the systems for an empty central pore. The standard error of the free energy profile is shown using a shaded region around the curve. b The panels circled in blue show a snapshot of the empty and filled states of the central pore for Lsc = 0.2 nm; the panel circled in red shows the filled state for Lsc = 1 nm. Water is represented as a transparent fluid, while the water molecules inside the secondary channels are explicitly shown to highlight the different levels of filling.
a Free energy profile of the system at the intrusion pressure (orange), extrusion pressure (green), and atmospheric pressure (blue) for secondary channel length, Lsc = 0.6 nm. Pressurizing the system amounts to tilting the free energy profile. We highlight the intrusion and extrusion barriers that would allow to observe these events in typical experimental timescales, i.e., approximately milliseconds. b Intrusion (black) and extrusion (red) pressures as a function of the length of the secondary channels. The intrusion and extrusion pressures for the system without secondary channels are reported for comparison (dotted lines). The inset shows pressure hysteresis, H = (pint − pext)/pint, with pint and pext being the intrusion and extrusion pressure, respectively, as a function of Lsc.
Figure 3b shows that the intrusion/extrusion pressures can increase by as much as 60 MPa when the secondary channel length is changed from 0.2 to 1.2 nm. Previous studies reported an increased pore hydrophobicity (higher pext), due to the presence of smaller cavities in the empty state31; this “superhydrophobic” effect depended on the surface fraction of the main pore covered by cavities and could be rationalized in terms of the Cassie–Baxter model43. Here, instead, the surface fraction is fixed and the intrusion/extrusion pressures are found to depend sensitively on the secondary channel length. pint and pext allow to quantify the previously unexplored effect of the length of secondary channels/pore interconnections on the hydrophilicity/hydrophobicity: short secondary channels (Lsc = 0.2) facilitate intrusion as compared to pores without lateral channels, while longer ones (Lsc > 0.4 nm) hinder it; extrusion is hindered for pores with Lsc < 1 nm and facilitated for pores larger or equal. Such dramatic changes tend to saturate with increasing Lsc.
The length of the secondary channels also affects the (dimensionless) pressure hysteresis, H = (pint − pext)/pint, which is related to energy dissipation in intrusion/extrusion cycles. In particular, hysteresis decreases with Lsc. Overall, Fig. 3b shows that pore connections are effective means of controlling intrusion and extrusion properties of HLS, which, in turn, determine their applicability as energy storage or dissipation devices. In particular, we propose that the length of secondary channels can be used as a design parameter for HLS, possibly extending the technological applications of these materials.
Spontaneous filling of sub-nanometric channels
The reported changes in pint and pext are rooted in the spontaneous filling of the secondary channels by water (Fig. 2, right), which is most surprising given their subnanometric size and their hydrophobicity. This result is counter-intuitive and even paradoxical, implying that larger cavities (the main and lateral pores) are harder to wet than subnanometric ones (the secondary channels), at odds with classical capillarity, with mean field calculations of independent nanometer-sized cavities in contact with simple liquids19,44, and with experiments30 and simulations31 of larger cavities. Figure 4a shows that the number of filled secondary channels depends on Lsc, with most of the cavities being filled for Lsc = 0.2 nm and very few of them (but not zero!) being filled for Lsc = 1.2 nm. The wetting of secondary channels cannot be explained within a classical capillarity framework as becomes apparent by estimating the intrusion pressure via the Kelvin–Laplace equation
where γLV is the liquid–vapor surface tension, θ the Young contact angle of the material, and D the pore diameter. Equation (1) predicts pint ≈ 85 MPa for the present secondary channels and no dependence on their length. The non-negligible probability of filling the secondary channels at zero pressure is thus a striking result as is the fact that the filling probability depends on Lsc; this phenomenon calls for a different modeling which explicitly takes into account sub-nanometer effects due to water molecules arranging in a single file. To understand whether the filling of the sub-nanometer channels depends on their specific arrangement or chemistry, we simulated the filling of independent, 0.5 nm long pores with different contact angles. It was found that, while the probability of wetting depends quantitatively on these details—to be systematically explored in an upcoming work,—secondary channels were found in the wet state for a range of conditions, which makes the phenomenology rather general. Details are reported in the Supplementary Notes 5–6.
a Histogram of the filled secondary channels during molecular dynamics runs, for different secondary channel lengths, Lsc. A single file of water molecules occupies secondary channels, as shown by molecular dynamics snapshots in the inset (blue for the secondary channels with Lsc = 0.2 nm and in red for Lsc = 1 nm). b Number of hydrogen bonds created by the water molecules in the secondary channels (red) and the ones destroyed (black) in order to move the molecules there, for different Lsc in the filled state, using the empty state as a reference.
The anomalous wetting of secondary channels can be explained by the hydrogen bonding between individual molecules, which has to be considered when water is organized in a single file. The energy gain due to the formation of hydrogen bonds within single-file water molecules might exceed the energetic penalty arising from water molecules entering in an extremely confined and hydrophobic environment. On the other hand, as the length of the secondary channels increases, the energy benefit of forming hydrogen bonds no longer compensates the energy penalty of water entering the secondary channels. To support this interpretation, we computed the number of hydrogen bonds created and destroyed by the presence of water molecules in the secondary channels, as defined in other works45: for the shortest channels, wetting of the secondary channels leads to a favorable increase in the total number of hydrogen bonds in the system, while the opposite is true for the longest channels, see Fig. 4b and the Supplementary Notes 3–4. This “ångstroscale” filling of secondary channels can be observed only when their characteristic length is comparable to the hydrogen bond length; already for Lsc = 1 nm, corresponding to an occupancy of ca. 4 water molecules, the probability of filling is small. Figure 4b highlights that the competition between formation and destruction of hydrogen bonds is a substantial driving force for the filling of the secondary channels, showing a trend similar to the filling probability in Fig. 4a. However, there are other contributions to the energy which are not included in this simple model, such as the interactions of the confined water molecules with the solid. Also, although the trends remain qualitatively the same, the value of the crossover depends on the specific definition of hydrogen bond adopted, see Supplementary Notes 4.
In summary, hydrogen bonds bridging across the main pores are crucial to cause wetting of subnanometric secondary channels, which, in turn, regulate the wettability of the main pores, by creating hydrophilic patches which can connect the main pores with chains of hydrogen bonds. Indeed, if one models the filled secondary channels as water molecules trapped in simple cavities, the stability of the wet state is considerably increased, as shown in the Supplementary Note 7. The coupled wetting of the main pores and the of secondary channels allows the water front to advance more easily than without interconnections.
Discussion
Pore connectivity is not usually considered when analyzing the intrusion and extrusion processes of hydrophobic nanopores. Actually, we have shown that the length of secondary channels is a key parameter that can change the wetting properties of the main pore. Intrusion and extrusion pressures in these systems can vary by more than 60 MPa when comparing short, Lsc = 0.2 nm, and long, Lsc = 1.2 nm, secondary channels. The key variable controlling wetting is the filling of the secondary channels, which is found to depend on the formation of a single file of water molecules, linked through hydrogen bonds, which introduces an unexpected dependence of wetting on length. The wetting of secondary porosity is indeed surprising, as classical capillary theory predicts a huge intrusion pressure based on their subnanometric radius. Despite this, water spontaneously intrudes and, even for Lsc = 1.2 nm, secondary channels have a non-negligible probability of being filled. We have proposed an explanation of this unexpected behavior, showing that the increase in probability is related to the energy gain of having hydrogen bonds connecting the main channels through the secondary channels. Physical modeling, which explicitly taking into account sub-nanometric features such as hydrogen bonding is thus needed for the quantitative prediction of the secondary channel filling as a function of their length and radius and will be explored in future work, where we will quantify the unexpected wetting of these ångstrom-scale porosities. The spontaneous filling of the secondary channels dramatically affects the filling mechanism of the main pore, and, as demonstrated in Supplementary Note 7 for a simplified model, the main pore can be change all the way from effectively hydrophilic to effectively hydrophobic depending on the number of filled secondary channels. We propose that the results described in this work could be experimentally verified in a variety of materials, including the mesoporous silica SBA-15, which has subnanometer pores connecting the main ones; in this material, the wall thickness, and hence the length of the secondary channels, can be controlled35. These findings lay the foundations for a different paradigm in the design of nanoporous materials for energy storage and dissipation, supplying a route to engineer the intrusion and extrusion pressures and the hysteresis in HLS via pore interconnections.
Methods
Molecular dynamics setup
The atomistic structure of our system is obtained from a slab of fixed atoms with an fcc arrangement, into which the porous structure was excavated. The 7 cylindrical pores have diameter of 1.54 nm, which is the characteristic size of silicogermanate zeolite ITQ-33 pores46, a hydrophobic zeolite of ITT type. Secondary channels have a diameter of 0.77 nm, also in this case, the zeolite ITQ-33 has been taken as a reference to consider a realistic case of practical relevance. Simulations were run using LAMMPS47. The slab was immersed in SPC/E water48, whose interaction with the wall was set to obtain a contact angle of 104∘26, see Supplementary Note 1. We considered 5 different systems, modifying the distance between the main pores, i.e., the length of the secondary channels Lsc, between 0.2 and 1.2 nm.
Restrained molecular dynamics
Restrained molecular dynamics was used to compute the free energy profiles as a function of water filling of the main pore. We used a cylindrical control region that encompassed the central pore to impose different pore fillings via RMD. An annular region encompassing the 6 lateral pores was used to impose their filling throughout the simulations. The harmonic potential constant was set to 1 kcal/mol. The simulations were run at 310.5 K using a Nosé–Hoover chain thermostat49, while pressure was controlled by a free liquid–vapor interface far away from the porous slab26, see Fig. 1. A 1 ns equilibration time was used while the production run lasted 0.5 ns.
Data availability
Raw data for this work are available in Zenodo with the DOI identifier https://doi.org/10.5281/zenodo.6519981.
Code availability
All the relevant code for the data analysis are available from the authors upon reasonable request.
References
Eroshenko, V., Regis, R.-C., Soulard, M. & Patarin, J. Energetics: a new field of applications for hydrophobic zeolites. J. Am. Chem. Soc. 123, 8129–8130 (2001).
Fraux, G., Coudert, F.-X., Boutin, A. & Fuchs, A. H. Forced intrusion of water and aqueous solutions in microporous materials: from fundamental thermodynamics to energy storage devices. Chem. Soc. Rev. 46, 7421–7437 (2017).
Sun, Y. et al. High-rate nanofluidic energy absorption in porous zeolitic frameworks. Nat. Mater. 20, 1015–1023 (2021).
Grosu, Y. et al. Mechanical, thermal, and electrical energy storage in a single working body: electrification and thermal effects upon pressure-induced water intrusion–extrusion in nanoporous solids. ACS Appl. Mater. Interfaces 9, 7044–7049 (2017).
Lowe, A. et al. Effect of flexibility and nanotriboelectrification on the dynamic reversibility of water intrusion into nanopores: pressure-transmitting fluid with frequency-dependent dissipation capability. ACS Appl. Mater. Interfaces 11, 40842–40849 (2019).
Eroshenko, V., Piatiletov, I., Coiffard, L. & Stoudenets, V. A new paradigm of mechanical energy dissipation. part 2: experimental investigation and effectiveness of a novel car damper. Proc. Inst. Mech. Eng., Part D: J. Automob. Eng. 221, 301–312 (2007).
Suciu, C. V. & Yaguchi, K. Endurance tests on a colloidal damper destined to vehicle suspension. Exp. Mech. 49, 383–393 (2008).
Kota, A. K., Kwon, G., Choi, W., Mabry, J. M. & Tuteja, A. Hygro-responsive membranes for effective oil–water separation. Nat. Commun. 3, 1–8 (2012).
Yang, H.-C., Hou, J., Chen, V. & Xu, Z.-K. Janus membranes: exploring duality for advanced separation. Angew. Chem. Int. Ed. 55, 13398–13407 (2016).
Roth, R., Gillespie, D., Nonner, W. & Eisenberg, R. E. Bubbles, gating, and anesthetics in ion channels. Biophys. J. 94, 4282–4298 (2008).
Giacomello, A. & Roth, R. Bubble formation in nanopores: a matter of hydrophobicity, geometry, and size. Adv. Phys.: X 5, 1817780 (2020).
Tortora, M. et al. The interplay among gas, liquid, and solid interactions determines the stability of surface nanobubbles. Nanoscale 12, 22698–22709 (2020).
Walter, T. H., Iraneta, P. & Capparella, M. Mechanism of retention loss when c8 and c18 hplc columns are used with highly aqueous mobile phases. J. Chromatogr. A 1075, 177–183 (2005).
Gritti, F., Brousmiche, D., Gilar, M., Walter, T. H. & Wyndham, K. Kinetic mechanism of water dewetting from hydrophobic stationary phases utilized in liquid chromatography. J. Chromatogr. A 1596, 41–53 (2019).
Coasne, B., Galarneau, A., Di Renzo, F. & Pellenq, R. Intrusion and retraction of fluids in nanopores: effect of morphological heterogeneity. J. Phys. Chem. C 113, 1953–1962 (2009).
Helmy, R., Kazakevich, Y., Ni, C. & Fadeev, A. Y. Wetting in hydrophobic nanochannels: a challenge of classical capillarity. J. Am. Chem. Soc. 127, 12446–12447 (2005).
Donne, A. L. et al. Intrusion and extrusion of liquids in highly confining media: bridging fundamental research to applications. Advances in Physics: X7 https://doi.org/10.1080/23746149.2022.2052353 (2022).
Laplace, P. S.Traité de mécanique céleste/par PS Laplace...; tome premier [-quatrieme], vol. 4 (de l’Imprimerie de Crapelet, 1805).
Giacomello, A., Schimmele, L., Dietrich, S. & Tasinkevych, M. Perpetual superhydrophobicity. Soft Matter 12, 8927–8934 (2016).
De Gennes, P.-G., Brochard-Wyart, F. & Quéré, D. Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves Vol. 315 (Springer, 2004).
Tinti, A., Giacomello, A., Grosu, Y. & Casciola, C. M. Intrusion and extrusion of water in hydrophobic nanopores. Proc. Natl Acad. Sci. USA 114, E10266–E10273 (2017).
Guillemot, L., Galarneau, A., Vigier, G., Abensur, T. & Charlaix, É. New device to measure dynamic intrusion/extrusion cycles of lyophobic heterogeneous systems. Rev. Sci. Instrum. 83, 105105 (2012).
Grosu, Y. et al. Viscosity at the nanoscale: confined liquid dynamics and thermal effects in self-recovering nanobumpers. J. Phys. Chem. C 122, 14248–14256 (2018).
Tinti, A., Camisasca, G. & Giacomello, A. Structure and dynamics of water confined in cylindrical nanopores with varying hydrophobicity. Philos. Trans. R. Soc. A: Math., Phys. Eng. Sci. 379, 20200403 (2021).
Khay, I. et al. High pressure intrusion–extrusion of licl aqueous solutions in silicalite-1 zeolite: influence on energetic performances. J. Phys. Chem. C 118, 3935–3941 (2014).
Camisasca, G., Tinti, A. & Giacomello, A. Gas-induced drying of nanopores. J. Phys. Chem. Lett. 11, 9171–9177 (2020).
Ryzhikov, A., Nouali, H., Daou, T. & Patarin, J. A drastic influence of the anion nature and concentration on high pressure intrusion–extrusion of electrolyte solutions in silicalite-1. Phys. Chem. Chem. Phys. 20, 6462–6468 (2018).
Confalonieri, G., Daou, T. J., Nouali, H., Arletti, R. & Ryzhikov, A. Energetic performance of pure silica zeolites under high-pressure intrusion of licl aqueous solutions: an overview. Molecules 25, 2145 (2020).
Bushuev, Y. G., Grosu, Y., Chora̧żewski, M. A. & Meloni, S. Subnanometer topological tuning of the liquid intrusion/extrusion characteristics of hydrophobic micropores. Nano Lett. 22, 2164–2169 (2022).
Galarneau, A. et al. Pore-shape effects in determination of pore size of ordered mesoporous silicas by mercury intrusion. J. Phys. Chem. C 112, 12921–12927 (2008).
Amabili, M. et al. Pore morphology determines spontaneous liquid extrusion from nanopores. ACS Nano https://doi.org/10.1021/acsnano.8b07818 (2019).
Trzpit, M. et al. Zeolites and Related Materials: Trends, Targets, and Challenges, Proceedings of the 4th International FEZA Conference, 561–564 (Elsevier, 2008).
Bushuev, Y. G., Sastre, G., de Julián-Ortiz, J. V. & Gálvez, J. Water–hydrophobic zeolite systems. J. Phys. Chem. C 116, 24916–24929 (2012).
Grosu, Y. et al. Hierarchical macro-nanoporous metals for leakage-free high-thermal conductivity shape-stabilized phase change materials. Appl. Energy 269, 115088 (2020).
Choi, M., Heo, W., Kleitz, F. & Ryoo, R. Facile synthesis of high quality mesoporous SBA-15 with enhanced control of the porous network connectivity and wall thickness. Chem. Commun. 12, 1340–1341 (2003).
Grosu, Y. et al. A highly stable nonhysteretic {cu2 (tebpz) MOF–water} molecular spring. ChemPhysChem 17, 3359–3364 (2016).
Martin, T. et al. Dissipative water intrusion in hydrophobic MCM-41 type materials. Chem. Commun. https://doi.org/10.1039/b109081j (2001).
Bonella, S., Meloni, S. & Ciccotti, G. Theory and methods for rare events. Eur. Phys. J. B 85, 97 (2012).
Giacomello, A., Casciola, C. M., Grosu, Y. & Meloni, S. Liquid intrusion in and extrusion from non-wettable nanopores for technological applications. Eur. Phys. J. https://doi.org/10.1140/epjb/s10051-021-00170-3 (2021).
Tinti, A., Giacomello, A. & Casciola, C. M. Vapor nucleation paths in lyophobic nanopores. Eur. Phys. J. https://doi.org/10.1140/epje/i2018-11658-y (2018).
Maragliano, L. & Vanden-Eijnden, E. A temperature accelerated method for sampling free energy and determining reaction pathways in rare events simulations. Chem. Phys. Lett. 426, 168–175 (2006).
Lisi, E., Amabili, M., Meloni, S., Giacomello, A. & Casciola, C. M. Self-recovery superhydrophobic surfaces: modular design. ACS Nano 12, 359–367 (2017).
Cassie, A. & Baxter, S. Wettability of porous surfaces. Trans. Faraday Soc. 40, 546–551 (1944).
Giacomello, A., Schimmele, L., Dietrich, S. & Tasinkevych, M. Recovering superhydrophobicity in nanoscale and macroscale surface textures. Soft Matter 15, 7462–7471 (2019).
Muthachikavil, A. V., Peng, B., Kontogeorgis, G. M. & Liang, X. Distinguishing weak and strong hydrogen bonds in liquid water—a potential of mean force-based approach. J. Phys. Chem. B 125, 7187–7198 (2021).
Corma, A., Díaz-Cabañas, M. J., Jordá, J. L., Martínez, C. & Moliner, M. High-throughput synthesis and catalytic properties of a molecular sieve with 18- and 10-member rings. Nature 443, 842–845 (2006).
Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19 (1995).
Berendsen, H., Grigera, J. & Straatsma, T. The missing term in effective pair potentials. J. Phys. Chem. 91, 6269–6271 (1987).
Martyna, G. J., Klein, M. L. & Tuckerman, M. Nosé–hoover chains: the canonical ensemble via continuous dynamics. J. Chem. Phys. 97, 2635–2643 (1992).
Humphrey, W., Dalke, A. & Schulten, K. Vmd: visual molecular dynamics. J. Mol. Graph. 14, 33–38 (1996).
Acknowledgements
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No. 803213). This project has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No. 101017858. The authors acknowledge PRACE for awarding us access to Marconi100 at CINECA, Italy.
Author information
Authors and Affiliations
Contributions
A.Gubbiotti, S.M., and A.G. designed the study. G.P. performed simulations. G.P., A.Gubbiotti, and A.G. analyzed data and wrote the paper. S.M. and Y.G. contributed to the discussion, reviewed and edited the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communication Physcis thanks Guillaume Fraux and the other, anonymous, reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Paulo, G., Gubbiotti, A., Grosu, Y. et al. The impact of secondary channels on the wetting properties of interconnected hydrophobic nanopores. Commun Phys 6, 21 (2023). https://doi.org/10.1038/s42005-023-01140-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-023-01140-0
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.