Abstract
Multi-stability is a widely observed phenomenon in real complex networked systems, such as technological infrastructures, ecological systems, gene regulation, transportation and more. Thus, even if the system is at equilibrium in a normal functional state, there might exist also a potential stable state having abnormal activity, into which the system might transition due to an external perturbation. Such a system can be regarded as unsustainable, due to the danger of falling into the potential undesired abnormal state. Here we explore, analytically and via simulations, how supporting the activity of a small fraction of nodes can turn an unsustainable system to become sustainable by eliminating the undesired potential stable state. We unveil a sustaining phase diagram in the presence of a fraction of controlled nodes. This phase diagram could provide how many controlled nodes are required for sustaining a given network as well as how strong the connectivity of the network should be for a given fraction of controllable nodes.
Similar content being viewed by others
Introduction
Biological, social, or technological complex systems experience, in certain cases, catastrophic failure causing the collapse of the whole system functionality. For instance, overload failures in power systems1,2, species extinction in ecological networks3,4,5, traffic jams in a city6, and cell death in cellular dynamics7,8. Such collapses can be caused by structural damages, causing the networks to lose their connectivity9,10,11,12,13,14,15. However, some systems may lose their functionality despite they are still connected due to sparse connectivity and/or functional disturbances16,17,18,19,20,21,22,23,24,25,26,27. Once a system collapses, the question is how it responds to this situation. Two types of systems can be distinguished. Some systems recover on their own and go back to a normal functional state, while others remain in their abnormal nonactive state, and can be recovered only by external recovery. The former kind is considered “sustainable” systems since they are permanently active even after disturbances. The latter type, on the contrary, is considered “unsustainable” systems, since even though they are stable, yet in the presence of external perturbations, they collapse and do not return spontaneously to their original state. In fact, what makes the difference between these two types, is the bi-stability character of the dynamics21. If there is another stable state, nonfunctional, then once the system reaches this state it stays in this state. However, when the active state is the only stable state, there is no danger to fall into another stable state since there is no such one.
The effects of controlling nodes’ activity have been explored from several points of view, including controllability theory28,29,30, propagation patterns of small perturbations across the network31,32,33, and global effects on the system state34,35,36,37,38. A recent study39 has shown that for certain systems and under certain conditions controlling even a ‘single’ node can move the whole system to a desired natural active state of the system. This happens when the signal of control manages to propagate from shell to shell around the source single node as in a domino effect to create a “macroscopic” impact. However, for other systems or under different conditions, a microscopic intervention can make only a local “microscopic” effect as one would expect. When this is the situation, a macroscopic intervention is required for creating a global change. However, a basic question is whether the global change in the system state, resulted by a macroscopic control, is just quantitative or could be even qualitative, i.e. eliminating the lower state, and if so, what is the required fraction of controlled nodes to make it.
In this study, we aim to explore the question of transforming an unsustainable system into a sustainable system, by supporting the activity of a fraction of nodes. The intervention that we discuss is done by forcing a fraction ρ of controlled nodes to have a high value of activity Δ. We develop a framework to predict for a given network structure and for a given intervention (ruled by ρ and Δ) if the system becomes sustainable. By defining a parameter β25, that captures the connectivity of the network, we construct and present a phase diagram in the (β, ρ) space. From this phase diagram, for a given network with a certain β, we can determine what is the minimal (critical) fraction of nodes ρc that is needed for sustaining the network. From a different point of view, we can determine as well, for a given fraction accessible to control (ρ), how strongly connected the network should be for becoming sustainable. We find that by controlling a small fraction of nodes, we enlarge considerably the “sustainable phase” compared to controlling a single node39. We further present a theory that bridges the two limits of macroscopic and microscopic sets of forced nodes, covering both extremes as well as the range in between. We demonstrate and apply our framework to three dynamic processes, cellular, neuronal, and spin dynamics, showing its generality. However, different systems show remarkably varying sustaining phase diagrams.
Results
Unsustainable networks
To find the conditions for which a network is unsustainable, we first analyze the dynamics of a free system without external intervention. We rely upon a general framework31,32,33 to model nonlinear dynamics on networks. Consider a system consisting of N components (nodes) whose activities xi (i = 1, 2, . . . , N) follow the Barzel–Barabási31 equation,
The first function, M0(xi), captures node i’s self-dynamics, describing mechanisms such as protein degradation40 (cellular), individual recovery41,42 (epidemic), or birth/death processes43 (population dynamics). The product M1(xi)M2(xj) describes the i, j interaction mechanism, representing e.g., genetic activation7,44,45, infection41,42, or symbiosis46. The binary adjacency matrix A captures the network, i.e., the interactions (links) between the nodes. An element Aij equals 1 if there is an interaction (link) between nodes i and j and 0 otherwise. The matrix A is symmetric and obeys the configuration model characteristics. The strength of the interactions is governed by the positive parameter λ.
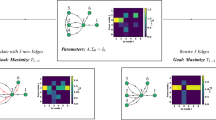
In Fig. 1, we demonstrate our problem on the example of gene regulation dynamics, which is explored and presented in detail below. For weak connectivity, expressed by low interaction strength or small density of links, there exists only the low-active state where all genes are suppressed, Fig. 1a, b, while for strong connectivity, there emerges an additional high-active state. However, the low-active state still exists, Fig. 1d, e, which allows the risk of collapsing from functionality into non-functionality as a result of some disturbances, see Fig. 1f. Therefore, such an active state is called unsustainable due to the potential failure into the inactive state. In this study, we show how supporting a small fraction of the system nodes (Fig. 1g, h, dark blue) eliminates the nonfunctional state and, as such, makes the system sustainable to perturbations, Fig. 1i.
a Diagram of regulatory dynamics showing two states, inactive x0 and active x1. For weak connectivity, only x0 exists, thus the system resides in the inactive phase. b For weak connectivity, there is no active stable state (cyan, very light), but just the inactive state (red). The vertical (z) coordinate represents the activity of each node. c Adding random perturbations (noise) to the activities does not help to activate the network since a functional stable state does not exist, thus the average activity stays low all the time. d For dense connectivity, both states are stable, such that there exists a bi-stable region (gray shade). e A system located in the bi-stable regime, demonstrates two stable states, active (cyan) and suppressed (red). Thus, x1 is unsustainable in this region since the inactive state x0 also exists. f An implication of the bi-stability is that adding random perturbations (noise) to the activities, results in spontaneous system transitions between the active (cyan) and inactive states (pink) since both are stable in the unsustainable phase. Here, as in (c) and (i), the noise was taken, for simplicity, to be discrete, since it is efficient enough for exposing if the system is sustainable. Stochasticity is a fundamental feature of gene expression appearing by randomness in transcription and translation56,57, thus adding a noise here reflects a realistic phenomenon. g, h Here, we consider the same system as in (d), but we control a fraction of the system (dark blue circles), ρ, and hold it with a constant high value, Δ. Due to this intervention, the low-functional state vanishes which makes the system sustainable. i When we control a fraction of nodes with high activity, perturbations such as those in (f) are not capable to deflect the system from the active state, since the inactive state disappears. Namely, the control makes the system sustainable.
Sustaining a network
To drive an unsustainable network to be sustainable, we consider a simple intervention. We force a set of nodes \({{{{{{{\mathcal{F}}}}}}}}\) (fraction ρ) to have a constant high activity value Δ (Fig. 1h), while all the rest in the complementary set \({{{{{{{\mathcal{D}}}}}}}}\) are governed by the original dynamics. Thus, such a forced system obeys the set of equations,
While in some systems, such a simple intervention is being a technical challenge, yet we consider this as a prototype case from which we can deduce others. For instance, if a constant control height of Δ works, then we can just keep the activity of the controlled nodes higher than Δ or equal, to sustain the system. Other interventions, such as adding flux, could be equivalently translated to holding the node’s activity with the new stable value caused by the flux. If we return to the above example of gene regulation, manipulation of gene expression is a common practice, e.g., using light47.
Next, we aim to track the states of the unforced nodes, i.e., the set \({{{{{{{\mathcal{D}}}}}}}}\). For finding the steady states of the forced system, we demand a relaxation, thus the derivative vanishes. In addition, we use a degree-based mean-field approximation42,48,49,50,51 assuming nodes having the same degree behave similarly. Thus, we replace the binary term Aij with the probability of link existence between i and j in the configuration model, kikj/(N〈k〉) where ki and kj are the degrees of i and j, respectively. Considering this, we define (see elaboration in the Section Methods) the order parameter Θ as
which represents the mean impact that an arbitrary free node gets from its arbitrary free neighbor. The variable \({x}_{j}^{* }\) stands for the activity of node j in relaxation, and \({{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{D}}}}}}}}\) means to count only links within \({{{{{{{\mathcal{D}}}}}}}}\), i.e., the unforced nodes. Using the defined Θ, and applying the mean-field approximation in Eq. (2) in relaxation, we obtain,
where R(x) = −M0(x)/M1(x), and \({k}_{i}^{{{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{F}}}}}}}}}\) is the number of forced neighbors (in \({{{{{{{\mathcal{F}}}}}}}}\)) of node i which is a free dynamic node (in \({{{{{{{\mathcal{D}}}}}}}}\)). Substituting this in the definition of Θ, we obtain a self-consistent equation for the order parameter,
where R−1 is the inverse function of R. This step assumes that R is an invertible function. Solving the self-consistent Eq. (5), we get all the states (both stable and unstable) of the system. This equation can be solved using any degree distribution and the specific selection of the nodes in \({{{{{{{\mathcal{F}}}}}}}}\) (see Section Methods).
To obtain, besides Eq. (5), more intuitive, simple, and useful expressions, we assume the following additional approximation based on a common mean-field (MF) approach. When the degree distribution is not very broad and/or the functions M2 and R are close to linear or constant, we insert the average into the functions25, i.e., \(\overline{{M}_{2}({{{{{{{\bf{x}}}}}}}})}={M}_{2}(\bar{{{{{{{{\bf{x}}}}}}}}})\) and \(\overline{R({{{{{{{\bf{x}}}}}}}})}=R(\bar{{{{{{{{\bf{x}}}}}}}}})\), to get an approximation for the leading order, see also the Section Methods. This allows us, using Eqs. (3) and (4), to obtain a very simple relation between the average steady state \(\bar{{{{{{{{\bf{x}}}}}}}}}\) of the free nodes and the connectivity β of the network for a given control characterized by ρ and Δ. We define the average activity \(\bar{{{{{{{{\bf{x}}}}}}}}}\) over all the neighbors within \({{{{{{{\mathcal{D}}}}}}}}\) by
and the connectivity β is defined as
combining both the interactions strength λ and the average neighbor degree over the whole network, κ = 〈k2〉/〈k〉. Using these terms, we finally obtain a simple equation for the states of a forced system, for κ ≫ 1 and random selection of the forced nodes,
where \(\rho =| {{{{{{{\mathcal{F}}}}}}}}| /N\) is the fraction of the controlled nodes. To get the free system states, we can just substitute ρ = 0, yielding \(\beta =R(\bar{{{{{{{{\bf{x}}}}}}}}})/{M}_{2}(\bar{{{{{{{{\bf{x}}}}}}}}})\). (For non-random selection of the forced nodes, but rather a degree-dependent selection, see Supplementary Note 2.)
Eq. (8) implies that forcing a fraction ρ of nodes to have an xi-value Δ changes the phase diagram of the system and creates a new phase diagram for a forced system. To demonstrate this change in the phase diagram, we go back to our main example of gene regulation. Applying the general equation in Fig. 2a to gene regulation yields that the free system, Fig. 2b, exhibits two regimes: an inactive state for weak connectivity, and a bi-stable regime (gray shade) above a certain β. In marked contrast, a forced system shows a remarkably different phase diagram, Fig. 2c, exhibiting three regimes: inactive for small β, bi-stability for intermediate β, and above a certain value of β only an active state. Neuronal and spin dynamics, Fig. 2d–g, have distinct phase diagrams which change as well by controlling a fraction of the system.
a The relation, Eq. (8), between the system state (〈x〉) and its connectivity (β) provides the phase diagrams of both free (ρ = 0) and controlled (ρ > 0) systems for any dynamics. Here we demonstrate this for three distinct systems. b, c Cellular dynamics. b A free system diagram shows a suppressed function at x0 for small β, and a bi-stable regime for large β, where x0 and x1 both exist and are stable. Thus the system is unsustainable and has a risk to fail into a nonfunctional state. c In contrast, a forced system, controlled by holding a fraction ρ of nodes with high-value Δ, shows a new phase diagram, having an s-shape curve, with a new region for large β in which only x1 appears (blue). Thus, a system in the blue region is now safe and not only active, but also sustainable. d, e Brain dynamics. d A free system exhibits three regimes: inactive for sparse topology, active for dense topology, and bi-stable in between. e Forcing the system with certain Δ and ρ pushes the twist of the s-shape to a lower β-value, and as such, makes the blue regime becoming sustainable rather than bi-stable. f, g Spin dynamics. f A free system has a zero inactive stable state for sparse connectivity, while for dense connectivity, there are two symmetric active states. g Controlled system shows a new phase diagram including a sustainable regime where only the positive stable state appears (blue shade). This dynamics does not fall into the formula in (a), however, a similar analysis can be done, see Supplementary Note 4 Section 4.3.
In all these three examples, a free system located at the high-active state within the bi-stable area (gray shade), is regarded as unsustainable. This is because there exists a potential inactive state. However, controlling a fraction ρ of nodes with high activity Δ, reshapes the phase diagram and creates an area (blue shade), in which the system becomes safer, that is, with no risk of failure into the low state. Hence the system becomes sustainable.
Application: cellular dynamics
As our main example in this paper, we apply our framework on the regulatory dynamics, captured according to Michaelis–Menten model44, by
Under this framework, \({M}_{0}({x}_{i})=-B{x}_{i}^{a}\), describing degradation (a = 1), dimerization (a = 2) or a more complex bio-chemical depletion process (fractional a), occurring at a rate B; without loss of generality, we set here B = 1. The activation interaction is captured by the Hill function of the form M1(xi) = 1, \({M}_{2}({x}_{j})={x}_{j}^{h}/(1+{x}_{j}^{h})\), a switch-like function that saturates to M2(xj) → 1 for large xj, representing j’s positive, albeit bounded, contribution to node i activity, xi(t).
When analyzing this system while it is forced by a fraction ρ of random nodes with activity Δ, we obtain, using Eq. (8),
In Fig. 3, we present in detail the results for cellular dynamics using simulations and theory when setting a = 1, h = 2. The phase diagram of a free system, derived from Eq. (10) by substituting ρ = 0, is shown in Fig. 3b. Note that \(\bar{{{{{{{{\bf{x}}}}}}}}}=0\) is a stable state of the free system, which is not obtained by substituting ρ = 0 in Eq. (10) but from the MF equation, see Supplementary Note 1. However, it can be obtained also from Eq. (10) by taking the limit ρ → 0. As explained above, the high-active state x1 is unsustainable for the full range, as demonstrated in Fig. 3c. Eq. (10) generates also the phase diagram for a forced system shown in Fig. 3d (thick curve) for ρ = 0.03 and Δ = 5, exhibiting an s-shape diagram which has now also a new only-active regime (blue shade). This regime is in the sustainable phase. In Fig. 3f, we demonstrate the forced system states in the three distinct regimes, and show that for β = 3.1, the external intervention makes the system sustainable rather than unsustainable in Fig. 3c. The implication of the low state disappearance is demonstrated in Fig. 1f, i, where the supported system is sustainable for large random perturbations in contrast to the uncontrolled unsustainable system. Note that the control also increases the level of the high state, x1, but this effect is minor. The s-shape, Fig. 3d, unveils a critical value of β = βc above which the system is sustainable. This βc depends on ρ, and this relation holds in the inverse direction as well, namely, for given β there is a required critical fraction ρc of controlled nodes to make a system sustainable. Therefore, we move to find the relation between the critical values of ρ and β at the transitions from the bi-stable region to both the sustainable phase, as well as the inactive region. As can be seen in Fig. 3d, both transitions are local extremum of \(\beta (\bar{{{{{{{{\bf{x}}}}}}}}})\), and hence they are found using Eq. (8) by
Eq. (11) provides βc as a function of both the fraction ρ and the force of control Δ. Using Eq. (10) we get βc or ρc for cellular dynamics. For gene regulation, the solution is not trivial (see Methods), however, in the limit of small ρ, when we get a small value of \(\bar{{{{{{{{\bf{x}}}}}}}}}\) at the transition, as in Fig. 3d, we obtain the scaling relation,
Indeed, in our simulations, for the values, a = 1, h = 2, we obtain, in Fig. 3k, ρc ~ β−2, where β = λκ. We discuss this result further below.
a We apply our framework to the regulatory dynamics captured by Michaelis–Menten model44. b Simulations (symbols) and theory (lines, Eq. (10) with ρ = 0) results for a free system of Erdős-Rényi (ER) structure with N = 104 and κ = 40 and for the parameters’ values a = 1 and h = 2. There is a bi-stable region (gray shade). In case that a ≥ h, there is no bi-stability38, thus here, we consider h > a to analyze system sustaining. c Demonstration of the activities of the system with β = 3.1 for ρ = 0. Both states are stable, therefore the system is unsustainable. d For a forced system by a fraction ρ = 0.03 of random nodes with activity Δ = 5, Eq. (8) provides a phase diagram (thick curve), exhibiting an s-shape curve which has now also a regime with only a single active state (blue shade). This regime is a sustainable phase. Note that simulations (symbols) are in agreement with the theory (lines). The network is the same as in (b). e The same as (d) with a larger fraction of controlled nodes, ρ = 0.11. Here we see that the unsustainable region almost vanishes, and the transition becomes almost continuous. This agrees with Eq. (14). f Activities for β = 1.5, 2.5, 3.1 in three regions, inactive (red diamond), unsustainable (cyan circle), and sustainable (blue triangle) correspondingly. The dark blue nodes are the forced nodes. The red nodes represent x0, the cyan nodes represent unsustainable x1, and the light blue nodes represent sustainable x1. g The new phase diagram in (β, ρ)-space for Δ = 5. The simulations were done on ER networks with N = 104 for 50 values of ρ, 50 values of β, for κ = 20, 60, 100, and averaged over ten realizations. In the color bar, the value 0 represents an unsustainable system, and 1 represents the other cases. The black lines are obtained from Eqs. (10) and (11). h The same as (g) with lower intervention force Δ = 1. As expected, in this case, a larger fraction of controlled nodes is needed to make the network sustainable. i (κ, λ)-space for a free system. j The sustaining phase diagram for ρ = 0.01 and Δ = 5. The light blue is the sustainable phase when forcing a fraction ρ = 0.01 of nodes, and the dark blue is the sustainable regime for holding a single node. The white lines represent the theory, Eqs. (10) and (11). k Horizontal trajectory in (κ, λ)-space for fixed λ = 0.1 and varying κ. Symbols are simulations and the line is theory obtained from Eqs. (10) and (11). The slope is according to Eq. (12). l Vertical trajectory in (κ, λ)-space for fixed κ = 20, 100 and varying λ. Note that the critical fraction for sustaining, ρc, for a given λ approaches 0, where it reaches the single-node sustainable phase in simulations (symbols). The theory, Eqs. (10) and (11) (continuous lines), deviate from the simulation results for small ρ. The dashed lines are from a different theory, see Supplementary Note 3, which captures also the limit of small ρ.
Figure 3e shows similar results as 3d for a larger fraction of controlled nodes, ρ = 0.11. One can see that for this value of ρ, the bi-stable area almost completely disappears. This suggests another critical fraction ρ0, above which the active state of the system becomes sustainable for any β. To find this ρ0, we notice that it captures a merge of local maximum and minimum, thus besides Eq. (11), also the second derivative should vanish,
These two conditions, Eqs. (11) and (13), together determine a tricritical point (β0, ρ0) in the (β, ρ)-space at which the three phases: inactive, unsustainable, and sustainable meet, and beyond which the system will not experience an abrupt transition at all, see Fig. 3g.
For the cellular dynamics, we find that (see Methods),
which for our values a = 1, h = 2, and for a large Δ, is equal approximately to 1/9, while using Δ = 1, it gets a higher value of 1/5, see Fig. 3g, h.
In Fig. 3g, h, we present the new sustaining phase diagram in (β, ρ)-space for networks with κ = 20, 60, 100 showing a good agreement between simulations and theory, Eqs. (10) and (11). Note that, as expected, for larger κ, the theory agrees better with the simulations. Furthermore, one can see that the tricritical point is in agreement with Eq. (14), and gets higher for smaller Δ, Fig. 3h. The symbols in Fig. 3g refer to the demonstrations in Fig. 3f exhibiting the system state in each region.
Next, we split the merged connectivity β and move to look at the 3D space (κ, λ, ρ), particularly on the (κ, λ)-space. This is since we want to test the system behavior also for low degrees, and thus we decouple β into two parameters κ and λ, Eq. (7). Moreover, we want to generalize the phase diagram to include the single-node reviving model39, where under certain conditions controlling one node revives the whole system into its high-active state. When it works, it also makes the system sustainable since it cancels the low-active state. Figure 3i shows the phase diagram of a free system with two areas as above in Fig. 3b. In Fig. 3j, we show the combined single-node reviving (dark blue), and fraction-reviving with ρ = 0.01 (light blue). The control of a small fraction of the system considerably extends the sustainable phase. The white lines represent the results of our theory, calculated via βc using Eqs. (10) and (11). Note that the theory works well for high κ while deviates for small values. The reason is the nature of the mean-field approximation, which works usually quantitatively only for a large degree. The reason is that if nodes have more neighbors, then different neighborhoods are more similar, as assumed by the mean-field theory.
In Fig. 3k, we cross the (κ, λ)-space horizontally for fixed λ = 0.1 while changing κ. Symbols represent simulations and the line represents the theory, obtained by Eqs. (10) and (11). This supports the scaling obtained in Eq. (12)ρc ~ β−2. See Fig. S3 for other values of a and h. It can be seen that for very small ρ there is an increasing deviation even though κ is large. This slight discrepancy becomes larger in Fig. 3l, where we move vertically with λ for fixed κ = 20 and κ = 100. Here the deviation of the theory (continuous line) for small ρ is significant. However, it gets better for larger degrees, as expected. This gap exposes the contradiction between our MF and simulations regarding the limit of ρ → 0, as discussed below.
The limit ρ → 0
Our MF theory, by definition, yields that ρ → 0 derives βc → ∞ as in a free system without intervention at all. However, it has been shown39 that for large enough λ even a single node impacts the network globally. The reason that our MF fails for very small ρ and not very large degree (see the continuous lines in Fig. 3l) is that when there are only one or few controlled nodes, the uniformity or homogeneity assumption of different nodes in the network, upon which the MF relies, is broken. The network gets a structure of shells around the few controlled nodes, as analyzed in ref. 39. Therefore, we developed here a modified shells MF which includes also the case of many controlled nodes rather than only one. This method bridges the microscopic and macroscopic intervention limits. It involves a combination of analytical and computational parts to cover both edges as well as the between range. A full analytical solution is still to be obtained. See Supplementary Note 3 for details. The dashed lines in Fig. 3l are obtained from this improved method, showing excellent agreement with simulations, thus, covering both extremes.
Large fluctuations
Another challenge for our MF theory is large fluctuations. This is when the network has a small average degree, but particularly for scale-free (SF) networks which exhibit a broad degree distribution, which represents large variations in node degrees. For these cases, though our MF approach predicts the transitions qualitatively, it has some deviation regarding the location of the critical points. To overcome the challenge of such networks, we step back in our theory derivations to Eq. (5), and use the order parameter Θ, Eq. (3), to determine the system states. This method does not assume the general parameter β = λκ, and even not the global parameter κ. But the analysis and solution depend on λ and on the full degree-distribution pk, Eq. (5). In Fig. 4, we present the advantage of this method compared to the above method, represented by Eq. (8). Figure 4a shows the very good agreement between simulations and theory, Eq. (5) for a scale-free network with γ = 3.5 and k0 = 15. In Fig. 4b, we present the (β, ρ) phase diagram for the same scale-free network as in Fig. 4a. The continuous lines represent the theory of Eq. (5), showing excellent agreement with the simulations results, while the dashed lines representing Eq. (8) fail. The SF’s phase diagram implies the higher susceptibility of SF to become sustainable compared to Erdős–Rényi (ER). For example, as seen in Fig. 4c and b, ρ0 that ensures the absence of the unsustainable phase is about 0.1 in ER while it is only about 0.03 in the presented SF. SF networks with smaller γ, or smaller k0, show some deviations from theory also for Eq. (5), see Fig. S4. Finally, we show in Fig. 4c that also in ER with a not very large degree, κ = 10, Eq. (5) supplies a significantly better accuracy (full line) compared to Eq. (8) (dashed line).
Results for scale-free (SF) networks and Erdős-Rényi (ER) with low degrees which have large fluctuations, and thus demand analysis using Eq. (5) rather than Eq. (8). a The order parameter Θ, Eq. (3), for a forced system with ρ = 0.015 and Δ = 5. The network here is scale-free with N = 104, minimal degree k0 = 15, and exponent γ = 3.5. The symbols are from simulations and the line is from theory, Eq. (5). b For the same network as in (a), the (λ, ρ) phase diagram shows a significantly narrower unsustainable regime compared to ER. The black continuous lines are from Eq. (5), while the dashed lines are from Eq. (8), which captures well ER networks but fails to predict SF. c Results for ER network with κ = 10, which is a smaller degree than in Fig. 3g. Also, here, the theory of Eq. (5) (full line) is better than Eq. (8) (dashed line).
Additional examples
Next, we consider other two types of dynamics to exhibit aspects that do not appear in the cellular dynamics as well as to demonstrate the generality of our framework.
Neuronal dynamics
As our second example, we consider neuronal dynamics governed by the set of equations given in Fig. 5a, based on a modification of the Wilson–Cowan model52,53, see Supplementary Note 4 Section 4.2. As can be seen in Fig. 5b (thin light lines), the system naturally exhibits an s-shape curve, including three dynamic phases. The inactive phase for small β, where there exists only the state x0, in which all activities are suppressed. The region of high β, where there exists only x1, in which the activities xi are relatively high. Thus, for high β, the system is “naturally sustainable”. In between these two extremes, the system features a bi-stable phase, in which both x0 and x1 are potentially stable, therefore the active state in this region is unsustainable. However, controlling a fraction of ρ = 0.02 with the activity of Δ = 15, creates a new s-shape curve with a more narrow bi-stable region (thick lines and symbols). Thus, a window of sustaining (blue shade) is created, in which the control drives the system to be sustainable. In Fig. 5c, we observe, in (κ, λ)-space, for ρ = 0.02, additionally to the three phases found for gene regulation (Fig. 3j), the naturally sustainable phase where the system is sustainable on its own without any intervention. Note also that our theory, Eqs. (8) and (11), predict the required λc to sustain the system given ρ = 0.02 for high degrees (white line). Figure 5d shows the (β, ρ) phase diagram for κ = 20, 60, 100.
a Neuronal dynamics based on Wilson–Cowan model52,53. b Phase diagram for dynamics of the forced system via fraction ρ = 0.02 and holding value Δ = 15 according to Eq. (8). The network is Erdős-Rényi (ER) with N = 104 and κ = 40. The forced curve is shifted left relative to the free system curve (thin and light lines), yielding a window of sustaining (blue shade) (c) (κ, λ)-space shows a sustaining phase diagram containing five phases. Our theory, Eqs. (8) and (11), predicts for high degrees well the transition between unsustainable and sustainable by fraction ρ = 0.02 and Δ = 15 (the white line). The light blue area is the sustainable phase for controlling a fraction ρ = 0.02, and the dark blue phase is the sustainable region when controlling a single node. d (β, ρ) phase diagram for κ = 20, 60, 100. e Model for spin dynamics based on Ising-Glauber model54. f While the free system (light and thin lines) shows a diagram with a zero regime and bi-stable symmetric regime, the forced system (thick lines) exhibits two regions: for a dense network (large β) coexistence of x0 and x1, and for a sparse network (small β) only x1 appears. Consequently, there is a range of sustaining (blue shade). Here ρ = 0.1 and Δ = 1. The network is ER with N = 104 and κ = 40. g The (κ, λ) phase diagram for ρ = 0.1 and Δ = 1. Here there is no sustainable phase when holding a single node since controlling a single node does not change the global system states in this dynamics. The simulations were averaged over 10 realizations of ER networks with N = 104. The white line represents the theory of Eq. (S4.41) in Supplementary Note 4 with Eq. (11). h The (β, ρ) phase diagram for fixed Δ = 1. Color represents simulations on ER with κ = 20, 60, 100 and N = 104. The results were averaged over ten realizations. The black line stands for the theory of Eq. (S4.41) in Supplementary Note 4 with Eq. (11).
Spin dynamics
As our final example, we explore the dynamics of spins connected by ferromagnetic interactions, captured by the equations of Fig. 5e, which are based on Ising-Glauber model54. This example is different from the two above examples since the interactions in this dynamics are “attractive” rather than “corroborative”. Moreover, the interactions act completely symmetrically towards both stable states in contrast to the above examples, where they only push toward the high-active state. In addition, the form of equations is not included in our framework, Eq. (1), however, a similar analysis holds for this dynamics, see Supplementary Note 4 Section 4.3.
Figure 5f shows the significant change in the phase diagram of the free system (thin lines) due to the controlled nodes (thick lines) with a fraction ρ = 0.1 having activity Δ = 1. In contrary to the symmetric states of a free system (thin and light lines), the forced system shows a region (blue shade) where x1 is sustainable. Note that this area is obtained for weak connectivity (small β) differently from the above examples. This is an outcome of the attractive nature of the interactions, since it causes competition between the controlled nodes, which pull up, and the free nodes, which pull down. The free nodes have a numerical advantage, however for small β, the natural negative solution is small (in absolute value), and for large enough Δ, the forced nodes win. In Fig. 5g, we show the phase diagram in (κ, λ) space as above. For spin dynamics, the phase of sustainability by a single node does not exist, due to the symmetric attractive interactions. The reason is that when the external signal propagates from the source node through neighbors, they have, on average, only one neighbor behind that pulls them up and more than one neighbor that pulls them down. Because of the symmetry between states, the numerical advantage wins. Thus, even if the intervention force Δ is high, its impact decays with distance and makes only a local impact in an infinite system. Figure 5h shows the (β, ρ) phase diagram, which has a different shape compared to the above examples as explained above. Note also that in this case, there is no tricritical point.
Discussion
In this paper, we study how dynamics that take place on a complex network is affected by dynamic interventions. Although a very broad knowledge has been accumulated on the structure of complex networks, the knowledge on dynamics evolving on complex networks is still being discovered. Our study deals with the goal of understanding the ways of influencing network dynamics via controlling a fraction of nodes.
We investigate the effect of a simple control of the system, i.e., forcing a fraction of nodes, ρ, to have a desired activity, xi = Δ. We show that such a simple intervention, even for small ρ and not large Δ, could have a crucial impact on the system’s dynamic behavior. We find that the control of a fraction of nodes, does not just pull up or down somewhat the natural states of the system, but under certain conditions, eliminates some of the potential system states. We show that this elimination of states can transform a functional but unsustainable system to become sustainable. This is because eliminating a potentially dysfunctional state by control removes the danger of a transition into a potentially undesired inactive state. We developed a general framework, applied to three kinds of dynamics, (i) cellular, (ii) neuronal, and (iii) spins dynamics, revealing the phase diagram of a controlled system, by which we can predict, for instance, the minimal fraction of nodes required to make the system sustainable.
Differently from “control theory” of complex networks29, which explores the ability to move a system into any desired state within a certain continuous volume, here we do not aim to move the system at all, but to eliminate a potential undesired inactive state of the system, and by this, the system stays in its natural stable active state, an easier mission allowing our analytical analysis. However, our framework is able to capture a global change in the system’s phase diagram, while the control theory of nonlinear dynamics on complex networks usually provides only local information29 rather than global.
Our fundamental and primary analysis of the impact of a simple intervention on network dynamics opens the door to future studies. For instance, one could explore other and more complex and/or realistic interventions, such as the non-random spread of controlled nodes, e.g. localized selection, or such as a different control, e.g., supplying some flux, constant or dynamic, into the controlled nodes instead of just forcing their activities to be constant as we considered here.
An additional natural generalization of this work is extending the scope governed by Eq. (1), since there is a variety of dynamics that show different patterns, e.g., a diffusive interaction, xj − xi, rather than multiplication as considered in Eq. (1).
Note also that networks with very broad degree distribution, such as scale-free networks with exponent lower than 3, or networks with a very low degree, challenge the quantitative accuracy of our theory, see Fig. 3a for low κ, and Fig. S4 for SF with γ = 2.5. These challenges demand further research.
Finally, it is worth noting that controlling a very small fraction of nodes can sustain a very large network. This is somewhat analogous to the static structural problem of percolation of interdependent networks, where a small fraction of reinforced nodes can significantly increase the robustness of the system55.
Methods
Forced system analysis
In this Section, we analyze the states of a forced system. For an analysis of a free system without control, see Supplementary Note 1.
To follow the impact of such a control as in Eq. (2), and testing if it makes the system sustainable, we analyze Eq. (2) for finding the system’s states while it is forced. The dynamics of the free nodes (\(i\in {{{{{{{\mathcal{D}}}}}}}}\)), according to Eq. (2), is
which by separating the sum between neighbors in \({{{{{{{\mathcal{D}}}}}}}}\) and neighbors in \({{{{{{{\mathcal{F}}}}}}}}\) turns to
To find the steady states of the system, we demand a relaxation, thus the derivative vanishes,
where \({x}_{i}^{* }\) represents the relaxation activity value of node i, and \({k}_{i}^{{{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{F}}}}}}}}}\) denotes the number of neighbors in \({{{{{{{\mathcal{F}}}}}}}}\) of the node i which is in \({{{{{{{\mathcal{D}}}}}}}}\). Arranging the terms, we obtain
where
Next, we apply the degree-based mean-field approximation42,48,49,50,51, replacing the binary value, Aij, by the probability of \(i\in {{{{{{{\mathcal{D}}}}}}}}\) and \(j\in {{{{{{{\mathcal{D}}}}}}}}\) to be connected given their degrees, which is \({k}_{i}^{{{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{D}}}}}}}}}{k}_{j}^{{{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{D}}}}}}}}}/(| {{{{{{{\mathcal{D}}}}}}}}| \langle {k}_{{{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{D}}}}}}}}}\rangle )\) because of the configuration model structure. This gives
Note that now the sum does not depend on i, hence we can write
by defining the order parameter,
which is the average impact of a node in \({{{{{{{\mathcal{D}}}}}}}}\) (free node) on a node in \({{{{{{{\mathcal{D}}}}}}}}\). Using Eqs. (21) and (22), we obtain a single self-consistent equation for the order parameter Θ,
which is Eq. (5) above. To solve this equation, we should replace the summation on nodes in \({{{{{{{\mathcal{D}}}}}}}}\) by some theoretically calculable term without need to measure nodes degree. Thus, we look for different expressions by writing Eq. (23) as
Averaging over all the possibilities of the pair \({k}^{{{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{D}}}}}}}}}\) and \({k}^{{{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{F}}}}}}}}}\), it gets the form
where \(\Pr ({k}_{j}^{{{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{D}}}}}}}}}=k,{k}_{j}^{{{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{F}}}}}}}}}={k}^{{\prime} })\) is the joint probability that node \(j\in {{{{{{{\mathcal{D}}}}}}}}\) has k neighbors in \({{{{{{{\mathcal{D}}}}}}}}\) (free nodes) and \({k}^{{\prime} }\) neighbors in \({{{{{{{\mathcal{F}}}}}}}}\) (forced nodes). This joint probability is determined by the degree distribution pk and the way of selection of the forced nodes (\({{{{{{{\mathcal{F}}}}}}}}\)). Next, instead of running over \((k,{k}^{{\prime} })\) (which are \({k}^{{{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{D}}}}}}}}}\) and \({k}^{{{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{F}}}}}}}}}\) respectively), we run over (k0, k) where here \({k}_{0}={k}^{{{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{V}}}}}}}}}\) is the degree of a free node, where \({{{{{{{\mathcal{V}}}}}}}}\) is the set of all nodes, and \(k={k}^{{{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{D}}}}}}}}}\) is the number of the free neighbors of a free node. Of course, for each node \({k}^{{\prime} }={k}_{0}-k\), that is \({k}_{i}^{{{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{F}}}}}}}}}={k}_{i}^{{{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{V}}}}}}}}}-{k}_{i}^{{{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{D}}}}}}}}}\). Performing this change of indexes, we obtain
and substituting Pr(k, k0) = Pr(k0)Pr(k∣k0) yields
The terms \(\langle {k}_{{{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{D}}}}}}}}}\rangle\), Pr(k0), and Pr(k∣k0) depend on the way of selection of the forced nodes besides the degree distribution pk. For now, we consider a completely random selection of controlled nodes. In this case, \(\Pr ({k}_{0})={p}_{{k}_{0}}\) (the degree distribution of the network) because \({{{{{{{\mathcal{D}}}}}}}}\) is random and therefore has the same degree distribution pk as the whole network \({{{{{{{\mathcal{V}}}}}}}}\). The probability that a neighbor is in \({{{{{{{\mathcal{F}}}}}}}}\) is ρ, thus \(\langle {k}_{{{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{D}}}}}}}}}\rangle =\langle {k}_{{{{{{{{\mathcal{V}}}}}}}}\to {{{{{{{\mathcal{D}}}}}}}}}\rangle =\langle k\rangle (1-\rho )\) as an average of binomial distribution, and \(\Pr (k| {k}_{0})=\left({{k}_{0}\atop {k}}\right){(1-\rho )}^{k}{\rho }^{{k}_{0}-k}\), binomial distributed. Substituting these, we finally obtain for a random selection of controlled nodes,
where \({p}_{{k}_{0}}\) is the degree distribution and 〈k〉 is the mean degree. This self-consistent equation is solvable theoretically based on the degree distribution. We use Eq. (28) to plot the theoretical lines in Fig. 4.
Small fluctuations MF
To get a simpler and informative equation, we apply another mean-field (MF) approximation25 that works well for small fluctuations, as shown in Figs. 3,5. According to this MF, we insert the average in Eq. (22) into the function M2(x), to obtain
where the average activity of the unforced nodes, \(\bar{{{{{{{{\bf{x}}}}}}}}}\), is defined by
Operating this average on Eq. (21) and using the MF approximation, we get
where
are the average degrees into \({{{{{{{\mathcal{D}}}}}}}}\) and into \({{{{{{{\mathcal{F}}}}}}}}\) respectively of node approached by link within \({{{{{{{\mathcal{D}}}}}}}}\). Substituting Eq. (29) into Eq. (31) we obtain an equation for the activity of a forced system,
The quantities \({\kappa }_{{{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{D}}}}}}}}}\) and \({\kappa }_{{{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{F}}}}}}}}}\) depend of course on the way of selecting the set \({{{{{{{\mathcal{F}}}}}}}}\) of controlled nodes. For now, we assume for simplicity that \({{{{{{{\mathcal{F}}}}}}}}\) is selected completely randomly, and find these quantities for this case. In Supplementary Note 2 we analyze the general case.
Random selection
Selecting the set of controlled nodes \({{{{{{{\mathcal{F}}}}}}}}\) randomly determines that the degree distribution of the controlled nodes, \({{{{{{{\mathcal{F}}}}}}}}\), the free nodes \({{{{{{{\mathcal{D}}}}}}}}\), and all of the nodes \({{{{{{{\mathcal{V}}}}}}}}\), are the same, pk. This allows us to analyze the quantities in Eq. (32), appearing in Eq. (33), since we can replace the average over subset of the network (\({{{{{{{\mathcal{F}}}}}}}}\) or \({{{{{{{\mathcal{D}}}}}}}}\)) by an average over all the network \({{{{{{{\mathcal{V}}}}}}}}\). Considering that an arbitrary node in \({{{{{{{\mathcal{V}}}}}}}}\) belongs to \({{{{{{{\mathcal{F}}}}}}}}\) with likelihood ρ, we obtain, using Wald’s identity,
For the second moment \(\langle {k}_{{{{{{{{\mathcal{D}}}}}}}}\to {{{{{{{\mathcal{D}}}}}}}}}^{2}\rangle\), we first change the average to be on \({{{{{{{\mathcal{V}}}}}}}}\), \(\langle {k}_{{{{{{{{\mathcal{V}}}}}}}}\to {{{{{{{\mathcal{D}}}}}}}}}^{2}\rangle\). Then we define a variable yj which is an indicator of whether neighbor number j of a given node belongs to \({{{{{{{\mathcal{D}}}}}}}}\), such that yj = 1 if neighbor j belongs to \({{{{{{{\mathcal{D}}}}}}}}\) and yj = 0 otherwise. Thus, \({k}_{{{{{{{{\mathcal{V}}}}}}}}\to {{{{{{{\mathcal{D}}}}}}}}}=\mathop{\sum }\nolimits_{j = 1}^{k}{y}_{j}\) where the index j runs over neighbors of an arbitrary node. The random variables yj are independent, and have the mean 1 − ρ, therefore,
Substituting Eqs. (34) and (35) in Eq. (32) provides
This result is very intuitive because this quantity represents the expected number of free neighbors of a free node approached via a free node as well. Hence, it has certainly one free neighbor, and since the average degree of an arbitrary neighbor is κ, it has κ − 1 more neighbors but a fraction ρ of them is expected to be controlled.
Next, we move to evaluate the second term in Eq. (32).
We already found the second term in Eq. (35). The first term is
Plugging Eqs. (35) and (38) into Eq. (37) gives
Substituting Eqs. (34) and (39) into Eq. (32) we get
This formula is intuitive as well, since it represents the number of forced neighbors of a free node approached via another free node. κ is the expected degree, and among the remaining κ − 1 neighbors, a fraction ρ is expected to be forced.
Substituting Eqs. (36) and (40) into Eq. (33), we get the mean-field equation for a forced system for a random selection of controlled nodes,
Taking the limit κ ≫ 1 and recalling β = λκ, this equation takes the form
Isolating β, we finally obtain Eq. (8) above,
which yields a relation between \(\bar{{{{{{{{\bf{x}}}}}}}}}\) and β, determining the average activity of the forced system for each topology captured by β. Also, the system states depend on the intervention characteristics, ρ and Δ. Note that substituting ρ = 0 in Eq. (43) recovers the case of a free system, see Supplementary Note 1. Recognizing the stable states of a forced system (ρ > 0) compared to those of a free system (ρ = 0), we can answer our main question of sustaining a system by holding a fraction of nodes. In the following Section, we find for cellular dynamics the sustaining window, i.e., a region where an unsustainable network becomes sustainable due to external control.
Sustaining cellular dynamics
Forced system
To examine the behavior of cellular dynamics (9) under sustaining, we seek to construct the forced system states according to Eq. (43),
This formula generates a new phase diagram for a forced system shown in Fig. 3d (thick curve) for ρ = 0.03 and Δ = 5, exhibiting an s-shape diagram which has now also a new active regime (blue shade), in which only x1 exists. This regime is regarded as the sustainable phase. Note that the simulation results (symbols) agree well with the theory. The simulations are for ER networks with κ = 40 and N = 104. The value of λ varies.
Sustaining window
For finding βc, above which the forced system is sustainable, according to Eq. (11), we take the derivative of β in Eq. (44) with respect to \(\bar{{{{{{{{\bf{x}}}}}}}}}\) to be zero as Eq. (11) demands, yielding
Denoting \(u=1+{\bar{{{{{{{{\bf{x}}}}}}}}}}^{-h}\), we obtain,
Arranging terms gives a solvable quadratic equation,
whose solutions are given by
Taking the solution which gives the smaller \({\bar{{{{{{{{\bf{x}}}}}}}}}}_{c}\) for the transition to the sustainable regime (see Fig. 3d), we get
Substituting this in Eq. (44) provides βc(ρ, Δ), yields a complicated expression. However, let us expand this in the limit of small ρ and, as a result small \({\bar{{{{{{{{\bf{x}}}}}}}}}}_{c}\) as can be seen in Fig. 3d, to get the scaling of βc and ρ in the limit of small ρ. To this end, we go back to Eq. (45) to obtain the leading order
and substituting this in Eq. (44), we finally obtain
which provides the scaling between the connectivity β and the fraction of control ρ at the transition from the unsustainable phase to the sustainable phase for small ρ in cellular dynamics. The inverse relation gives for a given β the critically required fraction ρc for sustaining a network,
In Fig. 3k, we present the results for a = 1, h = 2, thus we observe the scaling ρc ~ β−2 = (λκ)−2. In Fig. S3, we show results also for different values of a, h resulting in different exponents and a good agreement between simulations and theory.
Notice that, as we discuss in detail in Supplementary Note 3, the limits of small ρ and small 〈k〉 challenge our mean field that provides the scaling of (52), which is valid only for small ρ. Thus, even though the simulation results in Fig. 3k show the predicted exponent because of the large degrees, on the contrary, the results in Fig. 3l show a deviation from the predicted scaling because the MF assumption is broken due to the small ρ and small average degrees.
Tricritical point
Beyond some point (β0, ρ0), the unsustainable phase vanishes, and the transition between the high-active state and the low-active state becomes continuous, see Fig. 3e, g, h. This happens when the two transition points on the edges of the unsustainable region merge. In order for this to be fulfilled, there should be only a single solution to Eq. (46), therefore the term inside the square root has to equal zero. Thus we demand
yielding
which is the critical value of ρ above which the system is fully sustainable because the bi-stable regime disappears. Plugging this into Eqs. (49) and (44) provides the value βc of the critical point.
In our simulations in Fig. 3 we set a = 1, h = 2, thus we get ρ0 = 1/(1 + 8/(1 + Δ−h)), and setting Δ = 5 gives ρ0 ≈ 1/9, while using Δ = 1 yields ρ0 = 1/5. In general, for high Δ, we get ρ0 ≈ (h − a)2/(h + a)2.
Data availability
No datasets were generated or analyzed during the current study.
Code availability
All codes to reproduce, examine and improve our proposed analysis are available at https://doi.org/10.24433/CO.3390264.v1.
References
Yang, Y., Nishikawa, T. & Motter, A. E. Small vulnerable sets determine large network cascades in power grids. Science 358 (2017).
Zhao, J., Li, D., Sanhedrai, H., Cohen, R. & Havlin, S. Spatio-temporal propagation of cascading overload failures in spatially embedded networks. Nat. Commun. 7, 10094 –10099 (2016).
Courchamp, F. et al. Rarity value and species extinction: the anthropogenic allee effect. PLoS Biol. 4, e415 (2006).
Shih, H.-Y., Hsieh, T.-L. & Goldenfeld, N. Ecological collapse and the emergence of travelling waves at the onset of shear turbulence. Nat. Phys. 12, 245–248 (2016).
Jiang, J., Hastings, A. & Lai, Y.-C. Harnessing tipping points in complex ecological networks. J. R. Soc. Interface 16, 20190345 (2019).
Zeng, G. et al. Multiple metastable network states in urban traffic. Proc. Natl Acad. Sci. USA 117, 17528–17534 (2020).
Alon, U. An Introduction to Systems Biology: Design Principles of Biological Circuits (Chapman & Hall, 2006).
Jeong, H., Mason, S. P., Barabási, A.-L. & Oltvai, Z. N. Lethality and centrality in protein networks. Nature 411, 41 (2001).
Cohen, R., Erez, K., Ben-Avraham, D. & Havlin, S. Resilience of the internet to random breakdowns. Phys. Rev. Lett. 85, 4626–4628 (2000).
Albert, R. & Barabási, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47 (2002).
Watts, D. & Strogatz, S. Collective dynamics of ‘small-world’ networks. Nature 393, 440–442 (1998).
Barthélémy, M. Spatial networks. Phys. Rep. 499, 1 – 101 (2011).
Buldyrev, S. V., Parshani, R., Paul, G., Stanley, H. E. & Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 464, 1025–1028 (2010).
Leicht, E. A. & D’Souza, R. M. Percolation on interacting networks. Preprint at arXiv:0907.0894 (2009).
Gao, J., Buldyrev, S. V., Stanley, H. E. & Havlin, S. Networks formed from interdependent networks. Nat. Phys. 8, 40–48 (2012).
Motter, A. E. & Lai, Y.-C. Cascade-based attacks on complex networks. Phys. Rev. E 66, 065102 (2002).
Crucitti, P., Latora, V. & Marchiori, M. Model for cascading failures in complex networks. Phys. Rev. E 69, 045104–7 (2004).
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M. & Hwang, D.-U. Complex networks: structure and dynamics. Phys. Rep. 424, 175–308 (2006).
Dobson, I., Carreras, B. A., Lynch, V. E. & Newman, D. E. Complex systems analysis of series of blackouts: cascading failure, critical points, and self-organization. Chaos 17, 026103 (2007).
Achlioptas, D., D’Souza, R. M. & Spencer, J. Explosive percolation in random networks. Science 323, 1453–1455 (2009).
Menck, P. J., Heitzig, J., Marwan, N. & Kurths, J. How basin stability complements the linear-stability paradigm. Nat. Phys. 9, 89–92 (2013).
Majdandzic, A. et al. Spontaneous recovery in dynamical networks. Nat. Phys. 10, 34–38 (2014).
Zhang, X., Boccaletti, S., Guan, S. & Liu, Z. Explosive synchronization in adaptive and multilayer networks. Phys. Rev. Lett. 114, 038701 (2015).
Boccaletti, S. et al. Explosive transitions in complex networks’ structure and dynamics: percolation and synchronization. Phys. Rep. 660, 1–94 (2016).
Gao, J., Barzel, B. & Barabási, A.-L. Universal resilience patterns in complex networks. Nature 530, 307—312 (2016).
Behar, H. Fluctuations-induced coexistence in public goods dynamics. Phys. Biol. 13, 056006 (2016).
Danziger, M. M. et al. Dynamic interdependence and competition in multilayer networks. Nat. Phys. 15, 178–185 (2019).
Liu, Y.-Y., Slotine, J.-J. & Barabási, A.-L. Controllability of complex networks. Nature 473, 167–173 (2011).
Liu, Y.-Y. & Barabási, A.-L. Control principles of complex systems. Rev. Mod. Phys. 88, 035006 (2016).
Whalen, A. J., Brennan, S. N., Sauer, T. D. & Schiff, S. J. Observability and controllability of nonlinear networks: The role of symmetry. Phys. Rev. X 5, 011005 (2015).
Barzel, B. & Barabási, A.-L. Network link prediction by global silencing of indirect correlations. Nat. Biotechnol. 31, 720 – 725 (2013).
Harush, U. & Barzel, B. Dynamic patterns of information flow in complex networks. Nat. Commun. 8, 2181 (2017).
Hens, C., Harush, U., Cohen, R., Haber, S. & Barzel, B. Spatiotemporal propagation of signals in complex networks. Nat. Phys. 15, 403 (2019).
Cornelius, S. P., Kath, W. L. & Motter, A. E. Realistic control of network dynamics. Nat. Commun. 4, 1942–1950 (2013).
Sahasrabudhe, S. & Motter, A. E. Rescuing ecosystems from extinction cascades through compensatory perturbations. Nat. Commun. 2, 1–8 (2011).
Dobson, I., McCalley, J. & Liu, C.-C. Fast Simulation, Monitoring and Mitigation of Cascading Failure (Power Systems Engineering Research Center, 2010).
Duan, D., Bai, X., Rong, Y., Hou, G. & Hang, J. Controlling of nonlinear dynamical networks based on decoupling and re-coupling method. Chaos Solit. Fractals 163, 112522 (2022).
Sanhedrai, H. & Havlin, S. External field and critical exponents in controlling dynamics on complex networks. New Journal of Physics (2023).
Sanhedrai, H. et al. Reviving a failed network through microscopic interventions. Nat. Phys. 18, 338–349 (2022).
Barzel, B. & Biham, O. Binomial moment equations for stochastic reaction systems. Phys. Rev. Lett. 106, 150602–5 (2011).
Dodds, P. S. & Watts, D. J. A generalized model of social and biological contagion. J. Theor. Biol. 232, 587–604 (2005).
Pastor-Satorras, R., Castellano, C., Van Mieghem, P. & Vespignani, A. Epidemic processes in complex networks. Rev. Mod. Phys. 87, 925–958 (2015).
Gardner, T. S., Cantor, C. R. & Collins, J. J. Construction of a genetic toggle switch in Escherichia coli. Nature 403, 339 (2000).
Karlebach, G. & Shamir, R. Modelling and analysis of gene regulatory networks. Nat. Rev. 9, 770–780 (2008).
Schreier, H. I., Soen, Y. & Brenner, N. Exploratory adaptation in large random networks. Nat. Commun. 8, 1–9 (2017).
Holling, C. S. Some characteristics of simple types of predation and parasitism. Can. Entomol. 91, 385–398 (1959).
Wang, X., Chen, X. & Yang, Y. Spatiotemporal control of gene expression by a light-switchable transgene system. Nat. Methods 9, 266–269 (2012).
Pastor-Satorras, R. & Vespignani, A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 86, 3200–3203 (2001).
Boguná, M. & Pastor-Satorras, R. Epidemic spreading in correlated complex networks. Phys. Rev. E 66, 047104 (2002).
Barrat, A. Barthélemy, M. & Vespignani, A. Dynamical Processes on Complex Networks (Cambridge Univ. Press, 2008).
Dorogovtsev, S. N. & Goltsev, A. V. Critical phenomena in complex networks. Rev. Mod. Phys. 80, 1275–1335 (2008).
Wilson, H. R. & Cowan, J. D. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys. J. 12, 1–24 (1972).
Wilson, H. R. & Cowan, J. D. A mathematical theory of the functional dynamics of cortical and thalamic nervous tissue. Kybernetik 13, 55–80 (1973).
Krapivsky, P. L., Redner, S. & Ben-Naim, E. A Kinetic View of Statistical Physics (Cambridge Univ. Press, 2010).
Yuan, X. et al. Eradicating catastrophic collapse in interdependent networks via reinforced nodes. Proc. Natl Acad. Sci. USA 114, 3311–3315 (2017).
Raj, A. & Van Oudenaarden, A. Nature, nurture, or chance: stochastic gene expression and its consequences. Cell 135, 216–226 (2008).
Losick, R. & Desplan, C. Stochasticity and cell fate. Science 320, 65–68 (2008).
Acknowledgements
H.S. acknowledges the support of the Presidential Fellowship of Bar-Ilan University, Israel, and the Mordecai and Monique Katz Graduate Fellowship Program. We thank the Israel Science Foundation, the Binational Israel-China Science Foundation (Grant No. 3132/19), the NSF-BSF (Grant No. 2019740), the EU H2020 project RISE (Project No. 821115), the EU H2020 DIT4TRAM, and DTRA (Grant No. HDTRA-1-19-1-0016) for financial support.
Author information
Authors and Affiliations
Contributions
H.S. and S.H. designed the research and wrote the paper. H.S. performed computer simulations and analytical derivations.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communication Physics thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sanhedrai, H., Havlin, S. Sustaining a network by controlling a fraction of nodes. Commun Phys 6, 22 (2023). https://doi.org/10.1038/s42005-023-01138-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-023-01138-8
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.