Self-transport of swimming bacteria is impaired by porous microstructure

Abstract

Motility is a fundamental survival strategy of bacteria to navigate porous environments, where they mediate essential biogeochemical processes in quiescent wetlands and sediments. However, a comprehensive understanding of the mechanisms regulating self-transport in the confined interstices of porous media is lacking, and determining the interactions between cells and surfaces of the solid matrix becomes paramount. Here, we precisely track the movement of bacteria (Magnetococcus marinus) through a series of microfluidic porous media with broadly varying geometries and show how successive scattering events from solid surfaces decorrelate cell motion. Ordered versus disordered media impact the cells’ motility over short ranges, but their large-scale transport properties are regulated by the cutoff of their persistent motility. An effective mean free path is established as the key geometrical parameter controlling cell transport, and we implement a theoretical model that universally predicts the effective cell diffusion for the diverse geometries studied here. These results aid in our understanding of the physical ecology of swimming cells, and their role in environmental and health hazards in stagnant porous media.

Introduction

Bacterial communities are abundant in the stagnant waters of wetlands, including swamps, marshes, bogs, and fens, and they play a key role in biogeochemical cycles by functioning as both primary producers and decomposers^1,2. Most bacteria swim using thin, actuated flagella^3,4, and their resultant self-transport is vital to many of their ecological functions, especially in the stagnant porous sediments in which they live. In bulk fluid, bacteria swim in persistent random walk patterns^5,6,7, where otherwise straight-line swimming is decorrelated by flagellar-induced turns and Brownian rotational motion⁸. However, natural habitats of swimming cells are often characterized by pores that can range in size from that of a single cell to many times larger^9,10. In these porous microenvironments, cell motility is further disrupted due to interactions with nearby solid surfaces^{11,12,13,14,15,16,17}. While there has been significant emphasis on understanding the physical origins of cell-surface interactions, a clear consensus of their net effect on the self-transport properties of swimming bacteria in porous media has not been established.

Hydrodynamic and steric forces¹⁸ can cause bacteria and sperm to bias their motility toward flat substrates^19,20 and curved obstacles²¹, and flagellar contact mediates both plankton^22,23 and bacterial tumbling^24,25,26 near surfaces. The importance of such boundary-induced reorientation on swimmer migration through porous media has been illustrated by simulations and modeling of individual microswimmer dynamics^{15,27,28,29,30}. In particular, their reorientation dynamics upon contacting a surface (e.g., sliding versus specular reflection) are predicted to have a significant impact on their effective diffusion coefficients¹⁵. Recent experiments on bacterial self-transport in disordered 3D packed beds show that small pores comparable to the bacterial body size (≈1–10 μm) result in a cage-hopping behavior between pores³¹. Measurements of swimming microalgae in ordered microfluidic lattices with larger pores established that increasing the density of solid obstacles reduces the effective diffusion of the cells³². Other diverse transport behaviors have been reported ranging from simulations showing directional locking in ordered media³³ to experiments demonstrating subdiffusive transport of synthetic active particles in random media²⁸. Determining the pervasiveness of these transport phenomena, and in some cases their applicability to biological microswimmers remains challenging due to the vast landscape of potential pore geometries and swimmer behaviors.

The random walk behavior of swimming cells and active particles has motivated a number of diffusive models for transport in crowded environments^{15,27,28,29,30,34}, many of which are particular to specific propulsion mechanisms, cell-surface interactions, and pore microstructures³⁵. An overarching assumption in describing swimming cell transport in porous media is that their persistent motility is truncated approximately to the mean pore size of the medium, which inspired a general modeling framework for swimmer transport based on gas diffusion^12,36 and a search for the critical geometrical parameters of porous media that control swimmer behavior^15,34. However, these assumptions and models remain largely untested due to a lack of robust experimental measurements of cell trajectories and transport properties.

Here, we investigate the effect of porous microstructure on the self-transport of swimming bacteria (Magnetococcus marinus, strain MC-1) through thorough microfluidic experiments (Fig. 1a–f). MC-1 is a coccoid-shaped bacterium with a ≈1–2 μm diameter cell body that is propelled by a pair of flagellar bundles³⁷. High-fidelity cell tracking follows individual cells through ordered and disordered model porous media having a broad range of porosities and pore sizes that span natural cell environments^9,10,38,39. Direct measurements of cell motility and scattering angles from solid surfaces connect the micro-scale cell behavior to their large-scale transport coefficients. We show how the persistent random walks of the cells are broken by the porous microstructure, reducing the effective diffusion coefficients across all geometries. From these extensive experimental results, an effective mean free path emerges as a fundamental length scale of the porous media^12,15,34, which enables the accurate prediction of cell transport coefficients through a simple statistical model.

Fig. 1: Porous microstructure frustrates the random walks of swimming cells.

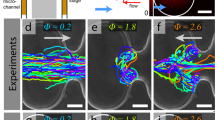
a–f Sample cell trajectories in porous microfluidic devices for various porosity, scale, and disorder of the obstacle lattice. See Table 1 for a full list of porous microfluidic geometries tested. Scale bars, 120 μm. a Cell trajectories in an open channel (porosity, σ = 1). b Ordered porous medium (σ = 0.55) with cylindrical pillars of diameter d = 85 μm, arranged in a hexagonal lattice with a lattice spacing c = 120 μm (scale, s = 1). c Disordered porous medium (σ = 0.55, s = 1), where d and average lattice spacing are similar to (b). d Porosity is varied by modifying the pillar diameters (d = 40 μm), while holding the lattice spacing constant (c = 120 μm). e Identical to (b), but with all features scaled up by a factor s = 1.5. f Identical to (c), but with increased porosity by reducing the pillar diameters to d = 20 μm. g–i Normalized polar probability density of cell swimming directions in various geometries: g ordered lattice with varying porosity (s = 1), h ordered lattice with varying scale (σ = 0.55), and i disordered media with varying porosity (s = 1). Instantaneous swimming direction vectors are averaged over a 1 s interval within the ballistic regime of the cell trajectories to obtain average swimming directions, 〈ϕ〉_1s. Cell trajectories were randomly sampled from the entire cell population (Supplementary Fig. 1), and the probability, p(〈ϕ〉_1s), is normalized by its maximum value, p_max(〈ϕ〉_1s).

Results

Cell trajectories rapidly decorrelate despite short-time pore-scale guidance

The long, meandering trajectories of swimming bacteria in bulk fluid (Fig. 1a) are drastically altered by interactions with porous microstructure (Fig. 1b–f). Upon collisions with pillars, cell swimming directions change abruptly (Fig. 1b–f), which leads to highly tortuous swimming paths in random media (Fig. 1c). However, in ordered media, cells can briefly follow paths aligned with the lattice structure (Fig. 1b). Beyond the effects of disorder, the observed random walks qualitatively appear to be diminished or exacerbated as porosity and feature scale vary (Fig. 1d–f), leading to a vast parameter space whose impact on bacterial transport remains poorly understood. These fundamental microstructural parameters were systematically varied (Table 1) to determine their impact on the short- and long-time transport properties of swimming bacteria. For short times, relative to their bulk persistence time (τ_p,0 = 4.6 s), the probability of the cell swimming direction averaged over 1 s, p(〈ϕ〉_1s), is homogeneous in open space (Fig. 1g, i) indicating that the cells swim in random directions (Fig. 1a). However, in ordered media, peaks in the orientation distribution emerge for sufficiently low porosities (Fig. 1g), which indicate that the bacteria align with the hexagonal lattice directions. This short-time guiding effect in ordered media is not dictated solely by porosity as it requires sufficiently small scale of the pore features (Fig. 1h). While alignment to the local pore structures may persist in random media, the swimming directions remain homogeneous across all porosities examined (Fig. 1i) by virtue of the random orientation of pores and throats.

Table 1 Geometric specifications of the microfluidic model porous media used in experiments.

Despite the observed sensitivity of the short-time swimming direction to the geometry, cells randomize their swimming direction after a finite persistent time, τ_p. For all the inspected geometries, the correlation functions of the swimming direction exponentially decay, according to $C(t)=\langle {{{{{{{\bf{p}}}}}}}}(t+{t}_{0})\cdot {{{{{{{\bf{p}}}}}}}}({t}_{0})\rangle ={e}^{-t/{\tau }_{p}}$ (Fig. 2a), where p is a unit vector describing the instantaneous cell swimming direction, obtained from their reconstructed trajectories. Strikingly, the combined effects of the intrinsic noise in the swimmer orientation (Fig. 2a, open) and discrete scattering encounters with the microstructure are simply characterized by a single decorrelation rate of the swimming direction, 1/τ_p. As the porosity is decreased, the rate of such encounters is increased and the swimming direction of the cells decorrelates faster (Fig. 2a). Taken together, these observations suggest that the pore size—rather than porosity, feature size scale, or the geometric order alone—regulates bacterial self transport (Supplementary Fig. 3). A microscopic viewpoint is required to fully understand how bacterial encounters with solid surfaces modify their trajectories and regulate the decorrelation process.

Fig. 2: Cell swimming direction decorrelates due to scattering from pillar surfaces.

a Swimming direction correlation functions (see “Methods”), C(t), for cells in a hexagonal lattice (scale, s = 1) exhibit an exponential decay across a range of porosities (0.37 ≤ σ ≤ 1). Dashed black lines show example fits to $C(t)={e}^{-t/{\tau }_{p}}$. b Yellow dotted line shows a sample cell trajectory with several scattering events from nearby pillars. The blue vector indicates the measured cell orientation upon entering the impact area (green circle) of the central pillar with an incident angle (θ_in) relative to the surface normal (white dashed line). The red vector indicates the cell orientation upon exiting the impact area with an outgoing angle (θ_out). The cell orientation changes by a scattering angle in the range 0^∘ ≤ α ≤ 180^∘. c Conditional probability, p(α∣θ_in), of cell scattering angle given the incident swimming angle measured in a hexagonal lattice (σ = 0.37, s = 1). d Ensemble mean cell scattering angles, $\tilde{\alpha }$, measured directly for various pillar diameters, d, and swimming speed ranges. Error bars show standard error of mean scattering angles.

Bacterial scattering is independent of pillar size and cell swimming speed

Robust cell trajectories from experiments enable us to quantify the bacterial scattering angle upon collision with a pillar surface (Fig. 2b). Focusing on hexagonal lattices, cell collisions with individual pillars were identified by defining an impact region within 2.5 μm from the pillar surface (comparable to the cell size). From the cell trajectories, the incident, θ_in, and outgoing, θ_out, angles of the cells relative to the pillar surface normal (Fig. 2b) were measured²³ by fitting straight lines to the cell position over seven frames just prior to entering and just after exiting the impact region, respectively. The scattering angle, α, characterizes the total change in cell orientation angle due to a collision with a pillar (Fig. 2b) and empirically appears to depend on their relative incident angles, θ_in, prior to impact (Fig. 2c). While body shape and flagellation can impact cell interactions with surfaces⁴⁰, ultimately, the statistics of the net bacterial scattering angle from an obstacle encapsulate the details of the hydrodynamic and steric interactions¹⁵ and are a primary determinant of transport⁸. Our results show that, when a cell approaches a pillar surface at a glancing, tangent angle (θ_in ≈ 90^∘), the cell’s orientation generally exhibits little change, and it leaves the surface oriented in approximately the same direction compared to its incident angle (α ≈ 0^∘; Fig. 2c). However, when a bacterium approaches perpendicular to the pillar surface (θ_in ≈ 0^∘), it is strongly scattered with a significant reorientation of the cell trajectory (α ≈ 120^∘). The scattering angle decreases approximately linearly with incident angle (Fig. 2c), and the scattering properties likely vary across microbial species due to flagellation, swimming style, and body shape and size²³. The cell scattering measurements were performed in situ across all pillar diameters tested (Table 1) and three different cell swimming speed ranges (Supplementary Fig. 1). Ultimately, the ensemble average scattering angle, $\tilde{\alpha }$, for the bacteria studied here was found to be independent of both the pillar diameter and the cell swimming speed (Fig. 2d). These measurements not only illustrate how cell scattering from pillar surfaces acts as the primary decorrelation mechanism in porous media, but also provide key quantitative scattering statistics necessary to model cell transport in such microstructured environments.

Porous microstructure hinders cell transport

In order to quantify the effects of porous media on the transport properties of swimming bacteria, we analyze the mean squared displacements (MSDs) of the cells across a wide range of pore structures. For short times (t ≪ τ_p), the MSDs universally overlap and grow as ~t² due to ballistic cell swimming motility, prior to scattering from pillars or reorienting due to flagellar noise and rotational Brownian motion (Fig. 3). The MSD scaling eventually transitions to ~t at large times (t ≫ τ_p) for all geometries, which indicates diffusive transport and stems from the decorrelation of the cell swimming trajectories (Fig. 2a). The MSDs from the measured 2D swimming cell trajectories are well characterized by an analytical fit (see “Methods”; Fig. 3a–c, dashed black curves)^35,41,42, which provides the effective translational diffusion coefficient, D, as well as the persistent swimming time, τ_p, of the cells (Fig. 4). The persistence times measured using this method closely correspond to those measured from the exponential decay of the swimming direction correlation functions, confirming the robustness of the analysis (Supplementary Fig. 2). While the MSDs of the swimming cells coincide for short times, a decrease in the porosity or scale decreases the size of the pore space and causes a more rapid decorrelation of cell motility. This effect is indicated by the earlier transition time of the MSD slope and accompanied by a decreased growth rate of the MSDs for t ≫ τ_p. These observations are universal across all geometries and bacterial swimming speed ranges (Fig. 3) and indicate that the porous microstructure hinders the diffusive transport of the cells, even in the ordered hexagonal geometries that promote short-time preferential swimming directions (Fig. 1g, h).

Fig. 3: Porous media universally hinders cell transport.

Measured mean squared displacements (MSDs) for swimming bacteria (50 ≤ V_s ≤ 80 μm/s) in a ordered lattice with varying porosity, b ordered lattice with varying scale, and c disordered lattice with varying porosity. In a–c, the dashed black lines show two example fits each to an analytical persistent random walk model (see “Methods”). Solid line segments indicate ~t² and ~t for the ballistic and diffusive regimes, respectively.

Fig. 4: Pore geometry sets persistent length and regulates diffusive self transport of swimming cells.

a Persistent swimming length of the cells, l_p, decreases with decreasing pore size, d_p. Dashed line shows l_p = d_p for reference. b Normalized effective cell diffusion coefficient, D/D₀, decreases with decreasing normalized effective pore size. l_m = d_p and l_m = l_f for gray and colored markers, respectively. D is measured from MSD fits in Fig. 3 (see also Supplementary Fig. 5), D₀ is the bulk diffusion coefficient, and dashed line is Eq. (3). c, d Effective mean free path is calculated as the mean distance for randomly sampled, theoretical straight paths (colored lines) from the central pillar (green) to the first intersecting pillar (red). Samples are shown in a hexagonal lattice for pillar spacing to diameter ratios of c/d = 1.2 in (c) and c/d = 1.7 in (d). Blue areas indicate coverage of all possible free paths. e Effective mean free path, l_f, grows faster than mean pore size, d_p, with increasing c/d for both ordered and disordered media with uniform and reflective scattering, and the results strongly agree with theory⁴⁷. Dotted lines indicate range of experiments. f Effective cell diffusion coefficients, D, decrease with decreasing effective mean free path, l_f, for all swimming speed populations and geometries. Dashed lines show Eq. (3). In (a), (b), and (f), markers correspond to key in (a), and error bars are the standard error computed by dividing data into random subsets (N = 3).

Effective pore size sets the effective cell diffusion

The effective cell diffusion coefficients decrease markedly by more than 500% across the porous geometries investigated (Supplementary Fig. 4). For their persistent random walk in 2D, the long-time diffusion coefficient of the cells is $D={V}_{s}^{2}{\tau }_{p}/2$, which can alternatively be expressed in terms their persistent swimming length l_p = V_sτ_p as D = V_sl_p/2 (Supplementary Fig. 5). Accordingly, cell populations with higher swimming speeds exhibit higher diffusion coefficients across all of the geometries examined (Supplementary Fig. 4). Swimming speed, V_s, is an intrinsic property of the cells and does not vary with changes in geometry. However, the bulk persistent swimming length, l_p,0 = V_sτ_p,0, sets a length scale below which we expect the porous media to dictate l_p (Fig. 4a; Supplementary Fig. 3). Our experiments clearly illustrate that ordered versus disordered porous media only marginally affect bacterial transport coefficients (Fig. 4a, Supplementary Fig. 4). Therefore, the effective pore size is the key parameter in determining the persistent swimming length (Fig. 4a) and transport coefficients (Supplementary Fig. 4) of the cells, rather than the porosity, scale, or order of the media alone.

Apart from random reorientations due to Brownian rotation and self-propulsion noise, motile bacteria in porous media generally swim in straight trajectories prior to interacting with a solid surface. The mean pore size, d_p, is a common geometric measure of the typical distance between such surfaces, and it is often quantified by the mean of the largest circle diameter, d_p, that can be inscribed in the void space (Table 1; “Methods”)^43,44,45,46. As the mean pore size decreases, reorientations due to cell-surface interactions becomes more prominent and decrease the measured persistent swimming length (Fig. 4a) and time (Supplementary Fig. 3). While the persistence length might be expected to be governed by l_p = d_p (Fig. 4a, dashed line), cells with higher swimming speeds exhibit persistence lengths that greatly exceed the pore size, especially for larger d_p. In the case of highly porous materials with large d_p, the probability of interacting with a small obstacle, d, compared to a relatively large obstacle separation, c, diminishes, allowing cells to transit multiple pores before scattering. Thus, we introduce an alternative characteristic length scale, stemming solely from the porous media geometry.

The effective mean free path, l_f, is defined here as the average value of randomly-sampled, theoretical straight paths between circular obstacles (Fig. 4c, d; see also Supplementary Methods), and it is akin to swimming cell trajectories with high persistence. The effective mean free path relative to the mean pore size increases monotonically with c/d, and l_f/d_p > 1 for both the ordered and disordered media explored here under a range of surface scattering conditions (Fig. 4e; see also Supplementary Methods).

While related metrics have been proposed separately in theoretical¹⁵ and simulation³⁴ works their relevance across disorder, scale, and porosity is not known, nor have they been rigorously vetted through experiments. Related to the mean free path, the maximal chord length of 3D media has been used to accurately describe the transport of active polymers in simulations, but only for disordered media with relatively low porosity³⁴. Separately, the Santalo equation, πA/P, describes the theoretical mean free path (void area, A; wetted perimeter, and P). However, it strictly applies only for reflective surface scattering⁴⁷, and its applicability has only been explored in theoretical studies of swimmers in 2D ordered media¹⁵. Despite the formal restrictions on this expression, a comparison of the measured πA/P for our ordered and disordered media empirically shows very good agreement with our computed l_f (Supplementary Fig. 6). This provides a simple approach to quantify the effective mean free path, and thus, we take l_f = πA/P going forward for both the ordered and disordered media studied here. Below, we show that l_f is an intuitive quantity that is adept at describing and predicting the transport of swimming cells in porous media (Fig. 4b, f).

Additive decorrelation rates dictate the self-transport in porous media

Based on classic models for gas diffusion³⁶, a general statistical framework for modeling the decorrelation of cell motility in porous media has been suggested¹², but not rigorously explored experimentally. Here, we reinterpret this model through the lens of our extensive experimental measurements: The effective mean free path is established as the relevant length scale that regulates the decorrelation of bacterial motility and thus their large scale transport in porous media. The total decorrelation rate of the bacterial swimming direction in porous media arises from the sum of two independent processes:

$$\frac{1}{{\tau }_{p}}=\frac{1}{{\tau }_{p,0}}+\frac{1}{{\tau }_{m}}.$$

(1)

The first process is the natural decorrelation rate, 1/τ_p,0, due to rotational Brownian diffusion and flagellar noise, which is related to the effective diffusion coefficient and persistence length in the bulk by ${D}_{0}={V}_{s}^{2}{\tau }_{p,0}/2={V}_{s}{l}_{p,0}/2$, and measured directly from experiments (Fig. 4f). The second process stems from bacterial scattering events due to interactions with solid surfaces:

$$\frac{1}{{\tau }_{m}}=\frac{(1-\langle \cos (\alpha )\rangle )}{{l}_{m}/{V}_{s}}.$$

(2)

It is mathematically equivalent to a run-and-tumble random walk⁸ and depends upon the cell swimming speed, V_s, and the average surface scattering angle, $\langle \cos (\alpha )\rangle$. Both of these parameters are measured directly from experiments, where we previously showed that the scattering statistics are independent of obstacle size (Fig. 2). This decorrelation rate is also a strong function of the effective pore size of the media, l_m, which dictates the typical distance that a cell can swim unimpeded. The resulting effective diffusion coefficient, D, is thus expressed as

$$D({l}_{m})=\frac{{D}_{0}}{\left(1+\frac{{l}_{p,0}}{{l}_{m}}(1-\left\langle \cos \right.(\alpha )\rangle)\right)},$$

(3)

shown in normalized form in Fig. 4b (dashed line).

The mean pore size is a typical choice for the relevant physical length scale of the media, l_m = d_p: Indeed, it yields a partial collapse of the data (Fig. 4b, gray markers) and is captured by the model (Eq. (1)) at small pore sizes, where cell-surface interactions are frequent. However, this local measure fails to predict effective diffusivity for relatively larger pore sizes. In highly porous environments, motile cells can travel several pores prior to interacting with small or sparse obstacles. Rather, the effective mean free path, l_f, computed purely from the geometry of the medium (Fig. 4c–e), provides a more relevant physical length scale, especially for swimmers with high bulk persistence (l_p,0 ≥ d_p). Choosing the effective pore size as l_m = l_f shows excellent quantitative agreement of the model with experiments across the broad ranges of porosities, pore sizes, order/disorder, and cell swimming speeds examined (Fig. 4b, colored markers; Fig. 4f). Thus, these results establish a comprehensive framework for predicting the transport coefficients of swimming cells in porous media with minimal parameters, including: (i) the cell motility in bulk fluid, V_s and τ_p,0, (ii) the average cell deflection from solid surfaces, $\langle \cos (\alpha )\rangle$, and (iii) the effective mean free path of the porous medium geometry, l_f.

Discussion

Our thorough microfluidic experiments illustrate how porous microstructure universally hinders the effective diffusion of the swimming bacteria MC-1, and they establish the essential parameters required to model and predict cell transport in stagnant saturated porous media. Varying the geometry, including porosity, scale, and disorder, revealed that the reduction of persistence length is the key mechanism hindering transport, and the effective mean free path of the medium (Fig. 4c–e) is the primary geometric scale that dictates bacterial transport coefficients. Precise measurements of cell-surface interactions were crucial to understanding long-time transport by revealing that MC-1 scattering is independent of pillar diameter. Subsequent scattering events reduced the effective cell diffusion coefficients, whereby the fastest cells experienced the most significant reduction as predicted by a modified Bosanquet model¹². The agreement of this model with extensive experimental evidence illustrates a reliable approach to forecast cell transport properties in porous media. Together with other recent works, our results solidify the effective mean free path as the critical length scale governing cell transport^15,34. With no fitting parameters, this model only requires knowledge of the cell swimming speed, bulk persistence time, mean surface scattering angle, and the effective mean free path, each of which are easily measured or calculated.

Microbes display a host of different behaviors mediated by steric, hydrodynamic, and flagellar interactions with surfaces, including a surprising bouncing-like motion in the case of MC-1 and MO-1¹⁶. A natural extension of the present work will be to determine how the transport of diverse microbial species with unique swimming strategies and surface behaviors¹⁷ are affected by porous microstructure through the framework established here. While our results for MC-1 are highly consistent with recent models of strongly scattering active swimmers in porous media¹⁵, previous simulations in ordered media have reported enhanced transport along preferential swimming directions in the case of weak surface scattering and strong persistence^15,33. We envision that the approach described here may be used to investigate a range of micro-swimmers with different surface scattering properties in combination with various ordered geometries and pillar shapes to determine the precise conditions under which preferential swimming paths might form and amplify transport. The effect of directed motility on cell transport through porous microstructures is highly relevant to microbial ecology in sediments and soils, and this approach may provide new insights into magnetotaxis⁴⁸ and chemotaxis⁴⁹ in porous media. Although the present experiments and modeling were restricted to quasi-2D microfluidic geometries, recently developed experimental approaches⁵⁰ could extend this work to model the naturally occurring 3D environments of swimming microbes.

Methods

Cell culturing

Magnetococcus marinus (strain MC-1) were grown in a semi-solid medium as previously described^37,51. A stock solution was prepared containing the following chemicals and solutions per liter: NaCl, 16.43 g; MgCl₂ ⋅ 6H₂O, 3.5 g; Na₂SO₄, 2.8 g; KCl, 0.5 g; CaCl₂ ⋅ 2H₂O, 1 g; HEPES, 2 g; NH₄Cl, 0.3 g; Wolfe’s mineral elixir⁵², 5 mL; 0.2% (w/v) aqueous resazurin, 0.6 mL; 0.01 M FeSO₄, 3 mL; 0.5 M KHPO₄ buffer with pH 6.9, 1.8 mL. The pH of the premade stock solution was adjusted to 7.0 using a 5% (w/v) NaOH solution, 1.6 g of noble agar (Difco) was added and mixed, and the stock solution was autoclaved, which fully dissolved the agar. After autoclaving, the stock solution was allowed to cool to approximately 45^∘C. The following solutions and chemicals were then added to the stock solution (per liter) to make the final cell growth medium: L-cysteine hydrate, 400 mg; vitamin solution⁵², 0.65 mL; 40% sodium thiosulfate pentahydrate solution (i.e., 10 mM of energy source), 5.6 mL; and 0.8 M NaHCO₃ (autoclaved dry; sterile water added after autoclaving to make the fresh stock solution), 2.8 mL.

For cell cultures, 10 mL of the medium was dispensed into sterile, 15 mm diameter and 125 mm long screw-capped autoclaved glass test tubes. The glass tubes with the medium were tightly capped and refrigerated over night allowing the agar to semi-solidify. During this time, the L-cysteine reduced the oxygen in the medium and formed an oxygen gradient relative to the air trapped at the top of the tube. The oxic-anoxic interface was evident by the transition from a pink hue to a transparent medium. 100 μL of cells from a previous culture was pipetted at the oxic-anoxic interface to inoculate the medium. All cultures were incubated at room temperature, and after approximately three days, a microaerobic band of bacteria formed at the oxic-anoxic interface of the tubes. For the microfluidic experiments, the cells were re-suspended in a swimming medium that is similar to the growth medium, except that it does not contain agar, HEPES, resazurin, vitamins, L-cysteine, and NaHCO₃.

Microfluidic devices and experiments

Model porous microfluidic devices were fabricated using standard soft-lithography techniques⁵³. The devices consisted of circular pillars in otherwise rectangular cross-section channels with various pillar arrangements (hexagonal order or random disorder), porosities, and sizes (Fig. 1a–f and Table 1). The devices had an inlet and an outlet to fill the chambers with swimming media and bacteria. In the ordered porous media, two different approaches were used to vary the lattice constant (c) and the pillar diameters (d): (i) varying the porosity (σ = 0.90, 0.81, 0.69, 0.55, 0.37) by keeping the lattice spacing constant (c = 120 μm) and changing the pillar diameters (d = 40, 55, 70, 85, 100 μm), and (ii) varying the scale (s = 0.5, 0.75, 1, 1.5, 2) by scaling all the dimensions up or down (c = 60, 90, 120, 180, 240 μm) at a constant porosity (σ = 0.55). The disordered porous media were generated by randomly displacing the cylindrical pillar locations from an originally hexagonal lattice. The new pillar locations were randomly sampled inside a hexagon with a circumradius of 0.9c centered at the original pillar location⁵⁴. Because this approach allows for overlapping pillars, the statistical properties of the resulting porous geometries were computed directly from computer-generated pillar arrangements using MATLAB. Specifically, for both the ordered and disordered media, the mean lattice spacing (c) and pore size (d_p), were measured using Delaunay triangulation, while the porosity (σ), void area (A), and wetted perimeter (P) were measured using polyshape objects. Standard theoretical relations for the ordered hexagonal media (non-overlapping) served to benchmark this approach (e.g., ${d}_{p}=2c/\sqrt{3}-d$) and were in excellent agreement with measured values (see Table 1).

For experiments, five different patches of pillar arrangements (2.6-mm long each) were located inside of a main channel having a total length of 25 mm, width of 2.2 mm, and depth of 10 μm. The channel depth was approximately one order of magnitude larger that the cell body size to ensure that cell interactions with obstacles were not artificially screened. Open spaces devoid of pillars (σ = 1) were located near the inlet and outlet of the channel for control experiments. The devices were filled with swimming media, and the channel outlet was subsequently sealed with wax to eliminate residual flows. 1 μL of cell suspension was taken from the oxic-anoxic transition interface of the glass culture tube, and pipetted into the channel inlet. North-seeking magnetotactic cells were guided into the channel using a hand held magnet, until the cell concentration reached about 50–100 cells/mm² by visual inspection. The remaining cells at the inlet were removed via pipette to avoid changes in cell concentration during the experiment.

Cell imaging and tracking

Imaging was performed at the center of each porous section (far from the side walls) within the main channel, as well as in the open channel section devoid of porous geometry (σ = 1). Cells were imaged using phase-contrast microscopy on an inverted microscope (Nikon Ti-E) with a ×4 magnification objective (0.13 NA). For each porous geometry, a 3600 frame video was recorded at 45 fps (5MP; Blackfly S camera, FLIR). This optical arrangement provided a large depth of focus relative to the channel depth and reduced light scattering around cylindrical pillars; it also enabled robust tracking of the ≈1 μm diameter bacteria throughout the depth of the microfluidic device and during collisions with pillar walls. Bacteria were tracked using a custom Kalman filter particle tracking algorithm (MATLAB, MathWorks)⁵⁵, yielding ≈ 2000 cell trajectories per video.

Statistical analysis of cell transport

The swimming speed of individual cells varies widely among the cell population and is in the range of 20 ≤ V_s ≤ 110 μm/s (Supplementary Fig. 1), where V_s is the mean swimming speed of a single cell averaged over its trajectory. Variations in the distribution of cell swimming speed significantly affect the perceived transport coefficients due to the strong dependence on V_s. For example, the effective diffusion coefficient that characterizes the random walk for swimming cells with a persistence time, τ_p, is $D={V}_{s}^{2}{\tau }_{p}/2$. In order to isolate the effect of swimming speeds from the effects of porous microstructure on cell transport, cell trajectories were separated into three sub-populations (Supplementary Fig. 1) having relatively narrow swimming speed ranges: 20–50 μm/s, 50–80 μm/s, and 80–110 μm/s. We primarily focus on the cells with swimming speeds in the range of 50–80 μm/s, unless stated otherwise.

The time correlation function of the cell swimming direction was computed as C(t) = 〈p(t + t₀) ⋅ p(t₀)〉, where p is a unit vector describing the instantaneous cell swimming direction obtained from their reconstructed trajectories. The correlation functions decay exponentially, $C(t)={e}^{-t/{\tau }_{p}}$, marking the finite persistence time, τ_p, of their random walk motility (Fig. 2). Mean squared displacements (MSDs) were determined from cell trajectories by dividing tracks into non-overlapping, equal-time segments (t), and computed as $MSD(t)=\langle {(x(t+{t}_{0})-x({t}_{0}))}^{2}+{(\,y(t+{t}_{0})-y({t}_{0}))}^{2}\rangle$. For a constant speed swimmer with a decorrelation rate 1/τ_p, the exact form of the MSD⁴¹ is $MSD(t)=4D[t-{\tau }_{p}(1-{e}^{-t/{\tau }_{p}})]$ with $D={V}_{s}^{2}{\tau }_{p}/2$. For simplicity, measured MSDs (Fig. 3) were fitted with the approximate form $MSD(t)\approx 4Dt(1-{e}^{-t/2{\tau }_{p}})$, which is asymptotically equivalent for both short and long times^42,56 (see also Supplementary Methods). Fitting yielded the effective diffusion coefficient, D, and the persistent time, τ_p, where the latter was in excellent agreement with τ_p measured from the correlation functions (Fig. 2 and Supplementary Fig. 2). The ensemble mean swimming speed, V_s, was computed by fitting the first 10 points of the MSDs in the ballistic regime (t ≤ 0.2 s), where $MSD={V}_{s}^{2}{t}^{2}$.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.