Introduction

Iron is one of the most abundant trace elements in the human body. The spatial distribution and valence of iron in tissues provides us with fruitful information that can reveal the molecular and cellular mechanisms of toxicity, metabolism, and disease related to metals inside the body at the cell level1,2. In the field of molecular biology, mass spectrometry (MS), such as inductively coupled plasma MS3 or matrix assisted laser desorption/ionization MS4, is used for quantitative analysis of molecules at the cell level, although the requirement of cell homogenization prevents in situ investigation. Optical methods such as Raman spectroscopy are frequently used as an in situ observation tool of biomolecules, including imaging of the detailed structure of individual cell5. Although these methods can detect metallic elements in a single cell, detailed information about metallic elements (e.g., valence change as a result of redox reactions or coupling to protein) can not be obtained. Another method to investigate metallic elements in cells is electron spin resonance (ESR) spectroscopy, which can resolve the oxidation state or coordination structure of ions from spectroscopic fingerprints. However, the limited spatial resolution and sensitivity of conventional ESR spectrometers prevent in situ inspection at the single-cell level.

To perform ESR spectroscopy for such a tiny sample, a microscale magnetometer can be an alternative detector of the ESR signal. For instance, scanning Hall probe microscope6,7,8,9, magnetic force microscope10,11,12, nitrogen-vacancy centers in diamond13,14,15, and superconducting quantum interference devices (SQUID)16,17,18,19 have been employed for this purpose. Unfortunately these magnetometers exhibits a trade-off between spatial resolution and sensitivity. For example, scanning probe microscopy and magnetometers based on single nitrogen-vacancy center can reach ultimate spatial resolution determined by their small size, but the sensitivity is reduced compared to magnetometers for bulk materials. Superconducting devices are a good example of a magnetometer which can have tunable spatial resolution and adjust the balance between the two competing factors. Because they are solid state devices fabricated on a substrate, the detector size is easily controlled from micrometer to centimeter scale by design. This is beneficial to inspect individual cells with typical size of tens of micrometer, since the probe size can easily be optimized to the target size. In addition, semiconductor fabrication technique enables us to fabricate an array of magnetometer on a single substrate. This will lead to realize a imaging device of a magnetic field with a cellular level spatial resolution.

With advances in superconducting technologies, two different types of superconducting ESR spectrometers have been actively investigated to detect a small number of electron spins either using superconducting resonators20,21,22,23,24 or superconducting magnetometers (e.g., SQUIDs25,26 or superconducting flux qubits27,28,29). We have previously demonstrated ESR spectrometers using superconducting flux qubits which can access areas of a few micrometers with a sensitivity of tens of spins/\(\sqrt{{{{{{{{\rm{Hz}}}}}}}}}\) (tens of pT/\(\sqrt{{{{{{{{\rm{Hz}}}}}}}}}\) in magnetic field unit)28.

In this work, we successfully detected the electron spins in iron-rich cultured neurons using a superconducting flux qubit. We attached the neurons cultured on an insulation layer to the flux qubit chip. As a function of temperature and an in-plane magnetic field, we observed the change in the magnetization of the cultured neurons. It is important to note that the spatial resolution of our sensor is close to the typical size of cells (10–20 μm), which enables us to investigate the sample with cellular level resolution. Thus, our results tantalizingly pave the way towards realizing ESR spectroscopy at the single-cell level. Single-cell ESR is especially useful to distinguish different characteristics of cells in an organ. Moreover, cells can uptake different levels of metallic ions, but, this information is invariably averaged out in bulk measurements. However, statistical and spatial distributions of ion concentrations can become available with single-cell ESR, which could then play an important role for understanding ion metabolism and transport in or between organs at the cell or protein level30. Ultimately, arraying a large number of flux qubits or moving the neuron laden insulation layer with a nano-manipulator suggest the exciting prospect of imaging the distribution of spins in tissues. This spatial technique could be employed to investigate metal depositions in pathological model tissues or cells to aid the understanding of cellular iron metabolism related to neuroferritinopathy, for example.

Results

Principle of magnetometry

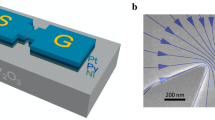
Figure 1 shows our experimental setup to detect a magnetization signal from neurons. We use a superconducting flux qubit as a sensitive magnetometer (Fig. 1a). On top of the qubit chip, the neurons cultured on a parylene-C film is laminated as shown in Fig. 1b. The neurons are magnetized by applying an in-plane magnetic field B∥. This magnetization shifts the qubit spectrum from the corresponding magnetic field that is experienced by the qubit (Fig. 1c). Thus, magnetization generated by the neurons can be detected by monitoring the change in the resonance frequency of the qubit with fixed flux operation point, B⊥. In this experiment, the neurons were cultured in an Fe3+-rich medium to enhance the signal intensity as detailed in Fig. 1d, e. See “Methods” for experimental details.

Fig. 1: Experimental setup for magnetometry of cultured neurons using a superconducting flux qubit.
figure 1

a Experimental setup. The flux qubit (blue) works as a sensitive magnetometer. The quantum state of the qubit is read out by a direct current superconducting quantum interference device (DC SQUID) with a room temperature readout circuit (sky blue). The flux qubit is excited by applying a microwave tone to an on-chip microwave (MW) line (purple). Cultured neurons (green) on a parylene-C film are attached to the qubit chip (orange arrow). An in-plane magnetic field B∥ (pink) is applied to polarize the electron spins in neurons, while a perpendicular magnetic field B⊥ (blue) is applied to control the operation flux of the qubit. b Stereomicroscope image of the qubit chip. The neurons cultured on a parylene-C film are indicated by the white arrow. Scale bar: 1 mm. Inset: Phase-contrast image of neurons on a parylene-C film. Scale bar: 100 μm. c The principle of magnetometry using a flux qubit. The qubit spectrum with (without) magnetic flux generated by the electron spins in neurons is shown by the blue (pink) curve. The magnetometry is performed by monitoring the change in the qubit resonance frequency at a fixed operation flux (sky blue). The green dotted rectangle corresponds to measured regions in Fig. 2a. It is worth mentioning that the direction of the shift depends on experimental details (e.g., direction of the in-plane field) and can be reverse. d, e Brightfield image of neurons cultured in medium containing d 0.2 μM (control) and e 50 μM of Fe3+ stained by nuclear fast red (cell soma; pink) and Prussian Blue with 3,3’-diaminobenzidine (Fe3+; dark brown). The white arrows in e indicate examples of the neurons with high Fe3+ concentration. Scale bars: 100 μm.

Full size image

Magnetometry of neurons

Figure 2 summarizes the measurement results of magnetization from neurons. The magnetometry was performed at different temperatures T and in-plane magnetic fields ∣B∥∣ to control the polarization of the electron spins in the neurons. The qubit spectra as a function of temperature at fixed in-plane magnetic field of 10 mT are shown in Fig. 2a. Due to parasitic circuit resonances, we only observed a clear qubit spectrum above 16 GHz. Overall, the spectra shift to the negative flux side with increasing temperature. This shift suggests that the qubit senses the decrease of the magnetization from the electron spins in the neurons with increasing temperature.

Fig. 2: Results of magnetometry.
figure 2

a Spectra of the flux qubit with neurons measured at 12.5, 25, 50, 100, and 200 mK. The temperature was adjusted from low to high in the experiment. The in-plane magnetic field was fixed at 10 mT. The color scale indicates the switching probability (see Methods) of the SQUID [20% (blue), 50% (white), and 80% (red)]. The switching probability of 50% (20 and 80%) corresponds to the ground (excited) state of the qubit. The arrows referenced to gray dashed line indicate the reduced magnetization induced shifts from the spectra at 12.5 mK. b Temperature dependence of the magnetization with an in-plane magnetic field of 10 mT. The sample was first heated to 200 mK from base temperature (yellow squares). The sample was then cooled from 200 mK to verify the experimental results (purple circles). Magnetization signal of pure parylene-C film is also plotted for comparison (brown triangles). c In-plane magnetic field dependence of the magnetization for different temperatures. d Temperature and in-plane magnetic field dependence of the magnetization as a function of ∣B∥∣/T. Original dataset is the same as c. The black dashed line is simulated magnetic flux shift. e Calculated energy diagram of electron spins in neurons as a function of magnetic field. Here, h is the Planck’s constant. The direction of the magnetic field was +z for this calculation. f Effective spin temperature as a function of the cold plate temperature. The dashed line is a guide for the eye, which indicates that the spin temperature is equal to the cold plate temperature. Error bars (standard error of curve fitting) in b–d, and f are smaller than the symbols.

Full size image

The amount of the flux shift as a function of the inverse temperature is summarized in Fig. 2b. In the high-temperature range, the magnetization, namely the magnetic flux shift increases almost linearly, while in the low-temperature range, the magnetization saturates. Figure 2b also indicates that the magnetization curve is well reproduced in both temperature sweep directions (warmup and cooldown) without hysteresis. It is important to note that a waiting time of >45 min is necessary after changing the temperature to thermalize the sample.

To investigate the temperature dependence in more detail, we measured the in-plane magnetic field dependence of the magnetization as shown in Fig. 2c, d. Here, the magnetization is plotted as a function of the ratio ∣B∥∣/T. To simulate field and temperature dependence, calculation of energy level structure is required. Electron spins induced by Fe3+ ions in cells are reported to have a energy level structure expressed by the Hamiltonian31

$$H={\mu }_{{{{{{{{\rm{B}}}}}}}}}{{{{{{{\bf{B}}}}}}}}g{{{{{{{\bf{S}}}}}}}}+D{S}_{z}^{2}+E\big({S}_{x}^{2}-{S}_{y}^{2}\big),$$
(1)

where μB is the Bohr magneton, B = B⊥ + B∥ is the magnetic field, g is the anisotropic g-factor tensor, S = (Sx, Sy, Sz) is the spin operator with the spin angular momentum S, D is the zero-field splitting, and E is the axial splitting. We used spin angular momentum S = 5/2, and the values of gx = 1.83, gy = 1.998, gz = 2.0151, D = 20.96 GHz, and E = 6.967 GHz reported in the literature31 to calculate the energy spectrum. An example of the energy level structure is plotted in Fig. 2e. Since the Hamiltonian has S = 5/2, it will result in six Zeeman-split levels En(n = 0, 1, 2, 3, 4, 5). As a result, the expected magnetization is calculated numerically by considering the population of the electron spins for each energy level. The simulation shows that the magnetization linearly increases as a function of the ratio B/T (Fig. 2d dashed line, Supplementary Note 1, and Supplementary Fig. 1) in our experimental conditions. This is consistent with lowest order two-level approximation, since the energy splitting between the first and second excited states (E2 − E1 > 70 GHz) is much larger than the energy scale of this experiment ~ 4 GHz.

However, the observed magnetization shown in Fig. 2d saturates with our experimental parameters whereas the simulated magnetization increases almost linearly (see Supplementary Fig. 1 for wider). We attribute this variation to the temperature of the spins in neurons deviating from the measured temperature of the cold plate in the dilution refrigerator. This might originate from the relatively low thermal conductivity of the parylene-C film, whose room-temperature value is 0.082 Wm−1K−1. Correcting for this deviation by assuming that there is no temperature discrepancy between the spin and thermometer temperature at 200 mK, we derive the effective spin temperature as shown in Fig. 2f. This reveals the spin temperature saturates around 40–90 mK in the low-temperature range. The saturation temperatures are different for the different magnetic fields. This observation might be related to the magnetic-field-dependent spin-lattice relaxation rate, as observed in solid state materials32, but a detailed discussion is beyond the scope of this letter. It should be noted that magnetometry of paramagnetic materials can be used as a thermometer in low-temperature ranges33.

Magnetometry of insulator film

To confirm the magnetization signal originates from the neurons, we performed magnetometry of pure parylene-C film. The contribution to the magnetization signal, measured by the qubit, from spins on the silicon substrate and in the insulator film is quantified by this experiment. Parylene-C films are reported to have unpaired electron spins with g-factor \({g}^{{\prime} } \sim\) 2 when they are damaged by an electron beam34. Figure 2b compares the results of magnetometry of the parylene-C film containing neurons with those of pure parylene-C film. This clearly shows that the magnetization signal from the parylene-C film is much smaller than the one originating from the neurons. Thus, we conclude that the magnetometry shown in Fig. 2a–d does indeed originate from the electron spins in the cultured neurons.

Conventional ESR spectroscopy of neurons

In addition, conventional ESR spectroscopy was performed for neurons cultured in the same condition as the qubit experiments to verify that the magnetization signal does indeed from the neurons. In general, neurons can have different constitutions spins like iron and copper. These spins can be separated in ESR spectrum by their different \({g}^{{\prime} }\)-factors. The spectrum shown in Fig. 3 has three large peaks corresponding to \({g}^{{\prime} }=\) 9.8, 4.3, and 2.0. The largest peak with \({g}^{{\prime} }=\) 4.3 is the signature of high spin state iron in cells with ± 3/2 transition (Fig. 2e, middle panel), while the small peak with \({g}^{{\prime} }=\) 9.8 can originate from ± 1/2 transition (Fig. 2e, bottom panel)31. The peak with \({g}^{{\prime} }=\) 2.0 might be interpreted as stemming from other metal ions, mostly copper, and radicals31. These peak structures are consistent with previous experiments31. Considering the peak height of the spectra, the contribution to the magnetization signal mainly comes from iron ions. This ESR spectrum thus conclusively confirms that the magnetization signal of Fe3+ ions in neurons can be measured by a superconducting flux qubit.

Fig. 3: Result of electron spin resonance (ESR) spectroscopy of neurons measured with a conventional X-band ESR spectrometer.
figure 3

The temperature of the sample is fixed at 10 K. Green, red, and blue arrow indicate ESR signals corresponding to \({g}^{{\prime} }=\) 9.8, 4.3, and 2.0, respectively. It should be noted that the shape of the spectrum is derivative-like due to the modulated magnetic field.

Full size image

Discussion

To estimate the number of measured neurons, we calculated the average distance between neurons to be 14 μm from the seeding condition (Fig. 1b; inset). This value is similar to the qubit size of 24 × 6 μm. Comparison of these two values leads to the conclusion that the sensing area of the qubit is expected to only have one neuron (10–20 μm). Thus, this method of magnetization detection is applicable to investigating the properties of a single neuron.

In general, it is possible to obtain material parameters from a magnetization curve, e.g., the spin angular momentum or g-factor. These parameters are key to identifying spin species in a sample. To obtain them, information about the magnetization curve, including the saturation regime, should be measured by lowering the temperature or by applying a larger in-plane magnetic field. As discussed earlier, the spin temperature saturates at >40 mK, which is higher than the cold plate temperature. According to the simulated magnetization curve (Supplementary Note 1 and Supplementary Fig. 1), we can observe the deviation from the linear dependence of the magnetization if the spins are cooled down to 12.5 mK at the magnetic field of 12.5 mT as indicated by the arrow in Supplementary Fig. 1. Consequently, using materials with higher thermal conductivity for insulation offers a route towards deriving the material parameters. The simulation also implies that the condition of 12.5 mK and 12.5 mT is still inadequate for observing the full saturation of the magnetization. Thus, application of a larger in-plane magnetic field is necessary to reach full saturation. However, the flux qubit in this work is made of aluminum, which becomes inoperational for in-plane fields >20 mT. To provide more insight into bio-spin systems, future development of flux qubits with compatibility to higher magnetic fields is required, for instance, by using niobium-based materials or thin superconducting film35.

In addition, the magnetization curve should give a number of electron spins in the sensing volume, as we demonstrated in previous experiments25,26,27,28,29. However, it is difficult to quantify the electron spins in neurons exactly in the present experiment. This is due to the lack of conversion factor between magnetization and the number of spins. However, if the parameter is combined with the slope of the flux qubit spectrum (conversion factor between magnetization and qubit frequency), we could then convert the change in the flux qubit transition frequency into the number of spins. Such a number of spin to magnetization conversion factor is attainable if the magnetometry up to the saturation regime is performed with a reference sample whose concentration is already known. This kind of quantitative analysis is especially important for expanding this method to spin imaging. For example, by comparing the results of magnetometry with stained microscope images like those in Fig. 1d, e, we can compare the distribution of electron spins whose parameters (e.g., g-factor) are identified with that of iron ions.

Although an exact conversion factor from magnetization to the number of spins is unknown, the number of detected spins can still be estimated by assuming the conversion factor from solid state materials25,26,27,28,29. This analysis yields the number of detected spins in neurons as 9 × 106. The detection volume for the qubit magnetization measurements is ~100 μm3 and hence a spin density of 9 × 1013 spins/mm3 can be extracted. In addition, the conventional ESR spectroscopy utilized in Fig. 3 can also render an estimate for the number of spins per unit volume of 2 × 1012–2 × 1013 spins/mm3. Consequently these two very different measurement protocols yield similar order of magnitude spin densities thus indicating their common origin. It should be noted that the lower spin density acquired from the ESR spectroscopy is due to the looser packing of cells in the large ESR tube.

The experimentally determined spin density can also be used to calculate the mass of iron in unit weight of cells in the neuron sample yielding 8 μg/g. This result can be compared to ESR spectroscopy of human brain tissue from literature which indicates an iron mass weight in the range 2–34 μg/g31,36. Consequently the overlap in these numbers confirms that the flux qubit does indeed detect magnetization from iron ions that is located in neurons.

In conclusion, we have demonstrated the detection of electron spins in cultured neurons using a superconducting flux qubit. By combining the ESR spectra obtained with a conventional spectrometer, the spin species is identified as iron in neurons. We emphasize that the typical size of the cells is close to the loop size of the qubit, which enables the investigation of individual neurons. Our device is also capable of detecting ESR signals if the excitation tone for the neurons is applied, as we previously demonstrated for solid-state spin materials25,26,27,28,29. The application of the excitation tone splits the spectrum composing the contribution to the magnetic field signal from different constituent spins due to their characteristic g\({}^{{\prime} }\)-factors at the single-cell level. Thus, the more detailed characteristics of the neurons would be visible from spectroscopic fingerprints in future experiments, including the detection of other metallic elements such as chromium, manganese, or copper.

Methods

Experimental setup

Figure 1a shows the experimental setup for magnetometry of cultured neurons. A superconducting flux qubit was fabricated on a silicon substrate. To read out the quantum state of the qubit, we inductively coupled a direct current superconducting quantum interference device (DC SQUID) to the qubit37. The measurement condition of the SQUID is tuned to have two states with finite (normal state) or zero voltage (superconducting state) depending on the magnetic flux through the SQUID loop. Since the flux qubit generates a magnetic flux depending on its quantum state, ground or excited state of the flux qubit can have one-to-one relationship to the two states of the SQUID. Switching probability is defined by the ratio of the number showing normal states to the total number of qubit readouts. The qubit was excited by a microwave tone applied through an on-chip microwave line. The neurons cultured on a polymeric film were attached by hand to the qubit chip as depicted in Fig. 1b.

Flux qubits are two-level systems with a hyperbolic resonance frequency dependence as a function of the perpendicular magnetic field through the loop of the qubit B⊥38,39 (Fig. 1c). To convert the change in the magnetization of the neurons into the change in the resonance frequency of the qubit, the qubit spectrum should have a finite slope. This condition is satisfied by adjusting the operation flux of the qubit as shown in Fig. 1c. Details of the sensing methodology employed for solid-state spin materials is available in our previous papers25,26,27,28,29.

The major difference between solid-state spin materials and neurons is the necessity of insulation between the spin sample and qubit device. We first confirmed that the resistance of the SQUID exhibited an irregular response at low temperatures for a device with neurons without an insulation layer between them. Thus, the measurement of the qubit state can not be performed without insulation.

To insulate the qubit device from neurons, a poly(chloro-p-xylylene) (parylene-C) film with the thickness of 2 μm is laminated on the qubit surface. Parylene-C is the mobile substrates for adherent cells with high biocompatibility, stiffness, optical transparency, and high electrical resistance40,41. These features are ideal to transfer the film with cells onto the qubit chip while keeping electrical insulation between them. The parylene-C film is developed on a glass substrate by chemical vapor deposition and then neurons are seeded on the parylene-C coated substrate. Cell culture was performed as described in previous work42. Neurons are dissected from hippocampi of 18-day-old Wistar rat embryos. The culture sample is fixed with glutaraldehyde by cross-linking the proteins. The solvent and water in the sample are removed using a freeze dryer. The neuron-laden parylene-C film is detached from the glass substrate and transferred onto the qubit chip. To make the alignment of neurons to the qubit easy, neurons are densely seeded on the parylene-C film with an initial density of 5000 cells/mm2 (Fig. 1b; inset). All animal experiments are approved by the Biological Safety and Ethics Committee of NTT Basic Research Laboratories (approval ID 2019-05), which are in compliance with the Guidelines for the Proper Conduct of Animal Experiments of the Science Council of Japan (Kohyo-20-k16-2, 2006).

For this experiment, we cultured the neurons in an Fe3+-rich culture medium to increase the number of the intracellular Fe3+ ions, as shown in Fig. 1d, e. As indicated by the white arrows in Fig. 1e, some neurons uptake a high amount of Fe3+ ions. The elevated level of intracellular Fe3+ (Supplementary Note 2 and Supplementary Fig. 2a) and the increased number of Fe3+-rich neurons (Supplementary Note 2 and Supplementary Fig. 2b) indicate that the culture in the Fe3+-rich medium results in high intracellular Fe3+ ions.

The flux qubit works as a magnetometer for unpaired electron spins originating from Fe3+ ions. To enhance the sensitivity of the magnetometry, the distance between the qubit and neurons should be minimized. To this end, after transferring the neuron-laden parylene-C film on the qubit chip, a small amount of ethanol was introduced to induce attachment via surface tension. Judging from an optical interference pattern formed by the gap between the qubit chip and the parylene-C film43, the typical distance between the qubit and neurons is estimated to be several micrometers, which is within the sensing volume of the flux qubit.

X-band ESR spectroscopy is performed using a commercial spectrometer, Bruker E500. ESR spectrum is obtained by using TE011 mode cavity with a Q-factor of 8000. A microwave signal at 9.38 GHz is sent to the cavity with the power of 8 mW at the generator. A magnetic field around 0.3 T is applied to samples with the magnetic field modulation (0.9 mT, 100 kHz). Samples are packed in quartz tubes with the diameter of 5 mm.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.