Abstract
Ultrafast folding proteins have become an important paradigm in the study of protein folding dynamics. Due to their low energetic barriers and fast kinetics, they are amenable for study by both experiment and simulation. However, single molecule force spectroscopy experiments on these systems are challenging as these proteins do not provide the mechanical fingerprints characteristic of more mechanically stable proteins, which makes it difficult to extract information about the folding dynamics of the molecule. Here, we investigate the unfolding of the ultrafast protein Engrailed Homeodomain (EnHD) by single-molecule atomic force microscopy experiments. Constant speed experiments on EnHD result in featureless transitions typical of compliant proteins. However, in the force-ramp mode we recover sigmoidal curves that we interpret as a very compliant protein that folds and unfolds many times over a marginal barrier. This is supported by a simple theoretical model and coarse-grained molecular simulations. Our results show the ability of force to modulate the unfolding dynamics of ultrafast folding proteins.
Similar content being viewed by others
Introduction
Most single-domain proteins exhibit an all-or-none folding behavior due to the high energy barriers that need to be overcome during the (un)folding process. The (un)folding of this type of protein is highly cooperative1, and equilibrium and kinetic experiments on this type of system where the equilibrium is perturbed either by temperature or a chemical denaturant are easily interpretable. For these proteins, the ensemble of states is mostly distributed between the folded and unfolded state, and therefore it is not possible to extract information about the folding mechanism, i.e., the myriad of conformations that are visited as the protein evolves towards the native state2. This becomes possible for ultrafast folding proteins, which lie on the other side of the cooperativity spectrum. They fold in timescales between milliseconds and microseconds and are characterized by their small size, typically helical structure, and low (<3kBT) free-energy barriers3. For this reason, there is a measurable population in the intermediate states of the protein, which could, in principle, be resolved by spectroscopy and, potentially, even at the single-molecule level.
After their initial applications to protein folding three decades ago, single-molecule force spectroscopy (smFS) techniques are now established as a means of accessing details of the (un)folding process that are distinct from those derived from traditional methods reliant on ensemble averaging4. smFS techniques either using optical or magnetic tweezers or an atomic force microscope (AFM), allow direct manipulation of an (un)folding reaction coordinate throughout the application of controlled mechanical forces5,6,7. Two-state and multi-state proteins often have easily interpretable signals upon mechanical unfolding, e.g., a saw-tooth pattern characterized by well-defined contour lengths in constant speed mode, or discrete jumps of measurable extension in the force–ramp, and force–clamp modes8,9,10. However, as the cooperativity of the protein decreases, proteins oppose less resistance to the external force, and these fingerprints become less predictable or disappear altogether. For example, Rief and his co-workers studied the prototypical ultrafast folder villin headpiece subdomain using optical tweezers11 They obtained continuous hump-like equilibrium transitions at a range of pulling speeds and completely featureless constant force traces at the midpoint. More recently, Perkins and his co-workers studied the computationally designed, three-helix bundle α3D12,13,14, which in bulk also folds in the microsecond regime15. α3D turned out to be extremely labile under force, resulting in a barely distinguishable peak of less than 12 pN. In previous work, we studied the reversible folding and unfolding protein gpW at a constant force under the AFM16,17. We resolved hopping transitions in an energy landscape with a low free energy barrier induced by the external force.
Here, we expand the realm of ultrafast folders studied using smFS examining the mechanical unfolding of the Engrailed Homeodomain (EnHD), a DNA binding domain of the transcription factor engrailed from Drosophila melanogaster. EnHD is a three-helix bundle of 54 residues that folds close to the protein folding speed limit, in the range of a few microseconds, and has been extensively characterized in bulk18,19,20. From the analysis of calorimetric and kinetic experiments, it has been predicted to have a marginal folding barrier21,22. Remarkably, EnHD did not fold into its conformation in a set of long-time-scale atomistic simulations, but another homeodomain exhibited a downhill free energy surface23. Our pulling experiments show that EnHD has weak mechanical stability, as expected for a protein that folds over a marginal free energy barrier. When subjected to a gradually increasing mechanical force (i.e., a force–ramp) the observed signature is not stepwise but sigmoidal. We interpret these results as a compliant mechanical response compatible with the simple theoretical adaptation of the Bell model and molecular simulations using a coarse-grained simulation model. The emerging picture is that of a very compliant protein that folds and unfolds many times over a marginal barrier induced by the applied force.
Results
Single-molecule force-extension experiments at a constant speed
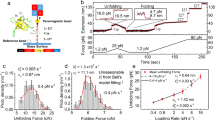
For our AFM experiments, we engineered a polyprotein where the protein EnHD (PDB code:1enh, Fig. 1a) is sandwiched between two pairs of I91 domains of human cardiac titin, resulting in the (I91)2-EnHD-(I91)2 construct. The I91 domains serve as mechanical handles when the polyprotein is subjected to a mechanical force (Fig. 1b). Importantly, the mechanical properties of I91, such as unfolding force and contour length (ΔLc), are well characterized and are clearly distinguishable in force spectroscopy measurements24,25. Thus, I91 serves as a molecular fingerprint for an adequate trace selection when the mechanical properties of the protein of investigation are difficult to recognize. In the case of EnHD, this is particularly important given its weak cooperativity, which may result in a featureless signal under force. Firstly, we conducted force-extension experiments where the EnHD polyprotein is forced to elongate at a constant velocity of 40 nm s−1. The unfolding of the molecule typically creates a sawtooth pattern in these experiments because the unfolding of each domain is composed of a stage of building up force while the domain remains resistant to the applied tension followed by a sudden drop on the registered force due to the triggering of unfolding. Registered measurements show the characteristic sawtooth pattern for I91 domains (Fig. 1c), and the analysis with the worm-like chain (WLC) model reveals mechanical stability of approximately in the range of 181 ± 8 pN (average ± SEM), although it depends on the unfolding speed, and a ΔLc of 28 ± 1 nm (average ± SD), in agreement with what is described in the literature26 (Supplementary Fig. 1). Conversely, no clear sawtooth pattern is detected for the unfolding EnHD. This suggests that EnHD has a very low mechanical resistance and unfolds at very low forces, so it goes virtually undetected in force-extension experiments.
a Representation of the crystal structure of the EnHD domain. b Scheme of the experimental setup. The EnHD is sandwiched between two titin homodimers, deposited in solution over a gold surface, and dragged by the AFM cantilever, resulting in the unfolding of the proteins. c Force-extension trace including the characteristic sawtooth pattern for the titin domains, and the initial featureless signal for EnHD. Stretching is conducted at a speed of 40 nm s−1.
Coarse-grained molecular dynamics simulations
These experimental results are consistent with coarse-grained molecular simulations using a structure-based all-atom simulation model (see Methods). First, in native conditions, the protein exhibits a unimodal free energy surface derived from the projection on the relevant reaction coordinate for folding, the fraction of native contacts, Q (Fig. 2a). Upon the application of an external force that pulls from the protein ends at constant extension speed, EnHD is very compliant, resulting in a low force peak (Fig. 2b). Because the units in the model cannot be compared directly with those in the experiment, we show the same result for pulling simulations on an immunoglobulin-like domain of titin used as a fingerprint for reference. The simulations recover the stark differences between a mechanically resistant protein and the featureless force-extension pattern for EnHD. We show snapshots of different conformations along the unfolding trajectory in Fig. 2d. The mechanical unfolding involves untangling the bundle, followed by the melting of the alpha helices. We have also run constant force simulations using our coarse-grained model. As we found for protein gpW16, force induces a small free energy barrier of approximately ~2 kBT that separates two well-defined minima in the protein landscape (Fig. 2a, c). We note that a similar hopping pattern between the folded and unfolded states is observed in experiments performed at a constant force of 8 pN (Supplementary Fig. 2a, b), although we were able to measure only a few of these events due to the complexity of low force experiments using our AFM. These transitions in the second timescale are mostly observed when the force perturbation is maintained to give sufficient time to cross the energy barrier induced by force. As we showed in our study of protein gpW27, the observation of transitions in the second timescale is consistent with the low barrier predicted by the simulations, if we consider that the dynamics under constant force are mainly determined by the apparatus. On the other hand, the change in extension between the native and mechanically unfolded states observed in the simulations is shorter than in experiments, likely due to the many simplifications in the coarse-grained model.
a Potential of mean force for the projection of coarse-grained simulations on the fraction of native contacts, Q. The black curve corresponds to the simulations in native conditions, and the red curve at the mechanical midpoint. b Force-extension curves from simulations at a constant pulling speed of 1e−3 nm/ps for EnHD (red) and titin (black). c Free energy landscape for both the end-to-end extension, L, and Q. Contour lines mark 0.5 kBT. d Cartoon representation of different conformations sampled during the mechanical unfolding, with timestamps relative to the numbering in. The green and blue beads correspond to the alpha carbons of the N and C-termini, respectively.
Single-molecule force–ramp experiments
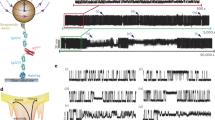
To further resolve the mechanical unfolding of the EnHD protein, we prepared force–ramp measurements at different values of the force loading rate. This approach gives accurate control of the applied force due to the intervention of a feedback loop that compensates for changes at a window of time below 1 ms. Thus, this protocol permits scanning a broad range of unfolding forces while controlling the force applied. The force protocol starts by pushing the cantilever against the gold substrate with a 10 pN force. Then, the cantilever slowly pulls from the protein at the desired loading rate (we used values of 1, 10, and 100 pN s−1), providing enough resolution to detect the unfolding response of our protein at both low and high forces. Finally, the rate is increased so that forces high enough to unfold I91 are reached more quickly. For two-state proteins, this type of experiment typically registers discrete jumps with lengths extensions that are force-dependent and that can be explained by models of polymer elasticity such as the worm-like chain (WLC) or freely-jointed chain28,29. However, for EnHD we obtained an unexpected sigmoidal unfolding pattern at forces below 20 pN (Fig. 3a and Supplementary Fig. 3). In the final part of the force-ramp traces, we observe the events corresponding to the four I91 titin repeats with a characteristic 24.5 nm length. Prior to the I91 unfoldings, the total change in the extension of the sigmoidal pattern matches the extension of EnHD of about 15 nm in the 20 pN range force (Fig. 3a), suggesting that this behavior corresponds to the unfolding of EnHD.
a Time series for the measured extension (top) and force (bottom) in a force-ramp experiment at 10 pN s−1 loading rate for EnHD. The inset highlights the signal corresponding to EnHD unfolding. b Same as a, but now including two consecutive low loading-rate force ramps separated by a force-quench to zero force. c Average force/length curve from multiple traces for EnHD and protein gpW (n = 29 independent traces from multiple experiments) at 10 pN s−1. Vertical dashed lines mark the mid-unfolding force (F1/2) for EnHD (red) at 7.6 pN, and gpW (brown) at 4.6 pN. Propagating baselines (black dashed lines) provide an estimated extension of about 7.5 nm for EnHD. The inset is the first derivative of the sigmoidal fit, indicating also mid-unfolding force.
To discard the possibility of any unspecific interactions between the protein construct and the surface, we repeat the cycle by quenching the force after the initial sigmoidal increase followed by another force-ramp at the same loading rate, which resulted in a similar sigmoidal increase very much like in the first event (Fig. 3b). This reproducibility in a single protein domain suggests that we are indeed looking at the mechanical unfolding of EnHD. The sigmoidal curves that we report have not been observed in the smFS literature before and must be interpreted with care. In Fig. 3c, we show the average of several force-ramp traces at 10 pN s−1, from whose derivative we estimate a mid-unfolding force F1/2 for this protein of 7.6 pN, which is close also to the value of the force at which we observed the hopping in force-clamp experiments (Supplementary Fig. 2b). Baseline propagation to F1/2 force value results in an extension of ~7.5 nm (Fig. 3c), which is comparable to the extension obtained by the WLC considering a contour length Lc of 19 nm and persistence length ρ of 0.4 nm. The F1/2 value of 7.6 pN is also in the same range as that for gpW also measured at ramps of 10 pN/s (F1/2 = 4.6 pN; see Fig. 3c, inset) and is also consistent with the value of the mid-unfolding force recently determined for α3D (F1/2 = 8.9 pN)14. These results suggest that EnHD has a mechanical resistance that is intermediate to those of gpW and α3D, demonstrating that the mid-unfolding force is a feature of ultrafast folding proteins, but, more importantly, shows that force–ramp experiments are suitable for the characterization of compliant unfolding patterns and that the unfolding midpoint is unique to each protein. Interestingly, the force-ramp perturbation is still sufficiently fast for EnHD to avoid slow transitions in the second timescale, such as those created by the entropic energy barrier, easily observable in the force–clamp regime.
A theoretical model for EnHD mechanical unfolding
To better understand the molecular event responsible for the sigmoidal signal, we have run stochastic simulations based on the Bell model at increasing force30,31. We set the model parameters using folding and unfolding rates in the order of the experimentally derived values for the in bulk at 25 °C18,20, and calibrate the position of the transition state to match the average experimental curve (Fig. 3c). In Fig. 4, we present the result of multiple stochastic simulations where folding and unfolding can occur multiple times in the timescale of the experiment. We represent the distance to the transition state (DTS) as a percentage of the total length. Using a transition state that is close to the unfolded state (i.e., at 90% of the distance between folded and unfolded) allows us to recapitulate the sigmoidal curves observed in the experiments (Fig. 4a). Other DTS are represented in Fig. 4b for comparison. We note that a short distance to the transition state would result in stepwise transitions, as observed for mechanically stable proteins like the titin domains, and a longer transition state would result in an almost linear unfolding. In our experiments, we have occasionally observed both types of transitions (Supplementary Fig. 4), suggesting a certain plasticity in the transition state of EnHD that would be consistent with its low free energy barrier. Using the atomistic coarse-grained model, we have run simulations that gradually increase the unfolding force (see Methods). The timescale that we cover in the molecular simulations is shorter than that in the experiments and in the stochastic model. Still, it is sufficient to reproduce the repetitive folding and unfolding, supporting our interpretation of the results (Supplementary Fig. 5).
a Force-extension plot from a simulation using the numerical Bell model with stochastic transitions (light green). Average experimental traces were obtained at 1 pN/s (orange). b Same Bell model are shown in (green) using different transition state distances and the average experimental traces are superimposed (orange).
Discussion
In the past decade, the study of proteins by smFS has revealed a variety of aspects in their folding dynamics that are mostly undetectable by traditional ensemble averaging methods. However, only recently have these methods been applied to proteins with low cooperativity, which are challenging due to their low unfolding forces and fast folding kinetics16. Here we have presented results on a protein with weak cooperativity, EnHD, using a combination of experiments, numerical modeling, and molecular simulations. Our results show that EnHD is a compliant protein that folds, overcoming a marginal free energy barrier induced by mechanical force. The mid-unfolding force obtained from both constant force and force-ramp experiments for EnHD is in the same range as other labile proteins like gpW16 and α3D14. From our force-ramp experiments, we obtain a novel sigmoidal signature that we interpret as multiple events of folding and unfolding of the protein, which occur repetitively in the timescale of the experiment.
In previous work, we investigated the instrumental effects in constant-force experiments on gpW16,17. Recent theoretical analysis indicates that folding and unfolding will be slowed down considerably both by the force probe and the smFS experiments32,33. Although a detailed analysis of these effects is beyond the scope of the current work, our results show folding and unfolding rates in the stochastic model up to two orders of magnitude slower than in bulk. Our previous analysis for gpW also indicated that despite introducing a slowdown in the dynamics, the apparent folding and unfolding measured by the instrument indeed trace the true molecular folding and unfolding events. We find that even in these conditions, the force-ramp experiments with EnHD result in a sigmoidal curve with multiple folding and unfolding events, that could be reproduced using a simple Bell model. We have discovered that the plasticity of the mechanical transition state is a feature of EnHD that defines the low cooperativity of this protein, making the unfolding highly compliant. Thus, this work shows how force can be used as a tool to investigate low-cooperativity proteins creating a mechanical signature that reveals the plasticity and compliance of the unfolding process. We believe that with greater improvements both in the time resolution of the instruments and in the design of cantilevers12,34, we anticipate that smFS experiments of folding and unfolding will continue revealing molecular details of weakly cooperative proteins.
Methods
Protein expression and purification
Gene encoding (I91)2-EnHD-(I91)2 chimeric polyprotein construct was designed and optimized for expression in Escherichia coli (Life Technologies). Here, two additional cysteine residues were added in the C-terminus, which helps for sample immobilization on the gold surface. Standard DNA manipulation protocols were used to clone the construct into the pQE80L expression plasmid (Qiagen). C41 strand competent cells of E. coli (Novagen) were used for protein expression. Transformed competent cells were grown in 1 L of LB media at 37 °C until an OD600 of around 0.6 was reached. Then protein expression was introduced by 1 mM of IPTG and further incubation at 37 °C for 4 h. Cells were then centrifuged, and a gentle cell lysis protocol was used to avoid damage to the expressed polyproteins. The sample was then purified first by HisTag affinity chromatography using a gravity column filled with HisPur Cobalt resin (Thermo Fisher Scientific) and second by size exclusion chromatography using a Superdex 200 HR column (GE Healthcare). The final elution buffer was HEPES 10 mM pH 7.0, NaCl 150 mM, and EDTA 1 mM. The sample was further concentrated using ultrafiltration Amicon 3k filters (Millipore). The final protein concentration was estimated to be around 1 mg mL−1 using a Nanodrop (Thermo Scientific). Then the samples were snap-frozen in liquid nitrogen and stored at −80 °C.
Single-molecule force spectroscopy (smFS)
All smFS force extension, constant force, and force ramp experiments were performed on an Atomic Force Spectrometer AFS-1 (Luigs Neumann). Biolever cantilevers from Olympus/Bruker were used with a spring constant of around 6 pN nm−1 for all constant force and force ramp measurements. The spring constant was measured before each experiment using the equipartition theorem within a software built-in procedure. Data was recorded between 0.5 and 4 kHz for the constant force and force ramp measurements. For those experiments that included quenching of force (Fig. 2c), the force was ramped at 1 pN s−1 until 45 pN (starting from 10 pN pushing F < 0). At this point, it was restored back to 10 pN pushing and ramped with the same rate until 45 pN again. During the combination of force–ramp and constant force experiments (Fig. 3), the force was ramped at a rate of 1 pN s−1 until reaching the 8 pN constant force. Then the protein was held for 20–30 s at the constant force before the ramp at 1 pN s−1 was continued. To reduce total experimental acquisition time, all traces include a rapid increase of the force rate to 30 pN s−1 at the end to quickly reach the high forces required to unfold Titin-I91 domains. All AFM experiments were carried out at room temperature (~24 °C) in HEPES buffer at pH 7.0. Typically, 40 µl of the protein sample (~µM concentration) was left for around 20 min for adsorption on a fresh gold-coated surface, using gold evaporation (Oerlikon UNIVX350). After the adsorption time, the sample was then rinsed off the gold surface with the HEPES buffer to remove the unbounded protein sample just before starting the measurements. Multiple traces are collected in each experiment and several samples were used in every condition. Data was collected and analyzed using Igor Pro 6.0 software.
Theoretical model
To interpret the force ramp experiments we use a simple model of two-state kinetics that allows for stochastic jumps between the folded and unfolded states depending on the force-dependent rates for folding and unfolding, kf (F) and ku(F). This dependence is described using the Bell model30, i.e. kf (F) = kf (0)exp(-βΔxfF) and ku(F) = ku(0)exp(βΔxuF), where kf/u(0) are the values of the folding and unfolding rates in bulk, Δxf/u is the distance to the from either state to the transition state and β is the inverse thermal energy. The extension of either the folded or the unfolded state at a given force are described using the WLC model, using a contour length of 19 nm and a persistence length of 0.4 nm. Simulations were run using a Gillespie algorithm35. Igor Pro 6.0 and Matlab v9.5 software were used for calculations and analysis.
Coarse-grained molecular dynamics simulations
We run molecular simulations using an atomistic structure-based model36. Briefly, the model keeps all the heavy atoms of the protein and represents interactions via harmonic terms for bonds, angles, and dihedrals. For atom pairs that are in contact in the native conformation, non-bonded interactions are represented by a Lennard-Jones potential. All other pairwise interactions are repulsive. Models were generated using the stand-alone version of the SMOG software package37, and simulations were performed using the Gromacs software package38, using a leap-frog stochastic dynamics integrator with a timestep of 5e−4 fs and a coupling constant of 1 ps (we note that the timescales of the model do not correspond to physical times). We first run simulations at multiple temperatures to estimate the folding temperature in the model. Then we run pulling simulations at a constant force and constant pulling speed using the pull code in Gromacs. Finally, we emulate the force–ramp mode by concatenating thousands of short simulation runs, each of which has an incrementally larger constant pulling force and starts from the last snapshot of the previous run. Results were analyzed using the MDtraj Python library39.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
Data supporting the findings of this study are available from the corresponding author upon reasonable request. Codes used to analyze the data are available upon request.
References
Guinn, E. J., Kontur, W. S., Tsodikov, O. V., Shkel, I. & Record, M. T. Probing the protein-folding mechanism using denaturant and temperature effects on rate constants. Proc. Natl Acad. Sci. USA 110, 16784–16789 (2013).
Carrion-Vazquez, M. et al. Mechanical and chemical unfolding of a single protein: a comparison. Proc. Natl Acad. Sci. USA 96, 3694–3699 (1999).
Garcia-Mira, M. M., Sadqi, M., Fischer, N., Sanchez-Ruiz, J. M. & Munoz, V. Experimental identification of downhill protein folding. Science 298, 2191–2195 (2002).
Schönfelder, J., De Sancho, D. & Perez-Jimenez, R. The power of force: insights into the protein folding process using single-molecule force spectroscopy. J. Mol. Biol. 428, 4245–4257 (2016).
Tapia-Rojo, R., Eckels, E. C. & Fernández, J. M. Ephemeral states in protein folding under force captured with a magnetic tweezers design. Proc. Natl Acad. Sci. USA 116, 7873–7878 (2019).
Schönfelder, J., Perez-Jimenez, R. & Muñoz, V. A simple two-state protein unfolds mechanically via multiple heterogeneous pathways at single-molecule resolution. Nat. Commun. 7, 11777–11777 (2016).
Bustamante, C., Alexander, L., Maciuba, K. & Kaiser, C. M. Single-molecule studies of protein folding with optical tweezers. Annu. Rev. Biochem. 89, 443–470 (2020).
Perales-Calvo, J., Giganti, D., Stirnemann, G. & Garcia-Manyes, S. The force-dependent mechanism of DnaK-mediated mechanical folding. Sci. Adv. 4, eaaq0243 (2018).
Alonso-Caballero, A. et al. Mechanical architecture and folding of E. coli type 1 pilus domains. Nat. Commun. 9, 2758 (2018).
Perez-Jimenez, R. et al. Probing the effect of force on HIV-1 receptor CD4. ACS Nano 8, 10313–10320 (2014).
Zoldak, G., Stigler, J., Pelz, B., Li, H. & Rief, M. Ultrafast folding kinetics and cooperativity of villin headpiece in single-molecule force spectroscopy. Proc. Natl Acad. Sci. USA 110, 18156–18161 (2013).
Edwards, D. T., Faulk, J. K., LeBlanc, M.-A. & Perkins, T. T. Force spectroscopy with 9-μs resolution and sub-pN stability by tailoring AFM cantilever geometry. Biophys. J. 113, 2595–2600 (2017).
Walder, R. et al. Rapid characterization of a mechanically labile α-helical protein enabled by efficient site-specific bioconjugation. J. Am. Chem. Soc. 139, 9867–9875 (2017).
Edwards, D. T., LeBlanc, M. A. & Perkins, T. T. Modulation of a protein-folding landscape revealed by AFM-based force spectroscopy notwithstanding instrumental limitations. Proc Natl Acad Sci USA 118, e2015728118 (2021).
Zhu, Y. et al. Ultrafast folding of alpha3D: a de novo designed three-helix bundle protein. Proc. Natl Acad. Sci. USA 100, 15486–15491 (2003).
Schönfelder, A. J., Sancho, D. D., Berkovich, R. & Best, R. B. Reversible two-state folding of the ultrafast protein gpW under mechanical force. Commun. Chem. 1, 59 (2018).
De Sancho, D., Schönfelder, J., Best, R. B., Perez-Jimenez, R. & Muñoz, V. Instrumental effects in the dynamics of an ultrafast folding protein under mechanical force. J. Phys. Chem. B https://doi.org/10.1021/acs.jpcb.8b05975 (2018).
Mayor, U., Johnson, C. M., Daggett, V. & Fersht, A. R. Protein folding and unfolding in microseconds to nanoseconds by experiment and simulation. Proc. Natl Acad. Sci. USA 97, 13518–13522 (2000).
Mayor, U. et al. The complete folding pathway of a protein from nanosecons to microseconds. Nature 421, 863–867 (2003).
Religa, T. L. et al. The helix turn helix motif as an ultrafast independently folding domain: the pathway of folding of Engrailed homeodomain. Proc. Natl Acad. Sci. USA 104, 9272–9277 (2007).
Naganathan, A. N., Sanchez-Ruiz, J. M. & Muñoz, V. Direct measurement of barrier heights in protein folding. J. Am. Chem. Soc. 127, 17970–17971 (2005).
Naganathan, A. N., Doshi, U. & Munoz, V. Protein folding kinetics: barrier effects in chemical and thermal denaturation experiments. J. Am. Chem. Soc. 129, 5673–5682 (2007).
Lindorff-Larsen, K., Piana, S., Dror, R. O. & Shaw, D. E. How fast-folding proteins fold. Science 334, 517–520 (2011).
Peters, D. T. et al. Unraveling the molecular determinants of the anti-phagocytic protein cloak of plague bacteria. PLoS Pathog. 18, e1010447 (2022).
Manteca, A. et al. Mechanochemical evolution of the giant muscle protein titin as inferred from resurrected proteins. Nat. Struct. Mol. Biol. 24, 652–657 (2017).
Perez-Jimenez, R., Garcia-Manyes, S., Ainavarapu, S. R. & Fernandez, J. M. Mechanical unfolding pathways of the enhanced yellow fluorescent protein revealed by single molecule force spectroscopy. J. Biol. Chem. 281, 40010–40014 (2006).
De Sancho, D., Schönfelder, J., Best, R. B., Perez-Jimenez, R. & Muñoz, V. Instrumental effects in the dynamics of an ultrafast folding protein under mechanical force. J. Phys. Chem. B 122, 11147–11154 (2018).
Oberhauser, A. F., Hansma, P. K., Carrion-Vazquez, M. & Fernandez, J. M. Stepwise unfolding of titin under force-clamp atomic force microscopy. Proc. Natl Acad. Sci. USA 98, 468–472 (2001).
Schlierf, M., Li, H. & Fernandez, J. M. The unfolding kinetics of ubiquitin captured with single-molecule force-clamp techniques. Proc. Natl Acad. Sci. USA 101, 7299–7304 (2004).
Bell, G. I. Models for the specific adhesion of cells to cells. Science 200, 618–627 (1978).
Edwards, D. T., LeBlanc, M.-A. & Perkins, T. T. Modulation of a protein-folding landscape revealed by AFM-based force spectroscopy notwithstanding instrumental limitations. Proc. Natl Acad. Sci. USA 118, e2015728118 (2021).
Nam, G. M. & Makarov, D. E. Extracting intrinsic dynamic parameters of biomolecular folding from single-molecule force spectroscopy experiments. Protein Sci. 25, 123–134 (2016).
Cossio, P., Hummer, G. & Szabo, A. On artifacts in single-molecule force spectroscopy. Proc. Natl Acad. Sci. USA 112, 14248–14253 (2015).
Edwards, D. T. et al. Optimizing 1-mus-resolution single-molecule force spectroscopy on a commercial atomic force microscope. Nano Lett. 15, 7091–7098 (2015).
Gillespie, D. T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81, 2340–2361 (1977).
Whitford, P. C. et al. An all-atom structure-based potential for proteins: bridging minimal models with all-atom empirical forcefields. Proteins 75, 430–441 (2009).
Noel, J. K. et al. SMOG 2: a versatile software package for generating structure-based models. PLoS Comput. Biol. 12, e1004794 (2016).
Abraham, M. J. et al. GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 1-2, 19–25 (2015).
McGibbon, R. T. et al. MDTraj: a modern open library for the analysis of molecular dynamics trajectories. Biophys. J. 109, 1528–1532 (2015).
Acknowledgements
This work has been supported by grants PID2019-109087RB-I00 to R.P.-J. and PGC2018-099321-B-I00 and RYC-2016-19590 to D.D. from the Spanish Ministry of Science and Innovation. This project has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No. 964764 to R.P.-J. D.D. receives support from Eusko Jaurlaritza (Basque Government) through the project IT1254-19. A.R. is the recipient of a doctorate fellowship from the Spanish Ministry of Science and Innovation. I.R.-O. acknowledges financial support from Donostia International Physics Center (DIPC).
Author information
Authors and Affiliations
Contributions
R.P.-J., V.M., and D.D. conceived the project and designed the research. A.R., A.O.-S., and J.S. cloned the protein and performed smFS experiments. A.R., D.D., V.M., and R.P.-J. analyzed smFS experiments. I.R.-O. and D.D. conducted computational molecular dynamics simulations. V.M. performed theoretical analysis. All authors contributed to writing and revising the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interest.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Reifs, A., Ruiz Ortiz, I., Saa, A.O. et al. Compliant mechanical response of the ultrafast folding protein EnHD under force. Commun Phys 6, 7 (2023). https://doi.org/10.1038/s42005-022-01125-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-01125-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.