Abstract
Combinatorial optimization problems are difficult to solve with conventional algorithms. Here we explore networks of nonlinear electronic oscillators evolving dynamically towards the solution to such problems. We show that when driven into subharmonic response, such oscillator networks can minimize the Ising Hamiltonian on non-trivial antiferromagnetically-coupled 3-regular graphs. In this context, the spin-up and spin-down states of the Ising machine are represented by the oscillators’ response at the even or odd driving cycles. Our experimental setting of driven nonlinear oscillators coupled via a programmable switch matrix leads to a unique energy minimizer when one exists, and probes frustration where appropriate. Theoretical modeling of the electronic oscillators and their couplings allows us to accurately reproduce the qualitative features of the experimental results and extends the results to larger graphs. This suggests the promise of this setup as a prototypical one for exploring the capabilities of such an unconventional computing platform.
Similar content being viewed by others
Introduction
The desire to solve complex combinatorial problems in an energy and time-efficient manner ignites the race to implement classical state-of-the-art optimisation techniques on traditional hardware. The implementation of the simulated annealing leads to a traditional classical solver, on complementary metaloxide-semiconductors (CMOSs) hardware results in the CMOS annealer1,2, and with field programmable arrays (FPGAs) it is known as the digital annealer machine3,4. The realisation of another physics-inspired method on graphics processing units (GPUs) underlies the simulated bifurcation machine5,6. With such mature dedicated hardware, the computational performance of classical optimisation methods can be studied on a large scale of hundreds of thousands of elements.
Novel computing paradigms can be based on novel physical platforms augmented by traditional hardware. In such a hybrid approach, the optimisation efficiency depends not only on classical algorithms, and the better quality of solutions is expected from natural internal processes in physical systems, while the classical hardware provides interactions between physical elements. For example, the FPGA operates in concert with the optical parametric oscillators7 and the spatial light modulator can create couplings between polariton condensates8,9 for solving hard optimisation problems.
To overcome the time limitations of traditional hardware, the pure passive unconventional computing architectures can be considered. In these architectures, the solution to the optimisation problem is found solely through an analogue system without exchanging information with the classical counterparts. The memristors (short for memory resistors) can perform matrix-vector multiplications according to Ohm’s and Kirchhoff’s laws in a completely analogue way10. Circuits of memristors (memristor crossbars) are used for simulating neural networks11,12,13 including Hopfield networks for solving hard optimisation problems14. A further improvement in power consumption over memristor-based Hopfield networks is expected for networks of phase-transition nano-oscillators with capacitive couplings15. These beyond-traditional hardware approaches16,17,18, as well as all-optical passive computing architectures with a similar principle of in-memory computing19,20,21,22, are naturally suitable for highly parallel calculations and offer orders-of-magnitude higher energy efficiency than classical devices. Many more physical systems are under intense investigation as quadratic unconstrained binary optimisation (QUBO) solvers in the post-CMOS era including lasers23,24,25,26, photonic simulators27, trapped ions28, photon and polariton condensates29,30, QED31,32, and others33,34,35.
The electronic and optical oscillator-based unconventional computing machines are generally applied to the minimization of spin Hamiltonians, to which many of the real-life optimisation problems can be mapped with a polynomial overhead36. One of the challenges in assessing the potential optimisation performance of such platforms is caused by the choice of instances of NP-hard problems. For example, minimising the Ising spin Hamiltonian on unweighted 3-regular graphs is proven to be NP-hard37, while for a subclass of Möbius ladder graphs, which are often chosen for testing non-traditional computing platforms7,15,33,34,35,38,39,40, the Ising model can be minimized in polynomial time41.
To develop new physics-inspired algorithms and explore non-trivial ways for escaping local minima of complex optimisation problems, the easy-to-assemble circuits of electronic oscillators could be considered. Although this is a well-studied classical system, there are only a mere handful of works with physical implementations of oscillator-based circuits, with most studies devoted to theoretical and numerical simplified models42, which do not necessarily represent internal physical processes that can be critical to optimisation performance. There exist many types of electrical oscillators one may use for computing. The vertex coloring problem of unweighted graphs has been recently addressed with small networks of five coupled relaxation oscillators with capacitive connections43. An integrated circuit of 30 relaxation oscillators with programmable couplings was implemented for solving the maximum independent set problem44. The all-electronic Ising Machine has been explored with weighted resistive couplings for four CMOS LC oscillators40 with larger network of 240 oscillators implemented on a chimera-graph architecture45.
In this work, we explore possible global optimisation mechanisms that could help evaluate the new small-size physical solvers by minimising the Ising Hamiltonian with fundamental passive electrical circuit elements: the resistor, the capacitor and the inductor, in the presence of nonlinearity. The electrical network of such RLC oscillators is an example of a purely classical computing system implemented on CMOS. For such electronic oscillator networks, we show the difference between the Ising minimization of the trivial problems, such as Max 3-regular cut on the Möbius ladder graphs, and the non-trivial, such as on the rewired Möbius ladder graphs and on random 3-regular graphs. The ground state success probability for non-trivial problems can be dramatically increased using the dynamic control of the inductance, the optimal value of which helps to efficiently escape the local minima. We discuss possible ways for creating easy-reconfigurable couplings between oscillators and possibilities for the large-scale on-chip integration of electronic circuits.
Other recent studies have utilized CMOS electronic relaxation oscillators and, through chip integration, engineered considerable system sizes44,46,47. Our implementation allows for the formulation of physically realistic equations of motion, and thus one emphasis of this paper is on the physics-based exploration of the energy minimizer as a dynamical-systems process.
Results
Experimental setup
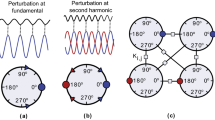
The basic idea is to drive a collection of nonlinear oscillators at a frequency that is roughly twice their natural frequency, ωd ≈ 2ω0, such that subharmonic resonance is induced in them (see also ref. 48). Subharmonic resonance is a nonlinear phenomenon and (in the case of an isolated oscillator) its onset occurs above a threshold amplitude in the driving signal49. It is characterized by an oscillator response that repeats every other driver period. Therefore, two response states are conceivable42, namely an oscillator response corresponding to either even or odd driving cycles. These two oscillator states will represent the basic “spin-up” and “spin-down” states of the Ising machine.
While the earlier work of ref. 42 proposed generic nonlinear oscillators driven by dedicated noise generators to induce parametric resonance, this is not feasible with the nonlinear RLC oscillators used here. Instead, we employ a single sinusoidal voltage signal (from a function generator) to drive all oscillators via capacitors into subharmonic resonance, as shown in Fig. 1. The oscillator consists of a varactor diode (NTE 618), featuring a nonlinear dependence of the capacitance on the voltage C(V), and an inductor, L. The coupling between a given pair of oscillators is achieved via resistors. Resistors connected straight across (red, labeled Rc(+)) favor in-phase oscillation between the two oscillators, whereas crossed resistors (blue, labeled Rc(−)) favor out-of-phase oscillation. The measured resistances of Rc-resistors were the same to within 1%, the inductor values to within 0.25%, and the capacitors to within 1%.
The main idea of coupling between nodes is illustrated here using a pair of oscillators, each consisting of a varactor diode, with capacitance C(V), and an inductor, L, in parallel. These are driven via capacitors, Cd, to induce subharmonic oscillations, for which ω = ωd/2. The two oscillators can be either positively coupled using the resistor pair labeled Rc(+) (red), or negatively using the resistor pair labeled Rc(−) (blue). The oscillations across each oscillator’s diode/inductor are measured as a floating voltage.
Figure 2a schematically depicts the experimental system for a network of eight subharmonic resonators. The main experimental challenge is to connect these eight oscillators via a programmable and reconfigurable coupling network. Our solution was to use a switch-matrix module that can be configured (via the terminal block) into a two-wire 8 × 32 cross-point matrix. The 8 analog-in channels of a data acquisition card (NI PXIe-6366) are synchronized to the start of the driving signal via a pulse generator and digitize the voltage profiles at all eight oscillators. The coupling scheme is illustrated in greater detail in Fig. 2b, which shows the example of a negative coupling between oscillator 1 and 3. There are eight inputs to the module arranged vertically on the left (three of which are depicted), and 16 used outputs arranged horizontally at the bottom (again three are shown). The first eight outputs (not shown) are responsible for positive coupling between oscillator pairs, and the next eight outputs (three shown) are responsible for the negative coupling. The latter is accomplished by crossing the wire at the bottom before feeding it back in to the respective oscillator. By closing that particular switch-pair (see solid circles), oscillators 1 and 3 are connected in the same manner as represented by the blue resistors in Fig. 1. While any oscillator pair can be independently coupled (either positively or negatively) in this way, note that this scheme does not allow for individual pairs to have different coupling strengths.
a Schematic of the basic experimental setup: the oscillator-system is driven sinusoidally, starting at the trigger of the pulse generator, which also initiates the data collection at the DAQ board. The oscillators are impedance-isolated from the AI channels of the DAQ via buffers. The coupling network connecting the oscillators is established via a terminal block (TB-2644) set to the 2-wire 8–32 configuration, and the switch-matrix unit (PXI-2532). b A more detailed view of the coupling network using the switch matrix: there are 8 inputs and 32 outputs in this configuration (16 of which are used). The inputs connect directly to the oscillators. The first eight outputs connect back to the inputs in a one-to-one fashion, but the second eight outputs shown in this figure cross the two wires before connecting back, as shown. The electrical switches at the cross-points of this switch-matrix module, represented here by open and closed red circles, can be programmed to be open or closed. As shown here, oscillators 1 and 3 would be negatively coupled.
Modeling the experimental system
As was shown in ref. 50, we can model the varactor diode, the nonlinear circuit element, as a parallel combination of three idealized components: a nonlinear capacitor of variable capacitance, C(V), a nonlinear resistor whose current-voltage relationship is given by ID(V), and a nonlinear dissipation resistance, Rl. We then apply the Kirchhoff loop rule using two loops around the circuit shown in Fig. 1, while also keeping mathematical track of the currents entering the nth node through the top capacitor and exiting through the lower capacitor. The detailed steps in the analysis are relegated to the “Methods” section; here we show only the final set of non-dimensionalized equations of motion governing this electrical network that will be used for the simulation results presented below. More specifically, the voltage dynamics for each oscillator (indexed by n) reads:
where the symbols are defined as follows in terms of the measurable circuit quantities: \({v}_{n}\) = Vn/A, with A being the amplitude of the driving signal and Vn the voltage across the diode; yn = Yn/(ACdω0), with Yn representing the current through the inductor. Similarly, iD = ID/(ACdω0), where ID(V) is the voltage-dependent current through the varactor diode. C(V) is the voltage-dependent capacitance of the diode, and c = C(V)/Cd. (Both functions, ID and C, are given in the Methods section.) Furthermore, \({\omega }_{0}=1/\sqrt{L{C}_{d}}\) and τ = ω0t, and Ω = ω/ω0 represent the dimensionalized time and driving frequency. Finally, τc = RcCdω0, and Bnm is either zero (no connection between that node pair) or 1 when the pair is negatively coupled.
Experimental Measurements
Let us begin by examining an antiferromagnetically coupled Möbius ladder graph for N = 6. The idea is to minimize the Ising Hamiltonian, which means finding the spin configuration {si = ±1} that yields the minimum energy for \({E}_{{{{{\rm{Ising}}}}}}=-\frac{1}{2}{\Sigma }_{i,j}{J}_{ij}{s}_{i}{s}_{j}\). Solving the Max 3-regular cut problem on an unweighted graph is trivially formulated as minimizing the Ising Hamiltonian by assigning Jij = −1 to connecting edges. This coupling network is shown schematically in Fig. 3a, where black (white) squares represent negative (zero) coupling between that pair of nodes. It is straightforward to see that this network that has a unique lowest-energy solution (up to a minus sign) of [1, −1, 1, −1, 1, −1]. When we drive the lattice with this coupling network at f = 380 kHz and Vd = 4 V, the system is driven to that lowest energy (E = −9), as seen in Fig. 3b, and we get the voltage response depicted in gray-scale in Fig. 3c. Some oscillators manage to transition to subharmonic resonance somewhat more quickly than others due to small spatial inhomogeneities, given that the subharmonic resonance is itself a nonlinear threshold process. We see, however, that after about 280 μs, or 50 subharmonic periods, the final alternating pattern firmly establishes itself. A time snapshot of the voltage profile across all six nodes—at a time indicated by the red dotted line in panel b—is shown in Fig. 3d. It is evident that the correct solution is encoded in that voltage profile. It should be mentioned that we computed the configurational energy from experimental data as outlined in the “Methods” section.
a The coupling matrix for N = 6 Möbius-ladder graph, where black (white) squares represent negative (zero) coupling. b The time evolution of the system’s energy, settling at the ground-state energy of E = −9 after around 50 subharmonic periods. c the N = 6 circuit response—time is plotted on the horizontal axis, node number vertically, and the voltage response is depicted in gray-scale. d The voltage profile encoding the ground state at particular instant of time, depicted as the red, dashed line in (c).
Note that for this network, there is no frustration, the optimization state is unique, and the electrical circuitry “finds” this state quickly and with complete reliability. This is true for any network that admits a single optimal solution without frustration. In such cases (i.e., for Möbius graphs when N/2 is odd), the circuit was found to perform with perfect accuracy. To demonstrate practical use for computing, however, the system also has to find solutions for the larger class of networks with frustration. In the frustrated ground state, some spins would have to be aligned in spite of being coupled antiferromagnetically. This would happen if N/2 is even in Möbius ladder graphs.
Let us now examine the N = 8 Möbius ladder, depicted in Fig. 4a. The experimental results for this network are displayed in Fig. 4b–d. Panel b shows the energy evolution of the state, as computed from Eq. (9). The energy does eventually reach the lowest possible value for this network (after about 130 subharmonic periods), but it does not reach it monotonically. Panels c and d reveal that the oscillator final response pattern encodes the state [1, 1, −1, 1, −1, −1, 1, −1], which is one of the degenerate ground states with an energy of E = −8. Note that this network does exhibit frustration—for instance, nodes 0 and 1 are negatively coupled, but this optimal state has those same two nodes oscillate in synchrony.
a The coupling matrix for N = 8 Möbius-ladder graph. b The time evolution of the system’s energy, settling at the ground-state energy of E = −8 after around 130 subharmonic periods; interestingly the system arrives there non-monotonically. c the circuit response encoding the solution of lowest energy, depicted as the temporal voltage snapshot in (d).
Figure 5 relates to a different 3-regular graph—comparing Figs. 4a and 5a reveals the coupling modifications. The raw data is shown (in the manner of previous figures) in panels c and d, which depict the initial and final time-interval responses. Figure 5b computes the configurational energy, according to Eq. (9) (in the “Methods” section) as before, at each period of oscillation. It is evident that after around 50 subharmonic periods (or about 250 μs), the electronic system has settled into the final state of the minimum energy, E = −8. Panels b–d also illustrate that in the evolution towards the final state, certain parts of the eventual state emerge much earlier than others. In this example, nodes 0 and 1 come into synchrony early, at around 70 μs, whereas nodes 3 and 4 do not snap into an anti-synchronous response until late, between 200 and 300 μs. This is illustrated in panel f, which plots the voltage profiles of nodes 3 and 4 (red and blue trace, respectively).
a Another 3-regular graph of N = 8. b Energy evolution of the network; we reach a ground state of energy E = −8 after around 45 subharmonic periods. c, d Early and late circuit response, respectively. e The final state, as encoded in the voltage profile. f Time-evolution of the voltage at node 3 (red) and 4 (blue).
As two final examples of 3-regular graphs, consider Fig. 6a, c. The driver frequency is again 400 kHz, the driver amplitude is gradually raised until a subharmonic pattern first emerges, and the steady-state circuit responses are shown in Fig. 6b, d, respectively. Both states encoded here in the voltage pattern match one of the optimized solutions for these graphs. For the two graphs they are, respectively, [1, 1, −1, 1, −1, −1, 1, −1] and [1, 1, −1, 1, 1, −1, −1, −1], both of which yield an energy of E = −8 for their respective networks.
It should be emphasized that these ground-state solutions in these 3-regular graphs compete with other patterns of fairly low energies, and such patterns can also emerge at or near the driver-amplitude threshold. In fact, when the driver is turned off and then on again, the same pattern does not always reappear even in the absence of changes to the driving conditions. A detailed statistical analysis has not been attempted yet but would clearly be an interesting topic for further study.
Furthermore, in order to attain the ground states, in some cases it proved necessary to randomly permute the inductors for the eight oscillators. The measured inductance values for all inductors agreed to within 0.25%, but even that low level of spatial “noise” in some instances proved sufficient to prevent the evolution to one of the correct ground states; here a mere rearranging of that noise would allow such states to manifest. In effect, our experimental results suggested the relevance of introducing some inductor noise to move the system out of local minima and nudging it towards the global minimum.
Numerical simulations
We now turn to numerical simulations of this system described by Eq. (1). Such simulations add three important facets to the picture: (i) they can, in principle, be used to map out more systematically the role of noise, initial conditions, and driving parameters, (ii) they allow us to more easily perform a statistical test, evaluating the efficiency of this computational scheme, and (iii) they allow an investigation of larger systems than can be currently implemented experimentally.
Our aim in this first proof-of-principle work is to reproduce in the simulations some of the experimental results shown previously. The numerical integration of Eq. (1) leads quickly to the correct ground state for networks without frustration. For instance, in the antiferromagnetically coupled ring with N = 8, this happens within roughly 10 subharmonic periods, or around 50 μs. This time is shorter than what we see in Fig. 3, but with higher driving amplitudes the experimental time can be reduced to align more closely with the simulations.
More importantly, Fig. 7 shows that the simulations perform well on the 3-regular graphs from before, depicted again in Fig. 7a.
Simulation results corresponding to the experimental setup of Fig. 5. a 3-regular graph of N = 8 coupling matrix, b energy evolution of the network; we reach an approximate ground state of energy E ≈ −8 after around 20 subharmonic periods. c, d Early and late circuit response, respectively. e, f Early and late time evolution of the voltage of the 8 oscillators starting from very small (~10−3 V) random initial conditions. The different colors represent different oscillators (4 in purple, 5 in green, 6 in light blue, 7 in maroon, and 8 in yellow). The time unit used is the driving period Td. The driving parameters used read ωd = 1.26ω0 and Vd = 3.1 V.
It is clear that the simulations manage to find one correct ground state of energy E ≈ −8 within roughly 20 subharmonic periods (Fig. 7b). Figure 7c, d shows the oscillation pattern of all eight oscillators at an early time and at long times, respectively. The corresponding voltage traces of the oscillators are displayed in the lower two panels, e and f. The same qualitative picture is observed for different initializations of the system. It is interesting to also note how the system overcomes metastable dynamics (i.e., between 10 and 20 subharmonic periods) to reach the desired lowest energy minimum. Comparing the numerical findings to the experimental results (Fig. 5), we see qualitative agreement in the final state and how it emerges via the establishment of the subharmonic response. For instance, in both experiment and simulation, we observe that a certain subset of oscillators moves into the subharmonic regime quickly, whereas others take significantly longer to snap into place. Furthermore, we find both experimentally and numerically that the final oscillator amplitudes are not always equal, and those oscillators that are lower in amplitude have not completely suppressed their alternate peaks and therefore exhibit a larger Fourier component at the driver frequency (Fig. 7f). The same phenomenon is apparent in Fig. 6, for instance, and indicates some limitations in the analogy of the electrical circuits, explored here, with Ising machines. Indeed, our oscillators are not “true spins” but rather are able to feature a more complex subharmonic response in their continuous time dependence. One way to overcome this issue of the heterogeneity of the oscillators’ amplitudes is to introduce feedback that drives all amplitudes to the same occupation51.
The one quantitative difference that we consistently observe is that in the simulations the final state can be obtained more quickly than in the experiments. One reason for the longer times in the experimental system could be the presence of a certain level of inhomogeneity between the oscillators. Furthermore, we did not incorporate temporal noise into the simulations. Another factor could be that varactor-diode dissipation is not precisely captured in the model. Nonetheless, it is evident that the key features of the experimental results are correctly reproduced in the numerics.
To explore the role of the driver (through the variation of its parameters) in greater detail, Fig. 8a shows the energy of the eventual state as a function of the two driving parameters— frequency ωd (x-axis) and amplitude Vd (y-axis). Evidently, we can distinguish between three qualitatively different regions. The dark blue region (I) corresponds to eventual states with an energy close to the ground-state energy (E ≈ −8) of the network in Fig. 4. The oscillator response pattern (Fig. 8b, first row) is very close to one of the degenerate ground states, i.e., the [1, 1, −1, 1, −1, −1, 1, −1], as expected. In this region, the variation in the energy values, originates mainly from the aforementioned discrepancies on the oscillator amplitudes.
a Dependence of the final energy for the Möbius-ladder network (Fig. 4) on the driving frequency ωd and the driving amplitude Vd. We observe the existence of three qualitatively different regions (dark blue, blue-green, yellow), which are marked with the representative data points I (ωd = 1.26ω0, Vd = 3.1 V), II (ωd = 1.5ω0, Vd = 2.2 V) and III (ωd = 1.65ω0, Vd = 4 V). The ensuing dynamics at the I,II,III points is shown in the three rows of (b). In particular, the first column shows the time evolution of the energy at the I, II, III points, whereas the second and third columns depict the corresponding circuit response at late times.
The situation is quite different in the green-blue region (II), appearing for smaller driving amplitudes and larger driving frequencies. These parameters lead to a steady state with an energy E ≈ −5.4, according to Eq.(9) in the Methods section, in which a subset of oscillators (here 2) performs smaller amplitude oscillations with the driving frequency, while the rest performs subharmonic oscillations (Fig. 8b, second row). The subharmonic oscillations are completely lost in the yellow regions of Fig. 8a. Note that this region includes apart from the small-frequency and small-amplitude region (where the subharmonic resonance is expected to be suppressed), also the high-frequency region with ωd > 1.65ω0 (III). For these parameter values the oscillators oscillate in phase, with the driving frequency ωd (Fig. 8b, third row), and thus lose the desirable analogy to Ising systems.
In terms of the optimal driving parameters, the experiments also show that the optimal operating regime frequency is near the lower edge of the subharmonic resonance curve, and as the frequency increases the ground state is no longer reachable, similar to what is indicated by the region of point II in Fig. 8. One difference is that in the experiment, the driver amplitude cannot be increased indefinitely. In fact, experimentally, it is advantageous to stay near the lower amplitude-threshold for subharmonic resonance. At higher amplitudes, other patterns— likely driven by inhomogeneities—become dominant. While simulation and experiment paint the same qualitative picture, differences in the details will likely become smaller with further fine-tuning of diode characteristics, especially concerning resistive dissipation. Nonetheless, it is important to stress that both experiments and current numerical simulations reach an optimal solution for 3-regular graphs, and they thus demonstrate the clear promise of this network of subharmonic LC-resonators as a purely passive unconventional computing architecture.
We now explore the numerical simulations for larger network sizes. Figure 9 shows results similar to Fig. 8a, but with N successively doubled, to N = 16 in panel a, to N = 32 in panel b, and finally to N = 64 in panel c. The color indicates the final energy reached for any given driving configuration. We notice that while the overall phase boundaries seem independent of graph size, the minimum energy state is reached less frequently for larger sizes. However, the region indicated by the dashed box near the lower amplitude threshold is seen to be most robust in returning the lowest energy.
Dependence of the network’s final energy on the driving frequency ωd and the driving amplitude Vd for Möbius-ladder networks of increasing sizes: a N = 16 with \({E}_{min}^{(th)}=-20\), b N = 32 with \({E}_{min}^{(th)}=-44\) and c N = 64 with \({E}_{min}^{(th)}=-92\). The dashed red box marks a region of the parameter space which appears to be most robust with respect to the increment of the network size.
In order to investigate the computational performance as a function of system size further, we now choose a driving condition consistent with the red dashed box in Fig. 9 and repeat the simulation 1000 times to perform a statistical analysis. The results are displayed in Fig. 10. The top panel, Fig. 10a, depicts difference between the average and minimum energies. Note the small residual difference in energy between the attained minimum and the theoretical minimum due to oscillator phases not perfectly mapping to 0 or π—see also Eq. (9). In Fig. 10b we compute the standard deviation in energies, and in panel c, the probability of reaching the energy minimum. In all three panels, we observe that up to N = 40, there is no appreciable size dependence and the computational success is near 100%. For larger networks, this success probability then begins to decrease monotonically. It should be noted that we did not attempt any annealing strategies for coaxing the system out of local minima, the use of which would likely increase the success probabilities.
a Dependence of the deviation ΔE of the final mean energy <E> (averaged over 1000 realizations) from the theoretical ground state energy \({E}_{min}^{(th)}\) as a function of N for Möbius-ladder networks. The red line marks the difference between the minimum energy Emin reached in simulations and the theoretical one. b Standard deviation, σE, of the final network energy after 1000 realizations as a function of the network size N. c Probability to reach the ground state network energy Emin in 1000 realizations for increasing network size N.
Discussion
In this study, a concrete experimental realization of a nonlinear electrical oscillator circuit is presented, operating under external drive in the regime of subharmonic resonance and allowing for a controlled selection of couplings, so as to realize different types of 3-regular graphs for small number of nodes systems, such as N = 6 and N = 8 (the case of higher N values was examined numerically). We have illustrated a concrete protocol so as to interpret this nonlinear coupled dynamical system as an effective spin-lattice and have shown that in such an interpretation, it is possible to reach the ground state energy, both in the case of unique minimizers and also in the presence of frustration. The role of noise in facilitating the departure from local minima and reaching the global minimum has been experimentally discussed. Importantly, the understanding of the RLC-characteristics of the relevant oscillator elements can, in principle, enable a Kirchhoff-law based theoretical model of the system that is found to be in very good qualitative agreement with the experimental observations. While here we have emphasized a proof-of-principle realization of the relevant setting, it is clear that the theoretical analysis enables a scaling of the system to higher numbers of nodes and, as shown herein, the consideration of both the advantages, but also the limitations of the subharmonic oscillator response in acting as an effective spin.
As indicated also above, this experimental realization provides a useful proof-of-principle, but also paves the way towards future efforts and associated questions. Clearly, issues related to scalability of considerations to large N, aspects related to the added wealth of phenomenology of the electrical oscillators (in comparison to simple spin variables) and its influence on the observed dynamics, as well as the role of noise and ensembles of realizations (and corresponding averaging) are among the many worthwhile avenues for further exploration. One can imagine, for instance, a large-scale implementation of this scheme that utilizes on-chip integration of the electronic circuits and coupling logic, especially in higher-frequency domains where inductive elements become less bulky. Such studies are currently in progress and will be reported in future publications.
It should also be noted that, while we numerically investigated Mobius graphs of larger sizes, these graphs have ground states that correspond to a principal eigenvector of the coupling matrix, which makes these problems somewhat simpler. For general 3-regular random graphs the optimality simplicity criterion will not hold. However, a suitably chosen annealing schedule of parameters would bring about a solution there as well, but it would have to be problem specific. Finding such schedules is an interesting future direction.
Methods
The circuit equations
Let us think of the left oscillator in Fig. 1 as oscillator n and the right one as oscillator m. Let us first consider the Kirchhoff loop rule on a “bowtie-shaped” path; we start with the circuit point in Fig. 1 at the bottom of the left inductor, move up across the inductor, go diagonally down (and right) across resistor Rc(−), up the right inductor, and finally diagonally down (and left) across Rc(−). For this closed path we can write the loop rule as, Vn − RcJnm + Vm − RcJmn = 0, where Jnm is the current through the resistor connecting the top of oscillator n to the bottom of oscillator m, and Rc = Rc(−). This implies that,
where we are not assuming the latter two currents to be the same. Let is now consider another Kirchhoff loop, this time starting at the left-bottom corner of Fig. 1, moving up across the signal generator, down across the left capacitor, Cd, down further across the parallel combination of diode and inductor, and finally down across the bottom capacitor, Cd. Here we can write,
Here the second and forth terms on the left side of Eq. (3) refer to the voltage drops across the top and bottom driving capacitors. We also know that,
Taking the time derivative of Eq. (3) and substituting Eq. (4), we get
Let us now consider these two currents. I+ is the current delivered to the nth oscillator via the top capacitor, and I− the current flowing back to the signal generator from the nth node. Where does this current, I+, flow next? Part of it goes through the parallel combination of diode and inductor, and part of it becomes Jnm. Now we examine the diode more closely. It can be effectively modeled as a parallel arrangement of a nonlinear resistor with a certain current–voltage relationship, ID(V), a nonlinear capacitor C(V) and a dissipation resistor Rl. These three will be specified in greater detail later. At present, we can therefore express I+ as,
where Y represents the current through the inductor. The minus sign is added to the first term because the diodes are oriented up in the forward direction in the circuit. It is evident that I− is the same as I+ except that the last term must be replaced by Jmn. Substituting Eq. (6) and its equivalent into Eq. (5), and also using Eq. (2), we arrive at:
We can also assume a sinusoidal driving signal, \({V}_{d}=A\sin (\omega t)\). Equation (7) describes a pair of nodes, but it can be naturally generalized to a network by adding up all the coupling currents, in which case the last term of the first equation in Eq. (7) would have to sum over all connected nodes m. We now non-dimensionalize these governing equations by introducing \({\omega }_{0}=1/\sqrt{L{C}_{d}}\) and τ = ω0t, as well as vn = Vn/A and Ω = ω/ω0. This then leads to Eq. (1).
Lastly, let us cite the functional forms for C(V) and ID(V) that were empirically obtained in ref. 50.
with β = 38.8 V−1 and Is = 1.25 × 10−14 A.
Here, \({V}^{{\prime} }=(V-{V}_{c})\), C_0 = 788 pF, α = 0.456 V−1, \({C}_{v}={C}_{0}\exp (-\alpha {V}_{c})\), Cw = − αCv, C = 100 nF/V2, and Vc = −0.28 V.
Configurational energy
In the context of Ising model, the energy of a N-particle spin configuration {Si}, also known as the state of the system, is given by:
In casting this coupled electrical resonator system in the form of the Ising problem, we note that there are only two stable states for our subharmonic resonators (with responses at even or odd periods of the driver), as explained previously. These are associated with spin-up and spin-down. However, transient resonator behavior can be described by superpositions of these. We associate these superpositions with angles that differ from 0 and π; for instance, a state that is an equal superposition of the even and odd states would be reasonably associated with an angle of π/2. Thus, we keep track of each oscillator’s response both at even and odd periods of the driver, A and B respectively, and from the ratio of these we compute an angle, \({\theta }_{n}(t)=2\arctan (A/B)\) at each measurement time, t. The energy formula then takes the form,
Data availability
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
Code availability
The Matlab code used for the numerical simulations in this work is available from the corresponding author on reasonable request.
References
Yamaoka, M. et al. A 20k-spin ising chip to solve combinatorial optimization problems with cmos annealing. IEEE J. Solid-State Circuits 51, 303–309 (2015).
Takemoto, T., Hayashi, M., Yoshimura, C. & Yamaoka, M. 2.6 a 2 × 30k-spin multichip scalable annealing processor based on a processing-in-memory approach for solving large-scale combinatorial optimization problems. In 2019 IEEE International Solid-State Circuits Conference-(ISSCC), 52–54 (IEEE, 2019).
Tsukamoto, S., Takatsu, M., Matsubara, S. & Tamura, H. An accelerator architecture for combinatorial optimization problems. Fujitsu Sci. Tech. J. 53, 8–13 (2017).
Matsubara, S. et al. Digital annealer for high-speed solving of combinatorial optimization problems and its applications. In 2020 25th Asia and South Pacific Design Automation Conference (ASP-DAC), 667–672 (IEEE, 2020).
Goto, H., Tatsumura, K. & Dixon, A. R. Combinatorial optimization by simulating adiabatic bifurcations in nonlinear hamiltonian systems. Sci. Adv. 5, eaav2372 (2019).
Goto, H. et al. High-performance combinatorial optimization based on classical mechanics. Sci. Adv. 7, eabe7953 (2021).
McMahon, P. L. et al. A fully programmable 100-spin coherent ising machine with all-to-all connections. Science 354, 614–617 (2016).
Berloff, N. G. et al. Realizing the classical XY hamiltonian in polariton simulators. Nat. Mater. 16, 1120–1126 (2017).
Kalinin, K. P., Amo, A., Bloch, J. & Berloff, N. G. Polaritonic xy-ising machine. Nanophotonics 9, 4127–4138 (2020).
Strukov, D. B., Snider, G. S., Stewart, D. R. & Williams, R. S. The missing memristor found. Nature 453, 80–83 (2008).
Hu, M. et al. Memristor-based analog computation and neural network classification with a dot product engine. Adv. Mater. 30, 1705914 (2018).
Yao, P. et al. Fully hardware-implemented memristor convolutional neural network. Nature 577, 641–646 (2020).
Lin, P. et al. Three-dimensional memristor circuits as complex neural networks. Nat. Electron. 3, 225–232 (2020).
Cai, F. et al. Power-efficient combinatorial optimization using intrinsic noise in memristor hopfield neural networks. Nat. Electron. 3, 409–418 (2020).
Dutta, S. et al. An Ising Hamiltonian solver based on coupled stochastic phase-transition nano-oscillators. Nat. Electron. 4, 502–512 (2021).
Yang, J. J., Strukov, D. B. & Stewart, D. R. Memristive devices for computing. Nat. Nanotechnol. 8, 13–24 (2013).
Li, Y., Wang, Z., Midya, R., Xia, Q. & Yang, J. J. Review of memristor devices in neuromorphic computing: materials sciences and device challenges. J. Phys. D: Appl. Phys. 51, 503002 (2018).
Kalinin, K. P. & Berloff, N. G. Nonlinear systems for unconventional computing. In Emerging Frontiers in Nonlinear Science, 345–369 (Springer, 2020).
Roques-Carmes, C. et al. Heuristic recurrent algorithms for photonic ising machines. Nat. Commun. 11, 1–8 (2020).
Shen, Y. et al. Deep learning with coherent nanophotonic circuits. Nat. Photonics 11, 441 (2017).
Prabhu, M. et al. Accelerating recurrent ising machines in photonic integrated circuits. Optica 7, 551–558 (2020).
Bernstein, L. et al. Freely scalable and reconfigurable optical hardware for deep learning. Sci. Rep. 11, 3144 (2021).
Babaeian, M. et al. A single shot coherent ising machine based on a network of injection-locked multicore fiber lasers. Nat. Commun. 10, 1–11 (2019).
Pal, V., Mahler, S., Tradonsky, C., Friesem, A. A. & Davidson, N. Rapid fair sampling of xy spin hamiltonian with a laser simulator. Phys. Rev. Res. 2, 033008 (2020).
Parto, M., Hayenga, W., Marandi, A., Christodoulides, D. N. & Khajavikhan, M. Realizing spin hamiltonians in nanoscale active photonic lattices. Nat. Mater. 19, 725–731 (2020).
Gershenzon, I. et al. Exact mapping between a laser network loss rate and the classical xy hamiltonian by laser loss control. Nanophotonics 1 (2020).
Pierangeli, D., Marcucci, G. & Conti, C. Large-scale photonic ising machine by spatial light modulation. Phys. Rev. Lett. 122, 213902 (2019).
Kim, K. et al. Quantum simulation of frustrated ising spins with trapped ions. Nature 465, 590–593 (2010).
Klaers, J., Schmitt, J., Vewinger, F. & Weitz, M. Bose–einstein condensation of photons in an optical microcavity. Nature 468, 545–548 (2010).
Kassenberg, B., Vretenar, M., Bissesar, S. & Klaers, J. Controllable Josephson junction for photon Bose-Einstein condensates. Phys. Rev. Res. 3, 023167 (2021).
Guo, Y., Kroeze, R. M., Vaidya, V. D., Keeling, J. & Lev, B. L. Sign-changing photon-mediated atom interactions in multimode cavity quantum electrodynamics. Phys. Rev. Lett. 122, 193601 (2019).
Marsh, B. P. et al. Enhancing associative memory recall and storage capacity using confocal cavity QED. Phys. Rev. X 11, 021048 (2020).
Böhm, F., Verschaffelt, G. & Van der Sande, G. A poor man’s coherent ising machine based on opto-electronic feedback systems for solving optimization problems. Nat. Commun. 10, 1–9 (2019).
Okawachi, Y. et al. Demonstration of chip-based coupled degenerate optical parametric oscillators for realizing a nanophotonic spin-glass. Nat. Commun. 11, 1–7 (2020).
Cen, Q., Ding, H., Hao, T. et al. Large-scale coherent Ising machine based on optoelectronic parametric oscillator. Light Sci Appl 11, 333 (2022).
Lucas, A. Ising formulations of many np problems. Front. Phys. 2, 5 (2014).
Garey, M. R., Johnson, D. S. & Stockmeyer, L. Some simplified np-complete problems. In Proc. Sixth Annual ACM Symposium on Theory of Computing, 47–63 (1974).
Takata, K. et al. A 16-bit coherent ising machine for one-dimensional ring and cubic graph problems. Sci. Rep. 6, 34089 (2016).
Yamamoto, Y. et al. Coherent ising machines-optical neural networks operating at the quantum limit. npj Quantum Information 3, 49 (2017).
Chou, J., Bramhavar, S., Ghosh, S. & Herzog, W. Analog coupled oscillator based weighted ising machine. Sci. Rep. 9, 1–10 (2019).
Kalinin, K.P., Berloff, N.G. Computational complexity continuum within Ising formulation of NP problems. Commun. Phys. 5, 20 (2022).
Xiao, T. P. Optoelectronics for refrigeration and analog circuits for combinatorial optimization. Ph.D. thesis, UC Berkeley (2019).
Parihar, A., Shukla, N., Jerry, M., Datta, S. & Raychowdhury, A. Vertex coloring of graphs via phase dynamics of coupled oscillatory networks. Sci. Rep. 7, 1–11 (2017).
Mallick, A. et al. Using synchronized oscillators to compute the maximum independent set. Nat. Commun. 11, 1–7 (2020).
Wang, T., Wu, L. & Roychowdhury, J. New computational results and hardware prototypes for oscillator-based ising machines. In Proceedings of the 56th Annual Design Automation Conference 2019, 1–2 (2019).
Moy, W. et al. A 1,968-node coupled ring oscillator circuit for combinatorial optimization problem solving. Nat. Electron. 5, 310–317 (2022).
Mallick, A. et al. Graph coloring using coupled oscillator-based dynamical systems. In 2021 IEEE International Symposium on Circuits and Systems (ISCAS), 1–5 (IEEE, 2021).
English, L. et al. Generation of localized modes in an electrical lattice using subharmonic driving. Phys. Rev. Lett. 108, 084101 (2012).
Nayfeh, A. & Mook, D. Nonlinear Oscillations (Wiley Interscience, New York, 1979).
Palmero, F., English, L., Cuevas, J., Carretero-Gonzalez, R. & Kevrekidis, P. G. Discrete breathers in a nonlinear electric line: Modeling, computation, and experiment. Phys. Rev. E 84, 026605 (2011).
Kalinin, K. P. & Berloff, N. G. Networks of non-equilibrium condensates for global optimization. New J. Phys. 20, 113023 (2018).
Acknowledgements
This material is based upon work supported by the US National Science Foundation under Grants DMS-1809074, DMS-2204702, PHY-2110030 (P.G.K.). K.P.K. acknowledges the financial support from Cambridge Trust and NPIF EPSRC Doctoral grant EP/R512461/1. N.G.B. acknowledges the grant from Julian Schwinger Foundation JSF-19-02-0005.
Author information
Authors and Affiliations
Contributions
L.Q.E. conducted the experimental work, and A.V.Z. the numerical work; K.P.K. and N.G.B. provided the theoretical foundations; P.G.K. guided and coordinated all aspects of the work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Yusuke Doi and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
English, L.Q., Zampetaki, A.V., Kalinin, K.P. et al. An Ising machine based on networks of subharmonic electrical resonators. Commun Phys 5, 333 (2022). https://doi.org/10.1038/s42005-022-01111-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-01111-x
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.