Abstract
High power lasers have become useful scientific tools, but their large size is determined by their low damage-threshold optical media. A more robust and compact medium for amplifying and manipulating intense laser pulses is plasma. Here we demonstrate, experimentally and through simulations, that few-millijoule, ultra-short seed pulses interacting with 3.5-J counter-propagating pump pulses in plasma, stimulate back-scattering of nearly 100 mJ pump energy with high intrinsic efficiency, when detuned from Raman resonance. This is due to scattering off a plasma Bragg grating formed by ballistically evolving ions. Electrons are bunched by the ponderomotive force of the beat-wave, which produces space-charge fields that impart phase correlated momenta to ions. They inertially evolve into a volume Bragg grating that backscatters a segment of the pump pulse. This, ultra-compact, two-step, inertial bunching mechanism can be used to manipulate and compress intense laser pulses. We also observe stimulated Compton (kinetic) and Raman backscattering.
Similar content being viewed by others
Introduction
High-power, chirped-pulse amplification (CPA) laser systems1 stretch initially ultra-short “seed” pulses before amplifying them by many orders of magnitude in amplifier chains, and then compressing them to ultra-short durations and peak powers currently as high as 10 PW2,3. Optical components in amplifier and compressor stages need to be large to avoid damage, which results in enormous and complex systems that are very expensive and difficult to maintain. Furthermore, extending the peak powers towards exawatts becomes increasingly challenging, which is driving a search for new technologies and methods of manipulating intense laser pulses.
Plasma has been identified as an alternative, ultra-robust and already broken-down, optically active medium for amplifying and compressing intense laser pulses4,5 or acting as robust optical elements to manipulate them6,7,8. An electron plasma Bragg grating can be readily created by the ponderomotive force of the beat wave of two counter-propagating laser beams. In plasma-based amplifiers, the grating is almost instantly produced by colliding a long pump pulse with a short and suitably detuned seed pulse to stimulate Raman or Brillouin amplification by resonantly exciting a third, longitudinal plasma density (Langmuir or ion-acoustic) wave, where the matching conditions ω0 = ω1 + ωp and k0 = k1 + kp are satisfied, where ω0,1,p and k0,1,p are, respectively, the frequency and wave-vector of the pump, seed and plasma wave9,10. The thus excited plasma grating scatters the pump to amplify the seed pulse. For a frequency-chirped pump, the resulting plasma grating has frequency and wave vectors that vary in space and time.
For sufficiently intense pump and seed pulses, where the “bounce frequency”, \({\omega }_{B}\approx 2{\omega }_{0}\sqrt{{a}_{0}{a}_{1}}\), of the electrons in the troughs of the ponderomotive potential exceeds the electron plasma frequency ωe, backscattering occurs kinetically4,5, which leads to a Compton amplification phenomenon analogous to that of the free-electron laser (FEL) instability11. Here, a0,1 = eE0,1/mcω0,1 are the respective normalised amplitudes of pump and seed pulses, with E0,1 being their electric fields. In this case, scattering is non-resonant, and ωp and kp do not correspond to a propagating plasma wave. Bunching and production of the grating can also be produced in a two-step modulator-buncher process, where the space-charge forces of the ponderomotively driven transient electron grating briefly impart momentum to the ions, which then ballistically evolve into an ion grating accompanied by electrons forming an overlapping grating7,12. This long-lived grating, also referred as a transient plasma photonic structure (TPPS), back-scatters the pump, as will be described below.
Parametric amplification in plasma has been studied extensively over the last three decades, both theoretically4,5,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34 and experimentally35,36,37,38,39,40,41,42,43,44,45,46,47,48,49. Several demonstrations of Raman amplification of seed in low-density plasma (np/nc ≪ 0.25, where np is the plasma density, and nc the critical plasma density)38,39,40,41,43,44,45,46,47,48,49 have been made. However, measured efficiencies have been relatively low (≈1−10%), which has been attributed to wave-breaking due to the low phase velocity of the beat wave29,39,42. This can be partially overcome by operating in the self-similar superradiant regime, where pump depletion truncates the interaction and only the front of the seed pulse grows5,25. The amplitude increase is linear rather than exponential with time. Similar superradiant amplification occurs in the Compton regime when the amplifying seed pulse duration, τp is comparable to the bounce period 2π/ωB4, as in the FEL superradiant regime50,51. Brillouin amplification, operating in the strongly coupled regime, where the ponderomotive potential exceeds the thermal pressure, has been shown to lead to the amplification of sub-picosecond, 1.06-μm laser pulses to intensities of 1 × 1017 W cm2 with an efficiency of ≈20%35.
Finally, several interesting applications of parametric amplification have been suggested, including storing light information within the plasma wave and retrieving it in a second step, which may find use in optical communications17,32.
This article presents an experimental study of amplification due to scattering off a local TPPS through a modulator-bunching process. As will be described, this TPPS forms only under specific conditions and acts as a partially reflective mirror that scatters the pump energy for several picoseconds. It should be emphasised that the process we describe here differs from that presented in the numerical work by Jia et al.52, where the development of an energy “tail” directly behind the seed is attributed to direct Brillouin amplification. The scattering process we present here (i) does not arise from a three-wave parametric process, because it does not involve a plasma wave, (ii) it occurs on a relatively long timescale, and (iii) it can potentially be efficient. The grating formation process is distinct from the one presented by Peng et al.12, where electrons are continually exposed to the ponderomotive potential of the beat wave produced by two infinitely long counter-propagating laser pulses, which similar to previously published theoretical work16 are identical (although their model is valid for unequal pulses of finite duration). Here, we show, both numerically and experimentally, the feasibility of producing a localised TPPS that persists for several picoseconds using a long-frequency-chirped pump pulse and a short-duration seed pulse. The scattered energy adds to that gained from Compton and/or Raman amplification, which contributes close to 50% of the total measured energy.
Results and discussion
An experimental investigation of these three mechanisms was undertaken using moderately intense, 6.5-ps duration, frequency-chirped pump pulses with a central wavelength of 795 nm, and 150-fs duration, fully-compressed seed pulses, which counter-propagate in a 3-mm wide hydrogen gas jet. The seed pulse central wavelength is 810 nm and incident energy is at most 15 mJ. For further details on the experimental set-up, see the Methods and Supplementary Fig. 1. A theoretical analysis, supported by particle-in-cell (PIC) simulations, is also presented below.
We have experimentally measured both the total back-scattered energies and individual spectra for a range of densities using chirped pulses at the highest pump energy available (3.5 J), corresponding to a maximum pump intensity of 1016 W cm−2. Key observations, presented in Fig. 1a, are: (i) the measured back-scattered energies increase when the seed pulse is present, as expected for a stimulated process; (ii) measured amplified seed energies increase with plasma density for positively chirped pump pulses, up to 90 mJ for densities ~1.5 × 1019 cm−3 (np/nc ≈ 8.6 × 10−3). However, for densities larger than 1 × 1019 cm−3, the Raman resonance is not satisfied (see Supplementary Fig. 2). For a negative chirp, the seed energy saturates around 20 mJ. These observations may appear unexpected and counter-intuitive, because for a negative chirp and for plasma densities below ~1 × 1019 cm−3, the Raman resonance is satisfied at an early stage of the interaction. For intensities that are initially below the threshold for entering the Compton regime, the seed amplitude can grow exponentially to the required level (see Supplementary Figs. 3, 4); and finally (iii) scattering off plasma density fluctuations or noise is strongly suppressed for a negative pump chirp. This shows, as illustrated in Fig. 1a, that some of the observed differences in seed amplification (for the different chirps) is because the scattered pump energy is integrated over all times and positions in the plasma.
a Back-scattered energy in the seed direction. Combined pump and seed shots are depicted by solid symbols, circle and triangle for positive frequency chirp, and square for negative frequency chirp. Empty symbols represent corresponding shots without the seed pulse i.e. scattering from noise. The different symbol shapes characterise different runs. The energy values are averages of three shots, with the error given as the standard deviation. Error on the inferred plasma density is estimated to be ±20%. Where the error bars are not visible, their lengths are smaller or equal to the symbol sizes. b, c are single-shot spectra. Solid (blue) line: seed spectrum after interaction; dotted (green) line: initial seed spectrum; dashed (red) line: spectrum of pump back-scattered signal without seed. Areas under the curves have been normalised to the measured energy, assuming that little energy falls outside the spectral window. b Pump with a positive frequency chirp, plasma density ~1.5 × 1019 cm−3 (np/nc ≈ 8.6 × 10−3); c Pump with a negative frequency chirp, plasma density ~1019 cm−3 (np/nc ≈ 5.7 × 10−3). The longest observable wavelength is ~880 nm because a different spectrometer grating was used compared to that in b. The inset in c displays the same data as c plotted on a magnified scale.
Another observation is that spectra of the scattered pump without seed show clear evidence of Raman-shifted spectral features, as illustrated in Fig. 1b, c, which confirms that the noise scattering mechanism is Raman back-scattering. When the seed pulse intercepts the pump, the spectrum of the total signal (the amplified seed plus the back-scattered light from the pump pulse) is confined to wavelengths solely within the initial seed spectral range, which might suggest that the main amplification mechanism is either Compton or Brillouin scattering. However, the amplification mechanism is clearly identified in 1-dimensional (1D) and 2-dimensional (2D) PIC simulations using the experimental parameters (see Methods).
Figure 2a, b show the envelope of the amplified seed electric field, for positively and negatively chirped pump pulses, respectively, from 1D simulations. Here, to identify the different contributions, we have divided the radiation fields into three segments: (orange) in advance of, (purple) within, and (green) trailing the seed pulse. An energy amplification of the seed pulse by a factor of ~14 and 20 is calculated for a positive and negative chirp, respectively (a middle (purple) region in Fig. 2a, b). Adding the energy contribution due to the scattered light trailing the seed, the amplification factors increase to 42 and 24, respectively. This is in qualitative agreement with the experimental observations, in particular the higher energies measured for the positive pump chirp.
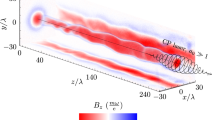
a, b are seed field envelopes after an interaction, for positively and negatively chirped pump pulses, respectively. The back-scattering produced in advance of the seed pulse is shown in orange, the amplified seed pulse in purple, and the scattered light trailing the seed pulse in green. Inset I shows the initial seed envelope. Insets II, III display the amplified seed pulses (purple region) on a magnified scale. c, d present the spectra obtained from a and b, respectively. The colour scheme associates spectra with temporal segments. The dotted black curve represents the initial seed spectrum. All spectra are normalised to the same value. e, f are the electron density spectra for positive and negative frequency chirp, respectively. Spectra are calculated at the time the seed pulse exits the plasma (seed propagates from top to bottom). The wave numbers are given in units of approximately the inverse beat wavelength, 2/λ0 = 1/400 nm−1. g, h are similar to e and f, but correspond to the ion density spectra. The electron density spectral amplitudes have been multiplied by factor four to be visible on the same scale as the ion density spectra. In f and h no spectral signature of the grating is visible when presented on the same scale as e and g.
Numerical calculation of the seed and scattered light spectra for the various temporal segments, shown in Fig. 2c, d, gives insight into the relevant processes. Early scattering of the pump is a result of Raman scattering from noise (the orange region in Fig. 2a, b), which is confirmed by the presence of the Raman Stokes line visible in the spectra at 880 and 840 nm, respectively, in Fig. 2c, d. Amplification over the seed pulse duration (purple) is attributed to Compton scattering. This is because the condition ωB ≥ ωe is satisfied when a0 ≥ 0.048 (3.8 × 1015 W cm−2)4. Brillouin amplification of the seed has been discounted because simulations with immobile ions lead to the same result, as illustrated in Table 1, summarising gain values for different numerical simulation configurations. In the case of a positive chirp, a clear Stokes satellite is observed at 890 nm (Fig. 2c), which has an amplitude larger than that of the initial seed spectrum. The difference between the seed pulse central frequency and the Stokes satellite is equal to ωe, which corresponds to a shift in wavelength by \({\lambda }_{{{{{{\mathrm{seed}}}}}}}\sqrt{{n}_{p}/{n}_{c}}\approx 75\,{{{{{{{\rm{nm}}}}}}}}\). This suggests that a fraction of the amplified seed energy may be transferred to the Stokes line by Raman forward scattering. However, this is not observed in the experiment because the growth rate of the instability may be lower than that of idealised simulations.
A key observation is that, for a positive chirp, a high level of back-scattered energy of the pump occurs in the trailing region behind the seed and appears as an apparent gain within the initial seed spectral bandwidth (green curves in Fig. 2c, d). This enhancement (apparent gain) is ascribed to the generation of a long-lived, localised electron and ion grating, or TPPS, that is formed close to the plasma entrance for the seed, at around 2.6 mm, as illustrated in Fig. 2e, f. This grating continues to back-scatter energy from the pump pulse into the trailing region behind the seed pulse. Back-scattering associated with this spectral feature at the seed wavelength, is very efficient: 17.5% of the pump energy is back-scattered while the grating persists. From the ratio of energy between the different segments in the simulations, we infer that the highest measured back-scattered energy, 90 mJ, up to 40 mJ, can be attributed to the (delayed) back-scatter from the TPPS, which is also consistent with the differences in energy between positive and negative chirps, observed experimentally. Figure 2e–h show electron and ion density spectra as a function of position, at the time the seed pulse exits the plasma slab (corresponding to the time t ≈ 10 ps in Fig. 3). A nonlinear TPPS is still clearly evident around 2.6 mm for the positive chirp (Fig. 2e, g). In contrast, no TPPS is clearly observed for a negative chirp (Fig. 2f, h), which may explain the lower gain.
Analysis is shown for a 27 μm region centred around the position 2.665 mm. The initial time corresponds closely to the time at which the seed crosses the plasma region of interest. The spectral amplitude of the fundamental wave number of the electron (green circle) and ion (orange square) gratings as a function of time is shown in a, for positive chirp and b, for the negative chirp. c, d present the phases of the electron and ion gratings at the fundamental wave number.
The TPPS is formed in the following sequence: the ponderomotive force associated with the local, quasi-stationary, laser beat wave drives electrons into a grating. Ions experience the strong associated space-charge fields and gain momentum from it. Depending on the position of the ions in the electrostatic potential, they gain phase-correlated momenta. After a short delay, an ion grating is formed inertially and electrons follow the ions to neutralise the charge7,8. The temporal evolution of the TPPS, for the 1D PIC simulations, is illustrated in Fig. 3. Figure 3a, c show the creation of a superposed electron and ion gratings, for a positively chirped pump. The seed and local pump wave frequencies are almost equal, leading to the formation of a quasi-stationary beat wave and a growing electron density modulation (see Supplementary Fig. 5). The space-charge fields of the electrons act as a modulator that imparts phase-correlated momenta to ions, which then bunch inertially. This two-stage process is similar to that in a klystron. The grating reaches its peak amplitude after 6 ps, as illustrated in Fig. 3a, and washes out due to the continual phase-space evolution of the ions, which is consistent with the phase of the grating starting to vary after 6 ps, as shown in Fig. 3c. The time scales are consistent with the duration of TPPS scattering observed in Fig. 2a. In contrast, Fig. 3b, d, shows that a grating does not form for a negative chirp. In this latter case, the relatively high phase velocity of the beat wave, combined with rapid electron wave-breaking, prevents the ions from gaining significant momentum and thus ballistically forming a grating. We have confirmed this by undertaking numerical simulations with immobile ions (Table 1, Gas (immobile ions)), which reduces the scattering behind the seed by two-thirds for the positive chirp case and highlights the role of the ions. Finally, the effect of the chirp sign on the back-scattered energy is suppressed for warm plasma, as illustrated in Table 1, which shows that thermal effects prevent the effective formation of a plasma grating. This underlines the differences between our work and that of refs. 12,52, which describes processes in warm plasma.
For a more quantitative comparison with our experimental measurements, we have undertaken 2D simulations, which are presented in Fig. 4. The intensity profile of the seed pulse before the interaction is illustrated in Fig. 4a, with its spectrum presented in Fig. 4d. The intensity profiles after interaction are shown in Fig. 4b, c for positive and negative pump chirps, respectively. Amplification factors of ≈8 and ≈6, for energy integrated over the initial seed pulse, are calculated for a positive and negative chirp, respectively. Including the scattered light both in advance of and also trailing the seed gives amplification factors of ≈24 and ≈17, respectively. This is consistent with the 1D simulations and the same physical processes can be identified from the spectra (Fig. 4e–g) i.e. 1D and 2D PIC simulations both qualitatively reproduce the larger amplification observed experimentally for a positive chirp, suggesting that scattering off a long-lived TPPS has an important role. Moreover, the spectrum of this scattered pump radiation almost fully overlaps the seed spectral range.
a Initial seed amplitude profile. b, c Amplified seed field envelopes after interaction with a pump beam with positive and negative frequency chirps, respectively. Pump back-scattering in front of the seed is not shown in full. The power spectrum of the initial seed is illustrated in d. Power spectra of the line-outs through the centre of the scattered signals are shown in e–g, for positive chirp and h–j, for negative chirp: e, h spectrum of the signal scattered in front of the seed; f, i spectrum of the amplified seed; g, j spectrum of the signal scattered into the trailing region behind the seed. All spectra are normalised by the largest peak value from the spectrum shown in h.
Conclusion
We have shown that amplification of an intense seed pulse in plasma depends on the sign of the chirp of an intense counter-propagating pump pulse and occurs through several distinct processes, including scattering off a TPPS, and the Compton and Raman instabilities. The measured scattered energy saturates around 20 mJ for a negative chirp, while, for a positive chirp, it grows to 90 mJ as the plasma density is increased, without any sign of saturation. PIC simulations show that almost half of the energy scattered from the pump can be due to the formation of a long-lived, localised, ion grating or TPPS. This is produced in a two-step, klystron-like process: when the pump pulse collides with the seed pulse, an electron grating is formed by the ponderomotive force of a local, nearly stationary, beat wave. Its space-charge force imparts phase-correlated momenta to the ions, which then ballistically evolve into an ion grating that is neutralised by overlapping electrons. 1D numerical simulations show the energy transfer is ≈17.5%, which should increase with higher densities. Furthermore, the grating survives the continuing propagation of the pump pulse through it and only washes out when the frequency detuning and/or pump intensity becomes large. In contrast, for a negative chirp, the beat wave becomes stationary somewhat later, and in the interim period, the plasma temperature rises, which suppresses the formation of the ion grating. The ability to produce and maintain robust gratings could provide a major advance for manipulating, reflecting, and compressing ultra-intense laser pulses.
Methods
Experimental layout
The experiments have been conducted at the Central Laser Facility at the Rutherford Appleton Laboratory using the two beams (referred to as pump and seed) from the Astra-Gemini laser system. The experimental layout is presented in Supplementary Fig. 1. The beams collide in a 3-mm wide hydrogen gas jet at an angle of 177∘ to avoid feedback into the laser amplifier chains. The 1–3.5 J, 6.5 ps duration pump pulse, chirped at a rate ∣α∣ = 1.15 × 1025 rad s−2, is focussed to a beam waist of 50 μm, which results in intensities of up to 1016 W cm−2. The pump spectrum is centred at 795 nm and has a bandwidth of 25 nm. The seed is 150 fs long and has an energy of up to 15 mJ, and a waist at a focus of 40 μm, which leads to a maximum peak intensity of 2.5 × 1015 W cm−2. To provide frequency detuning, the high frequencies of the seed pulse are filtered out in the compressor using a mask to produce a spectrum with a bandwidth of 10 nm centred at 810 nm. The pump beam serves the dual purpose of pre-ionising the gas medium to form a plasma with a density of up to 1.5 × 1019 cm−3, while acting as a source of energy for amplifying the seed pulse. The seed pulse is transported to a calibrated energy metre, and a small fraction is directed to a diagnostic system that includes a far-field imager (16-bit Andor CCD camera) and an imaging spectrometer (Shamrock spectrometer connected to a 16-bit Andor CCD camera) for analysing the seed focal spot, in addition to a frequency-resolved optical grating (FROG) diagnostic system, to enable full temporal characterisation.
Plasma density measurements
The plasma density, for low gas backing pressure, is estimated from the measured frequency shift between the pump pulse central frequency and the Raman Stokes peak frequency using the “positive chirp” data. A linear fit is used to evaluate the density at higher backing pressures, where the experimental data cannot be used. The relative error is estimated to be ±20%.
Numerical simulations
Numerical simulations have been performed using the fully relativistic PIC code OSIRIS in a static window53.
1D numerical runs use 32 particles per cell and per species with 60 cells per laser wavelength. The simulation domain length is 6.15 mm, with a gas/plasma length of 3 mm, including 200-μm up and down ramps. Depending on the simulated case, the domain is initially filled with either atomic hydrogen or plasma. The density in the main flat region is 1 × 1019 cm−3. The pump pulse is frequency-chirped with a 6.5-ps full-width-half-maximum (FWHM) intensity Gaussian envelope. The spectrum is centred at 795 nm with a 25-nm bandwidth. The seed uses a fifth-order polynomial function with a 150-fs FWHM duration. Laser pulse intensities match the experimental parameters.
2D numerical runs use four particles per cell and per species with 50 (longitudinal) × 6 (transverse) cells per laser wavelength. The simulation domain and plasma lengths are identical to the 1D case, with a transverse dimension of 0.252 mm. The pump and seed pulse waists are 50 and 40 μm, respectively. The seed temporal profile is identical to the profile for the 1D case. The pump temporal profile is a combination of two Gaussian functions that models the asymmetry observed in the measured experimental spectrum. The temporal profile is derived from fitting the experimental spectrum and assumes a linear frequency chirp to obtain a ≈ 6.5-ps full-width-half-maximum (FWHM) Gaussian envelope.
Data availability
Data associated with research published in this paper is accessible at https://doi.org/10.15129/537a07e7-8ef1-46ea-bf83-d44f895e688e.
References
Strickland, D. & Mourou, G. Compression of amplified chirped optical pulses. Opt. Comm. 56, 219 (1985).
Gales, S. et al. The extreme light infrastructure—nuclear physics (ELI-NP) facility: new horizons in physics with 10 PW ultra-intense lasers and 20 MeV brilliant gamma beams. Rep. Prog. Phys. 81, 094301 (2018).
Zou, J. et al. Design and current progress of the Apollon 10 PW project. High. Power Laser Sci. Eng. 3, e2 (2015).
Shvets, G., Fisch, N. J., Pukhov, A. & ter Vehn, J. M. Superradiant amplification of an ultrashort laser pulse in a plasma by a counterpropagating pump. Phys. Rev. Lett. 81, 4879 (1998).
Malkin, V. M., Shvets, G. & Fisch, N. J. Fast compression of laser beams to highly overcritical powers. Phys. Rev. Lett. 82, 4448 (1999).
Wu, H.-C., Sheng, Z.-M., Zhang, Q.-J., Cang, Y. & Zhang, J. Manipulating ultrashort intense laser pulses by plasma Bragg gratings. Phys. Plasmas 12, 113103 (2005).
Lehmann, G. & Spatschek, K. H. Transient plasma photonic crystals for high-power lasers. Phys. Rev. Lett. 116, 225002 (2016).
Lehmann, G. & Spatschek, K. H. Plasma-based polarizer and waveplate at large laser intensity. Phys. Rev. E 97, 063201 (2018).
Liu, C. S., Tripathi, V. K. & Eliasson, B. in High-Power Laser-Plasma Interaction Ch. 10 (Cambridge Univ. Press, 2019).
Drake, J. F. et al. Parametric instabilities of electromagnetic waves in plasmas. Phys. Fluids 17, 778 (1974).
Madey, J. M. J. Stimulated emission of Bremsstrahlung in a periodic magnetic field. J. Appl. Phys. 42, 1906 (1971).
Peng, H., Riconda, C., Grech, M., Su, J.-Q. & Weber, S. Nonlinear dynamics of laser-generated ion-plasma gratings: a unified description. Phys. Rev. E 100, 061201 (2019).
Amiranoff, F. et al. The role of the global phase in the spatio-temporal evolution of strong-coupling Brillouin scattering. Phys. Plasmas 25, 013114 (2018).
Chiaramello, M., Amiranoff, F., Riconda, C. & Weber, S. Role of frequency chirp and energy flow directionality in the strong coupling regime of Brillouin-based plasma amplification. Phys. Rev. Lett. 117, 235003 (2016).
Edwards, M. R., Jia, Q., Mikhailova, J. M. & Fisch, N. J. Short-pulse amplification by strongly coupled stimulated Brillouin scattering. Phys. Plasmas 23, 083122 (2016).
Lehmann, G. & Spatschek, K. H. Control of Brillouin short-pulse seed amplification by chirping the pump pulse. Phys. Plasmas 22, 043105 (2015).
Dong, M. & Winful, H. G. Area dependence of chirped-pulse stimulated Brillouin scattering: implications for stored light and dynamic gratings. J. Opt. Soc. Am. B 32, 2514 (2015).
Weber, S. et al. Amplification of ultrashort laser pulses by Brillouin backscattering in plasmas. Phys. Rev. Lett. 111, 055004 (2013).
Weber, S., Riconda, C. & Tikhonchuk, V. T. Low-level saturation of Brillouin backscattering due to cavity formation in high-intensity laser-plasma interaction. Phys. Rev. Lett. 94, 055005 (2005).
Yoffe, S. R. et al. Particle-in-cell simulation of plasma-based amplification using a moving window. Phys. Rev. Res. 2, 013227 (2020).
Balakin, A. A., Fraiman, G. M., Jia, Q. & Fisch, N. J. Influence of nonlinear detuning at plasma wavebreaking threshold on backward Raman compression of non-relativistic laser pulses. Phys. Plasmas 25, 063106 (2018).
Sadler, J. D. et al. Advantages to a diverging Raman amplifier. Comm. Phys. 1, 19 (2018).
Balakin, A. A. & Levin, D. S. Raman amplification of laser pulses near the threshold for plasma wave breaking. Plasma Phys. Rep. 43, 677 (2017).
Edwards, M. R., Toroker, Z., Mikhailova, J. M. & Fisch, N. J. The efficiency of Raman amplification in the wavebreaking regime. Phys. Plasmas 22, 074501 (2015).
Malkin, V. M. & Fisch, N. J. Key plasma parameters for resonant backward Raman amplification in plasma. Eur. Phys. J. Spec. Top. 223, 1157 (2014).
Chapman, T. et al. Driven spatially autoresonant stimulated Raman scattering in the kinetic regime. Phys. Rev. Lett. 108, 145003 (2012).
Trines, R. M. G. M. et al. Simulations of efficient Raman amplification into the multipetawatt regime. Nat. Phys. 7, 87–92 (2011).
Ersfeld, B., Farmer, J., Raj, G. & Jaroszynski, D. A. The role of absorption in Raman amplification in warm plasma. Phys. Plasmas 17, 83301 (2010).
Farmer, J. P., Ersfeld, B. & Jaroszynski, D. A. Raman amplification in plasma: wavebreaking and heating effects. Phys. Plasmas 17, 113301 (2010).
Hur, M. S., Yoo, S. H. & Suk, H. Envelope-kinetic analysis of the electron kinetic effects on Raman backscatter and Raman backward laser amplification. Phys. Plasmas 14, 033104 (2007).
Ersfeld, B. & Jaroszynski, D. A. Superradiant linear Raman amplification in plasma using a chirped pump pulse. Phys. Rev. Lett. 95, 165002 (2005).
Dodin, I. Y. & Fisch, N. J. Storing, retrieving, and processing optical information by Raman backscattering in plasmas. Phys. Rev. Lett. 88, 165001 (2002).
Tsidulko, Y. A., Malkin, V. M. & Fisch, N. J. Suppression of superluminous precursors in high-power backward Raman amplifiers. Phys. Rev. Lett. 88, 235004 (2002).
Malkin, V. M., Shvets, G. & Fisch, N. J. Detuned Raman amplification of short laser pulses in plasma. Phys. Rev. Lett. 84, 1208 (2000).
Marquès, J.-R. et al. Joule-level high-efficiency energy transfer to subpicosecond laser pulses by a plasma-based amplifier. Phys. Rev. X 9, 021008 (2019).
Lancia, L. et al. Signatures of the self-similar regime of strongly coupled stimulated Brillouin scattering for efficient short laser pulse amplification. Phys. Rev. Lett. 116, 075001 (2016).
Lancia, L. et al. Experimental evidence of short light pulse amplification using strong-coupling stimulated Brillouin scattering in the pump depletion regime. Phys. Rev. Lett. 104, 025001 (2010).
Vieux, G. et al. An ultra-high gain and efficient amplifier based on Raman amplification in plasma. Sci. Rep. 7, 2399 (2017).
Yang, X. et al. Chirped pulse Raman amplification in warm plasma: towards controlling saturation. Sci. Rep. 5, 13333 (2015).
Turnbull, D., Li, S., Morozov, A. & Suckewer, S. Simultaneous stimulated Raman, Brillouin, and electron-acoustic scattering reveals a potential saturation mechanism in Raman plasma amplifiers. Phys. Plasmas 19, 83109 (2012).
Vieux, G. et al. Chirped pulse Raman amplification in plasma. New J. Phys. 13, 063042 (2011).
Yampolsky, N. A. et al. Demonstration of detuning and wavebreaking effects on Raman amplification efficiency in plasma. Phys. Plasmas 15, 113104 (2008).
Ren, J., Cheng, W., Li, S. & Suckewer, S. A new method for generating ultraintense and ultrashort laser pulses. Nat. Phys. 3, 732 (2007).
Cheng, W. et al. Reaching the nonlinear regime of Raman amplification of ultrashort laser pulses. Phys. Rev. Lett. 94, 45003 (2005).
Balakin, A. A. et al. Laser pulse amplification upon Raman backscattering in plasma produced in dielectric capillaries. JETP Lett. 80, 12 (2004).
Dreher, M., Takahashi, E., Meyer-ter Vehn, J. & Witte, K. J. Observation of superradiant amplification of ultrashort laser pulses in a plasma. Phys. Rev. Lett. 93, 95001 (2004).
Ping, Y., Cheng, W., Suckewer, S., Clark, D. S. & Fisch, N. J. Amplification of ultrashort laser pulses by a resonant Raman scheme in a gas-jet plasma. Phys. Rev. Lett. 92, 175007 (2004).
Ping, Y., Geltner, I. & Suckewer, S. Raman backscattering and amplification in a gas jet plasma. Phys. Rev. E 67, 16401 (2003).
Ping, Y., Geltner, I., Morozov, A., Fisch, N. J. & Suckewer, S. Raman amplification of ultrashort laser pulses in microcapillary plasmas. Phys. Rev. E 66, 46401 (2002).
Bonifacio, R. et al. Physics of the high-gain FEL and superradiance. La Riv. del. Nuovo Cim. 13, 1–69 (1990).
Jaroszynski, D. A. et al. Superradiance in a short-pulse free-electron-laser oscillator. Phys. Rev. Lett. 78, 1699–1702 (1997).
Jia, Q., Barth, I., Edwards, M. R., Mikhailova, J. M. & Fisch, N. J. Distinguishing Raman from strongly coupled Brillouin amplification for short pulses. Phys. Plasmas 23, 053118 (2016).
Fonseca, R. A. et al. OSIRIS: a three-dimensional, fully relativistic particle in cell code for modeling plasma based accelerators. In International Conference on Computational Science 342–351 (Springer, 2002).
Acknowledgements
We acknowledge the support of the UK EPSRC (EP/J018171/1 and EP/N028694/1), the European Union’s Horizon 2020 research and innovation programme under Grant Agreement No. 871124 Laserlab-Europe. B.El. acknowledges support from the EPSRC (UK), grant EP/M009386/1. We would like to extend our thanks to the staff at the CLF for their valuable help. Also, the authors would like to thank the OSIRIS consortium (UCLA/IST) for the use of OSIRIS. 1D simulation results have been obtained using the EPSRC-funded ARCHIE-WeSt High-Performance Computer (www.archie-west.ac.uk). For the 2D simulation results, this research used the resources of the Supercomputing Laboratory at King Abdullah University of Science & Technology (KAUST) in Thuwal, Saudi Arabia. This work also used the ARCHER2 UK National Supercomputing Service (https://www.archer2.ac.uk).
Author information
Authors and Affiliations
Contributions
The project was initiated by D.A.J. The experiment was conceived by G.V. and D.A.J. The experiments and equipment calibration were undertaken by G.V., S.C., G.H.W, S.R.Y., F.G., M.P.T., C.P., G.M., J.M.D., T.K. and D.A.J. Experimental data were processed and analysed by G.V. Theoretical analysis, interpretation and simulations were carried out by G.V., B.Er., S.R.Y., B.El., M.S.H., E.B., G.L. and D.A.J. The manuscript was mainly written by G.V., B.El., B.Er., M.S.H., S.R.Y. and D.A.J., but all authors contributed to it.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vieux, G., Cipiccia, S., Welsh, G.H. et al. The role of transient plasma photonic structures in plasma-based amplifiers. Commun Phys 6, 9 (2023). https://doi.org/10.1038/s42005-022-01109-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-01109-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.