Abstract
Weyl semimetals show unique physical properties exemplified by the colossal anomalous Hall effect, arising from exotic quasiparticles called Weyl fermions emerging around the Weyl nodes. Manipulating these topologically protected Weyl nodes is anticipated to play a leading role towards the on-demand control of quantum properties in Weyl semimetals. We demonstrate non-volatile chirality switching in a ferromagnetic Weyl semimetal Co3Sn2S2 via all-optical magnetization reversal. When excited by circularly polarized mid-infrared light pulses, the sign reversal of the anomalous Hall conductivity stemming from the Berry curvature is observed, manifesting the switching of the chirality of the Weyl nodes accompanying with the magnetization reversal. Magneto-optical imaging measurements reveal that the mechanism of the magnetization/chirality switching is attributed to the helicity-dependent deterministic magnetization associated with the magnetic circular dichroism.
Similar content being viewed by others
Introduction
Weyl semimetals (WSMs) are topological quantum materials in which linear band crossings called Weyl nodes exist and act as pseudo-magnetic monopoles in the momentum space, where the magnetic charges of those monopoles are associated with chirality1,2,3,4,5. The low-energy quasiparticles in WSMs behave as chiral Weyl fermions characterized by spin- or pseudospin-momentum locking. The presence of Weyl nodes is manifested by non-trivial topological properties such as negative magnetoresistance ascribed to chiral anomaly and surface Fermi arcs that connect the Weyl nodes of opposite chirality. The existence of WSM requires the absence of either or both time-reversal symmetry and inversion symmetry. Magnetic WSMs (MWSMs) with spontaneously broken time-reversal symmetry exhibit a colossal intrinsic anomalous Hall effect (AHE) originating from the diverging Berry curvature at the Weyl nodes. The intrinsic anomalous Hall conductivity (AHC) arises from the unique electronic band topology, and therefore possesses dissipationless nature, making stark contrast to the extrinsic AHE which is originated by scattering processes6,7. Combined with the fully spin-polarized nature of the induced current, the intrinsic AHE has attracted great interests for its application to high-speed, low power-consumption spintronic applications including memory, logic devices, and quantum computing technology8,9.
To further exploit the functionalities of WSMs, on-demand manipulation of the topological properties is imperative. Besides static tuning with electric and magnetic fields, currents, and strain fields, light illumination provides another unique and promising route toward the control of those quantum functionalities. One approach is to exploit the coupling between Weyl fermions’ pseudospins and the polarization of light, which is a general feature of WSMs. This leads to novel optical and optoelectronic phenomena such as the circular photogalvanic effect10,11,12, bulk photovoltaic effect13, enhanced second-harmonic generation14, and terahertz (THz) emission15. Another approach is the light-induced modulation of the broken symmetry which the WSM originates from. This was demonstrated recently for inversion symmetry-breaking WSMs where the optical excitation causes, although transiently, a change in the crystal symmetry16,17,18. This controllability is a direct and unique consequence of the inversion symmetry-breaking origin of WSMs.
Compared to those WSMs, MWSMs have distinct aspects due to the coupling between band topology and magnetic orders. The energy, position, and chirality of Weyl nodes can be tuned by rotating the orientation of magnetic moments, causing the modulation of topologically non-trivial transport properties like AHE19,20. Switching between two ground states with opposite magnetization in MWSMs reverses the chirality of Weyl nodes and the sign of AHE in a non-volatile way. This would usually require an external magnetic field, while recently the electric current-induced switching of MWSMs has been realized by utilizing the spin-orbit torque in heterostructure devices21,22,23. By contrast, reports on optical control of MWSMs are scarce despite its potential ability for the non-volatile, freely reconfigurable, and ultrafast switching.
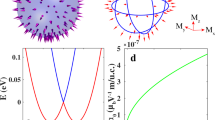
Here we demonstrate chirality switching in a thin film of a shandite compound Co3Sn2S2 via all-optical magnetization reversal by circularly polarized mid-infrared (MIR) light pulse excitation. Co3Sn2S2 is a recently identified MWSM that exhibits the chiral anomaly24, giant intrinsic anomalous Hall effect24,25, and Fermi arc surface state26,27. The unit cell consists of three stacked layers of the 2D kagome lattice of Co (Fig. 1a). The ferromagnetism arises from Co kagome layers with a strong anisotropy along the out-of-plane (c-axis) magnetic easy axis. The time-reversal symmetry-breaking WSM phase originates from spin-orbit coupling (SOC) and ferromagnetism24,25. When the SOC is absent, the valence and conduction bands inverse near the L points of the Brillouin zone, which forms nodal rings protected by the mirror symmetry. The MWSM phase emerges below the ferromagnetic phase transition temperature where the band degeneracy is lifted by exchange splitting. The nodal rings are gapped out by including SOC except for the protected spatial symmetry positions (red and blue spheres in Fig. 1b), which gives rise to pairs of linearly crossing bands (Fig. 1c). Several band calculations revealed that there are three pairs of Weyl nodes in the first Brillouin zone as shown in Fig. 1b, and the Weyl points of the spin majority band lies close to the Fermi energy. This condition provides unique opportunities to examine the physical properties characteristic to Weyl fermions.
a, Unit cell of Co3Sn2S2 where the cobalt atoms form a ferromagnetic kagome lattice. The magnetic moments are indicated by arrows along the c-axis. b Distribution of the Weyl points in the 3D Brillouin zone and the 2D momentum space projected in (001) direction. Red and blue represent the chirality (plus or minus) of each Weyl point. L points at the zone edge are indicated by black spheres. c Schematic band structure of Co3Sn2S2 in ferromagnetic phase including the nodal ring (black line) for that without spin-orbit coupling (SOC) and the Weyl points (red and blue spheres) for that with SOC. d Anomalous Hall conductivity and e that divided by longitudinal conductivity as a function of temperature. The Curie temperature, TC, is indicated by the arrow. f Anomalous Hall resistivity versus magnetic field curves at various temperatures. g Schematic of the terahertz (THz) Faraday rotation spectroscopy (\({\theta }_{F,{{{{{\rm{THz}}}}}}}\): the Faraday rotation angle) and near-infrared (NIR) Faraday microscope system with left-hand (\({\sigma }^{-}\)) and right-hand (\({\sigma }^{+}\)) circularly polarized MIR pump pulse. The mid-infrared (MIR) pump is incident normally to the sample, that is, parallel to the c-axis along which the magnetization (\(M\)) is oriented.
Results
Sample and setup
Our sample is a 23-nm-thick, c-axis oriented Co3Sn2S2 film grown by radio-frequency magnetron sputtering, which has been proven to show the transport properties equivalent to those of bulk single crystals28,29,30,31 (“Methods”). Figures 1d, e show the temperature dependence of the anomalous Hall conductivity \({\sigma }_{{xy}}\) and that divided by the longitudinal conductivity, \({\sigma }_{{xy}}/{\sigma }_{{xx}}\), respectively, the latter of which is equal to the tangent of Hall angle. The AHC and tangent of Hall angle increase below the Curie temperature, TC, of around 185 K, and reach more than 1500 Ω−1 cm−1 and 0.2, respectively, confirming the giant AHE which is equivalent to the value of bulk Co3Sn2S224,25. Hall resistivity curves as a function of magnetic field (\({\mu }_{0}H\), where \({\mu }_{0}\) is vacuum permeability) along the c-axis are displayed in Fig. 1f. Clear hysteresis loops observed below TC indicate that the out-of-plane direction is the easy magnetization axis and the coercive field reaches about 5 T at 100 K. The coercive force is larger than that of the bulk Co3Sn2S224,25,32 as is also reported for the Co3Sn2S2 thin flake33, which is partly attributed to the difference in magnetic anisotropy and domain wall pinning. The experimental setup is illustrated in Fig. 1g. For the evaluation of the AHC, the Faraday rotation measurement using the terahertz (THz) probe pulse was conducted. In addition, the magneto-optical microscope with near-infrared (NIR) light probe pulse visualizes the magnetization along the easy axis of the Co3Sn2S2 film. The MIR pump pulse (0.31 eV in photon energy) with left-hand circular (\({\sigma }^{-}\)), right-hand circular (\({\sigma }^{+}\)), and linear (\(X\)) polarization was used for the excitation of the sample (Methods for details).
Light-induced sign reversal of the anomalous Hall effect
The AHE of Co3Sn2S2 film with the MIR pulse excitation was examined by measuring the Hall conductivity in the THz frequency range34. The AHC of Co3Sn2S2 in the THz frequency range has been proven to reflect the intrinsic AHE which originates from the interband transition matrix element associated with the nodal rings connected to the Weyl nodes35. As plotted in Fig. 2a, the real-part AHC spectra of the single magnetic domain created by 60 mT field cooling are almost constant in the measured photon energy range and are in good agreement with AHC measured by dc transport at each temperature. Figure 2b represents the THz AHC spectra which were measured after the MIR excitation (0.31 eV in photon energy, 2.5 mJ cm−2 in fluence) at 27 K for the initially saturated film. The spectra manifest the helicity-dependent switching of the AHE, as \({\sigma }^{+}\) (\({\sigma }^{-}\)) polarization leads to a positive (negative) AHC. The AHC becomes zero by linearly polarized light excitation. Since the THz AHC spectra were measured after the MIR light excitation was switched off, the film sample is considered to be cooled down to 27 K before the AHC measurements. Thus, the zero AHC is ascribed to randomly oriented multi-domain state composed of ferromagnetic domains with two possible magnetic orientations (hereafter we refer to as demagnetization for convenience). For the data in Fig. 2b, because the spot size of the probe THz pulse is larger than the pump MIR pulse, the pump beam was swept before the measurements to cover the large spot of the THz probe pulse. However, the coverage is not perfect especially for the probe frequency below 6 meV, causing the reduced THz AHC in the lower frequency after sweeping \({\sigma }^{+}\) (red circles) and \(X\) (green circles) polarized light. A repetitive switching of the AHE is demonstrated by measuring the THz Faraday rotation angle, \({\theta }_{F,{{{{{\rm{THz}}}}}}}\), with the irradiation of circular-polarized light. \({\theta }_{F,{{{{{\rm{THz}}}}}}}\) versus time is plotted in Fig. 2c, with repeatedly changing the polarization of the pump between \({\sigma }^{-}\) and \({\sigma }^{+}\) by controlling the retardance of the waveplate between \(\lambda /4\) and \(3\lambda /4\). The square-wave like change of \({\theta }_{F,{{{{{\rm{THz}}}}}}}\) indicates the sign reversal of the AHC. The demonstrated sign reversal of the intrinsic AHE, which originates from the diverging Berry curvature around the Weyl nodes, manifests the non-volatile, light-induced chirality switching of the Weyl fermions around each Weyl node in MWSM, as illustrated in Fig. 2d.
a Optical anomalous Hall conductivity (AHC) (circles at several temperatures) of the uniformly magnetized film by field-cooling. Squares indicate the AHC measured by dc transport. b Optical AHC after sweeping the mid-infrared (MIR) pump pulses with the \({\sigma }^{-}\), \({\sigma }^{+}\), and \(X\) polarization. c Temporal evolution of terahertz (THz) Faraday rotation angle \({\theta }_{F,{{{{{\rm{THz}}}}}}}\) under MIR pulse excitation with the fluence of 1.99 mJ cm−2, along with the retardance of the waveplate where \(\lambda /4\) (\(3\lambda /4\)) corresponding to \({\sigma }^{-}\) (\({\sigma }^{+}\)) polarization. The sample temperature was set to 148 K by zero-field cooling, so the initial magnetization was M/M0 = 0 (multi-domain state). d Illustration of chirality switching of magnetic Weyl semimetals (MWSMs) by circularly polarized light. The chirality of each Weyl point is described as C = ± 1.
Change of magnetization with the chirality switching in Co3Sn2S2
As mentioned in the introduction part, the chirality of Weyl nodes in MWSMs is intimately coupled to the magnetization. Accordingly, the chirality switching should be associated with the all-optical magnetization switching (AOS) in Co3Sn2S2. To investigate the behavior of magnetization and its spatial distribution under the MIR excitation, we performed the magneto-optical imaging using NIR light pulse. Figure 3a shows magnetization images of the Co3Sn2S2 film after exposure to 104 pulses of \({\sigma }^{+}\) MIR light with various excitation fluences. The sample temperature was set to 100 K with the initial magnetization oriented to down (M/M0 = − 1) by 60 mT field-cooling, and the measurements were performed without applying a static magnetic field. Here, M/M0 denotes the magnetization relative to its saturated value (M/M0 = + 1 and −1 correspond to up and down magnetization, respectively), which was calibrated by the procedure described in Supplementary Note 1. A magnetization reversed domain (red) appears with a fluence of 0.48 mJ cm−2 on the initially saturated film (blue, M/M0 = − 1). When increasing the fluence, the area affected by the pump pulse expands while the central part becomes demagnetized. Similar to the THz AHC measurements, the images were taken more than 1 second after the MIR light excitation, therefore the film sample is considered to be cooled down to 100 K before the images were taken. Thus, the area that exhibits zero magneto-optical response (M/M0 = 0) should be viewed as a randomly oriented multi-domain state with each domain smaller than the spatial resolution of the imaging setup. The fluence dependence of the magnetization at the beam center is depicted in Fig. 3b. The reversal of the magnetization is identified when exceeding the threshold fluence at 0.45 mJ cm−2, resulting that the magnetization switching is efficiently activated in certain fluence region (shaded blue in Fig. 3b). Figures 3c, d display the magnetization image taken after \({\sigma }^{+}\), \({\sigma }^{-}\), and \(X\) polarized MIR light excitation for each position, with the initial magnetization set to up (M/M0 = + 1) and down (M/M0 = − 1), respectively. We can see that, in the outer ring regions of the affected areas, the deterministic magnetization control is realized depending on the light polarization; \({\sigma }^{+}\), \({\sigma }^{-}\), and \(X\) polarization which respectively leads to M/M0 = + 1, −1, 0. A comparison between Fig. 3c, d confirms the resultant magnetization to be independent of the initial magnetization. Since the light-induced magnetization reversal occurs only at the edge of the pump beam, a large area can be uniformly magnetized by sweeping the pump pulses over the film. This large area switching was demonstrated in Fig. 3e that was taken after sweeping the pump beam from right to left (indicated by black arrows). The complete magnetization switching by the swept laser is manifested by the line profile displayed in Fig. 3f, which is depicted along the vertical dashed line in Fig. 3e.
a Magnetization images of initially saturated (\(M/{M}_{0}\) = −1) Co3Sn2S2 film at 100 K after exposure to 104 pulses of \({\sigma }^{+}\) polarized mid-infrared (MIR) light under the indicated pump fluences. The color scale indicates the magnetization at each position \(M\) divided by the saturated value \({M}_{0}\), therefore \(M/{M}_{0}\) = −1(+1) corresponds to the spin down (up) state. b Magnetization at the beam center as a function of pump fluence. c Magnetization image after the spot excitation by \({\sigma }^{-}\), \({\sigma }^{+}\), and \(X\) polarized light at 100 K for the initially magnetization of M/M0 = + 1. d Same as (c), but the initial magnetization is opposite (M/M0 = − 1). e Line scans for \({\sigma }^{-}\), \({\sigma }^{+}\), and \(X\) polarized light. The laser beam was swept from right to left (indicated by black dotted arrows), and the magnetization pattern was subsequently imaged. For (c)–(e), the pump fluence was set to 0.69 mJ cm−2, and the color scale for (a) is also applied. f Line profile along the vertical dashed line in (e).
Multiple pulse accumulation effect
To understand the mechanism of the helicity-dependent magnetization control in Co3Sn2S2, we further examined a pulse-to-pulse accumulation effect. Figure 4a shows how the magnetization image evolves along the increase of the number of pump pulses with the fluence per pulse of 1.26 mJ cm−2 which is higher than the threshold fluence in Fig. 3b. The line profiles of the magnetization depicted from the images in Fig. 4a are also plotted in Fig. 4c. A single-pulse excitation causes only a circular demagnetized area in M/M0 = − 1 without showing the magnetization reversal. On the other hand, a multiple-pulse excitation leads to the deterministic magnetization in the outer ring region, where the magnetization increases toward M/M0 = + 1 by increasing the number of pulses. The magnetization reversal is completed by 103 pulses and no further change of the magnetization is observed by additional pulse irradiation (Supplementary Fig. 2 in Supplementary Note 2).
a Magnetization images of initially saturated film at 100 K after exposure to 1, 10, 100, and 1000 pulses of \({\sigma }^{+}\) polarized mid-infrared (MIR) light with a fluence of 1.26 mJ cm−2. The color scale indicates the magnetization at each position \(M\) divided by the saturated value \({M}_{0}\), therefore \(M/{M}_{0}\) = −1(+1) corresponds to the spin down (up) state. b Simulated magnetization images with single-pulse and multiple (104)-pulse excitations. c Line profiles of the magnetization from the central area and across the outer ring region depicted by images in (a). d Minimum laser fluence required to demagnetize the sample at the beam center by a single-pulse excitation (magenta circle). Dashed line represents the fitting curve describing the energy required to heat the sample to TC. Blue bars show the range of fluence where magnetization reversal is observed after 104-pulse excitation.
Discussion
Now we address the possible origin of the observed helicity-dependent switching of chirality and magnetization in Co3Sn2S2. AOS has been reported for a variety of ferrimagnetic36,37,38,39,40,41 and ferromagnetic materials42,43. AOS in ferrimagnets, which occurs with a single-shot excitation due to the transfer of angular momentum between magnetic sublattices, should differ from the present case, as atoms in Co3Sn2S2 do not form such sublattices. The observed AOS in this ferromagnetic Weyl semimetal rather resembles that of conventional ferromagnets. Accordingly, we consider two standard mechanisms of AOS in ferromagnets in order to explain the observed results. The first candidate is the inverse Faraday effect (IFE) where the effective magnetic field induced by the circular-polarized light results in the magnetization switching44. The mechanism of the AOS based on IFE combined with the laser-induced heating has been proposed45,46. This model in principle predicts a magnetization reversal even by a single-shot pulse excitation, while we do not observe such a magnetization reversal in the single-shot excitation case and only discern the demagnetization. Another plausible origin is the multi-shot accumulative AOS that occurs due to the magnetic circular dichroism (MCD)47,48. When a sample showing MCD is excited by circularly polarized light, the domains are selectively heated and thus have different probabilities of the magnetization switching. In this model, a single-shot pulse excitation of a uniformly magnetized sample causes randomly oriented domains at most (M/M0 = 0), but the repeated domain-selective laser-induced heating and subsequent cooling to the initial temperature can finally lead to a unidirectional overall magnetization with the orientation determined by the helicity of light.
The experimental result presented in Fig. 4a clearly indicates that the AOS occurs accumulatively by the multi-pulse excitation. We simulated this MCD-originated AOS (details are given in Supplementary Note 347). As presented in Fig. 4b, for a single-shot pulse excitation with a gaussian intensity profile, a circular demagnetized pattern is reproduced. On the other hand, with multiple (104)-pulse excitation, magnetization reversal progresses in the outer ring region because the accumulative AOS proceeds prominently in the area heated close to TC due to the maximum unbalance of switching probabilities. In contrast, the central area heated well above TC remains randomly oriented because domains of both magnetic orientations experience thermal demagnetization repeatedly. This explains that the radius of the ring pattern of the reversed magnetization (red region) spreads with increasing the pump fluence (Fig. 3a). The pump helicity dependence of the magnetization distribution (Fig. 3c, d) is also reproduced by the simulation (Supplementary Fig. 3). Note that the value of MCD at the pump photon energy (0.31 eV), defined as \(2({A}_{+}-{A}_{-})/({A}_{+}+{A}_{-})\) where \({A}_{+}\) (\({A}_{-}\)) is the absorption rate for \({\sigma }^{+}\) (\({\sigma }^{-}\)) polarized light, is estimated as large as 0.15 in the Co3Sn2S2 film (Supplementary Note 4 and Supplementary Fig. 4)35. Owing to this large MCD, the use of MIR light is likely better for accurate and efficient reversal of chirality and magnetization of Co3Sn2S2 compared to, for example, NIR light with about 1 eV showing the much smaller MCD. The giant magneto-optical response arising from the Weyl nodes in the MWSMs leads to a large MCD especially for low-frequency light, which is thought to favor the demonstrated switching. However, we would also like to note that the AOS in the present model and resultant chirality switching in MWSMs should be realized regardless of the microscopic mechanism of the MCD, whether it originates from linearly dispersing bands around Weyl nodes or from other bulk bands. In fact, the MCD in Co3Sn2S2 at photon energy 0.31 eV mainly arises from the interband transitions associated with bulk bands which are distinct from the nodal rings connected to the Weyl nodes35.
The present model predicts that the demagnetization by single pulse occurs when the temperature of the illuminated area is heated up to TC. Magenta circles in Fig. 4d present the experimentally obtained fluence threshold for the demagnetization at the beam center by a single-pulse excitation. Dashed line in Fig. 4d shows a fitting curve assuming that the absorbed pump pulse energy is consumed to heat the irradiated area of Co3Sn2S2 film up to TC, with adopting the literature value of the specific heat of the bulk Co3Sn2S249. The only fitting parameter is the absorption of the film sample for \({\sigma }^{+}\)-polarized pump pulse. The great consistency of the temperature dependence between the fitting and the experimental data verifies the above scenario. The obtained power absorption rate of the film, 47%, shows a reasonable agreement to the value of 35% estimated from the literature values of the optical longitudinal and Hall conductivity of bulk Co3Sn2S2 at 20 K35. Blue bars in Fig. 4d express the range of fluence at which AOS occurs after 104-pulse irradiation, adopted from the blue highlighted region in Fig. 2b. While the present model reproduces the observed AOS even semi-quantitatively, it is not sufficient to explain the threshold fluence for the multiple-pulse switching, which is substantially lower than the value of single-shot demagnetization. This efficient magnetization reversal compared to the demagnetization may suggest contributions of domain-wall motion, the effect of which has been investigated for the AOS in ferromagnetic materials50,51. For example, the thermal gradient between oppositely oriented magnetic domains due to MCD-induced non-equivalent heating can drive domain wall motions, which promote the magnetization reversal by expanding nucleated domains of opposite magnetic orientation. Other nonlocal effects such as dipolar fields should also affect the actual switching probability47. Further improvement of the models including these nonlocal effects is desirable to further elucidate the dynamics of the underlying mechanism. Although the observed chirality/magnetization switching is accumulative where the net magnetization gradually changes by cycles of the laser-induced heating and cooling events, two-step cumulative AOS where the repetitive laser pulse irradiation causes a helicity-independent demagnetization followed by a helicity-dependent remagnetization52 can be excluded as a mechanism for the present case by examining pulse-to-pulse magnetization under \({\sigma }^{+}\) and \({\sigma }^{-}\) excitation (Supplementary Note 5 and Supplementary Fig. 5). In the model of MCD-induced AOS (Supplementary Note 3), the deterministic magnetization results from the imbalance of hopping probabilities (Supplementary eq. (3) in SI) for two magnetic domains with opposite spins. This imbalance depends on the temperature dependence of energy barrier \(E\left(T\right)={VK}(T)\) (V: the grain volume, K: the out of plane magnetic anisotropy of energy density, in Supplementary eq. (4) in SI), how large the difference in elevated temperature between the two magnetic domains is, and how long they are held at elevated temperature (a parameter thot in Supplementary eq. (3) in SI). For the application of the chirality/magnetization switching to general MWSMs, the larger MCD, K, V, and thot are beneficial for the magnetization reversal, resulting in a smaller number of optical pulses required for the switching. If the difference between the initial temperature and the TC is large, the temperature difference between the two magnetic domains will be large, so magnetization reversal will be promoted with a smaller number of optical pulses. On the other hand, a large amount of pulse energy is required to bring about a large temperature rise, which can be disadvantageous in terms of energy efficiency. Appropriate design of these material parameters is crucial for the application of highly efficient magnetization/chirality switching, including the room temperature operation using MWSMs with higher Curie temperature.
The switching speed of the observed magnetization reversal is considered to be limited by the dynamics of the laser-induced heating and subsequent cooling. We performed a pump-probe measurement to evaluate this time-scale (Supplementary Note 6 and Supplementary Fig. 6). The result indicates that the demagnetization takes tens of picoseconds and the system returns to the initial temperature within hundreds of picoseconds. Considering that the magnetization reversal needs multiple heating and cooling events, the overall switching process requires nanoseconds in the present experimental condition, while further improvements, e.g., reduction of the pump spot size and improving of thermal contact may contribute to shorten the switching time.
Conclusions
In summary, we demonstrated the light-induced chirality switching in a MWSM, Co3Sn2S2, through an AOS process. Although the mechanism for the observed AOS is reasonably well described by a model that has been applied in conventional ferromagnetic materials, the intimate coupling between the chirality and the magnetization in the MWSM has made it possible to switch the chirality of Weyl nodes by light. This is further confirmed by the sign change of the THz AHC, underpinning the sign reversal of the Berry curvature distribution around the Weyl nodes that occurs concomitantly with the sign reversal of magnetization and thus the chirality of each Weyl node. Since the observed chirality/magnetization switching phenomenon originates from the inequivalent heating of oppositely oriented magnetic domains caused by MCD, the switching scheme should be applicable to a wide range of MWSMs regardless of the origin of MCD. The capability of magnetic/chirality domain control by light would also provide a platform for manipulating the domain structure and for exploiting the domain wall dynamics which are anticipated to be governed by the emergent axial gauge fields in MWSMs53,54.
Methods
Sample preparation and characterization
The 23-nm-thick c-axis-oriented Co3Sn2S2 films capped with an approximately 50-nm-thick insulating SiO2 layer were grown on double-side polished Al2O3 (0001) substrates by radio-frequency magnetron sputtering28. For the Co3Sn2S2 thin film samples prepared by this sputtering method, the ferromagnetic transition temperature, saturation magnetization, magnetic anisotropy parameter Ku, room temperature resistivity, residual resistivity at low temperature, anomalous Hall conductivity have been reported28,29,30,31,35, and all these values indicate properties were equivalent to those of bulk single crystals24,25,32. The compositional ratio was stoichiometric within the error bar range of energy-dispersive X-ray spectroscopy evaluation31. The structural characterization by transmission electron microscopy and X-ray diffraction using Cu Kα radiation have shown that the thin film samples were composed of c-axis oriented domains, while the anomalous Hall effect originating from the Berry curvature is less sensitive to the domain boundaries in the film. The c-axis orientation of the thin film samples ensures that the optical measurements performed in this study using c-axis propagating light reflect the in-plane optical responses perpendicular to the magnetic orientation. For the Co3Sn2S2 film used in this study, the thickness was estimated from thickness fringes around the Co3Sn2S2 (0006) peak. Electrical measurements for the evaluation of resistivity \({\rho }_{{xx}}\) and Hall resistivity \({\rho }_{{xy}}\) were carried out with the scratched Hall-bar sample in physical property measurement system (PPMS, Quantum Design). Conductivity \({\sigma }_{{xx}}\) and Hall conductivity \({\sigma }_{{xy}}\) were calculated from those resistivities.
Mid-infrared pump and THz Faraday rotation measurement
As a light source, we used a Yb:KGW-based regenerative amplifier (pulse energy 2 mJ, center wavelength 1030 nm, repetition rate 3 kHz, and pulse duration 170 fs). Half of the output was used to generate the mid-infrared pump pulse (pulse energy 17 μJ, center wavelength 4.0 μm, pulse duration 96 fs) by an optical parametric amplifier. The other half was used for the probe THz pulse. The fluence of the mid-infrared excitation was tuned by using two ZnSe wire-grid polarizers and the polarization was controlled by a liquid-crystal variable retarder. The pump pulse was focused using a CaF2 lens and normally incident to the sample. The spot size at the sample position was 90 μm in 1/e radius for the data shown in Figs. 3a and 4a, and 150 μm in 1/e radius for those in Figs. 2 and 3c–e. To obtain the Hall conductivity in the THz frequency range, we performed the Faraday rotation measurement with using time-domain THz polarimetry55. The THz probe pulses were generated by a 380-μm-thick GaP (110) crystal. The transmitted THz probe pulses were detected by electro-optic sampling in another GaP (110) crystal. The spot size of the probe THz pulse was evaluated for each frequency (or photon energy) taking into account the difference of diffraction limit. The values obtained by knife edge measurements at the sample position were 240 × 310 μm for 1 THz (4.14 meV) and 140 × 200 μm for 2 THz (8.27 meV) in 1/e radius. The Faraday rotation angle (\({\theta }_{F}\)) and ellipticity (\({\eta }_{F}\)) were obtained by measuring the parallel and perpendicular components of THz electric field by using wire-grid polarizers. The complex Hall conductivity is then converted by the equation \({\theta }_{F}\left(\omega \right)+i{\eta }_{F}(\omega )\cong {{{{{{\rm{\sigma }}}}}}}_{{xy}}({{{{{\rm{\omega }}}}}})d/\left[\left(1+{n}_{{{{{{\rm{sub}}}}}}}\right)c{\epsilon }_{0}+{\sigma }_{{xx}}\left({{{{{\rm{\omega }}}}}}\right)d\right]\) where \({n}_{{{{{{\rm{sub}}}}}}}\) is the refractive index of the substrate, \(c\) the speed of light, \({\epsilon }_{0}\) the vacuum permittivity, \({\sigma }_{{xx}}({{{{{\rm{\omega }}}}}})\) the longitudinal conductivity, and \(d\) the thickness of the film sample.
The Faraday rotation angle in Fig. 2c was measured during the mid-infrared pump irradiation while the Hall conductivity in Fig. 2b was measured after finishing the pump irradiation. For the data in Fig. 2c, the repetition rate of the pump pulse was reduced to 1.5 kHz using an optical chopper. The electric field perpendicular to the incident THz polarization (defined as \({E}_{y}\)) was measured using the THz probe pulse which was incident alternately to the pump pulse. Namely, \({E}_{y}\) was measured 0.33 ms after the pump pulse excites the sample where the sample was considered to be cooled down to the initial temperature. The measured \({E}_{y}\) was converted to the Faraday rotation angle plotted in Fig. 2c by an approximate expression \({\theta }_{F}={E}_{y}/{E}_{x}\), where \({E}_{x}\) is the transmitted THz electric field parallel to the incident polarization.
Magneto-optical microscopy using near-infrared light
For the magnetization imaging, the linearly polarized near-infrared (1030 nm) optical pulse was incident to the sample slightly non-collinear to the mid-infrared pump beam. The transmitted probe pulse was guided to a charge-coupled device (CCD) camera to take the polarization-resolved image of the sample with an analyzer (a glan-laser prism) placed before the CCD camera. The magnetization at each position was obtained by the calibration procedure as described in Supplementary Note 1. The typical spatial resolution was 3 μm by using a 5× objective.
Data availability
All relevant data are available from the authors upon request.
References
Burkov, A. A. Topological semimetals. Nat. Mater. 15, 1145–1148 (2016).
Jia, S., Xu, S.-Y. & Hasan, M. Z. Weyl semimetals, Fermi arcs and chiral anomalies. Nat. Mater. 15, 1140–1144 (2016).
Yan, B. & Felser, C. Topological materials: Weyl semimetals. Annu. Rev. Condens. Matter Phys. 8, 337–354 (2017).
Armitage, N. P., Mele, E. J. & Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 90, 015001 (2018).
Nagaosa, N., Morimoto, T. & Tokura, Y. Transport, magnetic and optical properties of Weyl materials. Nat. Rev. Mater. 5, 621–636 (2020).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539–1592 (2010).
Yang, K.-Y., Lu, Y.-M. & Ran, Y. Quantum Hall effects in a Weyl semimetal: possible application in pyrochlore iridates. Phys. Rev. B 84, 075129 (2011).
Roushan, P. et al. Topological surface states protected from backscattering by chiral spin texture. Nature 460, 1106–1109 (2009).
Qian, X., Liu, J., Fu, L. & Li, J. Quantum spin Hall effect in two-dimensional transition metal dichalcogenides. Science 346, 1344–1347 (2014).
de Juan, F., Grushin, A. G., Morimoto, T. & Moore, J. E. Quantized circular photogalvanic effect in Weyl semimetals. Nat. Commun. 8, 15995 (2017).
Ma, J. et al. Nonlinear photoresponse of type-II Weyl semimetals. Nat. Mater. 18, 476–481 (2019).
Rees, D. et al. Helicity-dependent photocurrents in the chiral Weyl semimetal RhSi. Sci. Adv. 6, eaba0509 (2020).
Osterhoudt, G. B. et al. Colossal mid-infrared bulk photovoltaic effect in a type-I Weyl semimetal. Nat. Mater. 18, 471–475 (2019).
Wu, L. et al. Giant anisotropic nonlinear optical response in transition metal monopnictide Weyl semimetals. Nat. Phys. 13, 350–355 (2017).
Gao, Y. et al. Chiral terahertz wave emission from the Weyl semimetal TaAs. Nat. Commun. 11, 720 (2020).
Sie, E. J. et al. An ultrafast symmetry switch in a Weyl semimetal. Nature 565, 61–66 (2019).
Luo, L. et al. A light-induced phononic symmetry switch and giant dissipationless topological photocurrent in ZrTe5. Nat. Mater. 20, 329–334 (2021).
Sirica, N. et al. Photocurrent-driven transient symmetry breaking in the Weyl semimetal TaAs. Nat. Mater. 21, 62–66 (2022).
Ghimire, M. P. et al. Creating Weyl nodes and controlling their energy by magnetization rotation. Phys. Rev. Res. 1, 032044 (2019).
Li, P. et al. Giant room temperature anomalous Hall effect and tunable topology in a ferromagnetic topological semimetal Co2MnAl. Nat. Commun. 11, 3476 (2020).
Tsai, H. et al. Electrical manipulation of a topological antiferromagnetic state. Nature 580, 608–613 (2020).
Takeuchi, Y. et al. Chiral-spin rotation of non-collinear antiferromagnet by spin–orbit torque. Nat. Mater. 20, 1364–1370 (2021).
Han, J. et al. Current-induced switching of a ferromagnetic Weyl semimetal Co2MnGa. Appl. Phys. Lett. 119, 212409 (2021).
Liu, E. et al. Giant anomalous Hall effect in a ferromagnetic kagome-lattice semimetal. Nat. Phys. 14, 1125–1131 (2018).
Wang, Q. et al. Large intrinsic anomalous Hall effect in half-metallic ferromagnet Co3Sn2S2 with magnetic Weyl fermions. Nat. Commun. 9, 3681 (2018).
Liu, D. F. et al. Magnetic Weyl semimetal phase in a Kagomé crystal. Science 365, 1282–1285 (2019).
Morali, N. et al. Fermi-arc diversity on surface terminations of the magnetic Weyl semimetal Co3Sn2S2. Science 365, 1286–1291 (2019).
Fujiwara, K. et al. Ferromagnetic Co3Sn2S2 thin films fabricated by co-sputtering. Jpn. J. Appl. Phys. 58, 050912 (2019).
Shiogai, J. et al. Robust perpendicular magnetic anisotropy of Co3Sn2S2 phase in sulfur deficient sputtered thin films. Phys. Rev. Mater. 5, 024403 (2021).
Ikeda, J. et al. Two-dimensionality of metallic surface conduction in Co3Sn2S2 thin films. Commun. Phys. 4, 117 (2021).
Ikeda, J. et al. Critical thickness for the emergence of Weyl features in Co3Sn2S2 thin films. Commun. Mater. 2, 18 (2021).
Shvetsov, O. O. et al. Lateral Josephson effect on the surface of the magnetic Weyl semimetal Co3Sn2S2. Phys. Rev. B 101, 035304 (2020).
Tanaka, M. et al. Topological Kagome magnet Co3Sn2S2 thin flakes with high electron mobility and large anomalous Hall effect. Nano Lett. 20, 7476–7481 (2020).
Shimano, R. et al. Terahertz Faraday rotation induced by an anomalous Hall effect in the itinerant ferromagnet SrRuO3. EPL Europhys. Lett. 95, 17002 (2011).
Okamura, Y. et al. Giant magneto-optical responses in magnetic Weyl semimetal Co3Sn2S2. Nat. Commun. 11, 4619 (2020).
Stanciu, C. D. et al. All-optical magnetic recording with circularly polarized light. Phys. Rev. Lett. 99, 047601 (2007).
Radu, I. et al. Transient ferromagnetic-like state mediating ultrafast reversal of antiferromagnetically coupled spins. Nature 472, 205–208 (2011).
Liu, T.-M. et al. Nanoscale confinement of all-optical magnetic switching in TbFeCo—competition with nanoscale heterogeneity. Nano Lett. 15, 6862–6868 (2015).
Lalieu, M. L. M., Peeters, M. J. G., Haenen, S. R. R., Lavrijsen, R. & Koopmans, B. Deterministic all-optical switching of synthetic ferrimagnets using single femtosecond laser pulses. Phys. Rev. B 96, 220411 (2017).
El-Ghazaly, A. et al. Ultrafast magnetization switching in nanoscale magnetic dots. Appl. Phys. Lett. 114, 232407 (2019).
Avilés-Félix, L. et al. Single-shot all-optical switching of magnetization in Tb/Co multilayer-based electrodes. Sci. Rep. 10, 5211 (2020).
Lambert, C.-H. et al. All-optical control of ferromagnetic thin films and nanostructures. Science 345, 1337–1340 (2014).
Mangin, S. et al. Engineered materials for all-optical helicity-dependent magnetic switching. Nat. Mater. 13, 286–292 (2014).
Kirilyuk, A., Kimel, A. V. & Rasing, T. Ultrafast optical manipulation of magnetic order. Rev. Mod. Phys. 82, 2731–2784 (2010).
Cornelissen, T. D., Córdoba, R. & Koopmans, B. Microscopic model for all optical switching in ferromagnets. Appl. Phys. Lett. 108, 142405 (2016).
John, R. et al. Magnetisation switching of FePt nanoparticle recording medium by femtosecond laser pulses. Sci. Rep. 7, 4114 (2017).
Gorchon, J., Yang, Y. & Bokor, J. Model for multishot all-thermal all-optical switching in ferromagnets. Phys. Rev. B 94, 020409 (2016).
Ellis, M. O. A., Fullerton, E. E. & Chantrell, R. W. All-optical switching in granular ferromagnets caused by magnetic circular dichroism. Sci. Rep. 6, 30522 (2016).
Schnelle, W. et al. Ferromagnetic ordering and half-metallic state of Sn2Co3S2 with the shandite-type structure. Phys. Rev. B 88, 144404 (2013).
Quessab, Y. et al. Helicity-dependent all-optical domain wall motion in ferromagnetic thin films. Phys. Rev. B 97, 054419 (2018).
Quessab, Y. et al. Resolving the role of magnetic circular dichroism in multishot helicity-dependent all-optical switching. Phys. Rev. B 100, 024425 (2019).
El Hadri, M. S. et al. Two types of all-optical magnetization switching mechanisms using femtosecond laser pulses. Phys. Rev. B 94, 064412 (2016).
Araki, Y. Magnetic textures and dynamics in magnetic Weyl semimetals. Ann. Phys. 532, 1900287 (2020).
Ilan, R., Grushin, A. G. & Pikulin, D. I. Pseudo-electromagnetic fields in 3D topological semimetals. Nat. Rev. Phys. 2, 29–41 (2020).
Shimano, R. et al. Quantum Faraday and Kerr rotations in graphene. Nat. Commun. 4, 1841 (2013).
Acknowledgements
This work was supported by JST CREST grant No. JPMJCR19T3, JPMJCR18T2, Japan. The authors thank Takashi Oka, Shun Okumura, and Hiroyuki Sudo for fruitful discussions.
Author information
Authors and Affiliations
Contributions
N.Y. and K.O. contributed equally to this work. R.S. conceived the project of this study. N.Y., K.O., and Y. H. carried out the optical experiments and analyzed the data. K.O. conducted the simulation with feedbacks from N.Y. and R.S. K.F., J.I., and A.T. fabricated and characterized the sample. N.Y. and R.S. wrote the manuscript with substantial feedbacks from all the coauthors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Rajyavardhan Ray and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yoshikawa, N., Ogawa, K., Hirai, Y. et al. Non-volatile chirality switching by all-optical magnetization reversal in ferromagnetic Weyl semimetal Co3Sn2S2. Commun Phys 5, 328 (2022). https://doi.org/10.1038/s42005-022-01106-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-01106-8
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.