Abstract
Quantum random number generators find applications in both quantum and classical communications schemes, particularly in security protocols where they can be used as a source of random seed or key material. In this work, we describe the implementation of a quantum random number generator on-board a nanosatellite deployed in low Earth orbit. Our generator samples shot noise from an entangled photon-pair source based on spontaneous parametric down-conversion, linking the entropy of the output to the quantization of the down-converted beam. We present analyzed data from the orbiting instrument alongside data taken from a ground-based engineering model where the statistical test suites indicate a good match to the output from a uniform distribution. Finally, we use the source to implement a prototype for an off-grid randomness beacon. This work paves the way to future low Earth orbit based public quantum randomness beacons.
Similar content being viewed by others
Introduction
Quantum random number generators (QRNGs) access the inherent randomness of quantum processes as a source of entropy in order to produce an unbiased and unpredictable output. These devices have been shown to have many prospective use cases, notably in cryptography1, simulation2, telecommunications3, and financial systems4.
In contrast to other physical random number generators, the unpredictability, which is a natural consequence of quantum mechanics, provides an abundant and uncomplicated source of randomness. Despite this relative availability, it is non-trivial to extract randomness from a quantum source due to the presence of technical noise arising from the imperfect nature of the measurement devices5.
In recent years, there have been many successful demonstrations of quantum random number generators in laboratories6,7,8, and several commercial products have entered the marketplace9. Besides this, there has been theoretical progress in more advanced QRNG schemes that allow public verification10, self-testing11 and even device-independent quantum random number generation12,13.
Of the many schemes to extract entropy from a photonic quantum system, we highlight: measuring the photon number statistics of a suitably attenuated source14, projective measurements of photon polarization orthogonal to the preparation basis15, and the measurement of interference between laser pulses with random phase16. Where entanglement is present, there are also opportunities to exploit the corresponding super-classical correlations to produce randomness which contains a degree of device independence12,13,17, or to generate so-called certified randomness17,18.
In this work, we describe the implementation of a quantum random number generator on an orbiting nanosatellite, SpooQy-119. While we are able to repurpose the satellite’s primary quantum optics payload for QRNG operation, constraints imposed by the resource-scarce platform restrict us to a simple scheme based on photon number statistics. In addition to the applications noted previously, orbiting random number generators enable the implementation of a resource known as a randomness beacon20. While a number of randomness beacons are currently accessible via the internet20,21, an orbiting beacon would be available to remote infrastructures with only sporadic, high-latency internet access, for example, monitoring stations connected via store-and-forward satellite services22,23. These installations could then make use of beacon pulses in applications such as time-stamping algorithms to increase the integrity of record-keeping, or for auditable input to a sampling process24. We describe here a proof-of-concept implementation of a public randomness beacon, and demonstrate the retrieval of beacon data via two distant ground stations, located in Switzerland and Singapore. Preliminary data from this publication was previously presented25, lacking detailed analysis and the demonstration of a prototype randomness beacon.
Results and discussion
The quantum optics payload on-board SpooQy-1 performs tomography on pairs of polarization-entangled photons generated from a spontaneous parametric down-conversion process. This paves the way to future implementation of entanglement-based quantum key distribution protocols such as Ekert9126 and BBM9227 in satellite-to-ground and satellite-to-satellite settings. For full details of the instrument, we refer readers to references19,28. Certified randomness can in principle be extracted from the correlation measurements of entangled photon pairs. However, the detection scheme on SpooQy-1 enables only the counting of coincident detections, and does not permit the time-stamping of individual events. Due to this design constraint, it is not feasible to utilize entanglement as a source of entropy for our QRNG. Instead, we take as our entropy source fluctuations in the discrete event rates captured during payload operation.
In the context of our QRNG implementation, it is sufficient to consider the production and detection of correlated photon pairs, with random detection times inherited from the statistical properties of the pump beam (see Fig. 1). The observation of shot noise in the measured event rate can be traced directly to the quantum description of the laser source, i.e., a coherent state [29, Chapter 8]. (see Supplementary note 1 for a discussion on shot noise as a randomness source).
A diode laser is used to pump (with mean photon counts/s, Sp) a spontaneous parametric down-conversion (SPDC) process based on bulk crystals. This results in the production of correlated pairs of photons, which inherit the random arrival time distribution from the pump field (see plotted call-outs). After removal of the pump light, these photon pairs are efficiently separated using a dichroic mirror (DM), and directed to two avalanche photodiode detectors (D1, D2) via two sets of optics implementing a polarization projection. Detectors D1 and D2 have mean photon counts/s, Si and Ss, respectively. Digitized electronic signals from the detectors are then combined with an AND gate, and coincident events are accumulated with a microcontroller (MC). For a detailed description of the optical payload, please refer to references19,28.
Photon pairs produced in the instrument are separated using a dichroic mirror and directed to two avalanche photodiodes. The digitized electronic signal from these detectors is routed to an AND gate and coincident detection events are recorded by a microcontroller.
Prior to detection, photons undergo polarization projection, implemented using a pair of liquid crystal polarization rotators and polarizers. This projection is used to select a measurement basis for each photon. When the same measurement bases are selected for both photons, the majority of coincident events are attributed to photon pairs. This approach allows accidental coincidences attributed to other sources (e.g., detector dark counts, stray light) to be rendered negligible by the use of a sufficiently short timing window. For example, in this implementation, they account for ~2% of the signal28,30, and this could be further reduced with more precise timing electronics.
As a direct consequence of the polarization entanglement generated by the optical system, any polarization basis measured simultaneously on both of the photons produce equivalent correlations. During QRNG operation, we select the diagonal basis to measure both of the photons. This detection scheme based on coincident events can be used to minimize the contribution from other entropy sources, significantly reducing the classical effect that would otherwise dominate the single detection channels. In the absence of any external noise source, random variations in the detected event rates can be traced to the quantization of the spontaneous parametric down-conversion field, which can be considered a uniform sampling of the photons in the pump beam. We use this as our raw entropy source.
Our approach resembles the work described by ref. 5, where random numbers are generated by sampling a coherent illuminating beam with a mobile phone camera. Due to the random inter-arrival times of the photons, the number of detected coincident events per unit of time may be expected to follow a Poisson distribution31. Care is taken to operate the instrument in a regime where the detectors are not saturated, preserving the Poissonian distribution of the source (see Supplementary note 2 for a discussion of how these statistics might be affected by detector recovery times). To extract uniform bits from this distribution we employ a Toeplitz hash-based extractor, as outlined in the Methods section.
To validate the uniformity of our QRNG’s output, a 35.6 kB sequence of random data generated in the laboratory is evaluated using the “Dieharder” test suite, and the result is visualized using the KS test (summarized in Fig. 2), alongside output generated using the C language RNG implementation32. In this analysis, the expectation for a random source is that the p value for each test should be distributed in the interval [0.01, 0.99]. Our data appears to conform to this expectation showing the empirically obtained p values remain close to the theoretical ideal line. This test also illustrates the limitations of such statistical analysis in assessing a random generator, specifically that such tests are restricted to the assessment of uniformity. The reader will note the similar performance obtained using the C RNG, which is pseudorandom and therefore entirely predictable with the knowledge of the seed.
We evaluate the (statistical) randomness of bits produced by our quantum random number generator. Data generated in laboratory setup passes all tests in the “Dieharder” suite (i.e., 0.01 < p < 0.99), illustrated here in the form of the KS test42 (blue curves) alongside a hypothetical ideal randomness source (black dashed line) and pseudorandom numbers generated using C RNG (yellow curves). This qualitative test sorts p values and plots them alongside values uniformly distributed over the interval [0,1].
Experiment performance in orbit
The experiment is repeated on-board SpooQy-1, after deployment in low Earth orbit. Due to the limited duty cycle of satellite operations and communication bandwidth, we are restricted to retrieve at most 256 random bits per trial. It is non-trivial to test the quality of randomness of such small datasets. For example, the “Dieharder” test is not suitable for these datasets33. However, one may estimate the quality of randomness of such short sequences of bits by observing the frequencies of occurrences of sub-strings of a particular length (namely the Borel normality condition)34, with a perfectly random sequence expected to produce a uniform distribution for each length. Figure 3 shows an analysis of 16896 random bits (i.e., the result of 66 trials in orbit), with the relative frequencies matching this expectation. For example, asymptotically the relative frequencies of occurrences of both 0 and 1 should be 50%, and occurrences of each of the strings 00, 01, 10, and 11 should be 25%. In our analysis of 66 trials, the occurrences of 0 and 1 are 49.8(3)% and 50.5(3)% respectively. The sequences 00, 01, 10, and 11 are observed with occurrences 24.5(4)%, 26.0(4)%, 24.3(4)%, and 25.0(4)% respectively.
We analyze 66 runs of randomness beacon containing total 16,896 bits generated in orbit. For a limited data set of this size, tests such as “Dieharder” provide little meaningful insight. Instead, it is useful to compute the relative frequencies of occurrences of all binary sub-strings of length 1, 2, 3, … (the so-called Borel normality condition34). This analysis indicates a uniform distribution within error bars limited by finite sample size.
Implementing a prototype randomness beacon
A randomness beacon20 is a public, periodically updated source of randomness provided as a resource for a variety of tasks which require a random input. The beacon publishes “pulses” of random bits on a pre-defined schedule, which are typically broadcast over the internet.
We implement a prototype randomness beacon with a 24-hour refresh interval on-board the nanosatellite SpooQy-1, with the goal of demonstrating the feasibility of distributing such a beacon to off-grid infrastructures. There are a few established functionality principles that a randomness beacon must satisfy in order to be useful20. These include the signing of each “pulse” using a public key traceable to the beacon originator, in order that the provenance of the beacon pulse can be confirmed. Pulses must also bear references to their parent in order to facilitate verification of the beacon’s integrity. While these features should be straightforward to implement on a dedicated satellite, SpooQy-1’s primary mission objectives laid stringent resource constraints on the QRNG subsystem. However, we were able to reinforce several standard elements of the satellite’s on-board radio to meet these requirements.
The on-board radio (Nanocom AX100, GOMspace) broadcasts a beacon signal at 30-second intervals, and is able to contain a simple data structure consisting of up to 256 generated random bits. The radio implements a hash-based message authentication code (HMAC), linking beacons to the satellite’s private key35. Alongside a timestamp, our data structure includes the current randomness beacon data in the form of 256 bits of full-entropy randomness. As computing a hash of the previous beacon data would be too computationally expensive for our highly constrained platform, we opt instead to include the full 256 random bits from the previous beacon, satisfying the requirement for linking to previous pulses.
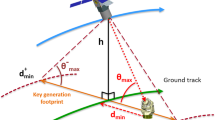
The satellite beacon is encoded using a proprietary data format, which can be decoded by the GOMspace GS100 ground station receiver36. Beacons were recorded at two ground stations, located at Windisch (Switzerland) and on the National University of Singapore’s Kent Ridge campus (Singapore). As our satellite was deployed from the ISS (International Space Station) orbit (inclination 51.6∘, period ~90 minutes), we typically observe six passes per day over the Switzerland site, and up to four passes over the Singapore site. Since the two ground stations are in different time zones, it yields a possibility for us to receive the same beacon at two different stations approximately 10 times in 24 hours. Ground track, locations of our ground stations, and a randomness beacon received by the ground stations on 12 January, 2020 are shown in Fig. 4.
We demonstrate a prototype orbiting randomness beacon. The ground track of our satellite is plotted against the world map, indicating the locations of our ground stations in Windisch (Switzerland) and Kent Ridge (Singapore). With an inclination of 51.6∘ and an orbital period ~90 minutes, the satellite is able to communicate with both ground stations 10 times within a 24-hour period. As our prototype randomness beacon updates every 24 hours, we are able to confirm the reception of identical beacons at both locations. Map graphics were generated using Cartopy43 with public domain data from Natural Earth.
As microsatellite-based broadband internet proliferates37, there may be an increased demand for satellite-based cryptographic infrastructures such as randomness beacons. To be truly useful, an orbital randomness beacon would require a higher refresh rate than demonstrated in this work (for example, the NIST beacon20 updates every 60 s), robust cryptographic authentication, and rigorous linking of sequential pulses38. While it was not possible to implement all of these on SpooQy-1, we believe that our proof-of-concept demonstration shows that such beacons can be hosted on-board low-resource satellites using existing technologies.
Conclusion
We have implemented a quantum random number generator on board an orbiting nanosatellite where the entropy is derived from the shot noise of photon correlations. QRNG output is tested using randomness testing suites, suggesting that the results are strongly indicative of highly uniform distribution. More comprehensive tests on the random bit string generated can be carried out once sufficient data is available. However, this work clearly shows the feasibility and practicality of this QRNG approach. We also implement a prototype randomness beacon, broadcasting randomness generated from a known and characterized quantum process.
Our results demonstrate the feasibility of implementing a sophisticated, photonics-based solution despite the challenges imposed by these small, resource-limited platforms. We hope that these results can pave the way towards more powerful QRNG implementations in orbit, including self-testing39 or even device-independent designs12.
Methods
In order to construct a randomness extractor, we must first estimate the available entropy of the sampled random signal. For a coincidence rate λ, with X a random variable corresponding to the number of events observed in one second, the probability of observing a particular outcome n is given by
The accessible entropy from this source is estimated using the min entropy of this distribution, given by
We extract uniform random numbers from this signal using a Toeplitz hashing extractor40 with extraction ratio g. With k bits encoding each event X, g must be less than \({H}_{\min }(X)/k\), with this value calculated following Equation (2). The result is uniformly distributed random bits5 with probability
Here m is the number of input low entropy bits and l is the number of extracted high entropy bits. The security parameter, ϵ > 0, is the probability of failure for the randomness extraction.
In our experiment, coincidence data is encoded in k = 16-bit registers. From analysis of 47, 422 seconds of data generated using a ground-based identical copy of the source, we estimate the quantum randomness per bit as g ≥ 1/4. We employ a Toeplitz matrix with dimensions l = 256 and m = 3072, yielding 256 bits of extracted randomness per 192 16-bit registers and achieving a generation rate of 80 bits/minute (see, Fig. 5). From equation (3), we expect the generated random bits to deviate from perfect randomness with probability at most 2−256. This means that one must collect and process 2256 random bits before being able to predict the next bit, assuming full control over, or knowledge of, the classical noise of the original source.
256 uniform random bits (y) are generated from 3072 input bits (x), captured as 192 16-bit integers. The extraction is performed using a 256 × 3072 Toeplitz matrix40 (M), which simultaneously removes any bias from the input sequence, and excludes the impact of non-quantum noise sources. Input and output integer sequences are shown here in greyscale representation, and we further expand 64 bits of the output to show a binary representation.
Figure 6a depicts detector coincident counts collected for 125 minutes in a laboratory setting using a source identical to that on the satellite. The raw data collected exhibits a slow-moving trend (orange curve). After removing the low-frequency components using fast Fourier transform (FFT) (cutoff frequency used 0.01 (Hz)), we obtain data which conforms well to a Poisson distribution (mean 1785 and Fano factor41 of 1 ± 0.013, Fig. 6c). This suggests that the remaining data consists of shot noise5. While resource constraints on the satellite do not permit the use of FFT algorithms, the use of only short-duration data blocks (192 samples of the coincident event rate) enables us to disregard these low-frequency contributions. This is confirmed by Fig. 6b, in which Fano factors of 192-point data blocks are shown to be within the range from 0.8 to 1.2, a signature of Poisson statistics reinforcing the absence of significant low-frequency effects.
a Raw coincident event rate and the moving average of the data points (orange curve) indicate the presence of a low-frequency component to the noise. b Histogram of Fano factors for each segment of 192 seconds length from the raw data in a. It shows that the Fano factors are centered ~1. This implies that in short time intervals the Poisson distribution is preserved. c The same data after removing low-frequency components by Fast Fourier Transform (FFT) filtering. d The histogram of the filtered coincidence data fit a Poisson distribution (red curve), indicating the remaining fluctuations are consistent with shot noise.
Data availability
The data that support the results of this work are available from the corresponding author on reasonable request.
Code availability
The code developed to analyze the data is available from the corresponding author on reasonable request.
References
Schindler, W. Random number generators for cryptographic applications. In Cryptographic Engineering, pp. 5–23. (Springer, 2009)
Hastings, W. K. Monte carlo sampling methods using markov chains and their applications. Biometrika 57, 97 (1970).
Bello, L. Debian open ssl predictable random number generator. Technical report (2008).
Schneier, B. Schneier’s cryptography classics library: applied cryptography, secrets and lies, and practical cryptography. (Wiley Publishing, 2007)
Sanguinetti, B., Martin, A., Zbinden, H. & Gisin, N. Quantum random number generation on a mobile phone. Phys. Rev. X 4, 031056 (2014).
Shen, L. et al. Randomness extraction from bell violation with continuous parametric down-conversion. Phys. Rev. Lett. 121, 150402 (2018).
Shi, Y., Chng, B. & Kurtsiefer, C. Random numbers from vacuum fluctuations. Appl. Phys. Lett. 109, 041101 (2016).
Herrero-Collantes, M. & Garcia-Escartin, J. C. Quantum random number generators. Rev. Mod. Phys. 89, 015004 (2017).
Quantum Random Number Generators: A Ten-year Market Assessment. Report IQT-QRNG-0121, Inside Quantum Technology https://www.insidequantumtechnology.com/product/quantum-random-number-generators-a-ten-year-market-assessment/ (2021).
Jacak, J. E., Jacak, W. A., Donderowicz, W. A. & Jacak, L. Quantum random number generators with entanglement for public randomness testing. Sci. Rep. 10, 1–9 (2020).
Ma, X. et al. Quantum random number generation. npj Quantum Inf. 2, 1–9 (2016).
Liu, Y. et al. Device-independent quantum random-number generation. Nature 562, 548–551 (2018).
Marangon, D. G., Vallone, G. & Villoresi, P. Source-device-independent ultrafast quantum random number generation. Phys. Rev. Lett. 118, 060503 (2017).
Dynes, J. et al. Testing the photon-number statistics of a quantum key distribution light source. Opt. Express 26, 22733–22749 (2018).
Jacak, M. M., Jóźwiak, P., Niemczuk, J. & Jacak, J. E. Quantum generators of random numbers. Sci. Rep. 11, 1–21 (2021).
Shakhovoy, R. et al. Quantum noise extraction from the interference of laser pulses in an optical quantum random number generator. Opt. express 28, 6209–6224 (2020).
Agresti, I. et al. Experimental device-independent certified randomness generation with an instrumental causal structure. Commun. Phys. 3, 1–7 (2020).
Acín, A. & Masanes, L. Certified randomness in quantum physics. Nature 540, 213–219 (2016).
Villar, A. et al. Entanglement demonstration on board a nano-satellite. Optica 7, 734–737 (2020).
Kelsey, J., Brandão, L.T., Peralta, R., Booth, H. A reference for randomness beacons: format and protocol version 2. Technical report, National Institute of Standards and Technology (2019).
Wang, G., Nixon, M. Randchain. Practical scalable decentralized randomness attested by blockchain. In 2020 IEEE International Conference on Blockchain (Blockchain), pp. 442–449 (2020).
Hamamoto, N., Arimoto, Y., Hashimoto, Y., Ide, T., Sakasai, M. High speed and global store and forward communication system using leo satellites. In Proceedings of 1994 3rd IEEE International Conference on Universal Personal Communications, pp. 418–422 (1994).
Allery, M., Ward, J. The potential for’store-and-forward’communications using small satellites in low earth orbits. In 3rd European Conference on Satellite Communications-ECSC-3, pp. 230–235 (1993).
Hevia, A. & Gómez, C. Why me? shedding light on random processes via randomness beacons. Commun. ACM 63, 49–50 (2020).
Reezwana, A., Islam, T., Grieve, J.A., Wildfeuer, C.F., Ling, A. Generating quantum random numbers on a cubesat (spooqy-1). In: CLEO: Applications and Technology, pp. 3–3 (2020).
Ekert, A. K. Quantum cryptography based on bell’s theorem. Phys. Rev. Lett. 67, 661 (1991).
Bennett, C. H., Brassard, G. & Mermin, N. D. Quantum cryptography without bell’s theorem. Phys. Rev. Lett. 68, 557 (1992).
Villar, A., Lohrmann, A. & Ling, A. Experimental entangled photon pair generation using crystals with parallel optical axes. Opt. express 26, 12396–12402 (2018).
Fox, M. Quantum Optics: an Introduction. Oxford university press (2006).
Zafra, A.V. Building entangled photon pair sources for quantum key distribution with nano-satellites. PhD dissertation, National University of Singapore (2019).
Mandel, L. Fluctuations of photon beams: the distribution of the photo-electrons. Proc. Phys. Soc. 74, 233 (1959).
Ritchie, D.M., Kernighan, B.W., Lesk, M.E. The C Programming Language. (Prentice Hall Englewood Cliffs, 1988).
L’Ecuyer, P. & Simard, R. Testu01: A C library for empirical testing of random number generators. ACM Trans. Math. Softw. (TOMS) 33, 1–40 (2007).
Ian Caludet, C. Borel normality and algorithmic randomness. In: Developments in Language Theory, p. 113 (1993).
GOMSPACE: Ax100–Long-range Software Configurable VHF/UHF Transceiver. (2016).
Nanocom GS100 Datasheet. GOMSPACE; gs-ds-nanocom-ax100-3.3.docx3.3; 12 August 2016. https://gomspace.com/UserFiles/Subsystems/datasheet/gs-ds-nanocom-ax100-33.pdf Accessed 2016-08-12.
Levchenko, I., Xu, S., Wu, Y.-L. & Bazaka, K. Hopes and concerns for astronomy of satellite constellations. Nat. Astron. 4, 1012–1014 (2020).
Fischer, M.J., Iorga, M., Peralta, R. A public randomness service. In: Proceedings of the International Conference on Security and Cryptography, pp. 434–438 (2011).
Lunghi, T. et al. Self-testing quantum random number generator. Phys. Rev. Lett. 114, 150501 (2015).
Ma, X. et al. Postprocessing for quantum random-number generators: entropy evaluation and randomness extraction. Phys. Rev. A 87, 062327 (2013).
Fano, U. Ionization yield of radiations. ii. the fluctuations of the number of ions. Phys. Rev. 72, 26 (1947).
Massey Jr, F. J. The kolmogorov-smirnov test for goodness of fit. J. Am. Stat. Assoc. 46, 68–78 (1951).
Met Office: Cartopy: a Cartographic Python Library with a Matplotlib Interface. Exeter, Devon. https://scitools.org.uk/cartopy (2010–2015).
Acknowledgements
This research was carried out at the Centre for Quantum Technologies, National University of Singapore, and supported by the National Research Foundation, Prime Minister’s Office, Singapore under the grant NRFCRP12-2013-02.
Author information
Authors and Affiliations
Contributions
A.R., T.I., X.B., C.W., A.L., and J.G. contributed equally to the work.
Corresponding author
Ethics declarations
Competing interests
The authors declare that there are no competing interests. James A. Grieve is a Guest Editor for Communications Physics, but was not involved in the editorial review of, or the decision to publish this article.
Peer review
Peer review information
Communications Physics thanks Juan Carlos Garcia-Escartin and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Reezwana, A., Islam, T., Bai, X. et al. A quantum random number generator on a nanosatellite in low Earth orbit. Commun Phys 5, 314 (2022). https://doi.org/10.1038/s42005-022-01096-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-01096-7
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.