Introduction

In the collisionless space and astrophysical plasma environments, the energy transfer and dissipation largely rely on wave-particle interaction. The interaction becomes especially efficient when a streaming particle observes the Doppler-shifted plasma waves at its cyclotron frequency, a process named cyclotron resonance1. The resonance condition is

$$\omega -{k}_{\parallel }{v}_{\parallel }-\varOmega =0,$$
(1)

where ω is the wave angular frequency, k∥ is the wavenumber in the background magnetic field direction, \({v}_{\parallel }\) is the particle’s parallel velocity, and Ω is the particle’s cyclotron frequency. When Eq. (1) is satisfied, the particle is locked in phase with the waves to enable a sustained wave-particle energy exchange. Accordingly, a resonant velocity Vr is defined by

$${V}_{{{{{{\rm{r}}}}}}}=(\omega -\varOmega )/{k}_{\parallel },$$
(2)

to represent the parallel velocity of resonant particles.

Cyclotron resonance plays a key, if not dominant role in shaping the particle dynamics in the near-Earth and planetary space environments. Two branches of plasma waves, namely, the electromagnetic ion cyclotron (EMIC) waves at frequencies slightly below the ion gyrofrequency2,3 and the whistler-mode chorus waves below the electron gyrofrequency4,5, are especially important in accelerating positively-charged ions6,7,8 and energetic electrons9,10,11, respectively. The latter process is also a major mechanism responsible for the formation of Earth’s and Jupiter’s radiation belts12,13,14. Resonant particles can be also decelerated in the perpendicular direction, which indicates pitch angle variation and, consequently, precipitation into the planetary atmosphere15,16,17,18,19,20,21,22.

Observational identifications of the cyclotron resonance have been made possible after the launch of the Magnetospheric Multiscale (MMS) four-spacecraft constellation23. Based on the MMS high-resolution (~150 ms) data of energetic ions, Kitamura et al. report that during an EMIC wave event24, the ion fluxes show periodic stripes in their gyro-phase spectra at energy and pitch-angle ranges matching the resonance condition in Eq. (1). These phase-bunching features are unambiguous manifestation of wave-particle cyclotron resonance8,24. More recently, spacecraft observations have also identified the formation of proton hills in phase space, which has been attributed to cyclotron resonance and believed to cause the frequency chirping of the observed EMIC waves25.

The resonance condition in Eq. (1), however, is derived based on a linear assumption that neglects the effect of the wave field on particle’s angular velocity. This implicit assumption can be understood by revisiting the equation of particle motion in the electromagnetic fields of parallel-propagating plasma waves,

$$\frac{{m{{{{{\rm{d}}}}}}}{{{{{\bf{v}}}}}}}{{{{{{{\rm{d}}}}}}t}}=q\left[{{{{{{\bf{E}}}}}}}_{{{{{{\bf{1}}}}}}}+{{{{{\bf{v}}}}}}\times \left({{{{{{\bf{B}}}}}}}_{{{{{{\bf{0}}}}}}}+{{{{{{\bf{B}}}}}}}_{{{{{{\bf{1}}}}}}}\right)\right],$$
(3)

where the particle velocity v includes the parallel \({{{{{{\bf{v}}}}}}}_{{{{{{\boldsymbol{\parallel }}}}}}}\) and perpendicular v⊥ components, B0 is the background magnetic field, E1 and B1 are the wave electric and magnetic fields (both in the plane perpendicular to B0), respectively. In deriving Eq. (1) from (3), only the background Lorentz force \({q{{{{{\bf{v}}}}}}}_{{{\perp }}}\times {{{{{{\bf{B}}}}}}}_{{{{{{\bf{0}}}}}}}\) is used to compute the particle’s angular frequency \(\varOmega =q{B}_{0}/m\) without considering the modification from the wave-associated forces (Lorentz force \({q{{{{{\bf{v}}}}}}}_{\parallel }\times {{{{{{\bf{B}}}}}}}_{{{{{{\bf{1}}}}}}}\) and electric force \({q{{{{{\bf{E}}}}}}}_{1}\), see “Methods” section for the detailed derivation). Therefore, the resonance condition in Eq. (1) applies only if the wave field is weak (\({B}_{1}/{B}_{0} \, < \, 0.01\), as a rule of thumb) or the particle’s perpendicular velocity is large (\({{{{{{\bf{v}}}}}}}_{{{\perp }}}\gg {{{{{{\bf{v}}}}}}}_{\parallel }\)). These assumptions are critical in the development of the classical cyclotron resonance theory26,27,28, in which the particle motion is described by a pendulum equation (Eq. (17) in the “Methods” section) to accommodate a single resonance island in phase space.

On the other hand, the resonant velocity in Eq. (2) can be modified significantly if the wave amplitude is large enough. Recent simulations29,30,31,32 have indeed shown that particles with small pitch angles can experience anomalous resonance at conditions different from Eq. (1), which highlights the importance of the wave-associated \({q{{{{{\bf{v}}}}}}}_{\parallel }\times {{{{{{\bf{B}}}}}}}_{{{{{{\bf{1}}}}}}}\) force in nonlinearly modifying the conventional theory. The resonance condition may also be revised by the wave electric field, since the electric force \({q{{{{{\bf{E}}}}}}}_{{{{{{\bf{1}}}}}}}\) can become comparable to the background Lorentz force for low-energy (tens or hundreds of eV) particles in large-amplitude waves. The role of the electric force in modifying the particle angular velocity has been explored theoretically33, which suggests that particles with parallel velocities much lower than the resonant velocity in Eq. (2) can still follow trapped trajectories in the velocity phase space. The trapping motion of these particles indicates a resonant behavior, although they were termed “nonresonant ions” in Berchem & Gendrin33 because of their deviation from the resonance condition in Eq. (1). Moreover, the modification of the particle’s angular velocity reaches the extremum when the phase difference \(\zeta\) between the perpendicular velocity and wave magnetic field equals 0 or 180°, which indicates the presence of two resonance islands centered in the direction parallel and antiparallel to the wave magnetic field33. The two-island scenario has also been obtained via a Hamiltonian formalism34,35,36, although such adjustments have not attracted sufficient attention due to the lack of observational evidence.

Here, we present MMS observations of large-amplitude EMIC waves with in-phase and antiphase relationships between the magnetic field and ion flux oscillations at energy and pitch-angle ranges incompatible with the cyclotron resonance condition. These two kinds of phase-bunched signatures are both reproduced by test-particle simulations, which provide direct evidence of the occurrence of anomalous resonance and the revision of the classical resonance condition. Since the low-energy particles usually have high phase-space densities (PSDs) in space plasmas37, their anomalous resonant behavior could impact the wave-particle energy transfer and consequently the evolution of plasma waves.

Results

Observations

The EMIC waves were observed by the MMS constellation on January 14, 2020 when the spacecraft traveled outbound in the dawnside magnetosheath. The four satellites observed nearly identical features (see Supplementary Figs. 1–4) due to their minor separations (typically 10–40 km), and therefore, we average the data over four spacecraft to improve the statistical significance. The utilized data include three-dimensional ion distributions from Fast Plasma Investigation, the magnetic field measurements from Flux Gate Magnetometer, and the electric field measurements from Electric field Double Probes38,39. The Hot Plasma Composition Analyzer data are also used to distinguish different ion species40, which shows a 99.5% contribution of protons to the plasma density. Therefore, we focus mostly on wave-proton interactions.

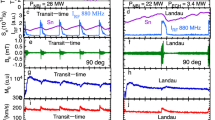
Figure 1 presents the overview of electromagnetic field and particle observations from 19:23:30 to 19:23:50 UT. The magnetic field in Geocentric Solar Eclipse (GSE) coordinates, shown in Fig. 1a, oscillated at a period of ~2.5 s, although the field strength (green line) hardly varied during this time interval. To better describe the field fluctuations, a field-aligned coordinate (FAC) is defined with the axial direction ([−0.45, 0.05, 0.89] in GSE) given by the background magnetic field B0 (determined via a lowpass elliptic filter at 0.05 Hz). The perpendicular ⊥2 direction is determined by the cross product of B0 and the sunward direction, and the ⊥1 direction completes the triad. The wavelet power spectrum of the perpendicular B1 field is given in Fig. 1b, which shows the peak wave power at 0.4 Hz between the local proton (red line) and helium-ion gyrofrequencies (blue line). The B1 and E1 wave fields, filtered within the 0.25~0.65 Hz frequency range, are shown in Fig. 1c, d. Obviously, B1⊥2 leads in phase than B1⊥1 by ~90°, which, together with their nearly identical amplitudes, indicate the left-hand circular polarization of the waves. The negligible fluctuations in \({E}_{1\parallel }\) and in \({B}_{1\parallel }\) (with \({B}_{1\parallel }/{B}_{1\perp }\) ∼ 0.15) also indicate the concentration of the wave field in the perpendicular plane. Figure 1e shows the 3-s running-averaged Poynting flux \({{{{{\bf{S}}}}}}={{{{{{\bf{E}}}}}}}_{{{{{{\bf{1}}}}}}}\times {{{{{{\bf{B}}}}}}}_{{{{{{\bf{1}}}}}}}/{\mu }_{0}\), which, as expected, is predominantly in the antiparallel direction. Therefore, the perpendicular wave fields (hereinafter referred to, for simplicity, as B1 and E1) can be used to estimate the wave phase speed \({v}_{{{{{{\rm{w}}}}}}}\)24. Based on Faraday’s law, we have

$$\left|{v}_{{{{{{\rm{w}}}}}}}\right|=\frac{\omega }{{{{{{\rm{|}}}}}}{k}_{\parallel }{{{{{\rm{|}}}}}}}=\frac{|{E}_{1\perp {{{{{{\rm{B}}}}}}}_{1}}|}{{B}_{1}},$$
(4)

where \({E}_{1\perp {{{{{{\rm{B}}}}}}}_{1}}\) is the E1 component perpendicular to both B0 and B1. The estimated phase speed is given in Fig. 1f. In other words, we have observed the hydrogen-band EMIC waves propagating unidirectionally in the spacecraft rest frame (labeled by subscript s) at the averaged velocity \({v}_{{{{{{\rm{ws}}}}}}}\)= −165 km s−1. Given the measured plasma bulk velocity of 35 km s−1 in the field-aligned direction, the wave phase velocity in the plasma rest frame (subscript p) is \({v}_{{{{{{\rm{wp}}}}}}}\)= −200 km s−1. These parameters enable us to determine the wavelength of ~400 km, which is much larger than the spacecraft separation and therefore justifies our approach to average the four spacecraft observations.

Fig. 1: MMS observations of an electromagnetic ion cyclotron wave event.
figure 1

a Magnetic fields in the Geocentric Solar Eclipse coordinates, with the x, y, z components and total magnetic field strength indicated by the black, blue, red and green lines, respectively. b Wavelet power spectra of the \({\perp }_{1}-{\perp }_{2}\) components of B1. c Wave magnetic field. d Wave electric field. e 3-s averaged Poynting flux. In panels (c–e), the black, blue and red lines represent the ⊥1, ⊥2 and ∥ components in the field-aligned coordinates, respectively. f Wave phase speed. g–i Gyro-phase spectra of phase space density (PSD) for perpendicular-moving ions (pitch angles between 90°±11.25°) within the 53-, 441-, and 974-eV energy channels, respectively, with the phase of B1 indicated by the blue lines. j Energy spectrum of PSD in log scale for the ions with pitch angles between 90°±11.25° and phase angle between 150° and 180°. k, l Gyro-phase spectra of PSD for ions (pitch angles between 0°–50°) within the 974- and 1269-eV energy channels, respectively.

Full size image

Since the ion distributions are measured at the temporal resolution of 150 ms, or ~1/15 of the wave period, one can determine the gyro-phase of each ion captured by the spacecraft at any given time. Here, the gyro-phase definition is based on FAC coordinates, with 0° representing the ⊥1 direction. Figure 1g–i shows the gyro-phase spectra of perpendicular-moving ions (in the pitch-angle range of 90° ± 11.25°) within the 53, 441 and 974 eV energy channels, respectively. The ion counts in each bin were typically greater than 100, high enough to ensure the statistical significance in this event. These spectra are characterized by periodic occurrence of inclined stripes with enhanced PSDs, which match the phase angle ϕB of the wave magnetic field B1 as indicated by the blue lines. Such a phase-bunched feature applies for perpendicular-moving ions from 50 eV to 1 keV (see Fig. 1j for the energy spectrum of perpendicular-moving ions with gyro-phase between 150° and 180°), with the direction of enhanced ion PSDs rotating along with B1 in the left-hand manner. The strong oscillations in Fig. 1j are compatible with the picture of ion acceleration or deceleration by tens or even hundreds of eV (see the energy variations of the PSD contours). Given the negative PSD gradient over energy, one can expect that the ions with enhanced PSDs (moving along B1 direction, or ζ = 0°) have been accelerated most significantly, and those with reduced PSDs (moving against B1, or ζ = 180°) have been decelerated the most.

The phase-bunched signatures are also observed for ions moving in the quasi-parallel direction. Figure 1k, l shows the gyro-phase spectra of the quasi-parallel-moving ions (with pitch-angle ranging from 0° to 50°) within the energy channels of 974 eV and 1269 eV, respectively. These features, however, are distinguished from those observed in Fig. 1g–i for perpendicular-moving ions in that the ion PSDs were enhanced in the −B1 direction (rather than B1 in Fig. 1g–i) indicating the strongest ion acceleration at ζ = 180°.

Neither perpendicular-moving ions nor the quasi-parallel-moving ions discussed above satisfy the classical resonance condition in Eq. (1). Here, the resonant velocity, computed based on Eq. (2), equals 90 km s−1 in the spacecraft rest frame (55 km s−1 in the plasma rest frame), in which the parameters ωs = 2.7 s−1, vws = −165 km s−1, and Ω = 4.17 s−1 are determined from observations. This velocity corresponds to the pitch angles of 27° and 78° for protons with energies of 53 eV and 974 eV, respectively, which are very different from the phase-bunched protons shown in Fig. 1g (53 eV, with pitch angle of ~90°) and Fig. 1k (974 eV, 0–50° pitch angle). The significant deviation is examined in the next section via test-particle simulations.

Simulations

Test-particle simulations are performed to analyze the evolution of ion distributions based on Liouville’s theorem, which ensures constant particle PSDs along their trajectories41,42. After we adopt an initial condition (uniform magnetic field, gyrotropic Maxwellian ion distributions in the plasma rest frame) and prescribe the wave field (a Gaussian-profiled monochromatic wave packet traveling against the background magnetic field with equal phase and group velocities), the trajectories of ions with various energies and moving-directions can be traced backward in time from any time and location to identify their initial velocities prior to the wave appearance. The time- and location-dependent ion distributions, including those detected by a virtual spacecraft (moving at a constant speed in the plasma rest frame to accommodate the background flow observed by MMS), can be determined via Liouville’s theorem. The detailed simulation setup is described in the “Methods” section.

Figure 2 shows the virtual spacecraft observations of our simulation. Figure 2a presents the wave magnetic field, in which the first two wave periods are associated with weak B1 but significant \(\partial {B}_{1}/\partial t\), and the latter six periods (the shadowed time interval) with stronger wave field correspond to the shadowed interval in Fig. 1. The simulated gyro-phase spectra for perpendicular-moving ions, given in Fig. 2b–d for three energy channels, show phase-bunched signatures nearly identical to the observations in Fig. 1g–i. The peaks of the simulated ion PSDs are aligned with the wave magnetic field (the blue lines) in the shadowed interval, although they show minor phase differences before that (the wave magnetic field leads in phase, to be discussed later). The observed pitch angle (90°) ion energy spectrum (Fig. 1j) are also reproduced in our simulations (see Fig. 2e). The agreement between simulations and observations provides an opportunity to understand the wave-particle interactions via analyzing representative ion trajectories.

Fig. 2: Simulation results observed by the virtual spacecraft.
figure 2

a Wave magnetic field, with the ⊥1 and ⊥2 components indicated by the black and blue lines, respectively. b–d Gyro-phase spectra in the same format as in Fig. 1g–i. e Energy spectrum in the same format as in Fig. 1j. f, g Temporal variations of kinetic energy and ζ (phase difference between the particle perpendicular velocity and the wave magnetic field) for sample protons A (black) and B (red), with their final energy and pitch angle (when reaching the spacecraft) labeled in Fig. 2d. The dashed lines represent the variations after their spacecraft arrival. h, i Gyro-phase spectra in the same format as in Fig. 1k–l. j, k Temporal variations of kinetic energy and ζ for sample protons A′ (black) and B′ (red), in the same format as in (f, g). l Temporal variations of the particle trapping frequency (ωtr, black), resonance island expansion rate (ωex, red) and nominal gyrofrequency (Ω1, blue) associated with the wave field B1, calculated based on the typical proton with 441 eV energy and 90° pitch angle.

Full size image

We select two sample ions with the same energy (441 eV), pitch angle (90°) and gyro-phase (250°) when they reach the virtual spacecraft at slightly different times (see the white dots in Fig. 2c). Obviously, proton A belongs to the phase-bunched population with higher PSDs, which indicates that it has been accelerated from a lower energy than proton B’s initial energy (see their energy variations in Fig. 2f). Figure 2g shows the temporal variations of ζ, in which the motion of proton B is characterized by its faster gyromotion than the wave field rotation. Proton A, on the other hand, gyrates faster than the wave vector only during the initial stage; after t = t0 + 9 s, the increasing ζ suggests that the wave field observed by proton A rotates faster than proton A’s angular motion. The sign reversal of dζ / dt indicates the proton’s resonant behavior, since it is trapped within a wave-carried phase-space island (see the limited ζ range of proton A in Fig. 2g) when the waves are strong enough.

Figure 2h, i presents the simulation results of the gyro-phase spectra for the 974- and 1269-eV protons moving in the quasi-parallel direction, which shows similar signatures to the observations (Fig. 1k, l), phase-bunched in antiphase with the wave magnetic field. We also select from Fig. 2h two typical ions, protons A′ and B′, with the same energy (974 eV), pitch angle (7°) and gyro-phase (110°) when reaching the virtual spacecraft, to understand their trajectories in the wave field. Here, proton A’ represents the phase-bunched population with enhanced PSDs, which has been accelerated from a lower energy than proton B′ (see Fig. 2j for their energy variations). The ζ variations of the two ions, given in Fig. 2k, show that the gyromotion of proton B’ is always slower than the wave field, whereas proton A′ is transitioned from a traversing trajectory into a trapped orbit near ζ = 180° as the wave amplitude becomes sufficiently high at around t0 + 10 s. In other words, the simulation results (together with their similarities with the observations) indicate the coexistence of two resonance islands centered at ζ = 0 and 180°, respectively.

Note that the proton trajectories discussed above are made complicated by the Gaussian profile of the wave evolution. To better understand the trapping and traversing motion of the protons, we next remove the Gaussian profile to focus on the proton behavior in the waves with uniform amplitude of 4 nT. Figure 3a presents the phase-space trajectories of protons A, B, A′ and B′ (represented by blue, yellow, red, and pink lines, respectively) before they reach the spacecraft at the corresponding circles. The horizontal and vertical axes are ζ and dζ/dt, respectively. Proton A′s closed trajectory, together with its intersection with the dζ/dt = 0 line, indicates the proton’s trapping motion around a resonance island centered at ζ = 0 (which coincides with the phase-bunched region of enhanced ion PSDs, see Fig. 1h). Within this island, proton A experiences significant variations in pitch angle (see Fig. 3b for proton trajectories in the \({v}_{\parallel }\)–\({v}_{\perp }\) plane), kinetic energy (Fig. 3c) and parallel velocity (Fig. 3d). Proton A′ also follows a closed trajectory to indicate its trapping motion within a different resonance island centered at ζ = 180°. Note that the energy variation of proton A′ is rather small (see Fig. 3c) in this case, which corresponds to the less significant PSD variations as observed in Fig. 1k, l than in Fig. 1g–i. The trajectories of protons B and B′, on the other hand, are always below or above the dζ/dt = 0 line in Fig. 3a, which agrees with their traversing motions with monotonic ζ variations in Fig. 2g, k, respectively.

Fig. 3: Phase-space trajectories of typical protons in the plasma rest frame.
figure 3

a Trajectories in the dζ/dt-ζ phase space. b Trajectories in the \({v}_{\parallel }\)-\({v}_{\perp }\) plane, in which the velocities are normalized by the Alfvén velocity VA = 290 km s−1 (computed based on the averaged plasma density Ni = 11 cm−3 and magnetic field strength B0 = 43.5 nT). c Trajectories in the Energy-ζ phase space. d Trajectories in the \({v}_{\parallel }\)-\(\zeta\) phase space, in which \({v}_{\parallel }\) is also normalized by VA. The cyclotron resonant velocity, Vrp = 55 km s−1, is delineated by the dashed line. The circles indicate the proton phase-space locations when they reach the virtual spacecraft. The blue, yellow, red, and pink lines represent protons A, B, A′ and B′, respectively. The purple and green crosses represent protons C and D, respectively.

Full size image

Discussion

The coexistence of two resonance islands clearly differ from the one-island expectation27 of the conventional resonance theory. Moreover, the large deviations of protons A and A’ from the cyclotron resonance condition in Eq. (1) also highlights the role of the wave-associated forces in nonlinearly modifying the particle angular velocity. According to Berchem and Gendrin33, the time derivative of ζ can be derived from Eq. (3), as

$$\frac{{{{{{\rm{d}}}}}}\zeta }{{{{{{{\rm{d}}}}}}t}}=\omega -{k}_{\parallel }{v}_{\parallel }-\varOmega +{\varOmega }_{1}\left({v}_{\parallel }-{v}_{{{{{{\rm{w}}}}}}}\right)\frac{{{{{{\rm{cos }}}}}}\zeta }{{v}_{\perp }},$$
(5)

where the wave-associated forces, \({q{{{{{\bf{v}}}}}}}_{\parallel }\times {{{{{{\bf{B}}}}}}}_{{{{{{\bf{1}}}}}}}\) and \({q{{{{{\bf{E}}}}}}}_{{{{{{\bf{1}}}}}}}\), are both considered to have an additional (the fourth RHS) term to its conventional counterpart,

$$\frac{{{{{{\rm{d}}}}}}\zeta }{{{{{{{\rm{d}}}}}}t}}=\omega -{k}_{\parallel }{v}_{\parallel }-\varOmega .$$
(6)

Here \({\varOmega }_{1}=q{B}_{1}/m\) is the nominal gyrofrequency associated with the wave field B1. The detailed derivation is given in the “Methods” section. The inclusion of the additional term in the full resonance condition indicates that the resonant velocities at the island centers (ζ = 0 and 180°) equal

$${V}_{{{{{{\rm{r}}}}}}}^{{\prime} }=\frac{\left(\omega -\varOmega \right){v}_{{{{{{\boldsymbol{\perp }}}}}}}\mp {\varOmega }_{1}{v}_{{{{{{\rm{w}}}}}}}}{{k}_{\parallel }{v}_{\perp }\mp {\varOmega }_{1}}={V}_{{{{{{\rm{r}}}}}}}\pm \frac{\left({V}_{{{{{{\rm{r}}}}}}}\mp {v}_{{{{{{\rm{w}}}}}}}\right)}{\frac{{k}_{\parallel }{v}_{\perp }}{{\varOmega }_{1}}\mp 1},$$
(7)

respectively, which satisfy the first-order (dζ/dt = 0) and the second-order (d2ζ/dt2 = 0) resonance conditions simultaneously. The revised resonant velocity has an additional term in comparison to Eq. (2), which depends on the wave amplitude and the particle perpendicular velocity. In case Ω1 becomes large enough (or \({v}_{\perp }\) approaches zero), the resonant velocity \({V}_{{{{{{\rm{r}}}}}}}^{{\prime} }\) approaches \({v}_{{{{{{\rm{w}}}}}}}\) at ζ = 0, which has an opposite sign to Vr to indicate that the resonance island can even be shifted to the reversed direction.

To better understand the nonlinear shift in resonance condition, we launch resonant protons at ζ = 0 and 180° (protons C and D) in the prescribed field, both of which stay immobile in phase space (see the purple and green crosses in Fig. 3a, respectively) to indicate synchronized motions with the wave field. Since proton C rotates in the same direction as the wave magnetic field (and perpendicular to the wave electric field), the wave-associated forces must be in the opposite direction to the background Lorentz force \({q{{{{{\bf{v}}}}}}}_{\perp }\times {{{{{{\bf{B}}}}}}}_{{{{{{\bf{0}}}}}}}\). Here, the wave-associated forces are dominated by \({q{{{{{\bf{E}}}}}}}_{{{{{{\boldsymbol{1}}}}}}}\), since \({q{{{{{\bf{v}}}}}}}_{\parallel }\times {{{{{{\bf{B}}}}}}}_{{{{{{\bf{1}}}}}}}\) is negligible for protons with pitch angles close to 90° (see Fig. 3b for the parallel velocity of proton C). The comparable values between \({q{{{{{\bf{E}}}}}}}_{{{{{{\boldsymbol{1}}}}}}}\) and \({q{{{{{\bf{v}}}}}}}_{\perp }\times {{{{{{\bf{B}}}}}}}_{{{{{{\bf{0}}}}}}}\) reduce the proton’s angular velocity from Ω to warrant the occurrence of anomalous resonance at a lower, or sometimes even reversed, resonant velocity (see Fig. 3d). For the proton D with a small pitch angle (see Fig. 3b), the \({q{{{{{\bf{v}}}}}}}_{\parallel }\times {{{{{{\bf{B}}}}}}}_{{{{{{\bf{1}}}}}}}\) force plays a more important role in the generation of the additional resonance island centered at ζ = 180°. This island originates from the fact that \({q{{{{{\bf{E}}}}}}}_{{{{{{\boldsymbol{1}}}}}}}\) and \({q{{{{{\bf{v}}}}}}}_{\parallel }\times {{{{{{\bf{B}}}}}}}_{{{{{{\bf{1}}}}}}}\) for particles in the island center are both in the same direction as \({q{{{{{\bf{v}}}}}}}_{\perp }\times {{{{{{\bf{B}}}}}}}_{{{{{{\bf{0}}}}}}}\), which indicates an enhanced angular velocity and consequently an enlarged resonant velocity (see Fig. 3d).

We next discuss the condition when the aforementioned nonlinear effect on particle angular frequency becomes critical. The detailed derivation, which follows the Omura43 approach in dealing with chorus wave-electron interactions, is given in the “Methods” section. To apply the classical cyclotron resonance theory, the following criterion must be satisfied:

$$\sqrt{\frac{{B}_{1}}{{B}_{0}}}\ll \sqrt{\frac{{v}_{\perp }^{3}}{{\left|{v}_{{{{{{\rm{w}}}}}}}-{V}_{{{{{{\rm{r}}}}}}}\right|}^{3}}},$$
(8)

indicating that the resonance condition in Eq. (1) must be revised when the wave amplitude relative to the background field becomes strong enough. Moreover, particles with lower v⊥ would be more easily affected. For proton A, the left- and right-hand sides of Eq. (8) are 0.3 and 1.2, respectively. For proton A’, the right-hand side equals 0.06, even lower than the left-hand side. Their comparable values violate the criterion to indicate the occurrence of anomalous resonance. This criterion also provides a threshold for v⊥, which is ~500 km s−1 (equivalent to the velocity of a 1.5-keV proton) in this event. This threshold agrees with the observations in Fig. 1 that anomalous resonance (manifested by phase-bunched stripes) appears at energies below 1.5 keV.

Finally, we discuss the effect of wave amplitude variations to the resonance islands. Obviously, the width of the resonance island varies (proportional to the square root of B1, see Omura43) when the particle experiences a varying wave amplitude, which is also manifested by the transition of proton A’s trajectory from traversing to trapping orbits (see Fig. 2g). Moreover, the island center would be displaced in ζ from 0 or 180°, and the displacement would depend on the island expansion rate (an analogy to Albert26, see the “Methods” section for relevant derivations). In our simulation, the Gaussian profile of the wave packet indicates a significant B1 variation (and consequently a large island expansion rate, see the red line in Fig. 2l) during the initial wave periods, which leads to the displacement of the island center and therefore a deviation of the ion PSD peaks from the wave magnetic field direction (Fig. 2b–d). The deviation, similar to the case discussed in Shoji et al.25 and Omura et al.27, also indicates an ion current component in the wave electric field direction, which enables wave-particle energy transfer. As the island expansion rate reduces in the shadowed region, the phase-bunched PSDs become more aligned with the wave magnetic field.

Conclusions

We report observations of EMIC waves with phase-bunched enhancements of proton fluxes at energies below 1.5 keV. The phase-bunched signatures could either appear along or against the wave magnetic field direction, which indicate the coexistence of two resonance island at pitch-angle and energy ranges incompatible to the classical cyclotron resonance condition. The observed signatures are successfully reproduced by test-particle simulations, which shows that the electric and Lorentz forces associated with the wave field, usually neglected in the calculation of particle angular velocities, plays a crucial role in revising the trajectories of low-energy particles. The revision not only modifies the resonance condition but also leads to the coexistence of two resonance islands in the phase space. Given the high PSDs of low-energy particles in space plasmas, the occurrence of anomalous resonance also implies that our current understanding of the wave-particle energy exchange and the associated wave evolution, largely based on the classical picture of cyclotron resonance, may not be accurate especially in regions of weak magnetic field.

Methods

Simulation setup

The initial condition of our test-particle simulation is based on MMS observations before the wave amplitude grows (from 19:23:23 to 19:23:28 UT). The initial ion distributions are assumed to be Maxwellian,

$$f={n}_{0}{\left(\frac{m}{2\pi T}\right)}^{\frac{3}{2}}{{\exp }}\left(-\frac{m{V}_{{{{{{\rm{x}}}}}}}^{2}+{{mV}}_{{{{{{\rm{y}}}}}}}^{2}+{{mV}}_{{{{{{\rm{z}}}}}}}^{2}}{2T}\right),$$
(9)

with parameters determined via a best-fit procedure to match the observations in the 50–1000 eV energy range. These parameters include the proton temperature T = 130 eV and number density n0 = 8.5 cm−3. In the spacecraft rest frame, the ion distributions are also shifted to match the observed ion bulk velocity, (−20, 10, 35) km s−1 in the FAC coordinates.

The electromagnetic fields in the plasma rest frame are expressed as

$${{{{{\bf{E}}}}}}={{{{{{\bf{E}}}}}}}_{{{{{{\bf{1}}}}}}}={E}_{{{\max }}}{{\exp }}\left(-\frac{{\left(z-{v}_{{{{{{\rm{wp}}}}}}}t-{Z}_{0}\right)}^{2}}{{L}^{2}}\right)\left[-{{\sin }}\left({k}_{\parallel }z-{\omega }_{{{{{{\rm{p}}}}}}}t\right){{{{{\bf{x}}}}}},{{\cos }}\left({k}_{\parallel }z-{\omega }_{{{{{{\rm{p}}}}}}}t\right){{{{{\bf{y}}}}}}\right],$$
(10)
$${{{{{\bf{B}}}}}}={{{{{\bf{B}}}}}}_{{{{{\bf{0}}}}}}+{{{{{\bf{B}}}}}}_{{{{{\bf{1}}}}}}={B}_{0}{{{{{\bf{z}}}}}}+{B}_{\max }{\exp }\left(-\frac{\left(z-{v}_{{{{{{\rm{wp}}}}}}}t-{Z}_{0}\right)^{2}}{{L}^{2}}\right)\left[{\cos }\left({k}_{\parallel }z-{\omega }_{{{{{\rm{p}}}}}}t\right){{{{{\bf{x}}}}}},{\sin }\left({k}_{\parallel}z-{\omega}_{{{{{\rm{p}}}}}}t\right){{{{{\bf{y}}}}}}\right],$$
(11)

which describes the unidirectional propagation of a Gaussian-profiled wave packet against the background magnetic field at the phase velocity vwp = vws− vzs = −200 km s−1. In this model, the wave group velocity equals the phase velocity. The wave angular frequency \({\omega }_{{{{{{\rm{p}}}}}}}={\omega }_{{{{{{\rm{s}}}}}}}-k{v}_{{{{{{\rm{zs}}}}}}}=3.28\) s−1 in the plasma rest frame is determined based on a Doppler-shift of the observed \({\omega }_{{{{{{\rm{s}}}}}}}=2.7\) s−1, which corresponds to the wavelength \(\lambda =383\) km. The Gaussian-profiled wave packet is initially centered at \({Z}_{0}=5\lambda\) with a characteristic width \(L=3\lambda\). The maximum amplitude of the wave electric field is set to be Emax = 0.8 mV s−1, and the corresponding \({B}_{{{\max }}}={E}_{{{\max }}}/{v}_{{{{{{\rm{wp}}}}}}}\) equals 4 nT. Here, the background field \({B}_{0}=43.5\) nT is assumed to be uniform in the magnetosheath, which agrees with the observations and is distinct from studies in the inner magnetosphere where the field inhomogeneity becomes important25,27.

The virtual spacecraft, moving at a constant velocity of \(-{{{{{{\bf{v}}}}}}}_{{{{{{\bf{s}}}}}}}\) in the plasma rest frame, departs from the Z = 0 plane to obtain the proton velocity distributions every 0.3 s. To enable direct comparison between observations and simulations, the observational constraints (such as the uncertainty of ±11.25° in pitch-angle determination) are considered by tracing 81 evenly-distributed particles within each bin of finite widths in gyro-phase (30°), pitch angle (22.5°), and energy channel. In other words, a total number of 60,264 protons are traced. The resulting phase-space densities, determined via Liouville’s theorem for each particle, are then averaged in each bin to produce the gyro-phase spectra of proton PSDs in Fig. 2.

Derivation of the resonance theory

The derivation of the resonance condition starts from the basic equation of particle motion in the wave field (Eq. (3)). Here, we follow Berchem and Gendrin33 to describe the velocity vector v by parallel velocity \({v}_{\parallel }\), perpendicular velocity \({v}_{\perp }\), and phase angle \({\phi }_{{{{{{\rm{v}}}}}}}\), so that Eq. (3) can be decomposed into

$$\frac{{{{{{\rm{d}}}}}}{v}_{\parallel }}{{{{{{{\rm{d}}}}}}t}}=-\frac{q}{m}{B}_{1}{v}_{\perp }{{{{{\rm{sin }}}}}}\zeta =-{\varOmega }_{1}{v}_{\perp }{{{{{\rm{sin }}}}}}\zeta ,$$
(12)
$$\frac{{{{{{\rm{d}}}}}}{v}_{\perp }}{{{{{{{\rm{d}}}}}}t}}=-\frac{q}{m}\left({E}_{1}-{v}_{\parallel }{B}_{1}\right){{{{{\rm{sin }}}}}}\zeta ={\varOmega }_{1}\left({v}_{\parallel }-{v}_{{{{{{\rm{w}}}}}}}\right){{{{{\rm{sin }}}}}}\zeta ,$$
(13)
$$\frac{{{{{{\rm{d}}}}}}{\phi }_{{{{{{\rm{v}}}}}}}}{{{{{{{\rm{d}}}}}}t}}=-\frac{q{B}_{0}}{m}-\frac{q}{m}\left({E}_{1}-{v}_{\parallel }{B}_{1}\right)\frac{{{{{{\rm{cos }}}}}}\zeta }{{v}_{\perp }}=-\varOmega +{\varOmega }_{1}\left({v}_{\parallel }-{v}_{w}\right)\frac{{{{{{\rm{cos }}}}}}\zeta }{{v}_{\perp }},$$
(14)

in which the mirror force in the parallel direction is neglected in Eq. (12) due to the zero curvature of \({{{{{{\rm{B}}}}}}}_{0}\) in our setup. The time derivative of phase difference \(\zeta\) is expressed by

$$\frac{{{{{{\rm{d}}}}}}\zeta }{{{{{{{\rm{d}}}}}}t}}=\frac{{{{{{\rm{d}}}}}}{\phi }_{{{{{{\rm{v}}}}}}}}{{{{{{{\rm{d}}}}}}t}}-\frac{{{{{{\rm{d}}}}}}{\phi }_{{{{{{\rm{B}}}}}}}}{{{{{{{\rm{d}}}}}}t}}=\frac{{{{{{\rm{d}}}}}}{\phi }_{{{{{{\rm{v}}}}}}}}{{{{{{{\rm{d}}}}}}t}}+\omega -{{v}_{\parallel }k}_{\parallel }.$$
(15)

Substituting Eq. (14) into (15), we have

$$\frac{{{{{{\rm{d}}}}}}\zeta }{{{{{{{\rm{d}}}}}}t}}=\omega -{k}_{\parallel }{v}_{\parallel }-\varOmega +{\varOmega }_{1}\left({v}_{\parallel }-{v}_{{{{{{\rm{w}}}}}}}\right)\frac{{{{{{\rm{cos }}}}}}\zeta }{{v}_{\perp }},$$
(16)

which is labeled Eq. (5) in the main text.

In the classical theory of cyclotron resonance27, the fourth RHS term in Eq. (16) is neglected to derive the resonance condition in Eq. (1). The negligence enables the derivation of the particle motion in the format of the pendulum equation,

$$\frac{{{{{{{\rm{d}}}}}}}^{2}\zeta }{{{{{{\rm{d}}}}}}{t}^{2}}={\varOmega }_{1}{k}_{\parallel }{v}_{\perp }{{{{{\rm{sin }}}}}}\zeta ,$$
(17)

which is characterized by a trapping frequency \({\omega }_{{{{{{\rm{tr}}}}}}}=\sqrt{{k}_{\parallel }{v}_{\perp }{\varOmega }_{1}}\) if the \({v}_{\perp }\)variation is also neglected. Many previous studies25,27 have also considered the driver of the pendulum, which could originate from the field inhomogeneity, to enable the wave-particle energy transfer.

If we keep the nonlinear (the fourth RHS) term in Eq. (16), the full resonance condition in Eq. (7) can be accordingly derived, and the pendulum Eq. (17) can be replaced by

$$\frac{{{{{{{\rm{d}}}}}}}^{2}\zeta }{{{{{{\rm{d}}}}}}{t}^{2}}\,= \, \, {k}_{\parallel }{\varOmega }_{1}{v}_{\perp }\left(1+\frac{\left({v}_{\parallel }-{v}_{{{{{{\rm{w}}}}}}}\right)\left({v}_{\parallel }-{V}_{{{{{{\rm{r}}}}}}}\right)}{{v}_{\perp }^{2}}\right){{{{{\rm{sin }}}}}}\zeta \\ +\frac{{\varOmega }_{1}\left({v}_{\parallel }-{v}_{{{{{{\rm{w}}}}}}}\right)}{{v}_{\perp }{B}_{1}}\frac{{{{{{\rm{d}}}}}}{B}_{1}}{{{{{{{\rm{d}}}}}}t}}{{{{{\rm{cos }}}}}}\zeta -\frac{{\varOmega }_{1}^{2}}{2}\left[1+\frac{2{\left({v}_{\parallel }-{v}_{{{{{{\rm{w}}}}}}}\right)}^{2}}{{v}_{\perp }^{2}}\right]{{{{{\rm{sin }}}}}}2\zeta ,$$
(18)

in which the additional terms are contributed by the time derivatives of \({v}_{\parallel }\), \({v}_{\perp }\), ζ (given by Eqs. (12), (13), and (16)) and B1 (the second RHS term in Eq. (18)). The third RHS term in Eq. (18) is of higher order and can therefore be neglected.

Equation (18) suggests that the resonance island is centered at ζ = 0 or 180° only if the second RHS term vanishes (when the particle observes a constant wave amplitude). Otherwise, the island center would be displaced in ζ with the value depending on relative magnitude of the first two terms, which in turn relies on the characteristic frequencies ωtr, Ω1 and dB1/B1 dt. Here, dB1/B1 dt can be interpreted as the expansion rate \({\omega }_{{{{{{\rm{ex}}}}}}}={{{{{\rm{d}}}}}}{L}_{{{{{{\rm{r}}}}}}}/{L}_{{{{{{\rm{r}}}}}}}{{{{{{\rm{d}}}}}}t}\) of the resonance island since the island width Lr is proportional to ωtr or \(\sqrt{{B}_{1}}\)43. The temporal variations of the three characteristic frequencies are shown in Fig. 2i for our simulation. The island expansion could be also understood from the Hamiltonian perspective26 of a decreasing inhomogeneity factor as the wave amplitude increases.

Finally, we derive the criterion that the fourth RHS term in Eq. (16) can be safely neglected (which indicates that the conventional theory is an appropriate approximation). The derivation approach is similar to the one used in Omura43, which was developed to deal with the interaction between electrons and chorus waves. We first reorganize Eq. (16) into

$$\frac{{{{{{\rm{d}}}}}}\zeta }{{{{{{{\rm{d}}}}}}t}}=-\frac{{\varOmega }_{1}}{{k}_{\parallel }{v}_{\perp }}\left(\varOmega -\theta \right){{{{{\rm{cos }}}}}}\zeta -\theta ,$$
(19)

where \(\theta ={k}_{\parallel }({v}_{\parallel }-{V}_{{{{{{\rm{r}}}}}}})\) is simply \(-{{{{{\rm{d}}}}}}\zeta /{{{{{{\rm{d}}}}}}t}\) in the classical theory. For near-resonant particles, \(\theta\) is in the same order as the trapping frequency \({\omega }_{{{{{{\rm{tr}}}}}}}\). By assuming \(\theta \sim {\omega }_{{{{{{\rm{tr}}}}}}}\ll \varOmega\), Eq. (19) can be expressed as

$$\frac{{{{{{\rm{d}}}}}}\zeta }{{{{{{{\rm{d}}}}}}t}}\cong -{\omega }_{{{{{{\rm{tr}}}}}}}\left[{\left(\frac{{\varOmega }_{1}}{\varOmega }\right)}^{\frac{1}{2}}{\left(\frac{{k}_{\parallel }{v}_{\perp }}{\varOmega }\right)}^{-\frac{3}{2}}{{{{{\rm{cos }}}}}}\zeta +\widetilde{\theta }\right]$$
(20)

where \(\widetilde{\theta }=\frac{\theta }{{\omega }_{{{{{{\rm{tr}}}}}}}} \sim 1\). Therefore, the condition to neglect the first RHS term is

$${\left(\frac{{\varOmega }_{1}}{\varOmega }\right)}^{\frac{1}{2}}\ll {\left(\frac{{{k}_{\parallel }v}_{\perp }}{\varOmega }\right)}^{\frac{3}{2}}={\left(\frac{{v}_{\perp }}{-{V}_{{{{{{\rm{r}}}}}}}+{v}_{{{{{{\rm{w}}}}}}}}\right)}^{\frac{3}{2}},$$
(21)

which can also be expressed as Eq. (8). Similar conclusions can be also obtained via the modified Hamiltonian analysis35,36.