Abstract
Magnetic skyrmions, as a whirling spin texture with axisymmetry, cannot be propelled directly by a uniform perpendicular magnetic field. Therefore, reported skyrmion motions have been induced using other sorts of stimuli — typically, electric currents in magnetic metals. Here, we propose to drive skyrmion motion, in a uniform perpendicular field, by intrinsic repulsive interactions among an outer domain wall (DW) and magnetic skyrmions. Through micromagnetic simulations, we demonstrate that the uniform perpendicular magnetic field can indeed displace magnetic skyrmions alongside the leading DW. At a fixed field strength, the velocity of the skyrmion train evolves according to a 1 / (Ns + 1) relation with Ns denoting the number of skyrmions. Based on the Thiele equation, we elucidate, analytically, the mechanism of the driven magnetic skyrmion motion as well as the velocity equipartition phenomenon and reveal that the skyrmion–DW and inter-skyrmion repulsive interactions offer the driving force for skyrmion motion. This study underlines the role of spin textures’ interaction in skyrmion dynamics, and opens an alternative route for skyrmion manipulation especially relevant to insulating magnets. Given the correspondence between ferromagnetism and ferroelectricity, we anticipate that the scheme should also work for polar skyrmions in ferroelectrics.
Similar content being viewed by others
Introduction
Since their experimental discovery, magnetic skyrmions have drawn widespread attention of global researchers for their importance from both fundamental and applied perspectives1,2,3. Now, it is confirmed that magnetic skyrmions can be stabilized by several mechanisms1: 1) Dzyaloshinskii-Moriya interaction (DMI), 2) classic magnetic dipolar interaction, 3) frustrated exchange interaction, and 4) four-spin exchange interaction. Because of the integer topological charge (also called skyrmion number), magnetic skyrmions exhibit emergent electrodynamics4: electrons flowing across magnetic skyrmions gain a Berry phase and thus undergo an excess transverse deflection, which is measurable as a topological Hall resistance; conversely, magnetic skyrmions driven by the electrons’ spin transfer travel at a certain angle with respect to the current flow, experiencing skyrmion Hall effect. The two conjugate effects can be used to probe and harness magnetic skyrmions coded as data bits in e.g., racetrack memories5. Actually, magnons impinging on magnetic skyrmions can induce similar outcome6,7. Furthermore, magnetic skyrmions can be driven by thermal or field gradient to rotate like a ratchet8,9,10,11,12. As a global effect, the current-based driving scheme is associated with high power consumption and even overheating. Spin wave-based driving is strongly affected by the damping parameters of magnetic materials, while thermal and magnetic field gradients-based driving requires sophisticated control of the thermal and magnetic field distributions. The mentioned problems heavily undermine the potential of these routes in practical applications.
Despite a decade of intense research, there remain a gap and controversies between experiments and theory regarding magnetic skyrmion motion, such as the skyrmion-size dependency of skyrmion velocity. In real samples, the interplay of skyrmions and pinning sites/neighboring magnetic textures may play a dominant role in skyrmion motion, and lead to deviation of skyrmion behaviors from theoretical anticipation13,14. For the common magnetic skyrmions3, i.e., axisymmetric, on a ferromagnetic background, and originating from DMIs15,16, the inter-skyrmion, skyrmion–boundary, and skyrmion–DW interactions are repulsive17,18,19,20. In reality, the rectilinear motion of magnetic skyrmions along a nanotrack is guaranteed by the skyrmion–boundary repulsive interaction that cancels out the Magnus force19,20,21. Namely, these mutual interactions can influence skyrmion motion in a constructive or destructive manner. Mastering how to steer them will help avoid detrimental effects and possibly open avenues for skyrmion manipulation22.
Recently, based on a precise control of edge-magnetization rotation, Schäffer et al. have numerically demonstrated concomitant creation and propulsion of arbitrarily mixed sequences of topologically distinct magnetic objects, typically, skyrmions/DWs23 and skyrmion/antiskyrmions24. In their protocol, the rotating edge magnetization periodically imprints a fresh spin texture which pushes the entire train of spin textures forward by repulsive interactions. Their proposal possibly leads to a superior racetrack design where digital bits “1” and “0” are coded into topologically distinct spin textures, e.g., skyrmion and antiskyrmions. This redesigned racetrack architecture is more robust against positional fluctuation of data carriers and can be more densely packed.
Magnetic DWs ubiquitously exist in magnets required by the tradeoff between short-range exchange and long-range dipolar interactions. In chiral magnets, innate or induced, magnetic skyrmions can subsist, due to DMIs, as a metastable or even stable spin configuration3. Over a broad range of parameter space, magnetic skyrmions and DWs can coexist in the same magnet, especially in constricted geometry13,25. When harboring a DW, a given ferromagnet no longer exhibits mirror symmetry, and under a magnetic field, the DW will migrate to expand the domain parallel to the field26. Different from DWs, skyrmions, as localized topological solitons, embody revolution symmetry, and thus, in a perpendicular magnetic field, they will expand or contract without substantial displacement of their centers3,25,27. That is why no field-induced magnetic skyrmion motion is reported. In a perpendicular magnetic field, a DW will inevitably move to the skyrmions. As a result, the DW and nearby skyrmion must repel each other. Then, the skyrmion is supposed to move under the action of the repulsive force.
In this study, using micromagnetic simulations and analytically, we corroborate the above conjecture based on a magnetic nanotrack, which allows for the simultaneous realization of skyrmion–DW19,23,28, inter-skyrmion17,24,29, and skyrmion–boundary interactions18,20,30. Our simulations demonstrate that, irrespective of the helicity, i.e., Néel, Bloch, or their hybrid31 (Supplementary Fig. S1), a train of skyrmions can be set into coherent motion alongside a DW by a uniform perpendicular magnetic field, and noteworthily, their velocity drops to 1 / (1 + Ns) with Ns the number of included skyrmions. The analytical results derived from the Thiele equation agree with and explain the numerical findings. Skyrmion annihilation at the lateral edge is also seen at high magnetic fields, when the skyrmion–boundary repulsion cannot balance the Magnus force19,20. Compared to the scheme in refs. 23,24, in our proposal, although the DW is driven differently by a uniform magnetic field, the motion of the skyrmions train is propelled analogously by repulsive interactions. Thus, in principle, the motions of the trains in this study and in refs. 23,24 should bear much similarity. The velocity equipartition and 1 / (Ns + 1) relation are probably a generic feature of magnetic skyrmion motion due to repulsive interactions, regardless of the origin of the boundary force, setting an upper bound on the skyrmion velocity driven by repulsive interactions. These results have significant implications for the design of racetrack devices. Apart from magnetic skyrmions, the proposed field-drive of skyrmion motion appears valid for polar skyrmions in ferroelectric materials32,33, where an electric version of DMIs has been identified theoretically through symmetry analysis34. This is a point worthy of experimental exploration as polar topological structures may indicate unique dynamics unattainable in their magnetic counterparts35.
Results
Micromagnetic model and simulations
This study concentrates on common magnetic skyrmions3. To this end, DMI is incorporated in the free energy of the target system — a magnetic nanotrack, 60 nm wide and 1 nm thick. Perpendicular magnetic anisotropy (PMA) is also included in the model, allowing for the stabilization of magnetic skyrmions without applying a magnetic field. A uniform out-of-plane magnetic field serves as the external drive for skyrmion dynamics. Thus, the total free energy, E, comprises the contributions of exchange, dipolar, PMA, DMI, and Zeeman interactions.
To trace the dynamics of magnetic textures in the nanotrack, we numerically solve the Landau-Lifshitz-Gilbert equation36,37 (see “Methods”),
where m = M(r, t) / |M| with the magnetization vector M being a continuous function of the coordinate r and time t, and \({{{{{{\bf{H}}}}}}}_{{{{{{\rm{eff}}}}}}}={{{{{\boldsymbol{-}}}}}}\frac{1}{{\mu }_{0}{{{{{\rm{|}}}}}}{{{{{\bf{M}}}}}}{{{{{\rm{|}}}}}}}\frac{{{\delta }}E}{{{\delta }}{{{{{\bf{m}}}}}}}\) represents the effective field with μ0 denoting the vacuum magnetic permeability; γ and α stand for the gyromagnetic ratio and Gilbert damping constant, respectively.
For the clean nanotrack without defects, we carry out three sets of simulations, the first set with interfacial DMI, the second set with bulk DMI, and the third set with coexisting interfacial and bulk DMIs (this situation could occur in real magnetic heterostructures38) corresponding to Néel, Bloch, and hybrid skyrmions, respectively. In principle, magnetic materials with Cnv (T) symmetry permit occurrence of the interfacial (bulk) DMI39. To ensure the general validity of the results, various values of PMA strength Ku and DMI strength D are addressed individually in our simulations. Unless otherwise specified, the results presented are based on Néel skyrmions with Ku = 0.8 MJm−3 and D = 3.5 mJm−2.
To reveal the influence of defects, we also consider a granular nanotrack40 and a notched nanotrack41, in which the PMA strength Ku is randomly distributed over grains around an average value Ku0 = 0.8 MJm−3 with a Gaussian distribution of the deviation, ∆K = Ku – Ku0. The notched sample contains an edge notch on the top or bottom border in addition to randomly distributed grains.
Isolated skyrmion in magnetic field
In B20 magnets, the A phase, i.e., the skyrmion lattice state, emerges at a finite magnetic field1,39, which is equivalent to a PMA. The equilibrium size of skyrmions in this phase is a function of the field strength3. Later, it is seen that the size of isolated skyrmions in ultrathin multilayer films with an actual PMA also sensitively depends on the applied magnetic field25,27. Here, we numerically explore how a perpendicular magnetic field affects an isolated skyrmion. The results are presented in Fig. 1. Note that, in this study, we focus on the steady-state motion of magnetic textures and ignore the transient process to equilibrium. Hence, all results presented correspond to a certain equilibrium state, either static or dynamic.
a, b Equilibrium spin configurations of an isolated skyrmion in a magnetic nanotrack (width w = 60 nm, length l = 2000 nm) and square nanoelement (w = 300 nm) under different magnetic fields. Field strength H is indicated on each panel. Determined by the field polarity, the skyrmion either expands or contracts without a net displacement. The color scale for mz, the perpendicular magnetization component, is used throughout this paper. c Skyrmion size as function of field strength. Lines are guides to eyes. Strong edge confinement in the nanotrack suppresses expansion of skyrmion area. The strengths of perpendicular magnetic anisotropy and Dzyaloshinskii-Moriya interaction are Ku = 0.8 MJm−3 and D = 3.5 mJm−2, respectively.
Figure 1a shows evolution of the equilibrium skyrmion size with field strengths in the narrow nanotrack (60 nm wide). Very clearly, the skyrmion adapts itself to the magnetic field. For a positive field, the skyrmion expands with increasing field strength, and for a negative field, it shrinks with increasing field strength. This skyrmion size variation stems from the energy redistribution in the system. At the highest field, the circular skyrmion is elongated in the longitudinal direction, because of the transverse confinement imposed by the lateral edges30.
For comparison, we also examine the skyrmion size evolution in an extended area; as shown in Fig. 1b, where a 300 nm wide square magnetic nanoelement is used. At first glance, there is no substantial difference from the above situation. The field dependence of the skyrmion diameter follows the same tendency. However, the geometric confinement significantly affects field susceptibilities of the skyrmion size (Fig. 1c) and shape (Fig. 1a, b). Effectively, the role of confined geometry resembles a magnetic field opposite to the skyrmion core polarity2. In the square nanoelement, the skyrmion grows rapidly with increasing field strength and turns into a big bubble suddenly at a relatively small field; whereas in the nanotrack, the skyrmion grows slowly and fills the track width until very large fields. Overall, these findings are in accordance with reported results, and no translational motion of skyrmion is observed.
Single domain wall in magnetic field
After decades of research, the DW dynamics has been well comprehended. It is generally accepted that, at small fields, the DW travels at a speed directly proportional to the field strength, and above a threshold field, the DW velocity drops abruptly due to Walker breakdown31,42,43,44,45,46. Recently, it is further recognized that the chiral DW induced by DMI tilts during motion and the tilting modifies DW dynamics47.
We numerically simulate the DW motion in a perpendicular magnetic field and derive its velocity along the nanotrack. The DW’s snapshots, at several particular times after applying the field, are shown in Fig. 2a. As expected, DW tilting occurs. After entering the steady state, the DW proceeds at a uniform speed (203 nm per 1.7 ns in this case) with a fixed tilt angle.
a Domain wall (DW) motion and (b) DW–skyrmion pair motion in a positive field (field strength H = 400 Oe) through expansion of the up domain. The time after applying the field is indicated on each panel. Through a similar distance (∆x: 209 vs 203 nm), the DW–skyrmion pair spends twice as much time as the single DW (∆t: 3.4 vs 1.7 ns), meaning that the DW speed roughly halves when a skyrmion is carried. c Velocities of a single DW and a DW–skyrmion pair against field strength for various (Ku, D) as indicated, where Ku and D are the strengths of perpendicular magnetic anisotropy and Dzyaloshinskii-Moriya interaction. Lines are guides to eyes. Irrespective of the field strength and (Ku, D), the velocities of the DW–skyrmion pair are always nearly half of those of the single DW, suggesting the universality of the feature.
The DW velocity versus field curves, for a series of (Ku, D) combinations, are plotted in Fig. 2c, from which several signatures can be identified. We would like to note that, for clarity, the cut-off fields on the velocity–field curves in Fig. 2c are set to the skyrmion annihilation fields, although, for all (Ku, D), the DW breakdown fields are concertedly far larger than the skyrmion annihilation fields, as listed in Supplementary Table S1. Apparently, all curves rise monotonically with the field strength. After scrutiny, one can find slight nonlinearity on the curves. This nonlinear deviation stems from the DW tilting, as elucidated in ref. 47. For different (Ku, D), the curves distinguish from each other by the slopes. These results agree with the literature47.
Above a certain threshold field (see Supplementary Table S1), the Walker breakdown in DW motion occurs, which is clearly reflected in Supplementary Fig. S2a, where the total topological charge of the system oscillates with time around a value of 0.5 characteristic of an antivortex48. In this process, an antivortex-like spin texture is firstly nucleated42,49 at and then divided from an end of the DW and ultimately annihilated at the sample edge, as shown in Supplementary Fig. S2b.
Domain wall–skyrmions ensemble in magnetic field
To step further, we insert a skyrmion ahead of the DW in the nanotrack, which is then immersed in a perpendicular magnetic field. The field-induced dynamics of the DW–skyrmion pair is depicted in Fig. 2b. It is seen that the skyrmion moves together with the DW. Traversing a 209 nm interval, the pair spends 3.4 ns, having a velocity of 61.5 ms−1 at H = 400 Oe. Therefore, in a uniform perpendicular magnetic field, the DW and accompanying skyrmion can move cooperatively as a whole. It is easy to find that such synergistic motion does not occur to a DW–DW or skyrmion–skyrmion pair. While two DWs in a pair move oppositely, two skyrmions in a pair remain stationary in response to an applied perpendicular field.
By contrast, without the skyrmion, the single DW takes only 1.7 ns through 203 nm (Fig. 2a), having a velocity of 119.4 ms−1. That is, inclusion of the skyrmion slows down the DW by a factor of ~ 1/2. For a systematic comparison, we numerically simulate the motion of the DW–skyrmion pair at various (Ku, D) against the field strength. The velocity–field curves are plotted in Fig. 2c. Obviously, the DW–skyrmion pair is always slower than the single DW. After a careful inspection, it is found that the reduction in the DW velocity is ~1/2.
When the field is high enough, the skyrmion will touch the sample edge and be annihilated, as illustrated in Supplementary Fig. S3b. At the time of skyrmion annihilation20, the total topological charge of the system jumps from 1 to 0, as shown in Supplementary Fig. S3a. The reason for the skyrmion annihilation is that, above the threshold field (Supplementary Table S1), the edge repulsive force on the skyrmion can no longer offset the Magnus force that scales linearly with the skyrmion velocity19,20. Indeed, as long as the skyrmion is sufficiently fast, the Magnus force will necessarily surpass the edge confining force causing the skyrmion annihilation, regardless of the driving scheme.
In the following step, we place more skyrmions in front of the DW and see how this many-body ensemble behaves in the perpendicular magnetic field. The velocity–field curves, for the ensembles hosting 1–5 skyrmions, are shown in Fig. 3b, and exemplarily, the images of the ensemble with 5 skyrmions, at particular times after application of the field, are shown in Fig. 3a.
a Migration of the domain wall (DW)–skyrmions ensemble as a whole accompanying expansion of the up domain in a positive field (field strength H = 400 Oe). Here, the train consists of 5 skyrmions. The time after application of the field is indicated on each panel. Over the latter two durations (∆t: 8 ns, i.e., 8–16 and 16–24 ns), the ensemble travels equal distances (∆x: 174 nm), implying that at time t = 8 ns the steady state has been attained. Consequently, the ensemble velocity can be calculated as v = ∆x / ∆t. b Ensemble velocity against field strength for the number of skyrmions Ns = 0, 1, 2, 3, 4, and 5. Definitely, an increase in Ns leads to a reduction in the ensemble velocity. c Skyrmion diameters and spacings at different field strengths for Ns = 5. dSKi denotes the diameter of the ith skyrmion (SK) away from the DW. SDW–SK1 and SSKi–(i+1) signify the spacing between the DW and 1st skyrmion and the spacing between the ith and (i+1)th skyrmions, respectively. Lines are guides to eyes. The strengths of perpendicular magnetic anisotropy and Dzyaloshinskii-Moriya interaction are Ku = 0.8 MJm−3 and D = 3.5 mJm−2, respectively.
It is observed that the ensemble can still be moved forward by the external field when more than 1 skyrmions participate, as show in Fig. 3 and Supplementary Figs. S4–S6. For instance, in the DW/5-skyrmions case, the ensemble at 400 Oe travels 174 nm in every 8 ns (Fig. 3a). The velocity of the ensemble increases linearly with the applied field but falls slowly with the increasing number of skyrmions (Fig. 3b). Another striking feature is that, during motion, individual skyrmions in the ensemble have different sizes; the skyrmions farther from the DW turn out to be larger, as shown in Fig. 3a. However, their separations firstly decrease and then increase. To unveil more details, we derive the DW–skyrmion and inter-skyrmion spacings as well as the diameter of each skyrmion; the results for the DW/5-skyrmions ensemble are shown in Fig. 3c and Supplementary Fig. S4c for Néel skyrmions and in Supplementary Fig. S5c for Bloch skyrmions. It is clear that elevated field strength leads to enhanced spreading of the skyrmion sizes and smaller separations between two neighbors. Specifically speaking, with the increasing field strength, the skyrmions nearer to the DW become smaller and smaller while those far from the DW become bigger and bigger. This is because the skyrmions closer to the DW experience stronger repulsive forces (as indicated later). The most special skyrmion is the outermost one, which experiences only one repulsive force and is free to adjust its position and therefore is easier to be affected by the field. This trend holds universally for all ensembles with multiple skyrmions.
We perform some simulations to directly compare the effects of the repulsive forces and perpendicular magnetic field on the skyrmion size. The results are presented in Supplementary Fig. S7. In these simulations, a single skyrmion is placed between two stripe DWs in a 300 nm × 1000 nm magnetic nanotrack and a perpendicular magnetic field parallel to the skyrmion core polarity is applied until the equilibrium is attained. It is seen that the skyrmion is always compressed despite the same polarity of the applied field and skyrmion core. The higher the field strength, the smaller the skyrmion. Above a certain field, the skyrmion is annihilated under the continuous compression of the enclosing stripe DWs. These results are in sharp contrast with those in Fig. 1, where a higher field always brings about a larger skyrmion, suggesting that the repulsive forces can dominate over the magnetic field in determining the skyrmion size. These contrasting results corroborate the skyrmion-size variation in the ensemble.
To better understand the ensemble motion, the velocity–field curves in Fig. 3b are replotted as the velocity versus Ns (Fig. 4a). Apparently, for all field strengths, the ensemble velocities decrease with Ns in seemingly the same manner. Furthermore, we define the mobility of an ensemble u as \(u=\frac{{dv}}{{dH}}\)44, where v and H are the ensemble velocity and external magnetic field, respectively. Accordingly, each curve in Fig. 3b gives rise to a mobility value, which is plotted in Fig. 4b as a function of Ns. In this figure, the mobility values, ũ, from simulation data are well fitted by the formula,
where ũdw is the mobility of a single DW carrying no skyrmions. That means that, at a given field, the ensemble velocity is inversely proportional to the total number of the magnetic entities (i.e., DW and skyrmions) in the ensemble. The more the included skyrmions, the slower the ensemble. When carrying skyrmions, the original DW velocity is equally distributed amongst all magnetic entities in the ensemble.
a Ensemble velocity versus the number of skyrmions Ns at various field strengths. b Ensemble mobility versus Ns. Black dots are simulation results and red dots are given by ũdw / (Ns + 1) with ũdw representing the mobility of a single domain wall. Lines are guides to eyes. The strengths of perpendicular magnetic anisotropy and Dzyaloshinskii-Moriya interaction are Ku = 0.8 MJm−3 and D = 3.5 mJm−2, respectively.
Ensemble motion in granular nanotrack
The motion of the magnetic skyrmions in an ensemble, under a uniform perpendicular magnetic field, is driven by the interactions between neighboring magnetic entities. The DW–skyrmions ensemble in a granular nanotrack permits the coexistence of the skyrmion–DW, inter-skyrmion, skyrmion–boundary, and skyrmion–defect interactions. Therefore, the ensemble in a granular nanotrack driven by an applied perpendicular field offers a natural arena and model system to understand exotic skyrmion dynamics in complex real materials with unavoidable defects40. We numerically study the ensemble motions in a granular nanotrack (Fig. 5), and by considering various combinations of ΔK, Ns, and H, we obtain the following statistical results (Supplementary Tables S2 and S3). To ensure the general validity of the simulation results, we have considered three different realizations of the grain distribution (Fig. 5a) and correspondingly ensemble motions (Fig. 6a) for each individual combination of ΔK, Ns, and H by changing the randomseed value in the simulations.
a Three different realizations of the granular nanotrack with an average grain size of 20 nm by Voronoi tessellation. In each grain, the strength of perpendicular magnetic anisotropy Ku is randomly distributed around the average value Ku0 = 0.8 MJm−3 with a Gaussian distribution of the deviation ∆K (= Ku ‒ Ku0). In this figure, ∆K = 2%Ku0 is shown. The color code indicates the strength of Ku. b Under field strength H = 300 Oe, the ensemble can move, without pinning, in the sample with ∆K = 2%Ku0 (Ku0 = 0.8 MJm−3 and Dzyaloshinskii-Moriya interaction strength D = 3.5 mJm−2). However, different from in the clean sample, the ensemble travels different distances ∆x over the same time intervals ∆t. Accordingly, we derive the average ensemble velocity by fitting the positions against time.
a Ensemble velocity versus the number of skyrmions Ns for the granular nanotrack at two various field strengths (H = 300 Oe and 600 Oe). For each field strength, three different realizations (Rlzts.1‒3) of grain distribution are considered. Black triangles are the average value of v(1), v(2), and v(3), the ensemble velocities in the three different realizations of grain distribution. b Ensemble velocity versus Ns for the clean (∆K = 0, where ∆K represents the deviation of perpendicular magnetic anisotropy strength from its average value Ku0) and granular (∆K = 2%Ku0) nanotracks. c Difference of the ensemble velocities in the clean and granular nanotracks (defined as ∆v = v(clean) – v(granular)) against Ns, which are derived from panel b. Lines are guides to eyes. Ku0 = 0.8 MJm−3 and Dzyaloshinskii-Moriya interaction strength D = 3.5 mJm−2.
It is seen that, at H = 600 Oe, the larger the ΔK, the fewer skyrmions the DW can carry (Supplementary Table S2), and for a given ΔK, with the increase of Ns, some skyrmions will be annihilated during the ensemble motion (Supplementary Fig. S8). The skyrmion annihilation always occurs at the lateral edge instead of in the interior of the nanotrack. For ΔK = 2%Ku0 and smaller, the DW can drive 1 to 5 skyrmions through the entire track length without skyrmion annihilation. However, when ΔK rises to 3%Ku0, at most 4 skyrmions can be carried by the DW (Supplementary Fig. S9); if 5 skyrmions are placed in front of the DW, the skyrmion closest to the DW will be annihilated on the way (Supplementary Fig. S8).
During the ensemble motion, the size and lateral position of each skyrmion experience random fluctuations (Fig. 5b, Supplementary Figs. S8 and S9). When a skyrmion is pinned, the other skyrmions ahead of it will stall; nevertheless, the following DW and/or skyrmions will continue to move towards the pinned skyrmion (Supplementary Fig. S8). Consequently, the skyrmion just behind the pinned one is compressed, moves transversely due to the Magnus force, and eventually is destructed by the edge (Supplementary Fig. S8). The stochastic fluctuations of the skyrmions’ sizes and lateral positions as well as the pinning of any a skyrmion at a random site in the presence of ΔK underlie the skyrmion annihilation in the granular sample.
For ΔK = 2%Ku0 and Ns = 5, the ensemble under H = 200 Oe is pinned after traveling a short distance (Supplementary Fig. S10), whereas under H = 300 Oe, 400 Oe, 500 Oe, and 600 Oe the ensemble can move without pinning until reaching the right edge [see Fig. 5b for a typical example]. Namely, there exists a threshold field for the ensemble motion in a granular nanotrack, which is a function of ΔK and Ns.
Furthermore, for ΔK = 2%Ku0, we change Ns from 0 to 5 and examine the ensemble motions at H = 300 Oe and 600 Oe (see Fig. 5b for example), and the numerical results suggest that the 1 / (Ns+1) relation satisfied by the ensemble velocity in the clean nanotrack does not strictly holds in the granular nanotrack (Fig. 6).
Ensemble motion in notched nanotrack
For both DWs and skyrmions, edge defects might be equally important as the interior ones at least in some aspects41,49. As examples, we numerically study the dynamics of the DW/5-skyrmions ensemble (i.e., Ns = 5) in a notched granular nanotrack (ΔK = 2%Ku0) in a uniform perpendicular field (the results are shown in Supplementary Figs. S11–S15). We consider a series of notch depths (h, varying from 6 nm to 54 nm in a step of 6 nm) and various field strengths (H, ranging from 100 Oe to 600 Oe with a step length of 100 Oe), as listed in Supplementary Tables S4 and S5.
Our simulations indicate that, at H = 600 Oe, the ensemble is able to pass over the notch up to h = 42 nm (Supplementary Table S5 and Fig. S11). When moving to the notch, all skyrmions concomitantly shrink and later pass through the notch one by one. After overcoming the notch, every skyrmion expands to its original size. Despite a short delay, the DW can also pass through the notch. In the process, the skyrmion contracts or expands to adapt to the track-width variation caused by the notch. As the notch depth is increased to h = 48 nm (Supplementary Figs. S12 and S13), the skyrmion closest to the DW is annihilated when a certain far skyrmion (the 2nd and 1st farthest skyrmions for the bottom and top notches, respectively) traverses the notch. This annihilation event stems from the skyrmion clogging29 before the notch, which results in skyrmion contraction and transverse motion and ultimate destruction at the edge. In the case of a top notch (Supplementary Fig. S13), the farthest skyrmion becomes a meron50 after traversing the notch apex, where the track width is too small to harbor a skyrmion.
For each given notch depth, there is a particular threshold field for the ensemble motion (Supplementary Table S4). Taking the h = 30 nm as an example, for both top and bottom notches, at H = 300 Oe, the entire ensemble is stopped before the notch (Supplementary Fig. S14); at 400 Oe, all the five skyrmions can pass through the notch but the DW is pinned at the notch (Supplementary Fig. S15); however, at 500 Oe and higher, the entire ensemble can be driven to pass through the notch (Supplementary Fig. S11).
Thiele model of ensemble motion
In clean sample
Projecting Eq. (1) onto the ensemble translation mode under the assumption that each magnetic entity in the ensemble owns a rigid structure, i.e., m(r, t) = m[r – \({{{{{\mathcal{R}}}}}}\)(t)] and moves steadily, i.e., \({{{{{\mathcal{R}}}}}}\)(t) = vt (where \({{{{{\mathcal{R}}}}}}\)(t) and v are the center of mass and velocity of a magnetic entity, respectively), one obtains the Thiele equation42,51,
where FG and \({{{{{{\bf{F}}}}}}}^{{{{{{\mathcal{D}}}}}}}\) are the Magnus force and dissipative force on each magnetic entity, respectively, and F represents a force due to the external magnetic field, skyrmion–DW or inter-skyrmion repulsive interaction, edge confinement (skyrmion–boundary interaction), impurities (skyrmion–defect interaction), etc. Equation (3) dictates that all the forces on a uniformly moving magnetic entity are in balance.
Although the Magnus forces on individual skyrmions might be slightly different (because of the slightly different sizes of the latter), the Magnus force on each skyrmion can be balanced by the repulsive force on the same skyrmion due to the skyrmion–boundary interaction. From skyrmion to skyrmion, the repulsive forces on skyrmions change but are always equal in magnitude and opposite in direction to the Magnus forces, resulting in force balance in the transverse direction19,20. Generally, the skyrmion–boundary repulsive interaction and in turn the repulsive force on a skyrmion can vary in a certain range, self-adaptively, through fine-tuning of the skyrmion–boundary distance and the local spin configuration on the boundary20. Of course, if the Magnus force on a skyrmion is too large, the repulsive force imposed by the boundary will no longer be able to cancel it; then, as a result, the skyrmion will be annihilated at the edge (as shown in Supplementary Fig. S3).
In this study, we concentrate on the steady motion of an ensemble along a nanotrack, where the transverse motion of magnetic skyrmions is suppressed by the edge confinement as explained above, i.e., v = (v, 0). Hence, \({{{{{\mathbf{F}}}}}}^{{{{{\mathcal{D}}}}}}=\alpha {{{\leftrightarrow}}\atop{{{{{\mathcal{{D}}}}}}}}\cdot {{{{{\mathbf{v}}}}}}=\alpha \left({{{{{{\mathcal{D}}}}}}_{{xx}},{{{{{\mathcal{D}}}}}}_{{xy}}\atop{{{{{\mathcal{D}}}}}}_{{yx}},{{{{{{{\mathcal{D}}}}}}}_{{yy}}}}\right)\left({v}\atop{0}\right)=\alpha \left({{{{{{{{\mathcal{D}}}}}}}_{{xx}}}\atop{{{{{{{\mathcal{D}}}}}}}_{{yx}}}}\right)v\), where \({{{\leftrightarrow}}\atop{{{{{\mathcal{{D}}}}}}}}=\left({{{{{{{\mathcal{D}}}}}}}_{{xx}},}{{{{{{{\mathcal{D}}}}}}}_{{xy}}}\atop{{{{{{{\mathcal{D}}}}}}}_{{yx}},}{{{{{{{\mathcal{D}}}}}}}_{{yy}}}\right)\) is the dissipation dyadic of a magnetic entity42,51. Based on this fact, all forces in the transverse directions are disregarded in the following analysis.
To elucidate the numerical findings, Eq. (3) is applied to every magnetic entity in the ensemble, and considering solely the longitudinal forces (as illustrated in Fig. 7a), one has,
for e.g. a DW/3-skyrmions ensemble, where \({F}_{{{{{{\rm{dw}}}}}}}^{{{{{{\mathcal{D}}}}}}}\) and \({F}_{{{{{{\rm{sk}}}}}}i}^{{{{{{\mathcal{D}}}}}}}\) are the dissipative forces on the DW and ith skyrmion, respectively, \({F}_{i+1,i}\) and \({F}_{i,i+1}\) are the mutual repulsive forces between two neighbors in the ensemble (note that, for the DW i = 0; for the skyrmions i = 1, 2, 3, … Ns), and FH stands for the driving force on the DW exerted by the external magnetic field.
a Train of domain wall–skyrmions in steady motion. Here, the number of skyrmions Ns = 3 is taken as an example and the transverse forces are ignored. b Uniformly moving train of cuboid–balls in direct contact. c Uniformly moving train of cuboid–balls linked by springs. d Forces on every entity. For the domain wall–skyrmions train, FH is the field-induced force, which only acts on the domain wall; \(F^{{{{{\mathcal{D}}}}}}\) are the dissipative forces, which act on every magnetic entity in the ensemble; Fi,i+1 and Fi+1,i (i = 0, 1, 2, … Ns) are a pair of action and reaction forces, which arise from dipolar and/or exchange interactions between the magnetizations in neighboring magnetic entities. For the cuboid–balls train, FH is an applied pushing or pulling force, which directly acts on the cuboid; \(F^{{{{{\mathcal{D}}}}}}\) are the friction forces, which act on every entity in the ensemble; Fi,i+1 and Fi+1,i (i = 0, 1, 2, … Ns) are the action and reaction forces, which arise from direct contact of neighboring cuboid and balls or from mediation of the spring. Steady motion means that the entire ensemble moves at a uniform velocity v.
Adding together all equations in Eq. (4), one gets,
The general form of Eq. (5) is,
According to the Newton’s third law, \({F}_{i+1,i}={F}_{i,i+1}\), since they are a pair of action and reaction forces. Then, Eq. (6) becomes,
For an out-of-plane magnetic field, the Zeeman energy of the system is \({E}_{{{{{{\rm{z}}}}}}}={{\mu }_{0}M}_{{{{{{\rm{s}}}}}}}H{{{{{\mathscr{d}}}}}}w\left(l-2q\right)-{N}_{{{{{{\rm{s}}}}}}}{{\mu }_{0}M}_{{{{{{\rm{s}}}}}}}H{{{{{\mathscr{d}}}}}}{{{{{\mathcal{S}}}}}}\), where \({{{{{\mathscr{d}}}}}},\) w, and l denote the thickness, width, and length of the nanotrack, respectively, q is the position of the DW center, and \({{{{{\mathcal{S}}}}}}\) is the area of a skyrmion. Correspondingly, by definition, \({F}^{H}=-\frac{\partial {E}_{{{{{{\rm{z}}}}}}}}{\partial x}=2{\mu }_{0}{M}_{{{{{{\rm{s}}}}}}}H{{{{{\mathscr{d}}}}}}w\)42.
For steady ensemble motion, \({v}_{{{{{{\rm{dw}}}}}}}={v}_{{{{{{\rm{sk}}}}}}i}=v\), and specifically, \({F}_{{{{{{\rm{dw}}}}}}}^{{{{{{\mathcal{D}}}}}}}=\alpha {{{{{{\mathcal{D}}}}}}}_{{xx}}^{{{{{{\rm{dw}}}}}}}v\) and \({F}_{{{{{{\rm{sk}}}}}}i}^{{{{{{\mathcal{D}}}}}}}=\alpha {{{{{{\mathcal{D}}}}}}}_{{xx}}^{{{{{{\rm{sk}}}}}}i}v\). To express \({{{{{{\mathcal{D}}}}}}}_{{xx}}^{{{{{{\rm{dw}}}}}}}\) and \({{{{{{\mathcal{D}}}}}}}_{{xx}}^{{{{{{\rm{sk}}}}}}i}\) explicitly, we choose the following ansatzes for the DW47 and skyrmion27, respectively,
with \({{{{{\bf{m}}}}}}=({{\sin }} \; \theta {{\cos }} \; \phi ,{{\sin }} \; \theta {{\sin }} \; \phi ,{{\cos }} \; \theta )\), where θ and ϕ are the polar and azimuthal angles of magnetization, x and y are the Cartesian coordinates along the length and width directions of the nanotrack, and χ and Δ are the tilt angle and thickness of the DW, respectively; r is the radial distance relative to the skyrmion center at (x, y) and R is the skyrmion radius.
For the DW, \({{{{{{\mathcal{D}}}}}}}_{{xx}}=\frac{{\mu }_{0}{M}_{{{{{{\rm{s}}}}}}}{{{{{\mathscr{d}}}}}}}{\gamma }\iint {\left(\frac{\partial \theta }{\partial x}\right)}^{2}{{{{{\rm{d}}}}}}x{{{{{\rm{d}}}}}}y\), substituting Eq. (8) into which, one obtains \({{{{{{\mathcal{D}}}}}}}_{{xx}}^{{{{{{\rm{dw}}}}}}}=2\frac{{\mu }_{0}{M}_{{{{{{\rm{s}}}}}}}{{{{{\mathscr{d}}}}}}}{\gamma }\frac{w}{\triangle }\). For a skyrmion, \({{{{{{\mathcal{D}}}}}}}_{{xx}}=\frac{\pi {\mu }_{0}{M}_{{{{{{\rm{s}}}}}}}{{{{{\mathscr{d}}}}}}}{\gamma }\int \left[{\left(\frac{{{{{{\rm{d}}}}}}\theta }{{{{{{\rm{d}}}}}}r}\right)}^{2}+{\left(\frac{{{\sin }}\theta }{r}\right)}^{2}\right]r{{{{{\rm{d}}}}}}r\), substituting Eq. (9) into which, one arrives at \({{{{{{\mathcal{D}}}}}}}_{{xx}}^{{{{{{\rm{sk}}}}}}i}\approx 2{{\pi }}\frac{{\mu }_{0}{M}_{{{{{{\rm{s}}}}}}}{{{{{\mathscr{d}}}}}}}{\gamma }\frac{R}{\triangle }\)52.
As already noted, during the steady motion, the sizes of individual skyrmions in the ensemble are different. The skyrmions nearer to the DW are smaller because of increasingly stronger repulsions between two neighbors. For the ith skyrmion away from the DW, the radius \({R}_{i}\approx {R}_{1}+(i-1)\delta\) with R1 being the radius of the skyrmion closest to the DW and δ denoting the difference in radii of two neighboring skyrmions. Then, one finds \({\sum }_{1}^{{N}_{{{{{{\rm{s}}}}}}}}{{{{{{\mathcal{D}}}}}}}_{{xx}}^{{{{{{\rm{sk}}}}}}i}=2{{\pi }}\frac{{\mu }_{0}{M}_{{{{{{\rm{s}}}}}}}{{{{{\mathscr{d}}}}}}}{\gamma }\left[{N}_{{{{{{\rm{s}}}}}}}\frac{{R}_{1}}{\triangle }+\frac{{N}_{{{{{{\rm{s}}}}}}}({N}_{{{{{{\rm{s}}}}}}}-1)}{2}\frac{\delta }{\triangle }\right]\). After some algebra, one finally has the ensemble velocity that reads,
where \({v}_{{{{{{\rm{dw}}}}}}}=\frac{\gamma }{\alpha }H\triangle\) is the velocity of a single DW in field H42 and according to the simulation results \(\eta ={{\pi }}\frac{{R}_{1}+\frac{{N}_{{{{{{\rm{s}}}}}}}-1}{2}\delta }{w}\approx 1\).
From Eq. (10), it is obvious that the ensemble mobility \(u\approx \frac{{u}_{{{{{{\rm{dw}}}}}}}}{{N}_{{{{{{\rm{s}}}}}}}+1}\) (wherein \({u}_{{{{{{\rm{dw}}}}}}}=\frac{\gamma }{\alpha }\triangle\) represents the mobility of a single DW), which reproduces the empirical fitting formula [Eq. (2)] derived from numerical results.
In granular sample
For the ensemble motion in a granular nanotrack (as shown in Fig. 5), the DW and each skyrmion experience a random force due to the interactions with grain boundaries40. In the current-driven case, Gong et al.40 found that the random force on a skyrmion is opposite to the skyrmion velocity, i.e., \({{{{{{\boldsymbol{F}}}}}}}_{{{{{{\rm{sk}}}}}}i}^{{{{{{\mathcal{R}}}}}}}=-{F}_{{{{{{\rm{sk}}}}}}i}^{{{{{{\mathcal{R}}}}}}}{\hat{v}}_{{ski}}\) with \({F}_{{{{{{\rm{sk}}}}}}i}^{{{{{{\mathcal{R}}}}}}}=b\alpha {{{{{\mathcal{D}}}}}}{(\triangle K)}^{2}/J\), where b is a position-independent numerical factor and J is the current density. In the field-driven case, it is reasonable to assume that \({F}_{{{{{{\rm{sk}}}}}}i}^{{{{{{\mathcal{R}}}}}}}=c\alpha {{{{{\mathcal{D}}}}}}{(\triangle K)}^{2}/H\), where c is a position-independent proportion factor and H is the field strength. For the DW, we further suppose that the random force \({{{{{{\boldsymbol{F}}}}}}}_{{{{{{\rm{dw}}}}}}}^{{{{{{\mathcal{R}}}}}}}=-{F}_{{{{{{\rm{dw}}}}}}}^{{{{{{\mathcal{R}}}}}}}{\hat{v}}_{{{{{{\rm{dw}}}}}}}\) with \({F}_{{{{{{\rm{dw}}}}}}}^{{{{{{\mathcal{R}}}}}}}=\zeta c\alpha {{{{{\mathcal{D}}}}}}{(\triangle K)}^{2}/H\), where a dimensionless adjustment coefficient ζ appears because a DW has distinct structure and topological properties from a skyrmion. Now, Eq. (7) is extended to,
Immediately, one gets the ensemble velocity in the granular nanotrack,
It is easy to find,
where \({v}_{\left({{{{{\rm{clean}}}}}}\right)}\approx \frac{{v}_{{{{{{\rm{dw}}}}}}}}{{N}_{{{{{{\rm{s}}}}}}}+1}=\frac{\frac{\gamma }{\alpha }H\triangle }{{N}_{{{{{{\rm{s}}}}}}}+1}\), the ensemble velocity in the clean sample, is just Eq. (10).
As seen from Eq. (12), in the granular sample, the ensemble mobility is not constant (not as in the clean sample) but rather depends on the field strength. That is why the mobility–Ns curves are absent in Fig. 6 for the granular sample.
Now, some comparisons can be made with the simulation results. Let us pay special attention to Fig. 6c, from which the simulation values of ∆v at H = 300 Oe and 600 Oe are ~4.42 ms−1 and ~2.17 ms−1, respectively. The former value is roughly twice the latter, meeting a key expectation of Eq. (13), \(\frac{\varDelta v(300\,{{{{{\rm{Oe}}}}}})}{\varDelta v(600\,{{{{{\rm{Oe}}}}}})}=\frac{1}{300}/\frac{1}{600}=2\).
Equation (10) and (12) suggest that, under a given H, the ensemble in the granular sample is always slower than in the clean sample (Fig. 6b); the smaller the field, the larger the velocity drop (Fig. 6c). As a direct consequence, the ensemble velocity becomes zero at a nonvanishing field. In other words, in the granular sample, the ensemble starts to move only above a threshold field (compare Fig. 5b and Supplementary Fig. S10). By setting v(granular) to zero, one obtains the threshold field, \({H}_{t}={\left(\triangle K\right)[\left({N}_{s}+\zeta \right)c\frac{\alpha }{\gamma \Delta }]}^{\tfrac{1}{2}}\), which indicates that the larger the ΔK and Ns, the higher the threshold field (Supplementary Figs. S8 and S9). Additionally, the dependence of the threshold field on α is also not unexpected.
For both samples, clean and granular, the theoretical indications are consistent with the computational results, suggesting that the Thiele model considering the inter-skyrmion, skyrmion–DW, and skyrmion–defect interactions captures the core of the field-driven motion of the DW–skyrmions ensemble.
Discussion
The Thiele model captures the essence of field-driven dynamics of the DW–skyrmions ensemble, in which the repulsive forces between neighboring magnetic entities19,23,24 efficiently drive the skyrmions (without these internal forces, the skyrmions will not move) but as internal forces do not enter the final equation, Eq. (7), enabling the derivation of the ensemble velocity in the absence of explicit forms of the repulsive forces17,19. The equipartition of the original DW velocity among the DW and all skyrmions has its roots in the efficient transfer of the external force experienced by the DW amongst all the magnetic entities in the ensemble via the DW–skyrmion and inter-skyrmion interactions, as schematically illustrated in Fig. 7. Moreover, Eq. (4) reveals that the repulsive force acting on the jth (j = 1, 2,… Ns) skyrmion by the left-hand neighbor \({F}_{j,{j}-1}\) is equal in magnitude to \({\sum }_{j}^{{N}_{{{{{{\rm{s}}}}}}}}{F}_{{{{{{\rm{sk}}}}}}i}^{{{{{{\mathcal{D}}}}}}}\), namely, the closer the skyrmion to the DW, the larger the stress experienced by the skyrmion (see Fig. 7 for the detail), which underlies why the skyrmion closer to the DW has a smaller size, as shown in Fig. 3a, Supplementary Figs. S4a, S5a and S6a. Actually, this scenario resembles skyrmion contraction in a nanotrack with enhancing geometric confinement2,20.
As seen from Fig. 2c and 3b, attaching skyrmions to the DW can eliminate the nonlinearity on the velocity–field curves for the single DW, which is ascribable to the greatly reduced tilt angle of the DW in the presence of one or more skyrmions47. During motion, the DW tends to tilt with respect to the transverse direction and a skyrmion deflects sidewards to an edge of the nanotrack. The directions of the DW tilting and the skyrmion deflection match each other in such a way that the DW–skyrmion repulsive interaction suppresses the DW tilting.
The validity of the demonstrated field-drive of skyrmion motion is examined in a broad region of parameter space (Fig. 2c). The results of field-driven ensemble motion for various (Ku, D) as shown in Supplementary Fig. S4 solidifies the notion. Apart from the Néel type, the drive scheme also applies to Bloch and hybrid types of DW and skyrmions (as shown in Supplementary Figs. S5 and S6), being independent of the helicity. In fact, this point is implied in the analytic results based on the Thiele model, since in both ansatzes of the DW and skyrmion the azimuthal angles ϕ describing the DW and skyrmion helicities are not explicitly specified [see Eqs. (8) and (9)]. These results suggest that the proposed field-based drive of skyrmion motion is universally valid for common magnetic skyrmions3 stabilized by DMIs irrespective of the helicities.
We would like to note that, the repulsive interactions originate from the same rotational sense of magnetization in the common skyrmions, boundary magnetic textures, and DWs, as pointed out in refs. 21,22. The rotational sense of magnetization in a magnetic texture is determined by the DMI. In a given sample with DMI, all magnetic textures are homochiral and have the same rotation sense (either clockwise or counterclockwise, depending on the sign of DMI constant), which ensures that the interactions between any two neighboring magnetic textures are repulsive.
Of course, attractive inter-skyrmion, skyrmion–boundary, and skyrmion–DW interactions can also occur, but for a different type of magnetic skyrmions (from the common skyrmions3), i.e., the nonaxisymmetric skyrmions on a conical phase of chiral ferromagnets53, the guided motion of which along tunable channels enables a renewed design of conventional spintronic devices, e.g., racetrack memory22. We believe that, for this type of magnetic skyrmions, the field-based drive of ensemble motion proposed in this study is still valid.
For the repulsive interaction, the driving force FH exerted by H on the DW is transferred to every skyrmion and pushes the entire ensemble to the right (Fig. 7a), in which case the force balance on the DW and skyrmions in steady motion resembles that on the uniformly moving cuboid and balls in direct contact (Fig. 7b, d). For the attractive interaction, the applied perpendicular magnetic field needs be reversed to impose an opposite driving force which pulls the ensemble to the left. Correspondingly, each force will also reverse. In this case, the cuboid and balls in direct contact are no longer an appropriate counterpart to the DW–skyrmions ensemble. However, the force balance on the magnetic ensemble in both scenarios can be unitedly described by the cuboid and balls connected by springs (Fig. 7c, d).
It is noteworthy that in Newtonian mechanics the cuboid–ball and ball–ball interactions are transferred via direct contact (Fig. 7b) or by the springs (Fig. 7c), whereas in micromagnetism the DW–skyrmion and inter-skyrmion interactions arise mainly from dipolar and/or exchange interactions of magnetic moments17,20,30.
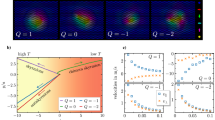
In an assembly consisting of a DW and two sets of skyrmions with opposite core polarities (Fig. 8a), one can selectively displace either set of the skyrmions along a certain direction by toggling the field direction, while leaving the other set undisturbed, as shown in Fig. 8. In the perpendicular field along +z (Fig. 8b), the DW experiences a driving force pointing to the right and thus moves to the set of skyrmions on the right side and departs the left set of skyrmions. When the DW departs one set of skyrmions, the increasing distance between the DW and that set of skyrmions leads to vanishing interaction strength between them. There is a considerable interaction between two magnetic textures only if their distance is small enough17,19,20. As a result, for the field along +z (Fig. 8b), the DW only interacts with the right set of skyrmions, and when the perpendicular field is reversed, i.e., along -z (Fig. 8c), the DW only interacts with the left set of skyrmions. Such operation is impossible in the current-driven motion where all skyrmions, whatever the core polarities, tend to shift in the same direction13,19,29. This behavior may enable the realization of field-controlled unidirectional devices.
a In such configuration, a domain wall sits in between two sets of skyrmions. b, c A perpendicular magnetic field (H) in a given direction will shift only one set of skyrmions in a certain direction without affecting the other set. Note that, one skyrmion or more can be included in each set. The strengths of perpendicular magnetic anisotropy and Dzyaloshinskii-Moriya interaction are Ku = 0.8 MJm−3 and D = 3.5 mJm−2, respectively. The field strength is H = 500 Oe and t is the action time of field.
Finally, we would like to discuss the relevance of these results to polar skyrmions32,33 in ferroelectric materials. Up to now, electric/spin currents, spin waves, and temperature and field gradients have proved capable of displacing magnetic skyrmions4,6,7,8,9,10,11,12,13,14. Amongst them, the most fascinating is the current-induced skyrmion motion, which holds promise in building compact, energy-efficient skyrmionic devices2. The field-drive of skyrmion motion conceived in this study represents an alternative route awaiting experimental exploration and might find use in magnetic insulators.
As the counterpart of magnetic skyrmions, polar skyrmions have been experimentally observed in both multilayered (PbTiO3/SrTiO3)32 and bulk (Bi0.5Na0.5TiO3)33 ferroelectrics. Theoretical strategies to robustly imprint skyrmions in simple ferroelectrics have also been put forward54. Furthermore, a group theory and first-principles computations study has shown that electric DMIs exist in ferroelectric materials and exhibits a one-to-one correspondence with their magnetic analogues34. These studies imply that electric skyrmions and DWs may appear in plenty of ferroelectrics as ordinary polar textures.
While polar DW motion triggered by various kinds of stimuli, especially, electric fields, is already demonstrated26,55,56,57,58, realization of driven polar skyrmion motion remains elusive because of the lack of available technological means. In ferroelectrics, there is no equivalent effect of spin-transfer or spin-orbit torque, and electric dipole waves, an analogue of spin waves, are observed just recently59 and await thorough exploration of their basic features. Latest investigations60,61 showed that polar skyrmions are sensitive to applied electric fields; typically, they expand or shrink depending on the field direction as do magnetic skyrmions in magnetic fields3,27 (Fig. 1). Therefore, field-based driving of polar skyrmions represents the most promising route; transplanting the proposed scheme to polar skyrmions seems feasible.
In conclusion, through micromagnetic simulations, we demonstrate that, in a perpendicular magnetic field, magnetic skyrmions in a nanotrack can moves coherently, when appropriately coupled to a single domain wall, and discover velocity equipartition among the DW and skyrmions. Based on Thiele’s analytic model, we reproduce the numerical results and find that the DW–skyrmion and inter-skyrmion repulsive interactions play a critical role in driving the skyrmion motion and partitioning the DW velocity. Recognizing recent advances in topological ferroelectrics, we are optimistic that the proposed scheme should also apply to polar skyrmions. Our study is expected to spark research efforts on magnetic (electric) field-based control of magnetic (polar35) skyrmions.
Methods
Micromagnetic energies
In this model, the total free energy, E, comprises the contributions of exchange, dipolar, PMA, DMI, and Zeeman interactions, i.e.,
Here, hd is the demagnetizing field and ℰdm is the DMI energy density. \({{{{{{\mathcal{E}}}}}}}_{{{{{{\rm{dm}}}}}}}={D}_{{{{{{\rm{i}}}}}}}\left({{{{{\bf{m}}}}}}\cdot \nabla {m}_{z}-{m}_{z}\nabla \cdot {{{{{\bf{m}}}}}}\right)\) for interfacial DMI2, \({{{{{{\mathcal{E}}}}}}}_{{{{{{\rm{dm}}}}}}}={D}_{{{{{{\rm{b}}}}}}}{{{{{\bf{m}}}}}}\cdot \left(\nabla \times {{{{{\bf{m}}}}}}\right)\) for bulk DMI1, and \({{{{{{\mathcal{E}}}}}}}_{{{{{{\rm{dm}}}}}}}={D}_{{{{{{\rm{i}}}}}}}\left({{{{{\bf{m}}}}}}\cdot \nabla {m}_{z}-{m}_{z}\nabla \cdot {{{{{\bf{m}}}}}}\right)+{D}_{{{{{{\rm{b}}}}}}}{{{{{\bf{m}}}}}}\cdot \left(\nabla \times {{{{{\bf{m}}}}}}\right)\) for coexisting interfacial and bulk DMIs. For simplicity, we assume that the DMI strengths Di = Db ≡ D in this study.
Numerical simulations
An initial, equilibrium magnetization configuration in the nanotrack is obtained by relaxing the entire system with a properly set near-equilibrium configuration to an energy minimum. The near-equilibrium configuration is easily realizable numerically using a micromagnetic tool, e.g., MuMax362. Subsequently, the Landau-Lifshitz-Gilbert equation36,37 is numerically solved to compute the dynamics of the resulting equilibrium magnetization configuration.
Numerical simulations are implemented using the finite-difference codes, MuMax362 and occasionally OOMMF63. Regarding the material parameters, exchange stiffness A = 15 pJm−1, saturation magnetization Ms = 580 kAm−1, and Gilbert damping constant α = 0.3 are fixed, whereas various values of PMA constant Ku and DMI strength D are addressed individually. In all simulations, the nanotrack is divided into a grid of 1 × 1 × 1 nm3 cubes, whose side length is small compared to the relevant feature sizes: the exchange length42 \(\scriptstyle \lambda = \sqrt{2A/\left({\mu }_{0}{M}_{{{{{{\rm{s}}}}}}}^{2}\right)}\approx 8.4\, {{{{{\rm{nm}}}}}}\), nominal skyrmion radius64 \(\scriptstyle R={{\pi }}D\sqrt{A/\left(16A{K}_{{{{{{\rm{eff}}}}}}}^{2}-{{{\pi }}}^{2}{D}^{2}{K}_{{{{{{\rm{eff}}}}}}}\right)}\approx 5.6\, {{{{{\rm{nm}}}}}}\), and DW thickness42 \(\scriptstyle \Delta =\sqrt{A/{K}_{{{{{{\rm{eff}}}}}}}}\approx 5.0\, {{{{{\rm{nm}}}}}}\), for the typical material parameters, where \({K}_{{{{{{\rm{eff}}}}}}}={K}_{{{{{{\rm{u}}}}}}}-(1/2){\mu }_{0}{M}_{{{{{{\rm{s}}}}}}}^{2}\) is the effective perpendicular magnetic anisotropy. Open boundary conditions are assumed.
Voronoi tessellation
The granular sample is implemented by Voronoi tessellation with average 20-nm grains, in which the PMA strength Ku is randomly distributed around an average value Ku0 = 0.8 MJm−3 with a Gaussian distribution of the deviation, ∆K = Ku‒Ku0. For every ∆K, three different grain distributions are examined to better assess the simulation results. For the notched samples, Ms is halved to 290 kAm−1 in the notch region.
Data availability
All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary information. Additional data related to this paper may be requested from the corresponding authors upon reasonable request.
Code availability
MuMax3 and OOMMF used to generate the results are open-source, public-domain codes which can be accessed freely at http://mumax.github.io/ (Release version 3.10) and https://math.nist.gov/oommf/ (Release version 2.0a3), respectively.
References
Nagaosa, N. & Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotech. 8, 899–911 (2013).
Fert, A., Reyren, N. & Cros, V. Magnetic skyrmions: advances in physics and potential applications. Nat. Rev. Mater. 2, 17031 (2017).
Bogdanov, A. N. & Panagopoulos, C. Physical foundations and basic properties of magnetic skyrmions. Nat. Rev. Phys. 2, 492–498 (2020).
Schulz, T. et al. Emergent electrodynamics of skyrmions in a chiral magnet. Nat. Phys. 8, 301–304 (2012).
Parkin, S. & Yang, S.-H. Memory on the racetrack. Nat. Nanotech. 10, 195–198 (2015).
Schütte, C. & Garst, M. Magnon-skyrmion scattering in chiral magnets. Phys. Rev. B 90, 094423 (2014).
Iwasaki, J., Beekman, A. J. & Nagaosa, N. Theory of magnon-skyrmion scattering in chiral magnets. Phys. Rev. B 89, 064412 (2014).
Jonietz, F. et al. Spin transfer torques in MnSi at ultralow current densities. Science 330, 1648–1651 (2010).
Kong, L. & Zang, J. Dynamics of an insulating skyrmion under a temperature gradient. Phys. Rev. Lett. 111, 067203 (2013).
Mochizuki, M. et al. Thermally driven ratchet motion of a skyrmion microcrystal and topological magnon Hall effect. Nat. Mater. 13, 241–246 (2014).
Kovalev, A. A. Skyrmionic spin Seebeck effect via dissipative thermomagnonic torques. Phys. Rev. B 89, 241101 (2014).
Zhang, S. L. et al. Manipulation of skyrmion motion by magnetic field gradients. Nat. Commun. 9, 2115 (2018).
Woo, S. et al. Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets. Nat. Mater. 15, 501–506 (2016).
Zeissler, K. et al. Diameter-independent skyrmion Hall angle observed in chiral magnetic multilayers. Nat. Commun. 11, 428 (2020).
Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 4, 241–255 (1958).
Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 120, 91–98 (1960).
Lin, S.-Z., Reichhardt, C., Batista, C. D. & Saxena, A. Particle model for skyrmions in metallic chiral magnets: Dynamics, pinning, and creep. Phys. Rev. B 87, 214419 (2013).
Iwasaki, J., Koshibae, W. & Nagaosa, N. Colossal spin transfer torque effect on skyrmion along the edge. Nano Lett. 14, 4432–4437 (2014).
Xing, X., Åkerman, J. & Zhou, Y. Enhanced skyrmion motion via strip domain wall. Phys. Rev. B 101, 214432 (2020).
Yoo, M.-W., Cros, V. & Kim, J.-V. Current-driven skyrmion expulsion from magnetic nanostrips. Phys. Rev. B 95, 184423 (2017).
Meynell, S. A., Wilson, M. N., Fritzsche, H., Bogdanov, A. N. & Monchesky, T. L. Surface twist instabilities and skyrmion states in chiral ferromagnets. Phys. Rev. B 90, 014406 (2014).
Leonov, A. O., Loudon, J. C. & Bogdanov, A. N. Spintronics via non-axisymmetric chiral skyrmions. Appl. Phys. Lett. 109, 172404 (2016).
Schäffer, A. F. et al. Rotating edge‑field driven processing of chiral spin textures in racetrack devices. Sci. Rep. 10, 20400 (2020).
Siegl, P. et al. Creating arbitrary sequences of mobile magnetic skyrmions and antiskyrmions. Phys. Rev. B 106, 014421 (2022).
Boulle, O. et al. Room-temperature chiral magnetic skyrmions in ultrathin magnetic nanostructures. Nat. Nanotech. 11, 449–454 (2016).
Shin, Y.-H., Grinberg, I., Chen, I.-W. & Rappe, A. M. Nucleation and growth mechanism of ferroelectric domain-wall motion. Nature 449, 881–884 (2007).
Romming, N., Kubetzka, A., Hanneken, C., von Bergmann, K. & Wiesendanger, R. Field-dependent size and shape of single magnetic skyrmions. Phys. Rev. Lett. 114, 177203 (2015).
Xing, X., Pong, P. W. T. & Zhou, Y. Skyrmion domain wall collision and domain wall-gated skyrmion logic. Phys. Rev. B 94, 054408 (2016).
Zhang, X. et al. Skyrmion-skyrmion and skyrmion-edge repulsions in skyrmion-based racetrack memory. Sci. Rep. 5, 7643 (2015).
Rohart, S. & Thiaville, A. Skyrmion confinement in ultrathin film nanostructures in the presence of Dzyaloshinskii-Moriya interaction. Phys. Rev. B 88, 184422 (2013).
Thiaville, A., Rohart, S., Jué, É., Cros, V. & Fert, A. Dynamics of Dzyaloshinskii domain walls in ultrathin magnetic films. Europhys. Lett. 100, 57002 (2012).
Das, S. et al. Observation of room-temperature polar skyrmions. Nature 568, 368–372 (2019).
Yin, J. et al. Nanoscale bubble domains with polar topologies in bulk ferroelectrics. Nat. Commun. 12, 3632 (2021).
Zhao, H. J., Chen, P., Prosandeev, S., Artyukhin, S. & Bellaiche, L. Dzyaloshinskii–Moriya-like interaction in ferroelectrics and antiferroelectrics. Nat. Mater. 20, 341–345 (2021).
Li, Q. et al. Subterahertz collective dynamics of polar vortices. Nature 592, 376–380 (2021).
Landau, L. & Lifshitz, E. On the theory of the dispersion of magnetic permeability in ferromagnetic bodies. Phys. Z. Sowjetunion 8, 153–169 (1935).
Gilbert, T. L. A phenomenological theory of damping in ferromagnetic materials. IEEE Trans. Magn. 40, 3443–3449 (2004).
Lu, J., Li, M. & Wang, X. R. Quantifying the bulk and interfacial Dzyaloshinskii-Moriya interactions. Phys. Rev. B 101, 134431 (2020).
Tokura, Y. & Kanazawa, N. Magnetic skyrmion materials. Chem. Rev. 121, 2857–2897 (2021).
Gong, X., Yuan, H. Y. & Wang, X. R. Current-driven skyrmion motion in granular films. Phys. Rev. B 101, 064421 (2020).
Yuan, H. Y. & Wang, X. R. Domain wall pinning in notched nanowires. Phys. Rev. B 89, 054423 (2014).
Thiaville, A. & Nakatani, Y. Domain-wall dynamics in nanowires and nanostrips, in Spin Dynamics in Confined Magnetic Structures III (Springer, Berlin, 2006), pp. 161–205.
Beach, G. S. D., Nistor, C., Knutson, C., Tsoi, M. & Erskine, J. L. Dynamics of field-driven domain-wall propagation in ferromagnetic nanowires. Nat. Mater. 4, 741–744 (2005).
Mougin, A., Cormier, M., Adam, J. P., Metaxas, P. J. & Ferré, J. Domain wall mobility, stability and Walker breakdown in magnetic nanowires. Europhys. Lett. 78, 57007 (2007).
Wang, X. R., Yan, P. & Lu, J. High-field domain wall propagation velocity in magnetic nanowires. Europhys. Lett. 86, 67001 (2009).
Wang, X. R., Yan, P., Lu, J. & He, C. Magnetic field driven domain-wall propagation in magnetic nanowires. Ann. Phys. (NY) 324, 1815–1820 (2009).
Boulle, O. et al. Domain wall tilting in the presence of the Dzyaloshinskii-Moriya interaction in out-of-plane magnetized magnetic nanotracks. Phys. Rev. Lett. 111, 217203 (2013).
Tchernyshyov, O. & Chern, G.-W. Fractional vortices and composite domain walls in flat nanomagnets. Phys. Rev. Lett. 95, 197204 (2005).
Nakatani, Y., Thiaville, A. & Miltat, J. Faster magnetic walls in rough wires. Nat. Mater. 2, 521–523 (2003).
Xing, X., Pong, P. W. T. & Zhou, Y. Current-controlled unidirectional edge-meron motion. J. Appl. Phys. 120, 203903 (2016).
Thiele, A. A. Steady-state motion of magnetic domains. Phys. Rev. Lett. 30, 230–233 (1973).
Hrabec, A. et al. Current-induced skyrmion generation and dynamics in symmetric bilayers. Nat. Commun. 8, 15765 (2017).
Leonov, A. O., Monchesky, T. L., Loudon, J. C. & Bogdanov, A. N. Three-dimensional chiral skyrmions with attractive interparticle interactions. J. Phys.: Condens. Matter 28, 35LT01 (2016).
Gonçalves, M. A. P., Escorihuela-Sayalero, C., García-Fernández, P., Junquera, J. & Íñiguez, J. Theoretical guidelines to create and tune electric skyrmion bubbles. Sci. Adv. 5, eaau7023 (2019).
Yang, T. J., Gopalan, V., Swart, P. J. & Mohideen, U. Direct observation of pinning and bowing of a single ferroelectric domain wall. Phys. Rev. Lett. 82, 4106–4109 (1999).
McGilly, L. J., Yudin, P., Feigl, L., Tagantsev, A. K. & Setter, N. Controlling domain wall motion in ferroelectric thin films. Nat. Nanotech. 10, 145–150 (2015).
Whyte, J. R. & Gregg, J. M. A diode for ferroelectric domain-wall motion. Nat. Commun. 6, 7361 (2015).
Rubio-Marcos, F., Campo, A. D., Marchet, P. & Fernández, J. F. Ferroelectric domain wall motion induced by polarized light. Nat. Commun. 6, 6594 (2015).
Gong, F. H. et al. Atomic mapping of periodic dipole waves in ferroelectric oxide. Sci. Adv. 7, eabg5503 (2021).
Das, S. et al. Local negative permittivity and topological phase transition in polar skyrmions. Nat. Mater. 20, 194–201 (2021).
Nahas, Y. et al. Topology and control of self-assembled domain patterns in low-dimensional ferroelectrics. Nat. Commun. 11, 5779 (2020).
Vansteenkiste, A. et al. The design and verification of MuMax3. AIP Adv. 4, 107133 (2014).
Donahue, M. J. & Porter, D. G. OOMMF User’s Guide Version 1.0 Interagency Report NISTIR 6376 (National Institute of Standards and Technology, Gaitherburg, MD: September 1999).
Wang, X. S., Yuan, H. Y. & Wang, X. R. A theory on skyrmion size. Commun. Phys. 1, 31 (2018).
Acknowledgements
X.X. is financially supported by the Guangdong Provincial Natural Science Foundation of China under Grant No. 2022A1515010605 and the National Natural Science Foundation of China under Grant No. 11774069. Y.Z. acknowledges the support by Guangdong Basic and Applied Basic Research Foundation (2021B1515120047), Guangdong Special Support Project (2019BT02X030), Shenzhen Fundamental Research Fund (Grant No. JCYJ20210324120213037), Shenzhen Peacock Group Plan (KQTD20180413181702403), Pearl River Recruitment Program of Talents (2017GC010293) and National Natural Science Foundation of China (11974298, 61961136006).
Author information
Authors and Affiliations
Contributions
X.X. conceived the study, performed the micromagnetic simulations, and did the derivation. X.X. and Y.Z. co-analyzed the results and co-wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Xin Gong and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xing, X., Zhou, Y. Skyrmion motion and partitioning of domain wall velocity driven by repulsive interactions. Commun Phys 5, 241 (2022). https://doi.org/10.1038/s42005-022-01020-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-01020-z
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.