Abstract
The kagome metals of the family AV3Sb5, featuring a unique structural motif, harbor an array of intriguing phenomena such as chiral charge order and superconductivity. CsV3Sb5 is of particular interest because it displays a double superconducting dome in the region of the temperature-pressure phase diagram where charge order is still present. However, the microscopic origin of such an unusual behavior remains an unsolved issue. Here, to address it, we combine high-pressure, low-temperature muon spin relaxation/rotation with first-principles calculations. We observe a pressure-induced threefold enhancement of the superfluid density, which also displays a double-peak feature, similar to the superconducting critical temperature. This leads to three distinct regions in the phase diagram, each of which features distinct slopes of the linear relation between superfluid density and the critical temperature. These results are attributed to a possible evolution of the charge order pattern from the superimposed tri-hexagonal Star-of-David phase at low pressures (within the first dome) to the staggered tri-hexagonal phase at intermediate pressures (between the first and second domes). Our findings suggest a change in the nature of the charge-ordered state across the phase diagram of CsV3Sb5, with varying degrees of competition with superconductivity.
Similar content being viewed by others
Introduction
Among the series AV3Sb5 (A = Rb, K, Cs)1,2,3, the Cs compound manifests the highest superconducting critical temperature Tc ≃ 2.5 K. CsV3Sb5 also features multi-gap superconductivity (SC) and more importantly, a time-reversal symmetry breaking (TRSB) chiral charge order (CO) below Tco = 94 K4,5,6,7, as reported by scanning tunneling microscopy8, polar Kerr rotation5, and muon spin relaxation/rotation (μSR) experiments4,6. A comprehensive understanding of the interdependence between CO and SC is thus essential, and can be studied by using an appropriate external perturbation. In the quest to obtain an efficient tuning knob, hydrostatic pressure was found to be optimal. Indeed, pressure suppresses the CO and results into an unusual but well-pronounced double superconducting dome in the temperature-pressure phase diagram. Compared to the Rb and K counterparts9,10,11, the double-peak behavior is most distinguishable in the case of CsV3Sb512,13,14,15 where Tc is roughly tripled to 8 K around the optimal pressure of 2 GPa from its value Tc = 2.5 K at ambient pressure. Thus, pressure tuned CsV3Sb5 offers a rich framework for studying the nature of the interplay between SC and CO.
To systematically characterize and to obtain a microscopic understanding of the complex temperature-pressure phase diagram of CsV3Sb5, here we report high-pressure zero-field (ZF) and transverse-field (TF) μSR as well as AC susceptibility (up to 1.75 GPa) measurements combined with first-principles calculations. TF μSR experiments serve as an extremely sensitive local probe technique to measure the magnetic penetration depth λ in the vortex state of bulk type-II superconductors. This quantity is directly related to the superfluid density ns via 1/λ2 = μ0e2ns/m* (where m* is the effective mass). ZF μSR has the ability to detect internal magnetic fields as small as 0.1 G without applying external magnetic fields, making it a highly valuable tool for probing spontaneous magnetic fields due to TRSB in exotic superconductors. The techniques of μSR and Density Functional Theory (DFT) complement each other ideally, as we are able to sensitively probe the fundamental microscopic properties of CsV3Sb5 with μSR experiments and correlate them with the pressure-evolution of the charge-ordered state calculated by DFT.
Results
Superfluid density as a function of pressure
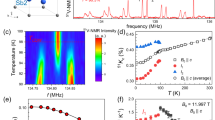
Figure 1a shows the TF-μSR time spectra of CsV3Sb5 well below (0.25 K) and above (10 K) Tc in the presence of an applied magnetic field of 10 mT for ambient as well as the highest applied pressure, 1.74 GPa. The weakly damped oscillations above Tc are essentially due to the randomly distributed local fields created by nuclear magnetic moments. The spectra below Tc show a sizable increase in relaxation because of the inhomogeneous distribution of internal fields arising due to the formation of the flux line lattice in the vortex state. The Fourier transform of the spectra, shown in Fig. 1b, gives the internal field distribution, which showcases a clear broadening in the superconducting state compared to the normal state. From the TF-μSR data, the superconducting relaxation rate σsc(T) is extracted. The latter is related to the magnetic penetration depth via \(\frac{{\sigma }_{{{{{{{{\rm{sc}}}}}}}}}(T)}{{\gamma }_{\mu }}=0.06091\frac{{\phi }_{0}}{{\lambda }^{2}(T)}\), where γμ = 2π × 135.5 MHz/T is the muon gyromagnetic ratio and ϕ0 is the flux quanta16,17 (details of the analysis of the TF-μSR data are given in the Supplementary Note 2). The resulting temperature dependence of the inverse squared magnetic penetration depth λ−2(T), measured under various hydrostatic pressures, are shown in Fig. 2a.
a Selected TF-μSR time spectra at 0.27 K (in the superconducting state) and 10 K (in the normal state) collected for ambient and 1.74 GPa pressure. Solid lines are the fits of the spectra considering both the sample and background parts, as described in the Supplementary Note 2. b The Fourier transform of the spectra shows an additional broadening of the peak due to an inhomogeneous distribution of internal fields, resulting from the appearance of a vortex lattice. c, d Representative ZF-μSR time spectra collected in zero field well below Tc (0.27 K) and above Tc (10 K) for 1.18 GPa (c) and 1.74 GPa (d). The solid lines are fits considering two relaxation channels, namely Gaussian-Kubo-Toyabe and a Lorentzian decay function. The error bars represent the standard deviation of the fit parameters.
a Temperature variation of the inverse squared magnetic penetration depth λ−2(T) for the applied hydrostatic pressures shown in the plot legend. The solid line is a two gap s + s-wave model fitting using the phenomenological α-model. b The temperature-pressure superconducting phase diagram of CsV3Sb5. The left axis shows Tc values obtained through TF-μSR and ac magnetic susceptibility measurements carried out under hydrostatic pressure conditions. The right axis presents the inverse squared London penetration depth at base temperature, i.e., λ−2(0) ∝ ns as a function of pressure. c Superconducting transition temperature Tc plotted as a function of the base-temperature superfluid density λ−2(0) for the three different regions of the phase diagram of b. The error bars represent the standard deviation of the fit parameters.
The λ−2(T) curves in Fig. 2a are well described by a two-gap model across the entire pressure range probed (see details in the Methods section). This indicates that the multi-gap nature of the superconducting state of CsV3Sb5, which was previously reported by various techniques for ambient conditions18,19,20,21, is robust against the application of hydrostatic pressure. As we show below, a sharp increase of both Tc and λ−2(0) occurs at pressures in the range 1.5–1.7 GPa, suggesting the complete suppression of the CO and thus a transition between the SC+CO state to the pure SC state. It is quite remarkable, therefore, that at the intermediate pressure 1.68 GPa, which is at the border between the SC+CO and pure SC phases, the temperature evolution of the penetration depth shows a prominent two-step like feature [purple curve in Fig. 2a]. This is a signature of inhomogeneity, whose origin can be either extrinsic, e.g., due to pressure inhomogeneity inside the cell, or intrinsic, due to phase separation caused by a first-order SC+CO to SC transition.
Figure 2b shows the pressure dependence of Tc and of the zero-temperature value of λ−2(0), which is directly proportional to the superfluid density ns. Interestingly, both λ−2(0) and Tc show a similar non-monotonic pressure dependence, featuring three distinct regions marked as I, II and III in Fig. 2b. Initially, as pressure increases, Tc shows an increase from 2.85(9) K at ambient pressure to 6.9(3) K at a critical pressure pc1 ≃ 0.63 GPa. Upon further increase in pressure, Tc shows a sharp and substantial decrease down to 2.87(7) K at 0.8 GPa. This marks the onset of Region II, where Tc increases only slightly with pressure. A sudden jump in Tc is seen around a second critical pressure pc2 ≃ 1.74 GPa, reaching a maximum value of \({T}_{{{{{{{{\rm{c}}}}}}}}}^{\max }\) = 8.0(1) K—which is almost three times larger than the ambient pressure value—and nearly saturating beyond this pressure. This regime is denoted as Region III in the T − p phase diagram.
The maximum Tc value of 8 K extracted from μSR is fairly close to the value obtained through electrical transport, AC and DC magnetization measurements14. Moreover, λ−2(0) qualitatively shows a similar trend to Tc with regard to pressure, also featuring a double-peak behavior. Indeed, there is a nearly threefold increase in the value of λ−2(0) from 6.5(1) μm−2 at ambient pressure to 17.3(9) μm−2 at 1.74 GPa, followed by saturation upon further increase in pressure. The relative variation of the λ−2(0) value at the highest applied pressure compared to its ambient pressure value is δλ−2(0)/λ−2(0) = 63%. This is rather unusual in comparison to BCS superconductors, where the superfluid density either depends weakly on pressure or remains pressure independent22. The sudden enhancement of Tc and λ−2(0) has an intimate connection with the collapse of CO at the critical pressure pc2, and is consistent with a first-order transition from the SC+CO phase to the pure SC phase. It is worth to mention that, in case of CsV3Sb5, clear M-dome like Tc vs. p phase diagram is observed because with pressure dispersion along c-axis increases, which weakens the nesting and hence vanishing the out of plane wave vector that results in first superconducting dome around pc1. However, for RbV3Sb5 and KV3Sb5, the dispersion along c-axis is already present at ambient pressure which may explain single superconducting dome and lower critical pressures for these systems.
Superconducting transition temperature vs. superfluid density
Figure 2c displays the correlation between the superconducting transition temperature Tc and the superfluid density λ−2(0) obtained from μSR experiments under different pressures. There are three distinct types of Tc[λ−2(0)] lines, each associated with one of the three regions of the phase diagram in Fig. 2b. For the data points belonging to Region I, we obtain a slope of 2.72 Kμm2, which is 3.5 times larger than the slope obtained for the data points from Region II (0.78 Kμm2). For Region III, λ−2(0) seems to be almost independent on Tc.
These linear relationships between Tc and λ−2(0) are characteristic of unconventional superconductors. In the present case, for Regions I and II, the Tc/λ−2(0) ratio lies far away from the values typically seen in BCS superconductors, where Tc/λ−2 ≈ 0.00025–0.015 Kμm2. The large values of Tc, despite the small values of the superfluid density in Regions I and II, are also signatures of unconventional SC, where Tc/λ−2(0) ~ 1–2023,24,25. Moreover, the change in the slope Tc/λ−2(0) from Region I to Region II, both of which display coexisting CO and SC, suggests a subtle modification in the CO state. Combined with the sudden suppression in Tc and λ−2(0) upon crossing the Region I to Region II boundary in Fig. 2b, this provides strong evidence for a distinct competition between SC and CO in these two regions. Finally, the fact that λ−2(0) is nearly independent of Tc in Region III can be attributed to the absence of a competing CO state in this region.
Spontaneous fields in the superconducting state
Zero-field μSR experiments have been successfully implemented to probe TRSB in well-known unconventional superconductors, e.g., Sr2RuO426,27,28, UPt329, LaNiC230, LaPt3P31. We have conducted ZF-μSR experiments for three different applied pressures: 0, 1.18, and 1.74 GPa. Representative ZF-μSR spectra above and below Tc for the pressures of 1.18 and 1.74 GPa are shown in Fig. 1c, d. Both display an increase in relaxation within the superconducting state. The data were fitted using the Gaussian-Kubo-Toyabe (GKT) depolarization function32 multiplied by an exponential decay function exp(−Λt). The Gaussian-Kubo-Toyabe function accounts for the random magnetic fields created by the nuclear moments. As was discussed previously for KV3Sb53, the exponential relaxation rate (−Λt) is sensitive to the temperature dependence of the electronic contribution to the muon spin relaxation. The temperature dependences of the electronic relaxation rate Λ(T) for the applied pressures of 0, 1.18 and 1.74 GPa are shown in Fig. 3.
a Electronic relaxation rate Λ(T) for CsV3Sb5 as a function of temperature obtained from ZF-μSR experiments carried out in the presence of three different applied pressures: (a) 0, (b) 1.18, and (c) 1.74 Gpa. Each pressure corresponds to a different Region (I, II, and III) of the T − p phase diagram of Fig. 2c. Solid lines through the data points are fits as described in the Methods section. The values for the superconducting transition temperature Tc are denoted by the vertical dashed black line. The error bars represent the standard deviation of the fit parameters.
At ambient pressure, we observe an enhancement of the exponential relaxation rate, with an onset slightly above Tc, by a small amount of ΔΛ0 = 0.024(8) μs−1. Since time-reversal symmetry is already broken by CO at TCO ≃ 95 K4,5,6, we speculate that the effect in the superconducting state is caused by the Meissner screening of the small fields induced by the CO loop currents created at TCO. A similar argument holds for 1.18 GPa (Region II), where both CO and SC coexist and the associated increase in electronic relaxation is ΔΛ1.18 = 0.011(2) μs−1.
However, at 1.74 GPa (Region III), where the CO is completely suppressed, we still observe an increase in Λ(T) with the onset of SC at Tc ≃ 8 K. The increase of Λ(T) with decreasing temperature in Region III is smooth, contrasting with the sharp increase observed in Regions I and II. As there is no CO at this pressure, a plausible origin for the enhancement of the internal field width is the spontaneous breaking of time reversal symmetry in the superconducting state. The increase in Λ by a magnitude of ΔΛ1.74 GPa = 0.031(3) μs−1 is associated with a characteristic field strength of ΔB = ΔΛ1.74 GPa/γμ = 0.04 mT. This value is comparable to what is observed in well-known TRSB superconductors, such as 0.05 mT for the chiral superconductor Sr2RuO427,28, 0.01 mT for the heavy-fermion superconductor UPt329, and 0.01 mT for the non-centrosymmetric superconductor LaNiC230. These results indicate that the SC state without CO breaks time-reversal symmetry. Indeed, a recent μSR investigation of the other kagome compounds, RbV3Sb5 and KV3Sb5, also reported evidence for TRSB in the pure SC state24.
Discussion
One of the intriguing findings of this paper is the observation of a double superconducting dome inside the region where SC and CO coexist, associated with a more than threefold enhancement of Tc and of the superfluid density, σsc(0) ∝ ns. Indeed, Fig. 2b shows that with increasing pressure, Tc and the superfluid density first increase up to 0.63 GPa, followed by a sudden drop in these parameters with further increase in pressure, defining the boundary between Regions I and II. Within Region II, Tc and ns increase slowly with increasing pressure up to 1.54 GPa, beyond which a dramatic enhancement is seen in these two quantities, marking the onset of Region III. This behavior is suggestive of a state of coexistence between competing SC and CO orders, which undergoes a transition to a pure SC state at pc2. Such a scenario would naturally explain why not only Tc but also ns displays a sudden change from Region II to Region III, as ns is suppressed in the coexisting state due to the partial gapping of the Fermi surface promoted by CO order.
Analogously, the strong variation of Tc and ns between pc1 and pc2 is indicative of a subtle modification in the nature of either the CO or the SC state from Region I to Region II. The SC state seems qualitatively the same in both regions: first, the λ−2(T) curves are indicative of a fully-gapped SC state in both regions. Second, the temperature dependence of the electronic relaxation Λ(T) is very similar in both Regions I and II (Fig. 3a, b). Consequently, it is plausible that the changes in Tc and ns are a consequence of a change in the CO state, in such a way that the CO of Region II competes more strongly with SC than the CO of Region I. Experimentally, it has been proposed that more than one CO state can be realized in these kagome metals7,8,13. Different theoretical calculations also suggest multiple nearby CO instabilities33,34,35,36,37,38,39. To investigate the possibility of a change in the nature of the CO state from Region I to Region II in CsV3Sb5, we performed DFT calculations at different hydrostatic pressures.
The AV3Sb5 compounds are predicted to have phonon instabilities at the M and L points of their hexagonal Brillouin zones40,41. Both of the unstable phonons transform as three-dimensional irreducible representations of the space group, which means that the high-temperature undistorted kagome lattice may lower its energy via lattice distortions along six independent atomic displacement patterns. Superpositions of these patterns give rise to a large family of candidate structures and bond order patterns, a subset of which are shown in Fig. 437.
a Pressure dependence of the difference in enthalpies between a charge-ordered state and that of the undistorted kagome lattice for different possible CO phases discussed in the text and shown in e–g. b Density of states (DOS) per formula unit calculated at ambient pressure for the different CO phases considered. c Variation of the DOS per formula unit at the Fermi level with pressure. The distinct types of CO states considered here display different bond order configurations and are named: d parent; e planar tri-hexagonal; f superimposed tri-hexagonal Star-of-David; and g staggered tri-hexagonal. Black, blue, green and red points in a–c correspond to these CO configurations respectively.
While there is growing evidence of time-reversal symmetry breaking in the CO phase, the predominant effect of pressure is expected to be on the lattice, and not directly on the properties of the CO state affected by TRSB. This is because interatomic force constants depend strongly on the bond lengths in ionic compounds, where there is a fine balance between the repulsive and the attractive components of the interatomic interactions. Moreover, the TRSB CO state is generally expected to induce a regular (i.e. time-reversal symmetry preserving) CO pattern of bond distortions due to nonlinear terms in the free energy36,39. For these reasons, despite the fact that our first-principles approach cannot directly account for TRSB, understanding how the crystal structure of CsV3Sb5 evolves under pressure using non-spin-polarized DFT calculations is a viable approach to elucidate the behavior of the CO in this material.
In Fig. 4a, we present the enthalpy per formula unit of the three lowest energy CO structures of CsV3Sb5 calculated from DFT as a function of pressure. The parent structure, without CO, is shown in Fig. 4d. Two of these CO phases, dubbed the (M00) + (0LL) “staggered tri-hexagonal” state (red, panel (g)) and the (MMM) + (LLL) “superimposed tri-hexagonal Star-of-David” phase (green, panel (f)), host a superposition of both M and L point lattice instabilities, and therefore have the 2 × 2 × 2 periodicity consistent with the available x-ray data. The third low energy phase, the so-called (MMM) “planar tri-hexagonal” phase (blue, panel (e)), is only associated with the M point instability. As a result, it has a 2 × 2 × 1 periodicity that seems inconsistent with the currently available experimental structure data.
Figure 4a shows that at pressures above 5 GPa, CO is completely suppressed, and we predict the undistorted kagome lattice to be the equilibrium structure. This is consistent with previous results that predicted the phonon instabilities at both M and L to vanish at pressures between 3 GPa and 5 GPa42. The threefold difference with respect to the experimental pc2 value is not unexpected. Indeed, an accurate prediction of the pressure at which the structural instabilities disappear is hard to achieve in DFT because of the large unit cell, the sensitivity of the electronic structure of the kagome layers on pressure, and lattice parameters errors due to the exchange correlation approximations. Nevertheless, the qualitative trends with pressure extracted from DFT are expected to be reliable.
While the staggered tri-hexagonal phase (red) has lower enthalpy than the other CO phases throughout the pressure range considered, the enthalpy differences between the distinct CO phases are on the order of a few meV’s per formula unit. This implies that entropic effects not captured by DFT are large enough to switch the ordering of these phases and cause the equilibrium structure to be a different phase from the one that minimizes the Kohn–Sham enthalpy. The two most likely candidates consistent with the experimentally observed 2 × 2 × 2 periodicity of the CO state are the staggered tri-hexagonal (red) and the superimposed tri-hexagonal Star-of-David phases (green). Since the energy difference between these phases become smaller with increasing pressure, it is plausible that there is a transition from one to the other under pressure.
To elucidate which of these two CO phases is realized in Region I, we compute their densities of states (DOS). As shown in Fig. 4b, there are important differences between the DOS curves of the staggered tri-hexagonal phase (red), the superimposed tri-hexagonal Star-of-David phase (green), and the undistorted kagome lattice (black). In particular, the latter has a larger DOS at the Fermi level, as well as van Hove singularities (signaled by the central “satellite” peaks in the DOS) closer to the Fermi level, when compared to the red and green curves (the blue curve, referring to the planar tri-hexagonal phase, is also shown for completeness). In contrast, the red curve has the smallest Fermi level DOS and farthest separated van Hove singularity peaks among the three curves. While the mechanism for SC in CsV3Sb5 remains under debate, one generally expects that a higher Fermi-level DOS correlates with a higher Tc. Moreover, if van Hove singularities are important for the SC mechanism, it is reasonable to assume that the closer their peaks are to the Fermi level, the higher the Tc will be. If these assumptions hold for CsV3Sb5, then a possible explanation for the unusual double-peak SC dome revealed by our μSR data is a transition from the superimposed tri-hexagonal Star-of-David phase (green) in Region I to the staggered tri-hexagonal phase (red) in Region II. This is because the latter should compete more strongly with SC due to the larger reduction in the DOS and further separation between the van Hove peaks. Similarly, because the undistorted lattice (i.e. without CO) has the highest DOS, this would also account for Tc being the highest when all types of CO are suppressed at pc2.
Conclusion
Our results uncover two different regions in the part of the phase diagram of the kagome metal CsV3Sb5 where both charge order and superconductivity are present. Based on our DFT calculations, we propose that two distinct types of CO order are realized: a superimposed tri-hexagonal Star-of-David phase at low pressures and a staggered tri-hexagonal phase at intermediate pressures, before CO is fully suppressed. These charge orders display different degrees of competition with superconductivity, which leads to the complex phase diagram featuring a double-peak in the pressure dependence of both the superconducting transition temperature and the superfluid density. Throughout the pressure range investigated, the nodeless multigap nature of the superconducting state remains persistent, in contrast to KV3Sb5 and RbV3Sb5, where a nodal gap emerges at higher pressures24. Furthermore, we show that once charge order is fully suppressed, the superconducting state breaks time-reversal symmetry, which makes this compound, together with its K- and Rb-counterparts, one of the rare cases of unconventional superconductors with spontaneously broken time reversal symmetry.
Methods
Sample growth
Single crystals of CsV3Sb5 used for for this study were grown by using self-flux method from Cs ingots (purity 99.9%), V 3-N powder (purity 99.9%) and Sb grains (purity 99.999%)43. The detailed description about the growth and characterization of crystals is provided elsewhere20,44,45.
μSR experiment
Muon spin relaxation/rotation (μSR) measurements under pressure were performed at μE1 beam line using GPD spectrometer at Paul Scherrer Institute, Switzerland. This spectrometer is a dedicated worldwide unique instrument for carrying out high-pressure μSR experiments. For μSR experiments, 100% spin polarized muons μ+ are implanted inside the sample one by one, where the spin of muon will Larmor precess around the local magnetic field Bint at the muon site. Detailed description about the μSR technique can be found elsewhere.46,47 In case of a superconductor, the characteristic length scale namely penetration depth can be determined by probing the inhomogeneous field distribution of vortex lattice. Heliox cryostat with a He-3 insert was used to access temperature down to 250 mK. Pressure upto 1.9 GPa were achieved using low and pre-defined background double wall pressure cell made from MP35N/CuBe alloy, specifically designed for high-pressure experiments48,49. Single crystals of CsV3Sb5 were filled with random orientations inside the pressure cell in a compact cylindrical area of height 12 mm and diameter 6 mm. Daphne 7373 was used as a pressure medium to ensure the hydrostatic pressure conditions as it solidifies at much higher pressure ~2.5 GPa. Low-temperature values of pressures were determined by tracking the superconducting transition of Indium, measured using ac susceptibility experiments (Supplementary Note 1). The fraction of muon stopping inside the sample was maximized to ~40%.
We performed transverse-field (TF) and zero-field μSR experiments at different pressures. Pressure cell is surrounded by four detectors: Forward, backward, left, and right with muon initial spin parallel to its momentum. The TF-μSR experiments were performed in field cooled condition to get homogeneous vortex lattice formation. Approximately 106 positrons were recorded for each data point. The asymmetry vs. time spectra were analyzed using the open software package MUSRFIT50.
Analysis of λ(T)
The temperature variation of magnetic penetration depth λ−2(T) is analyzed within the local (London) approach using following expression51:
where \(f={(1+E/{k}_{{{{{{{{\rm{B}}}}}}}}}T)}^{-1}\) is the Fermi distribution function. The temperature and angular dependence of gap is given by Δ(T, ϕ) = Δ0δ(T/Tc)g(ϕ), where Δ0 is the gap value at 0 K, \(\delta (T/{T}_{{{{{{{{\rm{c}}}}}}}}})=\tanh \{1.821[1.018{({T}_{{{{{{{{\rm{c}}}}}}}}}/T-1)}^{0.51}]\}\) represents the temperature dependence of gap. The angular dependence of the gap is represented by g(ϕ), which adapts a value 1 for isotropic s- wave model. We have fitted the λ−2(T) data at various pressures by separating it into two gaps:
In the above equation, x is the weight factor of the bigger gap Δ0,1. Supplementary Fig. 3 shows the pressure dependence of the superconducting gaps (Δ0,1 and Δ0,2) (Supplementary Note 3). In the regions where SC and CO coexists, i.e. Region I and II, fitting was done by considering the weight factor x as a global parameter for all pressures in the mentioned regimes. Similarly, for Region III, the fitting was done by assuming x as a global parameter in that region. The data at intermediate pressure 1.68 GPa is fitted by considering a linear combination of Eq. 2 with parameter values fixed from that obtained for 1.54 GPa (corresponding to the SC + CO state) and 1.74 GPa (corresponding to the SC state).
Analysis of ZF relaxation rate
Λ(T) at various pressures are fitted with following empirical relation:
where T* is a characteristic temperature below which the increase in electronic relaxation starts. Λ0 is the relaxation value above Tc, and ΔΛ is the change in relaxation after entering into the superconducting ground state. In Region I and II, the value of n is considerably high (14 and 15 respectively) indicating the step like increase in the relaxation rate. On the other hand, in Region III, where CO suppress completely, the value of n is 1 suggesting a linear increase in λ(T) below T* which coincides with Tc. As discussed in the main text, we conclude that in region III, T* corresponds to the time reversal symmetry breaking transition TTRSB.
DFT calculations
All DFT calculations were performed using Projector Augmented Waves (PAW) as implemented in the Vienna Ab initio simulation package (VASP) version 5.4.452,53,54. We used the PBEsol exchange correlation functional, with valence configurations of 5s25p66s1, 3s23p63d44s1, and 5s25p3 corresponding to Cs, V, ans Sb, respectively. Lattice parameters were found to be converged to within 0.001 Å using a plane wave cutoff energy of 450 eV, a Monkhorst-Pack k-point mesh of 20 × 20 × 10 in the primitive cell, and a 2nd order Methfessel–Paxton smearing parameter of 10 meV55. Different phases have different specific volumes, and hence at finite pressure, the phase that minimizes the enthalpy, rather than the Kohn–Sham energy only, is the equilibrium structure at that volume.
Bilbao Crystallographic Server and tools therein were used for symmetry analysis of various theoretically obtained crystal structures56.
Data availability
The data supporting the findings of this study are available within the paper and in the Supplementary Information. The raw data are available from the corresponding authors upon reasonable request. The raw data can also be found at the following link: http://musruser.psi.ch/cgi-bin/SearchDB.cgi.
References
Neupert, T., Denner, M., Yin, J.-X., Thomale, R. & Hasan, M. Charge order and superconductivity in kagome materials. Nat. Phys. 18, 137 (2022).
K., Jiang, et al. Kagome superconductors AV3Sb5 (A = K, Rb, Cs). arXiv https://doi.org/10.48550/arXiv.2109.10809 (2021).
Mielke III, C. Time-reversal symmetry-breaking charge order in a correlated kagome superconductor. Nature 602, 245 (2022).
L., Yu, et al. Evidence of a hidden flux phase in the topological kagome metal CsV3Sb5. arXiv https://doi.org/10.48550/arXiv.2107.10714 (2021).
Q., Wu, et al. The large static and pump-probe kerr effect with two-fold rotation symmetry in kagome metal CsV3Sb5. arXiv https://doi.org/10.48550/arXiv.2110.11306 (2021).
Khasanov, R. Time-reversal symmetry broken by charge order in CsV3Sb5. Phys. Rev. Res. 4, 023244 (2022).
Wang, Z. Electronic nature of chiral charge order in the kagome superconductor CsV3Sb5. Phys. Rev. B 104, 075148 (2021).
Zhao, H. Cascade of correlated electron states in the kagome superconductor CsV3Sb5. Nature 599, 216–221 (2021).
Wang, N. Competition between charge-density-wave and superconductivity in the kagome metal RbV3Sb5. Phys. Rev. Res. 3, 043018 (2021).
Zhu, C. C. Double-dome superconductivity under pressure in the V-based kagome metals AV3Sb5 (A = Rb and K). Phys. Rev. B 105, 094507 (2022).
Du, F. Pressure-induced double superconducting domes and charge instability in the kagome metal KV3Sb5. Phys. Rev. B 103, L220504 (2021).
Yu, F. Unusual competition of superconductivity and charge-density-wave state in a compressed topological kagome metal. Nat. Commun. 12, 1 (2021).
Wang, Q. Charge density wave orders and enhanced superconductivity under pressure in the kagome metal CsV3Sb5. Adv. Mater. 33, 2102813 (2021).
Chen, K. Double superconducting dome and triple enhancement of Tc in the kagome superconductor CsV3Sb5 under high pressure. Phys. Rev. Lett. 126, 247001 (2021).
Zhang, Z. Pressure-induced reemergence of superconductivity in the topological kagome metal CsV3Sb5. Phys. Rev. B 103, 224513 (2021).
Brandt, E. Flux distribution and penetration depth measured by muon spin rotation in high-Tc superconductors. Phys. Rev. B 37, 2349 (1988).
Brandt, E. H. Properties of the ideal ginzburg-landau vortex lattice. Phys. Rev.B 68, 054506 (2003).
Xu, H.-S. Multiband superconductivity with sign-preserving order parameter in kagome superconductor CsV3Sb5. Phys. Rev. Lett. 127, 187004 (2021).
Duan, W. Nodeless superconductivity in the kagome metal CsV3Sb5. Sci. China Phys. Mech. Astron. 64, 1 (2021).
Gupta, R. Microscopic evidence for anisotropic multigap superconductivity in the CsV3Sb5 kagome superconductor. npj Quantum Mater. 7, 1 (2022).
Nakayama, K. Multiple energy scales and anisotropic energy gap in the charge-density-wave phase of the kagome superconductor CsV3Sb5. Phys. Rev. B 104, L161112 (2021).
Das, D. Unconventional pressure dependence of the superfluid density in the nodeless topological superconductor α- PdBi2. Phys. Rev. lett. 127, 217002 (2021).
Uemura, Y. J. Universal correlations between Tc and \(\frac{{n}_{s}}{{m}^{* }}\) (carrier density over effective mass) in high-Tc cuprate superconductors. Phys. Rev. Lett. 62, 2317 (1989).
Guguchia, Z. et al. Tunable nodal kagome superconductivity in charge ordered RbV3Sb5. arXiv https://doi.org/10.48550/arXiv.2202.07713 (2022).
Mielke, C. Nodeless kagome superconductivity in LaRu3Si2. Phys. Rev. Mater. 5, 034803 (2021).
Luke, G. M. Time-reversal symmetry-breaking superconductivity in Sr2RuO4. Nature 394, 558 (1998).
Grinenko, V. Split superconducting and time-reversal symmetry-breaking transitions in Sr2RuO4 under stress. Nat. Phys. 17, 748 (2021).
Grinenko, V. et al. Unsplit superconducting and time reversal symmetry breaking transitions in Sr2RuO4 under hydrostatic pressure and disorder, Nat. Commun. 12, 3920 (2021).
Luke, G. Muon spin relaxation in UPt3. Phys. Rev. Lett. 71, 1466 (1993).
Hillier, A. D., Quintanilla, J. & Cywinski, R. Evidence for time-reversal symmetry breaking in the noncentrosymmetric superconductor LaNiC2. Phys. Rev. Lett. 102, 117007 (2009).
Biswas, P. K. Chiral singlet superconductivity in the weakly correlated metal LaPt3P. Nat. Commun. 12, 1 (2021).
Kubo, R. & Toyabe, T. Magnetic Resonance and Relaxation (North-Holiand Publishing Company, 1967).
Ratcliff, N., Hallett, L., Ortiz, B. R., Wilson, S. D. & Harter, J. W. Coherent phonon spectroscopy and interlayer modulation of charge density wave order in the kagome metal CsV3Sb5. Phys. Rev. Mater. 5, L111801 (2021).
Denner, M. M., Thomale, R. & Neupert, T. Analysis of charge order in the kagome metal AV3Sb5 (A = K,Rb,Cs). Phys. Rev. Lett. https://doi.org/10.1103/PhysRevLett.127.217601 (2021).
Feng, X., Jiang, K., Z., Wang, Z. & J., Hu. Chiral flux phase in the kagome superconductor AV3Sb5, Sci. Bullet. https://doi.org/10.1016/j.scib.2021.04.043 (2021).
Lin, Y.-P. & Nandkishore, R. M. Complex charge density waves at van hove singularity on hexagonal lattices: Haldane-model phase diagram and potential realization in the kagome metals AV3Sb5 (A = K, Rb, Cs). Phys. Rev. B 104, 045122 (2021).
Christensen, M. H., Birol, T., Andersen, B. M. & Fernandes, R. M. Theory of the charge density wave in AV3Sb5 kagome metals. Phys. Rev. B 104, 214513 (2021).
Subedi, A. Hexagonal-to-base-centered-orthorhombic 4Q charge density wave order in kagome metals KV3Sb5, RbV3Sb5, and CsV3Sb5. Phys. Rev. Materials 6, 015001 (2022).
Park, T., Ye, M. & Balents, L. Electronic instabilities of kagome metals: Saddle points and landau theory. Phys. Rev. B 104, 035142 (2021).
Cho, S. Emergence of new van hove singularities in the charge density wave state of a topological kagome metal RbV3Sb5. Phys. Rev. Lett. 127, 236401 (2021).
Qian, T. Revealing the competition between charge density wave and superconductivity in CsV3Sb5 through uniaxial strain. Phys. Rev. B 104, 144506 (2021).
Zhang, J.-F., Liu, K. & Lu, Z.-Y. First-principles study of the double-dome superconductivity in the kagome material CsV3Sb5 under pressure. Phys. Rev. B 104, 195130 (2021).
Yin, Q. Superconductivity and normal-state properties of kagome metal RbV3Sb5 single crystals. Chinese Phys. Lett. 38, 037403 (2021).
Ortiz, B. R. CsV3Sb5: A Z2 topological kagome metal with a superconducting ground state. Phys. Rev. Lett. 125, 247002 (2020).
Ortiz, B. R. New kagome prototype materials: discovery of KV3Sb5, RbV3Sb5, and CsV3Sb5. Phys. Rev. Mater. 3, 094407 (2019).
Yaouanc, A. & Reotier, P. D. de. Muon. Spin Rotation, Relaxation, and Resonance: Applications to Condensed Matter Vol. 147 (Oxford University Press, 2011).
Hillier, A. D. Muon spin spectroscopy. Nat. Rev. Method Primers 2, 4 (2022).
Shermadini, Z. A low-background piston–cylinder-type hybrid high pressure cell for muon-spin rotation/relaxation experiments. High Press. Res. 37, 449 (2017).
Khasanov, R. High pressure research using muons at the paul scherrer institute. High Press. Res. 36, 140 (2016).
Suter, A. & Wojek, B. Musrfit: A free platform-independent framework for μSR data analysis. Phys. Procedia 30, 69 (2012).
Serventi, S. Effect of two gaps on the flux-lattice internal field distribution: evidence of two length scales in Mg1−xAlxB2 from μSR. Phys. Rev. Lett. 93, 217003 (2004).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558 (1993).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Methfessel, M. & Paxton, A. High-precision sampling for brillouin-zone integration in metals. Phys. Rev. B 40, 3616 (1989).
Aroyo, M. I. Crystallography online: Bilbao crystallographic server. Bulgarian Chem. Commun. 43, 183 (2011).
Acknowledgements
We thank B. Andersen and M. Christensen for fruitful discussions. μSR experiments were performed at the Swiss Muon Source (SμS), Paul Scherrer Institute (PSI), Switzerland. H.L. was supported by National Key R&D Program of China (Grant No. 2018YFE0202600) and the Beijing Natural Science Foundation (Grant No. Z200005). T.B. and E.T.R. were supported by the NSF CAREER grant DMR-2046020. RMF (theory) was supported by the Air Force Office of Scientific Research under award number FA9550-21-1-0423.
Author information
Authors and Affiliations
Contributions
R.G., D.D., C.M., Z.G., F.H., and R.K. performed μSR experiments. R.G., D.D. and R.K. analyzed the μSR data. Q.Y., Z.T., C.G., and H.L. synthesized and characterized samples. R.M.F., T.B., and E.T.R. performed the theoretical analysis. R.K. and H.L. supervised the work at PSI. R.G., D.D., Z.G., and R.M.F. prepared the manuscript with notable inputs from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gupta, R., Das, D., Mielke, C. et al. Two types of charge order with distinct interplay with superconductivity in the kagome material CsV3Sb5. Commun Phys 5, 232 (2022). https://doi.org/10.1038/s42005-022-01011-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-01011-0
This article is cited by
-
Tuning of the flat band and its impact on superconductivity in Mo5Si3−xPx
Nature Communications (2024)
-
Superconducting diode effect and interference patterns in kagome CsV3Sb5
Nature (2024)
-
Evidence for time-reversal symmetry-breaking kagome superconductivity
Nature Materials (2024)
-
Pressure evolution of electron dynamics in the superconducting kagome metal CsV3Sb5
npj Quantum Materials (2023)
-
Bulk evidence of anisotropic s-wave pairing with no sign change in the kagome superconductor CsV3Sb5
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.