Introduction

Optical manipulation of materials has emerged as a powerful tool in engineering material properties on demand. A striking instance is the phenomenon of photo-induced superconductivity, in which superconductor-like behavior is observed after photoexcitation at temperatures far higher than the equilibrium transition temperature1. This effect has now been demonstrated experimentally in many different systems, including high-Tc cuprates2,3,4,5,6,7,8, iron-based superconductors9, fullerene superconductor K3C6010,11, and organic superconductor (BEDT-TTF)2Cu[N(CN)2]Br12. However, a theoretical explanation for this effect in each system is still subject to intense debate, with most interpretations coming essentially in three flavors.

The first class of theoretical ideas suggests that photoexcitation of the material leads to quasi-static modifications of the effective Hamiltonian13,14,15,16,17,18,19,20,21: examples include light distortion of the crystal lattice likely favoring superconductivity13 or melting of a competing charge density wave (CDW)6,22,23,24, which can even lead to metastable superconductivity6. The second approach argues that optical pumping provides a cooling mechanism for quasiparticles that allows signatures of superconductivity to persist up to higher temperatures25,26,27,28,29,30,31. The third interpretation has a Floquet-like out-of-equilibrium character32,33,34,35,36,37,37,38,39,40,41,42,43,44,45,46,47,48, where photoexcitation results in a parametric amplification of superconducting fluctuations.

Regarding the first category of theories, several experimental observations suggest that photo-induced superconductivity involves phenomena beyond simple modifications of the effective static Hamiltonian, and dynamical aspects play a crucial role. First, in the light-induced superconducting state of K3C60, the reflection coefficient exceeded unity. This observation indicates a type of light amplification not accessible in equilibrium38. Second, in the superconducting state of YBCO, pump-induced changes in reflectivity included a new peak at a frequency higher than the equilibrium Josephson plasmon (JP) edge2. Third, in the pseudogap state of YBCO, pumping leads to the appearance of the JP edge-like feature even though in equilibrium reflection coefficient appeared featureless49. Finally, recent experiments demonstrated exponential growth of JPs in YBCO following pump pulse both below and above Tc50.

Although the second class of ideas embodies a non-equilibrium character, to date, these ideas fail to provide a simple, intuitive interpretation of the mentioned experiments. On the other hand, all the experimental observations are well understood from the third theoretical approach that is based on periodically driven systems. Specifically, one starts by assuming that the pump pulse excites a collective mode, which in turn acts as a parametric drive to amplify low-energy plasmon excitations. From the perspective of nonlinear non-equilibrium optics, using the Floquet generalization of the Fresnel formalism, one can readily explain light amplification, enhancement of overdamped JPs, and appearance of new peaks and Fano-like features in reflectivity37,38,51.

The key to this Floquet picture is the existence of a coherently oscillating collective mode. Possible candidates can be a phonon that has been resonantly excited by light or an excited Higgs mode38,52,53, representing an order parameter amplitude fluctuation. In d-wave cuprate superconductors, the Higgs mode is unlikely an option because it is expected to have high energy and to be strongly damped due to nodal quasiparticles (for dynamical aspects related to the Higgs mode, see refs. 52,53,54,55,56,57,58,59). Therefore, the crucial question is whether, without resonantly exciting relevant collective modes, we can still expect well-defined low-frequency oscillations that follow impulsive photoexcitation, such as commonly used optical pumping at 1.55 eV5,6,8,9. The central result of our paper is that in systems with low-energy Josephson plasmons, such as in cuprates where the c-axis plasmon gap is in the terahertz range, long-lived oscillations generally occur even without resonant driving. Remarkably, the conversion of an incoherent pump to periodic dynamics is found both below and above the superconducting transition temperature, in both isotropic and anisotropic superconductors.

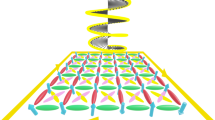
Before we turn to a detailed analysis, we first provide a physical picture of the mechanism that yields these oscillations despite incoherent photoexcitation. The key ingredient is plasmons in superconductors, representing fluctuations of the order parameter phase coupled to fluctuations of the electromagnetic field in the sample. This coupling renders plasmons to acquire a gap (Fig. 1) through the Anderson-Higgs mechanism60, which is closely related to the Meissner effect in static systems. In conventional superconductors, the plasmon gap is a large energy scale, it exceeds the quasiparticle gap, so that one often disregards the phase fluctuations. However, this scenario does not hold in a number of superconductors that exhibit light-induced superconducting behavior. For example, in K3C60, an isotropic three-dimensional superconductor, the plasmon gap is only about 20 THz38. Thus, the phase fluctuations might be essential there61,62. Besides, in cuprates, the strong anisotropy due to the layered crystal structure dramatically renormalizes the c-axis plasmon gap to be of the order of 1−2 THz, rendering Josephson plasmons the primary lowest-energy excitations.

Fig. 1: Summary of the main results.
figure 1

a The two building blocks of the effective description of non-equilibrium superconductors are the order parameter and the electromagnetic field in the sample, and the two entities are coupled. Upon photoexcitation, the electromagnetic field displays periodic fluctuation evolution, even if the order parameter dynamics is overdamped. b, c Schematic spectra of plasmons, which are gapped due to the Anderson-Higgs mechanism. Prior to photoexcitation (b), the plasmon distribution function is thermal; the thin blue curve captures the low occupation numbers. After photoexcitation (c), these plasmons proliferate (shown by the thick red-orange curve) through the creation of momentum-conserving pairs. d, e Schematics of time evolution of the electric field in the sample, which always has a zero expectation value. In equilibrium (d), the electric field has a non-zero thermal variance \({\langle {{{{{{{{\boldsymbol{E}}}}}}}}}^{2}\rangle }_{eq}\). After an impulsive optical quench (e), this variance becomes periodically modulated, with the frequency 2ωp being twice the plasmon gap.

Full size image

Motivated by d-wave cuprate superconductors, here we restrict the discussion to overdamped order parameter dynamics so that the Higgs-amplitude mode is strongly damped in our modeling. Despite this, we will demonstrate that the electromagnetic fluctuations in the sample exhibit coherent, oscillatory dynamics as they couple to the order parameter phase ([Fig. 1a). We consider photoexcitation with an ultrashort laser pulse, which is not tuned to a specific frequency and is not resonant with any eigenmode in the original system. The laser frequency is assumed to be much larger than any frequency of the relevant collective modes. Such an impulsive optical quench couples only to symmetry-even modes and, in particular, results in the proliferation of plasma fluctuations through the generation of momentum conserving plasmon pairs (Fig. 1c). Remarkably, even though the average electric field in the sample remains zero, the electromagnetic energy density exhibits well-defined oscillations at a frequency twice the plasmon gap (Fig. 1e). Such oscillations are well understood as two-plasmon impulsive stimulated Raman scattering, similar to what has been done for pairs of squeezed phonons in ferroelectrics63. The plasmons do not merely “heat up” after the photoexcitation, as their vacuum state is also being coherently squeezed (Fig. 1d, e). Physically, this phenomenon is analogous to exciting electromagnetic modes in a cavity with moving mirrors64,65,66. In the latter case, the system builds up strong electric field fluctuations with random phases. As a result, averaging over ensemble gives zero expectation value of the field but a non-zero energy density. A special feature of our system is the finite gap in the plasmon spectrum. Even though a whole continuum of (k, − k)-plasmon pairs gets excited, the total energy density picks up the net periodic dynamics with frequency twice the spectrum gap.

Results and discussion

To study the post-pulse evolution in both isotropic and anisotropic superconductors, we employ the time-dependent Ginzburg-Landau (TDGL) equation for overdamped stochastic dynamics of the superconducting order parameter67,68. We restore the gauge invariance through minimal coupling and use Maxwell’s equations for the electromagnetic field dynamics. We derive self-consistent dynamical equations for the order parameter, electromagnetic field, and their fluctuations to solve the stochastic equations. In this work, we aim to provide a physical picture of the interplay of light and matter degrees of freedom rather than to present a full microscopic description of the post-pulse evolution, which goes beyond our effective theory and requires the knowledge of, for instance, the dynamics of the quasiparticle distribution function68.

The TDGL approach has been widely used to understand non-equilibrium properties of superconductors69,70,71,72,73,74,75,76,77,78,79,80,81,82. In contrast to previous theoretical works, which neglect electromagnetic fluctuations because of a large plasmon gap, we treat the order parameter and the electromagnetic field on an equal footing because important classes of superconductors that exhibit light-induced superconductivity above Tc have a relatively small plasmon gap. This model is a non-perturbative theory that takes into account fluctuations at all relevant length scales and allows us to make experimentally verifiable predictions for a broad class of superconductors. Below we first outline in detail our theoretical approach and then present our main findings.

Equations of motion

To describe light-driven dynamics in layered materials, we employ a two-fluid model of superconductivity, where the superconducting fluid is coupled to the normal fluid of electrons through Maxwell’s equations83.

Superconducting fluid

The spontaneous symmetry breaking is described via the anisotropic gauge-invariant Ginzburg-Landau free energy (throughout the paper, we set ℏ = kB = 1):

$${{{{{{{\mathcal{F}}}}}}}}[\psi ]\, = \int {d}^{3}{{{{{{{\boldsymbol{r}}}}}}}}\left[\frac{1}{2{m}_{ab}}{\left|\left(-i{\nabla }_{ab}-\frac{{e}^{* }}{c}{{{{{{{{\boldsymbol{A}}}}}}}}}_{ab}\right)\psi \right|}^{2}\right.\\ + \left.\frac{1}{2{m}_{c}}{\left|\left(-i{\partial }_{z}-\frac{{e}^{* }}{c}{A}_{z}\right)\psi \right|}^{2}+\alpha | \psi {| }^{2}+\frac{\beta }{2}| \psi {| }^{4}\right].$$
(1)

Here α and β are the usual Landau parameters of the Mexican hat potential. mab and mc are the in-plane and out-of-plane Cooper pair masses, respectively. e* = 2e is the Cooper pair charge. The anisotropy parameter is defined as \(\gamma =\sqrt{{m}_{c}/{m}_{ab}}\): γ ≫ 1 in cuprates and γ = 1 for isotropic superconductors such as K3C60. In Eq. (1), the gauge-invariance is imposed through minimal coupling to the vector potential A = (Aab, Az). The order parameter dynamics is assumed to be overdamped (model A in the classification of ref. 67):

$$\tau \left[{\partial }_{t}+i\left({e}^{* }\phi +\delta \mu \right)\right]\psi ({{{{{{{\boldsymbol{r}}}}}}}},t)=-\frac{\delta {{{{{{{\mathcal{F}}}}}}}}}{\delta {\psi }^{* }({{{{{{{\boldsymbol{r}}}}}}}},t)}+\eta ({{{{{{{\boldsymbol{r}}}}}}}},t),$$
(2)

where the noise correlation function reads:

$$\langle {\eta }^{* }({{{{{{{{\boldsymbol{r}}}}}}}}}_{1},{t}_{1})\eta ({{{{{{{{\boldsymbol{r}}}}}}}}}_{2},{t}_{2})\rangle =2T\tau \delta ({{{{{{{{\boldsymbol{r}}}}}}}}}_{1}-{{{{{{{{\boldsymbol{r}}}}}}}}}_{2})\delta ({t}_{1}-{t}_{2}).$$
(3)

Here τ is a dimensionless coefficient characterizing the order parameter relaxation time. ϕ is the scalar potential; we choose the gauge where it is zero. The term with δμ = χ−1δρ, called electrochemical potential, describes the coupling between charge fluctuations δρ and the order parameter phase. χ represents the compressibility, a phenomenological parameter in our approach. The superconducting electric current density is given by:

$${j}_{s,\alpha }={\hat{m}}_{\alpha \beta }^{-1}\left[\frac{{e}^{* }}{2}{\psi }^{* }\left(-i{\partial }_{\beta }-\frac{{e}^{* }}{c}{A}_{\beta }\right)\psi +c.c.\right],$$
(4)

where \({\hat{m}}^{-1}=\,{{\mbox{diag}}}\,({m}_{ab}^{-1},{m}_{ab}^{-1},{m}_{c}^{-1})\) defines the mass tensor. We remark that in certain superconductors, such as K3C60, and well below T ≪ Tc, the coherent Higgs mode, neglected in Eq. (2), might be more essential than the plasma excitations. We relegate the study of such a situation, particularly the interplay between photoexcited Josephson plasmons and coherent Higgs oscillations, to future work.

Normal fluid

The normal current density reads

$${{{{{{{{\boldsymbol{j}}}}}}}}}_{n}=\hat{\sigma }({{{{{{{\boldsymbol{E}}}}}}}}-\nabla \delta \mu /{e}^{* })+{{{{{{{\boldsymbol{\xi }}}}}}}},$$
(5)

where \(\hat{\sigma }=\,{{\mbox{diag}}}\,({\sigma }_{ab},{\sigma }_{ab},{\sigma }_{c})\) is the normal-state conductivity tensor, assumed to be momentum- and frequency-independent. We included the Johnson-Nyquist noise to enforce the fluctuation-dissipation theorem84:

$$\langle {\xi }_{\alpha }({{{{{{{{\boldsymbol{r}}}}}}}}}_{1},{t}_{1}){\xi }_{\beta }({{{{{{{{\boldsymbol{r}}}}}}}}}_{2},{t}_{2})\rangle =2{\sigma }_{\alpha \beta }T\delta ({{{{{{{{\boldsymbol{r}}}}}}}}}_{1}-{{{{{{{{\boldsymbol{r}}}}}}}}}_{2})\delta ({t}_{1}-{t}_{2}).$$
(6)

Note that we neglected the relaxation of the normal current density, an approximation valid at low frequencies \(\omega \, \lesssim \, {\tau }_{{{{{{{{\rm{mf}}}}}}}}}^{-1}\), where τmf is the mean-free time. The charge conservation is expressed through the continuity equation:

$$\frac{\partial \delta \rho }{\partial t}+\nabla \cdot (\,{{{{{{{{\boldsymbol{j}}}}}}}}}_{n}+{{{{{{{{\boldsymbol{j}}}}}}}}}_{s})=0.$$
(7)

The Maxwell equations

In the gauge where the scalar potential is zero: \({{{{{{{\boldsymbol{E}}}}}}}}=-\frac{1}{c}{\partial }_{t}{{{{{{{\boldsymbol{A}}}}}}}}\) and B = ∇ × A. The remaining Maxwell equations read:

$$\nabla \cdot {{{{{{{\boldsymbol{E}}}}}}}}=4\pi \delta \rho ,$$
(8)
$$\nabla \times {{{{{{{\boldsymbol{B}}}}}}}}=\frac{1}{c}\frac{\partial {{{{{{{\boldsymbol{E}}}}}}}}}{\partial t}+\frac{4\pi }{c}(\,{{{{{{{{\boldsymbol{j}}}}}}}}}_{n}+{{{{{{{{\boldsymbol{j}}}}}}}}}_{s}).$$
(9)

Theory of dynamical Gaussian fluctuations

The above equations of motion can be formulated as stochastic first-order equations on eight real physical degrees of freedom q = (ψ1, ψ2, A, E), where ψ = ψ1 + iψ2. One can then write a single first-order Fokker-Planck equation on the cumulative distribution functional \({{{{{{{\mathcal{P}}}}}}}}[t;{{{{{{{\boldsymbol{q}}}}}}}}]\). One of the simplifications we employ in this work is that we assume that \({{{{{{{\mathcal{P}}}}}}}}\) remains Gaussian throughout the time evolution, i.e., \({{{{{{{\mathcal{P}}}}}}}}\) is fully characterized by time-dependent expectation values 〈q〉(t) and instantaneous correlators \({\langle {q}_{\alpha }({{{{{{{{\boldsymbol{r}}}}}}}}}_{1},t){q}_{\beta }({{{{{{{{\boldsymbol{r}}}}}}}}}_{2},t)\rangle }_{c}\). We further assume that the system is homogeneous in space so that in momentum space, one only has correlators of type \({\langle {q}_{\alpha }(-{{{{{{{\boldsymbol{k}}}}}}}},t){q}_{\beta }({{{{{{{\boldsymbol{k}}}}}}}},t)\rangle }_{c}\). The main technical result of this work is that we derive the first-order equations of motion on all of those correlators. The derivation, together with the final form of equations of motion, are relegated to the Supplementary Information, Supplementary Note 3 in particular. The obtained set of equations allows us to investigate fluctuating dynamics after photoexcitation events numerically.

Quenching protocol

We turn to discuss an impulsive optical quench. The effect of such incoherent photoexcitation is either to suddenly partially suppress the superconducting amplitude (Scenario I in Fig. 2) or to promptly perturb the superconducting free energy potential (Scenario II in Fig. 2). Scenario I captures quick condensate depletion as the laser pulse melts some of the Cooper pairs. In this scenario, the order parameter displays abrupt dynamics during the pump pulse but then evolves slowly on the time scale controlled by the TDGL relaxation time τ, cf. Eq. (2). Scenario II neglects partial condensate evaporation and describes photoexcitation as a sudden change to the coefficients of the Ginzburg-Landau free energy. The order parameter reacts relatively smoothly to this perturbation. In real materials, both scenarios are expected to play a role. Our numerical analysis of photoexcitation dynamics indicates that they give similar post-pulse phenomenology. For concreteness, throughout the rest of the paper, we primarily focus on the Scenario II [see Supplementary Note 5 for further discussion of Scenario I]. Specifically, we consider quenches in the quadratic coefficient α(t) of the free energy of the form:

$$\alpha (t)={\alpha }_{0}+\delta \alpha \exp (-t/{\tau }_{\alpha })\theta (t).$$
(10)

Here α0 is the pre-pulse value. δα encodes the strength of the photoexcitation. The case δα > 0 describes transient suppression of superconductivity and could be due to laser-heating of quasiparticles. The situation with δα < 0 represents transiently enhanced superconductivity and could arise in superconductors with competing orders, such as spin or charge density waves, which become suppressed by the photoexcitation. θ(t) is the Heaviside step function. τα is a phenomenological relaxation rate. One can easily generalize the present framework to various possible quenching protocols, including quenches in the sample temperature or modification of the dynamics in α(t) (for instance, use the Rothward-Taylor approach85). Regardless of the specific impulsive quenching protocol, our conclusions are insensitive to the functional form in Eq. (10).

Fig. 2: Theoretical modeling of an impulsive optical quench.
figure 2

We consider two situations: the laser pulse partially suppresses the order parameter expectation value (I) or it affects the coefficients of the Ginzburg-Landau free energy (II).

Full size image

We remark that, in case the laser frequency is comparable to those of the relevant collective modes, one might be interested in quenches of the external electromagnetic field that directly affects order parameter dynamics81. We leave the study of these quenches to future work.

Equilibrium collective modes

To understand how photoexcitation leads to coherent dynamics involving pairs of plasmons, we first establish the frequency of plasmons. Simple mean-field analysis shows that in anisotropic superconductors, the equilibrium c-axis JP gap is given by (see Supplementary Note 2):

$${\omega }_{c}=\sqrt{\frac{4\pi {({e}^{* })}^{2}}{{\gamma }^{2}{m}_{ab}}| \langle \psi \rangle {| }^{2}-{(2\pi {\sigma }_{c})}^{2}}-2\pi {\sigma }_{c}i.$$
(11)

Here 〈ψ〉 is the order parameter expectation value. This formula suggests that plasmons are present only below Tc, where 〈ψ〉 ≠ 0. However, one does expect that JPs constitute collective modes of the system above Tc as well. Within the Gaussian approximation, the plasmon frequency is given by a formula similar to Eq. (11) but with ∣〈ψ〉∣2 replaced by 〈∣ψ∣2〉. This equilibrium average of the square of the order parameter amplitude contains contributions from both the long-range expectation value 〈ψ〉 as well as from superconducting fluctuations. The Gaussian approximation, however, underestimates the JP dephasing arising from statistical fluctuations of the phase of the local superconducting order parameter. In the context of JPs in the vortex liquid state, this question has been analyzed by Koshelev and Bulaevskii86, who found that the lifetime of plasmons becomes shorter as the superconducting correlation length decreases.

Following these analyses, we expect to find three regimes of JP dynamics, as shown in Fig. 3a. (i) For T ≤ Tc, the plasmons develop due to the non-zero order parameter expectation value 〈ψ〉 ≠ 0. (ii) For moderate temperatures above Tc, Tc < T ≤ T*, the long-range coherence is absent 〈ψ〉 = 0, but strong superconducting fluctuations, as measured by 〈∣ψ∣2〉, provide large local superconducting amplitude and sufficiently long correlation length. In this case, we expect to find JPs with a frequency that is still larger than their decay rate. In the discussion below, we employ the Gaussian approximation to analyze plasmon dynamics in this regime, which we call pseudogap. Plasmon dissipation arising from scattering on statistical fluctuations of the order parameter86 can be included by renormalizing the effective normal fluid conductivity σc. (iii) For T > T*, plasmons become strongly overdamped. We remark that frequencies of the two other ab-plasmons are determined by the in-plane superfluid density, and for γ ≫ 1, they should have much larger energies and hence stronger damping. For this reason, we will not discuss them in the current paper.

Fig. 3: Post-pulse dynamics in isotropic superconductors.
figure 3

a Schematic phase diagram. Depending on model parameters, there exist three regimes: (i) for T ≤ Tc, the long-range order parameter expectation value is non-zero 〈ψ〉 ≠ 0, the plasmon gap is notable, and plasmon dynamics is coherent; (ii) Tc < T ≤ T*, no long-range order is present 〈ψ〉 = 0, but superconducting equilibrium fluctuations, as captured by 〈∣ψ∣2〉, are sufficiently strong, and the correlation length is sufficiently long so that plasmons are still essentially coherent excitations; (iii) T* < T, plasmons become overdamped. Quenches in I are shown in panels (d): the order parameter evolution (left), encoded in 〈∣ψ∣2〉(t), looks overdamped; in contrast, for t ≳ 1, we find that the electromagnetic field, as captured by \(\langle {{{{{{{{\boldsymbol{E}}}}}}}}}^{2}\rangle (t)-{\langle {{{{{{{{\boldsymbol{E}}}}}}}}}^{2}\rangle }_{eq}\), shows periodic dynamics (middle). The frequency of the oscillations, regardless of photosuppression or photostimulation of superconductivity, equals twice the plasmon equilibrium frequency 2ωp, as shown in the right panel, where we performed the fast Fourier transform (F.F.T.) of the tails of the curves in the middle panel, with an exponential fit subtracted. The stronger the photoexcitation, the larger the amplitude of oscillations. Quenches in II are shown in panels (c). The post-pulse evolution here is similar to quenches in I, since plasmons still represent coherent excitations in equilibrium due to the strong superconducting fluctuations. b Interestingly, provided the order parameter relaxation rate is small, one can get periodic dynamics in III via strong photostimulation of superconductivity: the post-pulse dynamics of the electromagnetic field displays oscillations, though with poorly defined frequency. This is because 〈∣ψ∣2〉(t), the quantity that defines the plasmon frequency, is changing in time. Besides this, the quasiparticle conductivity is large, which makes the oscillations to be damped, cf. Eq. (11). Parameters used: τ = 100, τE = 5, τα = 1, χ−1 = 0.1, κ = 5, σ = 1, Tr0 = 10−2 (b); τ = 5, τE = 1, τα = 1, χ−1 = 0.1, κ = 5, σ = 0.1, Tr0 = 10−2 (c); τ = 1, τE = 1, τα = 0.2, χ−1 = 0.1, κ = 25, σ = 0.1, Tr0 = 10−2 (d)—see Supplementary Note 1 for more details.

Full size image

Primary results

We first investigate photoexcitation dynamics in the symmetry-broken phase in isotropic superconductors. The summary of our results is shown in Fig. 3d. Let us discuss photo-enhancement of superconductivity first, corresponding to quenches with δα < 0, cf. Eq. (10). In response to such a pump pulse, 〈∣ψ∣2〉(t) is first transiently enhanced (t ≲ 0.2) and then quickly returns to its equilibrium value [see Supplementary Note 4 for more details]. The stronger the photoexcitation, the stronger this quantity develops. We also find that the recovery is exponential, in contrast to the slow power-law dynamics in incommensurate CDWs87. The character of the recovery is determined by the equilibrium collective modes: For superconductors, the plasmons are gapped, resulting in a quick exponential recovery, while it is gapless phasons (Goldstone modes) that are responsible for the slow evolution in CDWs. Now we turn to the dynamics of the electromagnetic field, which shows additional features. While the ensemble averaged electric field in the sample remains zero 〈E〉(t) = 0 (a homogeneous quench cannot result in the development of non-zero electric field since fluctuations with ±E are equally likely), the evolution of electromagnetic fluctuations, as captured by \(\langle {{{{{{{{\boldsymbol{E}}}}}}}}}^{2}\rangle (t)-{\langle {{{{{{{{\boldsymbol{E}}}}}}}}}^{2}\rangle }_{eq}\), is governed by three stages: (i) initial enhancement, signaling plasmon proliferation; (ii) transient suppression below the equilibrium value; and (iii) recovery. The second stage can be understood as follows. Since at longer times 〈∣ψ∣2〉(t) exceeds its equilibrium value and since this quantity determines the plasmon frequency at equilibrium, it renders the plasmons to be energetically costly, resulting in their eventual depopulation. Most remarkably, as 〈E2〉(t) recovers, it acts as a Raman mode and oscillates with a frequency twice the plasmon gap 2ωp [Eq. (11) with γ = 1]. We note that for the case of photosuppression of superconductivity, corresponding to quenches with δα > 0, the phenomenology of the transient dynamics is “flipped” compared to the case of photo-enhancement, but oscillations are still present.

Quenches in the pseudogap phase are shown in Fig. 3c, and we find that the phenomenology of transient dynamics is similar to that in the symmetry-broken phase. There are two qualitative differences: the plasmon frequency in the pseudogap phase might be notably smaller, and the plasmon lifetime is shorter since σ increases with increasing temperature. Above Tc, the order parameter expectation value 〈ψ〉 = 0 remains zero, even for quenches into the symmetry-broken phase. We conclude that in order to gain oscillatory dynamics, it is sufficient to have appreciable superconducting fluctuations rather than long-range coherence.

Since there are no coherent collective modes at equilibrium for T > T*, it would be compelling if one could induce periodic dynamics via photoexcitation, i.e., by putting the system out-of-equilibrium. Such a situation might indeed occur provided the order parameter relaxation rate is small [see Supplementary Note 6 for additional discussion], as shown in Fig. 3b. The possibility of achieving oscillatory evolution with strong photoexcitation, in an otherwise incoherent system, warrants further experimental studies.

Of particular experimental interest are cuprates, layered superconductors with the c-axis Josephson plasmon gap being in the terahertz range and γ ≫ 1. Furthermore, these materials have small out-of-plane quasiparticle conductivity, which renders the c-axis plasmons long-lived. Figure 4 shows our results for quenches in anisotropic superconductors. Similarly to the isotropic situation, the order parameter dynamics remains overdamped, regardless of the quenching protocol (Fig. 4a). We also find that the in-plane electric field displays no signatures of coherent evolution (Fig. 4b) (we recall that the in-plane plasmon gap is a large energy scale). However, the out-of-plane electric field, as captured by \(\langle {E}_{c}^{2}\rangle (t)-{\langle {E}_{c}^{2}\rangle }_{eq}\), demonstrates lasting oscillatory dynamics (Fig. 4d), with twice the c-axis Josephson plasmon frequency (Fig. 4c), 2ωc. Since it is natural to have small out-of-plane conductivity in anisotropic materials, we conclude that cuprates are promising materials to test our findings experimentally.

Fig. 4: Photoexcitation dynamics in anisotropic superconductors in the pseudogap phase above Tc.
figure 4

a Evolution of 〈∣ψ∣2〉(t) looks overdamped regardless of the quenching conditions. b Similarly, the in-plane electric field also displays overdamped dynamics due to the large in-plane plasmon gap ωab ≫ ωc. c, d In contrast, the out-of-plane electric field variance exhibits oscillations with frequency 2ωc (d), as shown in F.F.T. analysis in (c). These oscillations are long-lived because the out-of-plane normal conductivity σc is small. Parameters used: τ = 5, τE = 10−2, τα = 0.1, χ−1 = 0, κ = 103, σab = 0.1, σc = 10−5, Tr0 = 10−3, γ = 10.

Full size image

For experimental detection of these coherent dynamics, it is important to characterize the amplitude and the lifetime of the bi-plasmon oscillations, which can be affected by the quenching conditions. A stronger laser pulse, as encoded in ∣δα∣, would lead to a greater number of low momenta plasmons. As these plasmons are responsible for the periodic dynamics, there would be a larger amplitude of the oscillatory dynamics. Our simulations indicate that this amplitude grows linearly with the pulse strength. In isotropic superconductors, where the separation between longitudinal and transverse modes is possible, the former are excited stronger and constitute the primary source of temporal oscillations of the electric field variance. In anisotropic materials, such separation is not possible away from high symmetry directions, and all modes contribute to the bi-plasmon oscillations. In such systems, a different consideration is crucial for understanding which JPs are excited by the pulse: modes with larger in-plane currents have stronger damping due to the large anisotropy of the normal fluid conductivity. Dynamics of individual momentum components, n(q, t) = 〈E(−q, t) ⋅ E(q, t)〉, show that the strength of their oscillations, for example at q = 0, can even exceed the value of equilibrium fluctuations neq(q = 0) (Fig. 5b).

Fig. 5: Post-pulse dynamics of individual momentum harmonics.
figure 5

a Evolution of δn(q, t) = n(q, t) − neq(q), where n(q, t) = 〈E(−q, t) ⋅ E(q, t)〉, illustrates that the entire plasmon continuum gets excited. Low momenta modes are affected more strongly compared to large momenta ones. b Dynamics of δn(q, t) at q = 0 displays the bi-plasmon periodic dynamics. For typical model parameters, the relative amplitude of oscillating fluctuations can be ~100% of the thermal equilibrium fluctuations neq(0). Remarkably, during these oscillations, the thermal noise can be reduced by ~40% at the bottom of the first cycle, which is clear evidence for the vacuum squeezing. Parameters are the same as in Fig. 3c.

Full size image

The primary decay mechanism of oscillations is dephasing, which depends on details of the quenching protocol, including pulse duration and pulse frequency profile, as well as on the plasmon spectrum. During photoexcitation, the entire plasmon continuum is excited, with high-energy plasmons getting less populated compared to the low-energy ones (Fig. 5a). Since essentially all different frequencies above twice the plasmon gap contribute to the evolution of the electromagnetic energy density, these different modes dephase and render the oscillations damped. Dephasing is weaker and oscillations last longer for plasmons with flatter dispersion because, in this case, the impulsive photoexcitation produces plasmon pairs with frequencies that are closer to each other in energy [see Supplementary Note 5]. The dispersion of the relevant plasmons is expected to be flatter in type-II superconductors with a large Ginzburg parameter (see Supplementary Note 2), such as in cuprates.

As a final remark, the mechanism reported in this paper for converting incoherent pumping to long-lived oscillations relies only on the existence of a gapped phase mode in a U(1) symmetry-broken state. As such, in any scenario where such a gapped mode exists, we expect that any perturbation of the corresponding underlying order parameter, irrespective of transient enhancement or suppression, will lead to similar Raman-like oscillations. Potential examples include the relative phase mode of an unconventional superconductor88,89, structural phonon mode in a crystal53, or the pseudo-Goldstone mode thought to exist in the putative excitonic insulator Ta2NiSe590. In the latter, direct coupling of the excitonic condensate to phonons breaks the U(1) symmetry, explicitly making the Goldstone mode gapped.

Conclusion

Here we demonstrated how generic quenches of the superconducting order parameter result in oscillatory dynamics at frequency twice the plasma resonance. These oscillations are made up of pairs of plasma fluctuations and can directly act as a parametric drive to photons. As a consequence, experimental observables such as reflectivity and conductivity will be dynamically renormalized, as discussed in refs. 2, 3, 37, 50 on Floquet driven superconductors. In particular, in optical reflectivity, one expects the development of resonance at half the oscillation frequency, i.e., at the plasmon gap. Besides this, the parametric drive can result in amplification of reflectivity to values exceeding unity for large driving amplitudes38. This mode can manifest as a blue-shift of the effective plasma resonance in conductivity, as observed in ref. 43 for a bilayer superconductor. Apart from consequences for optical reflectivity, oscillations predicted here act as a Raman active mode and, thus, should be detectable as a modulation in the time-dependent optical properties. Besides, breaking inversion symmetry, for instance, with a magnetic field or electric current bias, would turn this Raman excitation into an IR one, emitting radiation that should be accessible with far-field optics. Our work implies that the presence of special collective modes, such as the Higgs-amplitude excitation or phonons, is not a prerequisite for providing a parametric drive in photoexcited superconductors. Importantly, our results are generic to a wide variety of superconductors, paving the way for future experimental discovery of Floquet quantum matter with unusual optical properties.