Abstract
Practical methodologies for qubit controls are established by two prerequisites, i.e., preparation of a well-defined initial quantum state and coherent control of that quantum state. Here we propose a quantum control method, realized by irradiating nonresonant nanosecond two-color (ω and 2ω) laser pulses to molecules in the pendular (field-dressed) ground state. The two-color field nonadiabatically splits the initial pendular ground state \(|\tilde{0},\tilde{0}\rangle \) to a superposition state of \(|\tilde{0},\tilde{0}\rangle \) and \(|\tilde{1},\tilde{0}\rangle \), whose relative probability amplitudes can be controlled by the peak intensity of one wavelength component (ω) while the peak intensity of the other component (2ω) is fixed. The splitting of the quantum paths is evidenced by observing degrees of orientation of ground-state-selected OCS molecules by the velocity map imaging technique. This quantum control method is highly advantageous because any polar molecule can be controlled regardless of the molecular energy structures.
Similar content being viewed by others
Introduction
Nowadays studies on controlling molecular rotation can be divided into two big branches. One is related to molecular spectroscopy. Gas molecules can be fixed in the laboratory-fixed frame by irradiating a moderately strong laser field1,2. Such a molecular ensemble is referred to as being aligned. In the aligned molecular ensemble, the molecular angular distribution is symmetric with respect to the plus–minus inversion of the aligned axis. A molecular ensemble with directional asymmetry is called being oriented. There are a number of studies on the realization of strong molecular alignment and orientation by combined electrostatic and laser fields3,4,5, a two-color laser field6,7,8,9,10, and a THz laser field11,12. The laser-induced molecular alignment and orientation techniques have enabled photoelectron spectroscopy13,14 and high-harmonic spectroscopy15,16,17 in molecule-fixed frames so that anisotropic properties including the molecular orbitals of sample molecules can be investigated.
The studies on molecular rotational dynamics are also connected to another big branch of quantum science, the so-called quantum computer or quantum simulator18, which has attracted widespread attention from many researchers in the relevant fields. Quantum computation has been pursued with various physical systems, including trapped cold ions19, nuclear magnetic resonance20, quantum dots21, and a superconducting circuit22. In addition, the molecular rotational state of polar molecules was proposed as a quantum platform23. The molecular rotational state is a suitable platform for a quantum computer18. Over the last decade, tremendous experimental efforts have been undertaken to prepare quantum platforms with cooled and trapped molecules24,25. In this platform, so-called pendular states (field-dressed states) are formed by applying an external electrostatic or magnetic field. A resonant microwave pulse can drive the transitions between the pendular states26,27. The driving frequency, intensity, and polarization need to be optimized, depending on the molecular species and the external field conditions. The resonant microwave electric field is widely used for coherent excitation of the molecular qubit system28. The pendular qubit states can also be controlled by optimally designed laser pulses29,30,31.
In this work, theoretically and experimentally, we show a different type of qubit control methodology for general molecules. We use nonresonant nanosecond two-color laser pulses, which are capable of completely controlling transition amplitudes of two laser-field-dressed states regardless of the energy structure of molecules.
Results
Theory of all-optical qubit control method by nonresonant two-color laser pulses
We describe our quantum control strategy when a sample molecule is well prepared in the rotational ground state. We use atomic units unless otherwise stated. In the purely adiabatic process, an initial field-free rotational state of a molecule designated by \(|J,M\rangle \) evolves into a field-dressed state, so-called a pendular state. Since the one-to-one correspondence between an initial field-free state and a field-dressed pendular state is physically ensured, a pendular state is conventionally expressed as \(|\tilde{J},\tilde{M}\rangle \) by using the corresponding initial quantum numbers J and M. Pendular states can be expanded by field-free rotational states as follows:
where CJ,M is an expansion coefficient obtained by diagonalizing a full time-dependent Hamiltonian matrix composed of a field-free Hamiltonian \({H}_{{{{{{\rm{rot}}}}}}}=B{\overrightarrow{J}}^{2}\) (with B the rotational constant of the molecule and \({\overrightarrow{J}}^{2}\) the squared angular momentum operator) and a laser-molecule interaction Hamiltonian Hint. In Eq. (1), higher-lying free rotational states need to be involved in the summation when a stronger laser field is applied. Considering a linearly polarized nonresonant two-color laser field6,7,9, the laser-molecule interaction Hamiltonian Hint is given by
Here Eω(t) and E2ω(t) are the envelopes of the ω and 2ω electric fields. ϕ is the phase difference between the two oscillating electric fields. θ is the angle between the molecular axis and the laser polarization. α∥ and α⊥ are polarizability components parallel and perpendicular to the molecular axis, while β∥ and β⊥ are hyperpolarizability components parallel and perpendicular to the molecular axis. Derivation of the interaction Hamiltonian can be found in ref. 10.
The first term of Eq. (2) generates molecular alignment by allowing transitions between field-free states via nonzero matrix elements \(\langle J,M| {\cos }^{2}\theta | J+2,M\rangle \). Since the cylindrical symmetry along the polarization direction is satisfied, transitions between different M states are not allowed. In the presence of only the alignment Hamiltonian, transitions between even- and odd-J states are not allowed, which also means that there is no transition between the two pendular states \(|\tilde{0},\tilde{0}\rangle \) and \(|\tilde{1},\tilde{0}\rangle \). The system is invariant under a plus-minus sign inversion of the polarization direction. The second term of Eq. (2) corresponds to the orientation Hamiltonian breaking the plus–minus sign inversion symmetry. In terms of the transition matrix elements, nonzero components \(\left\langle J,M| \cos \theta | J+1,M\right\rangle \), \(\langle J,M| {\cos }^{3}\theta | J+1,M\rangle \) and \(\langle J,M| {\cos }^{3}\theta | J+3,M\rangle \) allow transitions between even- and odd-J states. In this condition, a pendular state is given by the superposition of even- and odd-J states in Eq. (1). Analytic expressions of the nonzero matrix elements are given in ref. 10.
According to the Landau–Zener formula32, a nonadiabatic transition rate Γ(t) between two pendular states is
where ϵm(n) is an energy of a field-dressed state labeled by m(n), and dmn is the transition matrix element between the two states. Formerly, with nonresonant nanosecond laser pulses with moderately strong intensities of 1010−1012 W cm−2, it was believed that molecular rotational dynamics were adiabatic, because the rotational speed of molecules (1/(ϵm−ϵn)) is rapid enough in comparison to the field intensity variation so that Γ(t) is near zero. Therefore, the adiabaticity criterion can be considered as Γ(t) ~ 0. Over the past years, however, it was revealed that nonadiabatic transitions between a pair of pendular states \(|\tilde{0},\tilde{0}\rangle \) and \(|\tilde{1},\tilde{0}\rangle \) can be significant depending on the external field parameters9,10,33,34,35. This intrinsically inevitable nonadiabatic transition between pendular doublet states, though it is a technical issue to be overcome in the molecular orientation, can be a powerful tool to control the qubit state given by a superposition of \(|\tilde{0},\tilde{0}\rangle \) and \(|\tilde{1},\tilde{0}\rangle \).
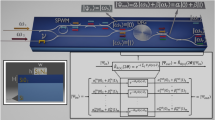
Figure 1 schematically shows our quantum control strategy. The second-harmonic pulse (2ω) has a shorter pulse duration than the fundamental (ω) pulse, due to the second-order frequency conversion process. Therefore, in the leading edge of the nanosecond two-color laser pulse, virtually only the ω pulse interacts with molecules. By the ω field becoming strong enough, the molecules in both \(|\tilde{0},\tilde{0}\rangle \) and \(|\tilde{1},\tilde{0}\rangle \) states show strong alignment along the polarization direction of the ω field1,2. In this condition, the two states are not mixed because the nonresonant-laser-based alignment Hamiltonian has no transition matrix elements between the two states. In the presence of only the strong alignment potential, the two states are almost degenerate in energy at t = t1−δt as shown in Fig. 1. Up to this moment, the population of the initial pendular ground state \(|\tilde{0},\tilde{0}\rangle \) is preserved through the adiabatic process. Any transitions to higher-lying pendular states \(|\tilde{J},\tilde{0}\rangle \) (\(\tilde{J}\ge 2\)) can be ignored by assuming a slow temporal variation of the laser intensity.
Temporal shapes of the ω and 2ω laser pulses and temporal variations of field-dressed eigenenergies (\({\epsilon }_{\tilde{n},\tilde{0}}\) (n = 0,1)) of the two pendular states are shown. Nonadiabatic splittings of the quantum state occur at the leading (t1) and the trailing (t2) edges of the 2ω laser pulse. Quantum path evolution of the initial pendular ground state \(|\tilde{0},\tilde{0}\rangle \) is schematically shown. The final state is given by Eq. (9).
The combination of the ω and 2ω fields forms an orientation potential via a hyperpolarizability interaction with the molecules6,7. As the 2ω intensity becomes significant, due to the orientation Hamiltonian, the transition matrix elements between the two states abruptly become nonzero. The degeneracy is clearly resolved as the 2ω intensity becomes stronger, and the two energy curves exhibit an avoided crossing at t1 as shown in Fig. 1. Since the energy gap between the two states is near zero at the crossing point t1, the two states can be mixed completely by the transition rate given by Eq. (3), such that the rotational state after t = t1 + δt can be expressed as \(a|\tilde{0},\tilde{0}\rangle +b|\tilde{1},\tilde{0}\rangle \) with relations ∣a∣2 = ∣b∣2 ~ 1/2 and ∣a∣2 + ∣b∣2 = 1. We note that, in the presence of the orientation potential, the two pendular states are oriented in opposite directions. While each pendular state shows strong orientation, the degree of molecular orientation is virtually zero because the two pendular states are completely mixed. To increase the degree of orientation, it is desirable to temporally synchronize the alignment and orientation potentials by optimizing the delay between the ω and 2ω pulses9,10,36.
The two energy curves cross again on the trailing edge of the 2ω pulse at t = t2. In between the crossing points of t1 and t2, the interaction can be considered adiabatic because the temporal variations of the energy curves are slow enough. Thus the adiabaticity criterion Γ(t) ~ 0 is satisfied.
At the second crossing point t = t2, the quantum states experience another nonadiabatic splitting. After the splitting at t = t2, the mixed quantum state adiabatically evolves until the laser pulses are completely turned off. Eventually, there are four quantum paths through the entire laser–molecule interaction process.
The final state \(|\psi ({t}_{{{{{{\rm{f}}}}}}})\rangle \) can be analytically expressed by using an initial state \(|\psi ({t}_{{{{{{\rm{0}}}}}}})\rangle \) and the following unitary propagation operator:
Here \({\hat{U}}_{{{{{{\rm{s}}}}}}}\) is a 2 × 2 unitary operator, nonadiabatically mixing an initial pendular ground state into a superposition state at time t1. Another mixing process at t2 can be given by the Hermitian conjugate of \({\hat{U}}_{{{{{{\rm{s}}}}}}}\) by assuming a temporally symmetric laser pulse. The unitary nature gives a 2 × 2 matrix in a generalized form, expressed as
In between the nonadiabatic transition points of t1 and t2, the two adiabatic quantum paths accumulate phases, which can be considered by a diagonal matrix \({\hat{U}}_{{{{{{\rm{e}}}}}}}\) given by
Therefore, the total unitary operator is given by
where Q ≡ (S0−S1)/2. In the right-hand side of Eq. (7), e−iP(P ≡ (S0 + S1)/2) is omitted because it introduces a uniform phase shift to the operator. When ∣a∣2 = ∣b∣2 = 1/2, Eq. (7) is
Eventually, the state \(|\tilde{0},\tilde{0}\rangle \) evolves into
and the state \(|\tilde{1},\tilde{0}\rangle \) evolves into
by the irradiation of the nonresonant two-color laser pulse. This result means that the final population in the pendular ground state \(|\tilde{0},\tilde{0}\rangle \) and the first excited state \(|\tilde{1},\tilde{0}\rangle \) can be controlled by the quantum phase difference \(Q=\int\nolimits_{{t}_{1}}^{{t}_{2}}({\epsilon }_{0}-{\epsilon }_{1}){\rm {d}}t\). The phase difference Q(Iω) is an increasing function of the peak intensity of the ω pulse because the energy gap of the two states for the time between t1 and t2 is an increasing function of the hyperpolarizability interaction. Therefore, the final state \(\left|\psi ({t}_{{{{{{\rm{f}}}}}}})\right\rangle \) (shown in Fig. 1) can be controlled by the peak intensity Iω of the ω pulse.
To validate this quantum control method, we have calculated the population dynamics by numerically solving the relevant time-dependent Schrödinger equation9,10. An OCS molecule is used as a sample. Nonresonant ω and 2ω laser pulses are used, whose pulse durations are set at 6 and 2 ns by FWHM, respectively. The polarizations of the two wavelengths are parallel. The ground state \(|\tilde{0},\tilde{0}\rangle \) is used as an initial condition. Numerical calculations are conducted by changing the peak intensity Iω of the ω pulse, while the peak intensity I2ω of the 2ω pulse is fixed at 0.8 × 1011 W cm−2. Throughout the simulations, the relative phase ϕ between the two wavelengths is set at zero to maximize the orientation potential, which is proportional to \(\cos \phi \)6,7. Without losing the concept of the underlying physical mechanism, the above simulation conditions are chosen to clearly demonstrate the nonadiabatic transitions at the leading and trailing edges of the 2ω pulse, so that the results are consistent with the analytic solution.
Figure 2a shows the populations of the two states \({\left|\left\langle \tilde{0},\tilde{0}| \psi \right\rangle \right|}^{2}\) and \({\left|\left\langle \tilde{1},\tilde{0}| \psi \right\rangle \right|}^{2}\) at the peak of the laser pulse, and those populations after the interaction are shown in Fig. 2b. At the peak intensity (Fig. 2a), more population transfer occurs by increasing Iω. The \(|\tilde{1},\tilde{0}\rangle \) state population reaches near 50% at Iω = 1.0 × 1012 W cm−2, which means that the two states are totally mixed in the first nonadiabatic transition process at t1. At the peak intensity of the pulse, the degrees of alignment between the ground state and the mixed state is consistent as shown in Fig. 2c. However, while the ground state shows strong orientation, the mixed state shows significantly reduced orientation as shown in Fig. 2d because the two oppositely oriented states are mixed.
a The pendular ground \(|\tilde{0},\tilde{0}\rangle \) (solid line) and excited \(\left|\tilde{1},\tilde{0}\right\rangle \) (dashed line) state populations at the peak tpeak of the two-color pulse, and b those populations after the laser pulse has passed completely at tf. The degrees of alignment c and orientation d at tpeak evaluated from the pendular ground state (blue-solid line) and the mixed pendular state \(\left|\psi \right\rangle \) (red-dashed line) obtained by solving the time-dependent Schrödinger equation. The results are shown as a function of the peak intensity Iω of the ω pulse.
Looking at the populations after the laser pulse has completely passed (Fig. 2b), they show oscillating behaviors as expected from the analytic solution. When the peak intensity Iω is above 1.0 × 1012 W cm−2 and the two states are completely mixed at the peak intensity of the laser pulse (∣a∣2 = ∣b∣2 ~ 1/2), the final populations oscillate between 0% and 100% as the peak ω intensity is further increased, which is consistent with the prediction from the analytic function (Eq. (9)). Creation of the four quantum paths and the interference between these paths cause the Iω-dependent modulation of the final state amplitudes.
Experimental observation
Figure 3 shows a summary of our observations of molecular orientation by the velocity map imaging (VMI) technique. OCS molecules in the rotational ground state are used as a sample (see Supplementary Methods). At the peak intensity of the two-color pulse, the molecules are ionized by a femtosecond probe pulse as shown in Fig. 3a. The 2-dimensional velocity distributions of the S+ fragment ions are observed, which reflect the angular distributions of the rotation-controlled neutral molecules. The typical S+ ion images are shown in Fig. 3c–f. In the center of the images, there appear low-energy fragment signals. These signals originate from the dissociation of OCS+ parent ions and are not a focus of the present study. In the concentric rings between 150 and 210 pixels, there appear signals upward and downward along the polarization direction. The up–down asymmetry along the polarization direction shows the evidence of orientation of OCS molecules. Orientation potential energies created by the two-color laser pulses are proportional to \(\cos \phi \), with ϕ the relative phase between the two wavelengths (shown in Fig 3b). The \(\cos \phi \) dependence of the orientation directions is seen in the comparisons between (c) and (d) or (e) and (f).
a Velocity-map imaging for observing molecular orientation. The pump and probe pulses are irradiated to OCS molecules in the rotational ground state. b Schematic representation of the relative phase ϕ between the two wavelengths. c–f Typical images of the S+ fragment ions observed in different conditions. g ϕ-independent degrees of alignment \(\left\langle {\cos }^{2}{\theta }_{2{{{{{\rm{D}}}}}}}\right\rangle \) and h ϕ-dependent degrees of orientation \(\left\langle \cos {\theta }_{2{{{{{\rm{D}}}}}}}\right\rangle \) for two peak ω intensities of 5.0 × 1011 W cm−2 (black) and 1.7 × 1011 W cm−2 (red).
The S+ ion images are measured by changing ϕ. We evaluate the degrees of alignment \(\langle {\cos }^{2}{\theta }_{2{{{{{\rm{D}}}}}}}\rangle \) (g) and orientation \(\langle \cos {\theta }_{2{{{{{\rm{D}}}}}}}\rangle \) (h) of the rotation-controlled neutral molecules from the ion distributions with θ2D the angle between the polarization direction of the two-color control pulse and the detected ion direction. When Iω is increased from 1.7 × 1011 to 5.0 × 1011 W cm−2, the degree of alignment is increased as shown in Fig. 3g, while the ϕ-dependent modulation amplitude of the degree of orientation is reduced as shown in Fig. 3h. Note that the degree of alignment is independent of ϕ within data fluctuations and is increased when the ω intensity is increased, which ensures that the experimental conditions such as the spatial overlap of the two-color beams are constant during the experiment. If the process is adiabatic, the degrees of alignment and orientation should increase by increasing the peak intensity of the ω pulse. The reduced degree of orientation means that the nonadiabatic transition between oppositely oriented two pendular states actually takes place as discussed in Fig. 2d. Since the nonadiabatic process is observed in the first half of the two-color pulse, another Hermitian conjugate nonadiabatic process should also take place in the second half of the two-color pulse.
Conclusions
In this study, using the ground-state-selected target OCS molecules, we demonstrated a qubit control method realized by nonresonant two-color laser pulses, rather than a resonant microwave. This approach has a strong advantage in that it does not require either resonance frequency tuning or an external field, and the quantum control can be all-optically achieved. Utilizing nonresonant laser pulses brings us a capability of qubit control regardless of molecular energy structures. Thus, this all-optical nonresonant field approach has tremendous potential for coherent control of rotational qubit states. This study paves the way to control multiple qubits by various methods utilizing nonresonant laser pulses.
Method
As a pump pulse for the quantum control, the fundamental (ω) and the second-harmonic (2ω) pulses from an injection seeded Nd:YAG laser (Spectra-Physics, LAB-130-10) are used. The duration of the ω pulse is 9 ns and that of the 2ω pulse is 6 ns by FWHM. The relative phase ϕ between the ω and the 2ω pulses is varied by changing the angle of a fused silica plate inserted in the beam path. The peak intensity of the 2ω pulse is fixed at 2.0 × 1011 W cm−2, while the ω intensity is changed by an attenuator consisting of a λ/2 waveplate and a polarizer. As a probe pulse, output from a Ti:sapphire amplifier is used with the center wavelength of 800 nm and the pulse width of 35 fs. The polarizations of the pump pulses are set parallel to the detector plane and that of the probe pulse is perpendicular to the detector plane. The pump and the probe pulses are collinearly focused by a 300-mm lens into the state-selected molecular beam.
Statistics and reproducibility
The S+ fragment ions are detected by a microchannel plate (MCP) backed by a phosphor screen and the images on the screen are recorded by a charge-coupled device camera. In Fig. 3g, h, both \(\langle {\cos }^{2}{\theta }_{2{{{{{\rm{D}}}}}}}\rangle \)’s and \(\langle \cos {\theta }_{2{{{{{\rm{D}}}}}}}\rangle \)’s are evaluated based on the angular distributions observed for S+ fragment ions as shown in Fig. 3c–f.
Code availability
The codes used in all theoretical simulations are available from the corresponding authors upon reasonable request.
References
Friedrich, B. & Herschbach, D. Alignment and trapping of molecules in intense laser fields. Phys. Rev. Lett. 74, 4623 (1995).
Friedrich, B. & Herschbach, D. Polarization of molecules induced by intense nonresonant laser fields. J. Phys. Chem. 99, 15686 (1995).
Sakai, H., Minemoto, S., Nanjo, H., Tanji, H. & Suzuki, T. Controlling the orientation of polar molecules with combined electrostatic and pulsed, nonresonant laser fields. Phys. Rev. Lett. 90, 083001 (2003).
Takei, D., Mun, J. H., Minemoto, S. & Sakai, H. Laser-field-free three-dimensional molecular orientation. Phys. Rev. A 94, 013401 (2016).
Holmegaard, L. Laser-induced alignment and orientation of quantum-state-selected large molecules. Phys. Rev. Lett. 102, 023001 (2009).
Kanai, T. & Sakai, H. Numerical simulations of molecular orientation using strong, nonresonant, two-color laser fields. J. Chem. Phys. 115, 5492 (2001).
Oda, K., Hita, M., Minemoto, S. & Sakai, H. All-optical molecular orientation. Phys. Rev. Lett. 104, 213901 (2010).
Lin, K. All-optical field-free three-dimensional orientation of asymmetric-top molecules. Nat. Commun. 9, 5134 (2018).
Mun, J. H. & Sakai, H. Improving molecular orientation by optimizing relative delay and intensities of two-color laser pulses. Phys. Rev. A 98, 013404 (2018).
Mun, J. H., Sakai, H. & González-Férez, R. Orientation of linear molecules in two-color laser fields with perpendicularly crossed polarizations. Phys. Rev. A 99, 053424 (2019).
Kitano, K., Ishii, N. & Itatani, J. High degree of molecular orientation by a combination of THz and femtosecond laser pulses. Phys. Rev. A 84, 053408 (2011).
Xu, L., Tutunnikov, I., Gershnabel, E., Prior, Y. & Averbukh, I. S. Long-lasting molecular orientation induced by a single terahertz pulse. Phys. Rev. Lett. 125, 013201 (2020).
Holmegaard, L. Photoelectron angular distributions from strong-field ionization of oriented molecules. Nat. Phys. 6, 428 (2010).
Meckel, M. Laser-induced electron tunneling and diffraction. Science 320, 1478 (2008).
Itatani, J. Tomographic imaging of molecular orbitals. Nature 432, 867 (2004).
Kanai, T., Minemoto, S. & Sakai, H. Quantum interference during high-order harmonic generation from aligned molecules. Nature 435, 470 (2005).
Vozzi, C. Generalized molecular orbital tomography. Nat. Phys. 7, 822 (2011).
Koch, C. P., Lemeshko, M. & Sugny, D. Quantum control of molecular rotation. Rev. Mod. Phys. 91, 035005 (2019).
Häffner, H., Roos, C. F. & Blatt, R. Quantum computing with trapped ions. Phys. Rep. 469, 155 (2008).
Jones, J. A. & Mosca, M. Implementation of a quantum algorithm on a nuclear magnetic resonance quantum computer. J. Chem. Phys. 109, 1648 (1998).
Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A 57, 120 (1998).
Song, C. Continuous-variable geometric phase and its manipulation for quantum computation in a superconducting circuit. Nat. Commun. 8, 1061 (2017).
DeMille, D. Quantum computation with trapped polar molecules. Phys. Rev. Lett. 88, 067901 (2002).
Lien, C. Y. Broadband optical cooling of molecular rotors from room temperature to the ground state. Nat. Commun. 5, 1 (2014).
Wu, Y., Burau, J. J., Mehling, K., Ye, J. & Ding, S. High phase-space density of laser-cooled molecules in an optical lattice. Phys. Rev. Lett. 127, 263201 (2021).
Will, S. A., Park, J. W., Yan, Z. Z., Loh, H. & Zwierlein, M. W. Coherent microwave control of ultracold 23Na40K molecules. Phys. Rev. Lett. 116, 225306 (2016).
Li, J.-R. et al. Tuning of dipolar interactions and evaporative cooling in a three-dimensional molecular quantum gas. Nat. Phys. 17, https://doi.org/10.1038/s41567-021-01329-6 (2021).
Carr, L. D., DeMille, D., Krems, R. V. & Ye, J. Cold and ultracold molecules: science, technology and applications. N. J. Phys. 11, 055049 (2009).
Zhu, J., Kais, S., Wei, Q., Herschbach, D. & Friedrich, B. Implementation of quantum logic gates using polar molecules in pendular states. J. Chem. Phys. 138, 024104 (2013).
Zhang, Z. Y., Liu, J. M., Hu, Z. & Wang, Y. Implementation of three-qubit quantum computation with pendular states of polar molecules by optimal control. J. Chem. Phys. 152, 044303 (2020).
Liu, J.-M., Wang, Y., Hu, Z. & Zhang, Z.-Y. Optical control of entanglement and coherence for polar molecules in pendular states. Opt. Express 27, 26588 (2019).
Wittig, C. The Landau–Zener formula. J. Phys. Chem. B 109, 8428 (2005).
Sugawara, Y., Goban, A., Minemoto, S. & Sakai, H. Laser-field-free molecular orientation with combined electrostatic and rapidly-turned-off laser fields. Phys. Rev. A 77, 031403(R) (2008).
Muramatsu, M., Hita, M., Minemoto, S. & Sakai, H. Field-free molecular orientation by an intense nonresonant two-color laser field with a slow turn on and rapid turn off. Phys. Rev. A 79, 011403(R) (2009).
Nielsen, J. H. Making the best of mixed-field orientation of polar molecules: a recipe for achieving adiabatic dynamics in an electrostatic field combined with laser pulses. Phys. Rev. Lett. 108, 193001 (2012).
Hossain, M. M., Zhang, X., Minemoto, S. & Sakai, H. Stronger orientation of state-selected OCS molecules with relative-delay-adjusted nanosecond two-color laser pulses. J. Chem. Phys. 156, 041101 (2022).
Acknowledgements
This study was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) [Grant No. 2020R1C1C1012953]. It was also supported in part by the Max Planck POSTECH/KOREA Research Initiative Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT[Grant No. 2016K1A4A4A01922028]. The experimental part of this study was supported by Grant-in-Aid for Specially Promoted Research No. 21000003 from MEXT and the Photon Frontier Network Program of MEXT.
Author information
Authors and Affiliations
Contributions
J.H.M., S.M., D.E.K., and H.S. contributed to discussions and the preparation of the manuscript. J.H.M. performed the calculations. J.H.M. and S.M. performed the experiments.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Jin-Ming Liu and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. This article has been peer reviewed as part of Springer Nature’s Guided Open Access initiative.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mun, J.H., Minemoto, S., Kim, D.E. et al. All-optical control of pendular qubit states with nonresonant two-color laser pulses. Commun Phys 5, 226 (2022). https://doi.org/10.1038/s42005-022-01005-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-01005-y
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.