Introduction

The development of Josephson junction (JJ) physics1 is of significance for exploiting exotic coherent macroscopic quantum phenomena and superconducting (SC) device applications in various quantum information technologies2. In particular, coherent coupling between two JJs is the key for SC circuit designs to engineer qubit-qubit couplings and realise exotic SC phases in multiple JJ arrays. Recently, the Andreev molecular state (AMS), a concept for producing short-range coherent coupling between two JJs on nanowires has been introduced3,4,5. In the two adjacent JJs, upper (JJU) and lower (JJL), on the nanowires sharing one SC electrode, as described in Fig. 1a, the respective Andreev bound states (ABSs)6,7 are hybridised because of the penetration of the ABS wave functions into the shared SC electrode, forming an AMS as the bonding and anti-bonding states. ABSs have been utilised for the Andreev qubit8,9,10, and AMS physics holds the possibility of producing short-range coherent coupling between qubits. In such a device, the ABS energy and supercurrent in JJU depend on not only δU, the phase difference on JJU, but also on the ABS energy and the phase difference, δL, of JJL. Consequently, the supercurrent in JJU can be controlled nonlocally by manipulation of JJL, which is referred to as the nonlocal Josephson effect3. The AMS has been observed in a double dot coupled with SCs11; however, experimental studies of superconducting transport related to the AMS, such as the nonlocal Josephson effect, have not been reported.

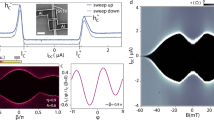
Fig. 1: Concept of this study and device structure.
figure 1

a AMS formation is shown. The ABSs of JJU and JJL penetrate the SC electrodes, as illustrated in the middle panel. When the separation of the two JJs is short, the ABSs in the respective nanowires are hybridised to form an AMS. b SEM image of the 3-terminal JJ on a double nanowire. The two JJs share the left SC electrode, but on the right side, the two SC electrodes were placed on the respective nanowires. c SEM image of sample B. The shared and lower SC electrodes in b are connected by a superconductor loop.

Full size image

When two nanowires are coherently coupled through an SC electrode, the coupling forms a nonlocal SC correlation on the double nanowire. Such nonlocal SC correlation is an essential ingredient for engineering time-reversal invariant topological SCs and can be applied in topological quantum computing with Majorana fermions or parafermions in SC-semiconductor hybrid systems12,13,14. The nonlocal SC correlation on double nanowires has been addressed in electrically tunable devices11,15,16. Experimental study of the nonlocal Josephson effect is a necessary step to address the phase control of the nonlocal SC correlation; it paves the way for realising time-reversal invariant topological SC devices.

Considering that multiple phase differences dominate the junction properties, the coupled JJs in Fig. 1a resemble multiterminal JJs17,18,19,20,21,22,23,24, providing a platform for topological physics25,26,27,28. In this sense, establishing the physics of the coupling between JJs will also help to develop multiterminal JJ physics, as studies on not only devices of a single normal conductor with multiple SC electrodes but also those of two or more coupled JJs on various independently controllable materials may be conducted.

Here, we report experimental evidence of the nonlocal Josephson effect using gate-tunable InAs nanowires to demonstrate the coherent coupling between two JJs on a double nanowire. Our results provide a means to nonlocally control the D.C. Josephson effect. Our strategy for this demonstration is to determine whether the SC correlation between any two SC electrodes exists and then measure the switching current in JJU dependent on δL.

Results

We have prepared two coupled JJ devices, named samples A and B. We have chosen an InAs double-nanowire structure, created using the selective area growth (SAG) method as this method allows the preparation of two spatially separated parallel nanowires with high yield compared to using self-assembled nanowires15,16,29. Additionally, aluminium is epitaxially grown on InAs nanowires, which provides a highly transparent interface30. The two SAG nanowires are spatially separated by 60 nm. JJU and JJL were formed on InAs nanowires U and L, respectively. The SC electrode on the left side is shared by the two JJs, but the two right SC electrodes contact nanowire U and nanowire L separately. Sample A has been fabricated into a 3-terminal JJ device (left shared SC, right upper SC, and right lower SC electrodes) on nanowires U and L. A scanning electron microscope (SEM) image of the same structure is shown in Fig. 1b. For sample B, JJL is embedded in an SC loop to change δL by a magnetic field (B) penetrating the SC loop. The two gate electrodes is used to electrically control JJU and JJL with gate voltages of VgU and VgL, respectively. The SEM image of sample B is shown in Fig. 1c. The junction of sample B has the same structure as that of sample A, but the shared and lower SC electrodes are connected to an SC loop. Sample A is used to confirm the SC correlation between any two SC electrodes and sample B to demonstrate the nonlocal control of the D.C. Josephson effect.

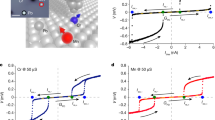
First, we have measured sample A at 10 mK to study the correlation between the SC electrodes. For this purpose, we have simultaneously measured VU and VL, the voltages of the upper and lower SC electrodes with the shared SC grounded by sweeping the bias currents IU and IL through JJU and JJL, respectively (see Fig. 2a). Figure 2b, c show the measured differential resistances dVU/dIU and dVL/dIL as functions of IU and IL, respectively. In the square region of −30 nA < IU < 30 nA and −60 nA < IL < 60 nA, dVU/dIU and dVL/dIL almost vanish in both figures, indicating that the supercurrent flows between the upper and the shared SC and between the lower and the shared SC. This means that the switching current is almost 30 nA for JJU and 60 nA for JJL.

Fig. 2: Three-terminal measurement of the two coupled Josephson junctions on the double nanowire.
figure 2

a Shows a schematic of the electrical circuit used for measurement of sample A. b, c show the differential resistances of JJU and JJL, respectively, as a function of IU and IL, measured simultaneously. The supercurrent flows in both JJs in the central blue regions of −30 nA < IU < 30 nA and −60 nA < IL < 60 nA. In the regions arranged with SCUS, SCLS, and SCUL extending outward from the central blue supercurrent region, the local supercurrent remains between a pair of the two SC electrodes with the dissipative current in the other pairs.

Full size image

From the supercurrent region, the three additional regions where the differential resistance is reduced are extended, as labelled with SCUS, SCLS, and SCUL in Fig. 2b, c. These diagonal features have also been reported in multiterminal Josephson junctions22,23,24. In these regions, the supercurrent flowing between any two contacts remains within these contacts, whereas the dissipative current flows between the other contacts. For example, in SCUS, there is considerable reduction, as seen in Fig. 2b, but not in Fig. 2c. In addition, SCUS is strongly dependent on IU but is slightly sensitive to IL. This means that the supercurrent between the upper and shared SC electrodes remains in SCUS with the dissipative current at JJL because ∣IL∣ > 60 nA. For similar reasons, SCLS can be assigned to the region where the supercurrent between the lower and shared SC electrodes remains.

As for SCUS and SCLS regions, the figures indicate that the differential resistance in the remained supercurrent regions is finite. For example dVU/dIU in SCUS is around 300 Ohm at IL ~ ±400 nA (see Supplementary Note 6, Supplementary Fig. S8). This can be assigned to the Joule heating effect derived from the normal transport in JJL. The heating increases the electron temperature in JJU, resulting in the phase diffusion which produces the finite differential resistance even in the supercurrent region31. Additionally, SCUS and SCLS have finite tilts on the VUVL plane. These tilts can be derived from the cotunneling of the quasiparticles. For example, when a finite potential difference on JJU is present, the current in JJU flows from the upper SC to the shared SC. Additionally, due to the cotunneling through the shared SC, the finite current also flows to the lower SC. This cotunneling current generates the finite tilt of SCLS.

We focus on the diagonal feature SCUL in which both dVU/dIU and dVL/dIL are slightly reduced, as shown in Figs. 2b, c. A supercurrent can exist in three pairs of upper, lower, and shared SC electrodes. The supercurrent in the upper and shared SC pair is assigned to SCUS, and that in the lower and shared SC pair is assigned to SCLS. Therefore, SCUL can be assigned to the supercurrent between the upper and lower SC electrodes. This result indicates that a nontrivial SC correlation exists between the upper and lower SC electrodes, although the shared SC electrode only intermediates two nanowires; no other material connects the two SC electrodes. This is a signature of the nonlocal SC correlation between the two JJs. However, the SCUL signal is small and vague because the dissipative current and nonequilibrium quasiparticles coexist with the supercurrent. In addition, if there is an electrical short between two NWs, similar experimental results would be obtained (see Supplementary Note 7). Therefore, a detailed discussion of the nonlocal SC correlation from these 3-terminal results is difficult.

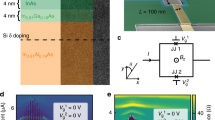
Then, we take the other strategy to control the phase difference δL in sample B. We have measured VU by changing IU and B at several VgU and VgL, the gate voltages on JJU and JJL, respectively (see Fig. 3a). Figure 3b represents VU vs. IU at B = 0 mT and several VgU. At IU = 105 nA for VgU = 0 V, the supercurrent region is switched to the normal region (see Supplementary Note 5). The switching current Isw decreases as VgU decreases, indicating that JJU can be controlled electrically. We roughly estimate the proximity SC gap of 0.1 mV as a product of the switching current and the normal resistance at 4 K at VgU = 0 V (see Supplementary Note 1, Supplementary Fig. S1). This is similar to the bulk Al gap energy (0.18 meV), meaning that the high transparent JJs are realised. VgU = −5 V provides about half of Isw at VgU = 0 V. Figure 3c indicates VU vs. IU at B = 1.9 mT and several VgL. VgL = −4.4 V provides about 0.9 of Isw at VgL = 0 V, meaning that Isw of JJU depends weakly on VgL in the present range.

Fig. 3: Switching current oscillation indicating a coherent coupling between two Josephson junctions.
figure 3

a Shows a schematic of the measurement circuit for sample B . b Illustrates the IU − VU curves obtained at several VgU points, indicating that the supercurrent in JJU can be tuned by VgU locally. c Indicates VU vs. IU at B = 1.9 mT and several VgL. The supercurrent in JJU is little controllable by VgL. d Shows VU as a function of IU and B. The boundary between the red and blue regions corresponds to the switching current in JJU as a function of B. The image clearly indicates the oscillation of the switching current in the JJU.

Full size image

We have measured VU vs. IU at various magnetic field strengths. The obtained values of VU as a function of IU and B are shown in Fig. 3d. As illustrated, the switching current around 100 nA, corresponding to the boundary between the blue and red regions, oscillates with B. The oscillation period is 0.22 mT, which reasonably agrees with the calculated value of 0.30 mT, derived from the superconducting loop area (6.88 μm2). The magnetic field changes only δL and the phase difference of JJL in the SC loop. Therefore, B would not affect the Isw of JJU if there were no nonlocal SC correlation between JJU and JJL. The obtained switching current oscillation has been reproduced in different devices on a single or double nanowire (see Supplementary Note 2, Supplementary Fig. S2). Furthermore we confirmed that this oscillation disappeared as the distance between the two junctions increased, as expected from the theory that the distance should be shorter than the coherence length of SC to form the coupling. Disappearance of the oscillation with the long distance implies that the single JJ on the single nanowire produces no oscillation of the switching current (see Supplementary Note 3, 4–7, Supplementary Figs. S3–7). Consequently, we present the observation of the nonlocal Josephson effect derived from the coupling between JJU and JJL through the shared SC electrode. Additionally, our observation of JJU switching current in sample B proves coherence of the coupling because the nonlocal phase modulation is observed on the supercurrent which is one of the phase coherent phenomena. We note that the switching current of JJU at a single B point is given by the maximum value of the current phase relation (CPR) of JJU with a fixed δL. Then the oscillation of Isw indicates that the coupling between the JJs modulates the maximum value of the CPR. Thus, we cannot conclude that the Andreev states in the JJs are fully hybridised for any δU and δL, but at least, we can insist that the coherent coupling exists and the hybridization modulates the supercurrent transport in our device.

To clarify that the Isw oscillation originates not only from the JJU, but also from the properties of JJL, we studied the gate voltage control of the nonlocal Josephson effect signal. We evaluate the peak-to-peak value (a difference of the maximum and minimum of Isw) and the average of Isw vs. B at the respective gate voltages. First, we indicate the VgU dependence of Isw vs. B with VgL = 0 V, indicating local gate control. Both the peak-to-peak value and the average of Isw change with VgU, as shown in Fig. 4a. Then, we move onto the VgL dependence with VgU = 0 V; this refers to nonlocal gate control. As shown in Fig. 4b, the average of Isw is almost constant, whereas the peak-to-peak value decreases as VgL decreases (see Supplementary Fig. S9). This indicates that the average is affected only by the local gate voltage; the oscillation is affected by both the local and nonlocal gate voltages. Therefore, the oscillation originates from the coherent coupling between the two JJs. We note that the nanowires grown directly on InP substrates have accumulated carriers at the interface with the InP substrate due to the misfit dislocations, potential impurities, and roughness originated from the etching process to make the insulating mask for the SAG growth32. Then nanowire carriers at the interfaces are hardly removed by the electrical gating and we cannot pinch off the nanowires.

Fig. 4: Local and nonlocal gate control of the switching current oscillation in JJU.
figure 4

a, b Show the peak-to-peak value in red and the average in blue of the switching current in JJU as a function of VgU and VgL, respectively. In the local gate control case in a, both the amplitude and average change with VgU. However, only the peak-to-peak value largely varies in the non-local gate control case in b. This means that the switching current oscillation is derived from the hybridisation between JJU and JJL.

Full size image

Discussion

Finally, we discuss the microscopic origin of the observed coherent coupling between JJU and JJL. In the literature3, the coupling in the ballistic junctions is dominantly formed by the double elastic cotunneling through the shared SC. The observed tilt of SCLS in Fig. 2 provides a ratio of the cotunneling current to the current in JJU as around 0.14. This value is similar to a ratio of the peak to peak value to the average of Isw found in Fig. 4. Therefore, the similarity between the cotunneling ratio and the oscillation ratio seems to imply that the coherent coupling in our devices is dominantly originated from the cotunneling process as theoretically expected in the ballistic JJs.

Although our experiments clearly provide evidence of existence of the nonlocal Josephson effect, we only addressed the nonlocal control of the switching current. In order to unveil the local and nonlocal transport on the coupled JJs, it is significant to evaluate the current phase relation, which gives the supercurrent as a function of local and nonlocal phase differences. In addition, microscopic mechanism to produce the coherent coupling should be revealed experimentally. Furthermore, the obtained results can be explained without relying on spin-orbit interactions. Then it is not revealed how the spin-orbit interactions in the InAs nanowires modulates the nonlocal Josephson effect. Recently the spin-orbit effects on the superconducting transport has been discussed in a strong magnetic field33. Then further research of the nonlocal Josephson effect under the in-plane strong magnetic field is necessary to unveil the spin-orbit effects.

In summary, we confirm the nonlocal superconducting correlation between two JJs in a 3-terminal device and observed the nonlocal Josephson effect in a double JJ device with a superconducting loop. These demonstrate that the short-range coherent coupling between the two different JJs can be formed through a superconductor. The observed coherent coupling is not just for the semiconductor-superconductor junctions but expected in various kinds of JJs coupled through superconductors. Our results pave the way to engineering short-range coherent coupling between superconducting qubits, such as the Andreev qubit8,9,10, and provide a building block for designing functional SC devices consisting of the two JJs on the different materials.

Methods

Sample growth

The SAG InAs double nanowires have been grown by molecular beam epitaxy (MBE)32,34,35,36,37,38. Prior to the InAs growth, nanowire structures have been patterned using standard electron-beam lithography on SiOx (30 nm)/Al2O3 (3 nm) layers on an Fe-doped InP(001) substrate which is insulating at low temperature. The patterns have been formed by dry-etching of the SiOx masking layer and wet-etching of the Al2O3 etch-stop layer. The patterned nanowires are along the [100] ridge direction. The processed InP surface has been further cleaned by ultraviolet-ozone and diluted HCl38. In a III-V MBE chamber, the patterned InP substrate has been desorbed at 520∘ C with a flux of As4 molecules. 80-nm-thick InAs nanowires were grown at a growth rate of 0.1 ML s−1 under As-rich growth conditions. After InAs growth, the substrate has been transferred to an interconnected MBE chamber and cooled to ~80 K using liquid nitrogen on a cold-head manipulator for Al layer growth. To achieve a continuous Al layer between two adjacent InAs nanowires along the [100] ridge direction, a 10-nm-thick Al layer has been first grown at +20∘ with respect to the [100] ridge direction, and another 10-nm-thick Al layer has been grown at -20∘ with respect to the [100] ridge direction. Immediately after Al growth, the substrate has been transferred to a loadlock within 5–6 minutes and exposed to O2 gas for oxidation of the Al surface to preserve a smooth and continuous Al layer prepared at a cryogenic temperature.

Device fabrication

Epitaxial aluminium is grown globally on the substrate, and the two parallel nanowires are intermediated by the Al film. In the fabrication process, we have removed the unnecessary epitaxial aluminium by wet etching with a type-D aluminium etchant to form JJs and superconducting loops. Then, we have grown a 20 nm-thick aluminium oxide layer through atomic layer deposition and fabricated a separate gate electrode on each nanowire with Ti 5 nm and Au 20 nm. Following the measurement, we have checked that the upper and lower SC electrodes are disconnected by SEM. Due to the interface quality of InP substrate and InAs nanowire32, we cannot pinch off the conductance by the top gate voltages.

Measurement

For the measurement of sample A, we have injected bias currents from the upper and lower SC electrodes, with the shared SC electrode grounded. When we have measured dVU/dIU (dVL/dIL), we have added a small oscillating current of 1 nA ΔIU(ΔIL) with 23 Hz on IU(IL) and detected the oscillation component of the voltage ΔVU(ΔVL) using the lock-in technique. For the measurement of sample B, we have only injected a DC bias current IU and detected VU. All measurements have been performed at 10 mK, the base temperature of our CryoConcept wet dilution fridge. The lines are filtered by low pass filters consisting of 2.7 kOhm resistance and proper electric capacitance. For the current bias, we have inserted a 1 MOhm resistance in between the device and the voltage source. This effectively forms a current source with 1 MOhm output impedance, which is sufficiently higher than the line resistance and the device resistances.