Introduction

Our modern networked societies are more dependent than ever on highly secure data transmission. Typical examples are constituted by the control of critical infrastructures—such as energy generation, communication, transportation and logistics – as well as the exchange of health data. The digital encryption methods used today offer a range of attack points that can be overcome with the help of quantum key distribution (QKD). It is therefore desirable to establish QKD in a future multi-level digital security architecture in addition to the technology already in use.

A global quantum communication network with satellite-based links is likely to have advantages over fiber-based networks in terms of long-distance QKD, since the exponential photon losses introduced by optical fibers are too detrimental for distances beyond a few hundred km1,2. Quantum repeaters3,4 have been proposed to push this limit further. Here, intermediate, untrusted repeater stations involving distillation and swapping5 steps reminiscent of quantum teleportation6 allow the fundamental limitations of direct quantum communication to be overcome. Although fiber-based quantum repeaters offer distances well beyond the direct communication limit, largely governed by the repeaterless bound7,8,9, and in principle allow for secure communication between arbitrary distances, they are still limited to around a few thousand km4,10 which precludes their use for global quantum networking.

In contrast, satellite-based free-space QKD (satQKD) benefits from a polynomial scaling with distance. In the field of satQKD, there are already multiple studies11,12,13 supporting numerous initiatives and missions both active and in planning14,15,16,17,18 phases from Europe, North America, and Asia rely on the BB84 and BBM92 schemes19. The most prominent example is the MICIUS which has realized many milestone demonstrations including teleportation from ground to satellite20, decoy-state BB84 QKD from satellite to ground21, and a long-distance, entanglement-based QKD with the BBM92 protocol22. The ranges in these experiments have been limited to the line-of-sight distance of the satellite which depends on its orbit. MICIUS has further demonstrated a beyond-line-of-sight QKD between Vienna and Beijing, operating as a trusted node23.

However, untrusted node operation for beyond-line-of-sight distances towards truly global scales requires the implementation of a quantum repeater protocol enabled by onboard quantum memories24,25. Furthermore, quantum memories do not only help increase the overall network range but also offer a solution to low detection rates in entanglement-based schemes26,27,28,29,30,31,32 and thus facilitate memory-assisted QKD (MA-QKD) protocols which can be thought of as a single-node quantum repeater link. By synchronizing otherwise probabilistic detections, a single repeater station with a quantum memory would change the scaling of the key rate from ηch to \(\sqrt{{\eta }_{{{{{{{{\rm{ch}}}}}}}}}}\) where ηch is the channel transmission. The development of systems for MA-QKD will not only enable the broad commercial use of satellite QKD, but will also promote the exploitation of other quantum technologies. Almost all key components for MA-QKD with untrusted satellites are already available or very well developed. This includes optical terminals, single-photon sources, and detectors. Only quantum memories have a relative research backlog33. These developments are forward-looking and promising, but at the same time, it is far from clear how to optimally devise schemes for satellite-based quantum key distribution with realistic resources.

In this work, we comprehensively analyze multiple quantum repeater schemes that rely on satellites with quantum memories for continental and intercontinental distances34, going beyond our earlier work24. We make use of an event-based Monte Carlo simulation that enables the analysis of quantum repeaters with multi-mode memories. We simulate achievable MA-QKD rates in different satellite and ground station geometries for current and near-future experimental parameters. In addition, the current work utilizes memory cutoff times35 to improve achievable key rates and stresses the importance of choosing them appropriately.

Results and discussion

For establishing quantum communication over intercontinental distances, it has been shown that making use of a satellite with a quantum memory can provide an advantage over systems without memory24,25, e.g., higher key rates for setups with only one satellite and shorter entanglement distribution times for multiple satellites. Quantum memories in principle suited for satellites have been demonstrated, e.g., in ref. 34. In this work, we build upon these earlier results and further analyze scenarios utilizing multiple satellites as repeater stations for a quantum repeater.

To this end, we have developed a large-scale numerical Monte Carlo simulation for quantum repeaters that can faithfully represent loss and imperfect quantum memories, as well as other sources of noise such as dark counts. While there are existing approaches dealing with the computation of key rates for different repeater setups4,29,30,36, the generalization of these methods to longer distances and other error models is by no means straightforward, e.g., an analytical approach also involves an intricate analysis of entanglement swapping strategies37. Another challenge lies in the fact that for setups with multiple repeater links, a trial to establish an entangled pair somewhere along the line being successful or not can potentially influence the wait times in quantum memories everywhere in the setup. Therefore, we have chosen a simulation as our approach.

To be specific and close to the considerations pertaining to realistic implementations, we focus on scenarios that make use of three satellites. When trying to reach very long distances, approaches with only one satellite will invariably reach a limit where the connection between ground stations becomes geometrically impossible or at least suffer from very high loss due to a shallow transmission angle through the atmosphere. While picking a higher orbit for a single satellite can extend the range, there is a significant trade-off in having to send photons to much longer distances. For a proper comparison, one needs to also take the different orbital periods into account, which we touch upon in our analysis in the “Effective rates for orbiting satellites" subsection of the Results and Discussion section.

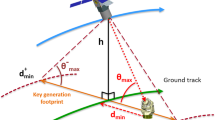
While the movement of the satellites is indeed essential (and will be considered later), first, we consider the following setup with a static satellite, which already contains a breadth of effects to analyze: Two ground stations A and B are separated by ground distance d. Three satellites are used to establish a secret key between them. The central satellite SC is positioned halfway between the ground stations at orbital height h, however, the other two satellites SA and SB can be positioned at the same orbital height at any distance from the ground station and the central satellite as depicted in Fig. 1a.

Fig. 1: Using multiple satellites to connect distant ground stations.
figure 1

a Using three satellites SA, SB, and SC to connect ground stations A and B (separated by a ground distance d allows reaching distances beyond the horizon of a single satellite. The positioning of the satellites is a new parameter to optimize in this scenario. b Total loss when trying to establish an entangled link between the ground station A and SC with an entangled pair source at SA. SA@x% denotes that satellite SA is positioned vertically above the point at x% of the total ground distance. With three satellites one can avoid sending qubits through the atmosphere at a very shallow angle by positioning the outer satellites closer to the ground stations. Orbital height h = 400 km, divergence angle θd = 3 μrad.

Full size image

The positioning of the satellites becomes an additional decision for such a setup with three satellites, which is not present when using only one satellite. The two main sources of loss are the elevation angle-dependent atmospheric loss ηatm(θ) and the distance-dependent diffraction loss ηdif. Picking the position of satellites SA and SB clearly comes with a trade-off between those two sources of loss. Positioning the satellite directly above the ground station minimizes the atmospheric loss, but also means photons will need to be sent over longer distances.

In Fig. 1b the total loss for establishing a link between A and SC with an entangled pair source at SA is shown for different positions of the satellites SA and SB. There is a trade-off between avoiding as much atmospheric loss as possible when SA is positioned right above A and the long distance between the satellites that causes. However, for the very tightly collimated, diffraction-limited beams we consider here (θd = 3 μrad) it becomes clear that for long distances it is advantageous to avoid as much atmospheric losses as possible. For a system with higher diffraction losses, this trade-off may not be as clear and would need to be reconsidered. A detailed discussion about the error model and a description of the protocols can be found in Supplementary Notes 1 and 2, respectively.

Scenario 1

In this scenario, we look at an approach where the outer satellites establish links between the central satellite SC and each ground station and SC connects them by entanglement swapping, see Fig. 1a. Hence, this is a protocol consisting of only two repeater links. For this setup, only SC needs to be equipped with the ability to store qubits in a quantum memory, so we consider that the central satellite has two quantum memories with n modes each as well as the ability to perform entanglement swapping. We assume that all quantum memories in both scenarios are directly heralding memories, i.e., it is immediately possible to tell whether loading a qubit into memory was successful. SA and SB both are equipped with an entangled pair source that allows them to distribute entangled pairs between their assigned ground station and SC.

The basic idea of this protocol is very similar to one with only a single satellite because only two repeater links are needed. Links are established between the central satellite and the ground stations and the central station has to wait for confirmation that a photon has arrived at each ground station before performing entanglement swapping. However, there are some subtle differences in terms of timing that need to be considered.

The main difference from protocols in refs. 29,30 is that the satellites with entangled pair sources do not have the information about whether a qubit has been loaded into memory successfully. Therefore, it makes sense for the source not to wait until confirmation from the satellite with the memory but to instead continuously send out entangled pairs. Therefore one central limitation lies in the maximum possible rate of entangled pair generation fclock by the source.

The continuous sending of pairs is conceptually similar to the up-link scenario considered in ref. 24 with the difference that here the entangled pair sources are located on board of satellites instead of being on the ground. However, here the waiting times cannot be eliminated completely as the central satellite still has to wait for confirmation that a qubit arrived at the ground station before performing the entanglement swapping operation.

Scenario 2

In this alternative scheme, we instead consider a setup that establishes four repeater links and uses three successive entanglement swapping operations to finally connect the ground stations A and B. This means all three satellites need to have the capability to store qubits in a directly heralded fashion. We assume that similar to the above scenario each satellite is equipped with two quantum memories with n modes each30. However, this time the satellites SA and SB contain emissive quantum memories (denoted by * in Fig. 2a) that are able to emit single photons that are entangled with an internal atomic excitation, i.e., a stored matter qubit32,38. Satellite SC, on the other hand, carries absorptive type quantum memories39,40 that are capable of catching a flying qubit for storage similar to the quantum memories in Scenario 1.

Fig. 2: Strategies for utilizing three satellites.
figure 2

a Illustration of the considered scenarios. Satellites SA and SB are equipped with entangled pair sources (EPS) and send qubits to the other satellite and the ground stations (dashed lines). In Scenario 1 only the central satellite SC has quantum memories and two repeater links are established. In Scenario 2 all of the satellites have quantum memories and a protocol with four repeater links are used. b Scenario 1: Choosing an appropriate cutoff time tcut—a maximum time a qubit is kept in a quantum memory—can be very beneficial to the key rate. The optimal value for tcut is distance-dependent and it is possible to choose a value that is too low. A dashed line indicates a BBM92 protocol with only one satellite and a clock rate of 20MHz with the same loss model. This plot is for a divergence of θd = 6 μrad as the effect is more pronounced in situations with high loss.

Full size image

The satellites that generate entangled states (SA and SB) continuously try to establish new links with their neighboring stations. This means that whenever a memory mode at SA is empty, a new entangled memory-photon pair is generated. The associated photonic qubit is then sent to the other station—either the associated ground station A or the central satellite SC. The memory qubit at SA will need to be stored at least until confirmation from the other repeater station is received to confirm whether this trial has been successful. For this protocol, we assume that the trial for multiple memory modes can run in parallel and independently of each other. However, in practice, it is likely that instead of spatially separated channels there will be a number of time slots available in a shared channel. As long as the number of available time slots is much larger than the number of memory modes, the effects of sharing a channel are negligible. This is in contrast to Scenario 1, where the amount of photons that can be sent through the channel in a given time (which we directly link to the rate of entangled state generation for our simulation) is actually a limiting factor.

Furthermore, one needs to pick a strategy for how the entanglement swapping operations are handled if multiple successfully established qubits are sitting in memory, which is a situation that can potentially occur at each of the three satellites. For this scenario, we chose to perform entanglement swapping as soon as it becomes available (i.e., there is no fixed order in which the satellites need to perform their Bell measurements) and always pick the eligible qubits that have sat in memory for the longest time. While this is likely not optimal (e.g., a more recently established entangled pair will have a higher fidelity), it completely eliminates the need for additional two-way communication (and therefore additional waiting times) between the satellites during the entanglement swapping process, that would arise from more involved strategies.

Compared to Scenario 1 this setup certainly introduces an operational overhead in the form of more qubits having to wait in quantum memories (and therefore dephase) as well as the need for additional operations. It is nonetheless interesting to consider as it is likely that this type of scheme will become more relevant once more advanced quantum repeater protocols, e.g., with added entanglement purification, become experimentally feasible.

Key rates

The asymptotic key rate is lower bounded by (see refs. 29,41,42):

$$r\left[1-h({e}_{X})-fh({e}_{Z})\right],$$
(1)

where r is the rate of bits obtained from successful coincidence measurements that correspond to valid entanglement swapping operations, h is the binary entropy function and eX(Z) is the quantum bit error rate in the X (Z) basis. We assume that the error correction inefficiency f is equal to 1. We let the simulation run until we have generated a large sample (105 for Scenario 1 and 104 for Scenario 2.) of long-distance links between A and B, which we use to calculate the sample mean for r and eX(Z).

Ultimately, a finite-size, composably secure analysis is essential for cryptographic applications43. Moreover, in a practical setting, the effects of finite data blocks on satellite quantum key distribution (see, e.g., refs. 12,44) can potentially be particularly significant if achievable block sizes in a single pass are limited. Nevertheless, the asymptotic rates are still informative since they provide an upper bound to the performance limit of satellite-based quantum repeater strategies and are reflective of performance for reasonable block sizes.

Cutoff times

In essence, using quantum memories for a quantum repeater allows one to trade some of the probability that measurements at the ground stations coincide for an overall higher rate of qubits that successfully arrived at their destination—with the entanglement swapping operation allowing one to connect two links that are more likely to be successful individually.

However, if qubits are stored in quantum memories for too long, the additional dephasing at some point becomes too detrimental and can reduce the achievable key rate. As an optimization, it is therefore important to add a mechanism to discard qubits that have dephased too much. One simple mechanism is to choose a cutoff time tcut > 0, which is the maximum time a qubit is allowed to sit in memory after a successful generation of an entangled link is confirmed. Such a cutoff mechanism has been previously proposed, e.g, in ref. 35, and its inclusion is one of the primary improvements of the protocol compared to the previous results in ref. 24. Discarding leftover qubits in memory after each cycle in the protocol in ref. 30 also has a similar effect to prevent too much dephasing noise from building upon the qubits in memory.

By carefully tuning the cutoff time, one can essentially choose how much of the trade-off mentioned above is acceptable. However, it should be noted that this is not the only possible mechanism for choosing when to discard dephased qubits. In fact, finding the optimal strategy at every time step has been shown to require resources that are scaling exponentially in the input size45.

In Fig. 2b the effect different choices of tcut can have on achievable distances and key rates is demonstrated. While the precise impact depends on many factors e.g., the relation of loss rates and memory quality, choosing an appropriate cutoff time is crucial to extend the reachable distance. It should be noted that choosing a too short cutoff time can actually be detrimental to the key rate, e.g., in Fig. 1b the achievable key rate is higher for tcut = 5 ms than for 2 ms in the 5000–7000 km range. This effect can be easily understood in the most extreme case as a very low tcut will essentially turn the protocol into a quantum repeater without memories.

Achievable key rates for realistic parameters

Having a numerical simulation opens up the possibility to investigate a large range of values for all relevant error parameters. However, in order to interpret the results, it is important to choose a meaningful parameter set. In Table 1 we list the parameters for our error model, which are considered the baseline for our simulation (see Supplementary Note 4 for additional results with brighter background light). These are chosen according to realistic ranges for current or near-term implementations.

Table 1 Base parameters for the simulation.
Full size table

As mentioned before, the position of the satellites SA and SB is a new decision that has to be made when using more than one satellite. In Fig. 3 the key rate of multiple positions is shown for the base parameter set in Table 1. For this parameter set, it is obvious that avoiding as much atmospheric loss as possible is worth the additional diffraction loss from the longer distance between SA and SC in Scenario 1, even for short communication distances. However, for the more involved Scenario 2 consisting of four repeater links, positioning SA directly above ground station A is not optimal. Hence, both the loss parameters and the precise choice of protocol influence the optimal satellite positions.

Fig. 3: Achievable key rates for different choices of positions of the satellites.
figure 3

This is a new parameter to optimize when using multiple satellites. Satellite SA is positioned vertically above varying percentages of the total ground distance. The dashed line indicates the BBM92 protocol with only one satellite and a clock rate of 20 MHz. a Scenario 1, a protocol with outer satellites distributing one pair between the ground station and the central satellite each. Here positioning the satellites SA and SB directly above the ground station to avoid as much atmospheric noise as possible proves beneficial. b Scenario 2, a protocol that establishes four links of entangled pairs between satellites and stations. Here, the distance-dependent trade-offs are more complex.

Full size image

One interesting thing to note is that for some configurations the key rate does not strictly decrease with the distance. This is due to a situation that can happen with multi-mode memories if multiple qubits sit in memory waiting for the other side to be ready for entanglement swapping. When the loss is much smaller for one repeater segment than the other (as is the case for the very asymmetric losses in Scenario 2), this is something that will happen often, even when using a cutoff time strategy. While most of the established pairs will not be swapped due to the high-loss segment not providing pairs fast enough, the average time a pair that does end up getting swapped is sitting in memory can end up being lower if both segments have comparable losses. Therefore, unintuitively an increase in the loss of the comparatively low-loss segment can lead on average to higher fidelity of swapped entangled pairs. Indeed, the local maxima for the case we consider here are found where the (distance-dependent) loss for the channel between A and SA is comparable to the inter-satellite loss between SA and SC. The key rates could likely be improved further by optimizing tcut at each data point, or modifying the swapping strategy when multiple qubits are waiting in memory.

In Fig. 4 we explore the effect of varying some parameters of interest, namely the divergence angle θd of the beams connecting ground stations and satellites, the quality of the quantum memories, and the orbital height of the satellites. Figure 4a, d show that naturally, a higher θd and therefore higher loss impact the key rate significantly. Despite the lower rates when a loss is small, Scenario 2 actually proves more resilient against higher loss rates. Fig. 4b and e clearly demonstrate that memory quality plays an important factor when determining reachable distances. While having satellites in higher orbits could be used to extend the reachable ranges even further, Fig. 4c and f demonstrate that there is a significant drop in key rates even for small θd.

Fig. 4: Exploring variations of the parameters.
figure 4

In each subfigure one parameter is varied, while the others are kept at their base value in Table 1. All plots are made for 1000-mode quantum memories. a–c show Scenario 1 (two repeater links), d–f show Scenario 2 (four repeater links). a/d Higher divergence angle θd = 4, 6, 8 μrad and therefore higher loss for SA satellite positions 0 (blue) and 0.2 (purple). b/e Various memory qualities with dephasing times Tdp of 1 s (blue), 100 ms (orange), 50 ms (pink), 10 ms (yellow), 5 ms (green), 4 ms (red), 3 ms (dark blue), 2 ms (black). c/f Differing orbital heights for all three satellites are 400 km (blue), 600 km (orange), 1000 km (pink), 1500 km (yellow), 2000 km (green).

Full size image

Effective rates for orbiting satellites

In the previous sections, we did not consider the movement of the satellites in an orbit around the Earth. While these static scenarios already show a wide range of effects and allow to draw conclusions about the importance of various parameters, the actual numbers obtained for the key rates would be more appropriate for far-future implementations with a large number of available satellites, which makes it likely to find sets of satellites close to optimal positions for large time periods. However, when analyzing near-term experiments with one or three satellites, the available time windows and changes of, e.g., diffraction and atmospheric losses along the path of the satellite become a vital component.

In the following, we look at a fixed ground distance d = 4400 km (i.e., right at the edge where a single satellite at the same orbital height h = 400 km can no longer see both ground stations at the same time). In Fig. 5a the total loss for establishing an entangled link between A and SC with an entangled pair source at SA as the setup of three satellites travels along its orbit is shown. This means that depending on the spacing between satellites in the orbit, there are time windows of about ~4–8 min where a signal can reach both ground stations. For comparison, the orbital period is ~92.4 min for this orbital height.

Fig. 5: Loss and key rates for a three-satellite network passing above ground stations d = 4400 km apart.
figure 5

The colors match the relative positions of the satellites in Fig. 3, such that when SC is exactly in the middle point between the ground stations SA will be at 0% (blue), 10% (orange), 20% (pink), or −10% (gray) of the total ground distance d. a Combined atmospheric and diffraction loss between A and SC (dashed lines) and along the whole optical path (solid lines). b The obtainable asymptotic key rate for Scenario 1 at points along the orbit if satellites were static at these positions.

Full size image

While the asymptotic key rates one would obtain with static satellites at various points along the orbit (as shown in Fig. 5b) are useful to get a sense of the performance of different setups, in order to estimate the actually obtainable rates one needs to analyse the effective quantum bit error rate of the raw bit strings collected at the ground stations. For each of the data points, we calculate the quantum bit error rate and average it weighted by the raw bit rate. We perform this for both scenarios with three satellites and also compare them to protocols with one satellite at higher orbits, as an alternative way to make key distribution at this distance possible. The obtainable raw bits per pass as well as the effective key rate (taking into account the time waiting for the satellites to come in range again) are summarized for a selection of satellite configurations in Table 2. For details of the calculations and additional results see Supplementary Note 3. It is worth noting that for the best working configurations around 104–106 raw bits per pass of the satellites can be expected, which would be sensible block sizes for finite key distribution protocols12 without having to accumulate bits over multiple passes.

Table 2 Effective rates for multiple configurations of orbiting satellites.
Full size table

Conclusion

In summary, we have developed a simulation for quantum repeaters that can deal with a variety of error models as well as multi-mode memories and setups with realistic protocols. This allows us to investigate scenarios that go beyond two repeater links (e.g., the protocol in Scenario 2 that uses four repeater links), for which no complete analytical description is known. We used this simulation to analyze the performance of schemes that use multiple satellites with quantum memories to perform QKD over long distances. Using more than one satellite allows one to reach distances that would be geometrically impossible with just one satellite. We have shown that reaching intercontinental distances with currently available or near-future experimental parameters is entirely feasible and even performing advanced schemes is reasonable, although the overhead of using multiple satellites is still very significant. In the future, we plan to use our simulation to analyze setups with actual experimental parameters to gauge the real performance that can be expected. Another direction would be to extend our approach to fully capture the effect of of changing conditions, e.g., as would be the case for analysing the full dynamics of moving satellites.

Methods

The main technique used to obtain our results is building on a substantial method involving a real-time Monte Carlo simulation. Our method focuses on high-level decision-making in creating protocols while faithfully including experimental parameters for many different physical implementations. This is in contrast to other large-scale simulations that put a much stronger emphasis on the network character of quantum networks, as being pursued, e.g., in refs. 46,47,48. We will report on substantial details and further applications of the simulation elsewhere. However, in the following, we briefly describe its basic working principles.

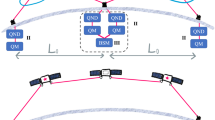
The simulation keeps track of the current situation, e.g., which pairs are currently established, at which stations the associated qubits are located and what the density matrix of each entangled pair is. All changes to the current situation happen via events that are scheduled in an event queue and resolved in order. For example, an event might be an entanglement swapping operation to connect two distant stations, or discarding a qubit that has been stored longer than the memory policy allows. Furthermore, a protocol determines the strategy of what events are scheduled. For instance, one component of the protocol might consist of scheduling an event that generates a new pair if the quantum memory is empty and generating a new pair is not already scheduled. An illustration of this scheme is depicted in Fig. 6.

Fig. 6: Schematic representation of the simulation framework.
figure 6

Events are scheduled in an event queue and resolved in order. The state of the simulation, i.e., the location of qubits and the quantum state of the entangled pairs, is changed when events get resolved. The figure shows as an example some of the information associated with an entanglement swapping event: at which station the entanglement swapping operation is performed, which entangled pairs are involved in the process, and which error model is relevant to the operation. The current state is monitored and new events are scheduled by the chosen protocol.

Full size image

We make use of two key methods that allow us to perform this simulation in a reasonable time frame. For one, we do not track individual photons that are much more likely to get lost than arrive at their destination when the loss is high. Instead, we use the known success probability of distributing a pair in one trial η and draw from a geometric probability distribution to determine how many sequential trials had to be performed in order to successfully establish one pair. This sampling from a probability distribution is why we call it a Monte Carlo simulation, even though other probabilistic aspects, e.g., dephasing noise in quantum memories and dark counts, are handled via the density matrix formalism. Secondly, we do not continuously update the effect of time-dependent dephasing noise in quantum memories, instead, we only update the quantum state when it becomes relevant, which is possible because we keep track of when it was last updated. This ensures that having many events happen in other parts of the simulation does not cause an undue amount of calculation for unaffected parts.