Abstract
Time-resolved studies with temporal resolution that separate molecular level dynamics from macroscopic changes, allow clear distinction between the time scales of the different degrees of freedom involved. Cooperative molecular switching in the solid state is exemplified by spin crossover phenomenon in crystals of transition metal complexes. Here we show the existence of a delay between the crystalline volume increase, and the cooperative macroscopic switching of molecular state. Using 100 ps X-ray diffraction, we track the molecular spin state and the structure of the lattice during the photoinduced low spin to high spin transition in microcrystals of [FeIII(3-MeO-SalEen)2]PF6. Model simulations explain the phenomenon with thermally activated kinetics governed by local energy barriers separating the molecular states. Such behaviour is different from that encountered in materials with no local energy barriers, where phase transformation can occur simultaneously with propagation of strain. Broadly, this motivates an optimised material design, scalable with size and intrinsic energetics.
Similar content being viewed by others
Introduction
Dynamical processes induced by a laser pulse in materials are intrinsically multi-scale in time and space. The difference of time scale is significant between the electronic processes, typically occurring within femtoseconds, the coherent atomic displacements ranging from few 10’s of femtoseconds to picoseconds reflecting the period of optical phonons, the volume expansion, and finally the slower kinetics dictated by activation energies. It is noteworthy that the macroscopic crystal deformations, such as global volume change, require collective atomic motions driving lattice deformations over long distances, i.e., acoustic wave propagation. The time scale is thus limited by the speed of sound in the crystal. The strain waves are triggered by laser-induced internal stress, generated by ultrafast lattice heating and/or instantaneous electronic change1,2. Recovery of the mechanical equilibrium with the sample environment occurs through wave propagation over the relevant length of the system (crystal size, light penetration depth,…). The associated acoustic time scale falls in the picosecond range for nanometers, and in the nanosecond range for micrometers in many materials of interest. Moreover, there may exist activation barriers at the local scale, which can further slow down the atomic rearrangements. As opposed to conventional time-averaging experiments, ultrafast time-resolved experiments are typically used to delineate the dynamics of the different degrees of freedom, such as change of electronic distribution, atomic reorganizations, as well as cell deformations3. They are key to understanding the non-equilibrium dynamics on material scale, and to harnessing the mechanisms that govern the properties of materials4,5,6,7.
The opportunity to photo-induce a phase transition with a laser pulse8,9 has opened up a vast field of research ranging from the melting of charge, spin and structural orders in electronically correlated materials10,11 to molecular switching in the solid state3,12,13,14. Recently, some attention has been turned to phase transitions that explore the possibility of combining the ultra-fast with the ultra-small15,16,17. We previously reported the size effect on an elastically-driven cooperative dynamical response in a switchable molecular crystal, a spin crossover (SCO) iron complex18. Owing to a positive elastic feedback from the expanding lattice on the volume-changing bistable molecules, the number of switched molecules is significantly enhanced and the lifetime of their photo-induced state is prolonged. The time scale of such dynamics showed to be scaling with the size, namely becoming shorter in micro- and nano-crystals than in bulk single-crystals (>100 μm). This suggested a central role of propagating volume expansion for the cooperative transformation at the scale of a crystallite19.
At thermal equilibrium, volume change and spin state switching occur together. In contrast, the out-of-equilibrium dynamics triggered by a laser pulse implies a sequence of processes with different intrinsic timescales. To establish the respective evolution of the elastic deformation of crystalline volume and the switching of molecular spin state, a simultaneous measurement of the two purportedly coupled parameters is required. To address this challenge, we used time-resolved X-ray diffraction (tr-XRD) on small crystallites. Our findings were corroborated with extended Monte Carlo simulations. They point to a bottleneck in the switching dynamics for SCO materials, and hint at a perspective for the design of functional spin-crossover nano systems.
Results
Phase transition and volume change in bulk single crystal
In this study, we focus on an SCO compound [FeIII(3-MeO-SalEen)2]PF6. The SCO materials serve as prototypical examples of cooperative switching between two molecular electronic states, Low Spin (LS) and High Spin (HS). The sample was previously identified as suitable candidate for the photo-induced out-of-equilibrium studies in solid-state from the angle of elastic properties that lead to strong cooperativity18. The crystalline structure of this material was characterized in previous studies (Supplementary Note 120,21). At the molecular level, the switching of electronic state of FeIII system, from LS (S = 1/2) to HS (S = 5/2) causes an increase of molecular volume, due to elongation of the Fe-Ligand bonds by around 0.15 Å between LS and HS states. The molecules in this compound are arranged in a closed-packed network20 (Fig. 1a). It is known that the relative stability between different macroscopic phases in such SCO crystals is ensured by the elastic intermolecular interactions of various strengths, resulting in more or less cooperative transformations22,23. In the present case, a strongly first-order phase transition is observed around 165 K, with a thermal hysteresis of 3 K, between the low-temperature LS phase and the high-temperature HS phase20. This phase transition is isostructural, as it does not imply any change of symmetry (same space group P-1 and Z = 2 for each phase), in a way similar to the gas-liquid transition24. The volume is a totally symmetric parameter and plays a central role for an isostructural phase transition. At thermal equilibrium, both the unit cell volume and the concentration of HS molecules show correlated jumps at the phase transition. This is usually observed for two totally symmetric degrees of freedom involved in changes associated with a phase transition without symmetry change25.
a [FeIII(3-MeO-SalEen)2]PF6 molecular lattices in Low Spin, LS (100 K, blue) and High Spin, HS (293 K, red) states, shown in the (a, c) plane. Ligands (in grey) are shown for the LS structure only. b X-ray diffraction (XRD) measurement on a single crystal: evolution on temperature, T, of the unit cell volume, V (T decreasing, plain black triangles, and T increasing, open circles) for extracting the thermal expansion parameters of the HS (red dotted line) and LS (blue dotted line) unit cell (Supplementary Note 120). Vertical black lines represent transition temperatures for T decreasing (Tdown) and T increasing (Tup). c–f Synchrotron x-ray powder diffraction on micro-crystals measured at ESRF, ID09 beamline: c Diffraction image measured at room temperature. d 1D powder patterns after azimuthal averaging of diffraction images (c) for the different temperature measured from 300 K to 100 K (upon cooling). e In yellow: temperature evolution of the magnetisation – temperature product MT as extracted from Superconducting Quantum Interface Device (SQUID) measurements; in grey: evolution of the HS fraction as extracted from the powder pattern refinement. Grey solid line is a guide for the eyes. f Temperature evolution of the mean unit cell volume as extracted from the powder pattern refinement. b, e and f: The vertical black line indicates transition temperature Tdown.
We performed XRD measurements on a single crystal (see Methods and Supplementary Note 2) between 100 K and 250 K, in order to quantify the volume jump (volume discontinuity at the first-order phase transition). The measured temperature evolution of the unit cell volume is displayed in Fig. 1b. It shows a significant volume jump of 1.6% (22 Å3 per unit cell) at the phase transition, taking place between the two thermal hysteresis limits Tdown = 163 K and Tup = 166 K, measured respectively upon cooling and upon heating (consistent with the values reported in the previous studies20). Below and above this discontinuity, the thermal expansion is also significant in both LS and HS phases. The same measurement allowed for determination of the thermal dependence of all six-unit cell parameters for each triclinic phase. Their extrapolated evolution can be described with a linear function of temperature T for both phases (Supplementary Figure 2 and Supplementary Table 1). The volume expansion coefficients for HS and LS phases were found to be respectively 0.31 Å3/K and 0.16 Å3/K (Fig. 1b). It is a considerable thermal expansion, leading to volume increase of 33 Å3 between 100 and 250 K, in comparison with 22 Å3 jump originating from the transition.
Powder XRD study at thermal equilibrium of micro-crystals
In the following, we will discuss measurements performed on micro-crystals of [FeIII(3-MeO-SalEen)2]PF6 embedded in a polymer thin film (see Methods). The small crystallites are plate-shaped, with average dimensions 3.5 µm × 0.35 µm × 0.13 µm21. The size is very much dependent on the synthesis conditions. Smaller crystallites are possible to obtain, but these were chosen to ensure diffraction patterns of sufficient quality for a quantitative analysis. The crystallites were dispersed in polyvinylpyrrolidone (PVP) polymer matrix and the composite films were spin-coated on a glass substrate, as described in26.
The powder XRD measurements were performed at ESRF, ID09 beamline. XRD images were recorded on a 2D detector in quasi-grazing reflection geometry at 0.2° incidence angle (see Methods). This experimental geometry was used to reduce the diffuse background due to scattering from the glass substrate and thereby enhance the diffraction from the thin film sample. A typical diffraction image is shown in Fig. 1c. The diffraction rings from the polycrystalline sample are clearly visible, with a patterning due to preferred orientation of the micro-crystals. Indeed, since the micro-crystals are plate-shaped, they tend to align with the shortest dimension (crystallographic c axis) perpendicular to the film surface. Several micro-crystals can also stack in-depth.
Temperature-dependent steady states measurements were first performed to characterize the XRD signatures of the phase transition in the polycrystalline sample. The measured diffraction patterns are shown in Fig. 1d. Strong diffuse background, mainly attributed to PVP (Fig. 1c) was removed, and the important peak broadening was ascribed mainly to a large X-ray footprint at the small angle of incidence. The latter made the analysis challenging, yet as detailed below, the full-pattern refinement was possible. This allowed for retrieval of key parameters, namely the phase fraction and the volume change.
To this end, we applied the Pawley approach27 using the Topas software28, and a similar method to the one recently applied for powder diffraction studies of photo-induced structural changes29,30. The refinements details are provided in Methods. In short, this method constrains the Bragg peaks positions according to the refined unit cell parameters, but allows the Bragg peaks intensities to vary freely. At room temperature, the sample is fully in the HS phase. At 100 K, it was not possible to fit the pattern satisfactorily considering LS phase only, therefore a biphasic state had to be considered, in contrast with the bulk single crystal. We ensured the stability of the refinement further by parametrization of the unit cell and peak intensities, as detailed hereafter. Firstly, to describe the volume evolution of both phases as a function of temperature T, the respective six unit cell parameters were forced to follow the thermal expansion determined with the single-crystal study and shown in Supplementary Figure 2. Consequently, the temperature T was the only parameter required to describe the evolution of all unit cell parameters. Secondly, the relative Bragg peak intensities Ihkl were fixed for both phases: Ihkl,HS, and Ihkl,LS were estimated from the refinements of the patterns at room temperature and 100 K, respectively. Thirdly, the complete powder patterns of a biphasic state (LS, HS) were fitted with the high spin fraction XHS as the only refined parameter (see Methods). In such a case, XHS accounts both for intensity changes and peak shifts, since the thermal expansion is phase-dependent.
The refined XHS is plotted in Fig. 1e as a function of temperature. A clear change of slope is observed at a temperature close to Tdown as defined above for the bulk single crystal. Above Tdown, the sample is almost fully in the HS phase, while a more rapid decrease of the HS fraction occurs below. Note that the absolute temperature on the sample between different setups (SQUID, XRD, optical spectroscopy), and also transition temperatures due to different sample batches of microcrystals, can vary by a few 10 s of K. In order to allow comparison between the different techniques, temperature scales are shifted for all XHS curves to have the change of slope at Tdown. To avoid confusion these rescaled temperatures will be referred to as T*. With this reference, the observed XHS evolution correlates very well with the M.T product (M, magnetisation and T, temperature) measured by SQUID (Superconducting QUantum Interference Device, see Methods), directly probing the evolution of the fraction of molecules in the HS state. Thus the spin state conversion in these micro-crystals shows two peculiar features: a gradual conversion (compared to abrupt in bulk), and incomplete conversion at low temperature. The residual XHS at T* = 100 K is equal to (34 +/− 3) %, which is consistent with the previous reports26. These two features may originate mainly from non-homogeneous stress due to surface interaction with polymers, resulting in a broad regime of phase coexistence21,31. The refined XHS also allows to calculate the average volume:
where VHS and VLS are the unit cell volume of the HS and LS phase respectively.
Concurrence of the gradual spin-state conversion and thermal expansion leads to a very smooth evolution of Vaverage. Yet, the latter slightly changes slope around T* = 160 K (Fig. 1f).
Thus parametrized powder pattern refinement allows extracting accurate values for both XHS(T) and Vaverage(T) simultaneously, and the ensuing discussion is hinged upon it. We should nonetheless mention some underlying assumptions. First hypothesis is that the LS and HS phases can be treated as separate diffracting domains. Explicitly, XHS quantifies the fraction of ordered HS domains, rather than counting the HS molecules. In case of random distribution of HS and LS molecules in the crystals, this model would lead to a misestimation of the real molecular fractions. A good correlation between XHS and the fraction obtained with SQUID, counting individual molecules irrespective of their spatial ordering, supports our assumption. The second hypothesis is that other structural distortions upon temperature within a given phase have negligible contribution to the changes of Ihkl. This is substantiated with measurements on a single crystal (Supplementary Figures 1.1 and 1.2) and therefore seems reasonable too.
Time-resolved XRD study of photoinduced dynamics
The tr-XRD images were recorded at 100 K with the setup described above. The crystallites were excited with 1 ps pump laser at 800 nm, as in previous optical studies18. The experimental time resolution was limited by the X-ray pulse duration to 100 ps. The details about the setup and data reduction are given in Methods.
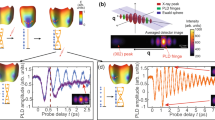
The time-resolved patterns covering several decades in time are shown in Fig. 2a. Photo-induced changes can be seen on these patterns for all positive delays, and they are emphasized in the difference patterns (Fig. 2b). The comparison with steady-state diffraction patterns measured at low and high temperature allows for a qualitative description. The shape of the difference patterns can be explained by a shift and a change of the diffracted intensity, from LS- to HS-Bragg peaks. These structural changes are clearly visible in Fig. 2b) for the intense peaks indexed (101), (01-1), and (102). In contrast, it is difficult to exploit the photoinduced change of (111) peak given the precision of our measurements. However, the peak shift to smaller q due to volume expansion would produce a similar difference pattern. Therefore, separating these two possible contributions requires more quantitative analysis as described below. A closer inspection of the difference patterns also gives some insight into the dynamics. First changes occur within the 100 ps time resolution. Thereafter, the difference patterns change shape, suggesting a sequence of processes with structurally distinct signatures.
a Time-resolved powder patterns and the corresponding difference patterns measured at the rescaled temperature T* = 100 K under high excitation fluence 380 μJ/mm2 (difference patterns are multiplied by 2 and shifted by 4 for clarity). Blue to red colors correspond to increasing time delay from negative to positive (detailed delays in Methods). b Integrated steady state patterns measured at room temperature (High Spin (HS) state, in red, plain line) and T* = 100 K (in blue, dotted line), offset for clarity by arbitrary values. Black lines are the result of powder pattern refinements (see Methods) and grey lines correspond to the residual (difference between experimental and refined patterns). Time-resolved differential pattern measured at T* = 100 K from −50 ps to 1 ms after photo-excitation under high fluence 380 μJ/mm2 (multiplied by 4 for clarity), showing the characteristic shape for volume expansion (peak shifts towards lower q values). Red and blue vertical lines indicate the position of major HS and Low Spin (LS) Bragg peaks, respectively. Time evolution of the unit cell volume (c), temperature change ∆Tlattice (d, see Methods), and relative HS fraction ∆XHS (e) as extracted from powder pattern refinement. Error bars correspond to 3σ, where σ is the refinement error as defined in Topas (see methods). f time evolution of ∆XHS at T* = 110 K (see Supplementary Note 7) as extracted from optical spectroscopy (adapted from18). In orange (squares): high excitation density (380 µJ/mm² and 410 µJ/mm² for X-ray diffraction (XRD) and optical density (OD) measurements, respectively), in dark green (triangles): low excitation density (60 µJ/mm² and 100 µJ/mm² for XRD and OD measurements, respectively). For this low fluence, the ΔXHS is multiplied by 2 for clarity.
In order to analyze the underlying structural dynamics, the same method of full-pattern refinement as in the temperature study was applied to the tr-XRD patterns. The refinement results are shown in Fig. 2c. The parametrized model was similar to that used in the temperature study. However, in addition to XHS, the lattice temperature becomes an adjustable parameter Tlattice, to account for the heating which drives the non-equilibrium lattice expansion in each phase (see Methods). The time evolution of the structural parameters obtained for the highest excitation density (380 µJ/mm²) reveals multistep dynamics. A small increase of ΔXHS estimated at 7%, accompanied by a small volume increase, is observed at the early step (i.e., within 100 ps time resolution). Even if the initial volume rise cannot be accurately determined due to the 100 ps time resolution, the maximum of the volume expansion is sufficiently pronounced and well resolved at around 300 ps. At this delay, for high excitation density, the refinement yields a value of ΔTlattice = (90 +/− 5) K, corresponding to ΔVaverage = 19 Å3. During this second step, ΔXHS increases very little, even at high excitation density. At such excitation, a more pronounced increase of ΔXHS occurs during a third step on the nanosecond time scale, with a plateau between t = 20 ns and t = 300 ns, corresponding to the maximum transformation ΔXHS = 23%. Finally, ΔXHS and volume decrease simultaneously, and recovery of the values at thermal equilibrium occurs on a sub-millisecond time scale. The most striking observation is the decoupling in time between the dynamics of volume change and ΔXHS: the increase of ΔXHS occurs two orders of magnitude later than the increase of volume. Importantly, their respective dependence on the excitation density is very different. Irrespective of excitation density, either low or high, the volume expansion exhibits a maximum around 300 ps. In contrast, ΔXHS exhibits a continuous decrease in the ns range at low excitation density, and a pronounced increase to a clear maximum at 20 ns for high excitation density (Fig. 2c). However, no significant increase of average volume is observed when ΔXHS reaches its maximum.
The validity of such analysis of non-equilibrium dynamics whereby Ihkl and the lattice expansion are a-priori assumed, can be questioned. Both affect mainly the refined XHS. In particular, the newly formed HS molecules might be homogeneously distributed within the crystal, rather than organized into separate diffracting phases. This homogeneous distribution would lead to a change of the average structure factor of each phase32, that is not taken into account in our analysis. Since the refinement of the structure factor (i.e Rietveld refinement) was not feasible with our data set, we instead allowed some freedom on the intensities of the LS peaks to account for a possible switching of randomly distributed LS molecules to the HS state. The resulting volume change and ΔXHS are plotted in Supplementary Figure 3. This approach leads to higher refinement errors and different ΔXHS (15%, instead of 25% in the two-domain model) but it retains the main features of the photo-induced dynamics: the maximum of volume change occurs around 300 ps while the maximum of ΔXHS change occurs around 20 ns. Moreover, as already stressed, the evolution of ΔXHS obtained by such analysis is consistent with previous optical measurements (Fig. 2f) that yield ΔXHS directly whether or not phase separation should take place. Such agreement strengthens the validity of the global analysis.
Monte-Carlo simulations of mechanoelastic model
In order to rationalize the experimental results, we applied the mechanoelastic model, also referred to as ball-and-spring model. In this two-dimensional model, molecules are mimicked with spheres (balls) whose radii reflect LS or HS state (10% increase in radius from LS to HS molecules, as observed on the Fe-Ligand bond length). The balls are connected by springs, which replicate elastic interactions occurring in the solid-state through the lattice (Fig. 3a). When molecules (balls) switch, they induce a local deformation of neighboring springs through a change of radii, that will propagate to the adjacent molecules (balls). Hence, the elastic force network accounts for both short- and long-range interactions in the model. The probabilities for switching a given molecule from LS to HS state, and the reverse, depend on the temperature and the local pressure through Arrhenius-like activation. This model was successfully used in previous studies to simulate the out-of-equilibrium self-amplification33,34, but in its simplest form cannot account for the time separation between the volume change and the increase of the HS fraction. Therefore in the following, we propose an extension of that model, taking into account thermal lattice expansion.
a [FeIII(3-MeO-SalEen)2]PF6 molecular lattice in Low Spin (LS) state, displayed in the (a, c) plane, ligands are hidden for clarity. The rounded blue contours encircle two molecules per unit cell. In Monte-Carlo (MC) simulations, elastic interactions are modeled by springs connecting the unit cells; diagonal springs prevent structural collapse in simulations. b Schematic representation of ball and spring model accounting for thermal volume expansion. The rounded blue and red contours replicate molecules in LS and High Spin (HS) state, respectively; short black and long magenta sticks replicate the thermal load on the springs. c Simulations of evolution of relative HS fraction ΔXHS and of the relative surface S/S0 (equivalent to volume in 2D box) following high (20%, orange, plain lines) and low (5%, dark green, dashed-dotted lines) fractions of switched sites at MC’s step zero. Dotted grey lines correspond to previous model, without initial spring length increase. In that case, the increase of HS fraction and the volume were not separated in time.
The elastic stresses originate not only from the molecular swelling upon LS to HS switch, but also from the lattice heating. The latter leads to the so-called thermo-elastic stresses that trigger thermal expansion1,35,36. It originates from the energy transfer between the photoexcited molecules and the thermal bath of lattice phonons37. Because the simulations rely on a harmonic potential, such phenomenon cannot be reproduced by a temperature increase alone, which only modifies the probability of switching. For this work, the Monte-Carlo (MC) model was extended to account for the thermal expansion by allowing distances between molecules to increase without changing the spin state. To factor this aspect of non-equilibrium thermodynamics in MC simulations, the springs were allowed to stretch beyond the HS and LS equilibrium distances at a given temperature (Fig. 3b). This mimics thermal lattice expansion. In practice, we started with a simulation assuming a homogeneous increase of temperature, with 15% increase for HS and LS spring lengths. Following this very first MC step, the spring lengths recover equilibrium positions exponentially, with the same time constant as the recovery of equilibrium temperature. Such extension of the insofar used model is a simple yet satisfactory approximation that allows independent treatment of volume change and spin transition.
Discussion
We now consider the implications of the observed multistep structural dynamics and propose a comprehensive scheme for the macroscopic photo-switching. In particular, we discuss the origin of a significant delay between the volume expansion process and the transformation from LS to HS phase.
The initial step of photo-excitation by a 100 fs laser pulse was described previously38. Direct photo-excitation from LS to HS molecular state is forbidden, so the 800 nm light is used to photo-excite a LS molecule to a short-lived intermediate singlet state, followed by an ultrafast intersystem crossing towards the HS state39. The latter is structurally relaxed on the ps time scale. The switched molecules are uniformly distributed in each microcrystal, since the photoexcitation is uniform both in the face parallel to the film surface and along the direction of the laser beam. The thickness (130 nm) is indeed much smaller than the penetration depth of laser light (approximately 5 μm at 800 nm18). Initial ΔXHS is small and it scales linearly with the excitation density18, here estimated at 7 % for the high excitation density (Fig. 2e). Importantly, the absorbed photon energy (1.55 eV) is much higher than the energy difference between HS and LS ground states (tens of meV). By consequence, most of the absorbed energy is dissipated through lattice heating. Complementary time resolved mid-IR measurements (Supplementary Note 4) that monitor the vibrational population of nascent HS molecules show that the incoherent energy transfer from large amplitude intramolecular vibrations of photoexcited molecules to the lattice is typically complete within 25 ps, which is reasonable for an insulating material (phonon-phonon interactions). During this initial process at the molecular scale, the volume is constrained, and uniformly distributed stresses are generated through both the swelling of switched molecules and the lattice heating. Subsequently, volume starts to expand through a coherent propagative process occurring at the microcrystal scale. Strain waves are launched directly from the surface of microcrystals to recover mechanical equilibrium with the environment, which is reached when the internal and the atmospheric pressure become equal1,2,36. Such strain wave picture is supported by the observation of a maximum of the volume expansion occurring at 300 ps, irrespective of the excitation density. It corresponds to the travel time of the volumic deformation through a microcrystal40. Thus, taking a sound velocity v ~ 4 * 10³ m.s−1 estimated from previous measurements on similar samples41 and L ~ 1.3 µm the average crystal dimension, the associated acoustic time scale is τ = L/v = 1.3*10−6/4*10³ = 330 ps. Moreover, the initial photo-switching of 7% of the molecules causes the average volume jump of only 1.5 Å3 (Fig. 1f), significantly smaller than the observed volume change of 19 Å3 at the maximum of volume expansion (Fig. 2c). It indicates that the lattice heating is dominant in this process. The estimated temperature rise at the surface due to imparted laser energy (Supplementary Note 5), ΔTlattice = 105 K, corroborates the experimentally found ΔTlattice = 90 K. After 300 ps, ΔVaverage decreases continually, due to heat transfer to the polymeric environment.
Even for the high excitation density, no significant increase of ΔXHS is observed during the acoustic step. It contrasts with ΔXHS = 23% on the 10–100 ns time scale, in agreement with previous optical measurements (Fig. 2e-f). A clear decoupling in time between the dynamics of volume expansion and molecular switching may be explained by a characteristic feature of SCO compounds, namely the existence of energy barriers between LS and HS state at molecular scale. They activate slower kinetics determined by Arrhenius-like probabilities, as introduced in the mechanoelastic model. Our simulations suggest that the delay of the activation is indeed independent of the size of the simulation box (Supplementary Note 6.2), unlike the time taken by the strain wave to travel through a microcrystal. At 300 ps, the molecular state is not equilibrated with the lattice thermal bath, and remains essentially frozen by local energy barriers. The volume expansion redistributes local pressure in a way that favors HS over LS (Supplementary Note 6.1), yet it does not cancel the effect of the energy barrier between these two molecular states and the transformation can only occur on longer time scale. Moreover, the occurrence of the second increase of ΔXHS depends in a non-linear fashion on the excitation density, experimentally and in the simulation (Figs. 2e and 3c). No such increase is observed at low excitation (Fig. 2e), in accordance with the threshold effect evidenced by optical measurements. Energy deposited by a laser pulse, controlling the initial density of photoexcited molecules, needs a certain value to trigger the phase transformation at the macroscopic scale. At low density, the photoexcited HS may relax to the ground LS state quasi-independently. At high density, the elastic interactions between photoexcited HS lead to a positive feedback and increase of XHS to a point where HS phase transformation can occur. This is a manifestation of cooperative response during the phase transformation. By contrast, a linear elastic response is observed for the propagating volume. The delay by almost two temporal decades between the two processes is relatively long. It is fair to assume that achieving a phase transition at the macroscopic scale requires more time than does the switching of independent molecules42. It is clear that the growth of the HS phase in the LS matrix will cost elastic energy and cause internal stresses at the interface between two phases. At the present stage, it is not possible to determine the exact physical picture of such kinetics of phase transformation. However, we can argue that it probably occurs by minimizing this elastic cost. Ultimately, addressing this question would require probing isolated single crystallites, for instance by electron microscopy14. Moreover, it is noteworthy that no additional volume increase is observed when ΔXHS reaches maximum. A part of the thermal energy stored in the lattice is spent on the latent heat of phase transformation. Consequently, the lattice temperature (Fig. 2d) and volume would decrease and counterweight the increase of volume originating from phase transformation.
Finally, after this step which occurs only at high excitation density (Figs. 2e and 3c), ΔVaverage and ΔXHS relax simultaneously on 10 µs time scale (50% decrease) to recover equilibrium with the environment. This is about two decades longer compared to a faster recovery under the effect of the low excitation. It is hence justified to suggest that the phase transformation associated with a sufficiently expanded volume prolongs the lifetime of the transient high spin state. Note that heat diffusion within the film could also contribute to the HS switching on long time scales18. Though photoexcitation is homogeneous in a given microcrystal, there exists an excitation gradient within the film. Temperature homogenization due to heat diffusion between crystallites proceeds on a great length scale (typically 10 µm). It can lead to a small yet measurable delayed increase of XHS in the range of few 10’s µs (see Supplementary Figure 7).
In conjunction with the earlier optical studies that revealed size-dependent switching time18, and a priori expectation that in the ever so smaller nanoparticles the macroscopic switching of the molecular state can be indefinitely fast, these results point to a bottleneck in the switching dynamics. Hence, our findings define the ultimate time scale for macroscopic transformation of molecular state in nanoscale objects for this class of solids. They do not obey the rule “the smaller the faster”17. This finding could motivate an optimised material design, scalable with size-dependent dynamics and intrinsic energetics. A perspective for the design of functional spin-crossover nano systems could reside in chemical leverage of the energy barriers by tuning the ligand field43, or other methods44.
Conclusion
First and foremost, these results demonstrate the capacity of time-resolved X-ray powder diffraction to simultaneously determine the photoinduced dynamics of average unit cell parameters and phase fraction in a molecular switchable material. A quantitative structural analysis30,45 allowed to establish a sequence of events by which photo-induced spin-state switching occurs from molecular to material scales. In particular, the experimental results support a scheme for the multiscale dynamics at a macroscopic scale whereby the volume expansion and the increase of switching molecules are clearly separated in time. The time scale of the dynamics of volume expansion scales with crystal size, which agrees with a propagative coherent picture of collective atomic motions such as longitudinal elastic waves, while the cooperative self-amplification upon phase transformation takes place later. The complete photo-induced cycle is drawn schematically in Fig. 4. It delineates time scales for multiscale dynamics triggered by a laser pulse at a molecular level and on the macroscopic scale. It emphasizes that the mechanisms involved in spin state switching through the excited state and the ground state are different. The photophysics of the excited state was largely covered in the literature, yet the cycle at the macroscopic level barely starts there. The figure depicts temporal decoupling at the macroscopic scale between the fast collective dynamics of volume dilation and the slow thermally activated kinetics of the LS-to-HS transformation. This bottleneck, where the molecules are frozen in their initial electronic state and intramolecular structure at acoustic time scale, may be discussed in terms of thermally activated kinetics at molecular scale, an intrinsic characteristic of SCO compounds. A model simulation accounting for this thermally activated kinetics, governed by local energy barriers separating LS and HS molecular state, reliably reproduced all important experimental features, the separation of time scales, and cooperative response of phase transformation (Fig. 3). The main lesson is that this situation is fundamentally different from that encountered in systems with no local energy barriers. In such a case, the transformation implies only ultrafast electronic redistribution and structural dynamics of atomic displacements on the optical phonon time scale. Those dynamics follow the propagation of volume expansion as observed recently in nano-crystals of a metal oxide undergoing insulator-to-metal transition, i.e., another isostructural first-order phase transition exhibiting large volume change30. In the case of SCO, the volume has to expand sufficiently to promote the thermally activated transformation towards the HS phase at the macroscopic scale. Should the energy barrier be very low, the macroscopic transformation would be limited by the propagation of volumic strain waves on the acoustic time scale.
1: laser induced charge transfer promotes Low Spin (LS) molecules (not shown for clarity) residing in LS lattice (blue) to a hot High spin (HS) state (shape and color coded consistently with Fig. 3) in less than 100 fs. 2: vibrational cooling of hot molecules with LS lattice (color-coded consistently with Fig. 3) takes place on the picosecond time scale. 3: volume expansion of heated lattice in 100’s ps, and coexistence of LS molecules (not shown) in thermally dilated LS lattice (blue) with photo-switched HS molecules (red) in thermally dilated HS lattice (red). HS and LS lattices superimposed to emphasize their likely coexistence (only average volume measured with X-ray diffraction). 4: shift of the switching regimes: LS molecules residing in the ground state switch to the HS state according to LS/HS occupancy probabilities modified by lattice expansion; the delay between expansion (300 ps, or less for nano-crystallites) and the switching (ns time-scale), due to incompressible Arrhenius-type kinetics sketched in the insert. 5: equilibrium recovery within μs time scale.
Methods
Single crystal X-ray diffraction
Temperature-dependent X-ray diffraction (XRD) study was performed on [FeIII(3-MeO-SalEen)2]PF6 single crystal using a laboratory SuperNova Agilent Technologies 4-circle diffractometer, with Cu-Kα microsource (λ = 1.5406 Å) and EosS2 CCD camera. The sample was cooled down using 800 Plus nitrogen flow cryostat from Oxford Cryosystems. To obtain good precision of cell parameter change with temperature, a set of short scans within 2 Å resolution was taken from 100 K to 250 K, with 2 to 5 K steps. Data reduction was performed with CrysAlisPro software. The single crystal had a plate shape, with a long dimension around 100 µm.
Samples
The FeIII compound was prepared in the form of a powder of pure microcrystals as previously reported21. The microcrystals (typical dimensions of 3.5 µm, 0.35 µm, 0.13 µm from Transmission Electron Microscopy) were processed in polyvinylpyrrolidone (PVP, MM = 45,000 gmol−1) thin films formed by spin-coating on glass substrate26.
X-ray diffraction on polycrystalline sample
Experimental setup
X-ray diffraction experiment was performed at ESRF, ID09 beamline during hybrid mode (7/8th continuous filling + 1 isolated electron bunch). The isolated electron bunch was used in the experiment. The ID09 setup was discussed in detail previously46. Briefly, fast rotating choppers were used to isolate X-ray single pulses (each 100 ps long) at 40 Hz repetition rate. The X-rays energy was centered at 18 keV (λ = 0.6888 Å) with 1.5% bandwidth. The beam size at sample position was 0.1 (horizontal) x 0.02 (vertical) mm2. Diffracted X-rays were integrated on a Rayonix MX170-HS CCD detector. Each image was recorded with 1000 shots exposure.
For the thermal study at equilibrium, the sample was cooled down using a nitrogen cryostream 700 Plus from Oxford Cryosystems and diffraction images were measured with 1 K steps from 293 K to 100 K.
For the time-resolved study, a synchronized laser (800 nm) at 40 Hz was used to excite the sample with 11° incident angle. Laser Beam size was 1.2 × 0.23 mm2, leading to a laser footprint on sample of (6.3 × 0.23) mm². The sample was cooled down to 100 K. Diffraction patterns were measured with 60 µJ/mm² and 380 µJ/mm² laser excitation, for time delays in the following lists, respectively:
[−50 ps, 0 ps, 50 ps, 100 ps, 300 ps, 1 ns, 3 ns, 10 ns, 30 ns, 100 ns, 300 ns, 1 µs, 3 µs, 10 µs, 100 µs, 300 µs, 1 ms]
[−50 ps, 0 ps, 50 ps, 100 ps, 200 ps, 300 ps, 700 ps, 1 ns, 1.5 ns, 3 ns, 5 ns, 7 ns, 10 ns, 30 ns, 100 ns, 300 ns, 1 µs, 3 µs, 10 µs, 30 µs, 100 µs, 300 µs, 1 ms]
Measurements were performed with shuffled delays, to detect any drift effects during the experimental time.
Data Reduction
The diffraction images were azimuthally integrated using pyFAI47. Background was subtracted using scikit-ued python library48. Negative reference patterns (−5 ns) were used to calculate differential patterns and averaging with trx python library (https://github.com/marcocamma/trx).
Powder patterns refinement
Full powder pattern refinements were performed after the data reduction step described above. Peak profiles and sample displacement were described from a fundamental parameter approach using expressions derived in49 with the TOPAS software28. The incident wavelength was fixed at λ = 0.6888 Å (E = 18 keV) and wavelength dispersion described by a gaussian convolution with FWHM = 10 mÅ (corresponding to Δλ/λ = ΔE/E = 1.5%). The beam height at sample position was fixed to 20 µm. Fixed incident angle αi was set to 0.2° for all scans. The latter parameters determine geometrical contribution to peak profiles (peak width). Sample displacement was refined once and fixed for a given temperature / time scan. Background subtracted patterns were refined on [0.3–1.9] Å−1 range. Typical Rwp was (19 +/− 2) %.
The refinement model includes two phases, namely ‘HS’ and ‘LS’ defined by a set of parameters xi(T) = xi,0 + xi,1T with x = a, b, c, α, β, γ and i = LS, HS. All parameters are given in Supplementary Table 1. Peak intensities {Ihkl,i} are refined according to equilibrium patterns measured at 300 K and 100 K for HS and LS phase, respectively. Based on the known structures and their temperature dependence, variations of Ihkl with temperature (due to variations of B-factors) are expected to have a negligible contribution to the powder patterns as measured in our experiment, and are thus neglected in the refinement model.
In the out-of-equilibrium patterns, the temperature T becomes refined parameter Tlattice, and XHS is also refined for each delay. In the study at thermal equilibrium, temperature is taken as a control parameter and thus not refined.
Magnetic susceptibility
Magnetic measurements were carried out using a Quantum Design SQUID magnetometer (MPMS5S Model) calibrated against a standard palladium sample. Data were collected between 250 and 50 K, at a rate of 0.67 K/min with a small number of microcrystals embedded in PVP, once removed from the glass substrate.
Data availability
Raw data were generated at the ESRF large-scale facility. Derived data supporting the findings of this study are available from the corresponding authors upon request.
References
Thomsen, C., Grahn, H. T., Maris, H. J. & Tauc, J. Surface generation and detection of phonons by picosecond light pulses. Phys. Rev. B 34, 4129–4138 (1986).
Wright, O. B. Ultrafast nonequilibrium stress generation in gold and silver. Phys. Rev. B 49, 9985–9988 (1994).
Lorenc, M. et al. Successive dynamical steps of photoinduced switching of a molecular Fe(III) spin-crossover material by time-resolved X-ray diffraction. Phys. Rev. Lett. 103, 028301 (2009).
Bargheer, M. et al. Coherent atomic motions in a nanostructure studied by femtosecond X-ray diffraction. Science 306, 1771–1773 (2004).
Baum, P., Yang, D.-S. & Zewail, A. H. 4D visualization of transitional structures in phase transformations by electron diffraction. Science 318, 788–792 (2007).
Braun, M. et al. Ultrafast changes of molecular crystal structure induced by dipole solvation. Phys. Rev. Lett. 98, 248301 (2007).
Morrison, V. et al. A photoinduced metal-like phase of monoclinic VO2 revealed by ultrafast electron diffraction. Science 346, 445–448 (2014).
Nasu, K. K. Multistabilities of the ground states, proliferations of excitons and photo-induced structural phase transitions. In: Nasu K. (eds) Relaxations of Excited States and Photo-Induced Structural Phase Transitions. Springer Series in Solid-State Sciences, vol 124. Springer, Berlin, Heidelberg https://doi.org/10.1007/978-3-642-60702-8_1 (1997).
K. Nasu (ed.) Photoinduced Phase Transitions https://doi.org/10.1142/5476 (World Scientific, 2004).
Zhang, J. & Averitt, R. D. Dynamics and control in complex transition metal oxides. Annu. Rev. Mater. Res. 44, 19 (2014).
Basov, D., Averitt, R. & Hsieh, D. Towards properties on demand in quantum materials. Nat. Mater. 16, 1077–1088 (2017).
Cailleau, H. et al. Acta Cryst. A66, 189–197, https://doi.org/10.1107/S0108767309051046 (2010).
Van der Veen, R.-M., Tissot, A., Hauser, A. & Zewail, A.-H. Unusual molecular material formed through irreversible transformation and revealed by 4D electron microscopy. Phys. Chem. Chem. Phys. 15, 7831–7838 (2013).
Van Der Veen, R.-M., Kwon, O.-H., Tissot, A., Hauser, A. & Zewail, A.-H. Single-nanoparticle phase transitions visualized by four-dimensional electron microscopy. Nat. Chem. 5, 395 (2013).
Sagar, D. M. et al. Femtosecond measurements of size-dependent spin crossover in Fe(II)(pyz)Pt(CN)4 nanocrystals. J. Phys. Chem. Lett. 7, 148–153 (2016).
Park, S. T. & van der Veen, R. M. Modeling nonequilibrium dynamics of phase transitions at the nanoscale: Application to spin-crossover. Struct. Dyn. 4, 044028 (2017).
Ridier, K. et al. Finite size effects on the switching dynamics of spin‐crossover thin films photoexcited by a femtosecond laser pulse. Adv. Mater. 31, 1901361 (2019).
Bertoni, R. et al. Elastically driven cooperative response of a molecular material impacted by a laser pulse. Nat. Mater. 15, 606–610 (2016).
Bertoni, R. et al. Cooperative elastic switching vs. laser heating in [Fe(phen)2(NCS)2] spin-crossover crystals excited by a laser pulse. CrystEngComm 16, 7269–7275 (2016).
Tissot, A., Bertoni, R., Collet, E., Toupet, L. & Boillot, M.-L. The cooperative spin-state transition of an iron(III) compound [FeIII(3-MeO-SalEen)2]PF6: thermal- vs. ultra-fast photo-switching. J. Mater. Chem. 21, 18347–18353 (2011).
Tissot, A., Rechignat, L., Bousseksou, A. & Boillot, M.-L. Micro- and nanocrystals of the iron(iii) spin-transition material [FeIII(3-MeO-SalEen)2]PF6. J. Mater. Chem. 22, 3411–3419 (2012).
Rat, S. et al. Solvatomorphism and structural-spin crossover property relationship in bis[hydrotris(1{,}2{,}4-triazol-1-yl)borate]iron(II). CrystEngComm 19, 3271–3280 (2017).
Buron-LeCointe, M. et al. Intermolecular control of thermoswitching and photoswitching phenomena in two spin-crossover polymorphs. Phys. Rev. B 85, 064114 (2012).
Chernyshov, D., Bürgi, H.-B., Hostettler, M. & Törnroos, K. W. Landau theory for spin transition and ordering phenomena in Fe(II) compounds. Phys. Rev. B 70, 094116 (2004).
Landau, L. D. and Lifshitz, E. M. Statistical Physics 3rd Edition Part 1, Elsevier https://doi.org/10.1016/C2009-0-24487-4 (1980).
Bertoni, R. et al. Femtosecond spin-state photoswitching of molecular nanocrystals evidenced by optical spectroscopy. Angew. Chem. 51, 7485–7489 (2012).
Pawley, G. S. Unit-cell refinement from powder diffraction scans. J. Appl. Crystallogr. 14, 357–361 (1981).
Coelho, A. A. TOPAS and TOPAS‐Academic: an optimization program integrating computer algebra and crystallographic objects written in C++. J. Appl. Cryst. 51, 210 (2018).
Azzolina, G. et al. Single laser shot photoinduced phase transition of rubidium manganese hexacyanoferrate investigated by x‐ray diffraction. Eur. J. Inorg. Chem. 3142–3147 https://doi.org/10.1002/ejic.201900598 (2019).
Mariette, C. et al. Strain wave pathway to semiconductor-to-metal transition revealed by time resolved X-ray powder diffraction. Nat. Comm. 12, 1239 (2021).
Laisney, J. et al. Mechanical-tuning of the cooperativity of SC particles via the matrix crystallization and related size effects. J. Mater. Chem. 8, 7067 (2020).
Collet, E. et al. Ultrafast spin-state photoswitching in a crystal and slower consecutive processes investigated by femtosecond optical spectroscopy and picosecond X-ray diffraction. Phys. Chem. Chem. Phys. 14, 6192–6199 (2012).
Enachescu, C. et al. Theoretical approach for elastically driven cooperative switching of spin-crossover compounds impacted by an ultrashort laser pulse. Phys. Rev. B 95, 224107 (2017).
Bertoni, R. et al. Temperature dependence of the cooperative out-of-equilibrium elastic switching in a spin-crossover material. Phys. Chem. Chem. Phys. 21, 6606–6612 (2019).
Matsuda, O., Larciprete, M. C., Li Voti, R. & Wright, O. B. Fundamentals of picosecond laser ultrasonics. Ultrasonics 56, 3–20 (2015).
Ruello, P. & Gusev, V. E. Physical mechanisms of coherent acoustic phonon generation by ultrafast laser action. Ultrasonics 56, 21–35 (2015).
Lorenc, M. et al. Cascading photoinduced, elastic, and thermal switching of spin states triggered by a femtosecond laser pulse in an Fe(III) molecular crystal. Phys. Rev. B 85, 054302 (2012).
Cammarata, M. et al. Sequential activation of molecular breathing and bending during spin-crossover photoswitching revealed by femtosecond optical and X-ray absorption spectroscopy. Phys. Rev. Let. 113, 227402 (2014).
Hauser, A., Gütlich, P. & Spiering, H. High-spin→low-spin relaxation kinetics and cooperative effects in the [Fe(ptz)6(BF4)2 and [Zn1-xFex (ptz)6](BF4)2 (ptz = 1-Propyltetrazole) spin-crossover systems. Inorg. Chem. 25, 4245–4248 (1986).
Schick, D. et al. Ultrafast lattice response of photoexcited thin films studied by X-ray diffraction. Struct. Dyn. 1, 064501 (2014).
Parpiiev, T. et al. Ultrafast non-thermal laser excitation of gigahertz longitudinal and shear acoustic waves in spin-crossover molecular crystals [Fe(PM–AzA)2(NCS)2]. Appl. Phys. Lett. 111, 151901 (2017).
Boukheddaden, K., Shteto, I., Hôo, B. & Varret, F. Dynamical model for spin-crossover solids. I. Relaxation effects in the mean-field approach. Phys. Rev. B 62, 14796–14805 (2000).
Feringa, B. L. & Browne, W. R. (eds). Molecular Switches. Second Edition. 2, 792 (Wiley-VCH, Weinheim, 2011).
Galego, J., Garcia-Vidal, F. & Feist, J. Suppressing photochemical reactions with quantized light fields. Nat. Commun. 7, 13841 (2016).
Freyer, B. et al. Ultrafast inter-ionic charge transfer of transition-metal complexes mapped by femtosecond X-ray powder diffraction. J. Chem. Phys. 138, 144504 (2013).
Cammarata, M. et al. Chopper system for single pulse experiments with synchrotron radiation. Rev. Sci. Instrum. 80, 015101 (2009).
Ashiotis, G. et al. The fast azimuthal integration Python library: pyFAI. J. Appl. Crystallogr. 48, 510 (2015).
René de Cotret, L. P. & Siwick, B. J. A general method for baseline-removal in ultrafast electron powder diffraction data using the dual-tree complex wavelet transform. Struct. Dyn. 4, 044004 (2017).
Rowles, M. R. & Buckley, C. E. Aberration corrections for non-Bragg–Brentano diffraction geometries. J. Appl. Cryst. 50, 240–251 (2017).
Acknowledgements
M.Lo. gratefully acknowledges the Agence Nationale de la Recherche for financial support under grant ANR-16-CE30-0018 (“Elastica”). M.-L.B. thanks Amandine Bellec and Eric Rivière for their assistance in the profilometry and magnetic measurement. Parts of this research were carried out in the frame of the IM‐LED LIA (CNRS). The work of C.E. was supported by a grant of the Romanian Ministry of Research, Innovation and Digitisation, CNCS/CCDI-UEFISCDI, Project No. PN-III-P4-ID-PCE-2020-1946, within PNCDIII. M.Lo. and L.S. acknowledge the support by PHC Brancusi program.
Author information
Authors and Affiliations
Contributions
C.M. and M.Lo. coordinated the project. A.V., C.M., E.T., M.Lo., R.B., M.C. carried out the experiment at ESRF. M.C. and M.Le. developed the setup. A.V. and C.M. with the help of E.T. performed X-ray data analysis. X.D., M.Lo., and J.K. carried out midIR experiment and J.K. analysed the data. Crystals were characterized and synthesized by F.Y. and M.-L.B. Monte-Carlo simulations were carried out by L.S. and C.E. with help of A.V. The discussion was extensively commented by H.C. and R.B. The manuscript was written by C.M., A.V. and M.Lo. with significant suggestions from E.C., H.C., R.B., M.-L.B., C.E., critical reading by B.C., M.W., and help from all co-authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Aditya Sood and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Volte, A., Mariette, C., Bertoni, R. et al. Dynamical limits for the molecular switching in a photoexcited material revealed by X-ray diffraction. Commun Phys 5, 168 (2022). https://doi.org/10.1038/s42005-022-00940-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-00940-0
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.