Abstract
A coherent Ising machine (CIM) is an open-dissipative Ising solver using optical pulses generated from a degenerate optical parametric oscillator as analog magnetizations. When solving real-world optimization problems with CIM, this solver has two difficulties: mutual coupling induced amplitude inhomogeneity and absence of natural way to implement Zeeman terms. For the approximate Gaussian formulation of CIMs with amplitude control feedback, we add artificial Zeemam terms using the target amplitude information. Here we show, for 16-spin CIM with Zeeman terms, the amplitude control increases the performance, particularly when Zeeman terms are competing against mutual coupling coefficients.
Similar content being viewed by others
Introduction
As the Moore’s law stagnates, special purpose accelarators to solve particular problems are expected to mitigate increasing time and energy costs for computation. Finding ground states of non-planar Ising models has been known to be NP hard in computational complexity theory, and has also drawn attention since various combinatorial optimization problems can be mapped into Ising Hamiltonian. There have been various attempts to use CMOS accelerators or physical systems for solving Ising problems1,2,3,4,5,6,7,8,9. A coherent Ising machine (CIM)10,11,12,13,14,15,16,17,18 uses the optical pulses in degenerate optical parametric oscillators (DOPOs) as binary spins to find the ground state of Ising problem
In CIM, optical pulses are mutually coupled by dissipative circuits rather than unitary gates to realize \({\tilde{J}}_{rr^{\prime} }\) coupling. There have been various attempts to use it for solving combinatorial optimization problems, including traveling salesman problem19, lead optimization in drug discovery20, multiple-input multiple-output optimization for wireless communication21, and compressed sensing for medical imaging22. In the attempts to use CIMs for real world problems, there have been two difficulties, the inhomogeneity of amplitudes23 and the lack of natural Zeeman terms, which are denoted as \({\tilde{h}}_{r}\) in Eq. (1). Particularly, in a previous attempt20, implementation of Zeeman terms with mean absolute amplitudes didn’t work if the additional parameter to represent the strength of Zeeman terms deviated from the optimal value. On the other hand, the correction of pulse-amplitudes’ inhomogeneity using the feedback technique has been suggested24, and used for solving random weight problems25,26,27. In this paper, we extend the model of amplitude controlled CIM and propose the implementation scheme of Zeeman terms.
Results and discussion
Coherent Ising machine
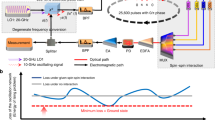
A coherent Ising machine with measurement feedback coupling has a ring cavity structure shown in Fig. 1a. Ising spins are represented by the signal pulses generated by χ(2) degenerate optical parametric amplification in periodically poled LiNbO3 (PPLN) waveguide device. Small parts of generated signal pulses are extracted by outlet coupler and their amplitudes are measured by optical homodyne detection. With the measured amplitudes (we denote as \({\tilde{\mu }}_{r}\) for r-th pulse), the coherent amplitude of feedback pulse to the r-th signal pulse is calculated in the digital circuit (FPGA) to the form of matrix vector product \({\sum }_{r^{\prime} }{\tilde{J}}_{rr^{\prime} }{\tilde{\mu }}_{r^{\prime}}\). By using intensity and phase modulation, the amplitudes of the feedback pulses are set to the calculated values. The feedback pulses are injected from the injection coupler.
a CIM with measurement and feedback (cited from ref. 16, SHG, ADC, FPGA, DAC, IM/PM, PPLN, and LO represent second harmonic generation, analog-to-digital converter, field programmable gate array, digital-to-analog converter, intensity modulator/phase modulator, periodically poled lithium niobate, and local oscillator, respectively). b χ(2) interaction of optical modes via virtual excitation of valence band electronic state. c Effective potential V(μ) of mean amplitude μ for p = 0.5 and 2 (g2 = 10−3).
We present the quantum theoretical model of measurement-feedback CIM, that are obtained by assuming the round-trip-time (Δt) is much smaller than the linear dissipation time. When we normalize the linear dissipation time to 1, The master equation of r-th DOPO is written as
Here, \({\hat{a}}_{r}\) is the annihilation operator of the r-th signal mode. The first term on the right hand side (R.H.S.) represents the linear dissipation of the signal mode. The second and third terms show the effect of χ(2) nonlinear interaction between signal and pump modes shown in Fig. 1b. When the r-th pump mode is coherently excited, the r-th signal mode has the parametric gain represented by the Hamiltonian \({\hat{H}}_{r}=\frac{i\hslash }{2}p({\hat{a}}_{r}^{{{{\dagger}}} 2}-{\hat{a}}_{r}^{2})\). Inversely, the signal mode photons are converted into the pump mode photon by two photon absorption (see Supplementary Note 1). The amplitude μ of a solitary DOPO follow the equation of motion \(\frac{d\mu }{dt}=-\frac{\partial V(\mu )}{\partial \mu }\), where V(μ) is the effective potential \(V(\mu )=(1-p)\frac{{\mu }^{2}}{2}+\frac{{g}^{2}}{4}{\mu }^{4}\) 23. As shown in Fig. 1c, below the oscillation threshold (p < 1), the effective potential has a minimum at μ = 0. On the other hand, it has two minima above the threshold (p > 1). When we assume that the DOPO has the spin value \(\sigma =\frac{\mu }{| \mu | }\), it transits from fluctuating random value for p < 1 to the stable value representing the low energy phase of spin.
To realize coupling of optical pulses, as shown in Fig. 1a, the measurement feedback CIM has two couplers added to the ring cavity, which are called outlet coupler and injection coupler. We assume two couplers have the same reflectance RB (we assume RB ≪ 1) which is related to the coupling induced linear dissipation rate j via j = RBΔt. By the outlet coupler and homodyne detection, the master equation has the additional terms which represent measurement-induced linear loss and state-reduction28:
The first term of R.H.S. represents the additional loss by adding outlet coupler, and the second term represents the impact of homodyne measurement. Wr are real random numbers representing the quantum vacuum noise incident from the open port of the outlet coupler. By homodyne measurement, one of the real numbers is selected from normally distributed vacuum noise, and measured values satisfy \(\overline{{W}_{r}(t){W}_{r^{\prime} }(t^{\prime} )}={\delta }_{rr^{\prime} }\delta (t-t^{\prime} )\) under ensemble averaging. Related to the injection coupler, the master equation has the following terms28,29:
The first term of R.H.S. represents the additional loss by injection coupler, and the second term represents the coherent feedback injection. The total master equation of measurement feedback CIM is written as \(\frac{\partial \hat{\rho }}{\partial t}={\sum }_{r}{\left(\frac{\partial \hat{\rho }}{\partial t}\right)}_{DOPO,r}+{\left(\frac{\partial \hat{\rho }}{\partial t}\right)}_{S.R.}+{\left(\frac{\partial \hat{\rho }}{\partial t}\right)}_{F.B.}\).
Gaussian approximation of positive-P model
When the two photon absorption coefficient g2 is small, the direct calculation of quantum master equation using photon number states requires huge computational cost (Above-threshold photon number has the order of g−2 for single DOPO.). Instead, we use the positive-P distribution function30, which is the generalization of Glauber–Sudarshan diagonal P function31,32. To model measurement-induced state reduction in positive-P simulation, we consider the following form instead of Eq. (3),
Here, \({\hat{X}}_{r}=\frac{{\hat{a}}_{r}+{\hat{a}}_{r}^{{{{\dagger}}} }}{\sqrt{2}}\) and \({{\Delta }}{\hat{X}}_{r}={\hat{X}}_{r}-\langle {\hat{X}}_{r}\rangle\). The outlet-coupling loss, measurement induced mean amplitude shift33, and measurement induced fluctuation reduction33 are introduced in the form of Gaussian measurement theory34,35.
The master equation composed of Eqs. (2), (4) and (5) is exactly converted to the positive-Pc-number stochastic differential equations (CSDEs). As shown in Supplementary Note 2, we used Gaussian approximation by neglecting higher order fluctuation products, to the positive-P CSDEs (shown as Supplementary Eqs. (S10) and (S11)). By adding amplitude control24,26 and Zeeman terms, we obtained following equations of Gaussian approximated positive-P (GAPP) model,
Here, μr is the mean amplitude, nr and mr represent variances of quantum fluctuations of r-th optical pulse. The auxiliary parameter er is introduced to reduce amplitude inhomogeneity24,26 by modulating the mutual coupling term as shown in Eq. (7). τ(t) is the target value of normalized squared amplitudes24,26. β is the strength to fix squared amplitudes to the target value.
Performance without amplitude control and Zeeman terms
Here, we start with simple examples with no amplitude control (β = 0 and er∣t=0 = 1) and no Zeeman terms \({\tilde{h}}_{r}=0\). First, we consider antiferromagnetically coupled two DOPOs \(\tilde{J}=-\left[\begin{array}{ll}0&1\\ 1&0\end{array}\right]\). The ground state energy (E0) is −1 and in the ground state configuration two spins have the opposite sign. We consider the time development starting from μr = mr = nr = 0. The parametric excitation p depends on time as \(p(t)=1+\tanh \frac{t+2}{10}\) (Fig. 2a, Supplementary Note 3). The time step was set to Δt = 2 × 10−3. Single run of time development for g2 = 10−3 and j = 2 is shown in Fig. 2b, c. With antiferromagnetic \({\tilde{J}}_{rr^{\prime} }\) matrix, the two DOPOs have the oppositely signed mean amplitudes μr (Fig. 2b). In Fig. 2c, the variances \(\langle {{\Delta }}{\hat{X}}_{r}^{2}\rangle ={m}_{r}+{n}_{r}+\frac{1}{2}\) are always smaller than 1 both for r = 1, 2. For two DOPOs, we calculate the success probability Ps. If energy calculated from Eq. (1) and spin values \({\sigma }_{r}=\frac{{\mu }_{r}}{| {\mu }_{r}| }\) at the final time step of the run is equal to the exact ground state energy (E0 = − 1), the run was counted as success. In Fig. 2d, we show the g2 dependent success probability obtained from GAPP. For each run, we simulate the time development until t = 4 for the coupling coefficient j = 2. The results from photon number expansion of effective density matrix (EDM) (See Methods and Supplementary Note 4) is shown with black circles. Although the results from GAPP deviate from those of EDM for large g2 due to the use of Eq. (5) and the Gaussian approximation to neglect higher-order fluctuation products, the deviation from EDM model is smaller than those of Gaussian approximated truncated Wigner (GATW) model26 (See Methods and Supplementary Note 5) shown with red broken line. Positive-P Gaussian simulation is the better approximation to the density matrix simulation than GATW. This is because we need to truncate higher order terms of Fokker-Planck equation to derive CSDEs in GATW. With the blue line, we show the GAPP results without measurement induced state-reduction, that used \({(\frac{\partial \hat{\rho }}{\partial t})}_{S.R.}\to \frac{j}{2}{\sum }_{r}([{\hat{a}}_{r},\hat{\rho }{\hat{a}}_{r}^{{{{\dagger}}} }]+{{{{{{{\rm{h.c.}}}}}}}})\) instead of Eq. (5). From this comparison measurement induced state-reduction enhances the performance of measurement feedback CIM.
a Time-dependent parametric excitation (p). Broken line shows the threshold for solitary degenerate optical parametric oscillator (DOPO). b, c Time development of mean amplitudes (μ1, μ2) and variances (\(\langle {{\Delta }}{\hat{X}}_{1}^{2}\rangle ,\langle {{\Delta }}{\hat{X}}_{2}^{2}\rangle\)) of anti-ferromagnetically coupled 2-spin GAPP model. Inset shows the minima of effective potential that two DOPOs have chosen. d t = 4 success probability of 2-spin antiferromagnetically coupled DOPOs. e t = 4 mean success probability of 3-spin system with randomly generated \({\tilde{J}}_{rr^{\prime} }\). In d, e, blue lines show the results of GAPP without measurement-induced state reduction (wo/S.R.).
Next, we considered 3-spin random system, where each independent component of \({\tilde{J}}_{rr^{\prime} }(r \, > \, r^{\prime})\), i.e., \({\tilde{J}}_{12},{\tilde{J}}_{23},{\tilde{J}}_{31}\) are randomly chosen from 21 discrete values (−1, −0.9, ⋯ , 0.9, 1)26,36. We prepared up to 107 instances and solved each instance only once (107 instances for GAPP, GATW and 105 instances for EDM). The ground state energy for each instance was obtained by brute-force search. The mean success probabilities \(\overline{{P}_{s}}\) are shown in Fig. 2e. GAPP is also the better approximation of density matrix simulation than GATW. When g2 is small, the impact of measurement induced state-reducton was smaller than 2-spin system.
Setting target amplitude
Next, we introduce the model with amplitude control24 and zero Zeeman terms, \({\tilde{h}}_{r}=0\). We use the following target function for normalized squared amplitude (Supplementary Note 6),
This is the approximated form of squared amplitude in solitary DOPO (In Supplementary Note 6, we compare it with the exact steady-state values in ref. 37.). To see the effectiveness of amplitude control with Eq. (12), we consider the one-dimensional ring with antiferromagnetic nearest-neighbor and next-nearest-neighbor coupling38, where \({\tilde{J}}_{rr^{\prime} }=-1\) if \(r-r^{\prime} \equiv \pm 1,\pm 2({{{{{{{\rm{mod}}}}}}}}N)\), and \({\tilde{J}}_{rr^{\prime} }=0\) for other \(r-r^{\prime}\). The N = 16 ring and the ground state are shown in Fig. 3a. For β = 10, 1, 0.1 and β = 0 (no amplitude control), success probabilities are plotted for various j in Fig. 3b. We used g2 = 10−3 in these simulations. Each run was simulated until t = 10 and we used the final measured value \({\tilde{\mu }}_{r}\) to calculate the energy in Eq. (1), via \({\sigma }_{r}=\frac{{\tilde{\mu }}_{r}}{| {\tilde{\mu }}_{r}| }\). When the CIM has the ground state energy (E0 = − 16), the run was counted as success. In Fig. 3b, we obtained higher peak success probability when the strength of amplitude control β is large. Particularly when we used β = 10, the peak value was more than five times larger than the conventional CIM (β = 0) without amplitude control. In Fig. 3c, d, the time development of mean amplitudes is shown for j = 2 and β = 0, 10. The amplitude control with the target function in Eq. (12) solved the problem of amplitude inhomogeneity, and realized the larger success probability even for the frustrated lattice.
a N = 16 one-dimensional ring with nearest-neighbor and next-nearest-neighbor antiferromagnetic coupling. Sites with blue and red arrows show up-spin (σ = 1) and down-spin (σ = − 1) states respectively. The pairs of two same sign spins under antiferromagnetic coupling are shown with gray lines. b Success probability as the function of coupling coefficient j with various β. c, d Time evolution of mean amplitudes without (β = 0) and with amplitude control (β = 10).
Zeeman biased model
We consider a simple model, the anti-ferromagnetically and fully connected four DOPOs (\({\tilde{J}}_{rr^{\prime} }=-1(r \, \ne \, r^{\prime} ),{\tilde{J}}_{rr}=0\)) with non-zero Zeeman terms, \({\tilde{h}}_{r}\,\ne\, 0\). The ground state has two up-spins and two down-spins with zero Zeeman term11, but with uniform strong bias it has a ferromagnetic order (Fig. 4a). We set the strength of Zeeman bias as the parameter, \({\tilde{h}}_{r}=\zeta\). In Fig. 4b, we show the ζ dependent success probability for β = 10 and 0. We fixed the coupling and nonlinear saturation to j = 2, g2 = 10−3. With amplitude control (β = 10), the success probability is increased from that with no amplitude control (β = 0). However, even with β = 10, the success probability has dropped at two spots, around ζ = 1 and around ζ = 3. This is understood in terms of the ground state transition for varying ζ. As shown in Fig. 4c, when ζ ∈ (1, 3) the ground state has three up-spins and one down-spin. There is a dip in success probability when ζ is slightly smaller than 1, where there is only small difference between the ground state energy (E0) with two up-spins and two down-spins and the first excited state energy (E1) with three up-spins and one down-spin. The first excitation state is excited by the fluctuations because of small energy difference. On the other hand, at ζ = 1 both states (two up-spins and two down-spins, three up-spins and one down-spin) are ground states and are counted as success. Therefore, the success probability was almost one for both β = 10, 0. In Fig. 4d, we show the probability for the system in the first excited state (we call P(E1)), and the energy gap between ground state (E0) and first excitation state (E1). When E1 − E0 is close to zero, the probability to find the first excitation state P(E1) increases.
a The ground state (Left) without (Right) with uniform bias. Sites with blue and red arrows show up-spin (σ = 1) and down-spin (σ = −1) states respectively. b Success probability as a function of uniform Zeeman bias ζ. c Ground state energy E0 and mean energy obtained by the simulation of β = 10 coherent Ising machine (CIM). d Probability to find first excitation state P(E1) (black line, left axis) and the excitation energy E1 − E0 (red broken line, right axis).
Complete graph with random weights and random Zeeman terms
Next, we consider the system of N = 16 complete graph with a random weight matrix. Each component of \({\tilde{J}}_{rr^{\prime} }(r \, > \, r^{\prime})\) and \({\tilde{h}}_{r}\) is randomly chosen from 21 discrete values (−1, − 0.9, ⋯ , 0.9, 1). We show three examples of random instances in Supplementary Note 7. In the numerical simulation, we calculated mean success probability \({\overline{P}}_{s}\) by generating 105 problem instances and performing the simulation only once for each instance. The success was judged at t = 20 by comparison between the CIM energy calculated from \({\sigma }_{r}={\tilde{\mu }}_{r}/| {\tilde{\mu }}_{r}|\) and the ground state energy (E0) obtained from the brute-force search. For g2 = 10−3, we show the j-dependent success probability for β = 10, 1, 0.1, 0 (Fig. 5a). The peak success probability was the largest when we use the strongest amplitude control β = 10. However, as different from the results in Fig. 3b, β = 0.1 had slightly better peak success probability than β = 1. In this case, the β dependence has two peaks as shown in Fig. 5b.
a Coupling strength j dependent success probability. b β (strength of amplitude control) dependence (j = 2). c Comparison of j-dependence for β = 10 coherent Ising machine (CIM) and previously considered models, conventional CIM which doesn't have amplitude control and Zeeman terms, and β = 10 amplitude controlled CIM with Zeeman terms provided by Eq. (13). d Dependence on the relative size of Zeeman terms ζ (j = 2). e The success probability (Ps) and the probability to find first excitation (P(E1)) of one random instance (I1). f The excitation energy of the first excitation state from the ground state (E1 − E0) in I1-instance.
Next, we compare our approach which uses target amplitude to realize Zeeman terms (Eq. (7)) with two models. The first one is conventional CIM14,15,17, that has no amplitude control and no Zeeman terms (\(\beta =0,{\tilde{h}}_{r}=0\)). Each component of \({\tilde{J}}_{rr^{\prime} }(r \, > \, r^{\prime})\) is chosen from 21 discrete uniform values (−1, −0.9, ⋯ , 1). The second one is the model using mean field to represent Zeeman terms20,39,
In Fig. 5c, we compare our realization of Zeeman terms, the realization using mean absolute amplitude20,39 (both have β = 10 amplitude control), and conventional CIM with no amplitude control and no Zeeman terms. For 16-spin random \({\tilde{J}}_{rr^{\prime}}\) matrix, the simulation with our method had the slightly better performance than the one with mean absolute amplitude. Under amplitude control, two realizations of Zeeman terms had the better peak performance than the conventional CIM. The comparison with auxiliary spin method to realize Zeeman terms7,21 is shown in Supplementary Note 8.
In Fig. 5d, we calculated the mean success probability when we change the relative magnitudes of Zeeman terms, by multiplying ζ to \({\tilde{h}}_{r}\), i.e., \({\tilde{h}}_{r}/\zeta \in [-1,-0.9,\cdots \, ,0.9,1]\). For certain values of ζ, particularly when ζ is an integer value, there are small peaks of performance. As we saw in Fig. 4, if the ground states degenerate accidentally, the success probability increases because all degenerate states with ground state energy E0 are counted as success. The small peaks of performance are the results of the fact that degeneration occurs more likely for integer ζ than for fractional ζ. The characterstics for large ζ explicitly depended on whether we used the amplitude control or not. With amplitude control the mean success probability increased for large ζ. On the other hand without amplitude control (β = 0) the success probability decreased. In Fig. 5e, f, we show the ζ dependent success probability Ps, and characteristics related to the first excitation state with energy E1 for one random instance (I1), whose \({\tilde{J}}_{rr^{\prime} }\) matrix and \({\tilde{h}}_{r}\) vector are shown in Supplementary Note 7. As shown in Fig. 5e, the dip of the success probability Ps is closely related to the increase of probability in finding the first excitation state P(E1), which increases when the energy gap (E1 − E0) is close to zero (Fig. 5f).
Conclusion
We show the numerical simulation results of measurement feedback CIM modeled as GAPP model, with correction of amplitude inhomogeneity whose target amplitude is also used for implementing Zeeman terms. For N = 16 frustrated system with nearest-neighbor and next-nearest-neighbor coupling and N = 16 complete graphs with random weights and Zeeman terms, the suggested CIM with amplitude control has the improved performance than the CIM without amplitude control. Particularly as the magnitudes of Zeeman terms \({\tilde{h}}_{r}\) increased with fixed \({\tilde{J}}_{rr^{\prime} }\), the success probability increased with amplitude control, whereas the success probability decreased without amplitude control. Studying the dependence on saturation coefficient g2 is also important (Supplementary Note 9), since large g2 is expected to reduce energy to solution and GAPP is more accurate than GATW model26 in such a region. The method in the paper will be effective in the application for compressed sensing22. Recently, the experimental measurement feedback CIM with N ~ 100, 000 spins was achieved40. GAPP will be applied to such a large N system. For current experimental CIM, where the round-trip time Δt is not much smaller than the photon lifetime, the discrete model41 can be more accurate method to simulate experimental system.
Methods
Effective density matrix (EDM) equation
To simulate measurement feedback CIM with density matrix equation, we add the terms to represent effective increase of single mode fluctuation that occurs when the fluctuation (∝Wr) in Eq. (4) is ensemble-averaged (related to the last term of Eq. (8) in ref. 28),
Here, \({j}_{1r}=\frac{j}{8}{\sum }_{r^{\prime} }{\tilde{J}}_{rr^{\prime} }^{2}\). The effective density matrix equation is \(\frac{\partial \hat{\rho }}{\partial t}={\sum }_{r}{\left(\frac{\partial \hat{\rho }}{\partial t}\right)}_{DOPO,r}+{\left(\frac{\partial \hat{\rho }}{\partial t}\right)}_{S.R.}+{\left(\frac{\partial \hat{\rho }}{\partial t}\right)}_{F.B.}+{\left(\frac{\partial \hat{\rho }}{\partial t}\right)}_{F.B.,SMF}\). The total density matrix \(\hat{\rho }\) is written as direct products of the density matrices of each DOPO (we use \({\hat{\rho }}^{(r)}\) to represent r-th DOPO), since DOPOs are coupled via mean amplitudes \(\langle {\hat{a}}_{r}+{\hat{a}}_{r}^{{{{\dagger}}} }\rangle\) and real random numbers Wr. For r-th DOPO, density matrix can be expanded using photon number states \(|{N}_{r} \rangle ({N}_{r} = 0,1,{\cdots})\), as \({\hat{\rho }}^{(r)}={\sum }_{{N}_{r}{N}_{r}^{\prime}}{\rho }_{{N}_{r},{N}_{r}^{\prime}}^{(r)}\left|{N}_{r}\right\rangle \left\langle {N}_{r}^{\prime}\right|\). The time development equations of \({\rho }_{{N}_{r},{N}_{r}^{\prime}}^{(r)}\) are provided in Supplementary Note 4. In Fig. 2d, e, each run started from the vacuum state where only \({\rho }_{0,0}^{(r)}=1\) components are non-zero and a run was counted as success when the energy calculated from \({\sigma }_{r}=\frac{{\mu }_{r}}{| {\mu }_{r}|}\) and Eq. (1) is identical to the ground state energy from the brute-force search. Here, \({\mu }_{r}=\frac{\langle {\hat{a}}_{r}+{\hat{a}}_{r}^{{{{\dagger}}} }\rangle }{2}\) were calculated as \(\frac{1}{2}{\sum }_{{N}_{r}}\sqrt{{N}_{r}+1}{({\rho }^{(r)})}_{{N}_{r}+1,{N}_{r}}+{\rho }_{{N}_{r},{N}_{r}+1}^{(r)}\left.\right)\).
Equations of Gaussian approximated truncated Wigner (GATW) simulation
In GATW simulation, we used following two equations to represent r-th DOPO.
Here, \({\mu }_{r}=\langle {\hat{X}}_{r}\rangle /\sqrt{2}\) are the mean amplitudes, and \({V}_{r}=\langle {{\Delta }}{\hat{X}}_{r}^{2}\rangle\) are the in-phase variances. The derivations of these equations are provided in Supplementary Note 5. In Fig. 2d, e, the time development started from the vacuum state, \({\mu }_{r}=0,{V}_{r}=\frac{1}{2}\), and a run was counted as success when the energy calculated from \({\sigma }_{r}=\frac{{\mu }_{r}}{| {\mu }_{r}| }\) and Eq. (1) is identical to the ground state energy from the brute-force search.
Data availability
Y.I. can provide the raw data in the article if formally requested.
References
Johnson, M. W. et al. Quantum annealing with manufactured spins. Nature 473, 194 (2011).
Utsunomiya, S. et al. Mapping of Ising models onto injection-locked laser systems. Opt. Express 19, 18091 (2011).
Kroeze, R. M. et al. Spinor self-ordering of a quantum gas in a cavity. Phys. Rev. Lett. 121, 163601 (2018).
Aramon, M. et al. Physics-inspired optimization for quadratic unconstrained problems using a digital annealer. Front. Phys. 7, 48 (2019).
Böhm, F. et al. A poor man’s coherent Ising machine based on opto-electronic feedback systems for solving optimization problems. Nat. Commun. 10, 1 (2019).
Yamaoka, M. et al. New computing paradigm for analyzing increasingly complex social infrastructure systems. Hitachi Rev. 64, 525 (2015).
Goto, H. et al. High-performance combinatorial optimization based on classical mechanics. Sci. Adv. 7, eabe7953 (2021).
Patel, S. et al. Ising model optimization problems on a FPGA accelerated restricted Boltzmann machine. Preprint at https://arxiv.org/abs/2008.04436 (2020).
Ahmed, I. et al. A probabilistic compute fabric based on coupled ring oscillators for solving combinatorial optimization problems. IEEE J. Solid State Circuits 56, 2870 (2021).
Wang, Z., Marandi, A., Wen, K., Byer, R. L. & Yamamoto, Y. Coherent Ising machine based on degenerate optical parametric oscillators. Phys. Rev. A 88, 063853 (2013).
Marandi, A., Wang, Z., Takata, K., Byer, R. L. & Yamamoto, Y. Network of time-multiplexed optical parametric oscillators as a coherent Ising machine. Nature Photon. 8, 937 (2014).
Takata, K., Marandi, A. & Yamamoto, Y. Quantum correlation in degenerate optical parametric oscillators with mutual injections. Phys. Rev. A 92, 043821 (2015).
Takata, K. et al. A 16-bit coherent Ising machine for one-dimensional ring and cubic graph problems. Sci. Rep. 6, 34089 (2016).
Inagaki, T. et al. A coherent Ising machine for 2000-node optimization problems. Science 354, 603 (2016).
McMahon, P. L. et al. A fully programmable 100-spin coherent Ising machine with all-to-all connections. Science 354, 614 (2016).
Yamamoto, Y. et al. Coherent Ising machines-optical neural networks operating at the quantum limit. npj Quantum Inf. 3, 1 (2017).
Hamerly, R. et al. Experimental investigation of performance differences between coherent Ising machines and a quantum annealer. Sci.Adv. 5, eaau0823 (2019).
Yamamoto, Y., Leleu, T., Ganguli, S. & Mabuchi, H. Coherent Ising machines-quantum optics and neural network perspectives. Appl. Phys. Lett. 117, 160501 (2020).
Yasuda, H., Hasegawa, M. & Aihara, K. A study on performance of hopfield-tank neural networks running on coherent Ising machine. Energy 2, 9 (2016).
Sakaguchi, H. et al. Boltzmann sampling by degenerate optical parametric oscillator network for structure-based virtual screening. Entropy 18, 365 (2016).
Singh, A. K., Jamieson, K., Venturelli, D., & McMahon, P. Ising machines’ dynamics and regularization for near-optimal large and massive MIMO detection. Preprint at https://arxiv.org/abs/2105.10535 (2021).
Aonishi, T., Mimura, K., Okada, M. & Yamamoto, Y. L0 regularization-based compressed sensing with quantum-classical hybrid approach. Quantum Sci. Technol. 7, 035013 (2022).
Leleu, T., Yamamoto, Y., Utsunomiya, S. & Aihara, K. Combinatorial optimization using dynamical phase transitions in driven-dissipative systems. Phys. Rev. E 95, 022118 (2017).
Leleu, T., Yamamoto, Y., McMahon, P. & Aihara, K. Destabilization of local minima in analog spin systems by correction of amplitude heterogeneity. Phys. Rev. Lett. 122, 040607 (2019).
Leleu, T. et al. Scaling advantage of nonrelaxational dynamics for high-performance combinatorial optimization. Preprint at https://arxiv.org/abs/2009.04084 (2020).
Kako, S. et al. Coherent Ising machines with error correction feedback. Adv. Quantum Technol. 11, 2000045 (2020).
Reifenstein, S., Kako, S., Khoyratee, F., Leleu, T. & Yamamoto, Y. Coherent Ising machines with optical error correction circuits. Adv. Quantum Technol. 16, 2100077 (2021).
Wiseman, H. M. & Milburn, G. J. Quantum theory of optical feedback via homodyne detection. Phys. Rev. Lett. 70, 548 (1993).
Shoji, T., Aihara, K. & Yamamoto, Y. Quantum model for coherent Ising machines: stochastic differential equations with replicator dynamics. Phys. Rev. A 96, 053833 (2017).
Drummond, P. D. & Gardiner, C. W. Generalised P-representations in quantum optics. J. Phys. A 13, 2353 (1980).
Glauber, R. J. Coherent and incoherent states of the radiation field. Phys. Rev. 131, 2766 (1963).
Sudarshan, E. C. G. Equivalence of semiclassical and quantum mechanical descriptions of statistical light beams. Phys. Rev. Lett. 10, 277 (1963).
Wiseman, H. M. & Milburn, G. J. Quantum theory of field-quadrature measurements. Phys. Rev. A 47, 642 (1993).
Eisert, J., Scheel, S. & Plenio, M. B. Distilling Gaussian states with Gaussian operations is impossible. Phys. Rev. Lett. 89, 137903 (2002).
Clements, W. R. et al. Gaussian optical Ising machines. Phys. Rev. A 96, 043850 (2017).
Goto, H. Quantum computation based on quantum adiabatic bifurcations of Kerr-nonlinear parametric oscillators. J. Phys. Soc. Jpn. 88, 061015 (2019).
Milburn, G. & Walls, D. F. Production of squeezed states in a degenerate parametric amplifier. Opt. Commun. 39, 401 (1981).
Hamerly, R. et al. Topological defect formation in 1D and 2D spin chains realized by network of optical parametric oscillators. J. Mod. Phys. B 30, 1630014 (2016).
Takesue, H. et al. Simulating Ising spins in external magnetic fields with a network of degenerate optical parametric oscillators. Phys. Rev. Applied 13, 054059 (2020).
Honjo, T. et al. 100,000-spin coherent Ising machine. Sci. Adv. 7, eabh0952 (2021).
Ng, E. et al. Efficient sampling of ground and low-energy Ising spin configurations with a coherent Ising machine. Phys. Rev. Res. 4, 013009 (2022).
Author information
Authors and Affiliations
Contributions
Y.I. and Y.Y. modeled the system. Y.I., M.D.S.H.G., and S.K. worked on the evaluation of the formulation. M.D.S.H.G. and T.A. made comments and provided information from the application side.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Inui, Y., Gunathilaka, M.D.S.H., Kako, S. et al. Control of amplitude homogeneity in coherent Ising machines with artificial Zeeman terms. Commun Phys 5, 154 (2022). https://doi.org/10.1038/s42005-022-00927-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-00927-x
This article is cited by
-
Overdamped Ising machine with stochastic resonance phenomena in large noise condition
Nonlinear Dynamics (2024)
-
Effective implementation of \(\text{L}{0}\)-regularised compressed sensing with chaotic-amplitude-controlled coherent Ising machines
Scientific Reports (2023)
-
Recent progress on coherent computation based on quantum squeezing
AAPPS Bulletin (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.