Abstract
Low loss microresonators have revolutionised nonlinear and quantum optics over the past decade. In particular, microresonators with the second order, chi(2), nonlinearity have the advantages of broad spectral tunability and low power frequency conversion. Recent observations have highlighted that the parametric frequency conversion in chi(2) microresonators is accompanied by stepwise changes in the signal and idler frequencies. Therefore, a better understanding of the mechanisms and development of the theory underpinning this behaviour is timely. Here, we report that the stepwise frequency conversion originates from the discrete sequence of the so-called Eckhaus instabilities. After discovering these instabilities in fluid dynamics in the 1960s, they have become a broadly spread interdisciplinary concept. Now, we demonstrate that the Eckhaus mechanism also underpins the ladder-like structure of the frequency tuning curves in chi(2) microresonators.
Similar content being viewed by others
Introduction
Nonlinear and quantum optics in the ring microresonators have attracted a great deal of attention over the past few years1,2. Its applications include classical and quantum information processing3,4,5, precession spectroscopy1 and exoplanet discovery6. While the third-order nonlinear response (Kerr effect) of microresonators remains the workhorse of research in this area, the second-order, χ(2), nonlinearity is attracting an increased attention2,7,8. χ(2) response is generally stronger than Kerr and offers greater flexibility with the spectral tunability and access to a range of quantum effects5,9,10,11. The respective material and fabrication issues have matured significantly12, and the phase-matching by the self-induced gratings in Si3N4 has been demonstrated13,14,15.
With all the innovations in mind, the temperature, T, control of the refractive index to provide the signal-idler-pump energy conservation, ℏωs + ℏωi = ℏωp, remains an essential method of the frequency tuning of the down-converted signal in microresonators since their very early days16,17 and till now18,19. For the total (material+geometry) resonator dispersion being well approximated by the second-order expansion, the index matching curves, T vs ωs,i, take the parabolic shape. It was demonstrated already in Ref. 17, and then has become a staple for many results on frequency conversion in χ(2) microresonators, see, e.g., 19,20,21 and references therein. Recent parametric down-conversion results in the thin-film quasi-phase-matched20 and whispering gallery22 LiNbO3 microresonators have also used the pump laser frequency as a control parameter leading to the parabolic ωp vs ωs,i tuning curves20,22. In what follows, we develop a theory underpinning the pump-frequency-tuning approach.
A distinct feature of the tuning process in microresonators is that the signal and idler frequencies vary discretely, i.e., with a jump, when one signal-idler pair switches to the next in sequence19,20,22. This discreteness raises some interesting questions. For example, is there a bifurcation scenario leading to the stepwise mode-number switch, or this is a bifurcation free parameter-drag effect, and what could be the locking interval in the parameter space providing the device operation in the desired pair of the resonator modes? Our theory answers the above questions and reveals that the instability scenario, or rather a ladder-like sequence of the instabilities, behind the tuning of the parametric frequency conversion in microresonators is known in the contexts of fluid dynamics and pattern formation as the Eckhaus instability23,24,25,26. The term of the Eckhaus, or so-called secondary, instability is used to describe the bifurcation that changes the period of a nonlinear wave23,24,25,26,27,28,29,30. We also find an explicit condition on the power vs loss balance which explains the cutting of the optical parametric oscillator (OPO) tuning parabola at one or both of its ends and limits the achievable spectral separation between the signal and idler photons.
Results and discussion
Model and classification of OPO regimes
Frequencies of the modes in high-finesse resonators are rigidly linked to the quantised set of the wavenumbers. Therefore, the step in frequency also implies the abrupt change of the spatial period, as it happens in the Eckhaus instability scenario. Accounting for the quantisation of the spectrum calls for the model formulation and methodology different from the continual models of transverse nonlinear optics27,31,32,33,34,35, fibre-loop28,29,36 and bow-tie37,38,39 cavities, cf. with the soliton and frequency conversion theories in the high-finesse microresonators40,41,42,43,44,45,46,47,48.
We now set the model in a transparent and rigorous manner. We assume that the pump laser frequency, ωp, is tuned around the frequency, ω0b, of the resonator mode with the number 2M. 2M equals the number of wavelengths fitting along the ring circumference. We also express the multi-mode intra-resonator electric field centred around ωp and its half-harmonic, ωp/2, as
respectively. Here, \(\vartheta =\left(0,2\pi \right]\) is the angular coordinate, and θ is its transformation to the reference frame rotating with the rate D1/2π. ‘a’ and ‘b’ mark the half-harmonic, i.e., signal, and pump fields, respectively. μ = 0, ±1, ±2, … is the relative mode number, and the resonator frequencies are
where, D1ζ/2π are the free spectral ranges, FSRs, and D2ζ are dispersions. In what follows, we choose D1 = D1a. The frequency, i.e., phase, matching parameter for the non-degenerate parametric process is defined as
Here, nm is the effective refractive index taken for the frequencies of the modes with the absolute numbers m = M ± μ (signal and idler) and 2M (pump), c is the vacuum speed of light and R is the resonator radius. For example, ε0 = 2ω0a − ω0b = 0 corresponds to the exact matching for the degenerate parametric conversion, nM = n2M.
Coupled-mode equations governing the evolution of aμ(t), bμ(t) are8,42,44
where \({\widehat{\delta }}_{\mu ,\mu ^{\prime} }=1\) for \(\mu =\mu ^{\prime}\) and is zero otherwise. \({{{{{{{\mathcal{H}}}}}}}}\) is the pump parameter, \({{{{{{{{\mathcal{H}}}}}}}}}^{2}={{{{{{{\mathcal{F}}}}}}}}{{{{{{{\mathcal{W}}}}}}}}/2\pi\), where \({{{{{{{\mathcal{W}}}}}}}}\) is the laser power, and \({{{{{{{\mathcal{F}}}}}}}}={D}_{1b}/{\kappa }_{b}\) is finesse44. δμζ are the detuning parameters in the rotating reference frame, \({\delta }_{\mu a}=({\omega }_{\mu a}-\frac{1}{2}{\omega }_{p})-\mu {D}_{1a}\) and δμb = (ωμb − ωp) − μD1a. δ0b is the pump detuning that is the main control parameter19,20,22. The parameter values used to scale our results to physical units are listed in the caption of Fig. 1.
a, b is an illustration of the generic comb with the spatial period 2π/ν. c, d is the staggered comb with the period π/ν. Red and green colours mark the signal and pump combs, respectively. The resonator parameters7 are: linewidths: κa/2π = 1 MHz, κb/2π = 2 MHz; repetition rates: D1a/2π = 21 GHz, D1b/2π = 20 GHz; dispersions: D2a/2π = −100 kHz, D2b/2π = −200 kHz; nonlinear coefficients: \({\gamma }_{a,b}/2\pi =300\,{{\mbox{MHz}}}/\sqrt{{{\mbox{W}}}}\).
Simple algebra reveals that all modal detunings in the half-harmonic signal can be expressed via δ0b and the respective phase-matching parameters,
While δμa and εμ do not depend on the repetition-rate difference, δμb does,
Depending on the pump power, the classical half-harmonic signal can be either zero or not. This is reflected in the structure of Eq. (4) and its solutions. Three types of solutions we should highlight are
-
(i)
no-OPO state:
$${a}_{\mu }=0,{b}_{0}=\frac{-i{\kappa }_{b}{{{{{{{\mathcal{H}}}}}}}}}{2{\delta }_{0b}-i{\kappa }_{b}},{b}_{\mu \ne 0}=0;$$(7) -
(ii)
degenerate OPO state:
$${a}_{0}\;\ne\; 0,{b}_{0}\;\ne\; 0,{a}_{\mu \ne 0}=0,{b}_{\mu \ne 0}=0;$$(8)and a family of
-
(iii)
non-degenerate OPO states:
$${a}_{\pm \nu }\;\ne\; 0,{b}_{0}\;\ne\; 0,{a}_{| \mu | \ne | \nu | }\approx 0,{b}_{\mu \ne 0}\approx 0.$$(9)
Though Eq. (4) does not have a closed analytical solution for the non-degenerate OPO, the experimental data demonstrate that the states with the ∣b0∣2 and ∣a±ν∣2 powers strongly dominating across the whole spectrum both exist and can be tuned to change from one ν to the other, and therefore, they represent the practically desirable regimes of the microresonator operation18,19,20,21. The explicit expressions for the non-zero modes in Eqs. (8) and (9) are introduced later.
In the fluid dynamics context23,24,25, the transition from the no-OPO to an OPO state would correspond to the Benjamin–Feir instability (emergence of the signal), while moving from the OPO state operating in the ±ν pair of modes to the ±(ν + 1) pair would be the Eckhaus instability, see, e.g., Ref. 23 that elucidates the difference between the two. The general form of Eq. (4) is not tractable analytically regarding the issue of the interplay between the different OPO states, and, therefore, in the next section, we derive the reduced model that allows such analysis to be carried out in a transparent form.
Apart from the OPO regimes listed above, Eq. (4) allows for the multi-mode frequency comb solutions that could be either stationary or time-dependent. The left column of Fig. 1 schematically illustrates a solution of Eq. (4) corresponding to the generic frequency comb with the spatial period 2π/ν. The structure of Eq. (4) also admits a family of the spectrally staggered combs, see the right column in Fig. 1, and we will show below that the non-degenerate OPO states are, in fact, approximations of the staggered combs.
Method of slowly varying amplitudes
Here we assume a condition that is quite common for the frequency conversion experiments in χ(2) microresonators. If a resonator is made to operate close to the μ = 0 phase-matching, i.e., ∣ε0∣ ~ κζ, then the simultaneous control of the repetition-rate difference between the pump and signal, D1b − D1a, is hard to achieve. Therefore, μ(D1b − D1a) easily becomes the dominant frequency scale in Eq. (4), i.e., μ∣D1a − D1b∣ ≫ ∣δ0b∣, κζ, ∣ε0∣, γab0. For example, for a bulk-cut (R ~ 1 mm)22 and integrated (R ~ 100 μm)19 LiNbO3 resonators, (D1b − D1a)/κζ ~ 103 and ~10, respectively. Thus, the above conditions work very well for the former starting from ∣μ∣ = 1 and for the latter from ∣μ∣ ~ 10.
Now, the natural methodological step is to separate the fast and slow time scales in the pump sidebands,
where Bμ are the slowly varying amplitudes. Then, the μ = 0 part of Eq. (4) becomes
and the μ ≠ 0 part is
Here, Δμζ are the auxiliary dimensionless detuning parameters,
which include the losses and, hence, are complex-valued. We note that Δμζ are free from D1b − D1a which has been absorbed by the fast oscillating exponents, see Eq. (10).
Integrating the ∂tBμ equation, while assuming that aμ is a slow function of time, we express the pump sidebands via the signal ones,
Substituting Eq. (14) into Eqs. (11) and (12) would make up the Kerr-like nonlinear terms. These terms represent the so-called cascaded Kerr nonlinearity49, which is, however, negligible in the leading order, because it scales inversely with μ(D1b − D1a). Hence, Eqs. (11) and (12), and the whole of the master system, Eq. (4), simplify to
Thus, the pump sidebands, bμ≠0, play no significant role in the frequency conversion when the repetition-rate difference, μ(D1b − D1a), is large. The latter simply is not featured in Eq. (15). The pumped mode, b0, is driven by the sum-frequency processes of the ±μ signal sidebands, which feeds back to the equations for the signal sidebands a±μ via the b0-terms. The absence, in the leading order, of the sum-frequency interaction between the sidebands with ∣μ1∣ ≠ ∣μ2∣ hints that the generation of the isolated sideband pairs should be a preferential regime over the broadband frequency combs.
Our approach is different from, e.g., the method when the whole of the high-frequency field is adiabatically eliminated by one way or the other so that the low-frequency field becomes driven by the cascaded Kerr effect, see, e.g., 28,38,49. The transition from Eq. (4) to Eq. (15) reduces the phase-space dimensionality of the pump field to one, but does not eliminate it entirely, and retains the leading order quadratic nonlinearity.
Solutions and thresholds
The reduced model, Eq. (15), allows examining in detail the properties of the OPO states (this section) and studying their instabilities with respect to each other (next section). In what follows we keep using μ as the running sideband index and ν designates a specific OPO state. Fixing ∂ta±ν = ∂tb0 = 0, and after some engaging algebra with Eq. (15), the explicit solutions for the non-degenerate OPO states are found in the following form,
where, H is the dimensionless pump parameter, and qν = 2 for ν ≠ 0. Eq. (16) with ν = 0 also covers for the degenerate case, but q0 = 1. Two possible solutions for the sideband amplitudes are found by taking modulus squared of the equation for \({e}^{i{\phi }_{\nu }}\),
The recent microresonator theories19,45,50 reported the double-valued solutions for the degenerate case. The non-degenerate case was also considered in19, but only for the zero detunings and exact phase-matching, while Eq. (16) and stability analysis that follow depend critically on the full account and ability to vary both of those flexibly.
The bifurcation points from the no-OPO to OPO regimes, i.e., Benjamin–Feir instabilities, are conditioned by the zeros of the sideband powers,
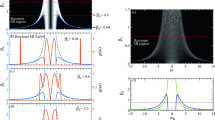
The laser power \({{{{{{{{\mathcal{W}}}}}}}}}_{\nu }\) at the OPO threshold is then calculated from \({{{{{{{{\mathcal{W}}}}}}}}}_{\nu }=8\pi {\kappa }_{a}^{2}{H}_{\nu }^{2}/{{{{{{{\mathcal{F}}}}}}}}{\gamma }_{a}^{2}\). The left column in Fig. 2 shows \({{{{{{{\mathcal{W}}}}}}}}={{{{{{{{\mathcal{W}}}}}}}}}_{\nu }\) vs δ0b, for the negative, zero, and positive phase-mismatch ε0. The minimum of \({{{{{{{\mathcal{W}}}}}}}}\) near δ0b = 0 exists in all three cases. For ε0 ≤ 0, this minimum is provided by the ν = 0 mode, i.e., the no-OPO state losses its stability to the degenerate OPO first. The second minimum of \({{{{{{{\mathcal{W}}}}}}}}\) at δ0b = − ε0, i.e., δ0a = 0 (see Eq. (6)), also happens for ν = 0.
a–c Instability boundaries of the no-OPO state relative to the excitation of the sideband pairs ±μ (Benjamin–Feir instability), where μs are indicated. Red and blue lines correspond to the super- and sub-critical bifurcations, respectively. d–f The existence and stability ranges of the degenerate, ν = 0, OPO state. The black colour marks the range of the stable operation of the degenerate OPO. The discretely varying blue-to-orange colour map shows the range of the non-degenerate OPOs. The full white lines delimit the range of the oscillatory (Hopf) instabilities leading to the breathing combs. Red and blue lines correspond to the super- and sub-critical bifurcations, respectively, see Eq. (18). The grey dashed line marks Eq. (20).
The top row of Fig. 3 shows the results of numerical simulations of Eq. (4) across the regions of the unstable no-OPO state for the relatively small input powers marked with the black dashed lines in the first column of Fig. 2. The ε0 = 0 case in Fig. 3a demonstrates how the degenerate OPO is first excited from the no-OPO state and then switches, in a cascaded manner, to the non-degenerate OPOs. Figure 3b shows how this scenario can happen twice for ε0 < 0. We note that the two cascades in Fig. 3b occur in the reverse order. The right-to-left cascade involves oscillations of the μ = 0 and other modes (breathing comb), while all the left-to-right cascades in Fig. 3a–c appear as the direct transitions between the neighbouring non-degenerate OPO states, as it is expected to happen in the Eckhaus instability scenario. We recall that we consider the near-phase-matching between the μ = 0 modes in the pump and signal fields. It leads to the Rabi-like oscillations between the a0 and b0 modes, which acquire small gain in the narrow interval of detunings and give birth to the breather states, see Refs. 46,47 for details of the theory of the χ(2) Rabi oscillations.
Signal mode numbers (a–c), i.e., the ladder of Eckhaus instabilities, and power of the generated sidebands (d–f) vs detuning for the pump powers shown by the black dashed lines in the left column of Fig. 2: (a, d) \({{{{{{{\mathcal{W}}}}}}}}=5\) nW (−53 dBm), ε0 = 0; (b, e) \({{{{{{{\mathcal{W}}}}}}}}=316\) nW (−35 dBm), ε0 = −5κb; (c, f) \({{{{{{{\mathcal{W}}}}}}}}=31.6\) nW (−45 dBm), ε0 = 5κb. a–c Numerically simulated, Eq. (4), excitation of the signal sidebands (field 'a') vs pump detuning, δ0b. The numbers inside the panels indicate the respective sideband orders. The vertical dashed lines mark the instability boundaries of the states ν relative to the excitation of the ν + 1 sideband pair, i.e., λν,ν+1 = 0 conditions, see Eqs. (22) and (23). The colour scale shows the sideband power. d–f Red and blue lines show the sideband powers vs δ0b as given by the analytical solutions in Eq. (17): \(| {a}_{\nu }^{+}{| }^{2}+| {a}_{-\nu }^{+}{| }^{2}\) (red) and \(| {a}_{\nu }^{-}{| }^{2}+| {a}_{-\nu }^{-}{| }^{2}\) (blue). Black circles show the numerically computed sideband powers corresponding to the data in the top row. The detuning range around δ0b ≈ 0.5κb in the middle column corresponds to the breather states.
For ε0 > 0, the minimum of \({{{{{{{\mathcal{W}}}}}}}}\) is also found at δ0b ≈ 0, but now it happens for ν ≠ 0, see Fig. 2b. Thus, here, the no-OPO state transits directly to the non-degenerate regime. Fixing δ0b = 0 in Eq. (17) gives \(16{H}_{\nu }^{2}={\varepsilon }_{\nu }^{2}/{\kappa }_{a}^{2}+1\), where εν = ε0 + ν2D2a. Hence, the minimum threshold power, \({H}_{\widehat{\nu }}^{2}=1/16\), for the Benjamin–Feir instabilities is achieved at the exact phase-matching, \({\varepsilon }_{\widehat{\nu }}=0\), where \(\widehat{\nu }\approx \sqrt{-{\varepsilon }_{0}/{D}_{2a}}\), ε0D2a < 0. Figure 3c demonstrates how the below threshold OPO switches directly to the non-degenerate state and passes through the cascade of νs.
Solving \({H}^{2}={H}_{\nu }^{2}\), Eqs. (18), one could find either two or four real values of δ0b where the ±ν sidebands bifurcate from zero, cf., Fig. 3d, f with Fig. 3e. In the left column of Fig. 2, the different colours mark the parts of the \({H}^{2}={H}_{\nu }^{2}\) thresholds where either \(| {a}_{\nu }^{+}{| }^{2}=0\) (red) or \(| {a}_{\nu }^{-}{| }^{2}=0\) (blue). The points of transition between the two colours are found by setting
Tuning the pump laser across the red boundaries and moving into the instability interval leads to \(| {a}_{\nu }^{+}{| }^{2}\) gradually increasing from zero, which corresponds to the soft-excitation regime (supercritical bifurcation), see Fig. 3d. Entering the instability tongue across the blue boundary leads to \(| {a}_{\nu }^{+}{| }^{2}\) popping out stepwise and \(| {a}_{\nu }^{-}{| }^{2}\) bifurcating from zero sub-critically (hard excitation), see Fig. 3e, f.
The right column in Fig. 2 shows the existence and stability ranges of the degenerate, ν = 0, OPO states. They bifurcate from the no-OPO state super-critically along the red line and sub-critically from the blue line. The parameter range where the \(| {a}_{0}^{+}{| }^{2}\) and \(| {a}_{0}^{-}{| }^{2}\) solutions coexist is located between the blue and dashed-grey lines. Generalising for arbitrary ν, the dashed-grey boundary is found from
Eckhaus instabilities and OPO tuning
While the top row in Fig. 3 shows the sequential switching between the modes with different numbers and intervals of the pump detuning that select a particular sideband pair, the bottom row shows the changes of the sideband amplitudes computed from Eq. (4) and maps them on the analytical solutions for the OPO states. Apart from the oscillatory instabilities around δ0b/κb ≈ 0.5 in Fig. 3b, e, all the insatiabilities of a given OPO state converge to the nearby stable one. In other words, these instabilities lead to the ν → ν + 1 swaps and, hence, to the change of the spatial period and frequency of the waveform in the resonator, i.e., these are the discrete spectrum Eckhaus instabilities.
By taking the OPO state with an arbitrary ν ⩾ 0, adding small perturbations \({\hat{a}}_{\mu }(t)\), where ∣μ∣ ≠ ν, and linearising the slowly varying amplitude model (15) we find
where b0 is a function of ν in accordance with Eq. (16). Solving Eq. (21) with \({\hat{a}}_{\mu }(t)={\tilde{a}}_{\mu }\exp \{t{\lambda }_{\nu ,\mu }\}\) and \({\hat{a}}_{-\mu }^{* }(t)={\tilde{a}}_{-\mu }\exp \{t{\lambda }_{\nu ,\mu }\}\) yields a set of the sideband-pair growth rates,
Thus, Eq. (22) describe the growth rates of the Eckhaus instabilities in the microresonator OPO, i.e., destabilization of the non-degenerate OPO state corresponding to the ±ν sideband pair through the excitation of any other pair ±μ. The instability threshold is reached when λν,μ becomes zero, while the generation of the ±ν sideband pair is stable if the pump frequency is tuned to provide δ0b such that \({\delta }_{\nu a}^{2}\;\leqslant \;{\delta }_{\mu a}^{2} + \frac{1}{4}{\kappa }_{a}^{2}\). The oscillatory bifurcations, i.e., the birth of breathers highlighted by the white lines in Fig. 2, correspond to ν = μ, and, therefore, are exempt from the above theory.
To find conditions of the switching from one sideband pair to the next, we set μ = ν ± 1. For D2a < 0 (normal dispersion), the interval of stable generation of the ±ν sideband pair is found as
where \({\varepsilon }_{\pm}={\varepsilon}_{0}+{\kappa }_{a}^{2}/2D_{2a}(1\pm 2\nu)\). The instability boundaries, λν,ν±1 = 0, as given by the above condition, are shown in Figs. 3 and 4a by the white dashed vertical lines and they match perfectly with the transitions found from the numerical modelling of Eq. (4).
The detuning corresponding to the midpoint of every step on the Eckhaus ladder, i.e., the left plus right limits divided by two, is \({\delta }_{0b}\approx-{\varepsilon }_{0}-{D}_{2a}({\nu }^{2}+\frac{1}{2})\). Thus, the latter reproduces the characteristic parabolic shape of δ0b vs ν in Fig. 4a. Recalling Eqs. (2) and (3), one can show that the same parabola is described by
Thus, the analysis done so far has demonstrated that a sequence of the OPO regimes achieved by the scan of the pump frequency follows the steps of the Eckhaus instabilities ladder and the phase-matching condition, cf., Eqs. (3) and (24). It also reveals that the size of the Eckhaus ladder’s steps and the tuning curve’s discreetness are controlled by the second-order dispersion. We shell note that the applicability of Eq. (22) extends beyond the second-order expansion applied for ωμ, Eq. (2), while Eq. (24) relies on it. Therefore, the microresonators with dispersion dominated by the higher orders could be an interesting case to consider in future.
a Ladder of Eckhaus instabilities for high powers. Numerically computed, Eq. (4), spectra of the optical parametric oscillator (OPO) signal vs pump detuning, δ0b, for the pump laser power \({{{{{{{\mathcal{W}}}}}}}}=3\) mW (4.8d Bm) and ε0 = 5κb, see the horizontal white dashed line in Fig. 2a. The white vertical dashed lines map the sequence of the Eckhaus instability thresholds, λν,ν±1 = 0, see Eqs. (22) and (23). The colour scale shows the sideband power in dBm. b–d show the details of the spectra of the pump (green) and OPO signal (red) corresponding to the dashed green lines in (a). Spectra in (c) and (d) are the staggered combs. d corresponds to the non-degenerate OPO state that is very well approximated by Eq. (17). The vanishing power levels have been included in (d) in order to demonstrate that the non-degenerate OPO states belong to the staggered comb family.
Figure 4a shows a sequence of the OPO transitions for the power which is much higher than in Fig. 3 (cf. black and white lines in Fig. 2b). The Eckhaus ladder in Fig. 4a is shown up to ν = 30, but extends up to ν = νmax = 120. The data in the top row of Fig. 3 also demonstrate that, for ε0 > 0, the parabolic tuning curve is also cut at its minimum. The power reduction, from the levels in Fig. 4a to the ones in Fig. 3, does not change the shape of the parabola but reduces its extent in ν and δ0b. Since the value of νmax sets the practical limit for the OPO tunability, it is now mandatory to apply our theory to elaborate this point further.
First, we should recall that the data in Fig. 3 have confirmed that Eqs. (16) and (17) provide an excellent approximation for the OPO states. Figure 4d includes the much weaker, practically negligible, part of the spectrum and, thereby, explicitly reveals the degree of accuracy of Eqs. (16) and (17). It also uncovers that the non-degenerate OPO states belong to the family of staggered combs. It follows from Eq. (16) that the power of the signal sidebands, a±ν, depends on the laser power, \({H}^{2} \sim {{{{{{{\mathcal{W}}}}}}}}\), and the power of b0 does not, and only its phase does. Indeed, \({b}_{0}^{\pm }={e}^{i{\phi }_{\nu }^{\pm }}{\kappa }_{a}{\Delta }_{\nu a}/{\gamma }_{a}\), where \({\phi }_{\nu }^{\pm }={\phi }_{\nu }(| {a}_{\nu }^{\pm }{| }^{2})\). This is a reason why H2 does not explicitly enter the Eckhaus instability rate, see Eq. (22). However, the limits of existence of \(| {a}_{\nu }^{\pm }{| }^{2}\;\geqslant \;0\), and, hence, of \({b}_{0}^{\pm }\) in Eq. (21) do critically depend on H2 as is given by Eq. (20).
Substituting the detunings δ0b = −εν (corresponding to the numbered tips in the left column of Fig. 2) in Eq. (20) yields \(4{\kappa }_{b}^{2}{H}^{2}={({\varepsilon }_{0}+{\nu }^{2}{D}_{2a})}^{2}\). From here one can work out the power dependencies of the minimal, \({\nu }_{\min }\) vs \({{{{{{{\mathcal{W}}}}}}}}\), and maximal, \({\nu }_{\max }\) vs \({{{{{{{\mathcal{W}}}}}}}}\), mode numbers corresponding to the ±ν OPO states. Recalling that the dispersion is normal, D2a < 0, the maximal number is
The \({\nu }_{\min }\) is conditioned by the sign of ε0. It is zero for ε0 ⩽ 0 and \({\nu }_{{{{\min}}}}^{2}\approx (-{\varepsilon }_{0}+2{\kappa }_{b}H)/{D}_{2a}\) if ε0 > 0, see Fig. 3. The plots of \({\nu }_{\max }\), \({\nu }_{\min }\) vs the laser power are shown in Fig. 5.
The pump power dependencies of the maximal, \({\nu }_{\max }\), and minimal, \({\nu }_{\min }\), mode numbers corresponding to the ±ν OPO states that can be generated by the pump-frequency tuning method. \({\nu }_{\min }\) is different from zero only for ε0 > 0. \(\widehat{\nu }\approx \sqrt{-{\varepsilon }_{0}/{D}_{2a}}\) corresponds to the lowest possible excitation threshold for ε0 > 0, see text between Eqs. (18) and (19). Dispersion is normal, D2a < 0, see Fig. 1 for other parameters.
For the whispering gallery and integrated LiNbO3 resonators, the mode number change by one corresponds to the wavelength step ~0.1 nm22 and 2 nm20, respectively. Hence νmax = 50 corresponds to the wavelength difference between the signal and idler 10 and 200 nm, respectively. The pump-frequency tuning data in Ref. 20 report up to 200-nm signal-idler separations. The experimental reports of the parabolic pump-frequency tuning curves in the microresonator18,19,20, fibre-loop36, and bow-tie38 OPOs do not contain the data sufficient for making a comparison with the reported here power-dependent parabola cut-off at \({\nu }_{\max }\) and \({\nu }_{\min }\). Therefore, further research into this problem is necessary.
Conclusions
We have demonstrated that the degenerate OPO transiting to the ladder of the non-degenerate OPO states via a sequence of Eckhaus instabilities is a universal OPO tuning scenario if the repetition-rate difference between the signal and pump fields, ∣D1b − D1a∣, dominates over all other frequency scales. The emerging combs are most typically staggered, with the two dominant sidebands in the signal field, which corresponds to the non-degenerate OPO regime, see Figs. 1, 3 and 4. For the high-finesse whispering gallery resonator used as an example in our work, this scenario covers the span of the pump laser powers from nano to milli Watts. The more complex frequency combs start to appear for the pump powers above 3mW, see δ0b ≈ −20κb in Fig. 4a, b. Apart from increasing the pump power, the ways to facilitate the microresonator OPOs to operate in the non-staggered comb could be, e.g., using resonators with the better-matched repetition rates taken relative to the losses, i.e., having smaller ∣D1b − D1a∣/κa,b, and using pumping into the modes with the odd numbers8,45,49,50.
The slowly varying amplitude model, Eq. (15), that we derived and employed here was the key step that has allowed us to solve the problem of switching between the OPO operating in the ±ν sideband pair to any other mode pair ±μ, where ν ≠ μ. This model relies on the aforementioned dominance of the repetition-rate difference, ∣D1b − D1a∣, which drives the fast oscillations of the pump sidebands, see Eq. (10). It also reveals that the growth rate of the Eckhaus instability does not depend on ∣D1b − D1a∣ in the leading order, see Eq. (22). Regarding the quadratic nonlinearity, the slowly varying amplitude model highlights the dominant role of the terms responsible for the nonlinear mixing of the central mode of the pump field with all the signal sidebands.
Our methodology has also let us derive the equation for the maximally allowed sideband order generated by the pump-frequency tuning method in the microresonator OPOs, which is easy to apply and use as a practical guideline for the parametric down-conversion experiments. All our analytical results are in excellent agreement with the numerical modelling of the full coupled-mode system, see Eq. (4).
Methods
Numerical integration of the coupled-mode model, see Eq. (4), has been performed using a fourth-order Runge–Kutta method. The procedure was optimised by applying the fast Fourier transform algorithm to the nonlinear terms in the real space to compute the sums in Eq. (4), see Ref. 44 for details. The data shown in Figs. 3 and 4 were obtained for 256 optical modes in the ‘a’ and ‘b’ fields, i.e., for μ = −127, … 128. The initial conditions were the no-OPO state in the μ = 0 modes and random perturbations in the rest of the spectrum.
Data availability
The data supporting the findings of this study are available from the authors upon reasonable request.
Code availability
The codes used for this study are available from the first author (dp710@bath.ac.uk) upon reasonable request.
Change history
21 October 2022
A Correction to this paper has been published: https://doi.org/10.1038/s42005-022-01033-8
References
Diddams, S. A., Vahala, K. & Udem, T. Optical frequency combs: coherently uniting the electromagnetic spectrum. Science 369, 267 (2020).
Strekalov, D. V., Marquardt, C., Matsko, A. B., Schwefel, H. G. L. & Leuchs, G. Nonlinear and quantum optics with whispering gallery resonators. J. Opt. 18, 123002 (2016).
Corcoran, B. et al. Ultra-dense optical data transmission over standard fibre with a single chip source. Nat. Commun. 11, 2568 (2020).
Raja, A. S. et al. Reconfigurable radiofrequency filters based on versatile soliton microcombs. Nat. Commun. 12, 5867 (2021).
Kues, M. et al. Quantum optical microcombs. Nat. Photon. 13, 170 (2019).
Obrzud, E. A microphotonic astrocomb. Nat. Phot. 13, 31 (2019).
Szabados, J. et al. Frequency comb generation via cascaded second-order nonlinearities in microresonators. Phys. Rev. Lett. 124, 203902 (2020).
Bruch, A. W. et al. Pockels soliton microcomb. Nat. Photonics 15, 21 (2021).
Fabre, C. & Treps, N. Modes and states in quantum optics. Rev. Mod. Phys. 92, 035005 (2020).
Alves, G. B., Barros, R. F., Tasca, D. S., Souza, C. E. E. & Khoury, A. Z. Conditions for optical parametric oscillation with a structured light pump. Phys. Rev. A 98, 063825 (2018).
Vashukevich, E. A., Losev, A. S., Golubeva, T. Y. & Golubev, Y. M. Squeezed supermodes and cluster states based on modes with orbital angular momentum. Phys. Rev. A 99, 023805 (2019).
Zhu, D. et al. Integrated photonics on thin-film lithium niobate. Adv. Opt. Photon. 13, 242 (2021).
Billat, A. et al. Large second harmonic generation enhancement in Si3N4 waveguides by all-optically induced quasi-phase-matching. Nat. Commun. 8, 1016 (2017).
Hickstein, D. D. et al. Self-organized nonlinear gratings for ultrafast nanophotonics. Nat. Photonics 13, 494–499 (2019).
Lu, X. et al. Efficient photoinduced second-harmonic generation in silicon nitride photonics. Nat. Photonics 15, 131–136 (2021).
Eckardt, R. C., Nabors, C. D., Kozlovsky, W. J. & Byer, R. L. Optical parametric oscillator frequency tuning and control. J. Opt. Soc. Am. B 8, 646 (1991).
Schiller, S. & Byer, R. L. Quadruply resonant optical parametric oscillation in a monolithic total-internal-reflection resonator. J. Opt. Soc. Am. B 10, 1696 (1993).
Meisenheimer, S. K., Furst, J. U., Buse, K. & Breunig, I. Continuous-wave optical parametric oscillation tunable up to an 8um wavelength. Optica 4, 189 (2017).
Bruch, A. W., Liu, X., Surya, J. B., Zou, C. L. & Tang, H. X. On-chip chi(2) microring optical parametric oscillator. Optica 6, 1361 (2019).
Lu, J. et al. Ultralow-threshold thin-film lithium niobate optical parametric oscillator. Optica 8, 539 (2021).
Strekalov, D. V. et al. Phase matching for the optical frequency conversion processes in whispering gallery mode resonators. J. Mod. Opt. 63, 50 (2016).
Amiune, N. et al. Optical-parametric-oscillation-based chi(2) frequency comb in a lithium niobate microresonator. Opt. Express 29, 41378 (2021).
Stuart, J. T. & Di Prima, R. C. The Eckhaus and Benjamin-Feir resonance mechanisms. Proc. R. Soc. Lond. A 362, 27 (1978).
Cross, M. C. & Hohenberg, P. C. Pattern formation outside of equilibrium. Rev. Mod. Phys. 65, 851 (1993).
Bergeon, A., Burke, J., Knobloch, E. & Mercader, I. Eckhaus instability and homoclinic snaking. Phys. Rev. E 78, 046201 (2008).
Parra-Rivas, P., Gomila, D., Gelens, L. & Knobloch, E. Bifurcation structure of periodic patterns in the Lugiato-Lefever equation with anomalous dispersion. Phys. Rev. E 98, 042212 (2018).
Longhi, S. Travelling-wave states and secondary instabilities in optical parametric oscillators. Phys. Rev. A 53, 4488 (1996).
Ward, H., Taki, M. & Glorieux, P. Secondary transverse instabilities in optical parametric oscillators. Opt. Lett. 27, 348 (2002).
Liu, Z., Leo, F., Coulibaly, S. & Taki, M. Secondary instabilities in all fiber ring cavities. Phys. Rev. A 90, 033837 (2014).
Perinet, N., Verschueren, N. & Coulibaly, S. Eckhaus instability in the Lugiato-Lefever model. Eur. Phys. J. D 71, 243 (2017).
Oppo, G. L., Brambilla, M. & Lugiato, L. A. Formation and evolution of roll patterns in optical parametric oscillators. Phys. Rev. A 49, 2028 (1994).
Staliunas, K. Transverse pattern formation in optical parametric oscillators. J. Mod. Opt. 42, 1261 (1995).
Skryabin, D. V. Instabilities of cavity solitons in optical parametric oscillators. Phys. Rev. E 60, R3508 (1999).
Tlidi, M., Mandel, P. & Haelterman, M. Spatiotemporal patterns and localized structures in nonlinear optics. Phys. Rev. E 56, 6524 (1997).
Tlidi, M. & Mandel, P. Space-time localized structures in the degenerate optical parametric oscillator. Phys. Rev. A 59, R2575 (1999).
Roy, A., Jahani, S., Langrock, C., Fejer, M. & Marandi, A. Spectral phase transitions in optical parametric oscillators. Nat. Commun. 12, 835 (2021).
Hamerly, R. et al. Reduced models and design principles for half-harmonic generation in synchronously pumped optical parametric oscillators. Phys. Rev. A 94, 063809 (2016).
Mosca, S. et al. Modulation instability induced frequency comb generation in a continuously pumped optical parametric oscillator. Phys. Rev. Lett. 121, 093903 (2018).
Dietrich, C. M. et al. Higher-order dispersion and the spectral behavior in a doubly resonant optical parametric oscillator. Opt. Lett. 45, 5644 (2020).
Chembo, Y. K. & Yu, N. Modal expansion approach to optical-frequency-comb generation with monolithic whispering-gallery-mode resonators. Phys. Rev. A 82, 033801 (2010).
Herr, T. et al. Temporal solitons in optical microresonators. Nat. Photonics 8, 145 (2014).
Guo, X. et al. Efficient generation of a near-visible frequency comb via Cherenkov-like radiation from a Kerr microcomb. Phys. Rev. Applied 10, 014012 (2018).
Qi, Z. et al. Dissipative cnoidal waves (Turing rolls) and the soliton limit in microring resonators. Optica 6, 1220 (2019).
Skryabin, D. V. Coupled-mode theory for microresonators with quadratic nonlinearity. J. Opt. Soc. Am B 37, 2604 (2020).
Podivilov, E., Smirnov, S., Breunig, I. & Sturman, B. Nonlinear solutions for chi(2) frequency combs in optical microresonators. Phys. Rev. A 101, 023815 (2020).
Puzyrev, D. N., Pankratov, V. V., Villois, A. & Skryabin, D. V. Bright-soliton frequency combs and dressed states in chi(2) microresonators. Phys. Rev. A 104, 013520 (2021).
Skryabin, D. V., Pankratov, V. V., Villois, A. & Puzyrev, D. N. Photon-photon polaritons in chi(2) microresonators. Phys. Rev. Research 3, L012017 (2021).
Zhao, Y., Jang, J. K., Okawachi, Y. & Gaeta, A. L. Theory of chi(2)-microresonator-based frequency conversion. Opt. Lett. 46, 5393 (2021).
Skryabin, D. V. Sech-squared Pockels solitons in the microresonator parametric down-conversion. Opt. Express 29, 28521 (2021).
Villois, A., Kondratiev, N., Breunig, I., Puzyrev, D. N. & Skryabin, D. V. Frequency combs in a microring optical parametric oscillator. Opt. Lett. 44, 4443 (2019).
Acknowledgements
We acknowledge the financial support received from UK EPSRC (2119373).
Author information
Authors and Affiliations
Contributions
D.N.P. developed numerical codes, performed simulations, analysed data and prepared them for publication. D.V.S. developed the theory and wrote the text.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests. D.V.S. is a Guest Editor of the Collection ‘Microresonator Frequency Combs: New Horizons’ for Communications Physics, but was not involved in the editorial review of, or the decision to publish this article.
Peer review
Peer review information
Communications Physics thanks Mustapha Tlidi, Wenjie Wan and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Puzyrev, D.N., Skryabin, D.V. Ladder of Eckhaus instabilities and parametric conversion in chi(2) microresonators. Commun Phys 5, 138 (2022). https://doi.org/10.1038/s42005-022-00907-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-00907-1
This article is cited by
-
χ(2) nonlinear photonics in integrated microresonators
Frontiers of Optoelectronics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.