Abstract
Electronic instabilities drive ordering transitions in condensed matter. Despite many advances in the microscopic understanding of the ordered states, a more nuanced and profound question often remains unanswered: how do the collective excitations influence the electronic order formation? Here, we experimentally show that a phonon affects the spin density wave (SDW) formation after an SDW-quench by femtosecond laser pulses. In a thin film, the temperature-dependent SDW period is quantized, allowing us to track the out-of-equilibrium formation path of the SDW precisely. By exploiting its persistent coupling to the lattice, we probe the SDW through the transient lattice distortion, measured by femtosecond X-ray diffraction. We find that within 500 femtoseconds after a complete quench, the SDW forms with the low-temperature period, directly bypassing a thermal state with the high-temperature period. We argue that a wavevector-matched phonon launched by the quench changes the formation path of the SDW through the dynamic pinning of the order parameter.
Similar content being viewed by others
Introduction
Peierls proposed a mechanism for the formation of charge density waves (CDW)1: a spinless one-dimensional electron gas described by the Fröhlich-Hamiltonian is intrinsically unstable to the doubling of the unit cell. The spectrum of excitations develops an energy gap, and a CDW forms if the energy gain from the electronic instability is larger than the strain energy of the coexisting lattice distortion2 (see Fig. 1(a)). A one-dimensional electron gas with spins described by the Hubbard-Hamiltonian develops a spin density wave (SDW), whose existence requires no lattice distortion3. In multidimensional systems, nesting between planar sections of the Fermi surface stabilizes density waves4,5. Nevertheless, their explanation remains incomplete; especially the role of collective excitations during the density wave formation remains elusive. The ionic lattice distortions are necessary for the existence of CDWs6. Yet quasi-static measurements in chromium (Cr)—a prototypical system hosting a classical SDW, CDW7,8, a pseudogap9, and a quantum critical point10—assign the dominant role in electronic order formation to the itinerant instability with little impact from the ionic lattice11.
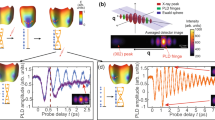
a The laser pulse quenches the spin density wave (SDW), which is coupled to the periodic lattice distortion (PLD) (solid line on the left), and launches a pair of longitudinal acoustic phonons (atomic positions (blue spheres) and their wavevector (black arrows)). Subsequently, the SDW bandgap (schematic energy diagram on the right) reopens and the coupled SDW-PLD state reforms in presence of the phonons. b Typical time-resolved X-ray diffraction data of the coherent satellite-peak (purple dots) for an incident pump fluence of 2 mJ/cm2. The data is fitted (purple solid line) with a damped harmonic oscillator in region II (blue shaded area), the fit is extrapolated to region I (red shaded area), and the extrapolated fit is subtracted from X-ray diffraction data. The residual is shown in orange and is proportional to the transient PLD amplitude coupled to the SDW through spin–lattice interaction. The inset shows typical diffraction data as measured on the two-dimensional detector for a single time delay. The coherent satellite-peak is in the center at Q002 – QL = 4.17 Å−1, the image spans 0.14 Å−1 horizontally, and the intensity drop towards the sides of the detector is due to the Ewald sphere intersecting the Bragg rod under an angle of 30 degrees.
Laser-induced quench and subsequent recovery of density waves offer a unique opportunity for studying the mechanisms of order formation in correlated systems12,13,14. A short laser pulse causes a spike in the electron temperature through the photon–electron interaction, which leads to density wave melting within 100 fs12. As the electron gas’s heat capacity is typically much smaller than that of the ionic lattice, the electronic subsystem cools via the electron–phonon interaction15, and the density wave recovers within picoseconds14,15. Often, a phenomenological description using the temperatures of different degrees of freedom captures the main features of the transition14. Here, we study the femtosecond quench and subsequent recovery of the SDW in Cr mediated by the generation and damping of an acoustic phonon (see Fig. 1a). We find the phenomenological Landau-model insufficient in describing the experimental observations. After a full quench induced by an electronic temperature increase of a few hundred kelvin above the Néel temperature, the SDW bypasses a state predicted by the model and observed experimentally in equilibrium. The SDW directly transitions into the low-temperature state. We hypothesize that the wavevector-matched acoustic phonons, launched by the laser quench, guide the system along a non-equilibrium path in the free-energy diagram. Measurements with two precisely timed pump-pulses support our hypothesis of phonon-assisted SDW formation.
Results
Time-resolved femtosecond X-ray diffraction
In a 28 nm thick epitaxial Cr film held at 115 K, the SDW ordering wavevector is perpendicular to the film surface, (001). The periodic lattice distortion (PLD)—the second harmonic of the SDW7—is incommensurate with the lattice and generates two diffuse X-ray scattering peaks around the 002 Bragg peak at a momentum transfer of Q002 ± QL. The interference between the diffuse scattering and Laue fringes results in coherent satellite-peaks (see Supplementary Note 1 and Supplementary Fig. 1). We excite the system with 45 fs full width at half maximum (FWHM) optical laser pulses (λ = 800 nm, see Fig. 1a) and monitor the satellite-peak intensity at Q002 – QL with ~10 fs X-ray laser pulses (λ = 1.4 Å)14,16,17 (see Fig. 1b and Methods). The time-dependent intensity consists of two components, an oscillation and an asymmetric distortion that is only present for time delays smaller than one ps (see Fig. 1b).
We analyze the time-resolved X-ray data by splitting it into two intervals (see Fig. 1(b)). In interval II (1 ps < t < 5 ps, blue shaded), we model the satellite-peak intensity as a damped harmonic oscillator
where the fitting parameter IF describes the baseline around which the intensity oscillates, and \({I}_{{{{{{{\mathrm{ph}}}}}}}},\omega\), t0, and tD are the oscillation’s amplitude, frequency, time offset, and damping time. To extract the non-oscillatory, asymmetric component of the PLD, we extrapolate the fit to shorter timescales (interval I: 0 ps < t < 1 ps) and subtract it from the data. The residual is the baseline around which the satellite-peak harmonically oscillates (see Fig. 1b, orange line).
Tracking the harmonic lattice vibration for probing the density wave order parameter
The coherent satellite-peak intensity is proportional to the amplitude of the dynamic PLD16 (see Supplementary Note 1), allowing us to quantitatively extract the dynamic lattice distortion \({A}_{{{{{{\rm{tot}}}}}}}\left(t\right)\) directly from the X-ray data. The harmonic oscillation of the satellite-peak intensity is consistent with an amplitude mode of the PLD6—equivalent to a standing wave consisting of two damped counterpropagating longitudinal coherent acoustic phonons. The laser quench launches an oscillating standing wave in the lattice with a wavevector, QL, of the pre-existing static PLD—the laser pulse releases the previously “frozen-in” standing wave14. By subtracting the harmonic oscillation from the total displacement, we determine the transient lattice displacement, \({A}_{{{\psi }}}\left(t\right)={A}_{{{{{{\rm{tot}}}}}}}\left(t\right)-{A}_{{{{{{\rm{ph}}}}}}}{{{{{\rm{cos }}}}}}\left(\omega (t-{t}_{0})\right){{{{{\rm{exp }}}}}}\left(-(t-{t}_{0})/{t}_{D}\right),\) around which the lattice elastically oscillates with the initial amplitude Aph (see Fig. 2b and Methods). X-ray diffraction measures the lattice distortions and does not directly measure itinerant electrons. Nevertheless, through spin–lattice interactions, the measured transient, non-oscillatory lattice distortion \({A}_{{{\psi }}}\left(t\right)\) probes the transient itinerant SDW order. The order parameter, \({A}_{{{\psi }}}\left(t\right)\) displays a quench, followed by a recovery (see Fig. 1b).
a Time-resolved total displacement \({A}_{{{{{{{\mathrm{tot}}}}}}}}\left(t\right)\) normalized by the ground state periodic lattice distortion (PLD) amplitude \({A}_{{{{{{{\mathrm{tot}}}}}}}}\left(t\right){/A}_{{{{{{{\mathrm{tot}}}}}}},{{{{{{\mathrm{GS}}}}}}}}\) (proportional to the X-ray satellite-peak intensity) as a function of the laser pump fluence shown as a color scale difference (color scale shown above the graph). b The amplitude of the transient order parameter, \({A}_{\psi }\left(t\right)\), normalized by the amplitude in the ground state, \({A}_{\psi ,{GS}}=\) \({A}_{{{{{{{\mathrm{tot}}}}}}},{{{{{{\mathrm{GS}}}}}}}}\), and shown for three different incident fluences: 1 mJ/cm2 (blue), 3 mJ/cm2 (green), and 5 mJ/cm2 (red). The inset shows the transient PLD amplitude for all fluences measured in a as a color scale difference (color scale shown above the right inset). c The spin density wave (SDW) quench amount \(\Delta {A}_{\psi }={A}_{\psi }\left(0{{{{{{\mathrm{ps}}}}}}}\right)-{A}_{\psi }\left(0.1{{{{{{\mathrm{ps}}}}}}}\right)\) (blue squares: data from a and green circles: higher statistics data) and the recovery amount (orange stars) determined from the transient PLD amplitude shown in b. The amplitude of the phonons (standing wave) Aph is also shown (magenta crosses). d The recovery time determined as the area indicated in the left inset in b, where \({\widetilde{A}}_{\psi }\)= [\(\left.{{A}_{\psi }\left(t-0.1{{{{{{\mathrm{ps}}}}}}}\right)-{A}_{\psi }\left(0.1{{{{{{\mathrm{ps}}}}}}}\right)}\right]/\left[{A}_{\psi }\left(2{{{{{{\mathrm{ps}}}}}}}\right)-{A}_{\psi }\left(0.1{{{{{{\mathrm{ps}}}}}}}\right)\right]\) is integrated from 0 to 1 ps. We choose the area because the exponential fit poorly reproduces the data at higher fluences due to the shoulder feature and the flat region. The uncertainty in b, c, d is estimated as the standard deviation of the data at time delays above 1 ps, where we expect the residual between the harmonic oscillator fit and the data to be zero.
Figure 2a shows the time-dependent intensity of the coherent satellite-peak as a function of the pump fluence. We first determine the phonon dynamics for each pump fluence by fitting the time-trace in interval II (1 ps < t < 4.5 ps). While the phonons' frequency (2.27 THz) and its damping time (3 ps) are independent of the fluence, the phonons' maximum amplitude increases with fluence. At 3.5 mJ/cm2 and above, the laser pulse launches the standing wave with the highest amplitude possible—approximately equal to the pre-quench amplitude of the PLD14 (see Supplementary Note 2, 3 and Supplementary Fig. 2a). All data collected for t > 1 ps is consistent with a damped harmonic oscillator, suggesting no phonon anharmonicity for all measured fluences.
Dynamics of the transient density wave order parameter
The precise measurement of the oscillatory lattice distortion in the time domain allows us to extract the subtle non-oscillatory lattice distortion that couples to the transient electronic order. For all measured fluences, this transient order parameter, \({A}_{{{\psi }}}\left(t\right)\), displays a quench followed by a recovery (see Fig. 2b). The amount by which the transient order reduces, ΔAψ, grows monotonically with the fluence before it saturates at a fluence of 3.5 mJ/cm2 (see Fig. 2c). The saturation signifies the critical fluence beyond which we observe a full quench of the order parameter, likely because the electronic temperature rises above TN at this critical fluence14. A complete quench also yields a standing wave with the maximum amplitude (see Fig. 2c and Supplementary Fig. 2a). While the recovery is monotonic for lower fluences, our data displays a “shoulder” for high fluences. A possible explanation for the shoulder is the phonon frequency dependence on charge carrier density, reported in a semimetal after the optical quench18. In metallic Cr, the magnitude of the carrier release is likely too small to modify the phonon frequency. Alternatively, no SDW recovery occurs at carrier temperatures above TN leading to a discontinuity of the SDW recovery when the carrier temperature falls below TN19. Finally, the total PLD amplitude \({A}_{{{{{{{\mathrm{tot}}}}}}}}\left(t\right)\) becomes negative at ~0.2 ps for high fluences (see Fig. 2a) when the atomic displacement passes through equilibrium (undistorted lattice) and the argument in the cosine approaches π (see Eq. 1). The shoulder feature occurs at 0.4 ps, where \({A}_{{{{{{{\mathrm{tot}}}}}}}}\left(t\right)\) becomes positive, indicating a strong coupling between the dynamic lattice distortion and the SDW recovery.
The order recovery time increases approximately linearly in the whole fluence range of 0–5.5 mJ/cm2 (see Fig. 2d). Yet the observed laser-induced dynamics of the lattice in our experiment remain exceptionally fast; the order vanishes within 100 fs and recovers within 500 fs, even at the highest measured fluences when the SDW and its coupled structural component are fully quenched (see Fig. 2b, highest fluence). In our experiment, X-ray diffraction is sensitive to the phase coherence of the density wave: disorder would broaden the satellite-peak and reduce its intensity at a fixed Q = Q002 – QL. The recovery of a coherent density wave in Cr is a few times faster than the recovery of phase coherence in other density-wave-systems after a full quench of the structural component20,21,22. Nicholson19 directly measured the SDW gap in Cr using time-resolved angle-resolved photoemission spectroscopy (tr-ARPES). Strikingly, our X-ray diffraction data and tr-ARPES show nearly identical time dependence, indicating persistent spin–lattice coupling out-of-equilibrium. It is this persistent coupling that we initially discover and then exploit to relate the SDW to the transient lattice distortion and to measure femtosecond dynamics of the SDW order parameter and wavevector with non-resonant X-ray diffraction.
Phonon-assisted density wave recovery
In the thin-film studied here, the interfaces restrict the temperature-dependent SDW period in Cr7 to two distinct values23. During quasi-static cooling, the SDW forms at TN = 290 K with the wavevector QH (7.5 PLD-periods across the film). At 230 K, the wavevector changes to QL (8.5 PLD-periods across the film) through an abrupt phase transition23. We correctly reproduce the quasi-static behavior using a phenomenological Landau model (see Fig. 3a, b and Methods)10,11,13,24,25,26. The superb momentum resolution of X-ray diffraction allows us to track the wavevector of the SDW during its formation out-of-equilibrium. Surprisingly, after a full laser quench, we observe no satellite-peak at Q002 – QH: the SDW immediately forms with the low-temperature wavevector QL (see Fig. 3b). The system directly bypasses a state expected from the free-energy diagram (compare gray and red lines in Fig. 3b, c). Additionally, the order recovers within 500 fs, suggesting the absence of an abrupt phase transition, which typically occurs on a significantly longer timescale (~100 ps)27,28.
a The Landau free-energy, \(F\left(\psi ,{Q}_{m}\right)\), as a function of the transient temperature of the electron gas, Te, and the order parameter ψ, shown for the wavevector Qm that minimizes the free-energy (color scale shown at the top). b The free-energy \(F\left({\psi }_{m},Q\right)\) as a function of the electronic temperature, Te, and wavevector Q, shown for the order parameter \({\psi }_{m}\) that minimizes the energy (color scale shown at the top). In a and b, the equilibrium (gray dashed line) and non-equilibrium (red solid line) paths during order formation are shown. c The wavevector dynamics revealed through measuring the satellite-peak intensity and position: in equilibrium, the spin density wave (SDW) forms with a smaller wavevector QH and then transitions to QL via an abrupt (first-order) phase transition (consistent with the energy barrier indicated by the gray dashed line in b. Out-of-equilibrium, the order immediately forms with QL, bypassing the state at QH (see red line in b). d A schematic phonon distribution during the formation of the SDW: in equilibrium the SDW forms at the Néel temperature (Tlattice = TN, top, gray), and out-of-equilibrium the SDW forms at a lower lattice temperature Tlattice < TN and in presence of wavevector-matched acoustic phonons at QL (red, bottom).
The addition of the wavevector shows that the Landau theory recently extended to ultrafast transitions may be inconsistent with experiments in the presence of collective vibrations. In equilibrium, the SDW forms in the presence of Bose-Einstein-distributed phonons at TN. Out of equilibrium, the SDW forms at a lattice temperature lower than TN and in the presence of wavevector-matched phonons at QL (see Fig. 3d). We hypothesize that the non-equilibrium phonon distribution dynamically pins the SDW through maintaining a periodic potential in the absence of the order parameter, thus modifying its formation pathway in the free-energy landscape. We test our hypothesis of the phonon-assisted SDW formation by exciting the system with two sequential laser pulses, which we showed can be used for controlling the vibrational state29. Each laser pulse launches a standing wave, and the delay between the laser pulses modifies the phase shift between the two standing waves and the amplitude of their harmonic superposition (see Fig. 4a). Varying the laser pulse delay by only 200 fs changes the superposition’s amplitude from 0 to 1.6 times the amplitude of the pre-quench PLD (see Fig. 4b, inset)29. When the laser pulse delay is larger than the SDW recovery time, the SDW recovers before the second pulse arrives, and we expect the second SDW-quench to be independent of the delay. Yet after the second quench, the SDW recovers faster for a larger phonon superposition amplitude (see Fig. 4b, Supplementary Note 4, and Supplementary Fig. 3a, b) (both the phonons' amplitude and recovery time are periodic functions of the pump-pump time delay (see Supplementary Note 4 and Supplementary Fig. 3c, d)), supporting our hypothesis of the phonon-assisted SDW formation.
a Typical time-resolved total displacement \({A}_{{{{{{{\mathrm{tot}}}}}}}}/{A}_{{{{{{{\mathrm{tot}}}}}}},{{{{{{\mathrm{GS}}}}}}}}\) normalized by its value in the ground state for two pump pulses arriving as indicated. The second pulse changes the phonon amplitude29. b The density wave recovery time, τ, as a function of the phonon amplitude, \({A}_{{{{{{{\mathrm{ph}}}}}}}}{/A}_{\psi ,{{{{{{\mathrm{GS}}}}}}}}\) normalized by the order parameter in the ground state, both measured after the arrival of the second pump pulse. Each pair of values is determined from a fit to the data measured with a fixed time delay between the two pump pulses; the analysis procedure is identical to the analysis used for single-pulse data (see Eq. (1)), with taking the arrival of the second pulse as time zero. The red line shows a linear fit with \(\tau \left({A}_{{{{{{\rm{ph}}}}}}}/{A}_{\psi ,{{{{{{\mathrm{GS}}}}}}}}\right)=b\left({A}_{{{{{{\rm{ph}}}}}}}/{A}_{\psi ,{{{{{{\mathrm{GS}}}}}}}}\right)+c\), with \(b=-0.046\) and \(c=0.35\). The dashed gray lines indicate the prediction intervals of the fit. Inset: The quench after the second pulse as a function of the phonon amplitude: the second pulse induces the same quench independent of the phonon amplitude. All pump-pump delays are larger than 0.5 ps, ensuring the electron-lattice equilibration completes before the second pulse arrives. Both pump pulses have the same intensity, 1 mJ/cm2, which only partially quenches the spin density wave.
Conclusions
In conclusion, our results show how a coherent ionic lattice vibration markedly modifies the pathway and the timescale of an electronic phase transformation, highlighting the opportunity for using collective excitations to guide electronic instabilities. Furthermore, we demonstrate how persistent spin–lattice coupling and non-resonant diffraction at X-ray lasers enable momentum-resolved interrogation of the transient electronic order in the presence of collective excitations.
Methods
Pump-probe X-ray measurements
The Cr film studied in this work was deposited onto a single-crystal MgO (001) substrate using DC magnetron sputtering at a substrate temperature of 500 °C and annealed for an hour at 800 °C. The growth process was optimized to yield both a smooth surface and good crystal quality of the sample. The film thickness was determined to be 28 nm by X-ray reflectivity. The Néel temperature of a thin film is 290 K (see also refs. 14,17). The pump-probe experiments were carried out at the XPP instrument of the LCLS with an X-ray photon energy of 8.9 keV, selected by the 111 diffraction of a diamond crystal. X-ray diffraction around the 002 Bragg peak (2θ = 60°) from each pulse was recorded by an area detector (CS140k) with a repetition rate of 120 Hz. Owing to the mosaic spread of the crystal in the film plane, several Laue oscillations appear on the area detector simultaneously. The satellite-peak intensity is defined as the normalized difference between the intensity in the ground state and the intensity in absence of the PLD. We determine the latter as the intensity at t = 0.1 ps for highest fluence, where the PLD crosses zero amplitude at high fluences. This normalized intensity is directly proportional to the total amplitude of the periodic displacement14. About 100 pulses were recorded for each time delay (30 fs steps in the time traces). For each time delay, the intensity was corrected for dark noise and normalized by the intensity measured in the region of the area detector where Laue oscillations were absent. The sample was excited by optical (800 nm, 45 fs), p-polarized laser pulses propagating nearly collinear with the X-ray pulses. The temporal resolution was estimated to be ~50 fs. The spot sizes (cross-section, FWHM) of the optical and X-ray pulses were 0.46 mm (H) × 0.56 mm (V) and 0.2 mm (H) × 0.2 mm (V), respectively.
Determining the order parameter from X-ray data
The laser pulse interacts with the carriers, raises their temperature, and perturbs the SDW. Because in thin metallic films the heat flow occurs at the Fermi velocity15, within ~30 fs the inhomogeneities in the excitation profile due to the limited penetration depth vanish. We assume that the laser quench launches the phonons (standing wave) and that the order parameter’s recovery has no impact on phonon amplitude and frequency. The uncertainty of our approximation is about 10% of the order parameter because the maximum slope of the recovery is about three times smaller than the maximum slope of the phonon oscillation (proportional to the velocity of the oscillating atoms), adding about 10% to the phonon energy (proportional to the atomic displacement). We chose the robust regression fit with the least absolute residual method to minimize the outlier’s influence and choose the upper and lower limits according to direct observation on the data shape. In the fit, different lower bounds for the harmonic oscillator fit ranging from 1 to 2 ps yield similar results. We subtract the extrapolated fit from the data, then add the PLD value at 4 ps to the residual. After 4 ps, the PLD represents an order parameter recovered to its new equilibrium value (slightly heated system). For fluences at around 11 mJ/cm2 this PLD amplitude vanishes14, indicating the absence of the order parameter recovery because the system remains above the Néel temperature (TN) (see Supplementary Note 2 and Supplementary Fig. 2b), in agreement with mean-field theory3,30. In summary, we describe the total measured dynamic periodic lattice distortion by
The subsequent heat transport from the film into the substrate occurs in ~0.3 ns16. The laser fluence was determined by comparing the data directly with the published data on the exactly the same films, where the fluence was determined by using the Bragg peak position as a thermometer14.
Landau-theory modeling
We use the Landau theory developed by McMillan for describing density waves31. It describes how density wave systems evolve microscopically, agrees with experiments in multiple CDW systems and SDW in Cr under quasi-static and pressure-driven conditions10,11, and was recently extended to ultrafast transitions13,24. We adapt the free-energy density to a thin-film Cr introducing terms similar to ref. 10 as
where \(\psi {e}^{i\phi }\) is the complex SDW order parameter with the real amplitude ψ (proportional to Aψ) and phase ϕ. Here, q is the natural nesting SDW wavevector given by the electronic instability, G the wavevector enforced by boundary conditions, and a, b, c, d, e, f the coefficients. The first two terms are the second-order free-energy expansion of Landau theory. We assume \(a\,{{\mbox{=}}}\,a_{0}\left(T_{{{\mbox{e}}}}{{\mbox{-}}}T_{{{\mbox{N}}}}\right)\), where Te is the transient temperature of the electron gas, TN is the Néel temperature, and b, c, d, e, f are temperature independent. The third term is electronic energy from finite spatial correlation length. We neglect the third term by assuming ψ is uniform across the thin film, \(\nabla \psi =0.\) The fourth term is the energy cost of changing SDW wavevector from the natural wavevector.
We use the fifth term to model the energy of the lock-in to the boundary conditions (possibly by impurities at the interfaces32), which restrict the available wavevectors of the SDW in a thin film. Specifically, we do not use G as a reciprocal space vector31, we use \({G=Q}_{L}\) and \({G=Q}_{H}\) to enforce the pinning by the interfaces. We replace the last term with \({f}_{L}{\psi }^{4}{\cos }\left(2\phi -2{Q}_{L}x\right)+{f}_{H}{\psi }^{4}{\cos }\left(2\phi -2{Q}_{H}x\right)\), \({{|f}}_{L}\left|\ > \ {{|f}}_{H}\right|\). This modification of McMillans formalism allows us to reproduce the experimentally observed quasi-static temperature dependence: the SDW forms with QH and subsequently transitions to QL via an abrupt phase transition evidenced through an energy barrier.
We integrate free-energy density F over the film thickness L by using \(\phi ={Qx}\) and find
The above equation is used to calculate the free-energy surface shown in Fig. 3a, b. We parametrize the model with the transient electronic temperature, Te: the electrons thermalize within few tens of fs after photoexcitation and remain thermalized among themselves during the electron phonon equilibration time19. The total system remains out of equilibrium because the lattice temperature \(T_{{{\mbox{lattice}}}}\) stays lower than the transient electronic temperature Te and only increases within ~0.5 ps during the electron–phonon coupling14,19. The transient change of the electronic temperature is ~5 times larger than the change in the lattice temperature14,19. For a given transient electronic temperature (value of a) and each value of the order parameter ψ, we minimize \(F\left(\psi ,Q\right)\) as a function of Q to determine the path of Q during the formation of the density-wave. Figure 3a shows this minimized \(F\left(\psi ,{Q}_{m}\right)\), which is dominated by the competition between the first two Landau terms. Similarly, for a given temperature and each value of the wavevector Q, we minimize \(F\left(\psi ,Q\right)\) as a function of ψ. Figure 3b shows this minimized \(F\left({\psi }_{m},Q\right)-{F}_{{\min }}({\psi }_{m},{Q}_{m})\). This function displays the competition between the natural wavevector q, and the two wavevectors restricted by the film geometry. As only two values QH and QL are possible, switching between the two requires overcoming an energy barrier.
Data availability
Raw data were generated at the Linac Coherent Light Source (LCLS), SLAC National Accelerator Laboratory large-scale facility. Derived data supporting the findings of this study are available from the corresponding author upon request.
Code availability
Code is available from the corresponding author upon request.
References
Peierls, R. E. Quantum Theory of Solids (Wiley, 2001).
Fröhlich, H. Electrons in lattice fields. Adv. Phys. 3, 325–361 (1954).
Overhauser, A. W. Spin density waves in an electron gas. Phys. Rev. 128, 1437–1452 (1962).
Lomer, W. M. Electronic structure of chromium group metals. Proc. Phys. Soc. 80, 489–496 (1962).
Moncton, D. E., Axe, J. D. & DiSalvo, F. J. Neutron scattering study of the charge-density wave transitions in 2H−TaSe2 and 2H−NbSe2. Phys. Rev. B 16, 801–819 (1977).
Gruner, G. Density Waves in Solids. 288pp. (CRC Press, 2009).
Fawcett, E. Spin-density-wave antiferromagnetism in chromium. Rev. Mod. Phys. 60, 209–283 (1988).
Corliss, L. M., Hastings, J. M. & Weiss, R. J. Antiphase antiferromagnetic structure of chromium. Phys. Rev. Lett. 3, 211–212 (1959).
Yeh, A. et al. Quantum phase transition in a common metal. Nature 419, 459–462 (2002).
Jaramillo, R. et al. Breakdown of the Bardeen-Cooper-Schrieffer ground state at a quantum phase transition. Nature 459, 405–409 (2009).
Feng, Y. et al. Itinerant density wave instabilities at classical and quantum critical points. Nat. Phys. 11, 865–871 (2015).
Eichberger, M. et al. Snapshots of cooperative atomic motions in the optical suppression of charge density waves. Nature 468, 799–802 (2010).
Yusupov, R. et al. Coherent dynamics of macroscopic electronic order through a symmetry breaking transition. Nat. Phys. 6, 681–684 (2010).
Singer, A. et al. Photoinduced enhancement of the charge density wave amplitude. Phys. Rev. Lett. 117, 056401 (2016).
Brorson, S. D. et al. Femtosecond room-temperature measurement of the electron-phonon coupling constant γ in metallic superconductors. Phys. Rev. Lett. 64, 2172–2175 (1990).
Singer, A. et al. Condensation of collective charge ordering in Chromium. Phys. Rev. B 91, 115134 (2014).
Singer, A. et al. Phase coexistence and pinning of charge density waves by interfaces in chromium. Phys. Rev. B 94, 174110 (2016).
Fritz, D. M. et al. Ultrafast bond softening in bismuth: mapping a solid’s interatomic potential with X-rays. Science (N. Y., N. Y.) 315, 633–636 (2007).
Nicholson, C. W. et al. Ultrafast spin density wave transition in chromium governed by thermalized electron gas. Phys. Rev. Lett. 117, 136801 (2016).
Zong, A. et al. Evidence for topological defects in a photoinduced phase transition. Nat. Phys. 15, 27–31 (2018).
Laulhe, C. et al. Ultrafast formation of a charge density wave state in 1T-TaS_{2}: observation at nanometer scales using time-resolved X-ray diffraction. Phys. Rev. Lett. 118, 247401 (2017).
Huber, T. et al. Coherent structural dynamics of a prototypical charge-density-wave-to-metal transition. Phys. Rev. Lett. 113, 026401 (2014).
Zabel, H. Magnetism of chromium at surfaces, at interfaces and in thin films. J. Phys.-Condens. Matter 11, 9303–9346 (1999).
Beaud, P. et al. A time-dependent order parameter for ultrafast photoinduced phase transitions. Nat. Mater. 13, 923–927 (2014).
Zhang, J. et al. Cooperative photoinduced metastable phase control in strained manganite films. Nat. Mater. 15, 956–960 (2016).
Harter, J. W. et al. Evidence of an improper displacive phase transition in Cd_{2}Re_{2}O_{7} via time-resolved coherent phonon spectroscopy. Phys. Rev. Lett. 120, 047601 (2018).
Abreu, E. et al. Dynamic conductivity scaling in photoexcited V2O3 thin films. Phys. Rev. B 92, 085130 (2015).
Singer, A. et al. Nonequilibrium phase precursors during a photoexcited insulator-to-metal transition in V2O3. Phys. Rev. Lett. 120, 207601 (2018).
Gorobtsov, O. Y. et al. Femtosecond control of phonon dynamics near a magnetic order critical point. Nat. Commun. 12, 2865 (2021).
Bardeen, J., Cooper, L. N. & Schrieffer, J. R. Theory of superconductivity. Phys. Rev. 108, 1175–1204 (1957).
McMillan, W. L. Microscopic model of charge-density waves in2H−TaSe2. Phys. Rev. B 16, 643–650 (1977).
Littlewood, P. B. & Rice, T. M. Metastability of the Q vector of pinned charge- and spin-density waves. Phys. Rev. Lett. 48, 44–47 (1982).
Acknowledgements
We thank Jerry Hastings for the discussions. The work was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contracts No. DE-SC0019414 (ultrafast X-ray data analysis and interpretation J.L., O.Y.G., B.G., A. S.), DE-SC0001805 (ultrafast X-ray scattering experiments, A.S., A.G.S., N.H., S.H., J.W., D.C., O.G.S.), and No. DE-SC0003678 (thin-film synthesis and characterization, ultrafast X-scattering, S.K.K.P., R.M., and E.E.F.). Use of the Linac Coherent Light Source (LCLS), SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515.
Author information
Authors and Affiliations
Contributions
A. Singer, O.G.S., and E.E.F. planned the project; A. Singer, S.K.K.P., A.G. Shabalin, N.H., S.H., R.M., J.W., D.C., J.M.G., D.Z., M.C. performed the pump-probe X-ray measurements; J.L. performed data analysis, interpretation of the results, and Landau modeling with help from O.Y.G., B.G., and A. Singer; S.K.K.P. and E.E.F. grew samples; and J.L., O.Y.G., and A. Singer wrote the paper. All authors contributed to discussions and gave comments on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Dmitry Khakhulin and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, J., Gorobtsov, O.Y., Patel, S.K.K. et al. Phonon-assisted formation of an itinerant electronic density wave. Commun Phys 5, 125 (2022). https://doi.org/10.1038/s42005-022-00902-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-00902-6
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.