Abstract
One of the most important topics in molecular biology is the genetic stability of DNA. One threat to this stability is proton transfer along the hydrogen bonds of DNA that could lead to tautomerisation, hence creating point mutations. We present a theoretical analysis of the hydrogen bonds between the Guanine-Cytosine (G-C) nucleotide, which includes an accurate model of the structure of the base pairs, the quantum dynamics of the hydrogen bond proton, and the influence of the decoherent and dissipative cellular environment. We determine that the quantum tunnelling contribution to the proton transfer rate is several orders of magnitude larger than the classical over-the-barrier hopping. Due to the significance of the quantum tunnelling even at biological temperatures, we find that the canonical and tautomeric forms of G-C inter-convert over timescales far shorter than biological ones and hence thermal equilibrium is rapidly reached. Furthermore, we find a large tautomeric occupation probability of 1.73 × 10−4, suggesting that such proton transfer may well play a far more important role in DNA mutation than has hitherto been suggested. Our results could have far-reaching consequences for current models of genetic mutations.
Similar content being viewed by others
Introduction
In their seminal paper, Watson and Crick proposed that the tautomerisation of DNA base pairs could produce stable errors in the genetic code1. The proposed mechanism for such tautomerisation is double proton transfer along the hydrogen bonds within base pairs, Guanine–Cytosine (G–C) or Adenine–Thymine (A–T)2,3. This mechanism is of particular interest due to what has been predicted to be a significant contribution from the quantum tunnelling of the protons through a potential barrier separating the nucleotide base pairs on the two strands of DNA4. The mechanism has been widely studied theoretically4,5,6,7 and, more rarely, experimentally8,9.
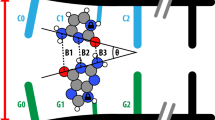
When the H-bond protons transfer across from a base site on one strand to the corresponding site on the other strand, each base changes from its standard canonical to its tautomeric form (see Fig. 1). If this tautomeric pair can survive the DNA cleavage process in the helicase (an enzyme that aids DNA strand separation), then each strand could pass through the DNA replication machinery (the replisome), whereby the tautomeric form of the base is mismatched with the wrong corresponding base on the copy strand1,10. Furthermore, this mismatched pair can evade fidelity check-points of the replisome by adopting a structure similar to a Watson and Crick base pair5,10, resulting in an erroneous mismatch and hence a point mutation (for example, G–C ↔ G*–C* → G*–T, where the star denotes the tautomeric form).
a Rendering of the canonical standard form taken from the reaction path of Slocombe et al.4 with permission from the Royal Society of Chemistry. b The energetic maximum along the reaction coordinate. c The potentially mutagenic tautomeric (enol-imino) non-standard form of the DNA base. Hydrogen atoms are shown in white, nitrogen in blue, carbon in grey, and oxygen in red.
The role of the double proton transfer mechanism has been hotly debated for over half a century, with several authors5,7,11,12,13 suggesting that it does not meet the criteria needed to survive the DNA replication process, since the tautomers would need to survive the nanosecond timescale of the Helicase cleavage process5,11,12. We present here a different and, we believe, more convincing argument. We show that the double proton transfer process takes place so quickly (in comparison with biologically relevant timescales) that the lifetimes of the tautomeric states do not play a significant part in determining the likelihood of a base pair mismatch. Rather, it is the ratio between the concentration of tautomeric base pairs to canonical base pairs present at chemical equilibrium that matters.
We assume, as previously observed6,14, that the two protons undergo asynchronous transfer, suggesting that the rate-determining process is the transfer of a single proton across the barrier, with the other proton then moving in the opposite direction to preserve electroneutrality. There is a substantial agreement in the literature that the proton transfer in G–C is an asynchronous process, while the step-wise proton transfer pathway (in which a proton transfer before the second one) has been ruled out in favour of the double proton transfer scheme4. The argument is that in the standard Watson–Crick configuration, the formation of the single proton transfer is either unstable or energetically unfavourable5,7,11,12. The thermodynamic equilibrium constant, Keq, is generally written as Keq = [G*–C*]/[G–C], which is the ratio between the concentration of products (tautomeric pair) and reactants (canonical pair) present at chemical equilibrium. However, the concentrations are modified by an activity coefficient. More correctly, a quantum activity coefficient, Γqm, needs to be included as a factor such that Keq-qm = Γqm × [G*–C*]/[G–C]. Which is exclusively a non-classical activity coefficient containing effects such as thermally enhanced tunnelling, zero-point energy, decoherence and dissipation, leading to an activity coefficient that is far from unity, in the same way that solvent effects can shift equilibrium15.
For G–C tautomerism, Keq can be readily obtained, either from the difference in Gibbs free energy, ΔG, between products and reactants via \({K}_{{{{{{{{\rm{eq}}}}}}}}}=\exp \left(-{{\Delta }}G/{k}_{{{{{{{{\rm{b}}}}}}}}}T\right)\) and calculated with ab initio methods, or measured experimentally. However, without an accurate estimate of the activity coefficient, we cannot determine the quantity of interest, [G*–C*]/[G–C]. Instead, we carry out a fully quantum mechanical calculation to obtain the G*–C* occupation probability within an open quantum system (OQS) approach. We find it to be several orders of magnitude greater than the observed rate (10−8 per base pair16) of spontaneous mutations through, for example, copying errors, suggesting that tautomerisation may well play an important role in point mutations.
Much recent theoretical effort has been devoted to investigating tautomerisation of A–T and G–C base pairs via double proton transfer, such as the use of path integral molecular dynamics8,14,17. Applying these methods suggests that proton delocalisation causes the strength of the hydrogen bonds in DNA base pairs to follow an anomalous temperature dependence due to the subtle balance of several quantum effects involved in the binding. The problem with such approaches is that while the proton dynamics are treated quantum mechanically, the coupling between them and the surrounding environment is dealt with via approximate “classical" thermostats. However, it is well known that crucial quantum effects such as decoherence and dissipation are not treated correctly in adiabatic, thermally uncoupled models of tunnelling6,18. Therefore, we employ in this work a fully OQS treatment of the dynamics, and subsequent populations, of the proton transfer in the G–C tautomerisation reaction. Our decision to study G–C rather than A–T is because the tautomeric state, A*–T*, is extremely unstable, with a fleetingly short lifetime, and therefore not as likely to play a role in mutagenesis4,5,7,13. Further discussion on the contention in the literature on the accuracy and nature of the proton transfer process in DNA can be found in Refs. 10 and 19.
Results
The system-bath model
We use an accurate description of the potential energy landscape of the double H-bond between the C and G bases4; we model the proton dynamics using an OQS model to account for dissipation and decoherence effects due to the surrounding cellular environment.
The proton transfer process is initially described by projecting the reaction pathway on a generalised reaction coordinate that connects the canonical to the tautomeric state via a single transition state4,20 on a chemically accurate potential energy surface (PES) in the form of an asymmetric double-well potential (Fig. 2, see Method section). The parameters of this potential are used to calculate the classical rate contribution within Eyring’s framework, which is outlined in the Methods section. Thus, the reaction is characterised by a ΔE (energetic asymmetry between the bottoms of the two potential wells) of 0.435 eV, a high forward barrier of 0.705 eV and a reverse barrier of 0.270 eV. The PES allows us to calculate the quantum tunnelling correction and estimate the lifetime of the tautomeric state. Figure 2 also shows the first ten energy eigenvalues for a single proton in this potential, six of which are entirely local to the G–C canonical configuration, with the seventh eigenstate the first to have a non-zero amplitude in the shallow (tautomeric) well.
The potential is used in the Hamiltonian of our OQS master equation in which the dynamics of the proton transfer are described following the Caldeira and Leggett quantum Brownian motion model21, in which the quantum system (a proton in the double-well potential) interacts with a surrounding infinite thermal bath of harmonic oscillators (representing the cellular environment). The bath degrees of freedom are then integrated over using the path integral formalism of Feynman and Vernon22.
The equivalent phase-space formulation of the Caldeira and Leggett master equation, also known as Wigner–Moyal–Caldeira–Leggett (WM–CL) equation, is written as21,23
and describes the time evolution of the Wigner function, W(q, p, t). The initial state is taken to be a non-equilibrium distribution localised in the reactant well.
where \({{{{{{{\mathcal{H}}}}}}}}={p}^{2}/(2m)+V(q)\), \({{{{{{{\mathcal{N}}}}}}}}\) is a normalisation constant, and \(\hat{h}(q)\) is a Heaviside step function that projects onto the product side of a transition state dividing surface (reaction barrier).
In Eq. (1), the phenomenological friction constant, γ, describes the strength of the coupling to the surrounding (Ohmic) heat bath21, kB is Boltzmann’s constant, T is the bath temperature, and the quantum ‘system of interest’ (the H-bond proton) has position q, momentum p and mass m. Eq. (1) also contains two terms describing the dissipation and decoherence that arise from the coupling of the proton with the bath. It is a deterministic dynamical equation that is rigorously valid only in the weak-coupling regime and in the high-temperature limit21.
However, for biologically relevant bath temperatures (T ≈ 300 K), the high-temperature limit is not a valid approximation. Consequently, our model requires a low-temperature correction applied in Eq. (1) whereby the thermal energy is replaced with the zero-point energy24,25,26,27,28,
where the high temperature limit is simply the leading term in the Taylor expansion of \(\coth x={\frac{1}{x}}+{\frac{x}{3}}-{\frac{{x}^{3}}{45}}+{\cdots}\)21,24,25,26,27,28. Here, ω is the frequency of the lowest energy eigenstate in the double-well potential. Making the replacement described in Eq. (3) permits the use of the WM–CL equation at lower temperatures, in which ω can be approximated by the second derivative of the potential around its global minimum (ω = 0.00367 a.u.). Figure 3 shows the breakdown of the high-temperature approximation for the G–C proton transfer potential. Further discussion on the low-temperature correction and its justification can be found in the Methods section. To account for this, we solve Eq. (1) with the factor kBT in the final term replaced by the right-hand side of Eq. (3).
Assuming that the bath is dominated by the thermal fluctuations of the surrounding water molecules, we can estimate the value of γ. Water has a collision spectrum in the range 3300−3900 cm−1 29, we take γ = 3900 cm−1.
Lifetime of the tautomer
In order to determine whether or not tautomerisation plays an important role in biology, we need to know the lifetime of the tautomeric state. Therefore, we calculate the quantum contribution, kQM, to the chemical reaction rate by monitoring how the flux of the probability changes between the left and right-hand well30,31,32,33,34. For a short time, we expect transient behaviour of the density with re-crossings of the transition state35 rather than exponential macroscopic decay of flux passing through the barrier. The phenomenological rate law applies only after a characteristic time τc in which this transient phase has ended.
The tunnelling factor, κ, calculated in the Methods section, is found to be very large (~105) indicating that the quantum contribution to the reaction rate is non-trivial. With this value, we obtain a forward and reverse reaction rate of kf = 7.61 × 105 s−1 and kr = 1.69 × 1013 s−1, respectively, whereas the half-life of the reactant and product is now 9.11 × 10−7 and 4.09 × 10−14 s, respectively. In an analogue system (the 7-azaindole dimer), ultraviolet femtosecond pulsed time-of-flight spectroscopy indicates that proton transfer can occur on a timescale of a few hundred femtoseconds36. Here, light is used to induce proton transfer and to probe the dynamics of the dimer. In addition, Douhal et al.36 demonstrate that the process is isotopically sensitive, indicating that quantum tunnelling can play a role in the dynamics. The experimental rates reported are much faster than the rates reported here, which is likely due to the initial ultraviolet pulse modifying the reaction profile. However, the experiment suggests that the proton transfer reaction rate can be fast and have a quantum component.
Comparatively, setting the quantum contribution in Eq. (8) to unity gives a classical forward and reverse reaction rate of kf = 7.596 s−1 and kr = 1.692 × 108 s−1. The classical equilibrium constant, Keq, is on the order of 10−8 which is in agreement with Gheorghiu et al.7, whereas the half-lifes of the reactant and product are 0.0913 and 4.1 × 10−9 s, respectively.
These quantum corrected half-lives are significantly shorter than the classical estimates, indicating the protons are sufficiently delocalised along the hydrogen bond and populate both states; the forward and reverse reaction rates are so quick that the system continuously converts between the canonical and tautomeric forms. This fast interconversion timescale suggests that an equilibrium description can be safely adopted.
We performed a sensitivity analysis of the reaction barrier (see Supplementary Note 5) and determined that increasing the barrier height significantly impacts the rate of the thermally activated proton ‘over-the-barrier’ hopping dynamics; namely, it causes a striking reduction in classical rate, but it affects the quantum tunnelling rate much less. Furthermore, the tunnelling correction remains so high that the equilibrium populations of the canonical and tautomeric forms would quickly be reached even if the barrier height was 50% higher than in our study.
We investigated the impact of the kinetic isotope effect (KIE) as a function of temperature (doubling the proton’s mass if replaced by a deuteron). See Supplementary Note 4 and Methods section. A strong dependence of the reaction rate on the reduced mass of the system can indicate tunnelling. Hence the kinetic isotope can be used to probe if quantum effects dominate37,38,39.
At low temperatures, the KIE rapidly increases, providing further evidence that the transfer process becomes increasingly dependent on the quantum (tunnelling) contribution. Meanwhile, at high temperatures, the KIE exponentially tails off. At biological temperatures the KIE = 30.
A high tunnelling factor and KIE has been observed in other models of OQSs18,40 probing proton transfer reactions. Furthermore, in a proton transfer reaction catalysed by enzyme soybean lipoxygenase, in the wild type, a high KIE of ~8041 has been experimentally observed and verified using theory42. Furthermore, the KIE increased to the values from 500–800 in the case of various mutants39,43,44,45. Consequently, the value of KIE reported here is within sensible bounds of experimentally observed values.
Tautomeric state occupation probability
This timescale of the proton transfer (10 fs−100 ns) is significantly shorter than the cleavage timescale in the helicase (t ≫ 100 ns). Therefore, the G–C base pair enters the active site of the helicase in thermal equilibrium between canonical and tautomeric states with its eigenstates populated according to a Maxwell–Boltzmann distribution, Weq(q, p) = W(q, p, t → ∞).
The tautomeric occupation probability can now be calculated by integrating the Wigner function at equilibrium over all momenta, p, and over position, q, spanning only the width of the shallow well (the product side of the barrier),
The top panel of Fig. 4 examines the probability of finding the thermal distribution in the tautomeric well. At 300 K we observe an tautomer occupation probability of 1.73 × 10−4. At biological temperature, the probability in the right-hand well for the Eω curve levels out as the zero-point energy of the oscillator dominates. On the other hand, if we neglect the low-temperature correction, the probability rapidly becomes negligible as the temperature drops. Incorporating the low-temperature correction shows that tunnelling can play a role even with little bath excitation due to zero-point energy corrections.
The energy change (ΔE = 0.435 eV, see Fig. 2) between the canonical and tautomeric states dictates that the classical thermal equilibrium constant for the model system would have to be \({K}_{{{{{{{{\rm{eq}}}}}}}}}=\exp (-({{\mbox{0.435}}}{{\mbox{eV}}})/{k}_{{{{{{{{\rm{b}}}}}}}}}T)=\,{{\mbox{5.4}}}\,\times \,{{\mbox{10-8}}}\). As we observe from the calculations of Fig. 4, there is a factor of ~104 difference between the thermalised tautomer occupation probability obtained from the two treatments.
While the surrounding environment quickly causes dissipation and decoherence of the quantum system (the transferring proton), it also initially provides a vital source of thermal activation, exciting the proton to higher energy eigenstates in the double-well that can promote tunnelling through to the tautomeric side and leaving a non-trivial population in this state once it reaches thermal equilibrium.
Discussion
We have explored the proton transfer mechanism in the H-bonds of the G–C base pair within an OQS model. In this approach, the quantum system (the H-bond proton in the double-well potential) undergoes dissipation and decoherence due to coupling to a surrounding heat bath (the cellular environment). The environment also acts as a source of thermal activation, exciting the proton to higher energy states that promote tunnelling across to the right-hand tautomeric state. At t → ∞, the thermal equilibrium distribution gives a probability of 1.73 × 10−4 for the proton being in the tautomeric form, which is more than four orders of magnitude larger than that predicted by classical and semiclassical studies previously reported for this system.
Purely classical calculations predict that the tautomeric state is rarely populated due to its high forward reaction barrier. Furthermore, the relatively small reverse reaction barrier suggests that the tautomer is classically unstable with a lifetime of the order Helicase cleavage timescale. However, in our OQS approach, the tunnelling factor obtained is on the order of 105, suggesting that the system readily interconverts between the canonical and tautomeric configuration via quantum effects.
Previously, it was suggested by Brovarets’ et al.5 and Gheorghiu et al.7 that if the tautomeric lifetime is much shorter than helicase cleavage timescale, little to no product would survive the process. Our investigations determined that the quantum rate is significantly higher than the classical rate for a wide range of bath coupling strengths. The tautomer’s lifetime calculated with quantum correction suggests that the equilibrium concentration of this species is quickly reached. We would also like to highlight that adding further dimensions into the system Hamiltonian could lead to potential corner-cutting effects46 which could further enhance the rate. Furthermore, the forward and reverse proton transfer processes are significantly quicker than the expected helicase cleavage timescale. Because of this effective equilibrium in the helicase active site, we can adopt the tautomer occupation probability as a metric to define the ratio of canonical to tautomeric concentrations.
Attempting to identify isotope effects in this system is problematic since investigating biological assays in deuterated solvents comes with a whole host of problems, for example, viscosity effects inhibiting correct protein function47. In addition, the impairment of gene expression at the transcription or translation level could preclude the measurement of the KIE discussed in the Methods section. Therefore, more direct measurements via nuclear magnetic resonance shifts, such as those applied to the G–T wobble mismatch, need to be applied9.
On the other hand, computational studies suggest that the monomeric form of the tautomers are stable and extremely long-lived due to their prohibitively large reaction barriers4,13,48,49. Based on previous evaluations4 of tunnelling in this system, we expect that the tautomeric population of the monomeric forms are unlikely to see any meaningful change while in transit from the helicase until it matches another base pair. Consequently, any last line of defence against the tautomer’s uptake would take place during the exonuclease proofreading process, during which slight modifications to the DNA structure caused by the tautomeric mismatch could be corrected.
The first50 structural evidence for the rare tautomer hypothesis was observed using X-ray crystallographic analysis of a DNA polymerase. Whereby the polymerase was observed mismatching C with A. The mismatch adopts a Watson–Crick-like configuration which can only be obtained via the movement of a single proton on one of the mismatched bases. The proton transfer product alters the hydrogen-bonding pattern such that the mispair forms an overall shape that is virtually indistinguishable from a canonical, Watson–Crick base pair in double-stranded DNA. It remains an open question if the proton transfer has contributions from quantum effects.
More recently, tautomerisation in DNA has been experimentally observed using NMR relaxation dispersion. Here, hairpin DNA duplex structures were observed to interchange between a wobble G–T and a Watson–Crick-like structure via tautomerisation (neutral) or ionisation (charged)9,51. This experimentally confirms that tautomerisation in DNA is a non-trivial effect.
A positive indication that tautomerisation might be facilitated by tunnelling was provided recently by Rangadurai et al.52. They extensively investigated the dynamics of the transition between a wobble and Watson–Crick-like G–T in duplex DNA by performing NMR relaxation dispersion in both H2O and D2O. The authors reported a KIE as the rate of exchange between the two conformations of the mismatch was ~3-fold slower in D2O than in H2O. This result provides the first experimental evidence supporting a transition state for tautomerisation involving proton tunnelling. However, before the observed KIE can be unequivocally attributed to proton tunnelling, further measurements will need to be conducted to investigate, for instance, its temperature dependence39. Since a definitive experimental hallmark of tunnelling is a temperature-independent rate at low temperature, the rate of classical over-the-barrier hopping becomes negligible at low temperatures, leaving only the quantum contribution37,38.
Experimental measurements of tautomerisation rates for G–C double proton transfer reaction are still not available. Nevertheless, we believe that our theoretical results force us to radically revise our understanding of the likelihood of point mutations in DNA, and we hope they will encourage new experimental measurements of the proton transfer reaction. Perhaps, a temperature-jump experiment, similar to investigations conducted on intramolecular proton transfer in heterocycles53, could elucidate the proton transfer rates.
One can note that our model predicts a rate of tautomerisation much higher than the overall rate of spontaneous mutations (~10−8)16, but this is consistent with the well-known presence of highly efficient DNA repair mechanisms. However, it is also difficult to comment on the overall efficiency of these repair mechanisms because other spontaneous mutations will also take place in DNA aside from tautomerisation54,55.
The high tautomer occupation probability might also be relevant to address the role of mutations in several theories of the origin of life, including the RNA-mechanism proposed by Eigen et al.56, in which single-stranded RNA phage replicases have error rates on the order of 10−4, suggesting that the early enzyme-controlled replication of nucleic acids may have been accuracy-limited by the tautomerisation reaction.
The low-temperature limit
To verify the validity of the low-temperature correction, we monitor some properties of the distribution (see Fig. 5). Here the thermal properties can be obtained by integrating Eq. (1) to t → ∞ at a given temperature. In the high-temperature case, Eq. (1) tends to a thermal average over the classical Hamiltonian. However, at low temperature, it is dominated by the quantum correction to the zero-point energy of the effective oscillator (Eq. (3)).
Comparing the thermal properties of the double-well potential as a function of the temperature to verify the validity of the low-temperature correction. a Showing the position-momentum uncertainty, in this system, 0.5 denotes the minimum uncertainty asserted by Heisenberg's uncertainty principle. b The S2 linear entropy. The low-temperature correction, Eω, is shown as the solid line in blue, whereas the high-temperature approximation, kBT, is shown in a dashed red line.
We note additionally that Heisenberg’s position-momentum uncertainty principle must also be upheld,
where
Within the atomic unit system, a minimally uncertain distribution will take on a value of 0.5, with a value less than this violating the uncertainty principle. The middle panel of Fig. 5 demonstrates that the high-temperature treatment becomes unphysical below ~600 K, whereby the distribution becomes increasingly point particle-like, violating the uncertainty principle. At low temperature, the linear trend continues to the origin, implying that at 0 K, the distribution is perfectly point-like, with zero uncertainty. On the other hand, incorporating the correction prevents the compression of the distribution in phase space at lower temperatures - demonstrating an asymptotic convergence to 0.5. At much higher temperatures shown in the plot, the two approaches converge.
If the system starts in a pure quantum state, the bath’s interactions will cause it to decohere, driving it to a mixed state57. The canonical quantum entropy via von Neumann entropy, \(S=-{{{{{{\mathrm{Tr}}}}}}}\,(\hat{\rho }\ln \hat{\rho })\) (where ρ is the density matrix) offers a measure of the statistical uncertainty represented by a quantum state. The von Neumann entropy is generally regarded as the preferred choice of a metric of coherence. However, in phase-space negative values can occur in the logarithm, which presents a problem with its evaluation. As a consequence, the von Neumann is too restrictive for our needs. Alternatively, the linearised entropy is a computationally convenient but accurate approach to measure coherence58,59. We can monitor the amount of decoherence using
Here, D corresponds to the number of degrees of freedom (unity in this case)58,59. For a pure, unmixed state, the S2 entropy takes on a value of zero. While the system evolves in contact with the bath, it begins to decohere, observed as an increase in linear entropy. If the bath coupling is turned off, we strictly observe no entropy change. As seen in the bottom panel of Fig. 5, the breakdown of the high-temperature approach is demonstrated as negative entropy values below ~600 K. Negative entropy implies that the system can be in a more ordered state than an unmixed, pure state, which is problematic. Whereas the low-temperature correction correctly implies S2 → 0. Further examinations on the low-temperature correction can be found in Supplementary Note 2.
Chemical reaction rate
In order to investigate the kinetics of the reaction, we need to determine the quantum contribution to the chemical reaction rate by monitoring the flux of the density passing through the transition state (barrier).
The tunnelling factor, κ, can be calculated using the classical and quantum contribution to the rate,
We obtain a quantum contribution, kQM, to the chemical reaction rate by monitoring the flux of the probability changes between the left and right-hand well30,31,32,33,34. The change can be determined by,
Here, \(\hat{h}(q)\) is the same Heaviside step function defined before, which delimits the left and right-hand well. The quantum contribution to the reaction rate is determined using Eq. (8) Hence, the full forward and reverse rate constants, kf and kr, are obtained from,
A reaction timescale can be obtained by inspecting the inverse of Eq. (10). Benchmarks of the methods can be found in Supplementary Note 3.
Kinetic isotope effect
We investigated the impact of the KIE to determine possible quantum effects. We investigated the KIE using the same parameters before but doubled the mass.
where \({k}_{{{{{{{{\rm{QM}}}}}}}}}^{{{{{{{{\rm{p}}}}}}}}}\) (\({k}_{{{{{{{{\rm{QM}}}}}}}}}^{{{{{{{{\rm{d}}}}}}}}}\)) is the rate for a proton (deuteron). We neglect any changes to the transfer energy landscape due to isotopic substitutions, such as zero-point energy and free energy contributions, and consider only the effect on the reaction rate due to modifications of the mass terms in Eq. (1).
Methods
Numerical methods
We solve Eq. (1) numerically using the method of lines approach in which q and p are discretised to a fixed equally spaced lattice with Nq points in range \([{q}_{\min },\,{q}_{\max }]\) and Np equally spaced points in range \([{p}_{\min },\,{p}_{\max }]\). See Supplementary Note 1. The partial derivatives in space are expanded using a second-order central finite difference approach. The outer coefficients are set to zero, corresponding to Dirichlet (reflecting) boundary conditions. To integrate the equations in time, we utilise the VCABM5 algorithm60, an adaptive fifth-order Adams–Moulton method implemented in the DifferentialEquations.jl ecosystem61. We find that VCABM5 offers a good trade-off between accuracy and speed. To simplify the numerical calculations, we drop the third-order potential terms in Eq. (1). Studies on other proton transfer reactions suggest that the reduced mass at the transition state is dependent on the proton transfer process and can fluctuate to a much heavier mass far from the transition state62. Depending on the reaction pathway, if the two protons transfer simultaneously or not, the reduced mass of the system can tend to one or two proton masses62. In our case, at the transition state, the motion of a single proton dominates4. Consequently, it is acceptable to assume that the mass of the proton mass is in, a very good approximation, the effective mass of the tunnelling particle in the asynchronous concerted process5. Furthermore, the collective classical rearrangement of the rest of the atoms of both bases can be neglected. We set the mass to a proton m = 1836 a.u., in contact with a thermal bath with T = 298.15 K.
The proton transfer potential
The double proton transfer reaction can be described as a PES obtained from ab initio quantum chemical methods (determined in Ref. 4—see discussions of the calculations within). We described this PES using a back-to-back double Morse potential given by
Table 1 contains all the parameters defining the potential corresponding to the tautomerisation reaction of G–C.
In the limits of the reaction coordinate away from the well minima, we require that the potential rapidly increases, creating a bounding wall. The wall corresponds to the strong repulsive force as the bond between the hydrogen and the hydrogen-bond donator atoms shorten. Here, the back-to-back double Morse potential captures these requirements while maintaining the reaction profile obtained from high-level density functional theory calculations. The bounded potential can then be inserted into our OQS approach and solve the dynamics and the steady-state solution.
The apparent single-dimensionality of the PES is due to the application of transition state theory to this system, which results in a single effective reaction coordinate being displayed to represent the minimum energy reaction pathway for tautomerisation. The approach of inserting the PES calculated from density functional theory into an OQS Hamiltonian has been successfully used before for proton transfer reactions6.
Data availability
The data presented in the figures of this article are available from the corresponding authors upon reasonable request.
Code availability
Numerical simulations were performed with Julia code that makes use of the differential equations package available on GitHub. The Julia source codes are available from the corresponding authors upon reasonable request.
References
Watson, J. D. & Crick, F. H. C. The structure of dna. Cold Spring Harbor Symp. Quant. Biol. 18, 123–131 (1953).
Löwdin, P.-O. Proton tunneling in dna and its biological implications. Rev. Mod. Phys. 35, 724–732 (1963).
Löwdin, P.-O. Quantum genetics and the aperiodic solid. In Advances in Quantum Chemistry (ed. Löwdin, P.-O.) Vol. 2 (Academic Press, 1966). http://www.sciencedirect.com/science/article/pii/S0065327608600763.
Slocombe, L., Al-Khalili, J. & Sacchi, M. Quantum and classical effects in dna point mutations: Watson–Crick tautomerism in at and gc base pairs. Phys. Chem. Chem. Phys. 23, 4141–4150 (2021).
Brovarets’, O. O. & Hovorun, D. M. Atomistic mechanisms of the double proton transfer in the h-bonded nucleobase pairs: Qm/qtaim computational lessons. J. Biomol. Struct. Dyn. 37, 1880–1907 (2019).
Godbeer, A., Al-Khalili, J. & Stevenson, P. Modelling proton tunnelling in the adenine–thymine base pair. Phys. Chem. Chem. Phys. 17, 13034–13044 (2015).
Gheorghiu, A., Coveney, P. & Arabi, A. The influence of base pair tautomerism on single point mutations in aqueous dna. Interface Focus 10, 20190120 (2020).
Pohl, R. et al. Proton transfer in Guanine–Cytosine base pair analogues studied by nmr spectroscopy and pimd simulations. Faraday Discuss. 212, 331–344 (2018).
Kimsey, I. J. et al. Dynamic basis for dg⋅ dt misincorporation via tautomerization and ionization. Nature 554, 195–201 (2018).
Kim, Y. et al. Quantum biology: an update and perspective. Quantum Reports 3, 80–126 (2021).
Brovarets’, O. O. & Hovorun, D. M. Why the tautomerization of the g ⋅ c Watson-Crick base pair via the dpt does not cause point mutations during dna replication? qm and qtaim comprehensive analysis. J. Biomol. Struct. Dyn. 32, 1474–1499 (2014).
Brovarets, O. O. & Hovorun, D. M. Can tautomerization of the a ⋅ t Watson-Crick base pair via double proton transfer provoke point mutations during dna replication? a comprehensive qm and qtaim analysis. J. Biomol. Struct. Dyn. 32, 127–154 (2014).
Soler-Polo, D., Mendieta-Moreno, J. I., Trabada, D. G., Mendieta, J. & Ortega, J. Proton transfer in Guanine-Cytosine base pairs in b-dna. J. Chem. Theory Comput. 15, 6984–6991 (2019).
Pérez, A., Tuckerman, M. E., Hjalmarson, H. P. & Von Lilienfeld, O. A. Enol tautomers of Watson-Crick base pair models are metastable because of nuclear quantum effects. J. Am. Chem. Soc. 132, 11510–11515 (2010).
Hill, T. Thermodynamics of small systems. in Dover Books on Chemistry (ed. Benjamin, W. A.) (Dover Publications, 1994). https://books.google.co.uk/books?id=Xa-yAAAAQBAJ.
Wu, W.-J., Yang, W. & Tsai, M.-D. How dna polymerases catalyse replication and repair with contrasting fidelity. Nat. Rev. Chem. 1, 1–16 (2017).
Fang, W. et al. Inverse temperature dependence of nuclear quantum effects in dna base pairs. J. Phys. Chem. Lett. 7, 2125–2131 (2016).
Liu, Y., Yan, Y., Xing, T. & Shi, Q. Understanding the large kinetic isotope effect of hydrogen tunneling in condensed phases by using double-well model systems. J. Phys. Chem. B 125, 5959–5970 (2021).
Srivastava, R. The role of proton transfer on mutations. Front. Chem. 7, 536 (2019).
Wales, D., Saykally, R., Zewail, A. & King, D. Energy Landscapes: Applications to Clusters, Biomolecules and Glasses (Cambridge University Press, 2003). https://books.google.co.uk/books?id=YQrB6s3LALEC.
Caldeira, A. O. & Leggett, A. J. Path integral approach to quantum brownian motion. Phys. A: Stat. Mech. Appl. 121, 587–616 (1983).
Feynman, R. P. & Vernon Jr., F. The theory of a general quantum system interacting with a linear dissipative system. Ann. Phys. 281, 547–607 (2000).
Wigner, E. On the quantum correction for thermodynamic equilibrium. Phys. Rev. 40, 749–759 (1932).
Burghardt, I. & Møller, K. B. Quantum dynamics for dissipative systems: a hydrodynamic perspective. J. Chem. Phys. 117, 7409–7425 (2002).
Agarwal, G. Brownian motion of a quantum oscillator. Phys. Rev. A 4, 739 (1971).
Haake, F. & Reibold, R. Strong damping and low-temperature anomalies for the harmonic oscillator. Phys. Rev. A 32, 2462 (1985).
Haake, F., Risken, H., Savage, C. & Walls, D. Master equation for a damped nonlinear oscillator. Phys. Rev. A 34, 3969 (1986).
Hughes, K. H. Dissipative quantum phase space dynamics on dynamically adapting grids. J. Chem. Phys. 122, 074106 (2005).
Gottwald, F., Ivanov, S. D. & Kühn, O. Applicability of the Caldeira-Leggett model to vibrational spectroscopy in solution. J. Phys. Chem. Lett. 6, 2722–2727 (2015).
Tanimura, Y. & Wolynes, P. G. Quantum and classical fokker-planck equations for a Gaussian-Markovian noise bath. Phys. Rev. A 43, 4131–4142 (1991).
Tanimura, Y. & Wolynes, P. G. The interplay of tunneling, resonance, and dissipation in quantum barrier crossing: a numerical study. J. Chem. Phys. 96, 8485–8496 (1992).
Zhang, J., Borrelli, R. & Tanimura, Y. Proton tunneling in a two-dimensional potential energy surface with a non-linear system–bath interaction: thermal suppression of reaction rate. J. Chem. Phys. 152, 214114 (2020).
Ishizaki, A. & Tanimura, Y. Multidimensional vibrational spectroscopy for tunneling processes in a dissipative environment. J. Chem. Phys. 123, 014503 (2005).
Montgomery Jr., J. A., Chandler, D. & Berne, B. J. Trajectory analysis of a kinetic theory for isomerization dynamics in condensed phases. J. Chem. Phys. 70, 4056–4066 (1979).
Hänggi, P., Talkner, P. & Borkovec, M. Reaction-rate theory: fifty years after kramers. Rev. Mod. Phys. 62, 251 (1990).
Douhal, A., Kim, S. & Zewail, A. Femtosecond molecular dynamics of tautomerization in model base pairs. Nature 378, 260–263 (1995).
Johannissen, L. O., Hay, S. & Scrutton, N. S. Nuclear quantum tunnelling in enzymatic reactions – an enzymologist’s perspective. Phys. Chem. Chem. Phys. 17, 30775–30782 (2015).
Johannissen, L. O., Iorgu, A. I., Scrutton, N. S. & Hay, S. What are the signatures of tunnelling in enzyme-catalysed reactions? Faraday Discuss. 221, 367–378 (2020).
Klinman, J. P. & Offenbacher, A. R. Understanding biological hydrogen transfer through the lens of temperature dependent kinetic isotope effects. Acc. Chem. Res. 51, 1966–1974 (2018).
Xie, W., Xu, Y., Zhu, L. & Shi, Q. Mixed quantum classical calculation of proton transfer reaction rates: from deep tunneling to over the barrier regimes. J. Chem. Phys. 140, 174105 (2014).
Glickman, M. H., Wiseman, J. S. & Klinman, J. P. Extremely large isotope effects in the soybean lipoxygenase-linoleic acid reaction. J. Am. Chem. Soc. 116, 793–794 (1994).
Li, P., Soudackov, A. V. & Hammes-Schiffer, S. Impact of mutations on the binding pocket of soybean lipoxygenase: implications for proton-coupled electron transfer. J. Phys. Chem. Lett. 9, 6444–6449 (2018).
Li, P., Soudackov, A. V. & Hammes-Schiffer, S. Fundamental insights into proton-coupled electron transfer in soybean lipoxygenase from quantum mechanical/molecular mechanical free energy simulations. J. Am. Chem. Soc. 140, 3068–3076 (2018).
Hu, S., Soudackov, A. V., Hammes-Schiffer, S. & Klinman, J. P. Enhanced rigidification within a double mutant of soybean lipoxygenase provides experimental support for vibronically nonadiabatic proton-coupled electron transfer models. ACS Catal. 7, 3569–3574 (2017).
Soudackov, A. V. & Hammes-Schiffer, S. Proton-coupled electron transfer reactions: analytical rate constants and case study of kinetic isotope effects in lipoxygenase. Faraday Discuss. 195, 171–189 (2017).
Pu, J., Gao, J. & Truhlar, D. G. Multidimensional tunneling, recrossing, and the transmission coefficient for enzymatic reactions. Chem. Rev. 106, 3140–3169 (2006).
Hohlefelder, L. S., Stögbauer, T., Opitz, M., Bayerl, T. M. & Rädler, J. O. Heavy water reduces gfp expression in prokaryotic cell-free assays at the translation level while stimulating its transcription. Biomed Res. Int. 2013, 592745 (2013).
Gorb, L., Podolyan, Y. & Leszczynski, J. A theoretical investigation of tautomeric equilibria and proton transfer in isolated and monohydrated cytosine and isocytosine molecules. J. Mol. Struct. 487, 47–55 (1999).
Podolyan, Y., Gorb, L. & Leszczynski, J. Ab initio study of the prototropic tautomerism of cytosine and guanine and their contribution to spontaneous point mutations. Int. J. Mol. Sci. 4, 410–421 (2003).
Wang, W., Hellinga, H. W. & Beese, L. S. Structural evidence for the rare tautomer hypothesis of spontaneous mutagenesis. Proc. Natl Acad. Sci. USA. 108, 17644–17648 (2011).
Kimsey, I. J., Petzold, K., Sathyamoorthy, B., Stein, Z. W. & Al-Hashimi, H. M. Visualizing transient Watson–Crick-like mispairs in dna and rna duplexes. Nature 519, 315–320 (2015).
Rangadurai, A., Szymanski, E. S., Kimsey, I., Shi, H. & Al-Hashimi, H. M. Probing conformational transitions towards mutagenic Watson–Crick-like g⋅ t mismatches using off-resonance sugar carbon r 1ρ relaxation dispersion. J. Biomol. NMR 74, 457–471 (2020).
Bensaude, O., Dreyfus, M., Dodin, G. & Dubois, J. Intramolecular nondissociative proton transfer in aqueous solutions of tautomeric heterocycles: a temperature-jump kinetic study. J. Am. Chem. Soc. 99, 4438–4446 (1977).
Kunkel, T. A. & Alexander, P. S. The base substitution fidelity of eucaryotic dna polymerases. mispairing frequencies, site preferences, insertion preferences, and base substitution by dislocation. J. Biol. Chem. 261, 160–166 (1986).
Zahurancik, W. J., Klein, S. J. & Suo, Z. Significant contribution of the 3’ → 5’ exonuclease activity to the high fidelity of nucleotide incorporation catalyzed by human dna polymerase epsilon. Nucleic Acids Res. 42, 13853–13860 (2014).
Eigen, M. & Schuster, P. A principle of natural self-organization. Naturwissenschaften 64, 541–565 (1977).
Zurek, W. H. Preferred states, predictability, classicality and the environment-induced decoherence. Prog. Theor. Phys. 89, 281–312 (1993).
Zurek, W. H., Habib, S. & Paz, J. P. Coherent states via decoherence. Phys. Rev. Lett. 70, 1187 (1993).
Włodarz, J. J. Entropy and wigner distribution functions revisited. Int. J. Theor. Phys. 42, 1075–1084 (2003).
Butcher, J. C. Numerical methods for ordinary differential equations in the 20th century. J. Comput. Appl. Math 125, 1–29 (2000).
Rackauckas, C. & Nie, Q. Differentialequations.jl–a performant and feature-rich ecosystem for solving differential equations in Julia. J. Open Res. Softw. 5, 15 (2017).
Schweiger, S. & Rauhut, G. Plateau reactions: double proton-transfer processes with structureless transition states. J. Phys. Chem. A 107, 9668–9678 (2003).
Acknowledgements
We are grateful for financial support from the Leverhulme Trust doctoral training centre grant number DS-2017-079. We acknowledge helpful discussions with the members of the Leverhulme Quantum Biology Doctoral Training Centre; particular thanks goes to Johnjoe McFadden. Further thanks go to Max Winokan and Antonio Pantelias, who both offered many productive conversations. The authors thank the University of Surrey for access to the Eureka HPC.
Author information
Authors and Affiliations
Contributions
M.S. and J.A-K. conceived and designed this research, L.S. built the computational apparatus. All the authors contributed to the preparation of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Peter R. Wills, Jose Javier Ruiz-Pernia and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Slocombe, L., Sacchi, M. & Al-Khalili, J. An open quantum systems approach to proton tunnelling in DNA. Commun Phys 5, 109 (2022). https://doi.org/10.1038/s42005-022-00881-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-00881-8
This article is cited by
-
Mimicking classical noise in ion channels by quantum decoherence
Scientific Reports (2024)
-
Low bias charge transport in DNA
Scientific Reports (2024)
-
A quantum physics layer of epigenetics: a hypothesis deduced from charge transfer and chirality-induced spin selectivity of DNA
Clinical Epigenetics (2023)
-
Environment assisted quantum model for studying RNA-DNA-error correlation created due to the base tautomery
Scientific Reports (2023)
-
Dynamical entropic measure of nonclassicality of phase-dependent family of Schrödinger cat states
Scientific Reports (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.