Abstract
Collective behaviour of electrons, frustration induced quantum fluctuations and entanglement in quantum materials underlie some of the emergent quantum phenomena with exotic quasi-particle excitations that are highly relevant for technological applications. Herein, we present our thermodynamic and muon spin relaxation measurements, complemented by ab initio density functional theory and exact diagonalization results, on the recently synthesized frustrated antiferromagnet Li4CuTeO6, in which Cu2+ ions (S = 1/2) constitute disordered spin chains and ladders along the crystallographic [101] direction with weak random inter-chain couplings. Our thermodynamic experiments detect neither long-range magnetic ordering nor spin freezing down to 45 mK despite the presence of strong antiferromagnetic interaction between Cu2+ moments leading to a large effective Curie-Weiss temperature of − 154 K. Muon spin relaxation results are consistent with thermodynamic results. The temperature and magnetic field scaling of magnetization and specific heat reveal a data collapse pointing towards the presence of random-singlets within a disorder-driven correlated and dynamic ground-state in this frustrated antiferromagnet.
Similar content being viewed by others
Introduction
Geometrically frustrated magnets with incompatible magnetic interactions between spins are characterized by strong quantum fluctuations and the absence of trivial order parameters related to broken symmetry. They are, therefore, extremely sensitive to perturbations such as quenched disorder, next-nearest-neighbor interactions, and magnetic anisotropy1,2. Strong quantum fluctuations preclude symmetry breaking phase transitions and lead to novel magnetically disordered ground states such as quantum spin liquids (QSLs)1,3,4,5,6. QSLs are characterized by quantum fluctuations, absence of long-range order even at T → 0, and exotic fractionalized excitations in contrast to spin-wave excitations found in conventional magnets7,8. These properties of QSLs are fingerprints of strong quantum entanglement. Triangular-lattice compound κ-(ET)2Cu2(CN)39 and 1-TaS210, kagome-lattice compound ZnCu3(OH)6Cl211, and hyperkagome-lattice compound PbCuTe2O612,13 are some of the most investigated candidate spin-liquid materials with unusual ground-state properties. Recently, enormous efforts have been devoted towards experimental realizations of QSLs on the honeycomb lattice ever since Alexei Kitaev proposed an exactly solvable highly anisotropic Kitaev model for S = 1/2 spins on this two-dimensional spin lattice14. In sharp contrast to an isotropic nearest-neighbor exchange model on the honeycomb lattice, which exhibits long-range order15, the ground state of the Kitaev model is a QSL with fractionalized Majorana fermions and gauge flux excitations16,17,18,19. The realization of this exotic state of matter is interesting not only from a fundamental physics point of view but also holds immense promise for potential applications in robust quantum computing technology20.
Despite tremendous experimental efforts, the observed signatures of QSL are far away from those of theoretically proposed QSLs states for a clean periodic system2,14,21. However, it has been suggested that some highly frustrated magnets show quantum disordered ground state due to randomness that might play an important role in destabilizing conventional Néel order at low T. There are several origins of randomness in magnetic insulators and the interplay between quantum fluctuation and randomness may lead to novel quantum ground states. The triangular-lattice YbMgGaO4 with anti-site mixing between nonmagnetic Mg2+ and Ga3+ ions22,23 and square lattice Sr2CuTe1−xWxO6 with a few percent of W on the Te site are some of examples of frustrated magnets with a randomness-induced quantum disordered ground state24,25,26. Interestingly, while most of the reported Kitaev magnets including 5d iridates A2IrO3 (where A = Na, Li) and ruthenate α-RuCl3 with 4d electrons show long-range order at sufficiently low temperature, the iridate H3LiIr2O6 and ruthenate α-Ru1−xIrxCl3, which are derived from a parent ordered magnet by substitution of nonmagnetic ions, do not exhibit long-range magnetic order27,28,29,30. Furthermore, some honeycomb-lattice magnets, like A3LiIr2O6 (A = H, D, Ag etc.), show scaling behavior in the field dependence of the specific heat27,31,32, which is ascribed to the existence of disorder, making these quantum materials interesting for studies of the effect of disorder on a QSL state32. A similar scenario is observed in three-dimensional spin lattice where quantum fluctuation is less pronounced. For instance, the oxynitride Lu2Mo2O5N2 with S = 1/2 spins on a pyrochlore lattice, which is derived from the spin-glass material Lu2Mo2O7 via random substitution of O2− and N3− anions, shows a dynamic ground state33,34.
Disorder in quantum magnets is usually unavoidable, yet very often it can act as a new prism in revealing many interesting quantum phenomena of the host material35,36,37,38. Frustrated magnets with the quenched disorder in the form of material defects or a broad distribution of exchange interaction strengths can exhibit a randomness-induced spin-liquid state. Understanding the impact of quenched disorder on the quantum fluctuations that drive quantum disordered states in antiferromagnets is an interesting area of study22,39,40,41. In the so-called random-singlet phase, singlets form due to a random distribution of antiferromagnetic exchange interaction between spin-1/2 defect sites, leading to a power-law distribution of exchange energies and density of states, which lead to unconventional scaling behavior in magnetic susceptibility and specific heat at low temperatures22,32,42. The signature of such novel random singlet state was initially observed in one-dimensional spin-chain organic compounds due to the presence of random antiferromagnetic Heisenberg exchange interaction43,44. Furthermore, there is also experimental evidence of a random singlet state in inorganic spin-chain compound BaCu2(Si1−xGex)2O745 wherein the random substitution of Ge in place of Si introduce the bond disorder in antiferromagnetic long-range ordered magnet BaCu2Si2O746. Theoretically, it has been proposed that such exchange randomness in the spin-chain compound is one of the key ingredients for quantum information processors which deals with properties of quantum entanglement in quantum materials47,48,49,50. In recent years, higher-dimensional quantum materials with intrinsic disorder either from spin vacancies, anti-site disorder or nonmagnetic impurities and dislocations or grain boundaries have drawn enormous attention to realize novel low-temperature phases including random singlet that is expected to be unique in disordered quantum many-body systems25,33,34. In frustrated magnets with quenched disorder, the majority of intrinsic S = 1/2 spins may constitute a dynamic liquid-like state while the remaining S = 1/2 moments act as defects and form a random network with exotic low-lying excitations that destabilize a glassy state and instead lead to a dynamic low-energy ground state32. Theoretically, it has been proposed that randomness in the frustrated lattice can induce spin-liquid-like states in a wide region of parameter space51. Experimentally, this phenomenon is much less explored due to a lack of suitable frustrated magnets, which leads one to look for candidate materials wherein the degree of randomness can be tuned in a controlled manner. In this context, 3d transition-metal frustrated S = 1/2 spin lattices are promising potential hosts of a randomness-driven quantum spin-liquid ground state.
Herein, we report crystal structure, neutron diffraction, magnetic properties, specific heat, and muon spectroscopy, as well as complementary density functional theory (DFT) and exact diagonalization (ED) results of the antiferromagnet Li4CuTeO6 (henceforth LCTO), where Cu2+ (S = 1/2) ions are arranged on a frustrated spin lattice with unavoidable anti-site disorder between Li+ and Cu2+. In LCTO, the majority of Cu2+ ions (84%) at the 2d crystallographic site form random-length strongly antiferromagnetic spin chains while a minority of Cu2+ ions (~7%) at defect 4g sites strongly antiferromagnetically couple to these spin chains, leading to significant frustration. The large and negative value of Curie–Weiss temperature reflects the presence of strong antiferromagnetic interaction between Cu2+ spins. Furthermore, we find that weaker interchain interactions effectively couple the chains in a random, disordered network at low T (low temperature). As a consequence, this compound neither undergoes a phase transition to long-range magnetic order nor spin-freezing down to at least 45 mK. Furthermore, specific heat and magnetization results reveal data collapse behavior, which suggests the presence of a random-singlet state32. Muon spin relaxation measurements corroborate a dynamic ground state in this frustrated magnet. This is attributed to the presence of subdominant interchain interactions that couple the chains in a disordered network. Our results thus establish that LCTO hosts a randomness-induced spin-liquid-like state in a frustrated magnet.
Results
Rietveld refinement and crystal structure
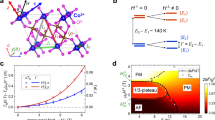
The room-temperature powder X-ray diffraction data were taken to confirm the phase purity of the polycrystalline samples of LCTO. The Rietveld refinement of the X-ray diffraction data was performed using GSAS software52, which confirms that LCTO crystallizes in a monoclicnic structure with the space group C2/m (No. 12)53. To deepen the analysis of the crystalline structure and in particular to determine the occupation of the mixed sites by the light elements a neutron diffractogram was measured at 300 K at an incident wavelength 1.28 Å. Figure 1a depicts the Rietveld refinement of neutron-diffraction data performed using fullprof which yields lattice parameters a = 5.2752(5) Å, b = 8.8163(8) Å, c = 5.2457(5) Å and α = γ = 90°, β = 113.172(8)°, in agreement with powder X-ray diffraction data (see Supplementary Table I) and previously reported values53. A unit cell of LCTO is shown in Fig. 1b. We found that among three crystallographic sites of Li, the sites 2d and 4g are partially shared with Cu2 and Cu3 sites, respectively, with Cu2 site occupancy p2 = 84% and Cu3 site occupancy p3 = 7%. This is likely due to the similar ionic radii of Li+ and Cu2+ ions. Cu2+ ions form distorted CuO6 octahedra with nearest-neighbor oxygen ions with Cu2 and Cu3 sites connecting to each other directly by corner- and edge-sharing, and indirectly via corner- and edge-sharing TeO6 octahedra in an a priori 3D lattice. However, a critical look at the crystal structure reveals only two plausibly strong exchange pathways: (i) a nearly-linear Cu–O–Cu superexchange (SE) bridge between Cu2 and Cu3 sites with a bond angle 173.3° and bond distance 4.12 Å, which is expected to yield a strong antiferromagnetic exchange \(J^{\prime}\) by Goodenough–Kanamori rules54,55, and (ii) a double Cu–O ⋯ O–Cu super-superexchange (SSE) bridge between two Cu2 sites going around a Te6+ ion with a large symmetric Cu–O ⋯ O bond angle of 138.6° and a small O ⋯ O distance 2.87 Å (well below the van der Waals radii sum ~3.04 Å), which is expected to yield a strong antiferromagnetic exchange J56,57,58,59,60 (Fig. 1b). The resulting 1D spin model is shown in Fig. 1c and consists of random-length linear spin chains of Cu2 (occupation probability p2) with exchange J running along the [101] direction, with randomly occupied Cu3 defect sites (occupation probability p3) displaced along ± b from each main-chain bond J introducing strong frustration by coupling to both neighboring Cu2 main-chain sites via a \(J^{\prime}\) exchange. All other SE and SSE pathways, which, if present, introduce 3D interchain couplings in general, are expected to have much smaller strength as they either proceed via very nearly 90° Cu–O–Cu and Cu–O ⋯ O angles, or involve O ⋯ O distances well above the O2− van der Waals radii sum. The powder ESR spectrum consists of two components, both featuring uniaxial symmetry, in agreement with the crystal symmetry. A fit of the spectrum with a powder-averaged Lorentzian shape (see Fig. 1d) yields principal g factors \({g}_{x,y}^{1}\) = 2.06 and \({g}_{z}^{1}\) = 2.31 for the component with larger intensity and \({g}_{x,y}^{2}\) = 2.06 and \({g}_{z}^{2}\) = 2.20 for the component with smaller intensity. The ratio of the intensities is 85:15, which is close to the ratio p2:2p3 of the occupied Cu2 and Cu3 sites as confirmed by the structural refinement.
a Rietveld refinement of neutron-diffraction data of LCTO at room temperature for the incident wavelength 1.28 Å. The solid circles represent the observed intensity (Obs.), whereas the black solid line is the calculated intensity (Cal.). The residual signal is denoted by a green solid line and is shifted vertically for clarity. b Visualization of one unit cell of LCTO where edge-sharing TeO6 and CuO6 octahedra connect Cu2+ ions on 2d (Cu2) sites with an exchange J through a Cu–O ⋯ O–Cu super-superexchange (SSE) bridge around Te6+. Additionally, corner-sharing CuO6 octahedra connect Cu2+ ions on 2d (Cu2) and 4g (Cu3) sites with an exchange \(J^{\prime}\) through a nearly-linear Cu–O–Cu superexchange (SE) bridge. c Resulting spin model of randomly depleted 1D spin chains of Cu2 sites with antiferromagnetic exchange J running along the [101] direction, to which randomly occupied Cu3 sites couple via an antiferromagnetic exchange \(J^{\prime}\) and introduce strong frustration. d The electron spin resonance (ESR) spectrum of LCTO measured at 250 K and 256.3 GHz (points). The fit (solid line) includes two components with uniaxial symmetry and a Lorentzian line shape.
Ab initio and exact diagonalization calculations
The expected interaction between Cu2+ moments are fully born out by ab initio DFT exchange-coupling calculations on a 2 × 1 × 2 supercell of LCTO using the local (spin) density approximation (LSDA) in an LSDA+U scheme with an effective Hubbard Ueff = 9 meV (see Supplementary Note 6 for details). By first assuming full occupancy of Cu2 sites and zero occupancy of Cu3 sites the main-chain Cu2–Cu2 antiferromagnetic exchange strength JDFT = 177 K was extracted, and then by introducing a single occupied Cu3 site the frustrating Cu2–Cu3 antiferromagnetic exchange strength \({J}_{{{{{{{{\rm{DFT}}}}}}}}}^{\prime}\) = 824 K was obtained. As expected, all other exchange interactions, which introduce 3D couplings between the chains, were found to have strengths below ~6 K, making them difficult to resolve by DFT. For T ≫ 6 K the frustrated 1D random-occupancy model of Fig. 1c is thus expected to hold, while at low T further frustrating interchain exchanges might be expected. Temperature-dependent thermodynamic quantities of the high-T random model obtained from DFT were calculated using ED by probability weighing ED results for different random-length chains of Cu2 spins with a different distribution of occupied Cu3 sites around them (see Supplementary Note 7 for details). This way, ED predictions for magnetic susceptibility χED, magnetic-specific heat Cmag,ED and magnetic entropy Smag,ED as a function of T, applied magnetic field μ0H (μ0 is the permeability of free space), g factor, and J and \(J^{\prime}\) exchange strengths at any given occupation probabilities p2 and p3 could be calculated to high accuracy.
Magnetic susceptibility
Figure 2a presents the experimental temperature dependence of the magnetic susceptibility (χ(T)) in an applied magnetic field μ0H = 1 T in the temperature range 1.9 K ≤ T ≤ 300 K. The magnetic susceptibility data do not indicate the presence of a phase transition down to 1.9 K. In order to estimate dominant magnetic interactions, the high-temperature 1/χ(T) data were fitted with a Curie–Weiss law (right y axis; Fig. 2a)
In Eq. (1), θCW and C are the Curie–Weiss (CW) temperature and the Curie constant, respectively. The CW fitting in the temperature range 180 K ≤ T ≤ 300 K yields θCW = −154 K and C = 0.39 cm3 Kmol−1. The estimated effective magnetic moment μeff = \(\sqrt{8C}\) = 1.76 μB is close to the expected value for a Cu2+ ion with S = 1/2 spin. The large negative θCW confirms the presence of dominant antiferromagnetic interactions between Cu2+ spins. To obtain a more quantitative estimate of the J and \(J^{\prime}\) exchange strengths, the χ(T) data were next fitted with the results of ED calculations on the random spin model of Fig. 1c. Fixing the ratio of experimental \(J/J^{\prime}\) to be the same as that found in DFT, \({J}_{{{{{{{{\rm{DFT}}}}}}}}}/{J}_{{{{{{{{\rm{DFT}}}}}}}}}^{\prime}\), which is expected to be a more robust DFT prediction than raw exchange strengths, and fixing the main-chain Cu2 site occupancy to the experimental value p2 = 84%, a good fit at T > 20 K is obtained (Fig. 2b) with only 3 free, sensible parameters: g = 2.28, \(J/{J}_{{{{{{{{\rm{DFT}}}}}}}}}=J^{\prime} /{J}_{{{{{{{{\rm{DFT}}}}}}}}}^{\prime}=1.38\), and p3 = 20%. We note that while fit parameters g and \(J/{J}_{{{{{{{{\rm{DFT}}}}}}}}}=J^{\prime} /{J}_{{{{{{{{\rm{DFT}}}}}}}}}^{\prime}\) are quite robust to perturbations like magnetic anisotropies or unwanted extrinsic contributions due to any impurities, the fitted value of p3 is substantially less so since the experimental data is limited to \(T\ll J^{\prime}\). Thus, the experimental value of Cu3 occupancy from neutron diffraction should be taken as definitive. The final estimates for the dominant exchanges are thus J = 244 K and \(J^{\prime}\) = 1140 K, with the discrepancy from DFT likely arising from the choice of Hubbard Ueff, which acts to rescale all exchanges. Importantly, for T < 20 K the high-T model of Fig. 1c starts to systematically deviate from the experiment, indicating the presence of further, most likely interchain, exchanges Jinter ≲ 10 K in strength acting between the random spin-chain fragments of the high-T model and dominating the physical response of LCTO at low \(T \; < \; 20\,{{{{{{{\rm{K}}}}}}}}\,\ll \,J,J^{\prime}\). In this regime most spin degrees of freedom of spin-chain fragments are expected to freeze out, leaving only their ground-state degrees of freedom to couple via Jinter exchanges in an emergent ≥ 2 dimensional (likely 3D) random lattice. Remarkably, though LCTO exhibits such quenched disorder, ultimately arising from partial Cu2+ site occupancy, that could lead to a spin-glass state at low T, the absence of glass-like freezing behavior is witnessed by the absence of any separation between zero-field-cooled and field-cooled susceptibility measurements in 100 Oe (inset of Fig. 2b). Furthermore, to confirm the absence of spin-freezing, we have performed ac susceptibility measurements down to 45 mK at different frequencies. It is observed that there is no peak or frequency dependence of the real part of the ac susceptibility (Fig. 2c and see Supplementary Fig. 3) in the temperature range 45 mK ≤ T ≤ 50 K, which strongly rules out the presence of spin-glass transition in Li4CuTeO661. Quenched Li/Cu anti-site disorder in the host lattice could, alternatively, also lead to unconventional scaling behavior of thermodynamic observables. Such a scenario has been proposed in several frustrated quantum materials22,25,32,62.
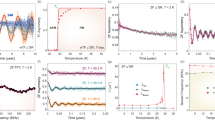
a The temperature dependence of the magnetic susceptibility (left y axis) and inverse magnetic susceptibility (right y axis) in a magnetic field μ0H = 1 T. The solid red line represents the Curie–Weiss (CW) fit. b The temperature dependence of magnetic susceptibility at 1 T with a high-T (high-temperature) fit using exact diagonalization (ED) results, and a low T fit using a power-law. The inset shows the zero-field-cooled (ZFC) and filed cooled (FC) susceptibility in a magnetic field of 100 Oe. c The temperature dependence of the real part of ac susceptibility in different frequencies down to 45 mK. d Data collapse for MT−0.15, where M is the magnetization and T is the temperature, as a function of μ0H/T.
As shown in Fig. 2d, a data collapse of MT−0.15, where M is the magnetization and T is temperature, as a function of μ0H/T is found in LCTO in a broad temperature range between 2 and 50 K (see Supplementary Note 3), which could be a sign of the presence of random singlets62. Furthermore, theoretically, it has been suggested that in the absence of the spin-orbit interaction, low-temperature magnetic susceptibility data of random-singlet states show a power-law χ ∝ T−γ behavior with γ < 124. The susceptibility data were fitted with a power-law χ ∝ T−γ in the low-temperature region, which yielded γ = 0.82 ± 0.01 (Fig. 2b). A similar power-law fit was also observed in the quasi-two-dimensional magnet Sr2CuTexW1−xO6, which is a promising candidate for realizing a random-singlet state on a square lattice25. A power-law fit of low-temperature magnetic susceptibility thus suggests the realization of a random-singlet state attributed to the presence of isolated magnetic moments in the host lattice25,32. The data collapse is a remarkable feature found also in other QSL candidates with a quenched disorder such as the honeycomb lattice H3LiIr2O627 and the triangular-lattice Y2CuTiO662. The data collapse behavior in the low-temperature region suggests the presence of random singlets in LCTO induced by quenched disorder as predicted theoretically32.
Specific heat
Figure 3a depicts the temperature dependence of specific heat in zero magnetic field. The absence of any anomaly in the entire temperature range of investigation rules out any phase transition down to 52 mK, which is much below both the CW temperature and the dominant J and \(J^{\prime}\) exchange interactions and thus indicates the presence of strong spin frustration that promotes a dynamic ground state in LCTO. The specific heat results in several magnetic fields upto 7 T are shown in Fig. 3b. It is observed that upon increasing the magnetic field the broad maximum shifts toward higher temperatures. Though similar to a Schottky contribution, which could arise from quasi-free spins, it, in fact, describes intrinsic spin physics due to both spins that appear isolated in the high-T spin model (Fig. 1c), and due to finite-length spin-chain fragments with an odd total number of spins, as the total spin of those cannot be lower than 1/2 by the rules for quantum addition of spin. In both cases, an applied field Zeeman splits the spin-1/2 ground state introducing a local-field-dependent energy gap that results in a specific heat peak whose position is proportional to the applied field. However, all spins, both those in finite-length spin-chain fragments, as well as nominally isolated spins, in fact couple together to form a frustrated 3D random spin lattice via weaker Jinter interchain exchanges, together shaping the intriguing, liquid-like low T behavior of LCTO at T ≲ Jinter.
a The temperature dependence of the specific heat (Cp) in zero magnetic field in a broad temperature range 0.052 K ≤ T ≤ 250 K. b The temperature-dependent specific heat in different magnetic fields upto 7 T. c The temperature dependence of magnetic-specific heat divided by temperature in zero field in a log-log scale where the red line is the power-law fit. Inset shows the temperature dependence of associated entropy change. d The scaling behavior of the magnetic-specific heat with \({C}_{{{{{{{{\rm{mag}}}}}}}}}{({\mu }_{0}H)}^{0.85}/T\) as a function of the scaled temperature T/μ0H for several fields.
In order to gain further insights into the magnetic properties relevant to this frustrated magnet and understand the ground-state degeneracy, it is important to extract the magnetic-specific heat. Therefore, we have considered the zero-field specific heat data (Cp) as a sum of intrinsic magnetic-specific heat (Cmag) due to exchange-coupled Cu2+ ions, and lattice specific heat (Clattice) due to phonons. After subtracting the lattice contribution (see Supplementary Note 5), the obtained magnetic-specific heat exhibits a clear broad maximum (see Supplementary Fig. 6) around 0.4 K releasing ~13% of entropy (inset in Fig. 3c), which is a typical signature of short-range spin correlations in spin liquid candidates27,62. Comparing this with ED results on the high-T model with no interchain coupling, which shows no such peak in zero field, and instead exhibits residual entropy at absolute zero due to unavoidable Kramers ground-state degeneracy of individual spin-chain fragments (see Supplementary Note 7), this clearly shows the dominant impact of frustrated interchain couplings Jinter at low T. Furthermore, it is observed that the temperature dependence of Cmag/T shows a T−0.5 power-law behavior (Fig. 3c) at low temperature, which suggest the presence of a random singlet state with strong low-lying excitations27,63. Next, the entropy was obtained by integrating Cmag/T in the temperature range 0.052 K ≤ T ≤ 2 K and is shown in the inset of Fig. 3c, with the contribution to entropy from specific heat below at T below the lowest measured T = 52 mK, estimated as S(52 mK) = Cmag(52 mK)/(0.5). The saturation entropy amounts to just 13% of expected total entropy for a spin-1/2 system, which could suggest the presence of a highly degenerate ground state, but also naturally arises just from the fact that many spin degrees of freedom inside individual spin-chain fragments already freeze out at these low \(T\ll J,J^{\prime}\), reducing the total number of available spin degrees of freedom and making individual spin-chain fragments behave as single effective spins in a frustrated random 3D spin lattice formed by weaker interchain interactions Jinter. The presence of these frustrated interactions is also seen from the shift of specific heat to lower T than predicted by theory if they were not present (see Supplementary Note 7 for a detailed comparison with ED calculations). The power-law behavior and the absence of any long-range ordering down to 52 mK in zero field data suggest that the antiferromagnet Li4CuTeO6 is a quantum spin liquid candidate.
Recently, Kimchi et al.32 suggested that quenched disorder in spin-liquid candidates can form a network of local moments in a random-singlet phase39,64 and the low-temperature-specific heat data recorded in various magnetic fields should collapse to a universal curve characterized by a parameter γ, where γ is defined by the relation \({C}_{p}/T\propto \frac{1}{{({\mu }_{0}H)}^{\gamma }}F(\frac{T}{{\mu }_{0}H})\) and F is a scaling function32. We scaled the magnetic-specific heat data of LCTO accordingly (see Fig. 3d) and we indeed find data collapse for γ = 0.85, which could be attributed to the presence of random singlets in the spin-liquid ground state. A similar data collapse is reported in a triangular-lattice Y2CuTiO6 with γ = 0.70, where 50% of Cu2+-sites are diluted by Ti4+ ions that yield quenched disorder62.
Muon spin relaxation
In order to gain microscopic insights into the intrinsic susceptibility and the ground-state spin dynamics, we performed zero-field (ZF) and transverse-field (TF) muon spin-relaxation (μSR) measurements on polycrystalline samples. μSR is a unique local-probe technique with a broad time window to track electron spin fluctuations. Therefore, ZF-μSR is one of the best tools to gain comprehensive microscopic information on magnetic ordering and spin dynamics of frustrated quantum materials. In Fig. 4a, we present ZF-μSR spectra at a few representative temperatures showing that muon asymmetry remains more or less unchanged for all temperatures, which confirms the absence of a phase transition down to 1.55 K65. The time dependence of the muon asymmetry provides information concerning internal field distributions at the muon stopping site. In multidomain or polycrystalline samples, static local field of nuclear origin Bloc is randomly oriented with respect to the initial muon spin direction. The corresponding local-field distribution can be approximated by a Gaussian shape. In this case, the muon relaxation function Pz(t) (also known as the Gaussian Kubo–Toyabe function (KT) is of the form
where σ gives the local-field distribution width.
a The time evolution of zero-field muon spin asymmetry curves for several temperatures where solid lines are the fits to Eq. (3). b The time evolution of muon spin asymmetry in zero field and in a longitudinal field (LF) of 50 G at 1.55 K with fits as discussed in the text. The simultaneous fit of zero-field and longitudinal field data to the Eq. (3) yields σ = 3.66 G and λ = 0.029 μs−1. c The temperature dependence of the longitudinal muon spin-relaxation rate in zero field. d The temperature dependence of Knight shift where red line is the fit of low-temperature Knight shift i.e., K ~ T−γ with γ = 0.75 in the applied field of 4900 G. Inset shows the scaling of the muon Knight shift (K) with bulk susceptibility with temperature as an implicit parameter. The solid line is the linear fit in two regions (see text). e The temperature dependence of the muon relaxation rate in the presence of a transverse field (TF) of 4900 G where the red line is the power-law T−0.2 fit in the low-temperature region. Error bars represent uncertainty of one standard deviation.
In LCTO, the presence of competing magnetic fields arising from electron spins provides dynamic muon spin relaxation in addition to relaxation due to quasi-static nuclear fields. Namely, a damping factor exp(− λ(T)t) characteristic of dynamical fields has to be added to the KT function to account for the experimental results. Therefore, the zero-field asymmetry spectra were fitted by the damped Gaussian Kubo–Toyabe relaxation function
where λ(T) is the dynamical muon spin-relaxation rate due to electronic spins. The fitting of the observed ZF asymmetry data (Fig. 4a) by Eq. (3) yields the nuclear field distribution width of approximately 3.66 G and the dynamical relaxation rate λ = 0.023 μs−1. In addition, the strong change of asymmetry spectra between zero field and a small longitudinal field of 50 G as shown in Fig. 4b also supports this model, as the applied field decouples the relaxation due to small static nuclear fields while it does not affect the relaxation due to larger but dynamical fields of electronic origin. The obtained temperature dependence of the muon spin-relaxation rate due to dynamical fields in ZF remains constant down to 1.55 K (Fig. 4c) without any signs of magnetic ordering, which suggests a dynamic ground state. We note that the presence of a disordered static local field at the muon site generally leads to the “1/3” tail in zero-field muon decay asymmetry of powder samples that is a hallmark of static magnetism. However, zero-field muon asymmetries do not show the “1/3” tail, which confirms the absence of spin-freezing66. In LCTO, the absence of any oscillation in ZF spectra (see Fig. 4a) also corroborates the absence of long-range magnetic ordering down to 1.55 K.
Next, we carried out muon rotation measurements in the presence of a large transverse field (TF) BT = 4900 G, which is much greater than the local fields. The observed experimental TF spectra were fitted using an oscillatory Gaussian decaying function
Here ϕ ~ π/3 is the initial phase of the oscillation, ν(T) is the frequency of muon precession originating from the local magnetic field and external transverse magnetic field, whereas λT(T) is the transverse muon spin-relaxation rate. In the presence of an external transverse field (BT), the total magnetic field experienced by muon can be defined as the sum of BT and Bloc. So, the mean precession frequency can be defined as ν(T) = γμ(BT + Bloc(T))/2π, where only the local magnetic field Bloc(T) changes with temperature (γμ = 2π × 135.53 MHzT−1 is the muon gyromagnetic ratio). The muon Knight shift (K) that is directly proportional to magnetic susceptibility (χ) via K = (ν(T) − ν0)/ν0 = Aχ, where ν0 = (γμ/2π) BT is the reference frequency and A is the coupling constant between the muon magnetic moment and the electron magnetic moments, thus captures intrinsic susceptibility relevant to the spin lattice. Inset of Fig. 4d depicts the muon Knight shift as a function of bulk magnetic susceptibility (χ) with temperature as an implicit parameter. It is seen that K as a function of χ exhibits two linear regions that are consistent with the observed crossover region in the temperature dependence of λT. Below T < 75 K, the linear fit (orange line) yields a coupling constant A = −114 Oe\({\mu }_{{{{{{{{\rm{B}}}}}}}}}^{-1}\) whereas we find A = −211 Oe\({\mu }_{{{{{{{{\rm{B}}}}}}}}}^{-1}\) from the linear fit (olive line) above 75 K. Furthermore, it is observed that the Knight-shift data follows K ~ T−0.75 power-law behavior at low T (see Fig. 4d), which is consistent with bulk magnetic susceptibility and confirms that such susceptibility is intrinsic to the system. This behavior further corroborates the presence of “random-singlets” in LCTO. μSR results do not indicate any static local fields of electronic origin down to 1.55 K. The measured muon asymmetry decay in zero field is, in fact, dominated by static nuclear fields, while relaxation due to dynamical fields of electronic origin remains hindered behind the nuclear relaxation due to exchange narrowing down to 1.55 K. This reveals spin fluctuations are fast even at T/θCW ≈ 0.01, which again suggests a dynamic ground state in LCTO. The temperature dependence of λT(T) is shown in Fig. 4e. Upon decreasing the temperature, the relaxation rate increases and a rather strong change of λT is observed in the temperature range 1.55 K < T < 10 K, which suggests the presence of a crossover region12. Above T > 20 K, λT varies very slowly with temperature as would be expected for a paramagnetic region. We note that the zero-field muon spin-relaxation rate due to electronic fields (Fig. 4c) is much lower than the transverse muon spin-relaxation rate (Fig. 4e) and its temperature dependence is different. As the former relaxation is only due to field fluctuations, while the latter is affected also by static local-field distributions induced by the applied transverse field, it is the induced local fields that are responsible for the increase of the transverse relaxation rate with decreasing temperature. This increase is characterized by a power-law T−0.2 at the lowest temperatures (Fig. 4e).
Discussion
Our investigation reveals the presence of a strong antiferromagnetic exchange interactions between spins of Cu2+ ions constituting a random frustrated spin-chain model with weaker interchain exchanges couplings forming an effective frustrated random 3D lattice of spin-chain fragments at low T. Remarkably, the material does not show any signature of a phase transition or spin-glass freezing down to at least 45 mK, which suggests a dynamical liquid-like ground state in this antiferromagnet. The scaling behavior of magnetization and specific heat data at low T reflects the presence of “random-singlets” in a quantum disordered ground state of LCTO. Magnetic materials with a dilute random network of S = 1/2 sites can be considered as a combination of two sub-systems where the majority of constituent spins develop spin-liquid or valence bond crystal, and the minority forms random singlets, and leaves out a random network of S = 1/2 sites. For such a system, in the ground state, spins do not undergo any long-range antiferromagnetic order. The spins that are strongly coupled rather constitute singlet pairs and the remaining spins are almost free due to the development of effective antiferromagnetic exchange interaction (J) with a power-law probability distribution, [P](J) ~ J−γ, between them in the low-T renormalization group flow of the random-singlet phase, where γ is a positive quantity related to the spin correlation length22. The small sub-system of spin-1/2 moments in the low-energy limit leads to unconventional scaling behavior in specific heat C[T] ~ T1−γ and spin susceptibility χ[T] ~ T−γ32. In the presence of an applied magnetic field, specific heat captures the modified distribution of energy through a field-dependent coefficient, i.e., \(C \sim T/{({\mu }_{0}H)}^{\gamma }\) at low temperatures. It is worth to mention that the temperature and field dependence of magnetic-specific heat displays T/μ0H data collapse for γ = 0.85 in LCTO, which is a bit higher than the observed γ = 0.5 for the honeycomb lattice H3LiIr2O6 and triangular-lattice LiZn2Mo3O8 but it is close to the observed γ = 0.7 for triangular-lattice Y2CuTiO6. The absence of strong spin-orbit interaction in Y2CuTiO6 and LCTO possibly plays a vital role resulting in data collapse with higher value of γ compared to H3LiIr2O6 and Li2Zn2Mo3O8. In addition, we also found a divergence in the low-temperature susceptibility of LCTO, which scales as T−γ with γ = 0.82 for bulk measurements and γ = 0.75 for local-probe muon Knight-shift measurements. This value of γ is comparable with the reported γ = 0.68 and 0.76 for Y2CuTiO6 and Sr2CuTe1−xWxO6, respectively24,25,62. Further theoretical and experimental studies are desired to shed additional insights into the magnetism and spin dynamics of this promising spin-liquid candidate and to clarify the degree to which the random-singlet picture might be modified due to the presence of an underlying spin-chain fragment structure with random connectivity. The chain fragments could conceivably contribute further ingredients to the low-temperature physics of LCTO, leading to novel phenomena outside the paradigm of the usually considered random-singlet states.
Conclusion
We have investigated the structure, thermodynamic and local magnetic properties of Li4CuTeO6 by employing X-ray, neutron diffraction, magnetization, specific heat, ESR, and muon spin-relaxation measurements. These were supported by state-of-the-art ab initio DFT and ED calculations to elucidate the high-T spin model and its thermodynamics. Li4CuTeO6 crystallizes in the monoclinic space group C2/m, wherein the Cu2+ site constitute spin chains with exchange J along the [101] direction of random length due to partial occupancy of the Cu2 site, with random additional Cu2+ ions on partially occupied Cu3 sites surrounding the main chains at positions displaced along ± b from the main-chain bond centers and coupling to two Cu2 sites on the main chain through an exchange \(J^{\prime}\). The large and negative CW temperature, θCW = −154 K, suggests the strong antiferromagnetic nature of the J and \(J^{\prime}\) exchange interactions between Cu2+ moments, which is confirmed by DFT and fits of ED calculations to experimental data for T > 20 K. These gradual deviations from these fits at low T reveals further frustrating 3D interactions between the random spin-chain fragments, which dominate the low T response. Specific heat experiments reveal the absence of long-range magnetic ordering down to 52 mK despite the presence of a large CW temperature, implying a highly frustrated spin lattice. The absence of spin-freezing despite the Li/Cu anti-site disorder reflects that Cu2+ moments remain fluctuating down to 45 mK. The zero-field and transverse-field μSR measurements support a dynamic ground state down to 1.55 K. Moreover, the existence of T/μ0H scaling as well as magnetization and specific heat data collapse indicate the presence of a spin-1/2 network of random singlets due to unavoidable anti-site disorder in the host lattice and frustrated weak 3D couplings. Our results demonstrate a randomness-induced spin-liquid state in a frustrated magnet. These results offer an exciting ground to explore novel quantum states with unconventional low-energy excitations in novel frustrated quantum materials with quenched disorder.
Methods
Polycrystalline samples of Li4CuTeO6 were synthesized by the conventional solid-state reaction route as outlined in ref. 53. To obtain a single phase of LCTO, stoichiometric amounts of Li2CO3 (Alfa Aesar, 99.0%), CuO (Alfa Aesar, 99.995%), and TeO2 (Alfa Aesar, 99.9995%) were mixed and the mixture was finely ground and pressed into a pellet, and after several intermediate steps, finally sintered at 850 °C for 30 h. The X-ray diffraction measurements were performed at 300 K by employing a Rigaku smart LAB X-ray diffractometer with Cu Kα radiation (λ = 1.54 Å). Due to the light mass of Li and O atoms, the analysis of X-ray powder diffraction data is not sufficient to determine the structural disorder and the mixed site occupancy. Therefore, neutron-diffraction measurements were performed at room temperature for the incident wavelength of 1.28 Å using crg-D1B Two-Axis Powder Diffractometer at the Institut of Laue-Langevin, France. Our neutron-diffraction studies detects neither spurious phases nor non-stoichiometry of oxygen. The neutron-diffraction results at 1.28 Å are shown in Fig. 1a, while the neutron-diffraction pattern, XRD pattern, and resulting refinements parameters are presented in Supplementary Notes 1 and 2. This suggests that the polycrystalline samples used in this study are of very high quality. The refined occupancy of all the atomic sites are within the experimental uncertainty of about 1%, thus ruling out the presence of non-stoichiometric oxygen.
Magnetization measurements were carried out using a Quantum Design, SQUID (MPMS) in the temperature range 1.9 K ≤ T ≤ 300 K under magnetic fields upto 5 T. The electron spin resonance (ESR) spectrum was measured at 250 K at the irradiation frequency of 256.3 GHz on a custom-built spectrometer with homodyne detection at the NHMFL, Tallahassee, USA. Thermoremanent measurements (see Supplementary Note 4) were performed using a Quantum Design, SQUID (MPMS) and the sample was cooled down from 100 to 2 K in either 1000 or 8 Oe, and turned down at 2 K. After 1 h, the signal was measured again (at t = 0). These results rule out the presence of a spin-glass transition and are shown in Supplementary Fig. 4.
Specific heat measurements were performed in a Quantum Design, Physical Properties Measurement System (PPMS) by the thermal relaxation method, in the temperature range 1.9 K ≤ T ≤ 240 K and in magnetic fields upto 7 T. Furthermore, specific heat measurements were carried out separately in the temperature range 0.052 K ≤ T ≤ 4 K in zero field and 3 T using a dilution refrigerator which was also used to measure ac susceptibility in the temperature range 0.045 K ≤ T ≤ 4 K at four different frequencies using a Dynacool PPMS instrument from Quantum Design, San Diego, USA.
μSR measurements were performed using the GPS spectrometer at the Paul Scherrer Institute, Villigen, Switzerland, on a polycrystalline sample with mass of ~1 g down to 1.55 K in zero field and in a transverse field of 4900 G.
DFT+U calculations on a 2 × 1 × 2 supercell of LCTO were carried out using the plane-wave DFT code67 using a local (spin) density approximation (LSDA) exchange-correlation functional in a LSDA+U scheme68 with an effective Hubbard Ueff = 9 eV, a 2000 plane-wave energy cutoff, and a 2 × 3 × 2 Monkhorst–Pack grid reciprocal-space sampling69. To extract exchanges total energies of ≥120 random collinear spin configurations were calculated and fitted to a symmetry-adapted spin model70. See Supplementary Note 6 for further details. ED calculations with upto N = 18 spins were carried out on > 13,000 distinct configurations of occupied Cu2 and Cu3 sites around finite-length spin-chain fragments in the high-T random 1D model of Fig. 1c, achieving a total probability between 60.2% and more than 98.8%, depending on parameters, that a randomly-chosen Cu2+ spin in LCTO is part of one of the ED calculated spin-chain fragments. Details of these ED calculations are presented in Supplementary Note 7.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request. The neutron-diffraction data can be found at https://doi.org/10.5291/ILL-DATA.EASY-1043.
References
Balents, L. Spin liquids in frustrated magnets. Nature 464, 199 (2010).
Anderson, P. W. Resonating valence bonds: a new kind of insulator? Mater. Res. Bull. 8, 153 - 160 (1973).
Ross, K. A., Savary, L., Gaulin, B. D. & Balents, L. Quantum excitations in quantum spin ice. Phys. Rev. X 1, 021002 (2011).
Ramirez, A. P., Hayashi, A., Cava, R. J., Siddharthan, R. & Shastry, B. S. Zero-point entropy. Nature 399, 333–335 (1999).
Khuntia, P. Novel magnetism and spin dynamics of strongly correlated electron systems: Microscopic insights. J. Magn. Magn. Mater. 489, 165435 (2019).
Nath, R. et al. Magnetization and spin dynamics of the spin S = 1/2 hourglass nanomagnet Cu5(OH)2(NIPA)4 ⋅ 10H2O. Phys. Rev. B 87, 214417 (2013).
Savary, L. & Balents, L. Quantum spin liquids: a review. Rep. Prog. Phys. 80, 016502 (2016).
Castelnovo, C., Moessner, R. & Sondhi, S. L. Magnetic monopoles in spin ice. Nature 451, 42 (2008).
Zhou, Y., Kanoda, K. & Ng, T.-K. Quantum spin liquid states. Rev. Mod. Phys. 89, 025003 (2017).
Klanjšek, M. et al. A high-temperature quantum spin liquid with polaron spins. Nat. Phys. 13, 1130–1134 (2017).
Khuntia, P. et al. Gapless ground state in the archetypal quantum kagome antiferromagnet ZnCu3(OH)6Cl2. Nat. Phys. 16, 469–474 (2020).
Khuntia, P. et al. Spin liquid state in the 3d frustrated antiferromagnet PbCuTe2O6: NMR and Muon spin relaxation studies. Phys. Rev. Lett. 116, 107203 (2016).
Chillal, S. et al. Evidence for a three-dimensional quantum spin liquid in PbCuTe2O6. Nat. Commun. 11, 2348 (2020).
Kitaev, A. Anyons in an exactly solved model and beyond. Ann. Phys. 321, 2 - 111 (2006).
Fouet, J. B., Sindzingre, P. & Lhuillier, C. An investigation of the quantum J1-J2-J3 model on the honeycomb lattice. Eur. Phys. J. B - Condens. Matter Complex Syst. 20, 241–254 (2001).
Do, S.-H. et al. Majorana fermions in the Kitaev quantum spin system α-RuCl3. Nat. Phys. 13, 1079–1084 (2017).
Takagi, H., Takayama, T., Jackeli, G., Khaliullin, G. & Nagler, S. E. Concept and realization of Kitaev quantum spin liquids. Nat. Rev. Phys. 1, 264–280 (2019).
Albuquerque, A. F. et al. Phase diagram of a frustrated quantum antiferromagnet on the honeycomb lattice: magnetic order versus valence-bond crystal formation. Phys. Rev. B 84, 024406 (2011).
Janša, N. et al. Observation of two types of fractional excitation in the Kitaev honeycomb magnet. Nat. Phys. 14, 786–790 (2018).
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. Non-abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008).
Kalmeyer, V. & Laughlin, R. B. Equivalence of the resonating-valence-bond and fractional quantum Hall states. Phys. Rev. Lett. 59, 2095–2098 (1987).
Kimchi, I., Nahum, A. & Senthil, T. Valence bonds in random quantum magnets: Theory and application to YbMgGaO4. Phys. Rev. X 8, 031028 (2018).
Zhu, Z., Maksimov, P. A., White, S. R. & Chernyshev, A. L. Disorder-induced mimicry of a spin liquid in ybmggao4. Phys. Rev. Lett. 119, 157201 (2017).
Liu, L., Guo, W. & Sandvik, A. W. Quantum-critical scaling properties of the two-dimensional random-singlet state. Phys. Rev. B 102, 054443 (2020).
Liu, L., Shao, H., Lin, Y.-C., Guo, W. & Sandvik, A. W. Random-singlet phase in disordered two-dimensional quantum magnets. Phys. Rev. X 8, 041040 (2018).
Hong, W. et al. Extreme suppression of antiferromagnetic order and critical scaling in a two-dimensional random quantum magnet. Phys. Rev. Lett. 126, 037201 (2021).
Kitagawa, K. et al. A spin-orbital-entangled quantum liquid on a honeycomb lattice. Nature 554, 341 (2018).
Do, S.-H. et al. Short-range quasistatic order and critical spin correlations in α-Ru1−xIrxCl3. Phys. Rev. B 98, 014407 (2018).
Baek, S.-H. et al. Observation of a random singlet state in a diluted Kitaev honeycomb material. Phys. Rev. B 102, 094407 (2020).
Do, S.-H. et al. Randomly hopping Majorana fermions in the diluted Kitaev system α-Ru0.8Ir0.2Cl3. Phys. Rev. Lett. 124, 047204 (2020).
Bahrami, F. et al. Thermodynamic evidence of proximity to Kitaev spin liquid in Ag3LiIr2O6. Phys. Rev. Lett. 123, 237203 (2019).
Kimchi, I., Sheckelton, J. P., McQueen, T. M. & Lee, P. A. Scaling and data collapse from local moments in frustrated disordered quantum spin systems. Nat. Commun. 9, 4367 (2018).
Uematsu, K. & Kawamura, H. Randomness-induced quantum spin liquid behavior in the S = 1/2 random-bond Heisenberg antiferromagnet on the pyrochlore lattice. Phys. Rev. Lett. 123, 087201 (2019).
Clark, L. et al. From spin-glass to quantum spin liquid ground states in molybdate pyrochlores. Phys. Rev. Lett. 113, 117201 (2014).
Gomilšek, M. et al. Kondo screening in a charge-insulating spinon metal. Nat. Phys. 15, 754–758 (2019).
Alloul, H., Bobroff, J., Gabay, M. & Hirschfeld, P. J. Defects in correlated metals and superconductors. Rev. Mod. Phys. 81, 45–108 (2009).
Yamaguchi, H. et al. Randomness-induced quantum spin liquid on honeycomb lattice. Sci. Rep. 7, 16144 (2017).
Dey, T. et al. Persistent low-temperature spin dynamics in the mixed-valence iridate Ba3InIr2O9. Phys. Rev. B 96, 174411 (2017).
Bhatt, R. N. & Lee, P. A. Scaling studies of highly disordered antiferromagnetic systems. Phys. Rev. Lett. 48, 344–347 (1982).
Kumar, R. et al. Sc2Ga2CuO7: a possible quantum spin liquid near the percolation threshold. Phys. Rev. B 92, 180411 (2015).
Khuntia, P., Kumar, R., Mahajan, A. V., Baenitz, M. & Furukawa, Y. Spin liquid state in the disordered triangular lattice Sc2Ga2CuO7 revealed by NMR. Phys. Rev. B 93, 140408 (2016).
Uematsu, K. & Kawamura, H. Randomness-induced quantum spin liquid behavior in the S = 1/2 random J1-J2 Heisenberg antiferromagnet on the honeycomb lattice. J. Phys. Soc. Jpn. 86, 044704 (2017).
Bozler, H. M., Gould, C. M. & Clark, W. G. Crossover behavior of a random-exchange Heisenberg antiferromagnetic chain at ultralow temperatures. Phys. Rev. Lett. 45, 1303–1306 (1980).
Scott, J. C., Garito, A. F., Heeger, A. J., Nannelli, P. & Gillman, H. D. Magnetic properties of poly(metal phosphinates): the effects of structural disorder on one-dimensional antiferromagnetic chains. Phys. Rev. B 12, 356–361 (1975).
Shiroka, T., Eggenschwiler, F., Ott, H.-R. & Mesot, J. From order to randomness: Onset and evolution of the random-singlet state in bond-disordered BaCu\({}_{2}{({{{{{{{{\rm{Si}}}}}}}}}_{1-x}{{{{{{{{\rm{Ge}}}}}}}}}_{x})}_{2}\,{{{{{{{{\rm{O}}}}}}}}}_{7}\) spin-chain compounds. Phys. Rev. B 99, 035116 (2019).
Shiroka, T. et al. Impact of strong disorder on the static magnetic properties of the spin-chain compound BaCu2SiGeO7. Phys. Rev. B 88, 054422 (2013).
Ma, S.-K., Dasgupta, C. & Hu, C.-K. Random antiferromagnetic chain. Phys. Rev. Lett. 43, 1434–1437 (1979).
Yao, N. Y. et al. Robust quantum state transfer in random unpolarized spin chains. Phys. Rev. Lett. 106, 040505 (2011).
Shu, Y.-R., Yao, D.-X., Ke, C.-W., Lin, Y.-C. & Sandvik, A. W. Properties of the random-singlet phase: from the disordered Heisenberg chain to an amorphous valence-bond solid. Phys. Rev. B 94, 174442 (2016).
Shu, Y.-R., Dupont, M., Yao, D.-X., Capponi, S. & Sandvik, A. W. Dynamical properties of the S = 1/2 random Heisenberg chain. Phys. Rev. B 97, 104424 (2018).
Watanabe, K., Kawamura, H., Nakano, H. & Sakai, T. Quantum spin-liquid behavior in the spin-1/2 random Heisenberg antiferromagnet on the triangular lattice. J. Phys. Soc. Jpn. 83, 034714 (2014).
Toby, B. H. EXPGUI, a graphical user interface for GSAS. J. Appl. Cryst. 34, 210–213 (2001).
Kumar, V., Bhardwaj, N., Tomar, N., Thakral, V. & Uma, S. Novel lithium-containing honeycomb structures. Inorg. Chem. 51, 10471–10473 (2012).
Goodenough, J. Magnetism and the Chemical Bond (R.E. Krieger Pub. Co, 1976).
Rocquefelte, X., Schwarz, K. & Blaha, P. Theoretical investigation of the magnetic exchange interactions in copper (II) oxides under chemical and physical pressures. Sci. Rep. 2, 1–5 (2012).
Rao, G. N. et al. Tellurium-bridged two-leg spin ladder in Ba2CuTeO6. Phys. Rev. B 93, 104401 (2016).
Whangbo, M.-H., Koo, H.-J. & Dai, D. Spin exchange interactions and magnetic structures of extended magnetic solids with localized spins: theoretical descriptions on formal, quantitative and qualitative levels. J. Solid State Chem. 176, 417–481 (2003). Special issue on The Impact of Theoretical Methods on Solid-State Chemistry.
Whangbo, M.-H., Dai, D. & Koo, H.-J. Spin dimer, electronic band structure and classical spin analyses of spin exchange interactions and ordered magnetic structures of magnetic solids. Solid State Sci. 7, 827–852 (2005). Selected articles from the 4th International Conference on Inorganic Materials.
Koo, H.-J. & Whangbo, M.-H. Analysis of the spin lattice model for the spin-gapped layered compounds Na3Cu2SbO6 and Na2Cu2TeO6 on the basis of electronic structure calculations. Inorg. Chem. 47, 128–133 (2008).
Bertani, R. et al. Halogen bonding in metal-organic-supramolecular networks. Coord. Chem. Rev. 254, 677–695 (2010). A Tribute to Fausto Calderazzo on the Occasion of his 80th Birthday.
Bieringer, M., Greedan, J. E. & Luke, G. M. Li4MgReO6 : an S = 1/2 antiferromagnet exhibiting spin-glass behavior. Phys. Rev. B 62, 6521–6529 (2000).
Kundu, S. et al. Signatures of a spin-1/2 cooperative paramagnet in the diluted triangular lattice of Y2CuTiO6. Phys. Rev. Lett. 125, 117206 (2020).
Song, P. et al. Evidence for the random singlet phase in the honeycomb iridate SrIr2O6. Phys. Rev. B 103, L241114 (2021).
Dasgupta, C. & Ma, S.-k Low-temperature properties of the random Heisenberg antiferromagnetic chain. Phys. Rev. B 22, 1305–1319 (1980).
Cantarino, M. R. et al. Dynamic magnetism in the disordered hexagonal double perovskite BaTi1/2Mn1/2O3. Phys. Rev. B 99, 054412 (2019).
Yaouanc, A. & De Reotier, P. D. Muon Spin Rotation, Relaxation, and Resonance: Applications to Condensed Matter, Vol. 147 (Oxford University Press, 2011).
Clark, S. J. et al. First principles methods using CASTEP. Z. Krist. 220, 567–570 (2005).
Anisimov, V. I., Aryasetiawan, F. & Lichtenstein, A. I. First-principles calculations of the electronic structure and spectra of strongly correlated systems: the LDA+U method. J. Phys.: Condens. Matter 9, 767–808 (1997).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).
Riedl, K., Li, Y., Valentí, R. & Winter, S. M. Ab initio approaches for low-energy spin hamiltonians. Phys. Status Solidi (B): Basic Res. 256, 1800684 (2019).
Acknowledgements
We thank DST, India for the PPMS facility at IIT Madras. P.K. acknowledges the funding by the Science and Engineering Research Board, and the Department of Science and Technology, India through Research Grants. A.Z. and M.G. acknowledge the financial support of the Slovenian Research Agency through Programme No. P1-0125 and Projects Nos. N1-0148 and J1-2461. A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by National Science Foundation Cooperative Agreement No. DMR-1644779 and the State of Florida. AMS thanks the NRF (93549) and the URC and FRC of the University of Johannesburg. Experiments at ILL were sponsored by the French Neutron Federation (2FDN), with data references from Easy Proposal No. 1043.
Author information
Authors and Affiliations
Contributions
P.K. conceived the investigation of Li4CuTeO6. P.K. designed the project and supervised the experiments presented in this work. J.K. and P.K. synthesized and structurally characterized the sample. J.K., P.K., A.M.S., Z.J., K.S., and M.S.R. carried magnetization and specific heat measurements. C.V.C, S.P., and L.M.-T. conducted the neutron-diffraction experiment. M.G. performed DFT and ED calculations. J. K., P. K., and M. G. analyzed magnetization and specific heat results. A.Z. and A.O. performed the ESR measurements, and A.Z. analyzed the results. J.C.O., P.K., A.Z., and J.K. carried out μSR investigation and analyzed the corresponding data. All authors discussed the results and finalized the paper. J.K. and P.K. wrote the paper, with the inputs from M.G. and A.Z.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Khatua, J., Gomilšek, M., Orain, J.C. et al. Signature of a randomness-driven spin-liquid state in a frustrated magnet. Commun Phys 5, 99 (2022). https://doi.org/10.1038/s42005-022-00879-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-00879-2
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.