Abstract
Engineering arrays of active optical centers to control the interaction Hamiltonian between light and matter has been the subject of intense research recently. Collective interaction of atomic arrays with optical photons can give rise to directionally enhanced absorption or emission, which enables engineering of broadband and strong atom-photon interfaces. Here, we report on the observation of long-range cooperative resonances in an array of rare-earth ions controllably implanted into a solid-state lithium niobate micro-ring resonator. We show that cooperative effects can be observed in an ordered ion array extended far beyond the light’s wavelength. We observe enhanced emission from both cavity-induced Purcell enhancement and array-induced collective resonances at cryogenic temperatures. Engineering collective resonances as a paradigm for enhanced light-matter interactions can enable suppression of free-space spontaneous emission. The multi-functionality of lithium niobate hosting rare-earth ions can open possibilities of quantum photonic device engineering for scalable and multiplexed quantum networks.
Similar content being viewed by others
Introduction
Engineering interaction Hamiltonian of photons with an ensemble of atoms or defect centers in solid-state photonics is of great interest from both fundamental and applied aspects. Recent advances in ion implantation enable deterministic engineering of multiple or arrays of ions in the crystalline matrix1. In the case of long one-dimensional arrays, the ability to control collective dynamics in such mesoscopic systems can lead to suppression of spontaneous emission and losses in the ensemble2,3. The rich physics of many-body interactions in these systems may lead to the discovery of different interaction regimes in solids for nonlinear quantum photonic applications such as on-chip photon-atom entanglement. The implementation of collective interactions in solid-state photonics can also help to overcome fundamental limitations of the current quantum communication devices stemming from probabilistic and not-scalable entangling interactions4.
It has been proposed that cooperative modes within emitter arrays can be harnessed to mediate tunable, long-range interactions between other impurities coupled to the chain5. In the cooperative regime, the strength of absorption or emission can scale quadratically with the atom number6. By tuning the inter-atomic separation, the dispersion relation can be engineered to observe localized photonic states. There has been limited research investigating collective interactions of light with solid-state emitters. The inhomogeneous broadening of optical transitions in solids and the lack of ability to deterministically control emitters’ locations and ensemble geometry had so far limited realization of controllable collective interactions in solid-state photonics. It has been shown that emission lifetime can change depending on the local concentrations of quantum dots and defects in diamond7,8.
Rare-earth ions (REIs) in crystalline solids exhibit inhomogeneous broadening as low as 10 MHz9,10,11 compared to 0.1–1 THz for defects in diamonds and quantum dots. Unlike defect centers and quantum dots, REIs are actual atoms with sub-nanometer footprints, and thanks to their internal electronic structures, the atomic excitations are relatively insensitive to the environment. These unique properties together with the telecom-band optical transitions of some REIs are of important interest for quantum applications, in particular, quantum light storage12,13,14,15 and microwave-to-optical transduction16,17. To date, world-record coherence time has been observed in rare-earth crystals exceeding 6 h18. The weak optical transition strength in REIs, however, prevents efficient optical pumping to a particular ground sub-level as the ground-state population lifetime is comparable to the excited state decay time. For this reason, nanophotonic cavities integrated on bulk yttrium orthosilicate (YSO) crystals have been considered to introduce Purcell enhancement of emission to improve the preparation efficiency13,19,20. This approach has resulted in enhancement factors of 70019, however, with the price of reducing the bandwidth and number of atoms available for interactions.
Integrated solid-state photonics based on silicon or lithium niobate (LN) materials provide salable platforms as hosts for REIs. Ion implantation in photonic materials has shown low inhomogeneous and homogeneous broadenings21,22,23. We have previously shown that it is possible to arrange REIs into an ordered array inside silicon nitride photonic resonators3. Integrating REIs with nonlinear crystals such as LN has also been demonstrated24,25,26. The LN photonic devices integrated with REIs can be promising candidates for multi-functional quantum optical devices where quantum light generation27, storage15, modulation28, and wavelength conversion29 can all occur within the same device.
When an ensemble of REIs inside micro-ring resonators forms an ordered array, in certain parameter regimes, ions can cooperatively interact with light30. In this regime, absorption and directional emission can increase without increasing the ion concentration. This is important because, in the case of REIs, high concentration leads to undesirable strong ion–ion interactions. This induces spin diffusion and dephasing31, lowering the coherence time of ions. In contrast, the cooperative interaction enables strong and broadband light-atom interactions at not-high atomic densities. Moreover, enhanced emission in this regime leads to increased pumping efficiency that can enable efficient quantum storage of light without affecting the memory bandwidth. The cooperative effect can also reduce the loss and increase the storage fidelity. For example, the emergence of dark states due to the coherent spin–spin interaction can be a promising candidate for photonic quantum memories32. When far from saturation, the collective effects are expected to lead to a memory unit with minimized transport and dephasing loss.
To deterministically create ion arrays, we use precision ion implantation. We select isotopically pure 169Tm2+ ions using a velocity selector (Wien filter) and use a focused ion beam (FIB) to implant ions with a beam spot size of 37 nm × 36 nm. Rare-earth Tm2+ change to Tm3+ after annealing. As the result, ions are localized in a segment of width and depth of about 36 nm across the waveguide as shown in Fig. 1a. The spatial and frequency spread of ions in each segment can be described by semi-Gaussian distributions. By repeating the implantation in multiple segments around the micro-ring, ordered arrays (with regular segment spacing) and disordered arrays (with random segment spacing) can be created. Although ions in each segment have different frequencies due to the inhomogeneous broadening, resonant excitation and resonant photoluminescence help to study the interaction of a narrow frequency class of ions. Moreover, Tm3+ are non-Kramers REIs in the crystalline matrix with the ability to, in principle, reach long coherence times as shown for other non-Kramers ions18. Also, the presence of optical transitions at both 0.8 μm and 1.6 μm enables applications in quantum communication33,34 for both free-space and fiber channels. Here, lithium niobate-on-insulator (LNOI) materials are chosen as the host materials for their multi-functional properties35,36 and ease of nanofabrication37,38 compared to other crystalline hosts. The applications of Tm-incorporated lithium niobate waveguides for integrated optical and quantum photonics have been highlighted by recent experimental studies25,39.
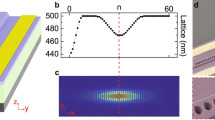
a Schematics of an LN micro-ring resonator incorporated with Tm3+ ion arrays engineered to have spacing close to λL/2neff. The top-right inset is an optical microscope image showing the fabricated LN micro-ring resonator with Au alignment marks used for implantation on a lithium niobate on insulator (LNOI) platform. Here, d = deff, λL, and neff represent the separation between neighboring ion segments, the wavelength where the light is commensurate with the atomic lattice, and the effective refractive index of the cavity mode, respectively; b Comsol simulation showing the fundamental TE mode confinement in the half-etched LN waveguide with the implanted Tm3+ ions. The width of the waveguide is 600 nm; c Stopping and Range of Ions in Matter (SRIM) software simulation showing the distribution of the implanted Tm ions in the LN layer. When implanted with 200 keV energy, the peak ion distribution lies around 51 nm below the top LN surface with a Gaussian distribution width of around 16 nm. The peak of the ion distribution corresponds to 0.1% ion concentration; d Mean atom–atom coupling rate (Ca) of an ordered array normalized to that of a disordered array. Δλin represents the width of the inhomogenous broadening of ions.
Results
LN Photonic micro-ring resonators integrated with Tm3+
The micro-ring resonators were fabricated by partially etching the LNOI wafer, and Tm ions were implanted into the ring resonator (Methods). Figure 1a shows the schematic figure of the fabricated micro-ring resonator with the Tm3+ arrays. Each ion segment is a rectangular box within which about Ns = 2.2 × 104 ions are randomly implanted. A collection of Ms = 1750 segments create an array with fixed segment spacing (ordered array) or random spacing (disordered array). To couple light into the micro-ring cavity via the bus waveguide, the LN layer was fully etched on the edges of the wafer to allow fiber-to-chip coupling. An additional input waveguide port (drop-port) designed on the other side of the micro-ring enables coupling of light to the micro-ring from the opposite side.
After the ions are excited using a pump injected from the drop-port, the scattered light in the clockwise and counter-clockwise directions inside the micro-ring can interfere to create a standing wave40. When the array is regularly spaced with spacing close to λL/2neff, where neff (=2.159) is the effective refractive index of the cavity mode (in this case TE mode) and λL is the wavelength where the light is commensurate with the atomic lattice, ions can experience the electric field from the other ions in the array with the same phase. In the commensurate lattice condition, the peak intensity of the standing wave perfectly coincides with the location of the ions in the arrays. Ideally, in this case, all the ions can coherently and cooperatively emit light even though the extent of the array is much larger than the light’s wavelength (~0.8 μm). Figure 1b shows the finite-element calculation of the E-field in the cross-section of the micro-ring. The etched sidewall angle of LN thin-film is 55∘ and the fundamental TE mode is well confined inside the partially-etched waveguide. As it is confirmed by the Stopping and Range of Ions in Matter (SRIM) simulation (Fig. 1c), the peak of ion concentration is around 51 nm below the top LN surface with a Gaussian distribution width of around 16 nm (Supplementary Note 4).
To see how the cooperative coupling changes with the lattice spacing, we define a mean atom–atom coupling (Supplementary Note 8) as
where \({{{{{{{\mathcal{N}}}}}}}}(\theta ,\omega )\) describes the angular distribution of atoms and inhomogeneous broadening of transition frequencies both described by Gaussian distributions, and R is the ring radius. Figure 1d shows the calculated value of Ca normalized to that of a disordered array. The enhanced atom–atom coupling is seen for ordered arrays in both the commensurate (d = λL/2neff) and the incommensurate (d ≠ λL/2neff) conditions. The effect of inhomogeneous broadening of width Δλin can be seen as broadening of Ca envelope. In our case, the periodic ion array is not exactly commensurate with the optical wavelength.
Cavity-induced Purcell enhancement of Tm at cryogenic temperatures
After the fabrication and implantation processes, we characterize the optical properties of the micro-ring and ions. We first measure the effect of micro-ring enhancing emission from the ions. The quality factor (Q) of the micro-ring resonator was measured to be about 2.2 × 104 at 796.85 nm, as shown in Fig. 2a. To measure the photoluminescence (PL) lifetime of Tm3+ ions in the micro-ring resonator, a pump light around 795 nm was pulsed (2 ms) and injected into the micro-ring from the drop-port. Because of the geometry of the designed drop-port, most of the pump light exiting the micro-ring is guided to one side of the bus waveguide. By positioning a lensed fiber on the other side of the waveguide, we can effectively screen the pump light while measuring the PL signal from Tm3+ ions. The emitted PL signal is then detected using a single-photon detector.
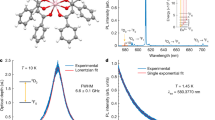
a The transmission signal at 796.85 nm showing the micro-ring cavity resonance and the corresponding Lorentzian fit (with asymmetry described by a linear parameter) with a loaded quality factor (Q) of 2.2 × 104. b Two photoluminescence (PL) decay curves of Tm3+ ions measured at room temperature (red) and 4 K (blue) from the LN micro-ring resonator of the disordered array, both pumped at 795 nm, are shown. The exponential time constant of the PL decay curves at room temperature (τRT) and 4 K (τ4K) are 226.3 μs and 177.7 μs, respectively. The inset shows PL lifetime at both room temperature (RT, red) and 4 K (blue) as a function of the resonant pump wavelength. Error bars defined here represent 95% confidence interval.
To study the effect of the cavity on light emission, a micro-ring with randomly spaced ion segments (with no periodic array structure) is used for PL measurement at both room temperature and 4 K. The temperature dependency of PL decay in presence of multidimensional decay processes41,42 provides means to measure the Purcell factor of ion emission by comparing decay rates at cryogenic and room temperatures in the same device. For rare-earth ions at room temperature, the ions’ homogeneous linewidth is much greater than the cavity linewidth that suppresses the Purcell effect41,43. At cryogenic temperatures, the homogeneous linewidth or the dephasing rate is expected to significantly decrease and be narrower than the cavity decay rate, where the Purcell factor can be fully recovered. Figure 2b shows the normalized PL intensity of Tm3+ ions pumped on the cavity resonance near the atomic transition (λpump = 794.5 nm) for both room temperature and 4 K. The lifetime of Tm3+ ions at 4 K is reduced compared to the PL lifetime at the elevated temperatures. The inset of Fig. 2b shows the PL lifetime as a function of the pump wavelength for both room temperature and 4 K. The data confirm the lifetime shortening at 4 K compared to room temperature emission. We attribute this lifetime shortening at 4 K to the Purcell enhancement provided by the micro-ring. In theory, taking into the account the Gaussian width of the ion implantation, we estimate the maximum Purcell factor of 0.25 ± 0.04 (Supplementary Note 6). Also, the experimental Purcell factor is calculated by τRT/τ4 K-1 ≈ 0.27 ± 0.1. The theoretical maximum Purcell factor is very close to the measured value. In the case of Tm ions in an LN crystal, the branching ratio of Tm ions for 3H4−3H6 transition is 0.7344,45 (Supplementary Note 5). In our care, because we use isotopically pure Tm ions, the transition probability for relaxation to 3H6 in LiNbO3 can be even higher. For this reason, we use the maximum theoretical Purcell factor (assuming a branching ratio of unity) for comparison to the experimental results.
Based on our previous studies46, we expect a negligible non-radiative decay at room temperatures. In the case of REIs doped in crystalline hosts such as LN, the nonradiative decay by the phonon decay processes is the dominant nonradiatve decay mechanism47,48. Based on the recent study also performed in a Tm:LNOI sample25, the nonradiative decay of Tm ions in LNOI waveguide is negligible compared to the bulk LN sample. Given that the measured PL lifetime in our implanted sample (at both room temperature and 4 K) is longer than the Tm-doped LNOI25,44, we conclude that nonradiative decay is negligible in our system. Otherwise, the experimental Purcell enhancement factor obtained above is an underestimation. The Purcell enhancement is a single-body effect provided by the mode confinement in the cavity. Below we discuss the results of cooperative emission as a collective effect resulting in an additional enhancement of light emission from an ordered ion array.
Array-induced enhanced light scattering
To verify the effect of the array on emission, we fabricated two identical micro-ring resonators with an identical number of ion segments. In one case, ion segments were randomly distributed along the micro-ring (also used for data in Fig. 2), while the other micro-ring hosts an ordered ion array (with loaded Q = 1.8 × 104).
Figure 3a shows the resulting normalized scattering signals for both the periodic array and the randomly distributed ensemble. The scattered signal is collected from the one edge of the bus waveguide while a CW pump is injected from the opposite end through the drop-port (Methods). On the atomic resonance condition, the periodic array shows about 60% more scattering compared to the disordered array. The scattering spectrum from the disordered array matches the absorption spectrum of Tm ions in LN waveguides25,39 with splitting due to 6Li and 7Li. The ordered array, however, shows peculiar oscillations originating from two distinct processes, as explained below.
a Normalized scattering data for the ordered ion arrays (blue) and disordered (randomly distributed) arrays (yellow) as a function of resonant pump wavelength. The scattering from the array near the atomic resonance (~795 nm) shows an enhancement of about 60% for the ordered array compared to the disordered one. The gray curve shows the calculated Bragg resonance that results from the ion implantation process (see text); b A zoomed-in scattering data near-atomic resonance shows modulation of the scattering signal with a period of λ/Ms, where Ms = 1750 is the number of ion segments in the array. The periodic oscillation is in agreement with the model of sinusoidal oscillation (solid line) with a double-peak Gaussian envelope of center and width corresponding to that of the disordered array (total width) data in a. The shaded regions indicate the predicted cavity resonances based on measurement of the cavity spectrum obtained from a different experiment run while taking into the account the uncertainty due to the drift in the cavity resonances. The dashed lines in both plots are guide to the eye.
Below 785 nm the signal and its oscillation are dominated by the Bragg scattering induced by the implantation process. Regardless of the ion’s optical transition, the process of ion implantation can damage the crystalline matrix inducing a slight change in the refractive index. Some of these damages can be recovered by the annealing process. But as high-temperature annealing is not an option (due to different thermal expansion coefficients of LNOI layers)49, a non-negligible index change near the implantation regions may remain. The modulation of the refractive index caused by the periodic implantation of ions can then manifest itself as Bragg-induced back-reflection of the pump light. This is why the reflection signal (originated from the ring) spans beyond the Tm emission band. We expect the signals from both Bragg and superradiance to show the same periodicity. As the result, the signals add up in the wavelength region of 785–790 nm while around 775 nm and 795 nm the Bragg and superradiance effects can primarily be observed, respectively. We note that in Fig. 3a, the fast oscillation with the periodicity of λL/Ms is not observed due to the low sampling of the pump wavelength.
Between 790–797 nm, which is the absorption window of Tm3+ ions, the effect of Bragg back-scattering is negligible compared to the collective scattering from the array. By fine scanning the pump wavelength near-atomic resonance (Fig. 3b), the scattered light intensity shows clear oscillations with a periodicity of λL/Ms, where Ms is the number of ion segments. The oscillation of the scattering signal is one signature of the cooperative resonance30 from the ion array. The theory used to model the oscillation in Fig. 3b is given by a modulated double-Gaussian profile centered around Tm transitions (λ1,2) described by \((A{e}^{-{(\lambda -{\lambda }_{1})}^{2}/(2{{\Delta }}{\lambda }_{in}^{2})}+B{e}^{-{(\lambda -{\lambda }_{2})}^{2}/(2{{\Delta }}{\lambda }_{in}^{2})}){\sin }^{2}(\frac{2\pi }{{\lambda }_{L}}{M}_{s}\lambda +{\theta }_{0})\), where λL/2 is the lattice spacing, Δλin is the width of the inhomogeneous broadening of ions extracted from Fig. 3a and A, B, and θ0 are free parameters.
As the free-spectral range of the cavity is about 0.8nm, the majority of points measured in Fig. 3 were obtained where the pump was off the cavity resonances (shaded regions in Fig. 3b). The drop-port coupling is only ~ 5% and the effect of the cavity resonances is expected to be small compared to the size of the oscillations observed in Fig. 3.
To verify that the near-resonance scattering signal is originated from the cooperative effect of ions, we also measure the emission lifetime of Tm ions for both ordered and disordered arrays at 4 K (Fig. 4a, b). Compared with the disordered array that does not exhibit a noticeable change in the lifetime near the Tm optical transitions, the ordered array shows reduced lifetime at 3H4 → 3H6 transitions (with splitting from 6,7Li centered around 793.5 nm and 794.5 nm). The maximum lifetime change is τ2/τ1 ≃ 1.25, which is expected to scale linearly with effective number of excitations, contributing to the cooperative emission. The data in Fig. 4b also show a minor trend as a function of pump wavelength. Near the cavity resonances shown as shaded regions, the enhanced Purcell factor is expected, which explains the lifetime reduction near 793.5 nm and 795 nm. It can be seen that near the atomic resonant frequencies, i.e., 794.5 nm and 793.5 nm, the lifetime is slightly higher. This can be explained by light re-absorption or radiation trapping50 also observed in our previous studies3,46 (For descriptions of error bars in Fig. 4a, b Supplementary Note 7).
a PL lifetimes of the Tm3+ ions as a function of wavelength in the periodic array, indicating the lifetime shortening near the atomic resonance as a result of cooperative resonances. The solid curve is a fit using a double-Lorentzian function with center wavelengths and widths matching that of scattering profile from the disordered array (Fig. 3a). The inset shows two PL decay curves of the Tm3+ ions: one away from the atomic resonance (red), the other close with the resonance (blue). τ is the exponential time constant of the PL decay curve; b PL lifetimes of the Tm3+ ions as a function of wavelength in the sample with disordered ion array, showing the lifetime is mainly unchanged near the atomic resonance; We note that the slight difference in quality factors of rings used in a and b causes small differences in Purcell-enhanced emission in the two cases and therefore the off-resonant lifetimes are not exactly the same. The shaded regions indicate the predicted cavity resonances based on measurement of the cavity spectrum obtained from a different experiment run while taking into the account the uncertainly due to the drift in the cavity resonances; c PL lifetimes of the Tm3+ ions as a function of input resonant pump power in the periodic array at a fixed wavelength of 794.4 nm. The lifetime linearly changes with the pump power that is a proxy for ion numbers in the array. Above some critical power, the lifetime remains unchanged as the pump saturates the ions. The y-intercept of the linear fit is ~224 μs. The lifetime data in a and b are taken with the pump power in the saturation region of c. Error bars defined here represent 95% confidence interval.
Figure 4c shows the result of decay time measurement as a function of pump power. As the pump power changes the fraction of ions excited, the lifetime linearly changes with the pump power below the saturation regime51. We discuss these results in more detail below.
Discussion
When emitters are confined to a region much smaller than the wavelength, directional and enhanced emission is expected that is accompanied by the lifetime modification52. Apart from the high atomic densities, low coherence time and small inhomogeneous broadening are required to reach this superradiance regime. In this regime, coherent emission can occur where atoms collectively emit photons with the same phase. As the result, the spontaneous emission rate is modified by the collective enhancement factor, η, which linearly scales with the number of collective excitations. Moreover, the total photon number directionally emitted in the detection mode is expected to scale quadratically with the number of collective excitations. This is accompanied by reduction in the free-space scattering.
In the case of rare-earth ions, high-density implantation gives rise to increased decoherence due to the dipole–dipole dephasing that suppresses the superradiant scattering from local ensembles. Instead, an array of local ensembles commensurate with the oscillation of the intra-cavity E-field collectively behaves as a high-density ensemble enabling observation of superradiance in the extended ensemble, or long-range superradiance. Due to the distribution of ion frequencies (i.e., inhomogeneous broadening), more ions are at the center of the absorption/emission spectrum. Therefore, at the center of the atomic resonance the highest collective effect is expected.
The lifetime shortening can occur due to both the cavity confinement and the collective effect. When the pump is off-resonant from the cavity resonance but still within the ions’ absorption spectrum, the pump can still be coupled to the cavity, and the lifetime shortening due to the collective effect can be observed. When the pump is on both atomic and cavity resonances, both cavity and collective effects contribute to the lifetime shortening. In the absence of the cavity, the interaction drops as 1/d3, for d being the atomic array spacing, while the micro-ring cavity leads to a semi-infinite-range (all-to-all) interactions between the emitters. This happens because all emitters efficiently couple to the same mode in a specific direction rather than a coupling via a free-space photon randomly emitted in all directions.
In the presence of the inhomogeneous broadening, mesoscopic cooperative decay of the symmetric and time-Dicke states52,53,54 can be observed as a simultaneous presence of sub and superradiant modes when all atoms are excited55. In our experiment, the signal-to-noise ratio is not high enough to confirm the slow decay signature of subradiant states after the initial fast decay. Also in arrays, excitation of subradiant states can be harder than the superradiant ones54,56,57 due to the complicated long-range interactions and many-body features of the atomic ensembles. Both inversion and pump-induced correlations between the atoms play a role in driving superradiant states51. At low pump powers, the interaction energy prevents efficient population of subradiant states. Uniform directional pumping along the cavity axis, gives rise to correlations that increase with duration or power of the pump light. Below saturation, we therefore take the pump power to be a proxy for η. In Fig. 4c we vary the pump power and measure the decay time. The results show that below saturation, the emission lifetime linearly decreases with the pump power. The data provide early evidence of cooperative effects of arrays in solids, and further investigation is needed to understand the complicated decay dynamics and the transition from sub- to super-radiance regime.
To theoretically describe the collective effects inside the cavity, we use the effective spin model58 and write an effective Rabi frequency for the nth ion segment in the array as \({{{\Omega }}}_{n}={{{\Omega }}}_{0}^{(n)}+3\pi {{{\Gamma }}}_{0}{\sum }_{m\ne n}{G}_{mn}\langle {\sigma }_{ge}^{(m)}\rangle\), where \({{{\Omega }}}_{0}^{(n)}\) is the Rabi frequency of the pump in the cavity at the ion segment n, \({\sigma }_{ge}^{(m)}\) is coherence between ground and excited states of atomic segment m, Gmn is the Green’s function of the mth ion at nth ion location, and Γ0 is the ion natural decay rate. The second term describes the scattering from all other segments that modify the local field of the nth segment, leading to an effective dipole–dipole interaction. The Green’s function of the ring can be determined as \({G}_{mn}\ =\ i\ \frac{2}{3}\ \frac{{g}_{0}^{2}}{{c}_{p}{{{\Gamma }}}_{0}}\ \exp (ikR| {\theta }_{n}-{\theta }_{m}| )\), where g0 is the single-atom vacuum Rabi frequency, cp is the mode phase velocity, R is the ring radius, and θi is the angular position of ion segment i. This clearly shows the role of the ring in creating an all-to-all infinite-range spin interactions (see Supplementary Note 8 for a detailed discussion).
In the limit of the non-depleted ion, i.e., σee ≈ 0, we can determine the steady-state coherence of the order-array equations of motion to arrive at \({\,{ < }\,\sigma }_{ge} > =-i{g}_{0}\sqrt{2\pi }{E}_{o}/(-i\delta +{{{\Gamma }}}_{0}/2+\frac{2\pi {g}_{0}^{2}}{\kappa }\eta )\). Here, κ is the cavity decay rate and the last term in the denominator is the effective coupling rate enhanced by η, the collective enhancement factor. The ratio of the scattering rate into the cavity mode compared to free space can then be calculated as \({\gamma }_{2}/{\gamma }_{1}=1+\frac{4\pi {g}_{0}^{2}}{\kappa {{{\Gamma }}}_{0}}\eta\), having the signatures of both cavity-enhanced emission via a Purcell effect and the cooperative array effect. Comparing the lifetimes of the Purcell-enhanced disordered array (Fig. 2b) and array-enhanced emission (Fig. 4a), we can estimate an experimental value for the collective enhancement factor η ≃ 1.8. In absence of imperfections such as inhomogeneous broadening, the enhancement factor is equal to the number of collective excitations. In our case, the enhancement factor quantifies the average effect of cooperative emission. The measured value of η > 1 suggests that at least two ions cooperatively emit. To identify the exact number of ions collectively emitting into the detection mode, one needs to measure lifetime for varying implantation density or segment number and perform numerical calculation in a multi-dimensional space7. The result can be improved by operating in the commensurate condition and enhancing the atom number and coherence time by, for example, multi-step implantation and annealing techniques59 and further operating at lower temperatures and higher magnetic fields39. Considering an enhancement of the coherence time at lower temperatures and higher magnetic fields by two orders of magnitude as evidenced previously39 and increasing the cavity Q to about one million (experimentally within reach24,26,29,37), a substantial increase in cooperative effects can be observed where η > 100 can be realized.
To the best of our knowledge, this is the first time the long-range cooperative resonance has been achieved in any solid-state photonic platform. The enhanced directional emission can reduce the noise (spontaneous free-space decay) when the system is used for quantum light storage. Moreover, the collective optical-density increase due to all-to-all infinite-range coupling leads to enhanced absorption, albeit with low densities avoiding density-associated dephasing. Despite the large inhomogeneous broadening of ions in solids compared to the laser trapped atomic arrays60,61, the deterministic ion localization, and significantly larger ion numbers and array lengths make it easier to study many-body and cooperative phenomena. Ideally, in the regime of strong atom–atom interactions dark states32,62,63 and blockade effects64 may emerge leading to a peculiar regime of light–atom interactions on-chip.
Methods
LN micro-ring resonator design and fabrication
The micro-ring resonators are fabricated on a 600 nm thick z-cut LNOI wafer using the same recipe described in our previous article26. The device pattern (bus waveguides, micro-ring resonators) is defined on a hydrogen silsesquioxane (HSQ) e-beam resist film by an electron beam lithography system with the dose of 2000 μC/cm2. Then, the 600 nm LN thin-film is half-etched using an Ar/Cl2/BCl3-based recipe for waveguides and micro-ring resonators. The width of the waveguide is 600 nm, and the waveguide dimension is designed such that the fundamental TE mode is still dominant while minimizing sidewall scattering loss, a significant loss channel of the LN waveguide37. The ring radius used is 50 μm, and the gap between the bus waveguide and the ring resonator is 430 nm, resulting in around 65% bus-ring coupling efficiency. Also, the gap between the ring and the drop-port waveguide is 535 nm, resulting in around 5% waveguide-to-ring coupling. For precision ion implantation, the Ti/Au alignment marks are deposited by the lift-off process. Five nanometer Ti layer is deposited below the 100 nm Au alignment marks as an adhesive layer. At this step, the sample is implanted with Tm2+ ions from Sandia National Laboratories. Finally, for stable light coupling to the waveguide, the remaining LN layer is fully etched with the same LN etching recipe, and the bottom Si layer is deep-etched (~80 μm) by the Bosch process for the fiber-to-chip coupling (U-grooves).
FIB implantation
To verify the collective effects, we use two micro-rings, one hosting an ordered array and one a disordered array of ion segments. The total number of ions and the total number of ion segments for both ordered and disordered samples are the same. Each ion segment has the same number of ions implanted with a fixed ion fluence. Also, both ordered and disordered samples have the same number of ion segments (Ms = 1750). The only difference between the two samples is the segment spacing and its regularity. In the ordered sample, the spacing is fixed and close to λL/2neff while in the disordered array the spacing between ion segments varies randomly around the micro-ring resonator (Supplementary Note 2).
When the spacing between each ion segment is λL/2neff (=184 nm), maximum cooperative interaction is expected. Because of the mismatch between the theoretical and experimental values of neff, the actual spacing between ion segments is 179.5 nm. Although this mismatch results in a lower cooperative effect, it allows us to distinguish the cooperative scattering signal from the Bragg scattering signal (Fig. 3a). As a reference, we also implant a ring resonator with a disordered array (with the same number of segments) where the spacing between ion segments was randomly varied for comparison. We use the focused-ion beam system in the Sandia National Laboratories with a minimum spot size as small as 10 nm for implantation. In our case of Tm2+ implantation, the mass spectrometry was first carried out using an AuSiTm source before the implantation to select a specific isotope and ion using a combination of electric and magnetic fields (Supplementary Note 1). The Tm2+ ions were implanted into rectangular segments of width 37 nm using the energy and fluence of 200 keV and 1 × 1014 ions/cm2, respectively. The obtained ion segments are much smaller than the optical wavelength (~0.8 μm), enabling a point-like approximation of each segment of ions. After the implantation process, post-implantation annealing is performed at 500 ∘C for 8 h under a Nitrogen atmosphere to repair crystal damage caused by the implantation. After the annealing procedure, Tm ions bond with the crystalline matrix and they change such that only Tm3+ ions with the optical transition of interest can create stable bonds.
Experimental setup for the scattering/reflection experiments
For the scattering and reflection experiments, the light around 790 nm is continuously pumped from a Ti:Sapphire laser (M Squared SolsTiS). The light is then split by a beam sampler with a ratio of 90% and 10%. The strong pump light (90%) is then injected to the drop-port of the micro-resonator using a lensed fiber. The scattering signal from the ions is then collected from the bus-waveguide on the other side of the micro-ring and measured using a Femto-watt detector or a single-photon detector (for PL lifetime measurements). The output scattering signal from ion arrays is normalized to the intensity of the other split-input light path (10%) (Supplementary Note 3).
Data availability
The results presented in this paper are available from the corresponding author upon reasonable request.
References
Sipahigil, A. et al. An integrated diamond nanophotonics platform for quantum-optical networks. Science 354, 847–850 (2016).
Asenjo-Garcia, A., Moreno-Cardoner, M., Albrecht, A., Kimble, H. & Chang, D. E. Exponential improvement in photon storage fidelities using subradiance and “selective radiance” in atomic arrays. Phys. Rev. X 7, 031024 (2017).
Nandi, A. et al. Controlling light emission by engineering atomic geometries in silicon photonics. Opt. Lett. 45, 1631–1634 (2020).
Chang, D. E., Jiang, L., Gorshkov, A. & Kimble, H. Cavity QED with atomic mirrors. N. J. Phys. 14, 063003 (2012).
Masson, S. J. & Asenjo-Garcia, A. Atomic-waveguide quantum electrodynamics. Phys. Rev. Res. 2, 043213 (2020).
Norcia, M. A., Winchester, M. N., Cline, J. R. & Thompson, J. K. Superradiance on the millihertz linewidth strontium clock transition. Sci. Adv. 2, e1601231 (2016).
Bradac, C. et al. Room-temperature spontaneous superradiance from single diamond nanocrystals. Nat. Commun. 8, 1–6 (2017).
Scheibner, M. et al. Superradiance of quantum dots. Nat. Phys. 3, 106–110 (2007).
Macfarlane, R., Meltzer, R. & Malkin, B. Optical measurement of the isotope shifts and hyperfine and superhyperfine interactions of nd in the solid state. Phys. Rev. B 58, 5692 (1998).
Thiel, C., Böttger, T. & Cone, R. Rare-earth-doped materials for applications in quantum information storage and signal processing. J. Lumin. 131, 353–361 (2011).
Ahlefeldt, R., Hush, M. R. & Sellars, M. Ultranarrow optical inhomogeneous linewidth in a stoichiometric rare-earth crystal. Phys. Rev. Lett. 117, 250504 (2016).
Rančić, M., Hedges, M. P., Ahlefeldt, R. L. & Sellars, M. J. Coherence time of over a second in a telecom-compatible quantum memory storage material. Nat. Phys. 14, 50–54 (2018).
Zhong, T. et al. Nanophotonic rare-earth quantum memory with optically controlled retrieval. Science 357, 1392–1395 (2017).
Hedges, M. P., Longdell, J. J., Li, Y. & Sellars, M. J. Efficient quantum memory for light. Nature 465, 1052–1056 (2010).
Saglamyurek, E. et al. Broadband waveguide quantum memory for entangled photons. Nature 469, 512–515 (2011).
Ortu, A. et al. Simultaneous coherence enhancement of optical and microwave transitions in solid-state electronic spins. Nat. Mater. 17, 671–675 (2018).
Bartholomew, J. G. et al. On-chip coherent microwave-to-optical transduction mediated by ytterbium in YVO4. Nat. Commun. 11, 1–6 (2020).
Zhong, M. et al. Optically addressable nuclear spins in a solid with a six-hour coherence time. Nature 517, 177–180 (2015).
Raha, M. et al. Optical quantum nondemolition measurement of a single rare earth ion qubit. Nat. Commun. 11, 1–6 (2020).
Chen, S., Raha, M., Phenicie, C. M., Ourari, S. & Thompson, J. D. Parallel single-shot measurement and coherent control of solid-state spins below the diffraction limit. Science 370, 592–595 (2020).
Weiss, L., Gritsch, A., Merkel, B. & Reiserer, A. Erbium dopants in nanophotonic silicon waveguides. Optica 8, 40–41 (2021).
Gritsch, A., Weiss, L., Früh, J., Rinner, S. & Reiserer, A. Narrow optical transitions in erbium-implanted silicon waveguides. arXiv https://doi.org/10.48550/arXiv.2108.05120 (2021).
Phenicie, C. M. et al. Narrow optical line widths in erbium implanted in tio2. Nano Lett. 19, 8928–8933 (2019).
Wang, S. et al. Incorporation of erbium ions into thin-film lithium niobate integrated photonics. Appl. Phys. Lett. 116, 151103 (2020).
Dutta, S., Goldschmidt, E. A., Barik, S., Saha, U. & Waks, E. Integrated photonic platform for rare-earth ions in thin film lithium niobate. Nano Lett. 20, 741–747 (2019).
Pak, D. et al. Ytterbium-implanted photonic resonators based on thin-film lithium niobate. J. Appl. Phys. 128, 084302 (2020).
Guo, X. et al. Parametric down-conversion photon-pair source on a nanophotonic chip. Light. Sci. Appl. 6, e16249–e16249 (2017).
Wang, C. et al. Integrated lithium niobate electro-optic modulators operating at CMOS-compatible voltages. Nature 562, 101–104 (2018).
Chen, J.-Y. et al. Ultra-efficient frequency conversion in quasi-phase-matched lithium niobate microrings. Optica 6, 1244–1245 (2019).
Furuya, K., Nandi, A. & Hosseini, M. Study of atomic geometry and its effect on photon generation and storage. Optical Mater. Express 10, 577–587 (2020).
Böttger, T., Thiel, C., Sun, Y. & Cone, R. Optical decoherence and spectral diffusion at 1.5 μm in ERR3+:Y2SIO5 versus magnetic field, temperature, and Er3+ concentration. Phys. Rev. B 73, 075101 (2006).
Ferioli, G., Glicenstein, A., Henriet, L., Ferrier-Barbut, I. & Browaeys, A. Storage and release of subradiant excitations in a dense atomic cloud. Phys. Rev. X 11, 021031 (2021).
Pant, M. et al. Routing entanglement in the quantum internet. npj Quantum Inf. 5, 1–9 (2019).
Wehner, S., Elkouss, D. & Hanson, R. Quantum internet: a vision for the road ahead. Science https://doi.org/10.1126/science.aam9288 (2018).
Zhu, D. et al. Integrated photonics on thin-film lithium niobate. Adv. Opt. Photonics 13, 242–352 (2021).
Boes, A., Corcoran, B., Chang, L., Bowers, J. & Mitchell, A. Status and potential of lithium niobate on insulator (LNOI) for photonic integrated circuits. Laser Photonics Rev. 12, 1700256 (2018).
Zhang, M., Wang, C., Cheng, R., Shams-Ansari, A. & Lončar, M. Monolithic ultra-high-q lithium niobate microring resonator. Optica 4, 1536–1537 (2017).
Luke, K. et al. Wafer-scale low-loss lithium niobate photonic integrated circuits. Opt. Exp. 28, 24452–24458 (2020).
Sinclair, N. et al. Optical coherence and energy-level properties of a tm 3+-doped li nb o 3 waveguide at sub kelvin temperatures. Phys. Rev. B 103, 134105 (2021).
Slama, S., Von Cube, C., Kohler, M., Zimmermann, C. & Courteille, P. W. Multiple reflections and diffuse scattering in Bragg scattering at optical lattices. Phys. Rev. A 73, 023424 (2006).
Ding, D. et al. Multidimensional Purcell effect in an ytterbium-doped ring resonator. Nat. Photonics 10, 385–388 (2016).
Genov, D., Oulton, R., Bartal, G. & Zhang, X. Anomalous spectral scaling of light emission rates in low-dimensional metallic nanostructures. Phys. Rev. B 83, 245312 (2011).
Gong, Y. et al. Linewidth narrowing and Purcell enhancement in photonic crystal cavities on an Er-doped silicon nitride platform. Opt. Exp. 18, 2601–2612 (2010).
Sun, Y., Thiel, C. & Cone, R. Optical decoherence and energy level structure of 0.1% tm 3+: Linbo 3. Phys. Rev. B 85, 165106 (2012).
Thiel, C., Sun, Y., Böttger, T., Babbitt, W. & Cone, R. Optical decoherence and persistent spectral hole burning in tm3+: Linbo3. J. Lumin. 130, 1598–1602 (2010).
Jiang, X., Pak, D., Nandi, A., Xuan, Y. & Hosseini, M. Rare earth-implanted lithium niobate: properties and on-chip integration. Appl. Phys. Lett. 115, 071104 (2019).
Kustov, E., Loschenov, V. & Basieva, I. Decay times of radiative and non-radiative transitions in rare-earth ions. Phys. Scr. 2014, 014032 (2014).
Weber, M. Radiative and multiphonon relaxation of rare-earth ions in Y2O3. Phys. Rev. 171, 283 (1968).
Li, S., Cai, L., Wang, Y., Jiang, Y. & Hu, H. Waveguides consisting of single-crystal lithium niobate thin film and oxidized titanium stripe. Opt. Exp. 23, 24212–24219 (2015).
Sumida, D. & Fan, T. Effect of radiation trapping on fluorescence lifetime and emission cross section measurements in solid-state laser media. Opt. Lett. 19, 1343–1345 (1994).
Glicenstein, A., Ferioli, G., Browaeys, A. & Ferrier-Barbut, I. From superradiance to subradiance: exploring the many-body Dicke ladder. Optica 47, 1541–1544 (2022).
Dicke, R. H. Coherence in spontaneous radiation processes. Phys. Rev. 93, 99 (1954).
Czarnik, J. W. & Fontana, P. R. Resonance radiation from interacting atoms. J. Chem. Phys. 50, 4071–4074 (1969).
Zhang, Y.-X. & Mølmer, K. Theory of subradiant states of a one-dimensional two-level atom chain. Phys. Rev. Lett. 122, 203605 (2019).
Shahbazyan, T., Raikh, M. & Vardeny, Z. Mesoscopic cooperative emission from a disordered system. Phys. Rev. B 61, 13266 (2000).
Solano, P., Barberis-Blostein, P., Fatemi, F. K., Orozco, L. A. & Rolston, S. L. Super-radiance reveals infinite-range dipole interactions through a nanofiber. Nat. Commun. 8, 1–7 (2017).
Reitz, M., Sommer, C. & Genes, C. Cooperative quantum phenomena in light-matter platforms. PRX Quantum 3, 010201 (2022).
Henriet, L., Douglas, J. S., Chang, D. E. & Albrecht, A. Critical open-system dynamics in a one-dimensional optical-lattice clock. Phys. Rev. A 99, 023802 (2019).
Rose, B. C. et al. Observation of an environmentally insensitive solid-state spin defect in diamond. Science 361, 60–63 (2018).
Sørensen, H. et al. Coherent backscattering of light off one-dimensional atomic strings. Phys. Rev. Lett. 117, 133604 (2016).
Corzo, N. V. et al. Large Bragg reflection from one-dimensional chains of trapped atoms near a nanoscale waveguide. Phys. Rev. Lett. 117, 133603 (2016).
Albrecht, A. et al. Subradiant states of quantum bits coupled to a one-dimensional waveguide. N. J. Phys. 21, 025003 (2019).
Zhong, J. et al. Photon-mediated localization in two-level qubit arrays. Phys. Rev. Lett. 124, 093604 (2020).
Ke, Y., Poshakinskiy, A. V., Lee, C., Kivshar, Y. S. & Poddubny, A. N. Inelastic scattering of photon pairs in qubit arrays with subradiant states. Phys. Rev. Lett. 123, 253601 (2019).
Acknowledgements
M.H. acknowledges support from National Science Foundation, Award No. 2101928-ECCS. H.A. acknowledges the support from Purdue University Start-up fund. The implantation in this work was performed at the Center for Integrated Nanotechnologies, an Office of Science User Facility operated for the U.S. Department of Energy (DOE) Office of Science. Sandia National Laboratories is a multimission laboratory managed and operated by National Technology & Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International, Inc., for the U.S. DOE’s National Nuclear Security Administration under contract DE-NA-0003525. The views expressed in the article do not necessarily represent the views of the U.S. DOE or the United States Government.
Author information
Authors and Affiliations
Contributions
D.P., A.N., and M.H. conceived the experiments. D.P. performed the simulations and fabricated the devices. M.T. and E.S.B. performed FIB implantation. D.P. and A.N. built the measurement setups. D.P. performed the measurements and analyzed the data. H.A. derived the theory of collective coherence of ions in periodic arrays. D.P. and M.H. wrote the manuscript with inputs from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pak, D., Nandi, A., Titze, M. et al. Long-range cooperative resonances in rare-earth ion arrays inside photonic resonators. Commun Phys 5, 89 (2022). https://doi.org/10.1038/s42005-022-00871-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-00871-w
This article is cited by
-
Cavity-enhanced narrowband spectral filters using rare-earth ions doped in thin-film lithium niobate
npj Nanophotonics (2024)
-
Phonon-mediated temperature dependence of Er3+ optical transitions in Er2O3
Communications Physics (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.