Abstract
Quantum networks allow us to harness networked quantum technologies and to develop a quantum internet. But how robust is a quantum network when its links and nodes start failing? We show that quantum complex networks based on typical noisy quantum-repeater nodes are prone to discontinuous phase transitions with respect to the random loss of operating links and nodes, abruptly compromising the connectivity of the network, and thus significantly limiting the reach of its operation. Furthermore, we determine the critical quantum-repeater efficiency necessary to avoid this catastrophic loss of connectivity as a function of the network topology, the network size, and the distribution of entanglement in the network. From all the network topologies tested, a scale-free network topology shows the best promise for a robust large-scale quantum internet.
Similar content being viewed by others
Introduction
Quantum networks are a paradigm of networks where the links and nodes obey the laws of quantum physics1,2,3. Namely, the quantum links can be quantum correlations4, quantum couplings or dynamics5,6, or even quantum causal relations7. Quantum nodes can be any system with quantum degrees of freedom. The nascent field of complex quantum networks4,8,9,10,11,12,13,14,15,16 is motivated both by the fundamental interest in understanding the nature and the properties of this object, as well as by the applied perspective of developing networked quantum technologies to fully harness their potential and their reach. The latter could be named for quantum-secure communications17,18, quantum-accelerated computation19,20,21, quantum-enhanced sensing and metrology22,23,24, and the development of a future quantum Internet1. However, quantum systems and states are vulnerable to noise in general. But how does this translate to the network realm, i.e., how robust are noisy quantum networks, and how is that robustness affected by the underlying graph? And how does it compare to the robustness of classical networks, which typically evolve, to non-trivial network topologies25,26,27, such as scale-free properties, topologies that are known to maintain their functionality against random failures28,29?
Networks are a set of nodes and links, where each link connects a pair of nodes. This naturally includes complex networks25,30 such as the current classical Internet31, a snapshot of which is presented in Fig. 1a. With the goal of investigating a quantum Internet, we consider quantum networks where the links correspond to entangled pairs of qubits, each lying in a different node. Now, imagine we want to realize a quantum operation, e.g., computing, communication, or metrology, between two distant nodes of a quantum network: how can they establish entanglement between them, with a certain target fidelity Ftarget, given the existing quantum correlations in the quantum network?
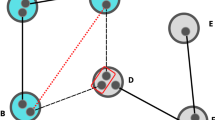
Depicted in a is a snapshot of the structure of Internet (at the level of autonomous systems using the dataset from31) clearly showing the scale-free properties of this complex network. This snapshot could in principle belong to a future quantum internet1, 48 which will, however, operate on different network principles. These differences can be seen even at the small scale. In b a small scale quantum-repeater network is shown, indicating how the connected components can intersect each other, in stark contrast to what is observed in a classical network. Here each node is represented by a black dot and the links by black lines. nij represents the number of entangled pairs associated with each link eij, which is chosen for this illustration to scale as r(l) = l. Two nodes vi and vj are connected at a distance l if there is a path between them such that for all links in that path satisfy the condition nij ≥ l, with l being the distance between node i and j. In c, d different connected components are displayed by blue green and red circle. c Illustrates a quantum network where one can only connect two nodes if nij ≥ l. The connected components clearly intersect each other. In contrast d illustrates a classical network where links can only be used to connect two nodes if nij ≥ 3. In this case the connected components do not intersect each other.
In our work, we consider an entanglement distribution network based on noisy quantum-repeater nodes, corresponding to the currently envisaged implementation of realistic long-distance quantum networks, distinctly from noiseless, pure-state, quantum networks4,12, and from networks based on quantum channels' upper-bound capacities9,10,11,12,14,15,16. Let us consider the general scenario where there are Nij noisy Bell pairs with fidelity Finitial connecting nodes vi and vj. If necessary, these noisy Bell pairs can be purified to yield nij = Nij/Nft pairs exceeding a given target fidelity Ftarget (where Nft is the number of initial pairs necessary to generate one Ftarget pair)32. Next, entanglement swapping between link vi and vj and link vj and vk consumes those Bell pairs to create a longer-range entangled pair between nodes vi and vk with fidelity \( {F}_{{{{{{{{\rm{target}}}}}}}}}^{2}\)33. That drop in fidelity means multiple pairs need to be available for entanglement purification to return the target fidelity Ftarget (again consuming more pairs). These entanglement swapping and purification operations continue at longer distances until we have connected the nodes/users who want to communicate in the network34. A critical question that arises is the resource consumption in such an approach. Fortunately, it is well known that resources required for the first-generation quantum-repeater network scale polynomially with the number of links l needed to connect the source node Alice and Bob35. To the leading order in this polynomial, we can define35,
as being the number of entangled qubit pairs in the entire chain necessary to create the connected entangled qubit pair with the desired fidelity Ftarget, and r(l) = lα is the number of entangled qubit pairs necessary to create the connected entangled qubit pair with the desired fidelity Ftarget per link. Above α represents the efficiency of the protocol which of course depends heavily on the experimental apparatus used for the repeater scheme and the noise present in it but values in the range [1, 2] are not uncommon (see Supplementary Note 1, Figs. S1 and S2 for further details).
In this work we will show that large-scale quantum networks based on noisy quantum-repeater nodes connected by noisy channels are prone to discontinuous phase transitions and that such transitions can be suppressed if the efficiency of the quantum-repeater protocol is above a certain threshold.
Results
The exploration of the connectivity of a quantum-repeater network requires the introduction of two types of connection between nodes, which we are going to call functional and structural connectivity. Functional connectivity in the quantum regime is the situation where a connection between the two nodes can be established with the required fidelity Ftarget. Structural connectivity on the other hand refers to the situation where a connection can be made since there is a path connecting the two nodes, but not necessary with fidelity Ftarget. We will illustrate these two concepts in Fig. 1b, c, d where the nodes v1 and v3 (and v3 and v5) can individually establish connections with sufficient fidelity Ftarget (functionally connected), but v1 and v5, while connected, can not (structurally connected). This means v1 does not belong to the same “functionally” connected component as v5 making it impossible to establish a connection between them with the required fidelity.
Standard Bernoulli percolation, a widely used technique to explore the robustness of classical networks25,36, can not be used in these quantum scenarios due to the quality of service Ftarget requirement (except in the limit α = 0). Although in Bernoulli-percolation theory, finding the largest connected component of a network is a computationally easy problem to solve25, finding the largest functional component of these networks is an NP-hard problem and can be related to the maximum clique-problem37 (see supplementary Note 2 for details). Our model is more manageable if one considers the case where all links operate with the same amount of purification and therefore using the same number of entangled qubit pairs in each link, nop. Let us call this quantity the operational number of entangled qubit pairs. The operational number of entangled qubit pairs is a free variable that one can tune in order to maximize network connectivity. It is also associated with an operational distance \({l}^{{{{{{{{\rm{op}}}}}}}}}={\left({n}^{{{{{{{{\rm{op}}}}}}}}}\right)}^{1/\alpha }\), meaning each link can be functionally used in paths of length lop or less.
Our concept of a quantum functional connection naturally suggests that we should choose the operational number of entangled qubit pairs nop as large as possible in order to increase the operational distance lop and therefore allow for nodes further away from each other to distribute Bell pairs with our required fidelity Ftarget. However, increasing the operational number of entangled qubit pairs reduces the probability of a given link having the required number of entangled pairs. Thus there is an important trade-off to consider. If the number of pairs distributed between nodes can be expressed as a function g(n), then the probability that a given link has the required operational number of entangled qubit pairs or more is given by,
which indicates that for nop larger than a certain value, most links are removed from the network and there is no giant component. Instead one needs to find the smallest value of nop, such that the operational distance is larger or equal to the diameter of the network d, (lop ≤ d). The diameter of the network is defined as the largest distance between any two nodes in the connected component25, therefore any two nodes (associated with the connected component) are able to establish a functional connection (see Fig. 2). This set of nodes is termed the backbone and serves two purposes, first, it can be used as a measure of the connectivity of the network, and second for large networks, they will behave similarly to classical communication networks. Routing developed for classical networks38,39 should be sufficient (although not necessarily optimal) to find a good path to connect two nodes with fidelity Ftarget. In such a situation our method guarantees the existence of at least one path connecting any two nodes in the backbone, but given the possible existence of several paths connecting two nodes, if the backbone is large, one could also use a multi-path routing approach to generate multiple entangled qubit pairs between them, using different routes, a strategy already proposed in relation to quantum networks9,10.
Illustration of how the quantum backbone can be computed where the numbers written in each link represents the number of entangled pairs contained in it. We begin in a with a D = 3 network and the operational distance lop = 0 meaning none of the links in the network need to be removed. As the operational distance lop is increased from 1b to 2c we see that we have removed links with nij < 2. Further in c we notice that the distance of the network increases from D = 3 to D = 4 due to the v5–v6 link being removed in b due to lack of resources. Then in d, e we continue to remove various links until we reach an operational distance that is largest than the diameter of the network. We are now left in e where the largest connected network component, termed our quantum backbone. Finally in f we superimpose this quantum backbone (shown in red) onto the entire network. The size of the backbone (number of nodes in the largest connected component of the backbone) is the number of red nodes nodes in f, namely 6.
One should vary the operational distances lop for any change in the network (like the removal of nodes and links) in order to maximize the size of the backbone. One wants to establish the repeater network with just enough resources to reach the diameter of the largest connected network component (lop = d ideally), but the question arises how the diameter of the network d and the operational distance lop change when now one considers that links can fail randomly with pext. The diameter of the network will depend on the probability that a link both has sufficient pairs to create our link (pop) and that there has not been any random failure in that link is given pext. The total probability that a link is both operational and not removed is therefore p = poppext, and for a given network one can write the diameter as \(\,{{\mbox{d}}}\,\left({p}^{{{{{{{{\rm{op}}}}}}}}}{p}^{{{{{{{{\rm{ext}}}}}}}}}\right)\). The operational distance on the other hand can be written solely as a function of the operational portability pop by inverting Eq. (2). This leads us to the equation,
At this point \({p}_{0}^{{{{{{{{\rm{op}}}}}}}}}\) we have the minimal number of resources required to reach the diameter of the network’s largest connected component. After we find \({p}_{0}^{{{{{{{{\rm{op}}}}}}}}}\), the size of the backbone can be easily computed as the number of nodes in the largest connected component of the network composed of only links with sufficient pairs to create the link, and the link was not removed due to random failures. In the example of Fig. 2, since there are no random failures the size of the backbone is 6. Adding random failures just means that we are starting with a network with some of the links already removed. Our approach is slightly simplistic in that we have only considered links (loss of nodes can also be incorporated). We are now at the stage where we can explore actual networks.
Quantum Erdős-Rényi networks
There are of course many well-known network models we could examine with the Erdős-Rényi model network probably being the simplest25,40. In the Erdős-Rényi model, N nodes are randomly connected to each other using L = cN/2 links, where c is the average number of links incident to each node. This model has been well explored in complex network theory25,40 and as such, it is a good starting point, especially as one can compute l(pop) and D(poppext) analytically41 when the number of nodes N → ∞ (asymptotic limit). Considering only bond percolation (loss of links) we show in Fig. 3 that the quantum backbone for a large Erdős-Rényi network is prone to an abrupt phase transition. We observe that the size of the quantum backbone actually drops abruptly as the probability of links not failing pext drops between a critical probability \({p}_{c}^{{{{{{{{\rm{ext}}}}}}}}}\). As it is usual in a first-order phase transition we observe hysteresis, therefore the critical probability \({p}_{c}^{{{{{{{{\rm{ext}}}}}}}}}\) is not well defined and the phase transition might occur in a range of probabilities between \({p}_{c1}^{{{{{{{{\rm{ext}}}}}}}}} \; < \; {p}^{{{{{{{{\rm{ext}}}}}}}}} \; < \; {p}_{c2}^{{{{{{{{\rm{ext}}}}}}}}}\), with \({p}_{{{{{{{{\rm{c1}}}}}}}}}^{{{{{{{{\rm{op}}}}}}}}},({p}_{{{{{{{{\rm{c2}}}}}}}}}^{{{{{{{{\rm{op}}}}}}}}})\) corresponding to the largest, (smallest) probability of links not failing where the phase transition might occur. This hysteresis region whose span grows with the size of the network is shown in Fig. 4 (see Supplementary Note 3 for the analytical calculations). We observe that, when the average number of entangled pairs in each link of the network is larger than a critical number of qubit pairs nc, the traditional percolation phase transition is recovered as shown in Fig. 4 (Supplementary Note 4 for details). The critical number of qubit pairs nc increases quickly with the size of the network (see Supplementary Note 4 for details). It is useful to mention that we have used α = 1 as a conservative value (see Supplementary Note 1). As α increases the average number of qubit pairs necessary to avoid the discontinuous phase transition will also increase.
Exploration of bond percolation on a quantum Erdős-Rényi network (ER) with average degree c = 6 where the number of entangled pairs in each link follows an exponential distribution with mean number 〈n〉. We plot the operational distance lop and the network diameter d versus the probability that links are both operational and not removed p = poppext, for \(\langle n\rangle ={\left(15\ln N\right)}^{\alpha }\) with α = 1 in a and \(\langle n\rangle ={\left(15\ln N\right)}^{\alpha }\) with α = 2 in b, respectively. The large colored dots indicate their intersection. Here the operational distance lop and network diameter d are scaled by \(\ln N\) for ease of comparison. Labelled are the curves lop(pop) for \({p}^{{{{{{{{\rm{ext}}}}}}}}}={p}_{{{{{{{{\rm{c1}}}}}}}}}^{{{{{{{{\rm{ext}}}}}}}}}\) (\({p}_{{{{{{{{\rm{c2}}}}}}}}}^{{{{{{{{\rm{ext}}}}}}}}}\)) which correspond to the smallest (largest) value of p indicating a stable lop(pop) = D(poppext) solution in the subcritical regime. Further the classical percolation critical probability pc gives the point where the networks breaks completely apart to become structurally disconnected meaning there is no giant set of nodes that can connect to each other with any fidelity. We generated one Erdős-Rényi network for each value of N, then dop(p) was determined by removing each link of the network with probability 1 − p. dop(p) was computed based on 100 runs for each value of p. The intersection between the two nodes at p0, is marked by blue dots for solutions in the supercritcal regime, and red dots for solutions in the subcritical regime. Next the size of the backbone (number of nodes in the backbone) is plotted as a function of in b for α = 1. intersection point found in a, b) there is a corresponding size in c, d. Finally the size of the backbone is plotted as a function of the probability that links are not removed pext in e, f for α = 1, 2. The functionally connected regime is represented as the blue region while the functionally subcritical regime is shown as the light red region. The blue/red stripped area represents the region where both the functionally connected and subcritical regimes are stable. The dark red region on the other hand represents the structurally disconnected regime for a network of size N = 105. Shaded region around each curve represents the standard deviation of the same.
Depicted are phase diagrams of \(\langle n\rangle /\ln N\) versus the probability that a link is not removed pext for a quantum Erdős-Rényi network network comprised of N = 104 (a), 105 (b), and 106 (c) nodes, respectively, with c = 6 average degree and α = 1. Here we assume the number of entangled pairs in each link follows an exponential distribution with mean 〈n〉. The functionally supercritcal regime is represented as the blue region while the functionally subcritical regime is the light red region. Further the stripped (blue/light red) area represents the region where both the functionally connected and subcritical regime are stable. The dark red region represents the structurally disconnected regime. Next the classical percolation critical probability pc is the point where the networks breaks completely apart, meaning there is no giant set of nodes that can connect to each other with any fidelity. Also shown are the critical mean resource number \({n}_{c}/\ln N\) for which the discontinuous phase transition is avoided.
Quantum scale-free networks
These observations lead to a natural question about how general our results are—especially in terms of the network model. As such it is useful to explore the scale-free Barabási-Albert quantum network whose classical counterpart is known to be more robust than the Erdős-Rényi25,42,43. In scale-free networks, the degree distribution follows a power law at least asymptotically. This promotes the existence of hub nodes with a degree much larger that the average one (see Fig. 1a for an example). Such distribution is observed in a diverse types of real-world networks27. The Barabási-Albert model44 is a simple example that allows us to generate and explore scale-free networks, based on the preferential attachment principle. This means that when links are added to the network they disproportionately connect to nodes with higher degrees27. In Fig. 5(a, b) we plot the operational distance lop(pop) and the diameter of connected component D(poppext) versus the probability a link is operational and not removed p = poppext for various network sizes N. Our results for the Barabási-Albert network show that we are in the supercritical regime for much lower values of pext, which highlights its ability to distribute entanglement even when a large number of links fail. This is to be expected, the Barabási-Albert network, and other scale-free networks, are known to be more robust than an Erdős-Rényi network43,44. More importantly in Fig. 5c we observe no discontinuous phase transition in the N = 103–105 region (unlike what occurred in the Erdős-Rényi situation Fig. 3, and therefore there is only one critical probability of links not failing \({p}_{{{{{{{{\rm{c1}}}}}}}}}^{{{{{{{{\rm{ext}}}}}}}}}={p}_{{{{{{{{\rm{c2}}}}}}}}}^{{{{{{{{\rm{ext}}}}}}}}}={p}_{c}^{{{{{{{{\rm{ext}}}}}}}}}\). This is exemplified in Fig. 5d by the absence of a region where both the subcritical and supercritical are stable solutions of Eq. (3). In fact, one can show that there is always a critical quantum-repeater efficiency αc such that for an efficiency large than the critical one α < αc the discontinuous phase transition is suppressed (our network used in Fig. 5a, b, c, d has αc > 1). It is useful to explore this αc parameter in a little more detail. When our resources are exponentially distributed, it is straightforward to show (supplementary Note 4 for details) that αc is given by
which establishes the existence of a sufficient repeater efficiency so that most of the classical behavior is recovered. Despite the suppression of the discontinuous phase transition for α < αc there are still a few differences between the various quantum cases. Unlike what one expects for a typical Barabási-Albert network 25,43 the point at each of the networks breaks apart, does not change significantly with the network size. To understand this, it is useful to look at the relation between \({p}_{c}^{{{{{{{{\rm{ext}}}}}}}}}\) and the classical percolation critical probability pc (which for the usual Barabási-Albert network tends to zero as N increases). When our resources are exponentially distributed, \({p}_{c}^{{{{{{{{\rm{ext}}}}}}}}}\) (or \({p}_{c2}^{{{{{{{{\rm{ext}}}}}}}}}\) for a discontinuous phase transition) is related to the classical percolation critical value pc by, (see Supplementary Note 5 and Fig. S3. for details)
with \({D}_{\max }\) being the critical network diameter, defined as the diameter of the network at the classical phase transition point \({D}_{\max }\mathop{=}\limits^{{{{{{{{\rm{def}}}}}}}}}D({p}_{c})\). This provides quite an interesting insight into this apparent change of behavior. It is well known that the classical percolation critical value pc tends to zero with the network size for the Barabási-Albert network43, but so does \({D}_{\max }\) (this is what prevents the suppression of the phase transition). This means that the decrease of \({p}_{c({c}_{2})}^{{{{{{{{\rm{ext}}}}}}}}}\) can be mitigated by increasing the average degree of the network \(\left\langle n\right\rangle\) proportionally with the critical network diameter to the power of α, \({({D}_{\max })}^{\alpha }\).
Exploration of bond percolation on a quantum Barabási-Albert network with N nodes and average degree c = 6 where the number of entangled pairs in each link follow an exponential distribution with mean 〈n〉. We simulated the the Bollobás variant of the Barabási-Albert model49 where we generated one Barabási-Albert network for each value of N. The diameter of the network D(p) was then determined by removing link from the network with probability 1 − pext, based on 100 runs for each value of p. We plot the operational distance lop(pop) and the network diameter D(p) versus the probability that links are both operational and not removed p = poppext for \(\langle n\rangle ={(10\ln (N))}^{\alpha }\) with α = 1 in a with the large colored dots indicating their intersection. Labelled are the curves Labelled are the curves lop(pop) for \({p}^{{{{{{{{\rm{ext}}}}}}}}}={p}_{{{{{{{{\rm{c}}}}}}}}}^{{{{{{{{\rm{ext}}}}}}}}}\) which correspond to the smallest value of p indicating a stable lop(pop) = D(poppext) solution. The intersection between two nodes at p0, is marked by blue dots for solutions in the supercritical regime, and red dots in the subcritical regime. Next the size of the backbone (number of nodes in the backbone) is plotted as a function of p in b. For each intersection point found in a there is a corresponding size in b. In c the size of the backbone is plotted as a function of the probability that links are not removed pext. The functionally supercritical regime is represented as the blue region while the functionally subcritical regime is shown as the light red region. The dark red region on the other hand represents the structural subcritical region for a network of size N = 105. We immediately observe that no discontinuous phase transition is seen (unlike in the Erdős-Rényi case). Finally in d we depict the phase diagrams of \(\langle n\rangle /\ln N\) versus y for N = 105 nodes including the curves for the critical probabilities \({p}_{c}^{{{{{{{{\rm{ext}}}}}}}}}\) and pc. Shaded region around each curve represents the standard deviation of the same.
Measuring the robustness of complex networks
Our exploration of the Erdős-Rényi and scale-free Bollobás quantum networks has highlighted how the topology of those networks plays a significant role in its robustness, meaning the ability to distribute entanglement in the presence of link failures, but how? We need to quantify this behavior using three important characterization parameters. The first two parameters are related to how many links need to be removed before the network breaks apart while the third is associated with the efficiency of the repeater protocol. These three parameters can be determined for both the Erdős-Rényi network and Barabási-Albert networks. It is also useful to determine these parameters for geometric networks. In a geometric network, nodes are distributed across a geometric space, and nodes that are closer are more likely to be connected than nodes further apart. This type of model is very natural in quantum communication networks, given the fact that direct quantum links spanning large distances are difficult to generate. We consider two types of geometric networks, geometric graphs45, where only nodes that are closer than a certain radius are connected to each other, and the Waxman model where the probability pij that two nodes connect to each other decays exponentially with the distance46 as \({p}_{ij}=\beta {e}^{-\frac{{r}_{ij}}{R}}\), with rij being the distance between node i and j, and R the average connection distance, and in our work we considered β = 1. Although we can describe these networks as a function of the number of nodes and links, for the geometric networks these parameters are associated with physical dimensions45. To give an example, a random geometric graph with a connecting radius of 266 km, an average degree c = 6, and a total number of 103 nodes correspond to a network spanning a physical distance on the order of 103 km. This conversion is explained in detail in supplementary Note 4 and displayed on the top axis of Fig. 6. With these four network topologies in mind—Erdős-Rényi, Barabási-Albert, geometric random graphs and Waxman model—we plot in Fig. 6 the classical percolation critical probability pc, \({D}_{\max }\), and αc versus N, for values of average degree c = 6, 8, 10. Our plots clearly show that scale-free networks are more robust according to all three parameters, that it is the only network that for the selected parameters is able to avoid the discontinuous phase transition for α > 1 with N > 103. The reasons for this are as follows. The classical percolation critical probability pc is the typical measure of the robustness of a network in the Bernoulli-percolation model. Scale-free networks are known to be extremely robust against random failures in the Bernoulli-percolation model as the hubs keep the network connected even when a large fraction of links are missing27. In contrast, the geometric random graphs seem to be the less robust networks according to this parameter. The lack of links connecting distant parts of the network hinders their robustness against random failures. Erdős-Rényi and scale-free networks are both small-world networks, meaning the distances between nodes in these networks grow with the logarithm of the number of nodes, and scale-free networks are something called ultrasmall networks because their network distances tend to be even lower27. On the other hand, geometric network models tend not to be small-world45. As expected the critical distance \({D}_{\max }\) is lower for the scale-free network and largest for the geometric networks. Scale-free networks are also more robust than other networks in terms of the critical quantum-repeater efficiency αc. This can be explained by the fact that αc depends on how the diameter of the network changes when links are removed from the network, Eq. (5). It can be seen from Fig. 3, and Fig. 4 that the diameter of the scale-free network grows considerably slower than that of an Erdős-Rényi network, explaining why this is the case. The diameters of the Waxman and geometric random graphs show similar behavior to the Erdős-Rényi network when nodes are removed. Quantum networks based on capacity channel upper-bounds15,16, can be seen as a special case of our model when the quantum-repeater efficiency is set to α = 0, a regime in which classical percolation tools can be used, and therefore there are no discontinuous phase transitions. Our results show the importance that the quantum-repeater protocol efficiency plays in a quantum internet, and the importance of choosing the right network topology to mitigate such effects. It is possible, however, to recover the classical behaviors for quantum networks with any topology and sizes for quantum repeaters that operate with α = 0. Realistically, it is unlikely that the first generations of quantum-repeaters networks will be close to that regime, especially when local gate inefficiencies are included. Our results provided a lower, and therefore more practical, threshold for the quantum efficiency required for the construction of a robust network.
There is one more important consideration we must address here in terms of the generality of our results. This relates to our choice of an exponential resource distribution used throughout the paper. The exponential resource distribution was primarily chosen for the ease of our calculations. Other distributions, uniform, for instance, show similar network behavior and our conclusion about the robustness of the Barabási-Albert networks remains unchanged (see Supplementary Note 4 for details). The form of the quantum repeaters, their operation, and how engineers of the future quantum Internet distribute resources throughout the network will determine what the resource distribution actually is. It is still an open question as to what the optimal resource distribution actually would be.
Shown are the three critical parameter the critical classical quantum-repeater efficiency, αc, the critical classical percolation probability, pc, and the critical network diameter \({D}_{\max }\). The critical classical quantum-repeater efficiency αc is the required quantum-repeater efficiency necessary to avoid the phase transition for a given network. The classical critical percolation probability, pc in the minimum probability that a link is not removed, in order to have the network in the connected regime. The relation between the critical classical percolation probability in our model \({p}_{c({c}_{2})}\) and the classical critical percolation probability, pc depends on the third parameter the critical network diameter \({D}_{\max }\), see Eq. ((5)). The critical network diameter \({D}_{\max }\) is the diameter of the network at the phase transition point. In the left, center, and right panel these are shown for the Erdős-Rényi (ER), Barabási-Albert (SF) geometric graphs (rgg), and the Waxman networks for N varying between 102.5–105. For a network to be robust we want αc and pc to be as large as possible with \({D}_{\max }\) to be as small as possible. We estimate the parameters above based on 100 network realization for each network model and value of c. For each network D(p) was computed based on 100 runs. Error bars show the standard deviation associated with each estimation. Show in the upper axis is estimation of the order of magnitude for physical range of the two geometric network (rgg and Waxman) assuming a connecting radius of 266 km (see Supplementary Note 6 and Note 7, and Table S1).
By introducing the quantum backbone, we derived a metric to measure the connectivity of a quantum network, and have shown how large-scale quantum networks based on noisy quantum-repeater nodes connected by noisy channels are prone to discontinuous phase transitions. This abrupt behavior breaks the network into disconnected pieces, severely limiting its operational reach. We found that the discontinuous phase transitions can be suppressed if the efficiency of the quantum-repeater protocol is above a certain value that depends on the topology and size of the network, αc. Furthermore, we have shown that the robustness of a quantum network can be fully characterized using three parameters, the classical percolation critical probability pc, the critical network diameter \({D}_{\max }\) and the critical quantum-repeater efficiency necessary to avoid the first-order phase transition, αc. Our results capture an inherent fragility that geometric networks possess, they tend to be more fragile than other networks. On the other hand, scale-free networks are more robust than all other networks according to these three parameters, and the required quantum-repeater efficiency necessary to avoid the first=order transition is not too large. We have shown that the right network topology combined with advanced repeater architectures47 provide potential solutions for the realization of robust quantum networks. Nevertheless, it does not mean a scale-free network will be sure of a feasible topology for a quantum network.
Discussion
One of the key requirements to generate a scale-free network in geometric spaces is the existence of direct links spanning long distances. As it as been mentioned before, those are problematic to generate for a quantum network. A combination of short links using optical fiber, and long links using communication through satellite might be enough to generate a scale-free-like quantum network, but more research needs to be done in this regard. Our work also does not consider multi-path purification protocols given the fact that they are still in their infancy. Multi-path purification protocols could be an interesting way to increase the reach of our network, but further research on this type of protocol would be required before we can perform analyses. Finally, it has been shown that scale-free networks although robust against target attacks can be very fragile against target attacks27. This phenomenon was also reported to be present in quantum networks15. Our model does not say anything about how robust these networks are against random attacks, and it would be an interesting question to address in future work. Our results provide a guiding principle for the design and development of a robust large-scale quantum Internet, at least against random failures, and provide a framework that can be generalized to study another type of failures or attacks.
Data availability
Data for a snapshot of the structure of Internet at the level of autonomous systems are available at http://www-personal.umich.edu/m̃ejn/netdata/as-22july06.zip.
Code availability
All codes in this work are available from the corresponding author on request.
References
Kimble, H. J. The quantum internet. Nature 453, 1023 (2008).
Caleffi, M., Cacciapuoti, A. S. & Bianchi, G. Quantum internet: from communication to distributed computing! in Proc. 5th ACM International Conference on Nanoscale Computing and Communication, NANOCOM ’18 (Association for Computing Machinery, 2018).
Van Meter, R. Quantum Networking (Wiley, 2014).
Perseguers, S., Lewenstein, M., Acín, A. & Cirac, J. I. Quantum random networks. Nat. Phys. https://www.nature.com/articles/nphys1665 (2010).
Inlek, I. V., Crocker, C., Lichtman, M., Sosnova, K. & Monroe, C. Multispecies trapped-ion node for quantum networking. Phys. Rev. Lett. 118, 250502 (2017).
Briegel, H.-J., Dür, W., Cirac, J. I. & Zoller, P. Quantum repeaters: the role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932–5935 (1998).
Brukner, Č. Quantum causality. Nat. Phys. 10, 259–263 (2014).
Brito, S., Canabarro, A., Chaves, R. & Cavalcanti, D. Statistical properties of the quantum internet. Phys. Rev. Lett. 124, 210501 (2020).
Pirandola, S. End-to-end capacities of a quantum communication network. Commun. Phys. 2, 51 (2019).
Pirandola, S. General upper bound for conferencing keys in arbitrary quantum networks. IET Quantum Commun. 1, 22–25 (2020).
Wu, A.-K., Tian, L., Coutinho, B. C., Omar, Y. & Liu, Y.-Y. Structural vulnerability of quantum networks. Phys. Rev. A 101, 052315 (2020).
Perseguers, S., Cirac, J. I., Acín, A., Lewenstein, M. & Wehr, J. Entanglement distribution in pure-state quantum networks. Phys. Rev. A 77, 022308 (2008).
Cuquet, M. & Calsamiglia, J. Entanglement percolation in quantum complex networks. Phys. Rev. Lett. 103, 240503 (2009).
Brito, S., Canabarro, A., Cavalcanti, D. & Chaves, R. Satellite-based photonic quantum networks are small-world. PRX Quantum 2, 010304 (2021).
Zhang, B. & Zhuang, Q. Quantum internet under random breakdowns and intentional attacks. Quantum Sci. Technol. 6, 45007 (2021).
Zhuang, Q. & Zhang, B. Quantum communication capacity transition of complex quantum networks. Phys. Rev. A 104, 022608 (2021).
Gisin, N. & Thew, R. Quantum communication. Nat. Photonics 1, 165–171 (2007).
Gisin, N., Ribordy, G., Tittel, W. & Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 74, 145–195 (2002).
Bennett, C. H. & DiVincenzo, D. P. Quantum information and computation. Nature 404, 247–255 (2000).
Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).
Zhong, H.-S. et al. Quantum computational advantage using photons. Science 370, 1460–1463 (2020).
Degen, C. L., Reinhard, F. & Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 89, 035002 (2017).
Caves, C. M. Quantum limits on noise in linear amplifiers. Phys. Rev. D. 26, 1817–1839 (1982).
Giovannetti, V., Lloyd, S. & Maccone, L. Quantum-enhanced measurements: beating the standard quantum limit. Science 306, 1330–1336 (2004).
Newman, M. Networks—An Introduction (Oxford University Press, 2010).
Dorogovtsev, S. N. & Mendes, J. F. Evolution of networks: From biological nets to the Internet and WWW (OUP Oxford, 2013).
Barabási, A.-L. et al. Network Science (Cambridge university press, 2016).
Cohen, R., Erez, K., ben Avraham, D. & Havlin, S. Resilience of the internet to random breakdowns. Phys. Rev. Lett. 85, 4626–4628 (2000).
Chen, Z., Wu, J., Xia, Y. & Zhang, X. Robustness of interdependent power grids and communication networks: a complex network perspective. IEEE Trans. Circuits Syst. II Express Briefs 65, 115–119 (2017).
Mezard, M. & Montanari, A. Information, Physics, and Computation (Oxford University Press, 2009).
Newman, M. E. J. Symetrized snapshot of the structure of autonamous systems. http://www-personal.umich.edu/m̃ejn/netdata/as-22july06.zip. (2006).
Bennett, C. H. et al. Purification of noisy entanglement and faithful teleportation via noisy channels. Phys. Rev. Lett. 76, 722–725 (1996).
Żukowski, M., Zeilinger, A., Horne, M. A. & Ekert, A. K. “event-ready-detectors” bell experiment via entanglement swapping. Phys. Rev. Lett. 71, 4287–4290 (1993).
Munro, W. J., Azuma, K., Tamaki, K. & Nemoto, K. Inside quantum repeaters. IEEE J. Sel. Top. Quantum Electron. 21, 78–90 (2015).
Muralidharan, S. et al. Optimal architectures for long distance quantum communication. Sci. Rep. 6, 20463 – (2016).
Sahini, M. & Sahimi M. Applications of Percolation Theory (CRC Press, 1994).
Karp, R. M. Reducibility among combinatorial problems. in Complexity of computer computations, 85–103 (Springer, 1972).
Kurose, J. F. & Ross, K. W. Computer networking: A top-down approach (Addison Wesley, 2010).
Tanenbaum, A. S. & Wetherall, D. Computer Networks, 5th edn. (Prentice Hall, 2011).
Erdős, P. & Rényi, A. On random graphs I. Publ. Math. Debr. 6, 290–297 (1959).
Riordan, O. & Wormald, N. The diameter of sparse random graphs. Comb. Probab. Comput. 19, 835–926 (2010).
Albert, R., Jeong, H. & Barabási, A.-L. Error and attack tolerance of complex networks. Nature 406, 378–382 (2000).
Callaway, D. S., Newman, M. E. J., Strogatz, S. H. & Watts, D. J. Network robustness and fragility: Percolation on random graphs. Phys. Rev. Lett. 85, 5468–5471 (2000).
Barabási, A.-L. & Albert, R. Emergence of scaling in random networks. Science 286, 509–512 (1999).
Dall, J. & Christensen, M. Random geometric graphs. Phys. Rev. E 66, 016121 (2002).
Waxman, B. Routing of multipoint connections. IEEE J. Sel. Areas Commun. 6, 1617–1622 (1988).
Muralidharan, S., Kim, J., Lütkenhaus, N., Lukin, M. D. & Jiang, L. Ultrafast and fault-tolerant quantum communication across long distances. Phys. Rev. Lett. 112, 250501 (2014).
Wehner, S., Elkouss, D. & Hanson, R. Quantum internet: a vision for the road ahead. Science 3622, eaam9288 (2018).
Bollobás, B. & Riordan, O. M. Mathematical results on scale-free random graphs. In Handbook of Graphs and Networks: From the Genome to the Internet (Wiley, 2003).
Acknowledgements
We thank Akshat Kumar for his feedback on Supplementary Note 2 and Marco Pezzutto for valuable discussions. We acknowledge the support from the JTF project The Nature of Quantum Networks (ID 60478). Furthermore, B.C. and Y.O. thank the support from Fundação para a Ciência e a Tecnologia (Portugal), namely through projects UIDB/EEA/50008/2020 and QuantSat-PT, as well as from projects TheBlinQC and QuantHEP supported by the EU H2020 QuantERA ERA-NET Cofund in Quantum Technologies and by FCT (QuantERA/0001/2017 and QuantERA/0001/2019, respectively), and from the EU H2020 Quantum Flagship projects QIA (820445) and QMiCS (820505). B.C. thanks the support from FCT through project CEECINST/00117/2018/CP1495. K.N. acknowledges support from the JSPS KAKENHI Grant No. 21H04880.
Author information
Authors and Affiliations
Contributions
B.C., W.M., K.N., and Y.O. contributed to the development of the initial concept, the design, and analysis of the networks performance as well as the writing of the manuscript. B.C. performed the network simulations.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Coutinho, B.C., Munro, W.J., Nemoto, K. et al. Robustness of noisy quantum networks. Commun Phys 5, 105 (2022). https://doi.org/10.1038/s42005-022-00866-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-00866-7
This article is cited by
-
Optimal quantum key distribution networks: capacitance versus security
npj Quantum Information (2024)
-
Identifying key players in complex networks via network entanglement
Communications Physics (2024)
-
Complex quantum network models from spin clusters
Communications Physics (2023)
-
Quantum NETwork: from theory to practice
Science China Information Sciences (2023)
-
Concurrence percolation threshold of large-scale quantum networks
Communications Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.