Abstract
The introduction of slippery lubricated surfaces allows for the investigation of the flow of highly viscous fluids, which otherwise will hardly move on standard solid surfaces. Here we present the study of the gravity induced motion of small drops of polymeric fluids deposited on inclined lubricated surfaces. The viscosity of these fluids decreases with increasing shear rate (shear thinning) and, more importantly, they exert normal forces on planes perpendicular to shear directions (elasticity). Despite the homogeneity of the surface and of the fluids, drops of sufficiently elastic fluids move downward with an oscillating instantaneous speed whose frequency is found to be directly proportional to the average speed and inversely to the drop volume. The oscillatory motion is caused by the formation of a bulge at the rear of the drop, which will be dragged along the drop free contour by the rolling motion undergone by the drop. This finding can be considered as a kind of new Weissenberg effect applied to moving drops that combines dynamic wetting and polymer rheology.
Similar content being viewed by others
Introduction
The motion of a drop on a solid surface is still attracting a lot of attention because of its implications on microfluidics and wetting1,2,3. On a tilted surface, the motion of a drop is the result of a balance between the down-plane component of the drop weight and the viscous resistance, plus a capillary force related to contact line pinning4,5,6. If the solid substrate is flat and chemically homogeneous, the drop moves with a constant speed, which is higher for low viscous liquids on hydrophobic surfaces7. The introduction of chemical and morphological defects may affect the drop motion either quantitively, or qualitatively by introducing dynamical nonlinearities. For instance, the resulting motion exhibits distinct stick and slip on a periodic array of hydrophilic and hydrophobic domains6,8, deviations at chemical steps between hydrophobic and hydrophilic regions9, anisotropy in the wetting of microwrinkled surfaces10,11, uni-directional liquid spreading on asymmetric nanostructure12,13, which can be exploited to passively guide the moving drops.
Inspired by the Nepenthes pitcher plant, effective strategies have been recently developed to produce very slippery surfaces that hardly pin sessile drops. They involve trapping a suitable low surface tension lubricating liquid inside a texture. The lubricant, if chosen correctly, allows a drop of another liquid to float on this mixed substrate14,15. Thus, a new class of materials is defined, also known as liquid-infused surfaces1,2,3, which are hemiliquid and hemisolid, where the intercalated lubricant is trapped by the solid cavities and therefore there is no contact between the drop and the solid substrate16. Since the lubricant surface is intrinsically smooth and free of chemical and morphological defects typical of solid surfaces, these lubricated surfaces exhibit very low contact line pinning and are then highly omniphobic17. For these features, they are used in various applications, including biomedical devices, sanitation, heat exchangers, and anti-ice materials1,18,19,20,21,22,23. However, the lubricant layer is not fully immobilized and depletes over time, implying a limited lifetime of this coating which depends on the specific function24.
The slippery nature of these hybrid surfaces allows investigating the dynamics of non-Newtonian drops. For example, lubricated surfaces have recently been shown to change the dynamic behavior of yield stress fluids such as condiments, lotions, toothpaste, and enable them to flow without shearing25. Generally, polymeric solutions are non-Newtonian fluids characterized by viscoelasticity: their viscosity decreases with increasing shear rate (shear thinning) and, more importantly, they exert normal forces on planes perpendicular to shear directions (elasticity)26. The most famous manifestation of fluid elasticity is probably the Weissenberg effect that occurs when a rotating rod is partially inserted into an elastic fluid, such as certain polymer solutions27,28: instead of being pushed outward forming a vortex as in the case of a Newtonian fluid like water, the solution is drawn towards the rod and climbs it up. This phenomenon can be easily explained assuming that there is an extra tension29 along the flow lines that arises from the stretching and alignment of the polymeric molecules along the flow lines28. If, as in the rotating rod experiment, the flow lines are closed circles, the extra tension along these lines “strangulates” the liquid and forces it inwards against the centrifugal forces and upwards against the forces of gravity. Because these solutions usually exhibit high viscosity, concentrated polymeric drops deposited on solid surfaces either barely move or leave traces behind. This explains why only a few reports30,31,32 have analyzed the motion of polymeric drops moving down an inclined solid surface, without observing major differences with respect to water drops. Moving drops of Xanthan (a stiff polymer) aqueous solutions characterized by a pronounced shear-thinning behavior show stationary motion whose velocity exhibits a sublinear relation with the driving force at high values, while for Newtonian fluids it is linear31. This behavior is shared by drops of polyacrylamide (a flexible polymer) solutions32. However, in contrast to solutions containing stiff polymers, drops of solutions containing flexible polymers exhibit remarkable elongation in steady motion32. Drops of elastic liquids presenting constant viscosity, also known as Boger fluids, moving on superhydrophobic and hydrophilic glass surfaces have also been investigated33,34. Boger fluid drops, with very high elasticity but otherwise identical properties to Newtonian ones, show no difference compared to Newtonian fluid drops while moving on hydrophilic glass surfaces. On the contrary, on a superhydrophobic surface, the Boger fluid drops are significantly slowed compared to the Newtonian drops because of the formation of single filaments between the main drop and micro-drops pinned on individual surface pillars. Furthermore, the low surface energy of a superhydrophobic surface allows decoupling the rolling, sliding and sticking motions of a viscoplastic drop35, i.e. of a material that behaves like a fluid only if an applied stress is beyond a critical (yield) stress, below which it behaves like a solid.
In this article, we explore the motion of viscoelastic drops on inclined slippery lubricated surfaces. An interesting phenomenon is observed: despite the homogeneity of the surface and of the polymeric solutions, the drop exhibits periodic oscillations superimposed to a uniform motion, with a frequency that is directly proportional to the average speed and inversely proportional to the drop volume.
Results and Discussion
Rheology of liquid solutions
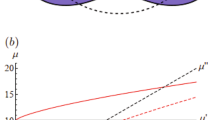
Solutions of Xanthan, a stiff rod-like polysaccharide, and polyacrylamide (PAA), a flexible polymer, are prepared in MilliQ water. Both solutions are reported to exhibit shear thinning and elastic effects (i.e. normal stresses)36,37,38. In this study, PAA of three different molecular weights are investigated: Mw ≈ 5–6 × 106 g mol−1 (Sigma-Aldrich) at concentration of 10,000 ppm (wt/wt), Mw ≈ 10 × 106 g mol−1 (polyacrylamide/acrylic acid [60:40], Polysciences, Inc.) at concentrations of 1500, 2500, and 5000 ppm (wt/wt) and Mw ≈ 18 × 106 g mol−1 (polyacrylamide/sodium acrylate [70:30], Polysciences, Inc.) at a concentration of 1000 ppm (wt/wt), which in the following are labeled as PAA5-6, PAA10, and PAA18, respectively. The Xanthan solutions have Mw ≈ 106 g mol−1 (Sigma-Aldrich) and two different concentrations: 1500 and 2500 ppm (wt/wt). The resulting solutions have concentrations ranging in the dilute or semi-dilute regime37,38,39 and their surface tensions are very similar to that of pure water. Consequently, drops are expected to be cloaked by a thin lubricant film once they are deposited on silicone or fluorinated oil-lubricated surfaces40,41. A glycerol solution at 70% (wt/wt) is used as a Newtonian reference for the motion of drops on slippery lubricated surfaces. The rheological properties of the mentioned solutions are characterized with a cone-plate rheometer (Kinexus lab+ Netzsch, Germany) and the main results are plotted in Fig. 1. More specifically, we measured the shear rate dependence of the viscosity μ and the first normal stress difference N1. This latter quantity is related to the vertical force that the fluid exerts perpendicularly to a moving disk, more precisely \({N}_{1}={\tau }_{11}-{\tau }_{22},\) where \({\tau }_{11}\) and \({\tau }_{22}\) are the diagonal elements of the stress tensor26. For a Newtonian fluid, N1 = 0, while N1 > 0 for an elastic fluid. As expected, at sufficiently high shear rates, all polymeric solutions, apart from PAA5-6, behave as a power-law fluid32. In agreement with previous studies, the corresponding N1 increases quadratically with the shear rate and, for a given molecular weight, N1 increases significantly with polymer concentration26. Finally, the N1 of Xanthan solutions is not negligible for concentrations greater than 1500 ppm42, being comparable to that of the low concentrated PAA10 and PAA18 solutions. As for their wetting properties, the apparent contact angle and the contact angle hysteresis of the polymeric solutions are comparable with the values for pure water.
Variation of the shear viscosity (a) and first normal stress difference (b) as a function of the shear rate for different polymeric aqueous solutions. Their composition is displayed in the legend of graph (b). Glycerol 70% wt/wt (full line) and silicone oil (dashed line) are also reported. Both are Newtonian fluids with N1 = 0. Error bars due to the rheometer precision are smaller than the data points.
Drop motion
Movies of drops moving downward tilted surfaces are acquired using a custom-made optical set-up (see Methods). A characteristic movie frame, with the drop appearing dark on a light background, is displayed in Fig. 2a, together with the indication of the front and rear points of the contact line, which are used to investigate the motion of the drop, and of the free contour of the drop. A sequence of snapshots extracted from the same movie is displayed in Fig. 2b. In the snapshots, the drop is enlarged and tilted so that it appears to lie on a horizontal surface. A careful inspection of the snapshots yields that the drop profile is not stationary but presents a localized bulge moving periodically along the semi-circular profile, as also displayed in Supplemental Movie 1 and characterized in the text below.
a Snapshot of a 30 μl polyacrylamide solution (PAA10/water 5000 ppm) drop moving downward on a 30° tilted surface. The free contour of the drop is indicated by a dashed curve of length p connecting the rear and front contact points. b Snapshots of the same drop taken at time intervals of 1/4 of the oscillation period; red lines highlight the evolution of the drop deformation.
The graph of Fig. 3 shows the time evolution of the front position of the contact line of different drops having volume Ω = 30 μl deposited on lubricated surfaces inclined by α = 30° (α = 15° for the PAA18 solution). The data refer to silicone surfaces with a nominal lubricant thickness of approximately 3 μm and are confirmed by measurements taken with the fluorinated oil (see Supplementary Note 1). The blue curve indicates a Newtonian glycerol/water solution having a viscosity μ = 18 mPa s. As expected, its linear trend confirms that the drop undergoes a uniform motion similar to those observed with water drops moving down-solid hydrophobic surfaces6. The linearity is better shown in Fig. 3b which reports the instantaneous variation δx of the front and rear contact points of the moving drop from the average linear trend obtained by fitting the corresponding curve reported in Fig. 3a with a straight line. The resulting mean velocity is also in good quantitative agreement with previous studies40,43,44 (see Supplementary Note 2).
a Time evolution of the front position of the contact line xf of drops of different solutions having volume Ω = 30 μL deposited on lubricated surfaces inclined by α = 30° (α = 15° for the polyacrylamide PAA18 and Xanthan solutions). b–i Time evolution of the instantaneous deviation δx of the front and rear contact points of drops of different solutions from the average linear trends reported in (a). Solid (open) symbols refer to the front (rear) contact point. The vertical dashed lines in panel (f), labelled from (i) to (iv), highlight the time instants corresponding to the snapshots in Fig. 2c.
As expected from the rheological characterization, PAA5-6 drops exhibit the same uniform motion as glycerol/water drops; see the purple curve in Fig. 3a and c. Interestingly, despite the much higher static viscosities, the average speed of PAA10 drops with concentration somewhat below 2500 ppm is also comparable to that of glycerol/water drops, within the uncertainty related to the fact that the curves refer to different surfaces that may present slightly different lubricant thicknesses44,45. This result can be rationalized by assuming that the viscosity of the moving PAA10 drops is much lower because of the shear dependence. If its viscosity is somewhat lower than that of the lubricant, the resulting motion will eventually be determined by the viscosity of the lubricant43. However, the most surprising result is the oscillatory motion of PAA10/water drops, which can be directly observed in Supplementary Movie 1. Nonuniform drop motions have already been reported in the literature, but in those cases the nonlinearity was due to engineered inhomogeneities in the substrate: the alternance of hydrophobic/hydrophilic stripes6 or the modulation of magnetic fields46, which induced spatial variations in the restoring forces acting on water and ferrofluid drops, respectively. In the case of viscoelastic drops, the oscillatory motion is a consequence of the rheology of these polymeric solutions.
These drops also undergo a rolling motion, which can be easily detected by adding ground coffee particles to PAA drops and tracking their motion relative to the drop with a high-speed camera as the drop moves across the surface40, as shown in Supplementary Movie 2. The unexpected oscillatory motions can be seen more clearly in the graphs (d)–(f) of Fig. 3, which show the time evolution of the instantaneous deviation δx of PAA10 drops at increasing concentrations. Similar behavior is also exhibited by PAA18 drops, Fig. 3g, and, more important, by the concentrated Xanthan solution, Fig. 3i. The diluted Xanthan solution instead shows a uniform motion, Fig. 3h, similar to that found with PAA5-6 drops, Fig. 3c. The various panels also indicate that the front and rear contact points appear to move in phase, suggesting that even the instantaneous center of the contact line follows the same motion. The oscillations they exhibit are probably related to the moving bulge in the drop profile displayed in the snapshots of Fig. 2b. This phenomenology can be qualitatively understood by noting that the shear rate is highest in the wedge region close to the rear contact point of the drop32,33,34. Due to the elasticity of the polymeric fluid, there is an extra tension normal to the drop contour that will locally pull it up, generating a bulge. This deformation is reminiscent of the convex profile of the free surface of a viscoelastic fluid flowing down an open, slightly inclined channel28; if the fluid is nonelastic, the free surface is instead flat. Once the bulge forms, it will be dragged along by the rolling drop. Then the oscillating time law is simply a consequence of the periodic conversion between the kinetic and gravitational potential energy of the deformed drop, as confirmed by solving the motion of a rigid wheel with a point mass fixed on its boundary. This can be considered as the simplest mechanical analog of the moving drop with the bulge rolling around its contour to assess the role of inertia by completely neglecting capillary forces and viscous dissipation (see Supplementary Note 3 and Supplementary Movie 3 for further details).
The graphs reported in Fig. 3 correspond to an overall displacement of about 3 cm. The distance from the drop dosing and the motion recording area is typically more than 3 cm, amply sufficient to neglect transient effects44. To experimentally confirm it, we have also used a 30 × 3 cm2 glass plate lubricated as the glass slides. As the separation between the deposition spot and the recording area is increased from 4 to 15 cm, no significant difference is observed in the resulting oscillatory motion (see Supplementary Note 4 for further details).
We tend to exclude the possibility that this motion is the result of an interplay between the polymeric drops and the lubricant layer. Actually, if we repeat the experiment by replacing the lubricated glass slide with one covered by a slippery solid surface made of smooth Teflon tape, the same oscillatory motion is observed (see Supplementary Note 5). However, the reproducibility becomes very poor and most of the time the PAA drops get pinned to the Teflon surface even though the drop volume is as high as 100 μl. However, when they move over a centimeter distance, they do exhibit oscillations similar to those reported in Fig. 3. Our measurements indicate that such oscillations only appear with solutions that have a significant first normal stress difference N1. Actually, the largest amplitude corresponds to the most concentrated PAA10 solution for which N1 is the highest, while no oscillations are observed for the PAA5-6 and Xanthan 1500 ppm solutions. We have tried to verify whether, for a given solution, the oscillation amplitude of drops of constant volumes varies with their mean speed, but no defined trend was observed (see Supplementary Note 6 for more details).
To shed more light on this novel motion, to the best of our knowledge, the graph of Fig. 4 plots the frequency of the periodic oscillations as a function of the mean drop speed. The data refer to PAA10 drops with a concentration of 2500 ppm having different volumes and deposited on surfaces tilted at different inclination angles (see also Supplementary Note 7 and 8 for more data on different surfaces and more concentrated solutions, respectively). It is evident the direct proportionality between f and U. Xanthan 2500 ppm data points are found to lie on the same straight line as PAA10 drops of similar volume. The direct proportionality between f and U confirms that the oscillations are related to the motion of the bulge in the drop profile mentioned above.
Oscillation frequency f as a function of the average drop speed U for the polyacrylamide solution PAA10 and Xanthan 2500 ppm drops of different volume deposited on lubricated surfaces impregnated with silicone oil of different viscosities. The dashed lines are linear fits to the data. The inset displays all the data in terms of the product \({fp}\) versus U, where p is the length of the drop free contour. The straight line has a slope equal to 1. The error bars represent one standard deviation.
The inverse of the slopes of the interpolating dashed lines of Fig. 4 yields a characteristic length λ. The values of λ are found to agree very well with the length of the free contours p of the corresponding drops: for instance, for 40 μL drops, λ = 8.6 ± 0.4 mm is practically coincident with the value p = 8.6 ± 0.2 mm derived from image processing. This conclusion is graphically confirmed by the inset, where the data are rescaled in terms of the product \({fp}\) versus U: all the data nicely collapse on a straight-line having slope equal to 1.
Conclusions
Recently, oscillations in the velocity have been reported in gravity-driven motion of large viscoplastic drops (Ω ∼ 250 µL) on superhydrophobic surfaces35. For the first time to our knowledge, our findings indicate that an oscillatory motion can also be observed on lubricated surfaces for smaller drops of viscoelastic fluids that exhibit shear-thinning and, more importantly, significant elasticity. This unexpected finding can be considered as a kind of new Weissenberg effect28, which is commonly associated with a viscoelastic fluid that climbs up a rotating rod, applied to moving drops. In addition to a proper rheology of the liquid drop, a key ingredient in our finding is a low contact line pinning, best achieved by impregnating a solid rough surface with a liquid lubricant. Interestingly, superhydrophobic dry rough surfaces, which are considered excellent water repellent, exhibit significant contact line pinning of elastic drops, resulting in enhanced friction33,34. Thus, the addition of a lubricant liquid makes the surface more similar to an ideal Young surface, perfect for addressing the dynamics of viscoelastic drops. Needless to say, more detailed modelling of the viscoelastic features that trigger the formation of the bulge and the restoring action played by the surface tension is required for a deeper understanding of the observed dynamics, which combines dynamic wetting with polymer rheology. We hope that this work will be a stimulus for such investigations.
Methods
Preparation of lubricated surfaces
For this work, slippery lubricated surfaces are prepared following the method described in46,47. A film of silicone oil having viscosity of 4.8 mPa s at T = 20 °C is spread on the surface of a microscope glass slide (76 × 26 mm2) and held at 300 °C for 10 min. After being cooled to room temperature, excess oil is washed away with acetone. The result of the thermal process is a thin, porous solidified silicone layer of about 200 nm thickness that we impregnate with silicone oils of different viscosities (4.8 mPa s and 95.6 mPa s). We have also considered fluorinated lubricated surfaces prepared according to this other procedure48: a ∼20 μm thick porous polytetrafluoroethylene (PTFE) membrane (Sterlitech Corp.) is applied to a microscope glass slide and wetted with ethanol to make it adhere smoothly by capillarity. Once the ethanol evaporates, the membrane is impregnated with fluorinated oil (Fomblin PFPE (Perfluoropolyether) Y LVAC 06/6) with viscosity 120 mPa s at T = 20 °C, using a dip coater (Kibron Inc. LayerX 274) and following the procedure reported in49. The withdrawal velocity during dip coating is set at 0.12 mm/min to ensure a controlled thickness of the liquid layer above the membrane of ∼0.5 μm. The lubricated surfaces prepared with these different methods are found to yield highly reproducible results in the drop motion. For silicone and fluorinated oil-lubricated surfaces, the apparent contact angle of sessile water drops is about 90° and 110°, respectively, and the contact angle hysteresis is less than 3° for both. The results on lubricated surfaces are compared with those obtained on solid substrates realized by covering a microscope slide with Teflon tape. Unlike lubricated surfaces, this surface presents a very high contact angle (≈120°), but the contact angle hysteresis is also very high (≈45°), resulting in larger pinning of the contact line.
Optical setup
The optical setup resembles that used in our previous study of sliding drops deviating at a chemical step9. The sample is mounted on a rotating support whose inclination angle α can be set by computer with 0.5° accuracy. Drops of volume Ω in the range between (10 ± 1) μl and (40 ± 1) μl are produced by means of a micropipette. The drop is illuminated by a white LED back-light. The lateral profile of the drop is viewed using a CMOS camera (Vision Research Phantom v7.3) mounted along the rotation axis of the stage and equipped with a macro zoom lens (Navitar Zoom 7000). Movies of the drop motion are acquired at sample rate intervals between 100 and 2000 fps and are analyzed through a custom-made LabVIEW script.
Data availability
All relevant data presented in this paper are available from the corresponding author upon reasonable request.
References
Mistura, G. & Pierno, M. Drop mobility on chemically heterogeneous and lubricant-impregnated surfaces. Adv. Phys.-X 2, 591–607 (2017).
Malinowski, R., Parkin, I. P. & Volpe, G. Advances towards programmable droplet transport on solid surfaces and its applications. Chem. Soc. Rev. 49, 7879–7892 (2020).
Lin, S. J., Li, B., Xu, Y., Mehrizi, A. A. & Chen, L. Q. Effective Strategies for Droplet Transport on Solid Surfaces. Adv. Mater. Interfaces 8, 2001441 (2021).
De Gennes, P. G., Brochard-Wyart, F. & Quéré, D. Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves. (Springer, 2004).
Le Grand, N., Daerr, A. & Limat, L. Shape and motion of drops sliding down an inclined plane. J. Fluid Mech. 541, 293–315 (2005).
Varagnolo, S. et al. Stick-Slip Sliding of Water Drops on Chemically Heterogeneous Surfaces. Phys. Rev. Lett. 111, 066101 (2013).
Podgorski, T., Flesselles, J. M. & Limat, L. Corners, cusps, and pearls in running drops. Phys. Rev. Lett. 87, 036102 (2001).
Varagnolo, S. et al. Tuning Drop Motion by Chemical Patterning of Surfaces. Langmuir 30, 2401–2409 (2014).
Semprebon, C. et al. Deviation of sliding drops at a chemical step. Soft Matter 12, 8268–8273 (2016).
Chung, J. Y., Youngblood, J. P. & Stafford, C. M. Anisotropic wetting on tunable micro-wrinkled surfaces. Soft Matter 3, 1163–1169 (2007).
Chen, Y., He, B., Lee, J. H. & Patankar, N. A. Anisotropy in the wetting of rough surfaces. J. Colloid Interface Sci. 281, 458–464 (2005).
Chu, K. H., Xiao, R. & Wang, E. N. Uni-directional liquid spreading on asymmetric nanostructured surfaces. Nat. Mater. 9, 413–417 (2010).
Hancock, M. J., Sekeroglu, K. & Demirel, M. C. Bioinspired Directional Surfaces for Adhesion, Wetting, and Transport. Adv. Funct. Mater. 22, 2223–2234 (2012).
Lafuma, A. & Quere, D. Slippery pre-suffused surfaces. EPL 96, 56001 (2011).
Wong, T.-S. et al. Bioinspired self-repairing slippery surfaces with pressure-stable omniphobicity. Nature 477, 443–447 (2011).
Daniel, D., Timonen, J. V. I., Li, R. P., Velling, S. J. & Aizenberg, J. Oleoplaning droplets on lubricated surfaces. Nat. Phys. 13, 1020–1025 (2017).
Daniel, D. et al. Origins of Extreme Liquid Repellency on Structured, Flat, and Lubricated Hydrophobic Surfaces. Phys. Rev. Lett. 120, 244503 (2018).
Anand, S., Paxson, A. T., Dhiman, R., Smith, J. D. & Varanasi, K. K. Enhanced Condensation on Lubricant-Impregnated Nanotextured Surfaces. ACS Nano 6, 10122–10129 (2012).
Kreder, M. J., Alvarenga, J., Kim, P. & Aizenberg, J. Design of anti-icing surfaces: smooth, textured or slippery? Nat. Rev. Mater. 1, 15003 (2016).
Leslie, D. C. et al. A bioinspired omniphobic surface coating on medical devices prevents thrombosis and biofouling. Nat. Biotechnol. 32, 1134–1140 (2014).
Li, J. S., Ueda, E., Paulssen, D. & Levkin, P. A. Slippery lubricant-infused surfaces: properties and emerging applications. Adv. Funct. Mater. 29, 1802317 (2019).
Regan, D. P. & Howell, C. Droplet manipulation with bioinspired liquid-infused surfaces: A review of recent progress and potential for integrated detection. Curr. Opin. Colloid Interface Sci. 39, 137–147 (2019).
Wang, J. et al. Viscoelastic solid-repellent coatings for extreme water saving and global sanitation. Nat. Sustain. 2, 1097–1105 (2019).
Peppou-Chapman, S., Hong, J. K., Waterhouse, A. & Neto, C. Life and death of liquid-infused surfaces: a review on the choice, analysis and fate of the infused liquid layer. Chem. Soc. Rev. 49, 3688–3715 (2020).
Rapoport, L., Solomon, B. R. & Varanasi, K. K. Mobility of Yield Stress Fluids on Lubricant-Impregnated Surfaces. Acs Appl. Mater. Interfaces 11, 16123–16129 (2019).
Ferry, J. D. Viscoelastic properties of polymers. 3rd edn, (John Wiley and Sons, Inc., 1980).
Garner, F. H. & Nissan, A. H. Rheological properties of high-viscosity solutions of long molecules. Nature 158, 634–635 (1946).
Bird, R. B., Armstrong, R. C. & Hassanger, H. Dynamics of polymeric liquids, Volume 1 Fluid Mechanics, 2nd Ed., (John Wiley and Sons, Inc., 1987).
Weissenberg, K. A continuum theory of rheological phenomena. Nature 159, 310–311 (1947).
Morita, H., Plog, S., Kajiya, T. & Doi, M. Slippage of a Droplet of Polymer Solution on a Glass Substrate. J. Phys. Soc. Jpn. 78, 014804 (2009).
Varagnolo, S., Mistura, G., Pierno, M. & Sbragaglia, M. Sliding droplets of Xanthan solutions: A joint experimental and numerical study. Eur. Phys. J. E 38, 126 (2015).
Varagnolo, S., Filippi, D., Mistura, G., Pierno, M. & Sbragaglia, M. Stretching of viscoelastic drops in steady sliding. Soft Matter 13, 3116–3124 (2017).
Xu, H., Clarke, A., Rothstein, J. P. & Poole, R. J. Sliding viscoelastic drops on slippery surfaces. Appl. Phys. Lett. 108, 241602 (2016).
Xu, H., Clarke, A., Rothstein, J. P. & Poole, R. J. Viscoelastic drops moving on hydrophilic and superhydrophobic surfaces. J. Colloid Interface Sci. 513, 53–61 (2018).
Kim, M., Lee, E., Kim, D. & Kwak, R. Decoupled rolling, sliding and sticking of a viscoplastic drop on a superhydrophobic surface. J. Fluid Mech. 908, A41 (2021).
Carre, A. & Eustache, F. Spreading kinetics of shear-thinning fluids in wetting and dewetting modes. Langmuir 16, 2936–2941 (2000).
Rafai, S., Bonn, D. & Boudaoud, A. Spreading of non-Newtonian fluids on hydrophilic surfaces. J. Fluid Mech. 513, 77–85 (2004).
Rafai, S. & Bonn, D. Spreading of non-Newtonian fluids and surfactant solutions on solid surfaces. Phys. A 358, 58–67 (2005).
Callaghan, P. T. & Gil, A. M. Rheo-NMR of semidilute polyacrylamide in water. Macromolecules 33, 4116–4124 (2000).
Smith, J. D. et al. Droplet mobility on lubricant-impregnated surfaces. Soft Matter 9, 1772–1780 (2013).
Sett, S., Yan, X., Barac, G., Bolton, L. W. & Miljkovic, N. Lubricant-Infused Surfaces for Low-Surface-Tension Fluids: Promise versus Reality. Acs Appl. Mater. Interfaces 9, 36400–36408 (2017).
Whitcomb, P. & Macosko, C. Rheology of xanthan gum. J. Rheol. 22, 493–505 (1978).
Keiser, A., Keiser, L., Clanet, C. & Quere, D. Drop friction on liquid-infused materials. Soft Matter 13, 6981–6987 (2017).
Keiser, A., Baumli, P., Vollmer, D. & Quere, D. Universality of friction laws on liquid-infused materials. Phys. Rev. Fluids 5, 014005 (2020).
Sharma, M., Roy, P. K., Barman, J. & Khare, K. Mobility of Aqueous and Binary Mixture Drops on Lubricating Fluid-Coated Slippery Surfaces. Langmuir 35, 7672–7679 (2019).
Rigoni, C. et al. Dynamics of ferrofluid drops on magnetically patterned surfaces. Langmuir 34, 8917–8922 (2018).
Eifert, A., Paulssen, D., Varanakkottu, S. N., Baier, T. & Hardt, S. Simple Fabrication of Robust Water-Repellent Surfaces with Low Contact-Angle Hysteresis Based on Impregnation. Adv. Mater. Interfaces 1, 1300138 (2014).
Hao, C. L. et al. Electrowetting on liquid-infused film (EWOLF): Complete reversibility and controlled droplet oscillation suppression for fast optical imaging. Sci. Rep. 4, 6846 (2014).
Sartori, P. et al. Motion of Newtonian drops deposited on liquid-impregnated surfaces induced by vertical vibrations. J. Fluid Mech. 876, R4 (2019).
Acknowledgements
We are particularly grateful to Andrea Ludovici for support in the acquisition of preliminary data, to Dr. Elisa Vettorato and Dr. Ilaria Fortunati for the rheological characterization and to Dr. Enrico Chiarello and Giorgio Delfitto for precious technical assistance. We thank Prof. Alberto Carnera and Dr. Stefano Lacaprara for useful discussions. This research was partially funded by the Italian Ministry of University and Research through PRIN2017 UTFROM and by the University of Padova through the STARS grant–EXODROP and the BIRD grant 2021-BiodivSeq,
Author information
Authors and Affiliations
Contributions
G.M. and M.P. conceived the project. P.S., M.D., and A.M. prepared the lubricated samples. P.S. and D.Fi. synthesized and characterized the viscoeleastic fluids, P.S., D.Fe., and A.Z. assembled the optical set-up. P.S., M.D., and A.M. acquired the videos and together with D.Fe. analyzed them. The paper was written by P.S, D.Fe., M.P., and G.M. All authors made comments.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sartori, P., Ferraro, D., Dassie, M. et al. Oscillatory motion of viscoelastic drops on slippery lubricated surfaces. Commun Phys 5, 81 (2022). https://doi.org/10.1038/s42005-022-00862-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-00862-x
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.