Introduction

Elastic and inelastic X-ray scattering have long provided detailed information on the static atomic arrangement in solids and the associated fundamental electronic, magnetic and lattice excitations. In recent years, conventional X-ray Thomson scattering has been increasingly supplemented by resonant elastic (REXS) and inelastic (RIXS) X-ray scattering which offer enhanced cross sections as well as atomic and bonding specificity. RIXS has been used to study the low-energy excitations in atoms and molecules1, in chemisorption systems2 and the momentum-dependent charge and spin excitations in solids3,4. REXS has been mostly utilized for diffractive imaging of the nanoscale charge5 and spin6 distributions in solids.

REXS and RIXS processes involve excitations of atomic core electrons into unfilled localized electronic valence states. The resonant x-ray absorption (XAS) step is followed by so-called spontaneous electronic decays resulting in the creation of photons or Auger electrons. The radiative (photon) and non-radiative (Auger) spontaneous decay probabilities are linked through the fluorescence yield which to a good approximation is an atomic core shell specific tabulated quantity7. Resonant X-ray scattering in the form of REXS and RIXS consists of two consecutive and linked absorption and emission processes. In the widely used Kramers-Heisenberg-Dirac (KHD) perturbation description of X-ray/matter interactions, absorption and emission, alone, are first order processes, while the link of the two processes in REXS and RIXS requires a second order perturbation treatment1,4. All first and spontaneous second order processes scale linearly with the incident intensity.

Of all X-ray processes, resonant absorption has the largest cross section. The spontaneous emission probability of a photon in the decay step is typically considerably smaller than that of an Auger electron in the soft X-ray range. This together with the random spontaneous emission direction of the photons causes a great reduction in the number of photons detected within the small solid angle of a spectrometer. For example, in L-edge RIXS measurements of the important 3d transition metal atoms, the photon emission probability given by the fluorescence yield, is of order Yf = 10−3–10−2 of the Auger decay probability7 and the solid angle of acceptance of state-of-the-art RIXS spectrometers is of order 10−5 of 4π steradians8. Thus the measured spontaneous RIXS signal is typically of order of a single photon for about 107 photons absorbed by a sample9.

The development of RIXS, which has the advantage over optical techniques of atomic specificity, has greatly benefitted from the increased brightness of modern synchrotron radiation sources which offer an incident photon flux within a bandwidth of 100 meV of order 1013 photons. Remarkably, however, even at such intensities, the photon degeneracy parameter, defined as the number of photons npk in the same polarization mode p and wavevector (direction) mode k, is still less than 110. This means that when an absorption event is triggered by an incident photon, there is no second photon available to influence, i.e. stimulate, the decay. This dilemma has only been overcome by the advent of X-ray Free Electron Lasers (XFELs) where individual pulses may contain coherent spikes (modes) of large degeneracy parameters10,11.

The benefit of X-ray stimulation may be seen by writing the RIXS emission cross section per atom, σRIXS, in KHD perturbation theory in a simplified “two-step” or “direct” RIXS form1,4 (see Methods) as,

$$\frac{d \sigma_{{{{{\mathrm{RIXS}}}}}}}{d \varOmega} = \frac{1}{4\pi} \underbrace{\frac{{{\Gamma}}_{{{{{\mathrm{X}}}}}}}{{{\Gamma}}_{{{{{\mathrm{X}}}}}}+ {{\Gamma}}_{{{{{\mathrm{A}}}}}}}}_{{\mbox{$Y_{{{{{\mathrm{f}}}}}}$}}} \left(1 + n_{\!p {{{{{\mathbf{k}}}}}}}\right) \, \sigma_{{{{{\mathrm{XAS}}}}}}$$
(1)

Here dΩ is the solid acceptance angle of the spectrometer, ΓX/ℏ the dipolar X-ray emission rate, ΓA/ℏ the Auger electron emission rate, Yf the fluorescence yield per atom7, and σXAS the spontaneous resonant absorption cross section per atom. The well-known factor 1 + npk, introduced by Dirac12, distinguishes the spontaneous decay probability induced by 1 virtual photon in the zero-point quantum vacuum and the stimulated decay probability driven by npk real photons in the polarization mode p and wavevector mode k contained in the mode volume Vpk = λ3ℏω/Δpk, where Δpk is the incident energy bandwidth. In the time-independent KHD theory, the stimulation rate depends on the incident bandwidth Δpk.

In the stimulation process, incident photons in a mode pk drive atomic decays and the emitted photons preserve the energy, polarization and direction of the driving photons, first pointed out by Einstein in 191713 in the derivation of Planck’s formula for the black body spectrum. Stimulation has two beneficial effects. If k is aligned with the acceptance cone dΩ of the spectrometer, the spontaneous RIXS cross section is directionally enhanced by 4π/dΩ  ≃ 105. In addition, the small spontaneous fluorescent yield Yf ≤ 10−2 is increased by the driving action of the stimulating photons.

The KHD perturbation formula (1) ignores changes in occupation of the electronic states during absorption and emission and its linear scaling with photon number breaks down for large npk14,15. Proper treatment by use of the time-dependent optical Bloch equations or the related Maxwell-Bloch theory16, shows that at large values of npk > 103 the stimulated fluorescence yield saturates at Yf npk → 1/2. The stimulated RIXS cross section therefore saturates at about half of the spontaneous absorption cross section, σRIXS → σXAS/2. The maximum enhancement of stimulated over spontaneous RIXS consist of a dominant solid angle contribution of 4π/dΩ ≃ 105 and a smaller “photon number” increase given by 1/(2Yf) which in practice is of order 50–500.

Pioneering studies with XFELs have utilized the large photon degeneracy parameter to create a large number of core holes, and the spontaneously emitted photons may then amplify by stimulation as they propagate in the sample, a process called amplified spontaneous emission (ASE)17,18,19,20,21. The direct or “impulsive” stimulation of the elastic REXS channel by a strong incident beam has also been observed in a thin film sample22,23. A stimulated inelastic RIXS signal has so far been detected only for atomic gas samples24 while similar studies for molecules remained inconclusive25. In related studies molecular products resulting from stimulated RIXS have been observed instead of the scattered X-rays themselves26,27.

In condensed matter, stimulated RIXS processes have not yet been demonstrated. This is mainly due to the increased complexity of electronic processes in solids, in particular the effect of inelastic cascading of photoelectrons and Auger electrons18,28,29. By use of XFEL-generated X-ray pulses centered around a strong XAS resonance of a solid sample, we here specifically address the interplay between pure photon driven, i.e. stimulated, valence to core transitions and intra-valence electron reshuffling effects due to inelastic scattering of photoelectrons and Auger electrons. This is accomplished by use of a transmission geometry through a thin film Co/Pd multilayer sample where the transmitted spectrum near the Co L3 XAS resonance is measured as a function of the incident intensity and energy distributions of 5 fs and 25 fs Full-Width-at-Half-Maximum (FWHM) pulses. A split pulse scheme is used for accurate pulse structure normalization. We observe the interplay between three different non-linear effects. The expected stimulated photon scattering enhancements in REXS and RIXS are accompanied by spectral changes due to inelastic scattering of the primary photo- and Auger-electrons. The latter effect leads to an electron redistribution near the Fermi energy that modifies the pure photon based stimulated REXS and RIXS spectra. The relative size of the three effects is quantified by use of a simple rigid density of states model for the studied Co/Pd sample which is in agreement with experiment. At our highest incident intensities of ≃300 mJ per cm2 per fs, the spontaneous RIXS signal is found to be enhanced by a factor of ≃106 for both 5 fs and 25 fs (FWHM) pulse lengths, close to the theoretical limit. Both stimulated gains are accompanied, however, by inelastic electron scattering which distorts the stimulated REXS and RIXS spectra due to changes in the valence band occupation near the Fermi energy. Their onset has previously been observed at lower intensities by detailed fluence-dependent XAS studies29. These secondary electron scattering effects are observed even for X-ray pulse lengths of 5 fs, indicating that their timescale is comparable to the “atomic clock” timescale set by the lifetime of the Co 2p core hole (1.5 fs).

Results and discussion

Experimental details

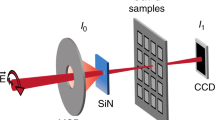
In order to reduce complexity, we study RIXS in a transmission geometry through a thin Co/Pd multilayer film, and detect the transmitted intensity in the forward scattering direction (momentum transfer q ≃ 0) with an energy resolving grating spectrometer, as illustrated in Fig. 1a.

Fig. 1: Experimental setup.
figure 1

a Simplified schematic of the experimental setup, which was also used in Chen et al.23. Linearly polarized Self-Amplified Spontaneous Emission (SASE) X-ray pulses are produced by an X-ray free electron laser. The X-ray pulses are split into two components with an X-ray beam splitter. One of the resultant X-ray beams passes through a blank SiN membrane while the other passes through a membrane with a Co/Pd magnetic multilayer. The beams emerging from the membranes in the forward direction are measured with a grating-based spectrometer which uses a Charge-Coupled Device (CCD) for photon detection. b Examples of single-shot spectra for a 25  fs pulse, recorded when the membranes and Co/Pd multilayers were removed from the X-ray paths. The spectra recorded from each beam align very well, demonstrating our ability to normalize the Co/Pd multilayer spectra by the bare membrane reference spectra.

Full size image

We used 5 fs and 25 fs (FWHM) linearly polarized X-ray pulses (see methods) produced through self-amplified spontaneous emission (SASE) at the Linac Coherent Light Source (LCLS)11. The pulses were directed to the Atomic Molecular and Optical station30 where they were split into two similar intensity pulses by a mirror with a sharp edge31. Both split pulses came to a focus near a Si chip containing 100 nm thick silicon nitride membrane windows. Half of the membranes had Co/Pd magnetic multilayers deposited on top of the SiN.

The multilayers were sputter deposited32 and had the metal layer sequence Ta(1.5)/Pd(3)/[Co(1)Pd(0.7)]x25/Pd(2), where the thicknesses in parentheses are in nm. One of the X-ray pulses passed through a membrane with the multilayer on top, while the other passed through a bare SiN membrane, acting as a reference as shown in Fig. 1a. The relative transmitted intensity through the sample had an energy-independent constant background, mostly due to Pd, which reduced the sample transmission to 55% of that through the bare SiN reference samples. The X-rays emerging from the membranes in the forward direction were detected at separate positions of a spectrometer with ≈1000 resolving power (see Methods). As shown in Fig. 1b, the photon energy content of the two X-ray beams was very similar, which enabled accurate normalization of our nonlinear X-ray transmission spectra, overcoming difficulties of earlier studies25.

The individual pulses contained coherent spikes as shown in Fig. 1b and their central X-ray photon energy was nominally set to 778 eV corresponding to the Co L3 resonance energy. As shown in the figure, the central pulse energy and spike structure varied pulse-to-pulse. The X-ray fluence onto the Co/Pd multilayers ranged from 0.1 through 9500 mJ per cm2 (see Methods). When the X-ray fluence exceeded about 50 mJ per cm2, the sample was damaged after the pulse through aftereffects of atomic diffusion or even explosion. Samples were therefore replaced every few X-ray shots and only the transmission spectrum of the first shot on each sample was analyzed. At low fluence (<10 mJ per cm2), spectra were recorded at the full 120 Hz repetition rate of LCLS for about five minutes and the samples were then replaced.

As shown in Fig. 1b, the incident pulses always contained photons at the resonant Co L3 absorption energy of E0 ≃  778 eV to produce Co 2p3/2 core holes. At low incident fluence, the transmitted spectrum is completely dominated by the dominant XAS intensity loss near E0, corresponding to the well-known strong XAS resonance29. Since in XAS, electrons are excited from Co 2p3/2 core electrons to empty 3d valence states above the Fermi level EF, this energy corresponds to the inflection point onset of the XAS resonance and serves as a natural demarcation line of the RIXS intensity below EF and the XAS and REXS intensities above EF.

The conventional spontaneous RIXS intensity from the sample is emitted into a 4π solid angle and is weak due to the Co fluorescence yield of only Yf = 8 × 10−3 7. At low incident fluence, RIXS emission at energies below E0 into the forward direction of our spectrometer is therefore completely negligible relative to the large XAS response. At high incident fluence, absorption above E0 will decrease due to stimulated REXS in the forward direction15,23, resulting in transmission increase at the resonant XAS energy. If the strong incident pulse also contains photons at energies below E0, the small spontaneous RIXS emission probability of Yf = 8 × 10−3 into 4π will be replaced by stimulated RIXS emission into the forward direction dΩ/(4π) (see Eq. 1), i.e. directly into the spectrometer. Then the stimulated RIXS increase into the spectrometer acceptance cone may be of order 106–107 so that it may become directly visible below E0 on the same intensity scale as the reduced XAS intensity above E0. This is the key to observing non-linear effects across the entire spectral energy range, containing both the XAS (REXS) and RIXS signatures in our experimental arrangement.

Experimental results

Figure 2 summarizes our experimental results. Of interest is the change in transmission through Co/Pd as a function of different incident pulse lengths, fluences and photon energy distributions. In practice, the incident intensity distributions have to overlap with the Co XAS resonance since any resonant non-linear response originates from the created Co 2p3/2 core holes.

Fig. 2: Summary of experimental results.
figure 2

a Comparison of the scaled spontaneous Co L3 Resonant Inelastic X-ray Scattering spectrum (RIXS, gray) for Co metal33 and the Co/Pd X-Ray Absorption Spectrum (XAS, black), both recorded at synchrotron light sources (low fluence limit). The red spectrum is the transmission version of the XAS spectrum. b Example of data extraction and normalization. The dashed gray line is the reference spectrum of a 25 fs pulse of 9490 mJ per cm2 fluence transmitted through the SiN window, multiplied by 0.55 to account for the constant non-resonant absorption of the Co/Pd sample. The blue curve is the measured transmission spectrum through the Co/Pd sample at the stated high fluence. The red curve is the spontaneous (low fluence) transmission spectrum, obtained by multiplying the red spectrum in (a) by the dashed-gray reference spectrum. Light blue shaded areas indicate non-linear gain and red areas non-linear loss. (c–h) show as dashed lines the reference spectra transmitted through the SiN for 5 fs and 25 fs pulses for different pulse shapes and fluences. The associated transmission difference spectra are shown as solid black lines. They were obtained by subtraction of the spontaneous low-fluence spectra from the non-linear high-fluence spectra for the respective transmission curves. The shading of areas corresponds to the procedure (blue minus red curves) illustrated in (b). Each spectrum is an average of many shots. The centers of three regions with non-linear response are denoted by dashed vertical lines and labeled α, β and γ.

Full size image

Figure 2 (a) shows low fluence spontaneous RIXS (gray curve) and XAS (black) spectra recorded with synchrotron radiation. The RIXS spectrum is that of Co metal, taken from Nilsson et al.33 and black curve is the polarization averaged XAS spectrum of our Co/Pd sample. It was recorded in the conventional synchrotron transmission geometry with the monochromator spectral resolution matched to our spectrometer in Fig. 1a. Any background below the Co absorption edge corresponding to 55% non-resonant absorption has been subtracted. We will refer to the shown spectra, scaled to the same unit peak value, as the spontaneous Co L3 XAS and RIXS spectra. Also shown as a red curve is the corresponding spontaneous resonant transmission spectrum given by

$${I}_{{{{{{{{\rm{trans}}}}}}}}}(\hslash \omega )={I}_{0}{{{{{{{{\rm{e}}}}}}}}}^{-{\sigma }_{{{{{{{{\rm{XAS}}}}}}}}}{\rho }_{{{{{{{{\rm{a}}}}}}}}}d}$$
(2)

where ρa = 91 atoms per nm3 is the atomic number density of Co and d = 25 nm the total Co thickness. In our case, the transmission at the Co L3 resonance is 32%.

Figure 2b illustrates the extraction of the transmission difference spectra to obtain the nonlinear relative to the spontaneous response. The dashed gray line is the reference transmission spectrum of a 25 fs pulse of 9490 mJ per cm2 fluence, which after beam splitting was transmitted through the SiN window. Its intensity was adjusted by a factor of 0.55, accounting for the non-resonant constant absorption of the Co/Pd sample. The red curve is the calculated spontaneous (low fluence) transmission spectrum through the Co/Pd sample for the reference pulse intensity and distribution, obtained by multiplying the red curve in (a) by the reference pulse transmission spectrum. The blue curve is the transmission spectrum measured for the indicated pulse length and high fluence. The shaded areas highlight the nonlinear changes in transmission, with light-blue areas indicating nonlinear transmission gain and red areas nonlinear transmission loss.

The experimental transmission difference spectra obtained with the procedure of Fig. 2b are shown in c–h for 5 fs and 25 fs X-ray pulses for different incident fluences and associated energy distributions of the pulses. The shown data for both 5 fs and 25 fs pulses correspond to multiple shots that were binned by the XFEL electron beam energy which is strongly correlated with the central photon energy of the X-ray pulses34. For each case, the dashed gray curves are the reference pulse spectra, scaled by 0.5 to emphasize the difference spectra shown as a solid black line. They represent the difference in transmission of Co/Pd for the respective pulse shapes and fluences and the low-fluence spontaneous transmission.

Figure 2c, d show the quality of our normalization procedure. At low fluences the calculated spontaneous transmission curves, obtained by multiplying the red curve in (a) with the pulse transmission function, are identical within noise with the measured transmission curves. In all high fluence cases, shown in Fig. 2e, f, g and h, the nonlinear response is negligible outside the Co L3 resonance region and exists only in the three regions indicated by vertical dashed lines, labeled in the figure. The central and bottom rows, respectively, show incident intensity distributions for 5 fs and 25 fs pulses, centered at similar central energy positions.

In the high-fluence spectra in Fig. 2e, f, g and h, the feature γ around the XAS peak position at 778 eV appears prominently as a transmission gain (blue) in all difference spectra. In contrast, the nonlinear features α and β show different behavior when the incident fluence distribution is shifted. As shown in Fig. 2g, h, the α feature disappears and the β feature becomes stronger when the incident distribution shifts to higher energy.

Assignment of non-linear features

We assign the lowest energy feature α, which is about 3.5 eV below the XAS peak, to stimulated RIXS. The feature is present only when there is sufficient incident intensity at its position, as shown in Fig. 2e and f. Since feature γ occurs at the XAS resonance position, we assign it partially to stimulated REXS, as suggested previously22,23. The blue shading of the stimulated RIXS and REXS intensities reveals a nonlinear increase in transmission. Since the RIXS and XAS intensities differ in practice by about six to seven orders of magnitude, the visibility of a RIXS signal reveals a large increase upon stimulation. As expected, the feature is absent when the incident pulse contains no photons at position α as in the bottom row of the figure.

Both stimulated REXS and RIXS spectral enhancements, however, are distorted by the presence of a third channel, seen as feature β. It is assigned to intra-valence band electron redistribution caused by secondary inelastic scattering of photo- and Auger electrons. This channel has previously been observed by detailed lower fluence XAS and X-ray magnetic circular dichroism studies29. In a solid, especially a metal, electron reshuffling around the Fermi energy, EF, may occur through electron excitations from below to above the Fermi energy (electron hole pairs). Upon deposition of sufficient energy by incident X-rays, such electron redistribution mimics a very high temperature Fermi-Dirac distribution over energies of 2 eV from the Fermi level29. Because of electron conservation, the decrease in electron population below EF is accompanied by an increase in electron occupation above EF. This adds to the stimulated REXS and RIXS channels in opposite ways.

Stimulated REXS and increased electron population above EF both reduce resonant absorption and increase transmission (blue shading). In stimulated REXS, the core electron excited into empty 3d states above EF is driven back into the core hole by stimulating photons, leading to a net loss of absorption15,22. Similarly, when valence electrons are excited across the Fermi level into empty 3d states through electron scattering, the absorption to these states is quenched. Both effects contribute similarly to the nonlinear response.

On the other hand, stimulated RIXS is due to 3d valence electrons from filled states below EF that are driven into core holes by stimulating photons. This makes the RIXS intensity observable through stimulation in the forward direction as a transmission increase. In the presence of electron excitations to states above EF, their loss in the filled states below EF quenches stimulated RIXS from this energy region. Hence the two effects partially compensate each other. This explains previous difficulties of observing stimulated RIXS in solids.

Quantitative model for the observed effects

The observed nonlinear effects can be accounted for by treating transition between core and valence states by a simple rigid density of states band model. Such a treatment is possible because of the local character of core hole excitations on Co atoms in the Co layers. The most important valence electrons in the nonlinear REXS/RIXS processes involve the Co 3d valence electrons owing to the dominance of atom-specific 2p3/2 ↔ 3d transitions. In equilibrium, the 3d band is filled with electrons below the Fermi level EF while states above EF are empty. In analogy to the description of molecular orbitals35, we shall denote filled electron states as 3d and empty states or holes as 3d*.

When Co atoms are excited through X-ray absorption, the final XAS core hole state is the intermediate state in REXS/RIXS. In our rigid band model the XAS process corresponds to 2p3/2 → 3d* transitions. In the REXS process, the excited electron transiently resides in the 3d* states before it decays back into the core hole. The spontaneous REXS process is incoherent since the decay is stochastically driven by the quantum mechanical zero point (ZP) field. The stimulated REXS process, in contrast, consists of a coherent up-down process driven by the concerted action of two or more photons between the initial and final states, which are the same. The RIXS process also starts with a 2p3/2 → 3d* XAS excitation to empty 3d* states. It is then followed by a 3d → 2p3/2 decay from filled valence states. The spontaneous RIXS decay is again driven by the ZP field while stimulated RIXS is driven by real photons and can therefore be enhanced.

The average lifetime of the intermediate Co core hole state is known to be τΓ ≃ 1.5 fs corresponding to a natural emission line width (FHHM) of Γ = ΓX + ΓA = ℏ/τΓ = 0.43 eV36. In contrast to optical transitions, the X-ray emission line width Γ is not determined by the dipolar width ΓX alone but contains a “ghost” contribution ΓA due to Auger decays. In the low fluence limit, the Auger decay process in Co atoms has a much larger probability, expressed by the small X-ray fluorescence yield Yf ≃ ΓX/ΓA which is only 8 × 10−3 7. This leads to the small spontaneous RIXS cross section relative to the XAS cross section as expressed by (1).

During an X-ray pulse of low incident fluence, the excitation of a specific Co atom in Co/Pd is not influenced by possible excitations of other Co atoms owing to the low probability of two or more Co atoms getting excited during the duration of a pulse. At high incident fluence, a significant fraction of all Co atoms in the sample gets excited during a pulse and for our impulsive stimulation geometry the broad energy bandwidth SASE pulses themselves can stimulate REXS and RIXS decays into the core holes. In addition, ASE can occur along the propagation path17,18,19,20,21. For our thin film samples, the ASE effect is quite weak in the forward direction because of the small Co thickness of 25 nm.

While ASE is expected to be weak for a thin film, another stronger indirect non-linear process can exist. It is triggered by primary photoelectrons and Auger electrons that multiply by inelastic scattering in random directions in the sample. At high incident fluence, the amplifying cascading effect is strong enough to create significant electron-hole excitations in the Co/Pd valence band. Whether this effect is observed depends on the relative timescale of the valence electron redistribution and the temporal width of the X-ray pulse. In Co/Pd the transfer of energy from the primary photo- and Auger-electrons to the entire valence electron sea proceeds in a cascade that ends up in an electron redistribution within a time of ≈10 fs29. Since this time is comparable to our pulse lengths such effects are expected to play a role. In addition, since the hot electron reservoir has not yet equilibrated with the lattice, an electron rearrangement has an extended energy range of about 2 eV around the Fermi level29.

Our identification of three dominant non-linear effects, namely stimulated REXS and RIXS and electron redistribution, may be used to quantitatively simulate the experimentally observed nonlinear transmission effects. We utilize the same procedure used to derive the experimental nonlinear spectra shown in Fig. 2. We can reference the assumed size and shape of the three nonlinear channels to the resonant X-ray absorption cross section which determines the sample transmission according to Eq. 2. The measured nonlinear transmission spectrum is then simply given by the change of the spontaneous transmission spectrum by the three nonlinear contributions.

In Fig. 3a we show the assumed spontaneous RIXS (gray), XAS (black) and transmission (red) spectra. The RIXS spectrum has been arbitrarily scaled to unit peak height. Also shown are the relative energy distributions and sizes of the three nonlinear contributions, assumed to represent those at the highest incident fluences in Fig. 2. We assume that the stimulated RIXS (magenta) and REXS (blue) contributions have the shape of the spontaneous spectra in (a) and have the same size of 18% of the resonant XAS peak value and area. The electron redistribution (green) is modeled by the difference of two Fermi-Dirac distributions that mimics previous experimental results29. It has a peak value of 20% of the resonant XAS value and 8% of the integrated XAS area.

Fig. 3: Model of nonlinear X-ray spectra.
figure 3

Here, spont. stands for spontaneous, stim./stimul. stand for stimulated, redist. stands for redistribution, rel. stands for relative, NL stands for nonlinear and EF is the Fermi energy. a Model Co L3 spontaneous Resonant Inelastic X-ray Scattering (RIXS, gray), X-Ray Absorption Spectrum (XAS, black) and transmission (red) spectra, and three assumed non-linear contributions, stimulated RIXS (magenta), electron redistribution (green) and stimulated Resonant Elastic X-ray Scattering (REXS, blue). The sizes of the nonlinear contributions are referenced to the unit value of the XAS peak. b Assumed incident pulse reference distribution (dashed), which allows all three nonlinear channels to contribute to the sum shown in black. c Shifted pulse reference distribution (dashed) which eliminates the stimulated RIXS contribution. The remaining two add up the sum shown in black. d Change of the spontaneous transmission spectrum (red) taken from (a), to the total nonlinear transmission one (black) for a wide incident energy distribution. The black curve is the red curve plus the the sum of all three nonlinear contributions. Colored arrows indicate nonlinear transmission gain (up arrows) and loss (down arrows) caused by the respective nonlinear channels.

Full size image

Depending on the energy distribution of the incident pulse, the three nonlinear contributions will contribute with different shapes and intensities. This is shown for two pulse distributions in Fig. 3b, c, modelled to reflect the two 25 fs high-fluence cases in Fig. 2f and h. When the incident distribution covers both the REXS and RIXS regions, all three nonlinear channels contribute and the resulting nonlinear transmission change is shown as a black line in Fig. 3b. When the RIXS energy region is inadequately covered, only the other two nonlinear channels contribute, as shown in Fig. 3c. Finally, we show in Fig. 3d the change of the spontaneous transmission spectrum in (a), shown again in red, by adding to it the three nonlinear contributions in Fig. 3b. The total nonlinear transmission spectrum (black) exhibits strong nonlinear effects whose spectral distortions are indicated by arrows.

Of particular interest is that now the stimulated RIXS spectrum, although, partly obscured by electron redistribution, appears on the same scale as the XAS effect. This arises from a stimulated amplification by a factor of order 106 relative to the spontaneous RIXS intensity (see sections Comparison of Experiment with Maxwell-Bloch RIXS Simulations and Comparison of Experiment with Kramers-Heisenberg-Dirac RIXS Theory). The close quantitative agreement of our simulations with experimental results for corresponding incident pulse distributions is underscored by their direct comparison on the same vertical scales in Fig. 4.

Fig. 4: Comparison of nonlinear spectra model to experiment.
figure 4

Here, spont. stands for spontaneous. a Experimental high-fluence non-linear effects for 25 fs pulses taken from Fig. 2f, h. b Simulated results with our model for similar incident intensity distributions, plotted on the same scale. The shown simulated curves are the black curves in Fig. 3b, c.

Full size image

The good quantitative agreement of theory and experiment allows us to determine the increase in stimulated over spontaneous RIXS for an incident intensity of about 300 mJ per cm2 per fs. At this value, the size of the stimulated RIXS intensity has a value of 18% of the spontaneous XAS intensity. We also find that the stimulated RIXS and REXS intensities are the same in our model. In the following we compare these values with calculations for the stimulated RIXS rate.

Comparison of experiment with Maxwell-Bloch RIXS Simulations

In Fig. 5a we show the two RIXS intensities for the highest fluence 5 fs and 25 fs pulses, deduced from the experimental data with help of our simulation model, in a logarithmic intensity versus fluence plot. The measured RIXS intensities, indicated by magenta (5 fs) and green (25 fs) filled circles, are referenced to the spontaneously absorbed intensity indicated by a black horizontal line of unit value. Another horizontal line indicates the fluorescence yield of Yf = 8 × 10−3 7, which corresponds to the spontaneous RIXS signal emitted into 4π, most of which is not seen by the detector.

Fig. 5: Experimental and simulated dependence of stimulated Resonant Inelastic X-ray Scattering (RIXS) amplification on X-ray fluence and X-ray intensity.
figure 5

Here, rel. stands for relative, spont. stands for spontaneous, stim. stands for stimulated, XAS stands for X-ray absorption spectrum, Yf is the fluorescence yield and Ωdet is the solid angle of acceptance of the spectrometer. a Dependence of stimulated RIXS amplification on fluence and pulse duration. The magenta and green circles are the experimentally determined stimulated RIXS intensities for 5 fs and 25 fs pulses relative to the spontaneous absorption rate. The error bars estimate the standard error in the absence of nonlinear effects. Also indicated as a horizontal line is the spontaneous RIXS rate emitted into 4π, i.e. the fluorescence yield Yf = 8 × 10−3 7. The correspondingly colored curves represent RIXS rates for L3 excitation of Co atoms, relative to the spontaneous absorption rate, calculated by use of a statistical Self-Amplified Spontaneous Emission (SASE) pulse description combined with a three level Maxwell-Bloch (MB) theory. The gray shaded region at the bottom indicates the fraction of the spontaneous RIXS signal typically seen by a detector with an angular acceptance of order 10−5 − 10−4. Vertical arrows indicate the two contributions to the observed stimulated RIXS relative to the absorbed rate. b The data in a are plotted as a function of incident intensity and comparison with the Kramers-Heisenberg-Dirac (KHD, blue) and MB (magenta and green) theories.

Full size image

As indicated by the horizontal gray line through the data points, the stimulated RIXS intensity is about 20% of the absorbed intensity, corresponding to a factor of about 20 increase in decay probability relative to the fluorescence yield, as indicated. More importantly, we also show a shaded gray band at the bottom that indicates the small fraction of the spontaneous RIXS signal typically seen by a detector with an angular acceptance of order 10−5−10−4 8. The gain advantage of stimulated RIXS predominantly arises from the solid angle enhancement rather than the factor 20 increase in decay probability. In fact, the stimulated decay probability will saturate at a maximum increase of a factor of 50 relative to fluorescence yield when at higher incident fluence absorption and emission equilibrate.

Also shown in Fig. 5a as magenta and green lines are the stimulated RIXS intensity increases predicted by the Maxwell-Bloch (MB) theory16 in conjunction with a statistical description of the SASE XFEL pulses37,38, discussed in Methods below. The statistical approach, which complicates data analysis, has typically been employed for the description of non-linear phenomena studied with SASE based XFELS39. The stimulated RIXS rate is again normalized to the spontaneous absorption rate, so that the theory reveals the expected linear increase with the number of stimulating photons per created core hole. At the highest fluence, the MB rate reveals a deviation from linearity due to saturated absorption. The theory is seen to underestimate the experimentally observed values by a factor of about 5.

In Fig. 5b we have recast the experimental results shown in (a) in terms of incident intensity, given by the fluence divided by the pulse length. The experimental data points then nearly merge and for an incident intensity of ≃300 mJ per cm2 per fs we find a stimulated RIXS intensity of about 20%, indicated by the horizontal gray line. This value corresponds to the total stimulated RIXS contribution shown as a magenta distribution curve in Fig. 3a. It is difficult to extract from the experimental data, alone, since it is partially hidden by the electron rearrangement intensity.

The additional blue line in Fig. 5b represents the description of stimulated RIXS by the KHD approximation given by (1) in conjunction with a simple model of the SASE pulses which we discuss next.

Comparison of experiment with Kramers-Heisenberg-Dirac RIXS Theory

In the RIXS literature which covers experiments ranging from molecules, polymers and chemisorption systems to solids with weak and strong valence correlations and solids in high pressure environments, the RIXS process is typically described in the KHD second order perturbation formalism1,2,3,4. It is outlined in Methods with emphasis on its simplification leading to (1). The essence of this “two-step” or “direct RIXS” simplification is the neglect of interference effects in the intermediate core hole state. This is typically a good approximation for solids1,4 while for free molecules, interference paths through vibrational intermediate states need to be included, leading mostly to relative intensity changes of the vibrational peaks1,40. The KHD perturbation approach is valid only as long as the stimulated rate increases linearly with npk and does not saturate. This condition is fulfilled over most of the fluence range as shown by the MB curves in Fig. 5a, with small changes due to saturation appearing only at the highest fluences.

The complete KHD theory expressed by Eq. 6 in Methods, distinguishes between exciting and stimulating photons. This distinction is absent in (1) since we normalize the RIXS to the XAS cross section, i.e. the system has already been “pumped” through absorption. The number of photons npk in (1) refers to those available in the mode pk to “dump” excited electrons back into the core hole through stimulation. Photons in the same mode are coherent and contained in the mode volume Vpk = λ3ℏω/Δpk, composed of the minimum lateral coherence area A = λ2 and longitudinal coherence length ℓ = λ ℏω/Δpk10. Since XFEL pulses are laterally coherent, only the longitudinal or temporal coherence is important in the present study.

Our impulsive stimulation geometry and the small energy separation \({{{{{{{{\mathcal{E}}}}}}}}}_{b}\,-\,{{{{{{{{\mathcal{E}}}}}}}}}_{a}\simeq 2\) eV allows us to adopt a particular convenient description of the incident SASE pulses which circumvents statistical modelling. Both pump and dump photons may be viewed as being contained in individual coherent and therefore transform limited spikes of temporal FWHM τ = 0.5 – 1 fs within the SASE pulses. When transformed into the energy domain, a flat-top temporal spike is converted into a sinc2 shaped energy distribution with the FWHM of the distributions related by τΔpk = 0.886h, where h = 4.14 fs eV is Planck’s constant. Because of the large energy width of several eV, REXS and RIXS can then be described by the average number of photons in individual temporal spikes which each cover a broad energy range that contains the absorption and emission regions. This allows us to express npk in terms of the average spike intensity Ipk which may be approximated as the incident fluence divided by the total temporal pulse length. This leads to the relation,

$${n}_{p{{{{{{{\bf{k}}}}}}}}}=\frac{1}{c}\frac{{\lambda }^{3}}{{{{\Delta }}}_{p{{{{{{{\bf{k}}}}}}}}}}{I}_{p{{{{{{{\bf{k}}}}}}}}}$$
(3)

For our geometry, the incident photons propagate into the forward direction so that the RIXS cross section per atom measured by the detector may be written as,

$$\sigma_{{{{{\mathrm{RIXS}}}}}} = \underbrace{\frac{d \varOmega_{{\det}}}{4\pi} \, Y_{{{{{\mathrm{f}}}}}}\, \sigma_{{{{{\mathrm{XAS}}}}}}}_{{{\mbox{spontaneous}}}}+ \underbrace{n_{\!p {{{{{\mathbf{k}}}}}}} \, Y_{{{{{\mathrm{f}}}}}}\, \sigma_{{{{{\mathrm{XAS}}}}}}}_{{{\mbox{stimulated}}}}$$
(4)

This formulation clearly shows the advantage of stimulated RIXS. The absence of the factor \(d\,{\Omega}_{\det}/4\pi\) in the stimulated case allows the finite-acceptance-angle detector to see a gain as soon as \({n}_{p{{{{{{{\bf{k}}}}}}}}} \, > \, d\,{\Omega }_{\det }/4\pi\). This fact is expressed in Fig. 5a by the stimulated gain exceeding the shaded gray region representing the relative spontaneous detection rate.

The stimulated gain calculated with the KHD theory assuming Δpk = 8 eV in (3) is shown as a function of incident intensity by a blue line in Fig. 5b. There is agreement with the experimental data. The agreement may be more realistically understood as follows. Equation 4 tacitly assumes that the RIXS response of all atoms in the sample is the same. It does not account for the actual attenuation of the incident intensity as it propagates through the sample. In a proper treatment, the stimulated response of a sample of finite thickness d should be described by the propagation of the stimulated linear response of thin slices of thicknesses much less than one X-ray absorption length (about 20 nm in our case). Since the incident intensity falls by a total factor of about 3 through our total Co thickness of 25 nm, our neglect of propagation overestimates the stimulated response by about a factor of 2. One may more realistically understand the good agreement of the blue line in Fig. 5b with experiment by an effective energy width Δpk = 4 eV or half of the assumed value. This increases npk according to (3) by a factor of 2 which is compensated a factor of 2 due to the neglected reduction of pulse propagation.

The stimulated REXS channel

Our modelling of the experimental results in Fig. 3 also provided information on the stimulated REXS channel, which at an incident intensity of ≃300 mJ per cm2 per fs was found to have the same intensity as the stimulated RIXS contribution according to Fig. 3a. The reason for the same contributions of stimulated REXS and RIXS in our case is derived in Methods. There we also discuss different formulations of stimulated REXS, in particular, the semi-classical existence of a coherent enhancement factor introduced in15. The equivalence of our present fully quantum mechanical treatment with the semi-classical one used in Chen et al.23 for the same Co/Pd samples is illustrated in Fig. 6.

Fig. 6: Experimental and simulated dependence of X-ray transmission on X-ray intensity.
figure 6

Here, rel. stands for relative. a Spontaneous (spont.) and nonlinear (NL) transmission spectra taken from Fig. 3d, with horizontal dashed lines indicating the relative peak transmission values. b Reproduced with permission Fig. 3a of Chen et al.23. Light blue open circles represent the transmission response simulated by statistical modelling of the Self-Amplified Spontaneous Emission (SASE) pulses in conjunctions with the two-level optical Bloch equations. The thick solid blue line links experimental data points, averaged over multiple shots, for the same Co/Pd multilayer samples used here.

Full size image

In Fig. 6a we have replotted the simulated transmission spectrum of Fig. 3d corresponding to an incident intensity of ≃300 mJ per cm2 per fs, with the spontaneous and nonlinear peak transmissions indicated by dashed red and blue horizontal lines. Their values agree with those given in Fig. 3a of Chen et al.23 which is reproduced in Fig. 6b. In both cases, the spontaneous transmission of 32% is found to change to about 62% through nonlinear effects.

Conclusions

Our studies show that both REXS and RIXS channels may be significantly enhanced by stimulation, also in solids. The most important enhancement comes from the direction-preserving nature of stimulated decays. This leads to angular enhancement factors for stimulated over spontaneous RIXS of order 104–105 due to the small acceptance angle of typical spectrometer. Relative to this number, the gain in stimulation-enhanced decay probability over the spontaneous fluorescence yield is relatively small. For the case of the Co L3 resonance, we observe about a 20 fold gain in the photon driven decay probability. This compares to the maximum possible enhancement of a factor of about 50, limited by saturation or equilibration of the absorption and emission channels.

As pointed out previously39, present RIXS experiments are complicated by the statistical SASE structure of XFEL pulses. Our statistical modelling of the pulses in conjunction with the Maxwell-Bloch theory underestimates the observed stimulated RIXS intensity by about a factor of 5. Statistical modelling is expected to yield better average fluence values for longer SASE pulses than used here, because of the greater number of coherent spikes. We also carried out MB calculations in the extreme two color limit, where for each pump photon at the absorption resonance, suitable dump photons at the emission energy were available. For the same incident X-ray intensity, this predicted a stimulated RIXS curve for the 25 fs SASE pulses that was more than a factor of five higher than the MB curve shown in Fig. 5.

The results of the simpler Kramers-Heisenberg-Dirac theory in conjunction with the assumption that the RIXS process is driven by individual SASE spikes whose short temporal duration provides the required bandwidth to cover both absorption and emission energies, was found to give good agreement with experiment. Since the energy losses probed with RIXS in solids are typically limited to a few eV, a beam consisting of a single few hundred attosecond spike26,41 may be a convenient source for future RIXS studies.

Our results have substantial implications for future RIXS and nonlinear X-ray investigations of solids because of the identified third nonlinear channel, caused by inelastic scattering of photo- and Auger electrons. The resulting valence electron redistribution effects distort the stimulated REXS and RIXS spectra due to overlapping spectral changes. For stimulated RIXS to become a robust technique for the study of low lying excitations in solids, future studies must find a way to mitigate this deleterious effect.

Methods

Adjustment and determination of X-ray fluence

The X-ray fluence at the Co/Pd multilayers was adjusted by changing the attenuation of a nitrogen gas attenuator42 before the Co/Pd multilayers as well as changing the spot size at the Co/Pd multilayers. The pulse energy at the Co/Pd multilayers was determined from the X-ray pulse energy measured with a gas detector42. The X-ray transmission efficiency from the gas detectors to the Co/Pd multilayers was estimated to be 10 percent. The X-ray spot size at the Co/Pd multilayers was measured through pinhole scans, giving a size of either 15 by 15 μm, or 20 by 150 μm, depending on the setting of the X-ray focusing mirrors.

Characterization of X-ray pulse duration

The average duration of X-ray pulses produced by LCLS in different modes was estimated using two different methods. The methods are complementary in that the first sets an upper limit on average pulse duration while the second sets a lower limit. In the first method, an X-band Transverse Deflecting Cavity measured the energy and temporal distribution of electrons in electron bunches after those bunches were used in the production of X-rays. The intensity profile of X-ray pulses was then derived from the time-resolved energy changes due to the XFEL lasing on the measured electron bunch43. This confirmed the 25 fs FWHM duration of the longer pulses and set an upper limit of 10 fs on the duration of the shorter pulses. In the second method, averaged pulse durations were estimated from the statistical correlation of X-ray spectra44,45. For the same operating modes as used for collecting data on the Co/Pd multilayers, we recorded spectra using the spectrometer of the Soft X-Ray Materials Science beamline46. For robustness of this analysis method, we limited the analysis to X-ray pulses where the central electron energy of the electron bunch generating the X-ray pulse was within the middle 10 percent of observed values. This gave a lower limit of 4.7 fs on the duration of the shorter pulses and 8.5 fs on that of the longer pulses.

Retrieval of X-ray spectra

Spectra were obtained from spectrometer CCD images by selecting the relevant region on the imaging detector and projecting along the axis of photon energy dispersion. The photon energy was calibrated by adjusting the coefficients of a linear relationship between spectrometer pixel position and photon energy such that a low fluence absorption spectrum measured at LCLS agreed with that measured on the same sample at beamline 13.3 at the Stanford Synchrotron Radiation Lightsource.

Kramers-Heisenberg-Dirac theory of RIXS

The KHD expression (1) arises in second order perturbation theory which gives the double differential resonant scattering rate as,

$$\frac{{{{{{{\mathcal{W}}}}}}}^{{{{{\mathrm{scat}}}}}}_{a \rightarrow b} }{d \varOmega_2 \, d (\hbar \omega_2)}\! = \underbrace{\frac{c\,n_{\!p_1{{{{{\mathbf{k}}}}}}_1}}{V_{p_1{{{{{\mathbf{k}}}}}}_1}}}_{{\mbox{${{\Phi}}_1$}}} \,\frac{d \sigma^{{{{{\mathrm{scat}}}}}}_{a \rightarrow b}}{d \varOmega_2 \, d( \hbar \omega_2)}$$
(5)

where Φ1 is the incident photon flux expressed by the photon degeneracy parameter, defined as the number of photons \({n}_{{p}_{1}{{{{{{{{\bf{k}}}}}}}}}_{1}}\) that are emitted from the mode volume \({V}_{{p}_{1}{{{{{{{{\bf{k}}}}}}}}}_{1}}={\lambda }^{3}\hslash {\omega }_{1}/{{{\Delta }}}_{{p}_{1}{{{{{{{{\bf{k}}}}}}}}}_{1}}\) with the speed of light c. In the dipole and rotating wave approximations, the double differential RIXS resonant cross section is expressed by1,

$$\frac{d{\sigma }_{a\to b}^{{{{{{{{\rm{RIXS}}}}}}}}}}{d{\varOmega }_{2}\,d({\hslash} {\omega }_{2})}= \frac{4{\pi }^{2}{\hslash} {\omega }_{1}{\hslash} {\omega }_{2}\,{\alpha }_{{{{{{{{\rm{f}}}}}}}}}^{2}}{{\lambda }_{2}^{2}}\,{{{{{{{{\mathcal{R}}}}}}}}}^{4}\,\left({n}_{{p}_{2}{{{{{{{{\bf{k}}}}}}}}}_{2}}\,+\,1\right)\\ \times \mathop{\sum }\limits_{b}^{{\omega }_{2}\le {\omega }_{1}}{\left|\mathop{\sum}\limits_{c}\frac{\left\langle b\right|\hat{{{{{{{{\bf{r}}}}}}}}}\cdot {{{{{\epsilon }}}}}_{{p}_{2}}^{* }\left|c\right\rangle \left\langle c\right|\hat{{{{{{{{\bf{r}}}}}}}}}\cdot {{{{{\epsilon }}}}}_{{p}_{1}}\left|a\right\rangle }{{\hslash} {\omega }_{1}-{{{{{{{{\mathcal{E}}}}}}}}}_{ca}+{{{{{{{\rm{i}}}}}}}}{{{\Gamma }}}_{c}/2}\right|}^{2}\\ \times \,L({\hslash} {\omega }_{1}\,-\,{\hslash} {\omega }_{2}\,-\,{{{{{{{{\mathcal{E}}}}}}}}}_{ba})$$
(6)

where \({{{{{{{{\mathcal{E}}}}}}}}}_{ij}={{{{{{{{\mathcal{E}}}}}}}}}_{i}\,-\,{{{{{{{{\mathcal{E}}}}}}}}}_{j}\) denotes the energy difference between two electronic states i and j, and

$$L(\hslash {\omega }_{1}\,-\,\hslash {\omega }_{2}\,-\,{{{{{{{{\mathcal{E}}}}}}}}}_{ba})=\frac{2}{\pi {{{\Gamma }}}_{b}}\frac{{{{\Gamma }}}_{b}^{2}/4}{{\left(\hslash {\omega }_{1}-\hslash {\omega }_{2}-{{{{{{{{\mathcal{E}}}}}}}}}_{ba}\right)}^{2}+{{{\Gamma }}}_{b}^{2}/4}$$
(7)

describes the final state Lorentzian energy distribution of unit integrated area and FWHM Γb. Its argument \(\hslash {\omega }_{1}\,-\,\hslash {\omega }_{2}\,-\,{{{{{{{{\mathcal{E}}}}}}}}}_{ba}\) links it to the Raman effect in optical spectroscopy. This expression is valid for negligible instrumental linewidth contributions.

In (6), αf ≃ 1/137 is the fine structure constant and \({{{{{{{\mathcal{R}}}}}}}}\) the radial 2p → 3d dipole matrix element, which is assumed to be the same for all transitions linking the core and valence manifolds. The remaining polarization dependent transition double matrix element depends on the angular momentum degeneracy of the core and valence states. The state \(\left|a\right\rangle\) is the initial electronic ground state of energy \({{{{{{{{\mathcal{E}}}}}}}}}_{a}\) and the states \(\left|c\right\rangle\) are the intermediate core hole states through which the system passes to the final state \(\left|b\right\rangle\) of energy \({{{{{{{{\mathcal{E}}}}}}}}}_{b}\). In RIXS, \(\left|b\right\rangle\) is another excited electronic state lying above the ground state by a relatively small energy separation \({{{{{{{{\mathcal{E}}}}}}}}}_{ba}={{{{{{{{\mathcal{E}}}}}}}}}_{b}\,-\,{{{{{{{{\mathcal{E}}}}}}}}}_{a}\). This energy difference extends from meV for vibrationally excited states to several eV for electronic excited states. The normalized Lorentzian of unit integrated area assures strict energy conservation between the initial state \(\left|a\right\rangle\) and final state \(\left|b\right\rangle\) which does not involve the intermediate states \(\left|c\right\rangle\).

The direct RIXS differential cross section is obtained by eliminating intermediate state interference effects by taking the sum over intermediate states c out of the squared absolute value in (6) and rewriting the expression in the three state RIXS form,

$$\begin{array}{lll} & & \frac{d \sigma^{{{{{\mathrm{dir}}}}}}_{{{{{\mathrm{RIXS}}}}}}}{d \varOmega_2 \,d (\hbar\omega_2)}=\frac{\lambda^2_1}{ 2\pi^3 } \left(n_{\!p_2{{{{{\mathbf{k}}}}}}_2} + 1 \right) \mathop{\sum}\limits_b \mathop{\sum}\limits_c \\ & &\times \underbrace{\frac{8 \pi^2 \hbar\omega_1 \alpha_{{{{{\mathrm{f}}}}}}}{\lambda^2_1} {{{{{{\mathcal{R}}}}}}}^2 | \left\langle c\right| \left(\hat{{{{{{\mathbf{r}}}}}}} \cdot {{\epsilon}}_{p_1}\right. \left| a \right\rangle |^2}_{{\mbox{absorption}}: \;{\Gamma}^{p_1}_{ac}} \frac{1}{{{\Gamma}}_c^2 } \frac{({{\Gamma}}_c/2)^2}{ \left(\hbar \omega_1 - {{{{{{\mathcal{E}}}}}}}_{ca} \right)^2 + ({{\Gamma}}_c/2)^2} \\ & & \times\underbrace{\frac{ 8 \pi^2 \hbar\omega_2 \alpha_{{{{{\mathrm{f}}}}}}}{\lambda^2_2} {{{{{{\mathcal{R}}}}}}}^2 \left| \langle b | (\hat{{{{{{\mathbf{r}}}}}}} \cdot {{\epsilon}}^*_{p_2}) | c \rangle \right|^2 }_{{\mbox{emission}}:\; {\Gamma}^{p_2}_{cb}}\frac{1}{{{\Gamma}}_b }\frac{ ({{\Gamma}}_b/2)^2 }{\left( \hbar \omega_2 - {{{{{{\mathcal{E}}}}}}}_{cb} \right)^2 + ({{\Gamma}}_b/2)^2} \end{array}$$
(8)

where the underbrackets define dipolar transition energy widths of the excitation (\({{{\Gamma }}}_{ac}^{{p}_{1}}\)) and decay (\({{{\Gamma }}}_{cb}^{{p}_{2}}\)) processes, specified below.

The direct double differential RIXS cross section contains two decay lifetime widths, those of the core hole intermediate state Γc and that of the final state Γb. The intermediate state width is given by Γc = Γ = ΓX + ΓA in (1). We can eliminate the final state width by integrating over all emission energies ℏω2 to obtain the compact expression,

$$\frac{d \sigma^{{{{{\mathrm{dir}}}}}}_{{{{{\mathrm{RIXS}}}}}}}{d\varOmega_2} = \frac{1}{4\pi} (1 + n_{\!p {{{{{\mathbf{k}}}}}}} ) \frac{ {{\Gamma}}^{p_2}_{cb}}{{\Gamma}} \underbrace{\frac{\lambda^2_1}{ \pi } \frac{{{\Gamma}}^{p_1}_{ac} }{{{\Gamma}} } \frac{({{\Gamma}}/2)^2}{(\hbar \omega_1 \! - \! {{{{{{\mathcal{E}}}}}}}_{ca})^2 \! + \! ({{\Gamma}} /2)^2}}_{{\mbox{$\sigma_{{{{{\mathrm{XAS}}}}}}^{p_1}$}}}$$
(9)

If we average the emission rate over polarization, we obtain \({{{\Gamma }}}^{{{{{{{{\rm{X}}}}}}}}}=\langle {{{\Gamma }}}_{cb}^{{p}_{2}}\rangle =\frac{1}{3}{\sum }_{{p}_{2}}{{{\Gamma }}}_{cb}^{{p}_{2}}\) which is the radiative emission width that determines the fluorescence yield Yf. If we similarly replace the XAS cross section by its polarization averaged value \({\sigma }_{{{{{{{{\rm{XAS}}}}}}}}}=\frac{1}{3}{\sum }_{{p}_{1}}{\sigma }_{{{{{{{{\rm{XAS}}}}}}}}}^{{p}_{1}}\), we obtain our desired expression (1) or

$$\frac{d{\sigma }_{{{{{{{{\rm{RIXS}}}}}}}}}^{{{{{{{{\rm{dir}}}}}}}}}}{d{\varOmega }_{2}}=\frac{1}{4\pi }\,\frac{{{{\Gamma }}}^{X}}{{{\Gamma }}}\,(1+{n}_{p{{{{{{{\bf{k}}}}}}}}})\,{\sigma }_{{{{{{{{\rm{XAS}}}}}}}}}$$
(10)

When the spontaneous (npk = 0) RIXS cross section is integrated over emission energies and angles, we see that it becomes the absorption cross section times the fluorescence yield, as required by energy conservation.

For the Co L edge the absorption and emission widths \({{{\Gamma }}}_{ac}^{{p}_{1}}\) and \({{{\Gamma }}}_{cb}^{{p}_{2}}\) in (8), averaged over polarization, need to be evaluated by considering the angular momentum degeneracies of the ground state \(\left|a\right\rangle\) and final (XAS) or intermediate (RIXS) state \(\left|c\right\rangle\). This consists of counting the electron and hole states per spin that contribute to a given transition, since the dipole operator conserves spin. Denoting the angular momenta for the core states as c and valence states as L, in Co metal there are Nh = 2.53d* holes in the 2(2L + 1) = 10 total states and Ne = 7.5 electrons6. The XAS and RIXS dipole transition widths are then obtained by taking the common prefactor in (8) to be

$$A=\frac{8{\pi }^{2}\hslash \omega \,{\alpha }_{{{{{{{{\rm{f}}}}}}}}}}{{\lambda }^{2}}\,{{{{{{{{\mathcal{R}}}}}}}}}^{2}=10\,{{{{{{{\rm{meV}}}}}}}}$$
(11)

This yields for the L = 2 → c = 1 emission dipole matrix element

$${{{\Gamma }}}^{X}=A\,\frac{L{N}_{{{{{{{{\rm{e}}}}}}}}}}{3(2L+1)(2c+1)}=3.3\,{{{{{{{\rm{meV}}}}}}}}$$
(12)

and with the value Γ = 430 meV36 gives the literature fluorescence yield of7

$${Y}_{{{{{{{{\rm{f}}}}}}}}}=\frac{{{{\Gamma }}}^{X}}{{{\Gamma }}}=7.7\times 1{0}^{-3}$$
(13)

Similarly we obtain for the c = 1 → L = 2 absorption matrix element

$${{{\Gamma }}}_{{{{{{{{\rm{XAS}}}}}}}}}=A\,\frac{L{N}_{{{{{{{{\rm{h}}}}}}}}}}{3(2L+1)}=3.3\,{{{{{{{\rm{meV}}}}}}}}$$
(14)

which happens to be same as ΓX since the difference in the angular momentum and electron/hole occupation factors cancel each other. The absorption matrix element for the L3 transition, only, is a factor of 2/3 smaller. The so obtained value, which is self consistent with the literature values of Γ and Yf, is about a factor of 2 larger than that obtained by curve-fitting of the L3 XAS resonance in Stöhr and Scherz15.

Kramers-Heisenberg-Dirac theory of REXS

Expression (6) also describes REXS with \(\left|b\right\rangle \,=\,\left|a\right\rangle\) and ℏω = ℏω1 = ℏω2. Since the final state is the ground state with infinitely long lifetime or infinitely narrow linewidth, the Lorentzian is replaced by a Dirac δ-function of the same unit integrated area, which accounts for energy conservation. While in spontaneous REXS, photons are emitted into random directions, stimulated REXS preserves the direction and polarization, k = k1 = k2 and p = p1 = p2, so that

$$\frac{{\sigma }_{{{{{{{{\rm{REXS}}}}}}}}}^{{{{{{{{\rm{stim}}}}}}}}}}{d\varOmega }=\, \frac{4{\pi }^{2}{(\hslash \omega )}^{2}\,{\alpha }_{{{{{{{{\rm{f}}}}}}}}}^{2}}{{\lambda }^{2}}\,{{{{{{{{\mathcal{R}}}}}}}}}^{4}\,{n}_{p{{{{{{{\bf{k}}}}}}}}}\\ \times {\left|\mathop{\sum}\limits_{c}\frac{| \langle c| \hat{{{{{{{{\bf{r}}}}}}}}}\cdot {{{{{\epsilon }}}}}_{p}| a\rangle {| }^{2}}{\hslash \omega \,-\,{{{{{{{{\mathcal{E}}}}}}}}}_{ca}\,+\,{{{{{{{\rm{i}}}}}}}}{{{\Gamma }}}_{c}/2}\right|}^{2}\delta (\hslash \omega \,-\,{{{{{{{{\mathcal{E}}}}}}}}}_{ca})$$
(15)

For a single intermediate state the stimulated REXS cross section is related to the XAS cross section according to,

$$\frac{\sigma^{{{{{\mathrm{stim}}}}}}_{{{{{\mathrm{REXS}}}}}}}{d \varOmega} \! =\, \frac{n_{\!p {{{{{\mathbf{k}}}}}}}}{4\pi {{\Gamma}}} \,\underbrace{\frac{ 8 \pi^2 \,\hbar\omega \, \alpha_{{{{{\mathrm{f}}}}}}}{ \lambda^2 } \, {{{{{{\mathcal{R}}}}}}}^2 \,|\langle a | \hat{{{{{{\mathbf{r}}}}}}} \cdot {{\epsilon}}_{p} | c \rangle|^2}_{{\mbox{${{\Gamma}}^p_{ca}$}}} \\ \times \underbrace{4 \pi \hbar\omega \, \alpha_{{{{{\mathrm{f}}}}}} \, {{{{{{\mathcal{R}}}}}}}^2 |\langle c | \hat{{{{{{\mathbf{r}}}}}}} \cdot {{\epsilon}}_{p} | a \rangle|^2 \frac{{{\Gamma}}/2}{(\hbar \omega - {{{{{{\mathcal{E}}}}}}}_{ca})^2 + {{\Gamma}}^2/4 }}_{{\mbox{$\sigma^p_{{{{{\mathrm{XAS}}}}}}$}}}$$
(16)

where \({{{\Gamma }}}_{ca}^{p}={{{\Gamma }}}_{ac}^{p}={{{\Gamma }}}_{{{{{{{{\rm{XAS}}}}}}}}}\) expresses a coherent up-down process determined by the XAS matrix element (14). We therefore have,

$${{{\Gamma }}}_{{{{{{{{\rm{REXS}}}}}}}}}^{{{{{{{{\rm{stim}}}}}}}}}={{{\Gamma }}}_{{{{{{{{\rm{XAS}}}}}}}}}={{{\Gamma }}}_{{{{{{{{\rm{RIXS}}}}}}}}}$$
(17)

This accounts for the same stimulated RIXS and REXS contributions in our model in Fig. 3 (a).

Finally, we need to comment on the agreement between the change of the nonlinear transmission shown in Fig. 6a and b. Our present formulation of the stimulated REXS cross section (16) leads to the intensity change in Fig. 6a. It is calculated by use of the matrix element for the Co L3 resonance ΓXAS = (2/3) × 3.3 = 2.2 meV. This corresponds to the assumption that the Co L3 XAS cross section written in the theoretical atomic form of (9) as

$${\sigma }_{{{{{{{{\rm{XAS}}}}}}}}}=\frac{{\lambda }^{2}}{\pi }\frac{{{{\Gamma }}}_{{{{{{{{\rm{XAS}}}}}}}}}}{{{\Gamma }}}\frac{{({{\Gamma }}/2)}^{2}}{{(\hslash \omega -{{{{{{{{\mathcal{E}}}}}}}}}_{ca})}^{2}\,+\,{({{\Gamma }}/2)}^{2}}$$
(18)

has a peak value of λ2ΓXAS/(πΓ) = 41.7 Mb per atom, concentrated within the natural linewidth of Γ = 430 meV. In contrast, the intensity change in Fig. 6b, adopted from Chen et al.23, was calculated in a solid state model, where the peak cross section was taken as the experimental Co metal value of 6.25 Mb, which is smaller due to broadening of the 3d valence orbitals by band-structure effects15. In the solid state model, the lower peak cross section is compensated by an increased collective atomic response, expressed by a forward scattering coherence factor Gcoh = λ2Na/(4πA)15. The two formulations give similar results and are linked according to,

$${n}_{pk}{{{\Gamma }}}_{{{{{{{{\rm{XAS}}}}}}}}}^{{{{{{{{\rm{atom}}}}}}}}}\simeq {n}_{{{\Gamma }}}\,{G}_{{{{{{{{\rm{coh}}}}}}}}}{{{\Gamma }}}_{{{{{{{{\rm{XAS}}}}}}}}}^{{{{{{{{\rm{solid}}}}}}}}}$$
(19)

Here npk is the degeneracy parameter or number of photons in the mode coherence volume Vpk = λ3ℏω/Δpk, while nΓ is the number of photons in an atom specific volume, defined through the natural decay linewidth Γ as VΓ = λ3ℏω/(2π2Γ). The photon numbers are just renormalized to different volumes as nΓℏω/VΓ = npkℏω/Vpk15. This may be viewed as an atomic conversion of the incident photons of mode bandwidth Δpk, into photons emitted with the natural decay linewidth Γ = Δpk/(2π2).

Three-Level Maxwell-Bloch theory

We used a one-dimensional three level Maxwell-Bloch model to estimate the strength of stimulated resonant inelastic X-ray scattering (see16 for an overview of this and related models). Multilevel Maxwell-Bloch models have been successfully used to describe the propagation of light through a variety of media that can be adequately treated as discrete, few-level systems, including the propagation of strong resonant X-ray pulses through atomic and molecular gases25,47.

We follow16 for our calculations. We write the amplitudes of the X-ray electric field as the real part of a slowly varying envelope, \({{{{{{{\mathcal{E}}}}}}}}(z,t)\) times a rapidly oscillating phase factor (Eq. 21.3 of16),

$$E(z,t)={{{{{{\mathrm{Re}}}}}}}\,\left[{{{{{{{\mathcal{E}}}}}}}}(z,t){e}^{i(kz-\omega t)}\right],$$
(20)

where \({{{{{{\mathrm{Re}}}}}}}\,[x]\) denotes the real part of x, k is the X-ray wavenumber, z is propagation distance, ω is the X-ray angular frequency and t is time. The material polarization (which is determined from the material state, as described below) is written in the same manner

$$P(z,t)={{{{{{\mathrm{Re}}}}}}}\,\left[{{{{{{{\mathcal{P}}}}}}}}(z,t){e}^{i(kz-\omega t)}\right],$$
(21)

where \({{{{{{{\mathcal{P}}}}}}}}(z,t)\) is the polarization envelope. Making the slowly varying envelope approximation and the change of variables

$$Z=z,\ T=t-z/v$$
(22)

gives an equation for the evolution of the envelope of the X-ray electric field16

$$\frac{\partial }{\partial Z}{{{{{{{\mathcal{E}}}}}}}}(Z,T)=i\frac{\omega }{2c{\epsilon }_{0}}{{{{{{{\mathcal{P}}}}}}}}(Z,T).$$
(23)

Assuming the material polarization does not depend strongly on Z, we can integrate this equation to get an approximate expression for the field of the X-ray pulse exiting the sample (where the sample extends from Z = 0 to l),

$${{{{{{{\mathcal{E}}}}}}}}(l,T)={{{{{{{\mathcal{E}}}}}}}}(0,T)+i\frac{\omega l}{2c{\epsilon }_{0}}{{{{{{{\mathcal{P}}}}}}}}(0,T).$$
(24)

As our sample has only a thickness of about one x-ray absorption length at the peak of the Co L3 absorption resonance, this approximation will be good to within a factor of 2.

Now we describe how we calculate the evolution of the Co/Pd material state. For this, we model the Co/Pd as a slab of discrete three-level atoms. The slab has the same thickness as our samples and the same density of three-level atoms as density of Co atoms in the actual samples. The three levels represent a ground state with energy E1 = 0 eV, a core-excited state with energy E2 = 778 eV (coinciding with the peak of the Co L3 resonance) and a valence-excited state with energy E3 = 2 eV (coinciding with a typical 3d excitation energy). The dipolar coupling between the ground state and the core-excited state is d12. The dipolar coupling between the core-excited state and the valence-excited state is d23. We chose the dipolar couplings in accordance with the linear X-ray absorption cross sections of our samples, as described at the end of this section. We let ρnm(t) denote the element in the nth row and mth column of the density matrix in the basis of eigenstates of the three-level atom in the absence of an applied X-ray field. From Equation 16.107 of16, we define a rotating coordinate representation of the density matrix through

$${\rho }_{nm}(t)={s}_{nm}(t){e}^{i{\xi }_{m}(t)-{\xi }_{n}(t)}.$$
(25)

Here, ξi(t) are arbitrary phase factors chosen to be convenient for the problem to be solved. We choose these according to Eq. 13.14 of16 with a single X-ray pulse acting to both excite and stimulate decay,

$$\hslash {\xi }_{1}(t)=0,\ \hslash {\xi }_{2}(t)=\omega t,\ \hslash {\xi }_{3}(t)=0,$$
(26)

where ω is the angular frequency of the applied X-ray field and ℏ is Planck’s constant divided by 2π. From Eqs. 13.8, 13.27 and 13.29 of16, we have a matrix which describes the time evolution of the system,

$$W=\frac{1}{2}\left[\begin{array}{ccc}0&{{{\Omega }}}_{{{{{{{{\rm{P}}}}}}}}}^{* }&0\\ {{{\Omega }}}_{{{{{{{{\rm{P}}}}}}}}}&2{{{\Delta }}}_{{{{{{{{\rm{P}}}}}}}}}&{{{\Omega }}}_{{{{{{{{\rm{S}}}}}}}}}\\ 0&{{{\Omega }}}_{{{{{{{{\rm{S}}}}}}}}}^{* }&2{{{\Delta }}}_{{{{{{{{\rm{R}}}}}}}}}\end{array}\right],$$
(27)

with the complex, time-dependent Rabi frequencies defined as

$${{{\Omega }}}_{{{{{{{{\rm{P}}}}}}}}}=-{d}_{12}{{{{{{{\mathcal{E}}}}}}}}/\hslash ,$$
(28)

and

$${{{\Omega }}}_{{{{{{{{\rm{S}}}}}}}}}=-{d}_{23}{{{{{{{\mathcal{E}}}}}}}}/\hslash .$$
(29)

The detunings are

$${{{\Delta }}}_{{{{{{{{\rm{P}}}}}}}}}={E}_{2}-{E}_{1}-\hslash \omega =0,$$
(30)

and

$${{{\Delta }}}_{{{{{{{{\rm{R}}}}}}}}}={E}_{3}-{E}_{1}.$$
(31)

The evolution of the density matrix elements is given by Eq. 16.116 of16,

$$\frac{d}{dt}{s}_{m^{\prime} m}= -i\mathop{\sum}\limits_{n}\left[{W}_{m^{\prime} n}(t){s}_{nm}(t)-{s}_{m^{\prime} n}(t){W}_{nm}(t)\right]\\ -\mathop{\sum}\limits_{nn^{\prime} }{{{\Gamma }}}_{m^{\prime} mn^{\prime} n}{s}_{n^{\prime} n}(t),$$
(32)

where Γ is a tensor chosen to phenomenologically model Auger decay. The entries of Γ are

$${{{\Gamma }}}_{2222}=-{{{\Gamma }}}_{1122}={{{\Gamma }}}_{{{{{{{{\rm{A}}}}}}}}},$$
(33)
$${{{\Gamma }}}_{1212}={{{\Gamma }}}_{2121}={{{\Gamma }}}_{2323}={{{\Gamma }}}_{3232}=\frac{{{{\Gamma }}}_{{{{{{{{\rm{A}}}}}}}}}}{2},$$
(34)

and zero otherwise. Once we have calculated s(t) for a particular time, we calculate the envelope of the material polarization for that time from Eq. (21.94) of16

$${{{{{{{\mathcal{P}}}}}}}}(t)=2N\left({d}_{12}{s}_{21}(t)+{d}_{32}{s}_{23}(t)\right).$$
(35)

We note that our choice of ΓA is a bit different from earlier gas phase modeling47. In our model, each atom is returned to the ground state after Auger decay instead of being transferred to a different state that interacts with X-rays differently. This reflects the fact that the energy of a core hole is rapidly transferred to valence electrons over a wide spatial range in our system and most electrons remain in the sample29. The impact of the valence electron changes are beyond the scope of our model, however.

We chose the dipole matrix element to correspond to the peak atomic L3 XAS cross section of σXAS = 41.7 Mb per atom as used for the KHD case. Using Eqs. (2.9.8) and (2.5.18) of14, along with the definition of the absorption cross section as the extinction coefficient divided by the atomic density, we obtain a formula for the absorption cross section at the peak of the resonance,

$$\sigma ({\omega }_{0})=\frac{2\pi {c}^{2}{\gamma }_{{{{{{{{\rm{sp}}}}}}}}}}{{\omega }_{0}^{2}\gamma },$$
(36)

where c is the speed of light, ω0 is the angular frequency at the center of the resonance, γ = Γ/(2ℏ) is half of the angular frequency FWHM of the absorption resonance, and γsp is a parameter proportional to the square of the dipole matrix element. In particular, γsp is given by Eq. (2.5.11) of14 as

$${\gamma }_{{{{{{{{\rm{sp}}}}}}}}}=\frac{{e}^{2}{\omega }_{0}^{3}\,{d}_{12}^{2}}{6\pi {\epsilon }_{0}\hslash {c}^{3}},$$
(37)

where ϵ0 is the permittivity of free space, and e is the charge of an electron. Combining these gives

$${d}_{12}=\sqrt{\frac{3\sigma ({\omega }_{0})\gamma {\epsilon }_{0}\hslash c}{{\omega }_{0}{e}^{2}}}=6.1\times 1{0}^{-12}{{{{{{{\rm{m}}}}}}}}.$$
(38)

The dipole matrix element between the model core and valence excited states was set to d23 = d12 as discussed earlier.

We now have the necessary equations to solve for the field of an X-ray pulse exiting a sample. We used the method of38 to generate simulated SASE pulses with 4 eV bandwidth and either 5 or 25 fs pulse durations. For each pulse duration, we simulated the interaction of the X-ray pulses with 20 different randomly generated SASE pulses and averaged the results. We assume the sample starts in the ground state,

$$s(0)=\left[\begin{array}{ccc}1&0&0\\ 0&0&0\\ 0&0&0\end{array}\right].$$
(39)

Next, we use Eq. (32) to solve for the evolution of the sample, then Eq. (35) to calculate the polarization as a function of time. Finally, we calculate the X-ray field exiting the sample from Eq. (24). The spectra of X-rays incident and exiting a sample is obtained from these time domain quantities by taking a Fourier transform. From these spectra, we extracted the stimulated inelastic scattering efficiencies shown in Fig. 5.