Abstract
Topological kagome magnets RMn6Sn6 (R = rare earth element) attract numerous interests due to their non-trivial band topology and room-temperature magnetism. Here, we report a high entropy version of kagome magnet, (Gd0.38Tb0.27Dy0.20Ho0.15)Mn6Sn6. Such a high entropy material exhibits multiple spin reorientation transitions, which is not seen in all the related parent compounds and can be understood in terms of competing magnetic interactions enabled by high entropy. Furthermore, we also observed an intrinsic anomalous Hall effect, indicating that the high entropy phase preserves the non-trivial band topology. These results suggest that high entropy may provide a route to engineer the magnetic structure and expand the horizon of topological materials.
Similar content being viewed by others
Introduction
The study of topological magnets is at the forefront of condensed-matter physics as they are promising platforms to study fundamental physics and to realize next-generation devices1,2,3,4,5. Materials with pristine Mn kagome lattices, RMn6Sn6 (R = rare earth element, see the left inset of Fig. 1a), have recently attracted great interest since they exhibit not only topological flat bands and relativistic bands, but also room temperature magnetism5,6,7,8,9,10,11,12,13,14,15. Depending on whether the R ion is 4 f magnetic or not, the RMn6Sn6 compounds show either ferrimagnetic (FIM) or antiferromagnetic (AFM) order at room temperature16,17,18. The interplay between the magnetism and nontrivial band topology in such kagome magnets can generate novel topological phases, e.g., the quantum-limit Chern phase in TbMn6Sn65. A recent study on quantum transport properties of the RMn6Sn6 material family with various R elements demonstrates a close relationship between rare earth magnetism and topological electronic structure, which suggests that the rare earth elements can effectively tune the Chern quantum phase in such kagome magnets6.
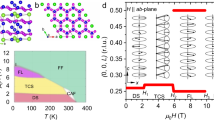
a (00 l) X-ray diffraction pattern of a HE166 single crystal. The left inset shows the Mn kagome layers and R sublattice in RMn6Sn6 kagome magnets. The right inset shows an image of a typical HE166 single crystal. b Energy-dispersive X-ray spectroscopy (EDXS) composition mapping for Gd, Tb, Dy, and Ho, showing uniform spatial distributions for each element.
The concept of high entropy alloy (HEA) is defined as a kind of solid solution containing more than five principle elements each of which has a concentration range of 5–35 at.%19. In such systems, the Gibbs energy is decreased by the increase of high configuration entropy. High-entropy oxides (HEOs) and high entropy intermetallics (HEIs) have been a recent research focus in this area and they are known to display a broad range of intriguing properties, including high thermoelectric performance20,21, superionic conductivity22, excellent mechanical performance23, superconductivity23, outstanding corrosion resistance23, etc. Recently, increasing attention is focused on the magnetic properties of HEOs and HEIs, as the coexistence of multiple magnetic elements is expected to generate unconventional complex magnetic orderings. However, the study on single crystalline high entropy topological magnets is still lacking.
In this work, we introduce the “high entropy” concept to the RMn6Sn6 kagome magnets by simultaneously including multiple rare earth cations. We have grown single crystals of a high-entropy phase with a composition of (Gd0.38Tb0.27Dy0.20Ho0.15)Mn6Sn6 (HE166) using a flux method. Magnetic measurements reveal that while this high-entropy phase shows similar magnetic transitions to those seen in the pristine compound TbMn6Sn6 (Tb166) at high temperatures, it exhibits an additional magnetic transition around 90 K. Magnetic susceptibility and neutron diffraction studies identify another FIM phase with tilted magnetic moments below 90 K, which is not seen in the relevant parent materials, i.e., GdMn6Sn6 (Gd166), Tb166, DyMn6Sn6 (Dy166), and HoMn6Sn6 (Ho166). Moreover, our magnetotransport measurements demonstrate an intrinsic anomalous Hall effect (AHE), indicating the survival of the Chern gapped Dirac fermions that are observed in the parent compounds.
Results and discussions
Synthesis and characterization of the high entropy RMn6Sn6 single crystal
As shown in the right inset of Fig. 1a, plate-like single crystals with 120° angles between some crystal edges were obtained via the flux method (see Single-crystal growth and characterizations in Methods session). The X-ray diffraction pattern of the HE166 single crystal along the c-axis (Fig. 1a) is very close to those of the parent compounds, indicating HE166 has a similar crystal structure to that of RMn6Sn6. To find whether local structure distortions in HE166 lead to inversion symmetry breaking, we conducted optical second harmonic generation (SHG) measurements. No SHG signal was observed, indicating that the inversion symmetry is preserved in the high entropy compound. The composition analysis using energy-dispersive X-ray spectroscopy (EDXS) shows while the nominal at.% of the four rare earth elements (Gd, Tb, Dy, and Ho) of the starting materials is the same, the actual composition of the HE166 single crystal is (Gd0.38Tb0.27Dy0.20Ho0.15)Mn6Sn6. The chemical composition mapping in the tens um scale clearly shows a homogeneous distribution of these four rare earth elements, as shown in Fig. 1b.
In general, one distinct feature of high entropy compounds is the severe lattice distortions arising from the mismatch of atomic mass, size, and bond state24,25. To evaluate the lattice distortions in HE166, we performed X-ray absorption fine structure (XAFS) spectroscopy studies on both HE166 and Tb166 (see Supplementary Fig. S1). From the fits to the Fourier transformed extended X-ray absorption fine structure (EXAFS) spectra (Supplementary Note 1 and Supplementary Fig. S2), we have extracted the mean-squared atomic displacements, σ2, (which reflects thermal and unresolvable static disorder) for various scattering paths in HE166 and Tb166, as shown in Supplementary Table S1. We find that the σ2 value of the Mn-HE path (Note that “HE” here refers to the high entropy lanthanide layer containing Gd0.38Tb0.27Dy0.2Ho0.15) in HE166 is one order of magnitude greater than that of the Mn-Tb path in Tb166, indicating HE166 has significantly increased lattice distortions than Tb166. This is consistent with the strong lattice distortion expected for a high-entropy phase.
Magnetic structure of the high entropy stabilized magnetic phase
The temperature dependences of magnetization of the HE166 crystal, measured with a magnetic field (0.1 T) applied along the in-plane direction and c-axis respectively under zero-field-cooling (ZFC) and field-cooling (FC) histories, are presented in Fig. 2a. We observed three striking magnetic transitions at ~420 K(T1), ~225 K (T2), and ~90 K (T3) in this sample. This is contrasted with the pristine parent compounds RMn6Sn6 which exhibit either a single FIM transition (R = Gd) or an FIM transition followed by a spin reorientation transition (R = Tb, Dy, and Ho). Previous neutron scattering studies17 have clarified the magnetic structures of these parent compounds and found that the rare earth magnetic sublattices are ferrimagnetically coupled to the Mn-sublattice. The initial FIM structure of RMn6Sn6 is independent of R, with the magnetic moments of R and Mn ions orientated along the in-plane direction, but the spin reorientation transitions lead to different FIM orders for R = Tb, Dy, and Ho. Below the spin reorientation transition temperature \({T}_{2}^{0}\), Tb166 displays an out-of-plane FIM order, whereas Dy166 and Ho166 show FIM orders with tilted magnetic moments, as illustrated in Fig. 2b. Both \({T}_{2}^{0}\) and the initial FIM transition temperature \({T}_{1}^{0}\) are dependent on R. According to the study by Kimura et al.,26 \({T}_{1}^{0}\) is 445 K for Gd166, 430 K for Tb166, 410 K for Dy166, and 385 K for Ho166, while \({T}_{2}^{0}\) is 320, 270, and 185 K, respectively, for Tb166, Dy166, and Ho166.
Temperature dependences of magnetization measured with a magnetic field (0.1 T) applied along the in-plane direction and c-axis through zero-field-cooling (ZFC) and field-cooling (FC) of HE166 (a) and Tb166 (d). b Illustration of spin structures of RMn6Sn6 and HE166 in their magnetic ground states. c The thermal variation of the neutron diffraction peak intensity for HE166. The error bars are determined by \(\sqrt{N}\), where N is the counting intensity. μ0 vacuum permeability. H magnetic field strength. c crystallographic c-axis of Tb166/HE166.
With the knowledge of the magnetic transitions of the RMn6Sn6 parent compounds, we can now better understand the magnetic transitions in HE166. Firstly, the initial transition at T1 ≈420 K should correspond to an FIM transition. The fact that the magnetization measured with an in-plane field is much greater than that measured with an out-of-plane field for \({T}_{2} \, < \, T \, < \, {T}_{1}\)indicates that the FIM state in this temperature range features magnetic moments oriented within the plane, consistent with the FIM state of Gd166 or the initial FIM state between \({T}_{1}^{0}\) and \({T}_{2}^{0}\) of Tb166, Dy166, and Ho166. Given that the transition at T1 in HE166 is as sharp as those transitions at \({T}_{1}^{0}\) in the parent compounds and the value of \({T}_{1}^{0}\) is dependent on the specific rare earth element as noted above, the possibility of magnetic phase separation due to the coexistence of multiple rare earth elements can be excluded.
Secondly, HE166 exhibits two spin reorientation transitions at T2 and T3 respectively. The first spin reorientation transition at T2 leads the magnetic moments to switch from the in-plane orientation to the c-axis, which is evidenced by the observation that the magnetization measured with an out-of-plane field is much greater than that measured with an in-plane field between T2 and T3, opposite to the magnetic anisotropic behavior seen in the in-plane FIM state within the \({T}_{2} < T < {{T}}_{1}\) temperature range. Such a spin orientation transition seems similar to that seen in the Tb166 parent compound whose spin orientation transition takes place at a temperature much higher than T2 of HE166 (i.e., 320 K). The second spin reorientation transition at ~90 K (T3) results in an increase in the in-plane magnetization, but a decrease in the out-of-plane magnetization, suggesting that the out-of-plane FIM order between T2 and T3 evolves into an FIM order with tilted magnetic moments as the temperature is lowered below T3. From the values of magnetization measured under FC histories for H ǁ c and H ⊥ c at 2 K and 0.1 T, the tilt angle θ of magnetic moments is roughly estimated to be ~30° with respect to the c-axis, smaller than the magnetic moments’ tilt angles of the FIM states of Dy166 and Ho166 where θ = 45° and 50° respectively (see Fig. 2b). Note that the θ values of Dy166 and Ho166 were determined using neutron diffraction refinements17. If we use their previously reported magnetization data of Hǁc and H⊥c at 0.1T26 to evaluate the moments’ orientation, we find the estimated tilt angle is ~45°, close to those determined by the neutron diffraction experiments, which justifies our approach of estimating the moments’ tilt angle for HE166. Furthermore, the spin reorientation transition below T3 also causes irreversible behavior in magnetization between ZFC and FC cooling measurements for both field orientations, indicating the tilted FIM state below T3 is characterized by domains.
The ferrimagnetism of HE166 as well as its spin reorientation transitions at T2 and T3 are further verified by neutron diffraction measurements. We have performed (0 0 L) and (1 0 L) scans at 300 and 6 K, and no incommensurate Bragg peaks were observed. Instead, Bragg peaks were observed only on nuclear-allowed reflections, consistent with the FIM characteristic found in the parent RMn6Sn6 compounds17. Figure 2c presents the temperature dependence of the integrated neutron scattering intensity of (100) and (002) Bragg peaks. The (002) scattering intensity monotonically increases down to T2 while there is a small decrease in the (100) intensity around 400 K followed by a nearly temperature-independent feature down to T2. Such a feature implies that right below T1 but above 400 K, magnetic moments have components along both the ab-plane and c-axis, while between T2 and 400 K spins align within the ab basal plane. The spin reorientation transition at T2 is manifested by the increase of (100) scattering intensity and the decrease of (002) intensity that reaches a minimum value around 100 K. This feature is consistent with the nearly zero in-plane magnetic moments measured around 100 K as shown in Fig. 2a. The spin reorientation transition at T3 (~90 K) is reflected by the increase in the (002) scattering intensity. This result indicates that the magnetic moments of the FIM state below T3 have both in-plane and c-axis components. Unfortunately, due to the strong neutron absorption by Gd and Dy elements, a limited number of Bragg peaks were collected, which makes it challenging to refine the spin structure and extract the exact spin orientations.
Since the first spin reorientation transition at T2 of HE166 shares similarity with the spin reorientation transition of Tb166, we reproduced Tb166 crystals and compared its magnetic anisotropy evolution with that of HE166 in detail. We anticipate achieving a deeper understanding of the tilted FIM state of HE166 through this comparison. In Fig. 2d, we present Tb166’s temperature dependences of magnetization measured under ZFC and FC histories with a magnetic field (0.1 T) applied along the ab-plane and the c-axis respectively. These data reveal an FIM transition at ~430 K\(({T}_{1}^{0})\), followed by a spin reorientation at ~315 K (\({T}_{2}^{0}\)), consistent with the prior report by Kimura et al.26. Its evolution of magnetic anisotropy with temperature also agrees well with the previously determined magnetic structure which features magnetic moments orientated along the ab-plane between 430 and 320 K, but the out-of-plane direction below 320 K.
In Fig. 3, we present the comparison of the isothermal magnetization data at different temperatures between Tb166 and HE166. For \({T}_{2}^{0}\left({T}_{2}\right) \, < \, T \, < \, {T}_{1}^{0}({T}_{1})\) (see Fig. 3a, b), the magnetic anisotropy manifested by the isothermal magnetization data clearly shows both HE166 and Tb166 are characterized by preferential in-plane spin orientations. When the temperature is close to \({T}_{2}^{0}\left({T}_{2}\right)\), the magnetic anisotropy becomes quite small for both systems (Fig. 3c, d). When the temperature is lowered below \({T}_{2}^{0}\left({T}_{2}\right)\), while the magnetic anisotropy of both systems is significantly enhanced with the spin-easy axis switching to the c-axis, the magnetic anisotropy of HE166 is much weaker than that of Tb166 (Fig. 3e, f). After HE166 evolves into a tilted FIM state below T3, its magnetic anisotropy is further weakened such that its magnetization can be polarized to saturations for both H ǁ c and H⊥c, with the ratio of saturated magnetization (Ms,c/Ms,ab) being ~1.24 at 7 T and 2 K, sharply contrasted with the large magnetic anisotropy of the FIM state below \({T}_{2}^{0}\) of Tb166 which exhibits field-induced magnetization saturation only for Hǁc (Fig. 3g, h). Moreover, HE166 also shows contrast with Dy166 and Ho166 in the magnetic anisotropy. Both Dy166 and Ho166 display very small magnetic anisotropy in their tilted FIM states, and their magnetizations measured with Hǁc and H⊥c exhibit similar polarization below 20 T26. These comparisons clearly show HE166 hosts a unique tilted FIM state whose magnetic anisotropy is moderate and lies in between those of Tb166 and Dy166/Ho166. Moreover, we also find a small variation of the Gd/Tb/Dy/Ho concentration in HE166 hardly has any effect on the magnetic transitions and the tilted FIM state described above, as demonstrated by the additional magnetization data measured on the (Gd0.37Tb0.28Dy0.19Ho0.16)Mn6Sn6 sample (see Supplementary Note 2 and Supplementary Figs. S3, S4).
Next, we turn to discuss why HE166 exhibits a tilted FIM state distinct from those FIM states seen in Gd166, Tb166, Dy166, and Ho166. As illustrated in Fig. 2d, the orientation of the magnetic moments is strongly dependent on the specific rare earth element in these parent compounds: Gd and Tb favor the in-plane and out-of-plane spin orientation respectively, whereas both Dy and Ho prefer θ = 45° or 50° tilted orientations. These facts indicate magnetic exchange interaction has essential differences among these four different parent compounds. As such, when these elements are mixed in the alloy phase, competing magnetic interactions due to the coexistence of Gd, Tb, Dy, and Ho should emerge. As indicated above, Gd, Tb, Dy, and Ho do not show the same concentration in the HE166 crystals and its actual composition is (Gd0.38Tb0.27Dy0.20Ho0.15)Mn6Sn6. Although the Gd concentration is the highest (38%), HE166 does not maintain an in-plane FIM order down to low temperatures as Gd166 does. Instead, it undergoes a spin reorientation transition similar to that in Tb166 at T2 though the Tb concentration is only 27%, indicating Tb plays a critical role in driving the spin reorientation transition at T2. However, the out-of-plane FIM order emerging below T2 does not sustain to low temperatures but evolves to a θ ≈30° tilted FIM state below T3. Apparently, the moments’ tilting below T3 is mostly driven by Dy and Ho, since their exchange interactions favor tilted spin orientations. Therefore, the double spin reorientation transitions, as well as the resulting tilted FIM ground state in HE166, can be viewed as a compromising consequence of the competing magnetic interactions. It should be emphasized that such competing magnetic interactions are enabled by the high entropy generated by randomly distributed four different rare earth elements. In other words, it is the high entropy that stabilizes the crystal structure and forbids phase separations, thus enabling the competing magnetic interactions and resulting in a long-range tilted FIM order which is not seen in any of the related parent compounds. This suggests high entropy materials offer a new route to engineer magnetic states.
Additionally, it is worth mentioning that the presence of tilted FIM below 90 K in HE166 is also likely connected with the magnetic fluctuations recently reported for Tb16615. Although early magnetic and neutron scattering measurements on Tb166 demonstrated its in-plane FIM order for \({T}_{2}^{0} \, < \, T \, < \, {T}_{1}^{0}\) and out-of-plane FIM order for \({T \, < \, T}_{2}^{0}\), the recent μSR study by Mieke et al15 shows its FIM order is accompanied by magnetic fluctuations in a wide temperature range and these magnetic fluctuations become weakened below 120 K and start to freeze out below 20 K, thus leading to the formation of an ideal static out-of-plane FIM order. Given that the out-of-plane FIM state of HE166 in the \({T}_{3} \, < \, T \, < \, {T}_{2}\) temperature range is analogous to that of Tb166, it might also bear magnetic fluctuations. In general, strong magnetic fluctuations often occur to a system on the verge of a magnetic phase transition. This implies that the out-of-plane FIM state of HE166 may not remain stable down to low temperature and has the possibility of transitioning to a different magnetic state in presence of external perturbations. Our observation of the magnetic transition from an out-of-plane FIM state to a tilted FIM state below 90 K in HE166 is indeed in line with such an implication. The competing magnetic interactions induced by the coexistence of Gd, Tb, Dy and Ho act as a perturbation, which drives the second spin orientation transition below 90 K.
The survival of the band topology
To explore the correlation between magnetism and the band topology in HE166, we also studied its magnetotransport properties. We measured both longitudinal resistivity ρxx and Hall resistivity ρxy as a function of the magnetic field at various temperatures (Fig. 4a). We have separated anomalous Hall contribution from the normal Hall contribution through the fit of the ρxy data to the empirical relation,
where \({\rho }_{{{{{{\rm{OH}}}}}}}\)(\({R}_{0}\)) and \({\rho }_{{{{{{\rm{AH}}}}}}}\)(\({R}_{s}\)) represent ordinary and anomalous Hall resistivity (coefficient), respectively. The anomalous Hall and longitudinal conductivity are derived by tensor conversion, that is, \({\sigma }_{{{{{{\rm{AH}}}}}}}={\rho }_{{{{{{\rm{AH}}}}}}}/({\rho }_{{{{{{\rm{xy}}}}}}}^{2}+{\rho }_{{{{{{\rm{xx}}}}}}}^{2})\) and \({\sigma }_{{{{{{\rm{xx}}}}}}}={\rho }_{{{{{{\rm{xx}}}}}}}/({\rho }_{{{{{{\rm{xy}}}}}}}^{2}+{\rho }_{{{{{{\rm{xx}}}}}}}^{2})\). The scaling relationship between \({\sigma }_{{{{{{\rm{AH}}}}}}}\) and \({\sigma }_{{{{{{\rm{xx}}}}}}}\) is plotted in Fig. 4b. As the signal-to-noise ratio is not very good below 100 K, we present only the data from 100 to 350 K in Fig. 4b. In this temperature region, \({\sigma }_{{{{{{\rm{AH}}}}}}}\) shows only relatively small variation with \({{\sigma }}_{{{{{{\rm{xx}}}}}}}\) (similar to the behavior seen in the parent compounds6), and strongly deviates from the screw scattering dominated scaling rule, i.e., \({\sigma }_{{{{{{\rm{AH}}}}}}}\)∝\({\sigma }_{{{{{{\rm{xx}}}}}}}\) (see the dashed lines in Fig. 4b), suggesting there exists an intrinsic AHE dominated by the Berry curvature in HE166. As shown in Fig. 4c, the intrinsic anomalous Hall conductivity, \({\sigma }_{{{{{{{\mathrm{int}}}}}}}}\), is further obtained by the fit to the Tian-Ye-Jin (TYJ) scaling law27,28,29:
a Hall resistivity of HE166 as a function of the magnetic field at various temperatures, measured with the current applied along the in-plane direction and the magnetic field perpendicular to the basal plane. b Anomalous Hall conductivity σAH versus longitudinal conductivity σxx. The dash lines represent \({\sigma }_{{{{{{\rm{AH}}}}}}}\)∝\({\sigma }_{{{{{{\rm{xx}}}}}}}\). c Tian-Ye-Jin (TYJ) scaling fit of \({\rho }_{{{{{{\rm{AH}}}}}}}\) vs \({\rho }_{{{{{{\rm{xx}}}}}}}\). \({\mu }_{0}\) vacuum permeability. H magnetic field strength. \({\sigma }_{{{{{{\rm{AH}}}}}}}({\rho }_{{{{{{\rm{AH}}}}}}})\) and \({\sigma }_{{{{{{\rm{xx}}}}}}}({\rho }_{{{{{{\rm{xx}}}}}}})\) are anomalous Hall and longitudinal conductivity (resistivity), respectively.
For each Mn layer, \({\sigma }_{{{{{{\rm{int}}}}}}}\) is about 0.034 \({e}^{2}/h\). Although this value is smaller than those of the relevant parent compounds whose \({\sigma }_{{{{{{\rm{int}}}}}}}\) is in the range of 0.07–0.27 \({e}^{2}/h\) per Mn layer5,6,8; it suggests that Chern gapped Dirac fermions survive in HE166 despite local disorders due to the random distribution of four rare earth elements. The difference of \({\sigma }_{{{{{{\rm{int}}}}}}}\) between HE166 and RMn6Sn6 likely results from their distinct chemical potentials.
The fact that the AHE is not clearly resolved in our Hall resistivity measurements below 100 K implies that the tilted FIM state below 90 K in HE166 does not further promote topological transport, but possibly suppresses it. This appears to suggest that the in-plane AFM component does not favor the nontrivial band topology as seen in other magnetic topological systems30,31. However, we note that Gd166/Dy166/Ho166, which shows either in-plane FIM or tilted FIM order, also exhibits topological transport properties similar to those of Tb1666. Therefore, the possibility of the band topology suppression by magnetic moments’ tilting in HE166 can be excluded. One possible origin of the suppression of AHE in the tilted FIM state of HE166 is the enhanced disorder scattering caused by the strong lattice distortions in the high entropy phase. As discussed above, the lattice distortions probed by XAFS in HE166 are indeed severe. Moreover, we also find the longitudinal resistivity \({{\rho }}_{{{{{{\rm{xx}}}}}}}\) of HE166 is much greater than that of Tb166, which provides further support for strong disorder scattering. The enhanced disorder scattering could significantly reduce the charge carriers’ anomalous transverse velocity driven by the Berry curvature such that the AHE is hard to be resolved when it becomes weak below 100 K.
In summary, we have synthesized a high entropy kagome magnet (Gd0.38Tb0.27Dy0.20Ho0.15)Mn6Sn6 using a flux method. Through magnetization and neutron scattering measurements, we find this compound undergoes three magnetic transitions at ~420, ~225, and ~90 K, respectively. The transition at 420 K results from an FIM ordering with magnetic moments aligned within the ab-plane, analogous to the initial FIM transitions in all the related parent compounds. The transitions at 225 and 90 K are spin reorientation transitions: the magnetic moments switch from the in-plane direction to the c-axis at 225 K but become ~30° tilted relative to the c-axis below 90 K. Such two-step spin reorientation transitions lead to a unique tilted FIM state with a moderate magnetic anisotropy, which is not seen in the parent compounds which exhibit either a single spin reorientation transition or no spin reorientation transition. Such a tilted FIM state in HE166 can be well understood in terms of the competing magnetic interactions enabled by the high entropy generated by randomly distributed Gd, Tb, Dy, and Ho. Furthermore, we observed an intrinsic AHE, suggesting that Chern gapped Dirac fermions survive in HE166 in spite of disorders. Our findings imply that (a) high entropy-enabled competing magnetic interactions provide a new route to magnetism tuning and (b) the band topology is insensitive to local disorders. This suggests the marriage of high entropy and magnetism in topological materials may be a promising strategy for fine-tuning the topological phases and expanding the family of novel topological materials.
Methods
Single-crystal growth and characterizations
Single crystals of HE166 and Tb166 used in this study were synthesized using an Sn flux growth method. For HE166, high-purity Gd, Tb, Dy, Ho, Mn, and Sn powders were mixed in the molar ratio of 1:1:1:1:24:96, placed in an alumina crucible covered with a piece of quartz wool on the top, and sealed in an evacuated quartz tube. Then the quartz tube was heated up to 1050 °C in a furnace and held at this temperature for one day, followed by cooling down to 600°C at a rate of 3 °C/h. After the tube was centrifuged to remove excess Sn at 600 °C, hexagonal-prism-like single crystals with a typical size of ~2 mm3 × 2 mm3 × 0.3 mm3 were obtained. A similar procedure was used to synthesize Tb166 crystals. We conducted room temperature X-ray diffraction measurements using a Malvern Panalytical Empyrean X-ray diffractometer (Cu Kα1 radiation) to confirm the grown crystals have the desired structure phase. The compositions of the grown crystals were analyzed using an energy-dispersive X-ray spectrometer.
Magnetic and magnetotransport measurement
The magnetic properties of the HE166 and Tb166 crystals were measured using a Quantum Design magnetic property measurement system (MPMS-3). The magnetotransport measurements were conducted using a standard four-probe method in a Quantum Design PPMS. The electric current was applied parallel to the (001) plane while the magnetic field was perpendicular to the plane. To eliminate the non-symmetricity of the electric contacts, the measured longitudinal resistivity and Hall resistivity are symmetrized/antisymmetrized using \({\rho }_{{{{{{\rm{xx}}}}}}}\left({{{{{\bf{H}}}}}}\right)=\left[{\rho }_{{{{{{\rm{xx}}}}}}}\left({{{{{\bf{H}}}}}}\right)+{\rho }_{{{{{{\rm{xx}}}}}}}\left(-{{{{{\bf{H}}}}}}\right)\right]/2\) and \({\rho }_{{{{{{\rm{xy}}}}}}}\left({{{{{\bf{H}}}}}}\right)=\left[{\rho }_{{{{{{\rm{xy}}}}}}}\left({{{{{\bf{H}}}}}}\right)-{\rho }_{{{{{{\rm{xy}}}}}}}\left(-{{{{{\bf{H}}}}}}\right)\right]/2\), respectively.
Single-crystal neutron diffraction measurements
Single-crystal neutron diffraction measurements were carried out on a triple-axis spectrometer (TRIAX) with an incident neutron wavelength of 1.638 Å (Ei = 30.50 meV) at the University of Missouri Research Reactor. A collimator setting of 60′ -60′ -S -40′ -40′ was used in this experiment and the single-crystal sample was measured in the (H 0 L) scattering plane, where H and L are in reciprocal lattice units (r. l. u.).
X-ray absorption fine structure spectroscopy
X-ray absorption fine structure spectra were collected at the beamline 10-ID32 of the Advanced Photon Source, Argonne National Laboratory (Argonne, IL). Single crystals of HE166 and Tb166 were measured in fluorescence mode for the Tb-L3 (7514 eV), Mn-K (6539 eV), and Sn-K (29,200 eV) edges, respectively, and analyzed using the Demeter package (Athena, Artemis, and Hephestus)33.
Data availability
The data that support the findings of this work are available from the corresponding author on reasonable request.
References
Franz, M. & Rozali, M. Mimicking black hole event horizons in atomic and solid-state systems. Nat. Rev. Mater. 3, 491–501 (2018).
Chang, C.-Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013).
He, K., Wang, Y. & Xue, Q.-K. Topological materials: quantum anomalous Hall system. Annu. Rev. Condens. Matter Phys. 9, 329–344 (2018).
Li, P. et al. Giant room temperature anomalous Hall effect and tunable topology in a ferromagnetic topological semimetal Co2MnAl. Nat. Commun. 11, 3476 (2020).
Yin, J.-X. et al. Quantum-limit Chern topological magnetism in TbMn6Sn6. Nature 583, 533–536 (2020).
Ma, W. et al. Rare earth engineering in RMn6Sn6 (R = Gd-Tm, Lu) topological Kagome magnets. Phys. Rev. Lett. 126, 246602 (2021).
Ghimire, N. J. et al. Competing magnetic phases and fluctuation-driven scalar spin chirality in the kagome metal YMn6Sn6. Sci. Adv. 6, eabe2680 (2020).
Asaba, T. et al. Anomalous Hall effect in the kagome ferrimagnet GdMn6Sn6. Phys. Rev. B 101, 174415 (2020).
Li, M. et al. Dirac cone, flat band and saddle point in kagome magnet YMn6Sn6. Nat. Commun. 12, 3129 (2021).
Ma, W. et al. Anomalous Hall effect in the distorted kagome magnets (Nd,Sm)Mn6Sn6. Phys. Rev. B 103, 235109 (2021).
Wang, Q. et al. Field-induced topological Hall effect and double-fan spin structure with a c-axis component in the metallic kagome antiferromagnetic compound YMn6Sn6. Phys. Rev. B 103, 014416 (2021).
Dally, R. L. et al. Chiral properties of the zero-field spiral state and field-induced magnetic phases of the itinerant kagome metal YMn6Sn6. Phys. Rev. B 103, 094413 (2021).
Xu, C. Q., Heitmann, T. W., Zhang, H., Xu, X. & Ke, X. Magnetic phase transition, magnetoresistance, and anomalous Hall effect in Ga-substituted YMn6Sn6 with a ferromagnetic kagome lattice. Phys. Rev. B 104, 024413 (2021).
Bykov, A. A., Chetverikov, Yu. O., Moskvin, E. V., Pirogov, A. N. & Grigoriev, S. V. Magnetic phase diagram of Y1−xTbxMn6Sn6 compounds. J. Magn. Magn. Mater. 424, 347–351 (2017).
Mielke III, C. et al. Intriguing magnetism of the topological kagome magnet TbMn6Sn6. Preprint at arXiv:210105763 (2021).
Venturini, G., Idrissi, B. C. E. & Malaman, B. Magnetic properties of RMn6Sn6 (R = Sc, Y, Gd−Tm, Lu) compounds with HfFe6Ge6 type structure. J. Magn. Magn. Mater. 94, 35–42 (1991).
Malaman, B. et al. Magnetic properties of RMn6Sn6 (R=Gd–Er) compounds from neutron diffraction and Mössbauer measurements. J. Magn. Magn. Mater. 202, 519–534 (1999).
Clatterbuck, D. M. & Gschneidner, K. A. Magnetic properties of RMn6Sn6 (R=Tb, Ho, Er, Tm, Lu) single crystals. J. Magn. Magn. Mater. 207, 78–94 (1999).
Miracle, D. B. & Senkov, O. N. A critical review of high entropy alloys and related concepts. Acta Mater. 122, 448–511 (2017).
Jiang, B. et al. High-entropy-stabilized chalcogenides with high thermoelectric performance. Science 371, 830–834 (2021).
Jiang, B. et al. Entropy engineering promotes thermoelectric performance in p-type chalcogenides. Nat. Commun. 12, 3234 (2021).
Bérardan, D., Franger, S., Meena, A. K. & Dragoe, N. Room temperature lithium superionic conductivity in high entropy oxides. J. Mater. Chem. A 4, 9536–9541 (2016).
Ying, T. et al. High-entropy van der Waals materials formed from mixed metal dichalcogenides, halides, and phosphorus trisulfides. J. Am. Chem. Soc. 143, 7042–7049 (2021).
Song, H. et al. Local lattice distortion in high-entropy alloys. Phys. Rev. Mater. 1, 023404 (2017).
Braun, J. L. et al. Charge-induced disorder controls the thermal conductivity of entropy-stabilized oxides. Adv. Mater. 30, 1805004 (2018).
Kimura, S. et al. High-field magnetization of RMn6Sn6 compounds with R = Gd, Tb, Dy and Ho. J. Alloy. Compd. 408–412, 169–172 (2006).
Tian, Y., Ye, L. & Jin, X. Proper scaling of the anomalous Hall effect. Phys. Rev. Lett. 103, 087206 (2009).
Ye, L. et al. Massive Dirac fermions in a ferromagnetic kagome metal. Nature 555, 638–642 (2018).
Zeng, C., Yao, Y., Niu, Q. & Weitering, H. H. Linear magnetization dependence of the intrinsic anomalous Hall effect. Phys. Rev. Lett. 96, 037204 (2006).
Guguchia, Z. et al. Tunable anomalous Hall conductivity through volume-wise magnetic competition in a topological kagome magnet. Nat. Commun. 11, 559 (2020).
Guguchia, Z. et al. Multiple quantum phase transitions of different nature in the topological kagome magnet Co3Sn2−xInxS2. npj Quantum Mater. 6, 1–8 (2021).
Segre, C. U. et al. The MRCAT insertion device beamline at the Advanced Photon Source. AIP Conf. Proc. 521, 419–422 (2000).
Ravel, B. & Newville, M. ATHENA, ARTEMIS, HEPHAESTUS: data analysis for X-ray absorption spectroscopy using IFEFFIT. J. Synchrotron Radiat. 12, 537–541 (2005).
Acknowledgements
Z.M., V.G., C.M.R., L.M., T.W.V., and R.Z. acknowledge the support from NSF through the Materials Research Science and Engineering Center DMR 2011839. Work at Michigan State University was supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division under Award # DE-SC0019259. C.M.R. and T.W.V. would like to express their gratitude to Drs. Mark Warren and Joshua Wright of Sector 10: MRCAT, at the Advanced Photon Source. MRCAT operations are supported by the Department of Energy and the MRCAT member institutions. This research used resources of the Advanced Photon Source, a US Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357.
Author information
Authors and Affiliations
Contributions
L.M. and Z.M. conceived the project. The crystal growth, XRD, EDXS, magnetic measurements, and magnetotransport measurements were carried out and analyzed by L.M. and Z.M. Single-crystal neutron diffraction measurements were conducted and analyzed by M.S., T.W.H., and X.K. The XAFS spectroscopy was carried out and analyzed by T.W.V. and C.M.R. The optical SHG measurements were performed by R.Z. and V.G. The paper was written by L.M. and Z.M. with inputs from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Min, L., Sretenovic, M., Heitmann, T.W. et al. A topological kagome magnet in high entropy form. Commun Phys 5, 63 (2022). https://doi.org/10.1038/s42005-022-00842-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-00842-1
This article is cited by
-
High-entropy engineering of the crystal and electronic structures in a Dirac material
Nature Communications (2024)
-
The role of electron correlations in the electronic structure of putative Chern magnet TbMn6Sn6
npj Quantum Materials (2023)
-
Quantum states and intertwining phases in kagome materials
Nature Reviews Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.