Introduction

There is a rich and constantly expanding taxonomy of unconventional superconducting phases, and increasingly sophisticated probes are needed to distinguish one such phase from another. A defining feature of any superconducting state is its collective mode spectrum, which encodes the dynamics of the order parameter. The collective modes of conventional (phonon-mediated) superconductors are well-established, consisting of two modes which correspond to fluctuations in the amplitude and phase of the order parameter. The first, called the Higgs mode1,2, is massive and resides at the edge of the quasiparticle continuum3,4, while the second, called the Anderson–Bogoliubov–Goldstone (ABG) mode5,6, is massless in a neutral system, in accordance with Goldstone’s theorem, but is lifted to the plasma frequency in the presence of long-ranged Coulomb interactions7, and is thus indistinguishable from the usual plasmon in real materials.

However, systems with more complex order parameters can exhibit a rich collective mode spectrum featuring other modes, such as additional Higgs modes in anisotropically gapped (e.g., d-wave) superconductors8, or Leggett modes in multi-band superconductors9. The presence of these additional modes in the spectrum can then be taken as a fingerprint of the underlying order parameter symmetry. That is, the dynamics of the order parameter can be studied to gain insight into its equilibrium structure. Such a scheme has only recently been proposed in the context of anisotropically gapped superconductors, where the spectrum of non-equilibrium Higgs modes can be used to deduce the orbital symmetry of the order parameter10,11.

In this article, we generalize this notion of “collective mode spectroscopy” to a particularly exotic class of unconventional superconductors, namely those which spontaneously break time-reversal symmetry in addition to global U(1) symmetry at the superconducting transition. These time-reversal symmetry breaking (TRSB) superconducting states are the subject of considerable current interest, and are believed to be realized in a number of bulk materials, including Sr2RuO412,13, UPt314,15, URu2Si216, UTe217,18, PrOs4Sb1219,20, and K-doped BaFe2As221, as well as engineered structures such as Bi/Ni bilayers22 and SnTe nanowires23. Moreover, recent theoretical proposals have suggested that such states may also be realized in moiré heterostructures24,25, and could be generically engineered in twisted bilayers of anisotropically gapped superconductors26,27.

In what follows, we identify two collective modes, the “generalized clapping modes,” which are unique to TRSB superconductors and subsequently derive their spectrum from a generally applicable microscopic weak-coupling theory. Our first key finding is that these modes are coherent collective excitations for a wide variety of TRSB states, even those which have point or line nodes in the superconducting gap. Owing to the universality of these modes in TRSB superconductors, they may serve as clear spectroscopic signatures which identify a TRSB superconducting state. To this end, we discuss a variety of existing experimental probes that can couple to these modes, and hence can be used as means to detect TRSB superconductivity in quantum materials. We pay special attention to the superconducting state of Sr2RuO4, where the generalized clapping mode spectrum could distinguish the two current leading candidate order parameters.

Results

Generalized clapping modes

TRSB superconducting states are characterized by a doubly-degenerate complex multi-component order parameter of the form Δ = Δ1 ± iΔ2 (see supplementary Note 1), and can be divided into two classes: (1) systems where both components Δ1 and Δ2 belong to the same multi-dimensional irreducible representation (irrep) of the crystalline point group, in which case ∣Δ1∣ = ∣Δ2∣ is required by symmetry, and (2) “mixed symmetry” systems where the two components belong to different irrep’s, which can arise due to either an accidental degeneracy between two pairing channels or two successive superconducting transitions (see Supplementary Note 1), in which case the ratio ∣Δ1∣/∣Δ2∣ is unconstrained.

Given this internal orbital structure of the order parameter, we would expect that in addition to the usual ABG and Higgs modes, there should be a massive mode corresponding to fluctuations of the relative phase between the two order parameter components around its equilibrium value of ±π/2. Further, we expect that there should be a second amplitude mode which corresponds to fluctuations of the relative amplitude ∣Δ1∣/∣Δ2∣ so there are a total of four real modes.

Historically, similar modes corresponding to “internal vibrations of the structure of the order parameter” were first recognized in 3He-A28, one of which was named the “clapping mode.” This was subsequently extended to the two-dimensional chiral p-wave (p + ip) superconductor29, where there are two such clapping modes which are degenerate and reside at a frequency \({{\Omega }}=\sqrt{2}{{{\Delta }}}_{0}\), with Δ0 the magnitude of the order parameter.

As argued above, we can anticipate analogous modes, which we call the generalized clapping modes, for any multi-component TRSB state on symmetry grounds alone30. Although it is intuitively obvious that the generalized modes should exist in principle, there is no reason to expect a priori that they are not overdamped by quasiparticle excitations. For a fully gapped superconductor, this requires that the frequencies of both modes lie below the quasiparticle continuum or, in the case of a nodal quasiparticle gap function, requires that the spectral function of each mode retains sharp features despite the presence of nodal quasiparticles. To establish that the generalized clapping modes are coherent, and thus experimentally detectable, for a generic TRSB state requires a derivation of their spectrum starting from a microscopic theory, which we furnish below. By studying the generalized clapping mode spectrum for a wide variety of TRSB order parameters we are able to establish the general features of these modes, which ultimately enable their use in the collective mode spectroscopy of real materials.

Weak-coupling theory

We begin with a single band of fermions subject to the attractive interaction \({V}_{{{{{{{\rm{kk}}}}}}}^{\prime}}=-{\sum }_{\ell = 1,2}{g}_{\ell }{\chi }_{{{{{{\rm{k}}}}}}}^{\ell }{\chi }_{{{{{{{\rm{k}}}}}}}^{\prime}}^{\ell }\) where gℓ > 0 are coupling constants and \({\chi }_{{{{{{\rm{k}}}}}}}^{\ell }\) are form factors which encode the orbital symmetry of the interaction. We take these to be real and normalized according to the inner product \(\int \frac{{{{{{\rm{d}}}}}}{\phi }_{{{{{{\rm{k}}}}}}}}{2\pi }\,{\chi }_{{{{{{\rm{k}}}}}}}^{\ell }{\chi }_{{{{{{\rm{k}}}}}}}^{\ell ^{\prime} }={\delta }_{\ell \ell ^{\prime} }\). We assume pairing in the \({S}_{{{{{{\rm{tot}}}}}}}^{z}=0\) sector, but within this sector our results are applicable to both singlet and m = 0 triplet pairing. We treat this system within the imaginary-time path-integral formalism by introducing a Hubbard-Stratonovich decoupling field Δℓ in each pairing channel and integrating out the fermions. One then arrives at the effective action for the order parameters Δℓ of

$$S=\mathop{\sum}\limits_{q}\left({g}_{1}^{-1}| {{{\Delta }}}_{q}^{(1)}{| }^{2}+{g}_{2}^{-1}| {{{\Delta }}}_{q}^{(2)}{| }^{2}\right)-{{{{{\rm{tr}}}}}}\log {{\mathbb{G}}}^{-1}.$$
(1)

The inverse fermion propagator is \({{\mathbb{G}}}_{k+q,k}^{-1}=(i{\omega }_{n}-{\xi }_{{{{{{\bf{k}}}}}}}\,{\tau }_{z}){\delta }_{q,0}+{\sum }_{\ell }{{{\Delta }}}_{q}^{\ell }{\chi }_{{{{{{\bf{k}}}}}}}^{\ell }\,{\tau }^{+}+{\sum }_{\ell }{\bar{{{\Delta }}}}_{-q}^{\ell }{\chi }_{{{{{{\bf{k}}}}}}}^{\ell }\,{\tau }^{-}\) where τi are the Pauli matrices in Nambu space, \({\tau }^{\pm }=\frac{1}{2}\left({\tau }_{x}\pm i{\tau }_{y}\right)\), and ξk = k2/2m − μ is the single-particle energy measured with respect to the Fermi level. We have also combined fermionic/bosonic Matsubara frequencies and momenta into the four-vectors k = (iωn, k) and q = (iΩm, q), where q corresponds to the center-of-mass momentum of the fermion pair and k corresponds to the relative momentum.

We assume g1, g2 are such that we find a saddle-point configuration in which both Δ(1) and Δ(2) are condensed with a relative phase of π/2, breaking time-reversal symmetry as discussed above. It will be convenient to change basis from (Δ(1), Δ(2)) → (Δ+, Δ−) according to \({{{\Delta }}}_{q}^{(1)}{\chi }_{{{{{{\bf{k}}}}}}}^{(1)}+{{{\Delta }}}_{q}^{(2)}{\chi }_{{{{{{\bf{k}}}}}}}^{(2)}={{{\Delta }}}_{q}^{+}{\chi }_{{{{{{\bf{k}}}}}}}^{+}+{{{\Delta }}}_{q}^{-}{\chi }_{{{{{{\bf{k}}}}}}}^{-}\) where the ± form factors are defined as

$${\chi }_{{{{{{\bf{k}}}}}}}^{\pm }={\eta }_{1}\,{\chi }_{{{{{{\bf{k}}}}}}}^{(1)}\pm i\,{\eta }_{2}\,{\chi }_{{{{{{\bf{k}}}}}}}^{(2)}$$
(2)

and η1,2 quantify the relative magnitude of each order parameter component. We choose to normalize them such that \({\eta }_{1}^{2}+{\eta }_{2}^{2}=1\) and can express both in terms of a “mixing angle” as \({\eta }_{1}=\cos \eta \) and \({\eta }_{2}=\sin \eta \).

Expanding around the saddle point with \({{{\Delta }}}_{q}^{+}={{{\Delta }}}_{0}=\,{{\mbox{const.}}}\,\) and \({{{\Delta }}}_{q}^{-}=0\), the mean-field equations are

$$\left(\frac{{\eta }_{1}^{2}}{{g}_{1}}+\frac{{\eta }_{2}^{2}}{{g}_{2}}\right)=-T\mathop{\sum}\limits_{k}\frac{| {\chi }_{{{{{{\bf{k}}}}}}}^{+}{| }^{2}}{{(i{\omega }_{n})}^{2}-{E}_{{{{{{\bf{k}}}}}}}^{2}}$$
(3)
$$\left(\frac{{\eta }_{1}^{2}}{{g}_{1}}-\frac{{\eta }_{2}^{2}}{{g}_{2}}\right)=-T\mathop{\sum}\limits_{k}\frac{{\left({\chi }_{{{{{{\rm{k}}}}}}}^{+}\right)}^{2}}{{(i{\omega }_{n})}^{2}-{E}_{{{{{{\rm{k}}}}}}}^{2}}$$
(4)

where \({E}_{{{{{{\bf{k}}}}}}}^{2}={\xi }_{{{{{{\bf{k}}}}}}}^{2}+| {{{\Delta }}}_{{{{{{\bf{k}}}}}}}{| }^{2}\) and the angle-dependent quasiparticle gap function is \({{{\Delta }}}_{{{{{{\bf{k}}}}}}}={{{\Delta }}}_{0}{\chi }_{{{{{{\bf{k}}}}}}}^{+}\). Given a particular set of pairing symmetries and coupling constants, these equations can be solved to determine the equilibrium values of η and Δ0 which characterize the condensate.

Effective action for fluctuations

Now, we move on to consider the fluctuations around this saddle point, which we parameterize as

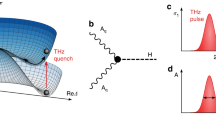
$$\begin{array}{lll}{{{\Delta }}}^{+}(x)&=&{{{{{{\rm{e}}}}}}}^{2i\theta (x)}\left({{{\Delta }}}_{0}+h(x)\right)\\ {{{\Delta }}}^{-}(x)&=&{{{{{{\rm{e}}}}}}}^{2i\theta (x)}\left(a(x)+ib(x)\right)\end{array}$$
(5)

where θ is the ABG phase mode, h is the Higgs mode, and the a and b modes are fluctuations in the relative amplitude and phase of the two order parameter components, i.e., the generalized clapping modes (see Fig. 1a). This parameterization suggests that we can equivalently think of the generalized clapping modes as being fluctuations in the degenerate time-reversed Δ− pairing channel, which are formally similar to Bardasis-Schreiffer modes31,32, as illustrated in Fig. 1b.

Fig. 1: Generalized clapping modes.
figure 1

a Schematic of the collective mode spectrum for a time-reversal symmetry breaking superconductor, featuring the massless Anderson–Bogoliubov–Goldstone mode (acoustic plasmon), massive relative phase mode (optical plasmon), and two massive amplitude modes. The A+ mode generically lies below the quasiparticle continuum. b Illustration of the collective modes: once the system condenses into e.g., the Δ1 + iΔ2 ground state, the corresponding order parameter Δ+ resides in a Mexican hat potential \({{{{{\mathcal{V}}}}}}[{{{\Delta }}}^{+}]\) with a finite expectation value. The Higgs (ABG) mode is then an amplitude (phase) fluctuation in this condensed pairing channel. In contrast, the time-reversed Δ− channel remains undcondensed and experiences a parabolic potential \({{{{{\mathcal{V}}}}}}[{{{\Delta }}}^{-}]\) centered around the minimum Δ− = 0. The generalized clapping modes are then the in-phase and out-of-phase fluctuations in this time-reversed uncondensed pairing channel.

Full size image

To organize our calculations in a manifestly gauge-invariant way, we minimally couple the system to an external (classical) gauge field and perform a unitary transformation \({{\mathbb{G}}}^{-1}\to U{{\mathbb{G}}}^{-1}{U}^{{{\dagger}} }\) with \(U={{{{{{\rm{e}}}}}}}^{-i\theta {\tau }_{z}}\) such that the ABG mode and gauge field only appear together as the gauge-invariant vector field V0 = A0 + ∂τθ and V = A − ∂θ (where we have set the electron charge equal to one). To quadratic order in these fields and setting q → 0, the action is

$$S= \mathop{\sum}\limits_{q}\left[\ {{{\Pi }}}^{00}{V}_{-q}{V}_{q}+{n}_{s}^{ij}\,{V}_{-q}^{i}{V}_{q}^{j}\right]\\ -\,\mathop{\sum}\limits_{q}\left[{{{{{{\mathcal{D}}}}}}}_{h}^{-1}\,{h}_{-q}{h}_{q}+{{{{{{\mathcal{D}}}}}}}_{a}^{-1}\,{a}_{-q}{a}_{q}+{{{{{{\mathcal{D}}}}}}}_{b}^{-1}\,{b}_{-q}{b}_{q}\right]\\ +\,\mathop{\sum}\limits_{q}\left[\ {\tilde{{{\Pi }}}}^{ha}\,{h}_{-q}{a}_{q}+{{{\Pi }}}^{0b}{V}_{-q}^{0}{b}_{q}\right]\,.$$
(6)

In the above, Π00 is the electronic compressibility, \({n}_{s}^{ij}\) is the superfluid density, \({{{{{{\mathcal{D}}}}}}}_{h,a,b}\) are the propagators for the Higgs, relative amplitude, and relative phase modes, and \({\tilde{{{\Pi }}}}^{ha}\) and Π0b are linear couplings between the Higgs/relative amplitude and ABG/relative phase modes which are non-vanishing in the q → 0 limit. This action is derived and the correlation functions which appear in it are evaluated in Supplementary Note 2.

To gain intuition, we begin by considering the familiar case of p + ip pairing in two dimensions. When the px and py components of the order parameter occur with equal amplitudes (η = π/4), as is dictated by symmetry in most cases of physical interest, we find that after analytically continuing to real-time the propagators for both the a and b modes have a pole at \({{\Omega }}=\sqrt{2}{{{\Delta }}}_{0}\), i.e., the two modes are degenerate. So, we see that the usual clapping modes previously studied in p + ip superconductors and 3He-A are indeed a special case of the generalized clapping modes a and b studied in this work. Moreover, at this point the gap is isotropic and the couplings \({\tilde{{{\Pi }}}}^{ha}\) and Π0b vanish so that the (generalized) clapping modes decouple from both quasiparticle excitations and other collective modes and thus are infinitely long-lived at zero temperature.

In real materials, anisotropic crystal fields can lead to deviations from the equal-amplitude η = π/4 state33, making it interesting to consider the collective mode spectrum of the p + ip state for general mixing angles. We plot the spectral functions of the a and b modes in Fig. 2a, b as a function of the mixing angle η and frequency Ω. We see that the two modes split as the mixing angle deviates from π/4, so that for generic mixing angles there are two generalized clapping modes corresponding to the relative amplitude and phase fluctuations.

Fig. 2: p-wave superconductor.
figure 2

Spectral functions (in units of the inverse normal state density of states at the Fermi level, ν−1) of a the relative amplitude and b phase modes for p + ip pairing as a function of frequency Ω (scaled to the typical gap 2Δ0) and the mixing angle η. Note that for an equal admixture of the px and py components (η = π/4) the two modes are degenerate at the frequency \(\sqrt{2}{{{\Delta }}}_{0}\). Away from this point, the modes split with a moving toward the gap edge (taking the character of an amplitude mode), and b moving toward zero frequency (taking the character of a phase mode). The minimum value of the gap for each mixing angle is represented by the gray dashed lines overlaid on each plot.

Full size image

Two-dimensional systems

We will now investigate the generalized clapping mode spectrum for several even parity two-component TRSB order parameters which are potentially relevant to experimental systems: the \({d}_{{x}^{2}-{y}^{2}}+i{d}_{xy}\) state, originally studied in the context of the cuprate high-temperature superconductors34,35, and now the subject of renewed interest due to its potential relevance to a number of moiré systems24,25,36, other heterostructures37, and its proposed realization in twisted bilayers of cuprates26 and other unconventional superconductors27; the s + idxy state, which has long been of interest in relation to the iron pnictide high-temperature superconductors38,39,40; and the \({d}_{{x}^{2}-{y}^{2}}+i{g}_{xy({x}^{2}-{y}^{2})}\) state which has recently been proposed as the order parameter of Sr2RuO441,42. The basic properties of each order parameter studied in this work are listed in Table 1.

Table 1 Time-reversal symmetry breaking order parameters.
Full size table

Because these are all mixed symmetry states where the mixing angle is unconstrained by point group symmetries, it is important to survey the generalized clapping mode spectra over the full range of η. We first turn our attention to the relative phase mode, the spectra of which we plot for each of the above order parameters in Fig. 3a–f. Crucially, we observe that the relative phase mode is a well-defined, coherent mode for all values of the mixing angle, with a sharp spectral function that can be seen in the line cuts in Fig. 3d–f. This even remains true for nodal order parameters, e.g., the d + ig state.

Fig. 3: Relative phase modes.
figure 3

Spectral functions of the relative phase mode as a function of frequency Ω (scaled to the typical gap 2Δ0) and the mixing angle η for a \(d+id^{\prime} \), b s + id, and c d + ig orders. The minimum value of the gap for each mixing angle is represented by the gray dashed lines overlaid on each plot. d, e, f Line cuts for several values of η for each order parameter, with the corresponding quasiparticle gap function around the Fermi surface shown in the inset.

Full size image

Next, we turn our attention to the relative amplitude mode. As we show in Supplementary Note 2, this mode is coupled to the Higgs mode even at zero momentum. The relative amplitude and Higgs modes then hybridize to form two orthogonal amplitude modes, which we call A+ and A−. We calculate the propagators DA±(Ω) for these modes in Supplementary Note 2, which we use to plot the spectral functions of each mode for various pairing symmetries, as shown in Fig. 4a–f.

Fig. 4: Amplitude modes.
figure 4

Spectral functions of the amplitude modes A± as a function of frequency Ω (scaled to the typical gap 2Δ0) and the mixing angle η for a, b d + ig, c, d \(d+id^{\prime} \), and e, f s + id orders. The minimum value of the gap for each mixing angle is represented by the gray dashed lines overlaid on each plot.

Full size image

For all of the pairing symmetries studied, the A− mode resides at or slightly below the gap edge, much like the conventional Higgs mode in a single-component superconductor. More interesting is the A+ mode, which lies well below the quasiparticle continuum for a wide range of mixing angles. This low-frequency amplitude mode represents a second novel collective excitation characteristic of TRSB superconducting states.

We also note that at η = π/4, the \(d+id^{\prime} \) state is fully gapped and chiral, and both generalized clapping modes are degenerate with a frequency of \({{\Omega }}=\sqrt{2}{{{\Delta }}}_{0}\), much like the chiral p-wave state in Fig. 243. As we will show below, this degeneracy is a general feature of chiral order parameters.

Three-dimensional systems

We now consider several TRSB superconducting states in three-dimensional systems: the 3d px + ipy state (i.e., a px + ipy order parameter defined over a spherical Fermi surface), better known as the Anderson–Brinkman–Morel (ABM) state of 3He-A44, which is also a minimal model for a Weyl superconductor, and thus may bear some qualitative similarities to the superconducting state of UTe218 and other candidate Weyl systems; the three-dimensional \({d}_{{x}^{2}-{y}^{2}}+i{d}_{xy}\) “double Weyl” superconducting state possibly realized in the “hidden order” phase of URu2Si245,46 or SrPtAs47,48; and finally the dxz + idyz state which is a candidate order parameter for Sr2RuO4 as well as the hidden order phase of URu2Si249,50.

All of these states are most naturally considered as equal-admixtures, i.e., with η = π/4, in which case the generalized clapping modes decouple from the Higgs mode. As seen in Fig. 5a–d, the generalized clapping modes are degenerate with one another in all cases. Unlike the two-dimensional case, however, the mode frequency is not \(\sqrt{2}{{{\Delta }}}_{0}\). By inspection of the analytic form of the generalized clapping mode propagators (see Supplementary Note 2), it is evident that the mode frequency is only \(\sqrt{2}{{{\Delta }}}_{0}\) if the order parameter is both chiral and isotropically gapped, whereas the ABM and 3d \(d+id^{\prime} \) (d + id) states exhibit point (line) nodes. We also note that this demonstrates that the generalized clapping modes remain coherent even for a system with line nodes in the superconducting gap, i.e., these modes’ survival seems largely insensitive to the nodal structure of the order parameter. Combined with the prior results for the chiral p + ip and \(d+id^{\prime} \) states in two-dimensions, we see that chiral order parameters are generically characterized by degenerate generalized clapping modes. In this way, the generalized clapping mode spectrum can be used to differentiate chiral states from mixed symmetry TRSB states, as further discussed below.

Fig. 5: Three-dimensional chiral superconductors.
figure 5

Spectral functions as a function of frequency Ω (scaled to the typical gap 2Δ0) for the relative amplitude and phase modes for the chiral (η = π/4) states a three-dimensional p + ip Anderson–Brinkman–Morel (ABM), b three-dimensional \(d+id^{\prime} \), and d + id state for a c fully three-dimensional system with a spherical Fermi surface (FS), and d quasi-two-dimensional system with a cylindrical Fermi surface. In all cases, the two clapping modes are degenerate, reflecting the chiral nature of the order parameter.

Full size image

Altogether, the results we have presented so far provide strong evidence that the generalized clapping modes are always well-defined sub-gap excitations in TRSB superconducting states. A rigorous proof of this conjecture would be an interesting direction for future research, but is beyond the scope of the present work. At a practical level, this universality is essential to these modes’ application in collective mode spectroscopy.

Having established that the relative phase and amplitude modes are typically well-defined collective excitations in TRSB superconductors, we now propose several means for their experimental detection.

Detection of relative phase modes

From the action (6), we see that the relative mode contributes to the charge density as ρ ~ i∂tb due to the non-vanishing linear coupling Π0b between b and the scalar potential. Since the relative phase mode resides at finite frequency, it is not affected by Coulomb interactions in the usual way and is not lifted up to the plasma frequency (similar to ref. 51).

One may then integrate b out of this action, renormalizing the electronic compressibility Π00(Ω) → Π00(Ω) + δΠ00(Ω) where

$$\delta {{{\Pi }}}^{00}({{\Omega }})=-{{{\Pi }}}^{0b}(-{{\Omega }})\,{{{{{{\mathcal{D}}}}}}}_{b}({{\Omega }})\,{{{\Pi }}}^{0b}({{\Omega }})/4$$
(7)

is the relative phase mode’s contribution to Π00(Ω). We plot this function for several pairing symmetries in Fig. 6a–d, where we see clear features at the relative phase mode frequency.

Fig. 6: ac compressibility.
figure 6

Imaginary part of the relative phase mode’s contribution to the electronic compressibility, Im δΠ00, given by Eq. (7), plotted as a function of frequency Ω (scaled to the typical gap 2Δ0) for a p + ip, b \(d+id^{\prime} \), c s + id, and d d + ig orders, in units of e2ν. All exhibit clear features at the clapping mode frequency. For the p + ip and \(d+id^{\prime} \) cases, the clapping mode peak is small (and is indicated by the arrows in the figure) near η = π/4 due to the suppression of the coupling to the scalar potential at η = π/4. For the same two cases, the large shoulder at higher frequencies arises due to the relative phase mode’s decay into, and coupling to, quasiparticles. We also note that within our model (where the basis functions are taken to be spherical harmonics), the results for the p + ip and \(d+id^{\prime} \) states are identical, which is an artifact of our highly symmetric model. In the s + id and d + ig cases, which are not subject to the same selection rules as the chiral states, the principal peaks are due to the relative phase mode.

Full size image

Taking into account Coulomb interactions and integrating out the ABG phase mode, the fully renormalized longitudinal dielectric function is

$${\epsilon }_{L}(\Omega ,{{{{{\bf{q}}}}}})=1+\frac{{n}_{s}}{m}\frac{{\tilde{{{\Pi }}}}^{00}({{\Omega }})}{{n}_{s}{{{{{{\bf{q}}}}}}}^{2}/m-{{{\Omega}}}^{2}{\tilde{{{\Pi }}}}^{00}({{\Omega }})}$$
(8)

where \({\tilde{{{\Pi }}}}^{00}({{\Omega }})={{{\Pi }}}^{00}({{\Omega }})+\delta {{{\Pi }}}^{00}({{\Omega }})\) is the renormalized compressibility and ns is the superfluid density. For frequencies much smaller than the plasma frequency, the dielectric function is \({\epsilon }_{L}({{\Omega }},{{{{{\bf{q}}}}}})\approx 1+{\tilde{{{\Pi }}}}^{00}({{\Omega }})/{{{{{{\bf{q}}}}}}}^{2}\), which includes a feature at the relative phase mode frequency that can be detected by probes sensitive to the density–density response function, as discussed below.

For most candidate TRSB superconductors, the superconducting gap, and hence the relative phase mode frequency, is in the terahertz regime. The ac electronic compressibility can be directly measured at THz frequencies using existing experimental techniques such as momentum-resolved electron energy loss spectroscopy (M-EELS)52,53,54,55, which enables direct experimental detection of the relative phase mode.

In such an experiment, the relative phase mode can be distinguished from trivial non-electronic modes by its dispersion and the fact that the peak corresponding to this mode should vanish above Tc. It can be shown that the relative phase mode disperses as \({{{\Omega }}}^{2}={{{\Omega }}}_{\,{{\mbox{b}}}\,}^{2}+\alpha {v}_{F}^{2}{q}^{2}\), where Ωb is the frequency of the mode and α is a constant dependent on the mixing angle and orbital symmetries of the order parameter. In light of these considerations, the observation of a sub-gap peak in the charge response, measured via M-EELS, which disperses with an electronic-scale wavelength would constitute smoking-gun evidence for the relative phase mode in a TRSB superconductor.

Alternatively, these modes may also be detected by sub-gap peaks in the microwave power absorption, as shown in refs. 56,57, and via magneto-optical measurements58. In fact, a collective mode of unknown origin has been observed in microwave power absorption measurements of the heavy-fermion superconductor UBe1359. To date, there is no evidence that the superconducting state of this system is TRSB, but a split transition has been reported in specific heat measurements of its Th-doped relative U1−xThxBe1360,61, which is suggestive of a multi-component order. In light of this, it could be interesting to revisit the order parameter symmetry of these compounds and whether time-reversal symmetry is broken. If so, ref. 59 might represent the first measurement of a generalized clapping mode.

In addition to the equilibrium probes discussed above, the relative phase mode should also be detectable out of equilibrium using time-resolved THz spectroscopy62. In fact, a recent experiment has claimed to observe the Leggett phase mode in the multi-band superconductor MgB2 using this technique63. However, another THz study of MgB2 attributed the same experimental signatures to other modes, complicating the identification of the Leggett mode64. In any case, further work is necessary to establish the precise experimental signatures of the relative phase mode in such an experiment.

If one were to observe a peak near the relative phase mode frequency in any of the experiments listed above, its origin can be further distinguished with the application of an external magnetic field. For most tetragonal two-component superconductors, there is a symmetry-allowed linear coupling to an external magnetic field \(\delta f=ig{H}_{z}({\bar{{{\Delta }}}}_{1}{{{\Delta }}}_{2}-{{{\Delta }}}_{1}{\bar{{{\Delta }}}}_{2})\)65. In terms of the relative phase φ between Δ1 and Δ2, this can be written as \(\delta f=gH\sin \varphi \approx -gH\delta {\varphi }^{2}\) where we have assumed that the fluctuations δφ are small around the equilibrium value of φ0 = π/2. Then, on very general grounds30, this coupling shifts the relative phase mode frequency from Ωb,0 at zero field to \({{{\Omega }}}_{b}^{2} \sim {{{\Omega }}}_{b,0}^{2}+gH\). That is, the frequency of an experimentally observed peak should vary linearly with small applied magnetic fields if it truly corresponds to the relative phase mode, and in this way, one may unambiguously assign an observed peak to the relative phase mode.

Detection of amplitude modes

The A± modes couple to electromagnetic fields in the same manner as the Higgs mode in a conventional single-component superconductor, through the non-linear coupling δS ~ A2A±. One method to detect amplitude modes using this coupling is via the observation of resonantly enhanced third-harmonic generation in a non-linear THz spectroscopy experiment, which has been successfully performed for both conventional66 and high-temperature superconductors67. Amplitude modes have also been detected in THz pump, optical probe experiments for conventional superconductors68 and cuprates69. However, despite the rapid development of THz spectroscopy of a probe of Higgs modes in superconductors, the impact of charge density fluctuations70, disorder71,72,73, and other modes74 on the THz response continue to be actively discussed, and the identification of the Higgs mode in unconventional superconductors remains controversial.

The A+ mode in TRSB superconductors is attractive on account of its low frequency, which should make it less heavily damped than conventional Higgs modes and easier to disentangle from the charge density fluctuations which onset at the gap edge75. Nonetheless, in light of the aforementioned controversy surrounding the THz detection of conventional Higgs modes, further work is necessary to establish the detailed THz response of the amplitude modes discussed in our work to facilitate comparison with potential future experiments.

Alternatively, the amplitude modes can be detected using microwave spectroscopy, or within linear response as a resonance in the optical conductivity in the presence of a background dc supercurrent76, as has been demonstrated in NbN77.

Like the relative phase mode discussed above, the observation of the low-frequency A+ amplitude mode is a direct signature of the TRSB superconducting state. Thus, the detection of this mode represents a different avenue in the emerging field of “Higgs spectroscopy”10,11,67 where non-equilibrium amplitude oscillations are used to gain insight into the symmetry of the condensate. However, in contrast to these pioneering works, generalized clapping modes can be detected in equilibrium and using a wide variety of experimental probes, as discussed above.

Discussion

To summarize, we have shown that fluctuations in the relative amplitude and phase of two-component TRSB order parameters are well-defined collective modes for a wide class of model order parameters with both spin-singlet and spin-triplet pairing (and possibly mixed-parity systems as well). Moreover, even for nodal gap functions, we have found that these modes are not overdamped by low-energy quasiparticles in the T → 0 limit. The frequency of each mode depends strongly on both the orbital symmetries of the two order parameter components and the relative amplitude of the two components in equilibrium.

Further, we have proposed a number of means to experimentally detect generalized clapping modes: the relative phase mode can be directly detected via measurement of the ac electronic compressibility (using e.g., M-EELS), the amplitude modes can be detected using ultrafast and non-linear THz spectroscopy as well as optical conductivity measurements (in the presence of a dc supercurrent), and both modes can be detected in microwave power absorption measurements. The observation of these modes in a given material would constitute robust evidence of a two-component TRSB order parameter.

Our work enables a variety of existing experimental techniques including ultrafast and non-linear optics, electron scattering, and microwave spectroscopy to be used as direct probes of TRSB in unconventional superconductors. These measurements can be thought of as a form of “collective mode spectroscopy,” where one obtains information about the structure of the order parameter from its collective mode spectrum. Given the relative scarcity of probes directly sensitive to TRSB in superconductors (previously limited to only Kerr rotation and muon spin relaxation), this represents a substantial expansion of the experimental tools available to characterize these exotic TRSB superconducting states.

Detection of the generalized clapping modes also offers the unique ability to estimate the relative magnitudes of each order parameter component through the frequency at which the mode resides (as seen in all of our results, the phase mode frequency is maximum for an equal admixture of order parameter components, and decreases as one component or the other becomes dominant). Moreover, observing these modes using ultrafast THz techniques would allow one to assess TRSB superconductivity in driven non-equilibrium superconductors. The exploration and manipulation of generalized clapping modes also represent a distinct direction in the wider, rapidly developing field of THz control of unconventional superconductors and their collective excitations74,78,79,80,81,82,83.

As mentioned above, the generalized clapping mode spectrum can be used to unambiguously distinguish chiral TRSB states from non-chiral states, as a generic TRSB superconductor has two non-degenerate generalized clapping modes, whereas it is only in the special case of a chiral state that the two modes are degenerate.

This capability is particularly well-suited to clarify the structure of the order parameter in Sr2RuO4—a problem of tremendous current interest. At the time of writing, the two leading candidate order parameters for this system are the mixed symmetry d + ig state (see Figs. 3c, f and 4e, f) and the chiral d + id state (see Fig. 5d), where the generalized clapping mode spectrum is plotted for the cylindrical Fermi surface relevant to Sr2RuO4). Quasiparticle interference84 and thermal transport85 measurements have demonstrated that the order parameter exhibits vertical line nodes along the zone diagonals (i.e., along the [110] direction), consistent with the d + ig scenario, and counter to the horizontal line nodes expected for a d + id state. In contrast, recent muon spin relaxation measurements failed to detect a splitting of the critical temperature under hydrostatic pressure86, which is only consistent with the chiral d + id order. Given these seemingly conflicting results, a measurement of the generalized clapping mode spectra, via e.g., microwave absorption measurements, could provide crucial insight into the chirality, or lack thereof, of the order parameter, and help the community converge on one candidate order parameter over the other.

Beyond its utility as a form of spectroscopy, the detection of generalized clapping modes is also interesting from a fundamental physics perspective, as the analog of the clapping mode in 3He-A has yet to be realized in any electronic system. Previously, the existence and detection of clapping modes were considered primarily in p + ip superconductors29,87,88, which have proven elusive to realize experimentally89. This work opens up a number of other materials platforms12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27 as candidate systems to finally realize these exotic collective modes in a solid-state system.

Finally, we speculate that our work may also be extended to the enigmatic pseudogap phase of the cuprate high-temperature superconductors where a non-zero Kerr rotation has been reported90, suggesting the existence of a TRSB phase above the superconducting transition. It has recently been suggested36,91,92,93,94 that the relative phase between two order parameter components can acquire a phase stiffness before either order parameter becomes phase coherent and condenses. In this scenario, the relative phase mode studied in this work could persist even above the superconducting transition, representing a distinctive collective excitation in a TRSB metallic phase.