Protocol designs for NOON states

Abstract

The ability to reliably prepare non-classical states will play a major role in the realization of quantum technology. NOON states, belonging to the class of Schrödinger cat states, have emerged as a leading candidate for several applications. Here we show how to generate NOON states in a model of dipolar bosons confined to a closed circuit of four sites. This is achieved by designing protocols to transform initial Fock states to NOON states through use of time evolution, application of an external field, and local projective measurements. The evolution time is independent of total particle number, offering an encouraging prospect for scalability. By variation of the external field strength, we demonstrate how the system can be controlled to encode a phase into a NOON state. We also discuss the physical feasibility, via ultracold dipolar atoms in an optical superlattice setup. Our proposal showcases the benefits of quantum integrable systems in the design of protocols.

Introduction

Quantum systems are widely considered to be the most promising foundation for the next generation of platforms in computing, communication, measurement, and simulation. This is primarily due to the properties of state superposition and entanglement. To realize the potential for progress, it is necessary to establish protocols that are capable of generating important quantum states.

The NOON state is a fundamental example. It is an “all and nothing” superposition of two different modes^1,2. For N particles, it has the form

$$\begin{array}{l}\left|{{{{{{{\rm{NOON}}}}}}}}\right\rangle =\frac{1}{\sqrt{2}}\left(\left|N,0\right\rangle +{e}^{i\varphi }\left|0,N\right\rangle \right)\end{array}$$

(1)

where the phase φ typically records information in applications. These include: in the fields of quantum metrology and sensing, performing precision phase-interferometry at the Heisenberg limit³ and overcoming diffraction limits in quantum lithography⁴; in tests of fundamental physics, NOON states are used to study Bell-type inequalities violation⁵; they offer promising applications in Quantum Communication and Quantum Computing⁶, and their utilization is expected to extend to areas such as chemistry and biology⁷. After early success, using photon pairs and Hong-Ou-Mandel (HOM) interferometry⁸, several schemes have followed for the production and detection of photonic NOON states^2,9,10,11,12. There are also proposals using other architectures, such as circuit QED¹³, trapped ions¹⁴, and Bose-Einstein condenstates¹⁵.

The creation of Bose-atom NOON states would enable new tests, using massive states, of the foundations for quantum mechanics. A step in this direction was taken with the demonstration of the matter-wave equivalent of the HOM effect^16,17. Prospects for creating Bose-atom NOON states using a double-well potential were first floated some time ago¹⁸. This early work considered an attractive system, which is prone to instability. In principle, a more robust repulsive system can be prepared to evolve to a high-fidelity approximation of a NOON state. However, the drawback here is that the process is associated with an extremely large time scale. Recently, new studies of the double-well system have been undertaken to reduce the time scale. One example proposes to adiabatically vary the system parameters through an excited-state phase transition during the process¹⁹. Another study employs periodic driving to lower the NOON-state evolution time²⁰. Nonetheless, the time to generate a NOON state in these examples still, increasingly, scales with the total number of particles.

Here we present an alternative to circumvent these issues. Our approach adopts a closed-circuit of four sites, with a Fock-state input of M particles in site 1, P particles in site 2, and no particles in sites 3 and 4, denoted as $\left|{{{\Psi }}}_{0}\right\rangle =\left|M,P,0,0\right\rangle$. The initial step is to create an uber-NOON state, with the general form

$$\left|\,{{\mbox{u-NOON}}}\,\right\rangle =\, \frac{1}{2}\left(\left|M,P,0,0\right\rangle +{e}^{i{\varphi }_{1}}\left|M,0,0,P\right\rangle \right.\\ \left.+\;{e}^{i{\varphi }_{2}}\left|0,P,M,0\right\rangle +{e}^{i{\varphi }_{3}}\left|0,0,M,P\right\rangle \right)$$

for a set of phases {φ₁,  φ₂,  φ₃}. This state may be viewed as an embedding of NOON states (1) within two-site subsystems. We then describe two protocols to extract a NOON state from an uber-NOON state, one through dynamical evolution followed by local projective measurement and post-selection, the other from dynamical evolution alone. The protocols are schematically presented in Fig. 1.

Fig. 1: NOON state generation scheme.

The four spheres on the left represent the initial state, with white indicating an empty site. Cyan and blue correspond to M and P particles, respectively. In time-evolved states, gradient colors are used to indicate that the state of a site is entangled with the rest of the system - superposition states for each step are shown in the framed legend. The bars connecting the spheres denote tunneling between nearest-neighbor sites, while the rectangles represent applied external fields to sites 1–3 (ν) and 2–4 (μ). In Protocol I, the system initially evolves for time t_m − t_μ, towards the u-NOON state. Then, a field is applied across sites 2–4 for time t_μ (dashed brown time line), to encode a phase. Finally, the light cyan halo portrays a projective measurement process at site 3, denoted by ${{{{{{{\mathcal{M}}}}}}}}$. The outcomes $\left|0\right\rangle$ and $\left|M\right\rangle$ signify which of two possible NOON states results across sites 2–4. Similarly in Protocol II, the system first evolves for time t_m − t_ν, then a field is applied to sites 1–3 for time t_ν to implement the phase π/2. Next, the system evolves for time t_m − t_μ, after which a field is applied to sites 2–4 to encode a phase during time t_μ. This results in a NOON state across sites 2–4, without performing a measurement procedure.

The approach taken has the following properties: (i) The system has long-ranged interactions, described by the Extended Bose-Hubbard Model (EBHM)²¹. There exists a choice of the coupling parameters for which this model is integrable²². As in other physically realized integrable systems^{23,24,25,26,27,28,29,30}, this property facilitates several analytic calculations for physical quantities. Here, integrability exposes the protocols available for NOON state generation. The execution time is found to be dependent on the difference between the two initially populated sites within the four-site system. It is independent of total particle number, opening a means for scalability.

(ii) The system can be controlled by breaking the integrability over small time scales. Encoding of the phase into a NOON state only requires breaking of integrability over an interval that is several orders of magnitude smaller than the entire execution time. This causes minimal loss in fidelity. (iii) With currently available technology, the system may be realized and controlled using dipolar atoms (e.g., dysprosium or erbium) with repulsive interactions, trapped in optical lattices^31,32. In this setup, the evolution times that we compute for NOON-state generation are of the order of seconds.

For the four-site configuration, the EBHM Hamiltonian is

$$H=\, \frac{{U}_{0}}{2}\mathop{\sum }\limits_{i=1}^{4}{N}_{i}({N}_{i}-1)+\mathop{\sum }\limits_{i=1}^{4}\mathop{\sum }\limits_{j=1,j\ne i}^{4}\frac{{U}_{ij}}{2}{N}_{i}{N}_{j}\\ -\frac{J}{2}\left[({a}_{1}^{{{{\dagger}}} }+{a}_{3}^{{{{\dagger}}} })({a}_{2}+{a}_{4})+({a}_{1}+{a}_{3})({a}_{2}^{{{{\dagger}}} }+{a}_{4}^{{{{\dagger}}} })\right],$$

(2)

where ${a}_{j}^{{{{\dagger}}} },\,{a}_{j}$ are the creation and annihilation operators for site j, and ${N}_{j}={a}_{j}^{{{{\dagger}}} }{a}_{j}$ are the number operators. The total number operator N = N₁ + N₂ + N₃ + N₄ is conserved. Above, U₀ characterizes the interaction between bosons at the same site, U_ij = U_ji is related to the long-range (e.g., dipole-dipole) interaction between bosons at sites i and j, and J accounts for the tunneling strength between different sites.

Below, we describe two protocols that enable the generation of NOON states, with fidelities greater than 0.9. A physical setup to implement them is also discussed.

Results

Insights into the physical behavior of Eq. (2) become accessible at the integrable coupling. Setting U₁₃ = U₂₄ = U₀ and U₁₂ = U₂₃ = U₃₄ = U₁₄, the system acquires two additional conserved quantities, Q₁ and Q₂, such that $2{Q}_{1}={N}_{1}+{N}_{3}-{a}_{1}^{{{{\dagger}}} }{a}_{3}-{a}_{1}{a}_{3}^{{{{\dagger}}} }$ and $2{Q}_{2}={N}_{2}+{N}_{4}-{a}_{2}^{{{{\dagger}}} }{a}_{4}-{a}_{2}{a}_{4}^{{{{\dagger}}} }$. Together with the total number of particles N and the Hamiltonian H, the system possesses four independent, conserved quantities. This is equal to the number of degrees of freedom, satisfying the criterion for integrability. Suppose that, initially, there are M atoms in site 1 and P atoms in site 2. We identify the resonant tunneling regime as being achieved when U∣M − P∣ ≫ J (see Methods for details), where U = (U₁₂ − U₀)/4. This regime is characterized by sets of bands in the energy spectrum (see Supplementary Note 1). In this region, an effective Hamiltonian H_eff (see Methods, Eq. (3)) enables the derivation of analytic expressions for several physical quantities.

In the settings discussed above, the system described by Eq. (2) provides the framework to generate uber-NOON states when N = M + P is odd³³. To encode phases, however, it is necessary to break the integrability in a controllable fashion. Here, we introduce two idealized protocols to produce NOON states with general phases by breaking the system’s integrability with externally applied fields. We call the subsystem containing sites 1, 3 as A, and the one containing sites 2, 4 as B. We denote three time intervals: t_m, t_μ, and t_ν. The first, corresponding to integrable time evolution, is associated with evolution to a particular uber-NOON state. The others, associated with smaller-scale non-integrable evolution, produce phase encoding. Both protocols are built around a general time-evolution operator

$${{{{{{{\mathcal{U}}}}}}}}(t,\mu ,\nu)=\exp \left(-\frac{it}{\hslash }[H+\mu ({N}_{2}-{N}_{4})+\nu ({N}_{1}-{N}_{3})]\right),$$

where the applied field strengths μ, ν implement the breaking of integrability. It is convenient to introduce the phase variable θ = 2μt_μ/ℏ, and to fix t_ν = ℏπ/(4Mν), with ℏ the reduced Planck constant.

Protocol I

In this protocol we employ breaking of integrability through an applied field to subsystem B and a measurement process. The protocol consists of three sequential steps, schematically depicted in Fig. 1:

• (i) $\left|{{{\Psi }}}_{1}^{\,{{{{{{\mathrm{I}}}}}}}\,}\right\rangle ={{{{{{{\mathcal{U}}}}}}}}({t}_{{{{{{{\mathrm{m}}}}}}}}-{t}_{\mu },0,0)\left|{{{\Psi }}}_{0}\right\rangle$;

• (ii) $\left|{{{\Psi }}}_{2}^{\,{{{{{{\mathrm{I}}}}}}}\,}\right\rangle ={{{{{{{\mathcal{U}}}}}}}}({t}_{\mu },\mu ,0)\left|{{{\Psi }}}_{1}^{\,{{{{{{\mathrm{I}}}}}}}\,}\right\rangle$;

• (iii) $\left|{{{\Psi }}}_{3}^{\,{{{{{{\mathrm{I}}}}}}}\,}\right\rangle ={{{{{{{\mathcal{M}}}}}}}}\left|{{{\Psi }}}_{2}^{\,{{{{{{\mathrm{I}}}}}}}\,}\right\rangle$,

where t_m = ℏπ/(2Ω) (see Methods) and ${{{{{{{\mathcal{M}}}}}}}}$ represents a projective measurement of the number of bosons at site 3 (which could be implemented, in principle, through site-selective imaging^34,35,36 or Faraday rotation detection^37,38,39). A measurement outcome of 0 or M heralds a high-fidelity NOON state in subsystem B. For other measurement outcomes, the output is discarded and the process repeated (post-selection).

Idealized limit

There is an idealized limit for which the above protocol has perfect success probability and output fidelity. Taking t_μ → 0, μ → ∞ such that θ remains finite, and using the effective Hamiltonian, provides explicit expressions for the uber-NOON states that result at steps (i) and (ii)

$$\left|{{{\Psi }}}_{1}^{\,{{{{{{\mathrm{I}}}}}}}\,}\right\rangle =\, \frac{1}{2}\left(\beta \left|M,P,0,0\right\rangle +\left|M,0,0,P\right\rangle \right.\\ \left.+\,\left|0,P,M,0\right\rangle -\beta \left|0,0,M,P\right\rangle \right)\\ \left|{{{\Psi }}}_{2}^{\,{{{{{{\mathrm{I}}}}}}}\,}\right\rangle =\, \frac{1}{2}\left(\beta \left|M,P,0,0\right\rangle +{e}^{iP\theta }\left|M,0,0,P\right\rangle \right.\\ \left.+\,\left|0,P,M,0\right\rangle -\beta {e}^{iP\theta }\left|0,0,M,P\right\rangle \right)$$

Note that due to the conservation of N₁ + N₃ and N₂ + N₄ under the effective Hamiltonian, Fock states such as $\left|M,0,P,0\right\rangle$ and $\left|0,M,0,P\right\rangle$ do not appear in the above expression. Next, the two possible states at step (iii) depend on the measurement outcome r at site 3:

$$\left|{{{\Psi }}}_{3}^{\,{{{{{{\mathrm{I}}}}}}}\,}\right\rangle =\left\{\begin{array}{l}\frac{1}{\sqrt{2}}\left(\beta \left|M,P,0,0\right\rangle +{e}^{iP\theta }\left|M,0,0,P\right\rangle \right),\quad r=0,\quad \\ \frac{1}{\sqrt{2}}\left(\left|0,P,M,0\right\rangle -\beta {e}^{iP\theta }\left|0,0,M,P\right\rangle \right),\quad r=M,\quad \end{array}\right.$$

with β = (−1)^(N+1)/2. These states are recognized as products of a NOON state for subsystem B with Fock basis states for subsystem A.

In the non-ideal case with non-zero t_μ and finite μ, there is a small probability that the measurement outcome r is neither 0 or M. Numerical benchmarks for the measurement probabilities and NOON state output fidelities are provided in a later section. Next, we describe a second protocol.

Protocol II

Now we specify an alternative protocol that does not involve measurements, so post-selection is not required. Employing the same initial state $\left|{{{\Psi }}}_{0}\right\rangle$, the following sequence of steps are implemented to arrive at a NOON state in subsystem B (illustrated in Fig. 1):

• (i) $\left|{{{\Psi }}}_{1}^{\,{{{{{{\mathrm{II}}}}}}}\,}\right\rangle ={{{{{{{\mathcal{U}}}}}}}}({t}_{{{{{{{\mathrm{m}}}}}}}}-{t}_{\nu },0,0)\left|{{{\Psi }}}_{0}\right\rangle$;

• (ii) $\left|{{{\Psi }}}_{2}^{\,{{{{{{\mathrm{II}}}}}}}\,}\right\rangle ={{{{{{{\mathcal{U}}}}}}}}({t}_{\nu },0,\nu)\left|{{{\Psi }}}_{1}^{\,{{{{{{\mathrm{II}}}}}}}\,}\right\rangle$;

• (iii) $\left|{{{\Psi }}}_{3}^{\,{{{{{{\mathrm{II}}}}}}}\,}\right\rangle ={{{{{{{\mathcal{U}}}}}}}}({t}_{{{{{{{\mathrm{m}}}}}}}}-{t}_{\mu },0,0)\left|{{{\Psi }}}_{2}^{\,{{{{{{\mathrm{II}}}}}}}\,}\right\rangle$;

• (iv) $\left|{{{\Psi }}}_{4}^{\,{{{{{{\mathrm{II}}}}}}}\,}\right\rangle ={{{{{{{\mathcal{U}}}}}}}}({t}_{\mu },\mu ,0)\left|{{{\Psi }}}_{3}^{\,{{{{{{\mathrm{II}}}}}}}\,}\right\rangle$.

Idealized limit

Similar to Protocol I, in the limit μ, ν → ∞, t_μ, t_ν → 0, and implementing ${{{{{{{\mathcal{U}}}}}}}}(t,\mu ,\nu)$ with the effective Hamiltonian produces

$$ \left|{{{\Psi }}}_{1}^{\,{{{{{{\mathrm{II}}}}}}}\,}\right\rangle =\, \frac{1}{2}\left(\beta \left|M,P,0,0\right\rangle +\left|M,0,0,P\right\rangle \right.\\ \left.+\,\left|0,P,M,0\right\rangle -\beta \left|0,0,M,P\right\rangle \right);\\ \left|{{{\Psi }}}_{2}^{\,{{{{{{\mathrm{II}}}}}}}\,}\right\rangle = \,\frac{1}{2}\left(\beta \left|M,P,0,0\right\rangle +\left|M,0,0,P\right\rangle \right.\\ \left.+\,i\left|0,P,M,0\right\rangle -i\beta \left|0,0,M,P\right\rangle \right);\\ \left|{{{\Psi }}}_{3}^{\,{{{{{{\mathrm{II}}}}}}}\,}\right\rangle = \frac{1}{\sqrt{2}}\left(\left|M,P,0,0\right\rangle +\beta {e}^{-i\pi /2}\left|M,0,0,P\right\rangle \right);\\ \left|{{{\Psi }}}_{4}^{\,{{{{{{\mathrm{II}}}}}}}\,}\right\rangle =\, \frac{1}{\sqrt{2}}\left(\left|M,P,0,0\right\rangle +{{\Upsilon }}\left|M,0,0,P\right\rangle \right)$$

where ${{\Upsilon }}=\beta \exp (i(P\theta -\pi /2))$.

Protocol fidelities

The analytic results provided above are obtained by employing the effective Hamiltonian in an extreme limit, with divergent applied fields acting for infinitesimally small times. Below we give numerical simulations of the protocols to show that, for physically realistic settings where the fields are applied for finite times, high-fidelity outcomes for NOON state production persist.

Throughout this section, we use $\left|{{\Psi }}\right\rangle$ to denote an analytic state, obtained in an idealized limit. We adopt $\left|{{\Phi }}\right\rangle$ to denote a numerically calculated state, obtained by time evolution with the EBHM Hamiltonian (2). Two sets of parameters are chosen to illustrate the results (expressed in Hz):

Set 1: {U/ℏ = 104.85, J/ℏ = 71.62, μ/ℏ = 30.02};

Set 2: {U/ℏ = 105.60, J/ℏ = 104.95, μ/ℏ = 27.42}.

For all numerical simulation results presented below, the initial state is chosen as $\left|{{{\Psi }}}_{0}\right\rangle =\left|4,11,0,0\right\rangle$, i.e. M = 4 and P = 11.

The fidelities of Protocols I and II are defined as⁴⁰ ${F}_{{{{{{{\mathrm{I}}}}}}}}=\big| \big\langle {{{\Psi }}}_{3}^{\,{{{{{{\mathrm{I}}}}}}}\,}| {{{\Phi }}}_{3}^{\,{{{{{{\mathrm{I}}}}}}}\,}\big\rangle \big|$ and ${F}_{{{{{{{\mathrm{II}}}}}}}}=\big| \big\langle {{{\Psi }}}_{4}^{\,{{{{{{\mathrm{II}}}}}}}\,}| {{{\Phi }}}_{4}^{\,{{{{{{\mathrm{II}}}}}}}\,}\big\rangle \big|$, respectively. This is computed for Pθ ranging from 0 to π, achieved by varying t_μ. In the case of Protocol II, we use ν = μ for both sets of parameters. The systems considered here can, in principle, be implemented using existing hardware—see Physical proposal.

Illustrative results are presented in Table 1, where it is seen that F_II is lower than F_I. This can be attributed to two primary causes. The first is that, while Protocol I takes τ_I ~ t_m to produce the final state, Protocol II requires double the evolution time τ_II ~ 2t_m. The longer evolution time contributes to a loss in fidelity. The second reason is that, the measurement occurring in the final step of Protocol I has the effect of renormalizing the quantum state after the collapse, which increases the fidelity of the resulting NOON state when a measurement of r = 0 or r = M is obtained. However, there is a finite probability that the measurement outcome is neither r = 0 nor r = M (see Supplementary Note 2).

Table 1 Fidelities for Protocols I and II.

In summary, both protocols display high fidelity results greater than 0.9. For Protocol I the outcomes are probabilistic (See Supplementary Note 2 for data). By contrast, the slightly lower fidelity results of Protocol II are deterministic. These results also reflect the trade-off between fidelity and total evolution time. The higher fidelity results associated with parameter Set 1, compared to Set 2, are produced through a long evolution time.

Readout statistics

A means to test the reliability of the system, through a statistical analysis of local measurement outcomes, is directly built into the design. This results from the system’s capacity to function as an interferometer³³. For both protocols, once the output state has been attained we can continue to let the system evolve under ${{{{{{{\mathcal{U}}}}}}}}({t}_{{{{{{{\mathrm{m}}}}}}}},0,0)$. This yields the readout states, denoted as $\big|{{{\Psi }}}_{\,{{{{{{\mathrm{RO}}}}}}}}^{{{{{{{\mathrm{I}}}}}}}\,}\big\rangle$, $\big|{{{\Psi }}}_{\,{{{{{{\mathrm{RO}}}}}}}}^{{{{{{{\mathrm{II}}}}}}}\,}\big\rangle$ respectively, for protocols I and II. In the idealized limits these are

$$\left|{{{\Psi }}}_{\,{{{{{{\mathrm{RO}}}}}}}}^{{{{{{{\mathrm{I}}}}}}}\,}\right\rangle =\left\{\begin{array}{l}\frac{c(\theta)}{\sqrt{2}}(\left|M,P,0,0\right\rangle +\beta \left|M,0,0,P\right\rangle)\hfill\\ +\frac{is(\theta)}{\sqrt{2}}(\beta \left|0,P,M,0\right\rangle -\left|0,0,M,P\right\rangle),{{\mbox{}}}\quad r=0,\hfill\\ \frac{c(\theta)}{\sqrt{2}}(\left|M,P,0,0\right\rangle -\beta \left|M,0,0,P\right\rangle)\hfill\\ -\frac{is(\theta)}{\sqrt{2}}(\beta \left|0,P,M,0\right\rangle -\left|0,0,M,P\right\rangle),{{\mbox{}}}\quad r=M,\\ \end{array}\right.$$

$$\left|{{{\Psi }}}_{\,{{{{{{\mathrm{RO}}}}}}}}^{{{{{{{\mathrm{II}}}}}}}\,}\right\rangle =\, \frac{1}{\sqrt{2}}s\left(\theta -\frac{\pi }{2P}\right)\left(\left|M,P,0,0\right\rangle +\beta \left|M,0,0,P\right\rangle \right)\\ -\frac{i}{\sqrt{2}}c\left(\theta -\frac{\pi }{2P}\right)\left(\beta \left|0,P,M,0\right\rangle -\left|0,0,M,P\right\rangle \right),$$

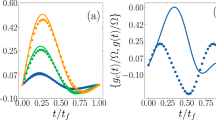
where $c(\theta)\equiv \cos \left(P\theta /2\right)$ and $s(\theta)\equiv \sin \left(P\theta /2\right)$. For $\left|{{{\Psi }}}_{\,{{{{{{\mathrm{RO}}}}}}}\,}^{I}\right\rangle$, the measurement probabilities at site 3 are ${{{{{{{\mathcal{P}}}}}}}}(0)={\cos }^{2}\left(P\theta /2\right)$ and ${{{{{{{\mathcal{P}}}}}}}}(M)={\sin }^{2}\left(P\theta /2\right)$. Combined with the probability of measuring r = 0, M in step (iii), we obtain four possibilities for the total probabilities as ${{{{{{{{\mathcal{P}}}}}}}}}_{{{{{{{\mathrm{I}}}}}}}}(0,0)={{{{{{{{\mathcal{P}}}}}}}}}_{{{{{{{\mathrm{I}}}}}}}}(M,0)=0.5{\cos }^{2}\left(P\theta /2\right)$ and ${{{{{{{{\mathcal{P}}}}}}}}}_{{{{{{{\mathrm{I}}}}}}}}(0,M)={{{{{{{{\mathcal{P}}}}}}}}}_{{{{{{{\mathrm{I}}}}}}}}(M,M)=0.5{\sin }^{2}\left(P\theta /2\right)$. Meanwhile, for $\big|{{{\Psi }}}_{\,{{{{{{\mathrm{RO}}}}}}}\,}^{II}\big\rangle$, the measurement probabilities at site 3 are ${{{{{{{{\mathcal{P}}}}}}}}}_{{{{{{{\mathrm{II}}}}}}}}(0)={\sin }^{2}\left(P\theta /2-\pi /4\right)$ and ${{{{{{{{\mathcal{P}}}}}}}}}_{{{{{{{\mathrm{II}}}}}}}}(M)={\cos }^{2}\left(P\theta /2-\pi /4\right)$. As a numerical check, we consider the same sets of parameters as in the previous section. We numerically calculate the above probabilities using the Hamiltonian (2), comparing the predicted analytic results with the numerical ones, as shown in Fig. 2. See Supplementary Note 2 for numerical probabilities of Protocol I, and related fidelity data. For results with Set 2, see Supplementary Note 3.

Fig. 2: Readout probabilities for Protocols I and II.

Comparison between analytic and numerically calculated probabilities for parameters of Set 1 for different values of Pθ. a Results for Protocol I. The pink dot and the blue “x” (green square and the blue “+”) depict the probabilities of measuring r = 0 (r = M) during the readout, having measured r = M or r = 0 in step (iii), respectively. b Results for Protocol II. The probabilities of measuring N₃ = 0 (N₃ = M) in the readout are shown as green (orange) triangles. The dotted line depicts the analytic predictions of the probabilities with respect to Pθ. The insets show the accordance between predicted and calculated probabilities in semilogarithmic scale.

Conclusions

We have addressed the challenging problem of designing protocols to facilitate NOON state creation. Our approach employs dipolar atoms confined to four sites of an optical superlattice. The setup allows for the interactions to be tuned, and to fix the couplings in such a way that the system is integrable. At these couplings, and for controlled perturbative breaking of the integrability, the theoretical properties of the system become very transparent.

The insights gained from integrability allowed us to develop two protocols utilizing a Fock-state input (see Supplementary Note 4). Protocol I employs a local measurement procedure to produce NOON states with slightly higher fidelities, over a shorter time, than Protocol II. However Protocol I is probabilistic, requiring post-selection on the measurement outcome. This is in contrast to the deterministic approach of Protocol II. For both protocols, phase-encoding is performed by breaking the system’s integrability, in a controllable fashion, at specific moments during the time evolution. And in both protocols the output states were shown to have high-fidelity in numerical simulations. We also identified a readout scheme, by converting encoded phases into a population imbalance, that allows verification of NOON state production through measurement statistics.

The approaches we have described, which are based on the formation of an uber-NOON state en route to the final state, have two significant advantages. One is that the evolution time does not scale with the total number of particles. Instead, it is only dependent on the difference in particle number of subsystems A and B in the Fock-state input. The other advantage is that all measurements are made on a local Fock-state basis.

We conducted an analysis of the feasibility of a physical proposal. It was demonstrated that the long-range interaction between dipolar atoms allows for an integrable coupling to be achieved, depending on the interplay between contact and dipolar interactions. Through the second-quantization procedure the values for the Hamiltonian parameters were provided, derived by numerical calculations. These are seen to be realistic both in the context of optical lattice setups and in comparison to literature. We also conducted an analysis of the system’s robustness in response to perturbation (see Supplementary Note 5 for a broader description).

Besides demonstrating the feasibility of NOON state generation, the physical setup we provide can also be employed in the study of thermalization processes and other many-body features of the EBHM. By establishing a link between integrability and quantum technologies, this work promotes advances in the field of neutral-atom quantum information processing.

Methods

Resonant tunneling regime

The Hamiltonian (2) has large energy degeneracies when J = 0. Through numerical diagonalization of the integrable Hamiltonian for sufficiently small values of J, it is seen that the levels coalesce into well-defined bands, similar to that observed in an analogous integrable three-site model^41,42. By examination of second-order tunneling processes in this regime (see Supplementary Note 1), an effective Hamiltonian H_eff is obtained.

For an initial Fock state $\left|M-l,P-k,l,k\right\rangle$, with total boson number N = M + P, the effective Hamiltonian is a simple function of the conserved operators with the form

$${H}_{{{{{{{{\rm{eff}}}}}}}}}=(N+1){{\Omega }}({Q}_{1}+{Q}_{2})-2{{\Omega }}{Q}_{1}{Q}_{2},$$

(3)

where Ω = J²/(4U((M−P)² − 1)) and U = (U₁₂ − U₀)/4. This result is valid for J ≪ U∣M − P∣, and it is this inequality that we use to define the resonant tunneling regime.

A very significant feature is that, for time evolution under H_eff, both N₁ + N₃ = M and N₂ + N₄ = P are constant. The respective (M + 1)-dimensional subspace associated with sites 1 and 3 and (P + 1)-dimensional subspace associated with sites 2 and 4 provide the state space for the relevant energy band (see Supplementary Note 1). Restricting to these subspaces and using the effective Hamiltonian (3) yields a robust approximation for (2).

Physical proposal

We propose a physical construction, consisting of ultracold dysprosium ¹⁶⁴Dy atoms trapped in an optical superlattice³⁵, to test the theoretical results. The trapping is accomplished by superimposing two 2D square optical lattices, one with “short” periodicity λ/2 and another with “long” periodicity λ_l/2 = λ, where the wavelength λ = 2π/k = 532 nm. The potential of the superlattice is given by

$$V({{{{{{{\bf{r}}}}}}}})= -\!{V}_{{{{{{{\mathrm{s}}}}}}}}{\sin }^{2}(kx)-{V}_{{{{{{{\mathrm{s}}}}}}}}{\sin }^{2}(ky)\\ +{V}_{{{{{{{\mathrm{l}}}}}}}}{\sin }^{2}\left(kx/2\right)+{V}_{{{{{{{\mathrm{l}}}}}}}}{\sin }^{2}\left(ky/2\right)+\frac{1}{2}m{\omega }_{z}^{2}{z}^{2},$$

where V_s and V_l are the depths of the short and long lattices, respectively. The trap frequency ${\omega }_{z}=\sqrt{{V}_{z}{k}^{2}/(2m)}$ of the harmonic confinement in z direction is controlled by the depth V_z of vertical counter-propagating laser beams with wavelength λ_l = 1064 nm, and m is the atom’s mass. We are interested in only one plaquette with four wells around the origin of the xy-plane, for which the potential of the ith well (i = 1, 2, 3, 4) in the harmonic approximation is given by

$${V}^{(i)}({{{{{{{\bf{r}}}}}}}})=\frac{1}{2}m{\omega }_{\,{{{{{{\mathrm{r}}}}}}}\,}^{2}[{(x-{x}_{i})}^{2}+{(y-{y}_{i})}^{2}]+\frac{1}{2}m{\omega }_{z}^{2}{z}^{2},$$

(4)

where the radial trap frequency ${\omega }_{{{{{{{\mathrm{r}}}}}}}}=\sqrt{2{V}_{{{{{{{\mathrm{s}}}}}}}}{k}^{2}/m}$ is determined by the depth of the short lattice. The ith well is centered at one of the (x_i, y_i) = (ζ_i−1d/2, ζ_id/2), ζ_i ≡ (−1)^⌊i/2⌋, positions in the xy-plane. The distance between nearest wells is d = λ/(2δ), where the parameter $\delta ={[1-{V}_{{{{{{{\mathrm{l}}}}}}}}/(2\pi {V}_{{{{{{{\mathrm{s}}}}}}}})]}^{-1}$ is constant, which results from the harmonic approximation and causes the sites to slightly approach each other. In our studies we consider V_l = V_s.

To establish equivalency between V(r) and the Hamiltonian of Eq. (2), we employ the standard second-quantization procedure. From this, we calculate the on-site interaction parameter U₀ as:

$${U}_{0} ={U}_{{{{{{{\mathrm{contact}}}}}}}}+{U}_{{{{{{{\mathrm{dip}}}}}}}}\\ =\kappa {\left(\frac{\eta }{\pi }\right)}^{3/2}\left(g-\frac{{C}_{{{{{{{\mathrm{dd}}}}}}}}}{3}f(\kappa)\right),$$

where the value of κ² ≡ ω_z/ω_r = 0.53 (0.56) establishes the cigar-shaped harmonic potential, η ≡ mω_r/(2ℏ), g ≡ 4πℏ²a/m, with a being the s-wave scattering length (tunable via Feshbach Resonance), ${C}_{{{{{{{\mathrm{dd}}}}}}}}\equiv {\mu }_{0}{\mu }_{1}^{2}$ is the coupling constant, where μ₀ is the vacuum magnetic permeability, μ₁ is the atomic magnetic moment, and f(κ) is a function that describes how the dipolar interaction behaves for different geometries (encoded in κ)⁴³. Taking site 1 as the “starting point’, the parameter U_1j, which accounts for the dipole-dipole interaction between atoms at sites 1 and j, is expressed as:

$$ {U}_{1j}= \frac{{C}_{{{{{{{\mathrm{dd}}}}}}}}}{4\pi }\int\limits_{0}^{\infty }{{{{{{{\rm{d}}}}}}}}rr\exp \left(-\frac{{r}^{2}}{4\eta }\right){J}_{0}(r{d}_{1j})Z(r),\\ Z(r)= \left(\frac{4}{3}\sqrt{\frac{{\kappa }^{2}\eta }{\pi }}-r\exp \left(\frac{{r}^{2}}{4{\kappa }^{2}\eta }\right)\,{{\mbox{erfc}}}\,\left(\frac{r}{2\sqrt{{\kappa }^{2}\eta }}\right)\right),$$

where J₀ is the Bessel function of first kind, d_1j = λ/(2δ), if j = 2, 4, and ${d}_{1j}=\lambda /(\sqrt{2}\delta)$, if j = 3. Here, the on-site dipolar interaction is given by ${U}_{{{{{{{\mathrm{dip}}}}}}}}=\mathop{\lim }\nolimits_{{d}_{ij}\to 0}{U}_{1j}\propto f(\kappa)$.

In this environment, the preparation of arbitrary initial Fock states, as in our protocols, may be accomplished^44,45 by changing one of the superimposed optical lattices’ phase with respect to the other, creating imbalances in the trapping potentials in a controllable way, such that the desired initial state becomes favorable within a Mott Insulator regime (see Supplementary Note 4).

Integrability condition

The physical setup above is able to simulate the EBHM. The ability to generate NOON states, however, relies on the particular case for which the EBHM is integrable; as explained previously, this can be accomplished by making U₀ = U₁₃, which we call the “integrability condition”. The approach is to first choose a value for the s-wave scattering length by changing the magnetic field. Then, from the condition just stated, one has to adjust ω_r by varying the laser beams intensities⁴⁶ such that, at some point, U₀ becomes the same as U₁₃. From this point every Hamiltonian parameter is evaluated only after the integrability condition is satisfied, which sets the intensity of the trapping scheme.

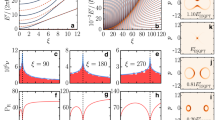
By considering a = 32.5 (30) a₀, the system becomes integrable at ω_r ≈ 2π × 54.110 (2π × 51.759) kHz, as is depicted in Fig. 3. This frequency implies a 2D-lattice depth of V_s ≈ 39.953E_R (36.558E_R), where E_R/ℏ = 2ℏ(kπ)²/(mλ²) = 26.894 kHz is the recoil energy, characterizing a deep lattice. This configuration infers a stable system^21,47. Then, by using this trapping frequency to calculate the Hamiltonian parameters, one finds U/ℏ ≈ 104.846 (105.600) Hz and J/ℏ ≈ 71.624 (104.953) Hz.

Fig. 3: Fulfillment of integrability condition.

The s-wave scattering length value is set, followed by a variation of the radial trapping frequency ω_r up to the point at which U₀ = U₁₃, corresponding to the frequency required for the system to be integrable. The red dashed (solid) and cyan long dashed (solid) depict U₀ (U₁₃) for a = 32.5 a₀ and a = 30 a₀, respectively, for different values of ω_r. By setting a = 32.5 a₀ (30 a₀), we find ω_r ≈ 2π × 54.110 kHz (51.759 kHz) as the frequency for integrability, which results in U₀/ℏ = U₁₃/ℏ ≈ 244.405 Hz (245.141 Hz). The points where U₀ = U₁₃ and the corresponding frequencies ω_r are highlighted by the dotted lines. The system is robust for small deviations from the integrable point (see Supplementary Note 5 for more details).

It is also important to highlight that the tunneling parameter J₁₃/ℏ ~ 3.2 × 10⁻⁴ Hz (J₁₃/ℏ ~ 7.7 × 10⁻⁴ Hz) between diagonal sites 1–3, which is nullified by the condition U₀ = U₁₃ in (2), is less than 1/t_m ~ 0.16 Hz (1/t_m ~ 0.35 Hz), relative to Set 1 (Set 2), ensuring the integrability requirement, considering J₁₃ = J₂₄, since U₀ = U₁₃ = U₂₄.

From this, one infers that the tunneling between different horizontal layers of the optical lattice is even smaller, since the distance between these layers is bigger than the distance between diagonal sites by a factor of $\sqrt{2}$.

Breaking of integrability

To produce a controllable breaking of integrability, it is sufficient to consider an additional 2D square long-lattice with the potential

$${V}_{{{{{{{{\rm{break}}}}}}}}}={V}_{b}{\sin }^{2}(kx/2+\varphi)+{V}_{b}{\sin }^{2}(ky/2+\epsilon \varphi),$$

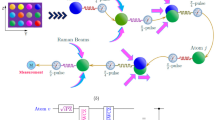
where the depth V_b = 10⁻³V_s and phase φ control the potential offset ${{\Delta }}=2{V}_{b}\sin \left(2\varphi \right)\sin \left[\pi /(2\delta)\right]$ of sites 1–3 (ϵ = +1) and 2-4 (ϵ = −1). When this additional long-lattice is switched on, the depth of the fixed long-lattice is ramped down to V_l → V_l − V_b to keep the parameter δ constant and it implements the terms $\mu =0.5\,{{\Delta }}\,\exp (-{k}^{2}/(8{\eta }_{r}))\,{\delta }_{\epsilon ,+1}$ and $\nu =0.5\,{{\Delta }}\,\exp (-{k}^{2}/(8{\eta }_{r}))\,{\delta }_{\epsilon ,-1}$. For φ = 15 mrad and the previously obtained radial trapping frequency, the parameters μ/ℏ and ν/ℏ can (non-simultaneously) assume the value of 30.016 (27.415) Hz. Therefore, considering M = 4 and P = 11, one should vary t_μ from 0 to ~4.8(5.2) ms to encode Pθ from 0 to π. Notice that for the case presented in Table 1, where Pθ = π/2, t_μ ~ 2.4(2.6) ms. Also, from the condition 2νt_ν/ℏ = π/(2M), corresponding to Pθ = π/2, t_ν ~ 6.5(7.2) ms. Figure 4 illustrates the complete trapping scheme.

Fig. 4: Trapping scheme of the four-site model.

a The 2D square optical lattice is generated with two sets of counter-propagating laser beams crossing at 90° with the other. The superlattice of the four-site model is achieved overlapping the 2D short-lattice (cyan) and long-lattice (blue). The vertical lattice (orange) provides confinement in z direction. An additional 2D square long-lattice (green) is used to implement the integrability break control. b Zoom into the region of the superlattice, which contains the four-site plaquette. c Breaking-of-integrability scheme. The system’s integrability can be broken by changing the phase difference between the superlattice and the additional 2D square long-lattice, effectively causing a potential imbalance ∣Δ∣ between wells 1 and 3 or wells 2 and 4, as in the detail. d The light gray background represents the trapping potential in the vicinities of the four-well system. The cigar-shaped of isosurfaces of the ground-state density, at a distance of d between nearest neighbors, are depicted in blue with direction of dipole aligned in the z-direction represented by purple arrows.