Abstract
Floquet-Bloch lattices are systems in which wave packets are subjet to periodic modulations both in time and space, showing rich dynamics. While this type of lattice is difficult to implement in solid-state physics, optical systems have provided excellent platforms to probe their physics: among other effects, they have revealed genuine phenomena such as the anomalous Floquet topological insulator and the funnelling of light into localised interface modes. Despite the crucial importance of the band dispersion in the photon dynamics and the topological properties of the lattice, the direct experimental measurement of the Floquet-Bloch bands has remained elusive. Here we report the direct measurement of the Floquet-Bloch bands of a photonic lattice with a single shot method. We use a system of two coupled fibre rings that implements a time-multiplexed Floquet-Bloch lattice. By Fourier transforming the impulse response of the lattice we obtain the band structure together with an accurate characterization of the lattice eigenmodes, i. e. the amplitudes and the phases of the Floquet-Bloch eigenvectors over the entire Brillouin zone. Our results open promising perspectives for the observation of topological effects in the linear and nonlinear regime in Floquet systems.
Similar content being viewed by others
Introduction
Optical waveguide arrays represent a class of periodic structures that have been the focus of intense research in the two past decades1,2. Such systems enabled direct observation with the light of many fundamental lattice phenomena such as Bloch oscillations3,4,5, Anderson localization6,7,8, discrete solitons9,10, and many others. Coupled waveguides have also been used to implement Floquet lattices in which photon wavepackets are subject to a periodic time modulation11,12,13,14. However, material constraints have limited the number of Floquet periods accessible in this configuration. Recently, discrete mesh lattices in time-multiplexed loop arrangements have been used to study elaborate Floquet–Bloch Hamiltonians with access to hundreds of both lattice sites and modulation periods15. So far, time-multiplexed fiber loop schemes have demonstrated a high degree of flexibility16,17 and they have been employed to investigate a number of effects such as parity-time symmetry18,19 or topological control of light propagation20,21 to cite a few. Note that photonics now offers a number of other possibilities to design and engineer the so-called synthetic mesh lattices, see ref. 22 for a recent review.
Time-multiplexed photonic mesh lattices are often implemented by connecting two appropriately designed fiber loops with a directional 50/50 fiber coupler23,24,25. In these systems, the phenomenon of discrete diffraction created at the fiber coupler results in the spreading of light wavepackets across the whole array as Floquet–Bloch waves26,27. The linear propagation of wavepackets in the Floquet–Bloch lattices is determined by their photonic band structure. Despite the importance of this band structure in the dynamics, its experimental determination is not an obvious task. In previous experimental works, the dispersive properties of the lattices have been indirectly deduced from the measurement in space and time of the group velocity and of the broadening experienced by many individual light wavepackets5,18,23. Recently, the measurement of the band structure in a different configuration based on the longitudinal optical modes of a single fiber ring has enabled the observation of synthetic spin–orbit coupling and quantum Hall ladders28,29. Beyond the only measurement of the band structure, the direct measurement of the amplitude and phase of the Floquet–Bloch eigenvectors would open the possibility of extracting experimentally fundamental properties such as winding and Chern numbers, of great importance to characterize the topological properties of a lattice.
In this paper, we report the experimental implementation of a method that allows the single-shot recording of the photonic band structure characterizing a Floquet–Bloch lattice realized with two coupled fiber loops. The experiment relies on the idea that the dispersive band structure of the lattice can be determined from the Fourier transform of its impulse response. The simultaneous measurement of the phase and of the amplitude of the impulse response of the lattice is achieved using a heterodyne technique. In addition to providing the dispersive band structure of the lattice (i.e., the dispersion relation connecting the quasi-energy and the Bloch momentum), our method provides the full and accurate characterization of the lattice eigenmode structure, i.e., the amplitudes and the phases of the Floquet–Bloch eigenvectors over the entire Brillouin zone. Let us notice that the idea that the eigenmode structure of a photonic mesh lattice can be determined using the optical heterodyne technique has been proposed in ref. 30. To the best of our knowledge, this idea has however never been implemented in practice and the fact that the full eigenmode structure of the photonic mesh lattice can be determined from the measurement of its impulse response has not been considered before our work.
Results and discussion
The lattice model and the associated photonic band structure
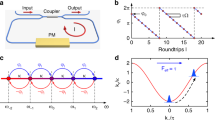
As shown in Fig. 1a, we consider a system of two coupled fiber loops, which are conceptually identical to those considered in previous experimental works15,23. The two fiber loops have an imbalanced path length ΔL = L2 − L1 which is chosen to be much shorter than the length L1 (resp. L2) of the short (resp. long) ring. When an optical pulse is injected into one of the loops, it is divided into two pulses after the coupler. These two pulses propagate along the short and long fiber rings before being split again at the fiber coupler. As discussed in detail in refs. 23,24, the dynamical evolution of the light pulses in this optical fiber system can be mapped onto the lattice shown in Fig. 1b. Each round trip of the pulses in the rings represents a time step, labeled by the integer m, while the separation of pulses within a time step can be mapped into the pseudo-real-space position of the lattice, labeled n. The timescale associated with the real-space position is given by ΔL, while the time step is determined by (L1 + L2)/2. The large difference between these two timescales permits a clear observation of the evolution of pulses at each time step at the output of the setup.
a Experimental setup showing the system of two coupled loops made with polarization-maintaining fibers (PMFs) having lengths L1 = 30.27 m and L2 = 30.72 m. The local oscillator used for the heterodyne measurement is a Brillouin fiber ring laser (BFRL) that is frequency detuned by ~10.8 GHz from the frequency of the signal circulating inside the loops. An electro-optic modulator is used to shape the pulses injected into the V loop. The losses in each loop are partially compensated by using Erbium-doped fiber amplifiers (EDFAs). A phase modulator (PM) can be used for a periodic modulation of the phase between −ϕ and +ϕ in the U loop. Light detection at the output of the fiber system is made using fast photodiodes (PDs). b Schematic representation of the Floquet–Bloch lattice on which the evolution of the light pulses circulating inside the loops can be mapped. The index n provides the position of the light pulses at the mth round trip in the Floquet–Bloch lattice. c Photonic band structure (Bloch momentum Q versus quasi-energy θ) for different values of the phase modulation ϕ within the U loop.
The space–time evolution of the complex amplitude of light pulses in the lattice shown in Fig. 1b is commonly described using a simple set of two coupled algebraic equations5,23:
\({u}_{n}^{m}=u(n,m)\) (resp. \({v}_{n}^{m}=v(n,m)\)) represents the complex amplitude of the pulses in the short (resp. long) loop at the nth position in the pulse train and at the mth round trip (time step) in the fiber loop system5,23. Φ(m) is an extra phase gained by the pulses in the shorter (U) ring owing to the addition of a phase modulator (PM in Fig. 1a). Its value changes sign at each time step (Φ(m) = (−1)m+1 ϕ), as depicted in Fig. 1b.
Following ref. 5, the Floquet–Bloch mode eigenstates (U, V)T of the lattice are obtained by decomposing \({u}_{n}^{m}\) and \({v}_{n}^{m}\) on a discrete basis of Fourier modes
This means that in reciprocal (Fourier) space, the variables n and m are conjugated with the “Bloch momentum” Q and the “quasi-energy” θ, respectively (see e.g. refs. 23,24).
Substituting Eq. (3) into Eqs. (1) and (2), it can be easily shown that the dispersion relation of the system presents two bands that are periodic both along the quasi-energy and momentum dimensions and that are given by23:
As shown, e.g., in ref. 23, one of the great advantages of the photonic lattice described in Fig. 1 is that the band structure can be easily modified by varying the value of ϕ.
The two bands are represented in Fig. 1c as a function of the parameter ϕ. For ϕ = 0 (equivalently, ϕ = 2π, blue lines in Fig. 2c), the lattice model has two bands that are gapped at the center of the Brillouin zone and touch at the edges due to the periodicity in quasi-energy. For other values of ϕ the bands can be fully gaped (red line) or touched in the center of the Brillouin zone (green line at ϕ = π). Considering a light wavepacket having a well-defined mean Bloch momentum Q0 together with a narrow momentum spread ΔQ, the group velocity of this wavepacket in the (n, m) (space–time) representation space is determined by the local slope of the excited band while the local curvature of the band determines the dispersive broadening of the wavepacket in space and time23,24.
The space–time evolution shown in (a) is measured in the U loop when a short pulse is injected in the V loop. The impulse response of the lattice shown in (a) is beaten against a reference laser field. This gives square pulses being modulated at ~10.8 GHz, as shown by the inset in (a). The fringe pattern expanding in space (n) and time (m) is numerically Fourier transformed in the two dimensions. This gives the 2D Fourier power spectrum plotted in (b) with one central component and two weak side bands at ~±10.8 GHz. The 2D Fourier spectrum plotted in (c) represents a zoomed view of the spectrum shown in (b) between 10.45 and 11.33 GHz. In terms of normalized units ("Bloch momentum” Q and “quasi-energy” θ), the photonic band structure of the lattice is measured for Q ∈ [−2π, 2π], θ ∈ [−2π, 2π]. The first Brillouin zone is depicted by the square region plotted in (c) with white dashed lines. The vertical color bar indicates the mapping from the normalized spectral power \(| \tilde{U}(Q,\theta ){| }^{2}\) to colors.
Measurement of the photonic band structure
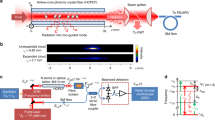
Our experimental determination of the band structure characterizing a Floquet–Bloch lattice is based on the single-shot simultaneous measurement of the phase and amplitude of the impulse response of the lattice. This is achieved using a heterodyne measurement where the wavefield at the output of the double loop system is beaten against a reference field, which is detuned from the frequency of the wavefield by ~10.8 GHz.
As shown in Fig. 1a, a single-frequency laser at 1550 nm is split into two arms by using a 99/1 fiber coupler. The high-intensity arm is directed towards the double ring system. A short square pulse with a duration of 1 ns and a peak power of ~6 mW is produced using an electro-optic modulator (EOM) before being injected into the two coupled fiber loops. Each fiber loop incorporates a narrow-bandwidth optical filter, an optical isolator, and an Erbium-doped fiber amplifier (EDFA) to partially compensate for all round-trip losses. The length L1 of the shorter loop is 30.27 m and the difference in loop lengths is ΔL = 0.45 m. With these values the average round trip time are \(\bar{T}=(2{L}_{1}+{{\Delta }}L)/(2v)\simeq 152.5\) ns and the time difference between the two loops is ΔT = ΔL/v ≃ 2.26 ns, v being the velocity of light in the fiber at 1550 nm. The choice of these values for the ring lengths is one of the key features of our experiment: the fiber ring lengths are more than one order of magnitude smaller than in other similar experimental setups23,24 to keep the whole physical distance covered by pulses circulating inside the loops smaller than the coherence length of the local oscillator delivering the reference field.
The local oscillator that delivers the reference field used in the heterodyne measurement is a Brillouin fiber ring laser (BFRL, pink dotted rectangle in Fig. 1a). A small part of the laser field extracted before the EOM is amplified at the Watt level using an EDFA and it is used as a pump field for the BFRL. The BFRL delivers a Stokes field with is frequency-downshifted with respect to the pump frequency by ~10.8 GHz, the frequency of acoustic waves propagating inside the optical fiber31. It is well known that BFRLs deliver a Stokes radiation having a linewidth much narrower than the one of their pump laser32,33. This feature, recently exploited for the improved operation of atomic clocks34, is used here to achieve a coherent beating between the narrow-bandwidth Stokes field and the pulses that propagate over the kilometric range associated with the tens of round trips made within the two coupled fiber loops. Assuming that the linewidth of our pump laser is ~300 kHz (constructor specification) and assuming that the linewidth of the BFRL is only determined by the narrowing property of Brillouin lasers, we estimate from Eq. (9) of ref. 32 that the linewidth of our local oscillator is around ~1 kHz, which means that its coherence length is around ~100 km.
Note that the fiber setup schematically shown in Fig. 1a is fully made with polarization-maintaining fibers (PMFs) and with PMF components. The laser field has a linear polarization state with a power extinction ratio better than 1:100 both in the BFRL and in the double loop system. The fact that the light polarization state does not fluctuate in the fiber system has the advantage to maximize the contrast of the beating signal between the local oscillator and the pulses at the output of the loop system. Moreover, the experimental results can be compared adequately with theoretical results provided by scalar models where vectorial (polarization) effects are ignored.
Figure 2a shows the spatiotemporal evolution measured at the output of the U ring after injection of a single initial pulse in the V ring and in the absence of phase modulation (Φ(m) = 0). The sequence of measured pulses shows trains of pulses separated by \(\bar{T}\). We use this time to order the pulses as a function of time step m (round trip number) in Fig. 2a, see “Reconstruction of the spatiotemporal diagrams from the time signal recorded in the experiments” in the “Methods” section for details. The output of the U ring is combined in a 99:1 beamsplitter with the BFRL local oscillator. A fast photodiode (Finisar 70 GHz XPDV3120) connected to a fast oscilloscope (Lecroy Labmaster 10Zi-A-65 GHz) is used to record the beat signal between the output of the coupled loop system and this oscillator, as shown in Fig. 1a. In this way, each individual pulse at the output of the loops has its amplitude that is fastly modulated in time at the beat frequency of ~10.8 GHz, see inset in Fig. 2a that shows the measured amplitude of the train of pulses at time step m = 2. The evolution of the relative phase between the light pulses within each round trip and between different round trips is encoded into the phase of the beat signal. The detection bandwidth of the photodiode is 50 GHz and the electrical bandwidth of the fast oscilloscope is 36 GHz. The beating signal is sampled at a rate of 80 GSa/s by the oscilloscope that has a memory depth of 512 Mpts. With these values, the beat signal is sufficiently well sampled for the proper quantitative determination of the band structure of the Floquet–Bloch lattice.
To obtain the dispersive band structure of the lattice, we perform the two-dimensional (2D) Fourier transform of the fringe pattern experimentally recorded and plotted in Fig. 2a. This fringe pattern is recomposed from a time signal having a duration of ~7.5 μs that corresponds to ~50 round trips of the light pulses inside the double loop system. The resulting 2D Fourier transform is computed numerically and shown in Fig. 2b. The plotted spectrum spreads horizontally between −15 and +15 GHz, but the spectrum computed numerically spreads over a wider frequency span of 80 GHz that is determined by the sampling rate of the oscilloscope. The vertical frequency range of the 2D spectrum is 6.5 MHz, which corresponds to the mean free spectral range \({{\Delta }}{\nu }_{{{\mathrm{FSR}}}}=1/\bar{T}\) of the double loop system. The 2D Fourier transform shown in Fig. 2b is composed of one vertical central band surrounded by two vertical side bands separated by 10.8 GHz from the central zero-frequency component.
Figure 2c represents a zoomed view of the 2D Fourier spectrum plotted in Fig. 2b around ~10.8 GHz. It reveals that this region of the spectrum displays the double band structure characterizing the Floquet–Bloch lattice implemented in the double-ring setup. The dashed square delimits the first quasi-momentum and quasi-energy Brillouin zone. All eigenstates of both bands are excited by the initial input pulse. Figure 2 shows that the band structure is straightforwardly determined only from the single-shot recording of the space–time pattern shown in Fig. 2a and the computation of its 2D Fourier transform. The measured shape of the bands agrees quantitatively with Eq. (4) for ϕ = 0 (\(\cos \theta =(\cos Q-1)/2\)). Note that Fig. 2 shows the spatiotemporal evolution and the measured band structure for the U ring. Analogously, the same kind of measurements can be done for the output of the V ring, as discussed in the subsection where we report the experimental determination of the eigenmode structure.
In Fig. 2c, the connection between the physical frequency νx (resp. νy) measured on the horizontal (resp. vertical) axis and the Bloch momentum (resp. the quasi energy) is given by the following simple relation: \(Q=2\pi ({\nu }_{x}-{\nu }_{x}^{0})/{{\Delta }}{\nu }_{{{\mathrm{B}}}}\) (resp. \(\theta =4\pi ({\nu }_{y}-{\nu }_{y}^{0})/{{\Delta }}{\nu }_{{{\mathrm{FSR}}}}\)). ΔνB = 1/ΔT = 443 MHz represents the width of the Brillouin zone. \({\nu }_{x}^{0}\) represents the central frequency of the Brillouin zone in the quasi-momentum dimension. In practice, its value slowly fluctuates from one recording to the other because the optical length of the fiber loop system is not actively stabilized with respect to the wavelength of the laser light. The slow and uncontrolled drift of \({\nu }_{x}^{0}\) arises from slow fluctuations of the difference in loop lengths ΔL on a timescale that typically falls in the second range. In practice, the value of \({\nu }_{x}^{0}\) is “manually” selected from one recording to the other in such a way that the band spectrum is symmetric with respect to the center of the Brillouin zone (Q = 0). The same phenomenon occurs along the vertical frequency direction because the mean length (2L1 + ΔL)/2 of the double loop system also fluctuates with respect to the laser wavelength. Consequently, from one recording to the next, there is a slow drift of the double band spectrum around the horizontal frequency axis. This drift effect is also corrected “manually” by adjusting \({\nu }_{y}^{0}\) in such a way that the band spectrum is symmetric with respect to the horizontal frequency axis (θ = 0). Active stabilization of the ring length to an integer multiple of the wavelength of the laser used to inject the pulses would unambiguously fix \({\nu }_{x}^{0}\) and \({\nu }_{y}^{0}\).
To explore other band structures, we now activate the PM inserted in the shorter loop (see Fig. 1a): the phase of the field in the shorter loop is modulated in time by a square signal oscillating between +ϕ and −ϕ at a period equal to the mean round trip time \(\bar{T}\) of light inside the loops. As shown in ref. 23, this modulation scheme permits to modify the band structure of the photonic lattice. Figure 3a, b shows the band structure measured experimentally in the U ring for ϕ = ϕ1 = π/2 and for ϕ = ϕ2 = 4π/5, respectively. Correspondingly, Fig. 3c, d shows the band structure numerically computed from the Fourier transform of the spatiotemporal evolution calculated using Eqs. (1) and (2) with a single pulse injected in the V ring as the initial condition, like in the experiment. A good quantitative agreement is found between experiments and theory in terms of the shape and occupation of the bands for the selected values of ϕ, see Supplementary Fig. S1 for additional plots showing the band spectra obtained for other values of ϕ.
a, b Experimental results showing the dispersive band structure of the photonic mesh lattice recorded with periodic square modulations of the phase with amplitudes ϕ1 = π/2 (a) and ϕ2 = 4π/5 (b). c, d Corresponding numerical simulations showing the band structure computed from the 2D Fourier transform of the impulse response of the system. Numerical simulations are made using Eqs. (1) and (2) with Φ1(m) = (−1)mπ/2 (c) and Φ2(m) = (−1)m4π/5 (d). The squares in white dashed lines represent the first Brillouin zone. The vertical color bar indicates the mapping from the normalized spectral power \(| \tilde{U}(Q,\theta ){| }^{2}\) to colors.
Experimental determination of the eigenmode structure of the Floquet–Bloch lattice
Measuring the impulse response of the photonic lattice by injecting a short pulse into the fiber system, we perform an excitation of the entire Brillouin zone that reveals the dispersive band structure of the lattice. We will see now that it also permits to extract quantitative information on the structure of its eigenmodes. Assuming that the PM inserted in the short loop is inactive (Φ(m) = 0), the substitution of Eq. (3) into Eqs. (1) and (2) provides not only the energy dispersion Eq. (4) but also the ratio R between the complex amplitudes of the Floquet–Bloch eigenmodes in the two loops:
The meaning of Eq. (5) can be better understood by analyzing numerical simulations of Eqs. (1) and (2). Figure 4a, b shows the computed spatiotemporal evolution of the lattice with Φ(m) = 0 and a single pulse injected in the V ring as initial condition: v(n = 0, m = 0) = 1, v(n ≠ 0, m = 0) = 0; u(n, m = 0) = 0 ∀ n. In these simulations, we have additionally added a term \(-\frac{\alpha }{2}{u}_{n}^{m}\) and \(-\frac{\alpha }{2}{v}_{n}^{m}\) in the right-hand side of Eqs. (1) and (2), respectively, to describe the fact that the losses in each loop are not perfectly well compensated by gain.
Numerical simulations of Eqs. (1) and (2) showing the impulse responses of the two loops (a, b) and their associated 2D Fourier transforms \(| \tilde{U}(Q,\theta ){| }^{2}\) (c), \(| \tilde{V}(Q,\theta ){| }^{2}\) (d). The squares in white dashed lines in (c, d) represent the first Brillouin zone. The simulations are made using a dissipation rate similar to the one measured in the experiment (α = 0.07) and no phase modulation (Φ(m) = 0 ∀ m). e Spectral power distributions \({P}_{U}(Q)=| \tilde{U}(Q,{\theta }_{+}(Q)){| }^{2}\) (orange line) and \({P}_{V}(Q)=| \tilde{V}(Q,{\theta }_{+}(Q)){| }^{2}\) (blue line) measured along the upper spectral bands in (c, d). f Spectral phase distributions \({\phi }_{V}(Q)={{{\mathrm{Arg}}}}(\tilde{V}(Q,{\theta }_{+}(Q)))\) (blue line) and \({\phi }_{U}(Q)={{{\mathrm{Arg}}}}(\tilde{U}(Q,{\theta }_{+}(Q)))\) (orange line) measured along the upper spectral bands in (c, d). g Time evolution of the mean optical power in each loop: <∣U(m)∣2> = ∑n∣U(n, m)∣2 (orange line), <∣V(m)∣2> = ∑n∣V(n, m)∣2 (green line) and time evolution of the global power in the two loops <∣U(m)∣2> + <∣V(m)∣2> (blue line). h Ratio between the spectral power distributions PV(Q)/PU(Q) (red line) measured in the upper bands and evolution of the ratio ∣R(Q)∣2 (red dashed line) between the power of the Floquet–Bloch eigenmodes (see Eq. (5)). The spectral phase difference Δϕ(Q) = ϕV(Q) − ϕU(Q) computed from the data shown in (f) is plotted in green dots. It follows a simple linear relation given by Δϕ(Q) = Q/2 that complies with the fact that Arg(R(Q)) = Q/2 (blue dashed line).
As shown in Fig. 4a, a symmetric evolution of the light power distribution ∣u(n, m)∣2 is observed in the U loop, while an asymmetric one is observed at the output of the other loop (V loop) where the light pulse is initially injected, see Fig. 4b. This asymmetric features between the injected and non-injected rings were already reported in the space–time domain in ref. 15. Figure 4c (resp. Fig. 4d) represents the 2D Fourier power spectrum \(| \tilde{U}(Q,\theta ){| }^{2}\) (resp. \(| \tilde{V}(Q,\theta ){| }^{2}\)) of the impulse response u(n, m) (resp. v(n, m)) shown in Fig. 4a (resp. Fig. 4b). Asymmetric features observed in space–time domain are also found in the 2D Fourier spectra shown in Fig. 4c and d for the U and V rings, respectively.
The origin of this asymmetry in the measured bands is a combination of two properties: (i) the fact that the relative amplitude and phase of the eigenvectors in the U and V rings depends on Q (see Eq. (5)), and (ii) the projection of the initial pulse, in the V ring, onto the eigenvectors. In the case displayed in Fig. 4c, d, the spectral power distribution of the bands, the distribution is symmetric in the U loop with respect to Q = 0, see Fig. 4c, and asymmetric in the V ring (see Fig. 4d). These features are exchanged when the initial excitation takes place in ring U.
From the 2D spectra shown in Fig. 4c, d, the spectral power distribution and the spectral phase distribution in the upper bands can be measured as a function of the Bloch momentum Q. The blue curve in Fig. 4e shows the spectral power distribution \({P}_{V}(Q)=| \tilde{V}(Q,{\theta }_{+}){| }^{2}\) measured for the V ring along the upper band of Fig. 4d whose dispersion is given by \({\theta }_{+}(Q)=+\arccos ((\cos (Q)-1)/2)\), see “Measuring the spectral power distribution and the spectral phase distribution in the photonic band structure” in the “Methods” section for the description of the method used for the computation of the spectral power. The orange curve in Fig. 4e shows, equivalently, the spectral power distribution of the upper band for the U ring: \({P}_{U}(Q)=| \tilde{U}(Q,{\theta }_{+}){| }^{2}\). The ratio PV(Q, θ+)/PU(Q, θ+) is displayed in the full red line in Fig. 4h. It nearly coincides with the dashed red curve, which displays ∣R(Q)∣2 computed from the analytical form given by Eq. (5). The slight difference between solid and dashed red curves in Fig. 4h arises from the fact that numerical simulations have been made by incorporating dissipative effects (α ≠ 0), while the expression of R is calculated for α = 0.
Analogously, by considering the argument of the 2D Fourier transform, we can compute the spectral phase distributions along the upper bands \({\phi }_{V}(Q)={{{\mathrm{Arg}}}}(\tilde{V}(Q,{\theta }_{+}(Q)))\) and \({\phi }_{U}(Q)={{{\mathrm{Arg}}}}(\tilde{U}(Q,{\theta }_{+}(Q)))\), for the V and U rings, respectively. In this case, for each value of Q, the phase is obtained at the value of the maximum spectral power density, see “Measuring the spectral power distribution and the spectral phase distribution in the photonic band structure” in the “Methods” section for details about the computation of the spectral phase. Figure 4f shows that the spectral phase in each band undergoes an excursion of ~40 radians over the entire Brillouin zone. Remarkably, the phase difference Δϕ(Q) = ϕV(Q) − ϕU(Q) follows a simple linear evolution (Δϕ(Q) = Q/2) plotted in green in Fig. 4h), which fully complies with the evolution of the argument of R(Q): Arg(R(Q)) = Q/2, from Eq. (5). A similar treatment can be done for the lower bands. The analysis we have just described based on numerical simulations shows how the eigenmode structure of the photonic mesh lattice can be measured from the Fourier transform of the impulse response of the lattice. Let us note that the results synthesized in Fig. 4 show that the eigenstate structure determined from an analytical calculation where α is set to zero (Eq. (5)) are robust to dissipative effects.
Figure 5 shows that all features revealed by numerical simulations reported in Fig. 4 are observed using our experimental methodology. Figure 5a, b shows the impulse responses measured at the output of loops U and V, respectively. Figure 5c, d displays the symmetric and asymmetric 2D Fourier spectra that are computed from the impulse responses plotted in Fig. 5b, respectively. Despite clear differences in the intensity distributions in the measured bands with respect to the bands computed from numerical simulations (compare Fig. 4e and Fig. 5e), the ratio PV(Q)/PU(Q) between the measured spectral powers is very close to the theoretical curve over the entire Brillouin zone, see Fig. 5h. The spectral phases ϕU(Q) and ϕV(Q) measured in the upper bands in Fig. 5c, d depict the same evolution as the one obtained from numerical simulations. Regarding the phase extracted of the upper bands extracted from the 2D Fourier transform protocol, Fig. 5f displays a large excursion in the phases ϕV,U(Q) over the Brillouin zone. Nevertheless, the phase difference Δϕ(Q) = ϕV(Q) − ϕU(Q) follows a simple linear relation in good agreement with results obtained from the model (Eqs. (1) and (2)): Δϕ(Q) = Arg(R(Q)) = Q/2.
Impulse responses were measured in the two loops (a, b) and their associated 2D Fourier transforms \(| \tilde{U}(Q,\theta ){| }^{2}\) (c) and \(| \tilde{V}(Q,\theta ){| }^{2}\) (d). The squares in white dashed lines in (c, d) represent the first Brillouin zone. Experiments are made without applying any phase modulation in the U loop (Φ(m) = 0 ∀ m). e Spectral power distributions \({P}_{U}(Q)=| \tilde{U}(Q,{\theta }_{+}(Q)){| }^{2}\) (orange line) and \({P}_{V}(Q)=| \tilde{V}(Q,{\theta }_{+}(Q)){| }^{2}\) (blue line) measured along the upper spectral bands in (c, d). f Spectral phase distributions \({\phi }_{V}(Q)={{{\mathrm{Arg}}}}(\tilde{V}(Q,{\theta }_{+}(Q)))\) (blue line) and \({\phi }_{U}(Q)={{{\mathrm{Arg}}}}(\tilde{U}(Q,{\theta }_{+}(Q)))\) (orange line) measured along the upper spectral bands in (c, d). g Time evolution of the mean optical power in each loop: <∣U(m)∣2> = ∑n∣U(n, m)∣2 (orange line), <∣V(m)∣2> = ∑n∣V(n, m)∣2 (green line) and time evolution of the global power in the two loops <∣U(m)∣2> + <∣V(m)∣2> (blue line). h Ratio between the spectral power distributions PV(Q)/PU(Q) (red line) measured in the upper bands and evolution of the ratio ∣R(Q)∣2 (red dashed line) between the power of the Floquet–Bloch eigenmodes (see Eq. (5)). The spectral phase difference Δϕ(Q) = ϕV(Q) − ϕU(Q) computed from the data shown in (f) is plotted in green dots. It follows a simple linear relation given by Δϕ(Q) = Q/2 that complies with the fact that Arg(R(Q)) = Q/2 (blue dashed line).
Conclusion
In this paper, we have reported experiments where the dispersive band structure characterizing a Floquet–Bloch lattice is measured in a single shot over the entire Brillouin zone by Fourier transforming the impulse response of the lattice. In addition, our method provides the full and accurate characterization of the lattice eigenmode structure, i.e., the amplitudes and the phases of the Floquet–Bloch eigenvectors over the entire Brillouin zone.
We believe that our experimental method will be useful not only for the accurate characterization of the linear dispersive properties of time-multiplexed photonic mesh lattices but also for the investigation of questions related to the influence of nonlinear effects on the propagation of Floquet–Bloch waves. A variety of nonlinear wave mixing phenomena at the origin of the broadening of spectral bands or of the nonlinear coupling between the Floquet–Bloch eigenmodes can be investigated using our experimental technique. In particular, it could be useful to explore the phenomenon of modulation instability in nonlinear topological photonic systems, as recently suggested in ref. 35.
Methods
Reconstruction of the spatiotemporal diagrams from the time signal recorded in the experiments
In the experiment, an electrical signal changing in time is recorded at the output of each fiber loop by using fast photodiodes. This signal is composed of sets of square pulses having peak amplitudes that slowly decay on average at each round trip while also spreading out in time due to the slight length imbalance between the two fiber loops, see Fig. 6. Using other words the recorded signal evolves on a slow timescale \(\bar{T}=(2{L}_{1}+{{\Delta }}L)/(2v)\) determined by the mean round trip time of light in the fiber loop system and on a faster timescale ΔT = ΔL/v determined by the difference length ΔL = L2 − L1 between the two loops. In the experiment, the two timescales \(\bar{T}\simeq 152.5\) ns and ΔT = ≃ 2.26 ns are well separated and it is appropriate to plot the dynamical evolution of light pulses using a representation where the slow evolution is decoupled from the fast one.
The recorded signal is sliced in a sequence of multiple time windows having all a duration \(\bar{T}\) equal to the mean round trip time of light in the double loop system. The space–time diagram is recomposed by concatenating the multiple time slices and by encoding the amplitude of the square pulses using a colormap. The index n provides the position of the light pulses at the mth round trip in the Floquet–Bloch lattice. A is the amplitude of the detected signal. The vertical color bar indicates the mapping from the amplitude A to colors.
This is achieved by using a method that is schematically shown in Fig. 6. The mean round trip time \(\bar{T}\) is measured in an accurate way and the recorded time signal is sliced into a sequence of time windows having all a duration \(\bar{T}\). The time segments obtained from this procedure are then concatenated in a space–time representation where the horizontal axis is associated with the fast timescale while the vertical axis is associated with the slow timescale. The spatiotemporal evolution of the light pulses in the photonic lattice is obtained in a last step where the amplitude of the square pulses is encoded by using a colormap.
Note that the voltage detected by the photodiode typically decays between ~300 mV and a few mV over ~50 round trips made by the light pulses inside the double loop system. This range of measured voltage keeps the photodiode in a linear response regime while also providing a reasonable signal-to-noise ratio over the whole measurement duration.
Measuring the spectral power distribution and the spectral phase distribution in the photonic band structure
The method used in our paper to measure the photonic band structure of the Floquet–Bloch lattice consists of Fourier transforming the impulse response of the lattice. In addition to providing the shape of the dispersive bands, this method provides the complex amplitude of the Floquet–Bloch eigenmodes. Here, we describe how the power and the phase of the eigenmodes are determined from the 2D band spectra that are computed by Fourier transforming the impulse response of the lattice.
The 2D Fourier power spectrum \(| \tilde{U}(Q,\theta ){| }^{2}\) computed from the impulse response of the U loop is shown in Fig. 7a. For any given value Q of the Bloch momentum, the power PU(Q) of a Floquet–Bloch eigenmode is determined by integrating the spectral power density in a narrow spectral region centered around the upper dispersive band using the following expression
where \({\theta }_{+}(Q)=+\arccos ((\cos (Q)-1)/2)\) provides the shape of the spectral band. Note that the knowledge of the analytical form of the function θ+(Q) is not required and that the value θ+(Q) simply represents the value of θ+ for which the spectral power density is maximum: \({\theta }_{+}(Q)=\max(| \tilde{U}(Q,\theta ){| }^{2})\). The value of Δθ is chosen in such a way that the average power given by Eq. (6) represents a smooth function of Q, as shown in Fig. 7b (Δθ = 0.1 in Fig. 7).
a Fourier power spectrum \(\tilde{U}(Q,\theta ){| }^{2}\) of the impulse response of the Floquet–Bloch lattice for the symmetric U loop. The vertical color bar in (a) indicates the mapping from the normalized spectral power \(| \tilde{U}(Q,\theta ){| }^{2}\) to colors. The spectral power of the Floquet–Bloch eigenmodes shown in (b) is determined by integrating the spectral power density between the orange dashed lines for each value of Q by using Eq. (6). The spectral phase shown in (c) is the argument ϕU(Q) of the Fourier modes at the frequencies where the spectral power density is maximum.
To determine the spectral phase ϕU(Q) of the Floquet–Bloch eigenmodes, we first locate the points in the upper part of the 2D spectrum (Fig. 7a) where the spectral power density is maximum: \({\theta }_{+}(Q)=\max(| \tilde{U}(Q,\theta ){| }^{2},\theta \, > \, 0)\). The spectral phase ϕU(Q) is simply computed as the argument of the Fourier modes at the points where the spectral power density is maximum: ϕU(Q) = Arg(\(\tilde{U}(Q,{\theta }_{+}(Q))\).
Data availability
The data that support the findings of this study are available from the corresponding author on reasonable request.
References
Garanovich, I. L., Longhi, S., Sukhorukov, A. A. & Kivshar, Y. S. Light propagation and localization in modulated photonic lattices and waveguides. Phys. Rep. 518, 1–79 (2012).
Christodoulides, D. N., Lederer, F. & Silberberg, Y. Discretizing light behaviour in linear and nonlinear waveguide lattices. Nature 424, 817–823 (2003).
Morandotti, R., Peschel, U., Aitchison, J. S., Eisenberg, H. S. & Silberberg, Y. Experimental observation of linear and nonlinear optical bloch oscillations. Phys. Rev. Lett. 83, 4756–4759 (1999).
Pertsch, T., Dannberg, P., Elflein, W., Bräuer, A. & Lederer, F. Optical bloch oscillations in temperature tuned waveguide arrays. Phys. Rev. Lett. 83, 4752–4755 (1999).
Wimmer, M., Miri, M.-A., Christodoulides, D. & Peschel, U. Observation of bloch oscillations in complex pt-symmetric photonic lattices. Sci. Rep. 5, 17760 (2015).
Pertsch, T. et al. Nonlinearity and disorder in fiber arrays. Phys. Rev. Lett. 93, 053901 (2004).
Lahini, Y. et al. Anderson localization and nonlinearity in one-dimensional disordered photonic lattices. Phys. Rev. Lett. 100, 013906 (2008).
Vatnik, I. D., Tikan, A., Onishchukov, G., Churkin, D. V. & Sukhorukov, A. A. Anderson localization in synthetic photonic lattices. Sci. Rep. 7, 4301 (2017).
Eisenberg, H. S., Silberberg, Y., Morandotti, R., Boyd, A. R. & Aitchison, J. S. Discrete spatial optical solitons in waveguide arrays. Phys. Rev. Lett. 81, 3383–3386 (1998).
Mandelik, D., Morandotti, R., Aitchison, J. S. & Silberberg, Y. Gap solitons in waveguide arrays. Phys. Rev. Lett. 92, 093904 (2004).
Rechtsman, M. C. et al. Photonic Floquet topological insulators. Nature 496, 196–200 (2013).
Maczewsky, L. J., Zeuner, J. M., Nolte, S. & Szameit, A. Observation of photonic anomalous Floquet topological insulators. Nat. Commun. 8, 13756 (2017).
Mukherjee, S. et al. Experimental observation of anomalous topological edge modes in a slowly driven photonic lattice. Nat. Commun. 8, 13918 (2017).
Bellec, M., Michel, C., Zhang, H., Tzortzakis, S. & Delplace, P. Non-diffracting states in one-dimensional Floquet photonic topological insulators. EPL 119, 14003 (2017).
Regensburger, A. et al. Photon propagation in a discrete fiber network: an interplay of coherence and losses. Phys. Rev. Lett. 107, 233902 (2011).
Chalabi, H. et al. Synthetic gauge field for two-dimensional time-multiplexed quantum random walks. Phys. Rev. Lett. 123, 150503 (2019).
Chalabi, H. et al. Guiding and confining of light in a two-dimensional synthetic space using electric fields. Optica 7, 506–513 (2020).
Miri, M.-A., Regensburger, A., Peschel, U. & Christodoulides, D. N. Optical mesh lattices with \({{{{{\mathcal{PT}}}}}}\) symmetry. Phys. Rev. A 86, 023807 (2012).
Regensburger, A. et al. Parity-time synthetic photonic lattices. Nature 488, 167 (2012).
Chen, C. et al. Observation of topologically protected edge states in a photonic two-dimensional quantum walk. Phys. Rev. Lett. 121, 100502 (2018).
Weidemann, S. et al. Topological funneling of light. Science 368, 311–314 (2020).
Yuan, L., Lin, Q., Xiao, M. & Fan, S. Synthetic dimension in photonics. Optica 5, 1396–1405 (2018).
Wimmer, M., Price, H. M., Carusotto, I. & Peschel, U. Experimental measurement of the berry curvature from anomalous transport. Nat. Phys. 13, 545 (2017).
Wen, Z., Lu, B., Wang, K., Qi, X. & Bai, J. Discrete optical propagation in one-dimensional synthetic mesh lattice. J. Opt. Soc. Am. B 37, 3152–3161 (2020).
Muniz, A. L. M. et al. Kapitza light guiding in photonic mesh lattice. Opt. Lett. 44, 6013–6016 (2019).
Bisianov, A., Wimmer, M., Peschel, U. & Egorov, O. A. Stability of topologically protected edge states in nonlinear fiber loops. Phys. Rev. A 100, 063830 (2019).
Gómez-León, A. & Platero, G. Floquet-bloch theory and topology in periodically driven lattices. Phys. Rev. Lett. 110, 200403 (2013).
Dutt, A. et al. Experimental band structure spectroscopy along a synthetic dimension. Nat. Commun. 10, 3122 (2019).
Dutt, A. et al. A single photonic cavity with two independent physical synthetic dimensions. Science 367, 59–64 (2020).
Tikan, A. M., Vatnik, I. D., Churkin, D. V. & Sukhorukov, A. A. Deriving eigenmode excitation spectrum of synthetic photonic lattices by means of optical heterodyning. Laser Phys. 27, 026203 (2017).
Smith, S. P., Zarinetchi, F. & Ezekiel, S. Narrow-linewidth stimulated brillouin fiber laser and applications. Opt. Lett. 16, 393–395 (1991).
Debut, A., Randoux, S. & Zemmouri, J. Linewidth narrowing in brillouin lasers: Theoretical analysis. Phys. Rev. A 62, 023803 (2000).
Geng, J. et al. Highly stable low-noise brillouin fiber laser with ultranarrow spectral linewidth. IEEE Photonics Technol. Lett. 18, 1813–1815 (2006).
Loh, W. et al. Operation of an optical atomic clock with a brillouin laser subsystem. Nature 588, 244 (2020).
Leykam, D., Smolina, E., Maluckov, A., Flach, S. & Smirnova, D. A. Probing band topology using modulational instability. Phys. Rev. Lett. 126, 073901 (2021).
Acknowledgements
This work was supported by the H2020-FETFLAG project PhoQus (820392), European Research Council (865151) via the project EmergenTopo, the French government through the Program Investissement d’Avenir (ISITE ULNE/ANR-16-IDEX-0004 ULNE), and IDEX-ISITE initiative 16-IDEX-0001 (CAP 20-25), managed by the Agence Nationale de la Recherche, the Labex CEMPI (ANR-11-LABX-0007), and the CPER Photonics for Society P4S.
Author information
Authors and Affiliations
Contributions
C.L., C.E., P.S., F.C., A.A., and S.R. have contributed equally to the design and the realization of the experiment. All the authors participated in the data acquisition that has been essentially performed by C. L. All authors participated in data analysis, numerical simulations, and have written the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Physics thanks Avik Dutt, Ulf Peschel, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lechevalier, C., Evain, C., Suret, P. et al. Single-shot measurement of the photonic band structure in a fiber-based Floquet-Bloch lattice. Commun Phys 4, 243 (2021). https://doi.org/10.1038/s42005-021-00750-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00750-w
This article is cited by
-
Nonlinear dispersion relation in integrable turbulence
Scientific Reports (2022)
-
Simulating topological materials with photonic synthetic dimensions in cavities
Quantum Frontiers (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.