Abstract
Spin Hall effect, an electric generation of spin current, allows for efficient control of magnetization. Recent theory revealed that orbital Hall effect creates orbital current, which can be much larger than spin-Hall-induced spin current. However, orbital current cannot directly exert a torque on a ferromagnet, requiring a conversion process from orbital current to spin current. Here, we report two effective methods of the conversion through spin-orbit coupling engineering, which allows us to unambiguously demonstrate orbital-current-induced spin torque, or orbital Hall torque. We find that orbital Hall torque is greatly enhanced by introducing either a rare-earth ferromagnet Gd or a Pt interfacial layer with strong spin-orbit coupling in Cr/ferromagnet structures, indicating that the orbital current generated in Cr is efficiently converted into spin current in the Gd or Pt layer. Our results offer a pathway to utilize the orbital current to further enhance the magnetization switching efficiency in spin-orbit-torque-based spintronic devices.
Similar content being viewed by others
Introduction
Spin Hall effect (SHE) that creates a transverse spin current by a charge current in a non-magnet (NM) with strong spin–orbit coupling (SOC)1 has received much attention because the resulting spin–orbit torque (SOT) offers efficient control of magnetization in NM/ferromagnet (FM) heterostructures of various spintronic devices2,3,4,5,6,7,8,9. Similar to the SHE, the orbital Hall effect (OHE) generates an orbital current, a flow of orbital angular momentum10,11,12,13. The OHE has distinctive features compared to the SHE; first, the OHE originates from momentum-space orbital textures, so it universally occurs in multi-orbital systems regardless of the magnitude of SOC12. For example, it has been reported non-trivial orbital current can be generated in 3d transition metals, graphene, or two-dimensional transition metal dichalcogenides13,14,15,16,17,18. Second, theoretical calculations show that orbital Hall conductivity is much larger than spin Hall conductivity in many materials, including those commonly used for SOT such as Ta and W10,11,13. This suggests that the spin torque caused by the OHE, or orbital Hall torque (OHT)19,20, can be larger than the SHE-induced spin torque, enhancing the spin-torque efficiency in spintronic devices. Recently, several experimental reports have claimed that significant SOT and magnetoresistance observed in FM/Cu/oxide structures, in which the SHE is known to be negligible, is of orbital current origin21,22,23,24. However, it seems that the underlying mechanism of the OHE and associated OHT are not yet fully understood. One issue is that there is no exchange coupling between orbital angular momentum (L) and local magnetic moment, and thus the orbital current cannot directly give a torque on magnetization. To make the OHT exerts on the local magnetic moment of the FM, the L must be converted to the spin angular momentum (S)19,20. Therefore, finding an efficient method of “L–S conversion” is crucial to utilizing the OHT for the manipulation of the magnetization direction.
In this article, we experimentally demonstrate two effective L–S conversion techniques of engineering SOC of either an FM or an NM/FM interface. We employ Cr as an orbital current source material because it has been theoretically predicted that Cr has a large orbital Hall conductivity \(\sigma _{{{{{{{{\mathrm{OH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}}\) of ~8200 (ħ/e)(Ω cm)−1 while having a relatively small spin Hall conductivity \(\sigma _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}}\) of −130 (ħ/e)(Ω cm)−1 with the opposite sign13. Here, ħ is the reduced Planck constant and e is the electron charge. For the Cr/FM bilayers, overall charge-to-spin conversion efficiency referred as effective spin Hall angle \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\), is expressed as19
where \(\sigma _{xx}^{{{{{{{{\mathrm{Cr}}}}}}}}}\) is the electrical conductivity of Cr and \(\eta _{L - S}\) is the L–S conversion coefficient. Here, we assume perfect transmission (\(T_{{{{{{{{\mathrm{int}}}}}}}}}\) = 1) of both spin and orbital currents through the Cr/FM interface. Note that the second term on the right side of Eq. (1) corresponds to the OHE contribution to \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\), which depends on the magnitude and sign of \(\eta _{L - S}\). We demonstrate how to achieve a large \(\eta _{L - S}\) by engineering the SOC of an FM or an NM interfacial layer. First, we employ a rare-earth FM of Gd with strong SOC, which increases the OHT in Cr/Gd heterostructures by ten times compared to that in Cr/Co heterostructures, indicating that the orbital current generated in Cr is efficiently converted to spin current in the FM Gd layer. Second, we modify the Cr/Co32Fe48B20 (CoFeB) interface by inserting a 1 nm Pt layer to facilitate L–S conversion. This leads to an enhancement in OHT, allowing us to demonstrate OHT-induced magnetization switching of perpendicular magnetization in Cr/Pt/CoFeB heterostructures. Since the OHE is expected to occur generally in various materials, our results demonstrating the significant OHT generated through the L–S conversion techniques broaden the scope of material engineering to improve spin-torque switching efficiency for the development of low-power spintronic devices.
Results and discussion
Orbital Hall torque generated by orbital current in Cr
To demonstrate the OHE in Cr and associated OHT, we investigate the current-induced spin-torque in Cr/FM heterostructures for two different FMs of Co and Ni. Figure 1a, b illustrates the role of \(\eta _{L - S}\) in \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\) of the Cr/FM samples, where \({{{S}}}_{{{{{{{{\rm{SHE}}}}}}}}}\) is the spin angular momentum generated by SHE and \({{{S}}}_{{{{{{{{\rm{OHE}}}}}}}}}\) is the spin angular momentum converted from orbital angular momentum due to OHE (\({{{L}}}_{{{{{{{{\rm{OHE}}}}}}}}}\)). Note that we assume that Ni has a greater \(\eta _{L - S}\) than that of Co (\(\eta _{L - S}^{{{{{{{{\mathrm{Ni}}}}}}}}} \, > \,\eta _{L - S}^{{{{{{{{\mathrm{Co}}}}}}}}}\)) because \(\sigma _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{Ni}}}}}}}}}\) is an order of magnitude larger than \(\sigma _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{Co}}}}}}}}}\)25,26. This is also supported by a recent first principle calculation demonstrating that the W/Ni bilayer exhibits a positive \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\) despite the negative \(\sigma _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{\mathrm{W}}}}}}}}\) of W20. This is attributed to the increased orbital current contribution to \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\) by the large and positive \(\eta _{L - S}^{{{{{{{{\mathrm{Ni}}}}}}}}}\). Figure 1a shows the case of a Cr/Co bilayer with \(\eta _{L - S}^{{{{{{{{\mathrm{Co}}}}}}}}}\) ~ 0, where \({{{S}}}_{{{{{{{{\rm{SHE}}}}}}}}}\) is dominant and thus \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\) is mainly determined by \(\sigma _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}}\) of negative sign. On the other hand, for the Cr/Ni bilayer having sizable \(\eta _{L - S}^{{{{{{{{\mathrm{Ni}}}}}}}}}\), non-negligible \({{{S}}}_{{{{{{{{\rm{OHE}}}}}}}}}\) caused by the conversion of \(\sigma _{{{{{{{{\mathrm{OH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}}\) contributes to \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\) (Fig. 1b). Since \({{{S}}}_{{{{{{{{\rm{OHE}}}}}}}}}\) is a positive value \((\eta _{L - S}^{{{{{{{{\mathrm{Ni}}}}}}}}} \, > \,0\,\& \,\sigma _{{{{{{{{\mathrm{OH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}} \, > \,0),\) opposite to \({{{S}}}_{{{{{{{{\rm{SHE}}}}}}}}}\), \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\) of the Cr/Ni heterostructures becomes positive when the magnitude of \({{{S}}}_{{{{{{{{\rm{OHE}}}}}}}}}\) is larger than that of \({{{S}}}_{{{{{{{{\rm{SHE}}}}}}}}}\). To test whether the orbital current generated in Cr gives rise to OHT, we perform in-plane harmonic Hall measurements of Co (3.0 nm)/Cr (7.5 nm) and Ni (2.0 nm)/Cr (7.5 nm) Hall-bar patterned samples (Fig. 1c). Figure 1d, e shows representative second harmonic Hall resistance (\(R_{xy}^{2\omega }\)) versus azimuthal angle (\(\varphi\)) curves under different external magnetic fields (\(B_{{{{{{{{\mathrm{ext}}}}}}}}}\)). \(R_{xy}^{2\omega }(\varphi )\) is expressed as27
where \(R_{{{{{{{{\mathrm{AHE}}}}}}}}}^{1\omega }\) and \(R_{{{{{{{{\mathrm{PHE}}}}}}}}}^{1\omega }\) are the first harmonic anomalous Hall and planar Hall resistances, respectively; \(B_{{{{{{{{\mathrm{DLT}}}}}}}}}\,(B_{{{{{{{{\mathrm{FLT}}}}}}}}})\) is the damping-like (field-like) effective field; \(B_{{{{{{{{\mathrm{eff}}}}}}}}}\) is the effective magnetic field, including the demagnetization field and anisotropy field of FM; \(R_{\nabla T}\) is the thermal contributions, and \(B_{{{{{{{{\mathrm{Oe}}}}}}}}}\) is the current-induced Oersted field. The \(R_{{{{{{{{\mathrm{AHE}}}}}}}}}^{1\omega }\) and \(R_{{{{{{{{\mathrm{PHE}}}}}}}}}^{1\omega }\) data are shown in Supplementary Note 1. Figure 1f shows the \({{{{{{{\mathrm{cos}}}}}}}}\varphi\) component of \(R_{xy}^{2\omega }\) divided by \(R_{{{{{{{{\mathrm{AHE}}}}}}}}}^{1\omega }\) [\(R_{{{{{{{{\mathrm{cos}}}}}}}}\varphi }^{2\omega }\)/\(R_{{{{{{{{\mathrm{AHE}}}}}}}}}^{1\omega }\)] as a function of \(1/B_{{{{{{{{\mathrm{eff}}}}}}}}}\) for the two FM/Cr samples, of which the slope represents BDLT and associated \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\). We find that the Co/Cr sample shows a negative slope, and thus a negative \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\). This is consistent with the negative \(\sigma _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}}\) reported both theoretically and experimentally28,29,30. In contrast, the Ni/Cr sample exhibits a positive slope, indicating a positive \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\). The sign reversal of \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\) in the Ni/Cr sample is attributed to the increased contribution of the orbital current in Cr by the L–S conversion in Ni (\(\sigma _{{{{{{{{\mathrm{OH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}}\eta _{L - S}^{{{{{{{{\mathrm{Ni}}}}}}}}} \, > \,0\)). Note that the \((2{{{{{{{\mathrm{cos}}}}}}}}^3\varphi - {{{{{{{\mathrm{cos}}}}}}}}\varphi )\) component of \(R_{xy}^{2\omega }\) divided by \(R_{{{{{{{{\mathrm{PHE}}}}}}}}}^{1\omega }\), representing \(B_{{{{{{{{\mathrm{FLT}}}}}}}}} + B_{{{{{{{{\mathrm{Oe}}}}}}}}}\), of the Ni/Cr sample is larger than that of the Co/Cr sample. This might also be related to the increased orbital current in the Ni/Cr sample as discussed in Supplementary Note 2.
a, b Schematic illustrations of the angular momentum transfer by spin current (red arrows) and orbital current (blue arrows) for Co (a) and Ni (b) ferromagnets (FMs). The spin (orbital) angular momentum is represented by S (L). The source of S and L is marked by the subscript of SHE (OHE) for spin Hall effect (orbital Hall effect). \({{{\eta }}}_{{{{L}}} - {{{S}}}}^{{{{{{{{\rm{Co}}}}}}}}({{{{{{{\rm{Ni}}}}}}}})}\) is the orbital-to-spin conversion efficiency of Co (Ni). c The \({{{R}}}_{{{{xy}}}}^{2{{{\omega }}}}({{{\varphi }}})\) measurement geometry for a Hall-bar sample. \(\varphi\) is the azimuthal angle of the external magnetic field (Bext) with respect to the current direction. d, e Azimuthal angle (φ) dependent second harmonic Hall resistance, \({{{R}}}_{{{{xy}}}}^{2{{{\omega }}}}({{{\varphi }}})\), under different Bext of Co (3.0 nm)/Cr (7.5 nm) (d) and Ni (2.0 nm)/Cr (7.5 nm) (e) samples. The solid lines are the fitting curves using Eq. (2). Each \({{{R}}}_{{{{xy}}}}^{2{{{\omega }}}}({{{\varphi }}})\) curve of Co/Cr (d) and Ni/Cr (e) is shifted by a y-axis offset to clearly show the Bext dependence. f \({{{R}}}_{{{{{{{{\rm{COS\varphi }}}}}}}}}^{2{{{\omega }}}}/{{{R}}}_{{{{{{{{\rm{AHE}}}}}}}}}^{1{{{{{{{\mathbf{\omega }}}}}}}}}\) as function of 1/Beff of Ni/Cr (red), Co/Cr (light-green), Ni/Pt (magenta), and Co/Pt (green) samples. Each solid line is the linear fitting line. The error bars in f are due to the standard deviation of the fitting of the \({{{R}}}_{{{{xy}}}}^{2{{{\omega }}}}({{{\varphi }}})\) versus φ curves using Eq. (2), which are smaller than the symbol size. g Cr thickness (tCr) dependent damping-like torque efficiency (ξDLT) of Ni/Cr (red) and Co/Cr (light-green) samples, where tCr ranges from 2 to 12.5 nm. The fitting results of orbital and spin diffusion lengths for Ni/Cr and Co/Cr are given in solid curves. The ξDLT’s of the reference Ni/Pt (magenta) and Co/Pt (green) samples are included for comparison. Lines are guides to eyes. All measurements are conducted at 300 K. The error bars in g are due to the standard deviation of the linear fitting of the cosφ components of Eq. (2) versus 1/Beff.
To verify whether the orbital current in Cr is the main cause of the measured torque, we perform two control experiments. First, we investigate the role of FM in determining \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\) by measuring the \(R_{{{{{{{{\mathrm{cos}}}}}}}}\varphi }^{2\omega }\)/\(R_{{{{{{{{\mathrm{AHE}}}}}}}}}^{1\omega }\) of the Co (3 nm)/Pt (5 nm) and Ni (2 nm)/Pt (5 nm) structures, in which Cr is replaced by Pt, which has positive \(\sigma _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{Pt}}}}}}}}}\) and \(\sigma _{{{{{{{{\mathrm{OH}}}}}}}}}^{{{{{{{{\mathrm{Pt}}}}}}}}}\)10,11,13,31. Figure 1f shows positive slopes and corresponding positive \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\)’s for both the FM/Pt samples, indicating that the sign change of \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\) in the FM/Cr samples is not due to the FM layer itself26. Note that the damping-like torque efficiency31, \(\xi _{{{{{{{{\mathrm{DLT}}}}}}}}} = (2e/\hbar )(M_{{{{{{{\mathrm{S}}}}}}}}t_{{{{{{{{\mathrm{FM}}}}}}}}}B_{{{{{{{{\mathrm{DLT}}}}}}}}}/J_{{{{{{{{\mathrm{Pt}}}}}}}}})\) where, MS is the saturation magnetization, tFM is the FM thickness, and JPt is the current density flowing in Pt (Supplementary Note 3), between the Co/Pt and Ni/Pt samples differs by a factor of two. This indicates that interface transmission (\(T_{{{{{{{{\mathrm{int}}}}}}}}}\)) plays a critical role in determining ξDLT in these samples, where the spin current is primarily generated by the SHE in the Pt layer32. It implies that \(T_{{{{{{{{\mathrm{int}}}}}}}}}\) can affect the ξDLT even in the FM/Cr sample, where the OHE is dominated. However, \(T_{{{{{{{{\mathrm{int}}}}}}}}}\) cannot account for the different signs of the \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\) (or ξDLT) between the Co/Cr and Ni/Cr samples since it can only reduce the magnitude of the ξDLT by diminishing the transmission of spin (or orbital) currents. Second, we examine the interfacial contributions33,34,35,36,37,38 to \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\) by measuring the Cr thickness (tCr) dependence of the ξDLT for the FM/Cr samples. If the positive \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\) of the Ni/Cr samples is due to the interfacial effect, ξDLT decreases with increasing tCr and eventually changes its sign to negative for thicker tCr’s where bulk Cr with negative \(\sigma _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}}\) dominates. However, this is not the case, as shown in Fig. 1g; for both FM/Cr samples, the magnitude of ξDLT increases with tCr, while maintaining its sign unchanged, which demonstrates that there is no significant interfacial contribution to \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\) in the FM/Cr samples. Note that we analyze the tCr dependence of ξDLT using a method of analyzing the SHE-induced SOT31, \(\xi _{{{{{{{{\mathrm{DLT}}}}}}}}}\sim \left[ {1 - {{{{{{{\mathrm{sech}}}}}}}}\left( {\frac{{t_{{{{{{{{\mathrm{Cr}}}}}}}}}}}{{\lambda _{{{{{{{{\mathrm{Cr}}}}}}}}}}}} \right)} \right]\), where, λCr is the spin or orbital diffusion length. The extracted λCr value is 6.1 ± 1.7 nm for the Ni/Cr and 1.8 ± 0.6 nm for the Co/Cr samples, which can be regarded as the orbital and spin diffusion lengths of Cr, respectively, since the ξDLT of the Ni/Cr (Co/Cr) sample is governed predominantly by the OHE (SHE). This result indicates that the orbital diffusion length is much greater than the spin diffusion length in Cr, as expected by theoretical calculations (Supplementary Note 4). These results corroborate that the OHE in Cr primarily governs the \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\) of the FM/Cr samples, providing an excellent platform to study L–S conversion engineering.
Efficient L–S conversion through rare-earth ferromagnet Gd
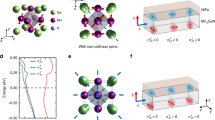
We now present two techniques to enhance the \(\eta _{L - S}\) of the Cr/FM structures. First, we introduce a rare-earth FM Gd, which is expected to have a large \(\eta _{L - S}\) due to its strong SOC39,40. Figure 2a illustrates the L–S conversion process in Cr/Gd heterostructures, where \(\eta _{L - S}^{{{{{{{{\mathrm{Gd}}}}}}}}}\) is negative because of its negative spin Hall angle41. In this case, \({{{S}}}_{{{{{{{{\rm{OHE}}}}}}}}}\) due to the orbital current (\(\eta _{L - S}^{{{{{{{{\mathrm{Gd}}}}}}}}}\sigma _{{{{{{{{\mathrm{OH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}}\) < 0) is the same sign as \({{{S}}}_{{{{{{{{\rm{SHE}}}}}}}}}\) (\(\sigma _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}}\) < 0), so they add up constructively with each other. This would result in enhanced \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\) in the Cr/Gd heterostructure compared to the Cr/Co heterostructure. To verify this idea, we prepare Hall-bar patterned samples of Gd (10 nm)/Cr (7.5 nm) and Co (10 nm)/Cr (7.5 nm) structures and conduct in-plane harmonic Hall measurements at 10 K to avoid any side effects due to the large difference in Curie temperatures between Gd (~293 K) and Co (~1400 K). Note that Cr is known to be antiferromagnetic at 10 K42, however, the exchange coupling of the Gd (Co)/Cr sample is negligibly small and therefore does not affect the harmonic Hall measurements (Supplementary Note 5). Figure 2b, c shows the \(R_{xy}^{2\omega }(\varphi )\) data measured under different Bext’s of the Gd/Cr and Co/Cr samples, respectively, which are well described by Eq. (2) as represented by solid curves. The \(R_{{{{{{{{\mathrm{AHE}}}}}}}}}^{1\omega }\) and \(R_{{{{{{{{\mathrm{PHE}}}}}}}}}^{1\omega }\) data are shown in Supplementary Note 1. Figure 2d shows \(R_{{{{{{{{\mathrm{cos}}}}}}}}\varphi }^{2\omega }\)/\(R_{{{{{{{{\mathrm{AHE}}}}}}}}}^{1\omega }\) versus \(1/B_{{{{{{{{\mathrm{eff}}}}}}}}}\) for the Gd/Cr and Co/Cr samples. We find two points; first, both samples exhibit negative slopes, indicating \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}} < 0\). Second, the Gd/Cr sample has a much larger slope or \(B_{{{{{{{{\mathrm{DLT}}}}}}}}}\) than that of the Co/Cr sample. The estimated ξDLT of the Gd/Cr sample is −0.21 ± 0.01, which is about ten times greater than that of the Co/Cr sample (−0.018 ± 0.002). Note that ξDLT of the Gd/Cr samples increases with the tCr (Supplementary Note 6), indicating that ξDLT originates from the orbital current in bulk Cr. The large enhancement of ξDLT or \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\) demonstrates that the OHT contribution can be increased by introducing FMs with large \(\eta _{L - S}\).
a Schematic illustration of the orbital-to-spin (L–S) conversion by \({{{\eta }}}_{{{{L}}} - {{{S}}}}^{{{{{\rm{Gd}}}}}}\) in the Cr/Gd heterostructure. The spin (orbital) angular momentum is represented by S (L). The source of S and L is marked by the subscript of SHE (OHE) for spin Hall effect (orbital Hall effect). b, c \({{{R}}}_{{{{xy}}}}^{2{{{\omega }}}}({{{\varphi }}})\) under different Bext of Gd (10 nm)/Cr (5 nm) (b) and Co (10 nm)/Cr (5 nm) (c) samples. Each \({{{R}}}_{{{{xy}}}}^{2{{{\omega }}}}({{{\varphi }}})\) of Gd/Cr (b) and Co/Cr (c) is shifted by a y-axis offset to clearly show Bext dependence. The solid lines are the fitting curves using Eq. (2). d \({{{R}}}_{{{{{{{{\rm{COS\varphi }}}}}}}}}^{2{{{\omega }}}}{{{{{{{\mathrm{/}}}}}}}}{{{R}}}_{{{{{{{{\rm{AHE}}}}}}}}}^{1{{{\omega }}}}\) versus 1/Beff of Gd/Cr (brown) and Co/Cr (blue-green) samples. Each solid line is the linear fitting line. All measurements are conducted at 10 K. The error bars in d are due to the standard deviation of the fitting of the \({{{R}}}_{{{{xy}}}}^{2{{{\omega }}}}({{{\varphi }}})\) versus φ curves using Eq. (2), which are smaller than the symbol size.
We estimate effective spin Hall conductivity \(\sigma _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}}({{{{{{{\mathrm{eff}}}}}}}}) = \sigma _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}} + \sigma _{{{{{{{{\mathrm{OH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}}\eta _{L - S}\) of the samples using the relation31 \(\sigma _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}}\left( {{{{{{{{\mathrm{eff}}}}}}}}} \right)\) = (ħ/2e)·(ξDLT × \(\sigma _{xx}^{{{{{{{{\mathrm{Cr}}}}}}}}}\)). The calculated \(\sigma _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}}({{{{{{{\mathrm{eff}}}}}}}})\) of the Gd/Cr sample is −999 (ħ/e)·(Ω cm)−1, which is much larger than the theoretical spin Hall conductivity of Cr13, \(\sigma _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}} =\) −130 (ħ/e)·(Ω cm)−1. The large \(\sigma _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}}({{{{{{{\mathrm{eff}}}}}}}})\) value of the Gd/Cr sample supports our claim that the enhanced ξDLT is due to the orbital current in Cr, subject to the effective conversion into spin currents in Gd (\(\sigma _{{{{{{{{\mathrm{OH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}}\eta _{L - S}^{{{{{{{{\mathrm{Gd}}}}}}}}}\)). On the other hand, the \(\sigma _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}}({{{{{{{\mathrm{eff}}}}}}}})\) of the Co/Cr sample is −86 (ħ/e)·(Ω cm)−1, which is comparable to the theoretical \(\sigma _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}}\) value. This is consistent with the fact that the orbital current contribution is negligible in the Co/Cr sample with \(\eta _{L - S}^{{{{{{{{\mathrm{Co}}}}}}}}}\) ~ 0. Furthermore, we observe that the ξDLT of the Gd/Cr sample decreases with increasing temperature (Supplementary Note 7). This can be attributed to phonon scattering since the orbital angular momentum is strongly coupled to the lattice through the crystal field potential20. At higher temperatures, more phonons are generated, reducing the OHE.
Magnetization switching by efficient L–S conversion through Pt interfacial layer
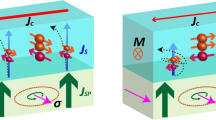
We next demonstrate another L–S conversion technique that modifies the NM/FM interface by inserting a Pt layer. This method has the advantage that it can be easily incorporated into perpendicularly magnetized CoFeB/MgO structures, which is a basic component of various spintronic devices43,44,45. Figure 3a illustrates the conversion process in a Cr/Pt/CoFeB structure, where the \({{{L}}}_{{{{{{{{\rm{OHE}}}}}}}}}\) originating from Cr is converted to \({{{S}}}_{{{{{{{{\rm{OHE}}}}}}}}}\) in the Pt layer. Since Pt has a positive \(\eta _{L - S}^{{{{{{{{\mathrm{Pt}}}}}}}}}\) due to positive \(\sigma _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{Pt}}}}}}}}}\), \({{{S}}}_{{{{{{{{\rm{OHE}}}}}}}}}\) would be positive (\(\sigma _{{{{{{{{\mathrm{OH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}}\eta _{L - S}^{{{{{{{{\mathrm{Pt}}}}}}}}} \, > \,0\)), while \({{{S}}}_{{{{{{{{\rm{SHE}}}}}}}}}\) is negative (\(\sigma _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{Cr}}}}}}}}} \, < \,0\)). Thus, the OHT due to \({{{S}}}_{{{{{{{{\rm{OHE}}}}}}}}}\) is the opposite of the spin Hall torque due to \({{{S}}}_{{{{{{{{\rm{SHE}}}}}}}}}\). To examine the effect of Pt insertion on OHT, we perform current-induced magnetization switching experiments as schematically illustrated in Fig. 3b. Figure 3c shows switching curves as a function of pulse current density (Jpulse) for Cr (10.0 nm)/Pt (0 or 1.0 nm)/CoFeB (0.9 nm)/MgO (1.6 nm) Hall-bar patterned samples. Note that an in-plane magnetic field Bx of +20 mT is applied along the current direction for deterministic switching of the perpendicular magnetization2,4,46. The Cr/CoFeB sample shows a counterclockwise switching curve consistent with negative \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\), caused primarily by the SHE in Cr. The switching polarity is reversed by introducing a Pt (1 nm) insertion layer. The clockwise switching curve of the Cr/Pt/CoFeB sample corresponds to positive \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\), which is the expected sign in the OHT scenario (Fig. 3a). The sign reversal of \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\) of the samples is also confirmed by perpendicular harmonic Hall measurements (Supplementary Note 8). Note that the switching polarity is abruptly reversed when tPt is greater than 0.6 nm (Supplementary Note 9), where Pt forms a continuous film that effectively converts orbital currents to spin currents. This makes the OHE dominant over the SHE.
a Schematic illustration of the orbital-to-spin conversion by \({{{\eta }}}_{{{{L}}} - {{{S}}}}^{{{{{\rm{Pt}}}}}}\) in the Cr/Pt/CoFeB heterostructure. The spin (orbital) angular momentum is represented by S (L). The source of S and L is marked by the subscript of SHE (OHE) for spin Hall effect (orbital Hall effect). b The magnetization switching measurement geometry for a Hall-bar sample, in which an in-plane magnetic field Bx is applied along the pulsed current Jpulse. c Magnetization switching curves of Cr (10.0 nm)/CoFeB (0.9 nm) and Cr (10.0 nm)/Pt (1.0 nm)/CoFeB (0.9 nm) samples under a Bx of +20 mT. The green and magenta symbols represent the samples without and with the Pt insertion layer, respectively. Open (closed) symbols indicate magnetization switching from down-to-up (up-to-down) directions. The switching polarity is indicated by an arrow in the center of curve. d tCr-dependent switching efficiency (\({{{{{{\xi }}}}}}^{{{{{{{{\rm{SW}}}}}}}}}\)) of the Cr/CoFeB (green) and Cr/Pt/CoFeB (magenta) samples. Lines are guide to eyes. All measurements are conducted at 300 K. The error bars in d are due to the standard deviation of fittings of BC = BP/cosθ which is (BP) estimation. Here, where BP is the domain wall propagation field, BC is the coercive field, and θ is the polar angle of the magnetic field (Supplementary Note 10).
The sign change in \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\) can be caused by the inserted Pt itself with positive \(\sigma _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{Pt}}}}}}}}}\). To rule out this possibility, we investigate the tCr dependence of the current-induced magnetization switching for the samples, where tCr ranges from 2.0 to 12.5 nm. Figure 3d shows the switching efficiency47,48 \(\xi ^{{{{{{{{\mathrm{SW}}}}}}}}}\,[ = (2e/\hbar )(M_{{{{{{{\mathrm{S}}}}}}}}t_{{{{{{{{\mathrm{CoFeB}}}}}}}}}B_{{{{{{{\mathrm{P}}}}}}}}/J_{{{{{{{{\mathrm{SW}}}}}}}}})]\) as a function of tCr. Here, \(t_{{{{{{{{\mathrm{CoFeB}}}}}}}}}\) is the CoFeB thickness, \(B_{{{{{{{\mathrm{P}}}}}}}}\) is the domain wall propagation field, and \(J_{{{{{{{{\mathrm{SW}}}}}}}}}\) is the switching current density (Supplementary Note 10). We find that the magnitude of \(\xi ^{{{{{{{{\mathrm{SW}}}}}}}}}\) for both samples increases with increasing tCr, while its sign remains unchanged for all tCr’s used in this study. Since the contribution of the spin current generated from Pt to \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\) in the Cr/Pt/CoFeB structures will decrease with increasing tCr, the similar thickness dependence of \(\xi ^{{{{{{{{\mathrm{SW}}}}}}}}}\) indicates that the \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\) of both samples predominantly originates from the Cr layer, not from the Pt interfacial layer; the SHE and OHE in Cr are the main sources of \(\theta _{{{{{{{{\mathrm{SH}}}}}}}}}^{{{{{{{{\mathrm{eff}}}}}}}}}\) for the Cr/CoFeB and Cr/Pt/CoFeB samples, respectively. These results demonstrate that the OHT can be effectively modified by interface SOC engineering and is capable of switching the perpendicular magnetization.
In conclusion, we experimentally demonstrate non-trivial OHT, spin torques originating from the orbital current in Cr, by introducing two effective ways of orbital-to-spin (L–S) conversion, which is a key ingredient of OHT generation. First, we employ a rare-earth FM of Gd having a larger L–S conversion efficiency than that of conventional 3d FMs. This greatly improves the SOT efficiency of the Cr/Gd bilayers compared to that of the Cr/Co bilayers. Second, we introduce a Pt interfacial layer in the Cr/CoFeB bilayers to facilitate L–S conversion. This allows the OHT to control the perpendicular magnetization in the Cr/Pt/CoFeB heterostructures. Since orbital currents can occur in various materials regardless of the SOC strength, our results provide a unique strategy based on orbital currents to develop material systems with enhanced SOT efficiency.
Methods
Film preparation and Hall-bar fabrication
Bilayers of FM (Co, Ni)/Cr, FM (Co, Ni)/Pt, Gd /Cr, and Co/Cr for harmonic measurements were deposited on Si/SiO2 or Si/Si3N4 substrates using DC magnetron sputtering under a base pressure of <2.6 × 10−5 Pa, while Cr/CoFeB and Cr/Pt/CoFeB structures for switching experiments were deposited on a highly resistive Si substrate using DC and RF magnetron sputtering under a base pressure of <4.0 × 10−6 Pa. An underlayer of Ta (1 nm)/AlOx (2 nm), or Ta (1.5 nm) layers were used to obtain smooth roughness; a capping layer of Ta (2–3 nm) was used to prevent further oxidation. All metallic layers and the MgO layer were grown with a working pressure of 0.4 Pa and a power of 30 W at room temperature. The AlOx layer was formed by deposition of an Al layer and subsequent plasma oxidation with an O2 pressure of 4.0 Pa and a power of 30 W for 75 s. Hall-bar-patterned devices with widths of 5, 10, or 15 μm were defined using photolithography and Ar ion-milling.
Spin–orbit torque characterization
In-plane harmonic measurement with AC current (frequency of 11 Hz) was performed to evaluate the spin–orbit torque of the heterostructures. Both \(R_{xy}^{1\omega }\) and \(R_{xy}^{2\omega }\) were recorded by two lock-in amplifiers at the same time while varying the azimuthal angle (\(\varphi\)) under a constant external field Bext and a current density Jx of 1 × 1011 A/m2.
Current-induced magnetization switching measurements
Magnetization switching experiments were conducted by applying a current pulse (pulse width of 30 μs) with a constant external magnetic field (Bx) of +20 mT. The magnetization state was checked by anomalous Hall resistance (RAHE) after applying the current pulse.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Sinova, J., Valenzuela, S. O., Wunderlich, J., Back, C. H. & Jungwirth, T. Spin Hall effects. Rev. Mod. Phys. 87, 1213–1260 (2015).
Miron, I. M. et al. Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 476, 189–193 (2011).
Liu, L. et al. Spin-torque switching with the giant spin Hall effect of tantalum. Science 336, 555–558 (2012).
Liu, L., Lee, O. J., Gudmundsen, T. J., Ralph, D. C. & Buhrman, R. A. Current-induced switching of perpendicularly magnetized magnetic layers using spin torque from the spin Hall effect. Phys. Rev. Lett. 109, 096602 (2012).
Demidov, V. E. et al. Magnetic nano-oscillator driven by pure spin current. Nat. Mater. 11, 1028–1031 (2012).
Emori, S., Bauer, U., Ahn, S. M., Martinez, E. & Beach, G. S. D. Current-driven dynamics of chiral ferromagnetic domain walls. Nat. Mater. 12, 611–616 (2013).
Ryu, K. S., Thomas, L., Yang, S.-H. & Parkin, S. Chiral spin torque at magnetic domain walls. Nat. Nanotechnol. 8, 527–533 (2013).
Manchon, A. et al. Current-induced spin-orbit torques in ferromagnetic and antiferromagnetic systems. Rev. Mod. Phys. 91, 035004 (2019).
Ryu, J., Lee, S., Lee, K. J. & Park, B.-G. Current-induced spin–orbit torques for spintronic applications. Adv. Mater. 32, 1907148 (2020).
Tanaka, T. et al. Intrinsic spin Hall effect and orbital Hall effect in 4d and 5d transition metals. Phys. Rev. B 77, 165117 (2008).
Kontani, H., Tanaka, T., Hirashima, D. S., Yamada, K. & Inoue, J. Giant orbital Hall effect in transition metals: origin of large spin and anomalous Hall effects. Phys. Rev. Lett. 102, 016601 (2009).
Go, D., Jo, D., Kim, C. & Lee, H.-W. Intrinsic spin and orbital Hall effects from orbital texture. Phys. Rev. Lett. 121, 086602 (2018).
Jo, D., Go, D. & Lee, H.-W. Gigantic intrinsic orbital Hall effects in weakly spin-orbit coupled metals. Phys. Rev. B 98, 214405 (2018).
Bhowal, S. & Satpathy, S. Intrinsic orbital moment and prediction of a large orbital Hall effect in two-dimensional transition metal dichalcogenides. Phys. Rev. B 101, 121112(R) (2020).
Canonico, L. M., Cysne, T. P., Molina-Sanchez, A., Muniz, R. B. & Rappoport, T. G. Orbital Hall insulating phase in transition metal dichalcogenide monolayers. Phys. Rev. B 101, 161409(R) (2020).
Bhowal, S. & Satpathy, S. Intrinsic orbital and spin Hall effects in monolayer transition metal dichalcogenides. Phys. Rev. B 102, 035409 (2020).
Bhowal, S. & Vignale, G. Orbital Hall effect as an alternative to valley Hall effect in gapped graphene. Phys. Rev. B 103, 195309 (2021).
Cysne, T. P. et al. Disentangling orbital and valley Hall effects in bilayers of transition metal dichalcogenides. Phys. Rev. Lett. 126, 056601 (2021).
Go, D. & Lee, H.-W. Orbital torque: torque generation by orbital current injection. Phys. Rev. Res. 2, 013177 (2020).
Go, D. et al. Theory of current-induced angular momentum transfer dynamics in spin-orbit coupled systems. Phys. Rev. Res. 2, 033401 (2020).
Ding, S. et al. Harnessing orbital-to-spin conversion of interfacial orbital currents for efficient spin-orbit torques. Phys. Rev. Lett. 125, 177201 (2020).
Kim, J. et al. Non-trivial charge-to-spin conversion in ferromagnetic metal/Cu/Al2O3 by orbital transport. Phys. Rev. B 103, L020407 (2021).
Tazaki, Y. et al. Current-induced torque originating from orbital current. Preprint at arXiv http://arXiv.org/abs/2004.09165 (2020).
Ding, S. et al. Observation of the orbital Rashba-Edelstein magnetoresistance. Preprint at arXiv http://arXiv.org/abs/2105.04495 (2021).
Amin, V. P., Li, J., Stiles, M. D. & Haney, P. M. Intrinsic spin currents in ferromagnets. Phys. Rev. B 99, 220405(R) (2019).
Wang, W. et al. Anomalous spin–orbit torques in magnetic single-layer films. Nat. Nanotechnol. 14, 819–824 (2019).
Avci, C. O. et al. Interplay of spin-orbit torque and thermoelectric effects in ferromagnet/normal-metal bilayers. Phys. Rev. B 90, 224427 (2014).
Du, C., Wang, H., Yang, F. & Hammel, P. C. Systematic variation of spin-orbit coupling with d-orbital filling: Large inverse spin Hall effect in 3d transition metals. Phys. Rev. B 90, 140407(R) (2014).
Chuang, T. C., Pai, C. F. & Huang, S. Y. Cr-induced perpendicular magnetic anisotropy and field-free spin-orbit-torque switching. Phys. Rev. Appl. 11, 061005 (2019).
Cui, B. et al. Current induced magnetization switching in Pt/Co/Cr structures with enhanced perpendicular magnetic anisotropy and spin Hall effect. Appl. Phys. Express 12, 043001 (2019).
Nguyen, M.-H., Ralph, D. C. & Buhrman, R. A. Spin torque study of the spin Hall conductivity and spin diffusion length in platinum thin films with varying resistivity. Phys. Rev. Lett. 116, 126601 (2016).
Zhang, W., Han, W., Jiang, X., Yang, S.-H. & Parkin, S. S. P. Role of transparency of platinum-ferromagnet interfaces in determining the intrinsic magnitude of the spin Hall effect. Nat. Phys. 11, 496–502 (2015).
Gambardella, P. & Miron, I. M. Current-induced spin-orbit torques. Philos. Trans. R. Soc. A 369, 3175–3197 (2011).
Emori, S. et al. Interfacial spin-orbit torque without bulk spin-orbit coupling. Phys. Rev. B 93, 180402(R) (2016).
Amin, V. P. & Stiles, M. D. Spin transport at interfaces with spin-orbit coupling: formalism. Phys. Rev. B 94, 104419 (2016).
Amin, V. P. & Stiles, M. D. Spin transport at interfaces with spin-orbit coupling: phenomenology. Phys. Rev. B 94, 104420 (2016).
Baek, S.-h. C. et al. Spin currents and spin-orbit torques in ferromagnetic trilayers. Nat. Mater. 17, 509–513 (2018).
Lee, H.-Y. et al. Enhanced spin-orbit torque via interface engineering in Pt/CoFeB/MgO heterostructures. APL Mater. 7, 031110 (2019).
Krupin, O. et al. Rashba effect at magnetic metal surfaces. Phys. Rev. B 71, 201403(R) (2005).
Stöhr, J. & Siegmann, H. C. Magnetism: From Fundamentals to Nanoscale Dynamics. Vol. 152 (Springer Series in Solid-state Sciences, 2006).
Ueda, K., Pai, C. F., Tan, A. J., Mann, M. & Beach, G. S. D. Effect of rare earth metal on the spin-orbit torque in magnetic heterostructures. Appl. Phys. Lett. 108, 232405 (2016).
Zabel, H. Magnetism of chromium at surfaces, at interfaces and in thin films. J. Phys. Condens. Matter 11, 9303–9346 (1999).
Ikeda, S. et al. A perpendicular-anisotropy CoFeB-MgO magnetic tunnel junction. Nat. Mater. 9, 721–724 (2010).
Torrejon, J. et al. Neuromorphic computing with nanoscale spintronic oscillators. Nature 547, 428–431 (2017).
Borders, W. A. et al. Integer factorization using stochastic magnetic tunnel junctions. Nature 573, 390–393 (2019).
Qiu, X. et al. Angular and temperature dependence of current induced spin-orbit effective fields in Ta/CoFeB/MgO nanowires. Sci. Rep. 4, 4491 (2014).
Lee, O. J. et al. Central role of domain wall depinning for perpendicular magnetization switching driven by spin torque from the spin Hall effect. Phys. Rev. B 89, 024418 (2014).
Mishra, R. et al. Anomalous current-induced spin torques in ferrimagnets near compensation. Phys. Rev. Lett. 118, 167201 (2017).
Acknowledgements
We acknowledge fruitful discussion with Hyun-Woo Lee, Kyoung-Whan Kim, and Daegeun Jo. We also thank Byoung Kook Kim at the KAIST Analysis Center for Research Advancement (KARA) for his support on the magnetic properties measurement. We acknowledge the Jülich Supercomputing Centre for providing computational resources under project jiff40. This work was supported by the National Research Foundation of Korea (2015M3D1A1070465, 2020R1A2C2010309, and 2020R1A2C3013302) and by the German Research Foundation (Deutsche Forschungsgemeinschaft)—TRR 173—268565370 (project A11), TRR 288—422213477 (project B06).
Author information
Authors and Affiliations
Contributions
The study was performed under the supervision of B.-G.P., S.L. and M.-G.K. fabricated samples and conducted the in-plane harmonic measurements and spin–orbit torque switching experiments with the help of D.K., J.-H.K., T.L., G.-H.L., N.J.L., J.K. and S.K. D.G. and Y.M. performed theoretical calculations. S.L., M.-G.K. and B.-G.P. performed data analysis with the help of D.G., K.-J.K. and K.-J.L. S.L., M.-G.K. and B.-G.P. wrote the paper with the help of all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Physics thanks Xiao-long Fan, Sashi Satpathy and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lee, S., Kang, MG., Go, D. et al. Efficient conversion of orbital Hall current to spin current for spin-orbit torque switching. Commun Phys 4, 234 (2021). https://doi.org/10.1038/s42005-021-00737-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00737-7
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.