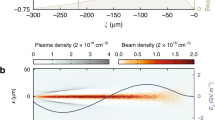
Abstract
Plasma-based accelerators are on the brink of a development stage, where applications of the beam for medical sciences, imaging, or as an injector for a future large-scale accelerator-driven light source become feasible. The requirements on electron beams for injection into a storage-ring are stringent regarding beam quality and reliability. Here, we propose a beam diagnostic technique for measuring lateral beam sizes with a few-μm resolution by applying a state-of-art single-photon camera to coherent synchrotron radiation that affords by a sub-femtosecond short bunch-length property. A sophisticated image processing algorithm enables the technique down to 5 photons/pixel for the visibility of 0.132. Results show the potential of the proposed system that achieves precise retrieval of the complex degree of coherence at an extremely low photon intensity similar to those expected towards the plasma-acceleration injectors.
Similar content being viewed by others
Introduction
Over the past decades, a compact accelerator using extremely high-gradient electric-field in an accelerating plasma cavity induced by a high-power laser or electron beams has been devised1,2,3 and actively studied4,5,6,7,8,9,10,11,12,13 for generating charged-particle beams stably with ultra-low-emittances in 6D phase space, and it demonstrates noticeable advances for dramatically improving the synchronization14 and the quality of the witness beam15,16 in laser-wakefield acceleration scenarios with external injection17,18,19. These achievements have been in the spotlight as a key technology for a low-energy and high-quality injector in lieu of or even superseding, a low repetition-rate injector based on conventional technology20,21. Recently, there is a global effort such as cSTART22, FLASHForward23, and Athenae24,25,26 projects aimed at designing a compact accelerator for exploiting plasma-wakefield acceleration technique as an injector of future large-scale accelerator-driven light sources. These novel injectors can generate electron beams with an extremely low-emittance on the order of γϵx,y = 0.05 mm-mrad for pC to sub-pC bunch charge levels at repetition rates of 10 Hz.
For the plasma-wakefield injectors, various techniques exist for measuring electron density distribution using an invasive manner based on a scintillating screen27,28 since, due to low repetition rates and low bunch-charge, the intensity of incoherent synchrotron radiation (ISR) generated at a bending magnet is insufficient for applying synchrotron radiation-based diagnostics. For instance, the estimated photon flux at the detector by ISR for the Athenae beam parameters is about 2.5 × 103 photons/s with a bandwidth of 105 nm, which is nine orders of magnitude lower than photon flux in third-generation medium-energy storage rings. However, these destructive monitors are not appropriate for such prospective applications that require electron beams continuously. The development of non-invasive diagnostics for measuring lateral beam sizes has been a long-standing and crucial challenge. Particularly, for commissioning and performance verification of the novel injector, it highly demands a spatial resolution of a few micrometers, which is necessary for measurements of lateral beam sizes of about 10 μm that corresponds to a betatron function βx,y of 1 m with the emittances listed in Table 1. A few-μm spatial resolution is only feasible by taking a profile detection methodology into a diffraction regime (interferometric technique). In general, this method, however, is not suitable for plasma-wakefield injectors because this technique requires essentially obstacles such as a double-slit, polarizer, and wavelength filter, which reduces the photon intensity by additional two orders of magnitude.
In this paper, we propose and demonstrate a non-invasive experimental methodology that enables determinations of absolute lateral size of high-quality beams at an extremely low intensity. This is only attainable with a few μm resolution by applying the interferometry technique on coherent synchrotron radiation (CSR). A sub-femtosecond short bunch-length in the plasma-wakefield accelerator offers a unique opportunity to gain prominent photon flux at the visible region by overwhelming the form factor limit \({\sigma }_{z} < \lambda /\sqrt{2}\pi\). The photon flux generated by the coherent nature is proportional to the square of the number of electrons so that, taking into account the obstacles with a bandwidth of 105 nm, the photon flux becomes 5.4 × 107 photons/s for the Athenae beams. This photon flux is not sufficient for precision phase retrieval of the interferometry patterns with conventional detectors that has a few e− noises per pixel, but it was overcome by utilizing a dedicated images processing algorithm and a state-of-the-art of single-photon camera. These two ideas enable the measurement of lateral beam sizes with a resolution of a few micrometers at an ever lower photon intensity. The goal of this project is to push the limits for the interferometric beam size monitor (IBSM) scheme in the low-intensity regime. The context for the present case study is the application of the scheme at plasma-driven electron injectors operating at low intensity and with extremely short electron pulses.
Results
The major beam parameters for the plasma-accelerator-based injectors relevant to our case study are listed in Table 1.
Figure 1 shows the setup of the IBSM diagnostics for a plasma-wakefield accelerator schematically. Synchrotron radiation from a bending magnet is guided to the beam diagnostics system and illuminates a double-slit to produce diffraction fringes. The diffraction fringes are imaged onto a camera by an objective lens. The location of the diagnostics is determined to be close to the incident angle of the electron beam to mitigate bunch lengthening effects caused by energy-dependent path difference (R56) in a bending magnet. With an acceptance of the beamline, order of ten of milliradian, the R56 is less than 0.004 fs/%. The light passes through a polarizer owing to σ- and π-polarization properties of synchrotron radiation, and a wavelength filter, as the spatial frequencies change with the wavelength, for obtaining an interference pattern close to a monochromatic polarized-ray.
The laser beam is separated by an electron-transparent mirror and is transferred to the laser diagnostics beamline to monitor the stability of the plasma. Electrons are guided to the user beamline by a bending magnet and synchrotron radiation is emitted perpendicular to the path in the magnet. The location of the diagnostics is determined to close to the incident angle of the electron beam by considering the bunch lengthening effect within the magnetic field of the bending magnet.
Photon intensity estimation and numerical simulations
The intensity distribution by a double-slit is found to be by using the basic theory of spatial coherence of light and the van Cittert–Zernike theorem which the Fourier transform of the intensity distribution function of a distant, incoherent source is equal to its complex degree of spatial coherence (also known as interferometric visibility) under certain conditions. Assuming a Gaussian distribution of a light source, the intensity distribution of photons at a screen with an objective lens can be presented for monochromatic light (see “Methods” for more details):
where I1 and I2 are the photon intensity at two holes, respectively, wx and wy are the slit opening in horizontal and vertical directions, and γ12 is the visibility (complex degree of spatial coherence), f is the focal length of the objective lens, Dx is the slit separation, ϕ represents the phase differences between the two incident waves, and I0 denotes the constant offset that is a preset value for a detector to compensate for negative values owing to random noise. For a Gaussian distributed source, when the photon intensity at two holes is identical, the absolute value of the complex degree of coherence can furthermore be simplified as
where σ is the rms beam size. This relation allows determining the absolute beam size directly. Because of its advantages of spatial high-resolution as well as simplicity, this technique is widely adopted for synchrotron radiation sources to measure the lateral beam size29,30,31,32,33,34. Furthermore, the technique has been advanced to retrieve electron-beam distribution in real spaces by applying an inverse-Fourier transformation of the complex degree of coherence35,36, to measure absolute beam sizes in the horizontal and vertical directions simultaneously by implementing a quadrature slit37,38, and to reconstruct the two-dimensional profile of transversely coupled beams by scanning the beam size over a 2π angle in the perpendicular plane to the beam axis39,40.
At low intensity, it is crucial to evaluate the influence of detector characteristics carefully such as nonlinear behavior determined by the complex phenomena of quantum efficiency and total noise because the resolution of the beam size measurement using the IBSM diagnostics relies on not only the detection precision of the intensity variation over the whole interferometry fringes but also the accurate measurements of amplitudes at global maximum and its neighboring minimum. The ratio of the amplitudes at two positions represents the modulus of the complex degree of spatial coherence. The total noise is given by the square root of the sum of the squares of shot noise Nshot, dark current noise Ndc, and readout noise Nr. Specifically, at low photon numbers, an intensified charge-coupled device and electron-multiplying charge-coupled device are commonly used but the intensifying mechanism generates a stochastic variation of the multiplied electron yield. Therefore, data acquisition with these devices has inevitable distortion of absolute quantity measurement to a specific single-photon signature. This effect also leads to an effective photon-number reduction as well41. We adopt the contemporary state-of-art single-photon scientific complementary metal–oxide–semiconductor (sCMOS) cameras from Hamamatsu (Orca-Fusion, QE = 80%, a dark current noise Ndc of 0.5 e−/pixel/s, and a readout noise Nr of 0.7 e−/pixel) and Teledyne (Prime BSI camera, QE = 95%, a dark current noise Ndc of 0.5 e−/pixel/s, and a readout noise Nr of 1.1 e−/pixel) and performed Monte-Carlo simulations with two specs to evaluate the effect of the quantum efficiency and total noise to the IBSM technique and to define the operating limit. The numerical simulation includes photon shot-noise which is caused by statistical quantum fluctuations and can be modeled by a Poisson process (see Methods for more details). The simulation results show that the higher quantum efficiency yields a better signal-to-noise (S/N) ratio when the intensity is greater than 5 photons/pixel. The Prime BSI camera was finally selected by the high quantum efficiency with a tolerable noise level. It also features pattern noise reduction technology and correlated noise reduction technology to ensure that it delivers clean, pattern-free images with minimal pixel defects, delivering improved image quality in low light conditions. The operating limit of the IBSM technique using the single-photon camera is about 5 photons/pixel at the peak, which corresponds to a S/N ratio of about 4. This is equivalent to a total flux of 2 × 104 photons/s that can be achieved at the cSTART injector by ISR and Athenae by CSR with a slit opening of 9 mm2 but it is relying on experimental settings.
To estimate the photon flux by ISR and CSR for two cases of the plasma-wakefield accelerator precisely, a numerical simulation is performed using SPECTRA code42 with beam parameters of Athenae and cSTART. Statistical errors in the visibility determination as a function of photon flux and the required bunch length to achieve the photon flux are investigated at various filter bandwidths. The resolution of this technique is determined by errors in the system such as noise of a camera, dispersion in a refractive lens, and the effect of bandwidth. The dispersion in a lens can be vanished by replacing the refractive optics with reflective optics (focusing mirrors). The effects of the camera noise and bandwidth were investigated by numerical simulations to estimate the spatial resolution of the system. Images were generated based on Monte-Carlo simulations (see “Methods”) and each image was analyzed based on least-square fitting using an analytical formula derived for Gaussian distribution (Eq. (1)).
Figure 2 evidences that taking the diminution of photon flux by the obstacles into account, the photon flux by ISR at the detector is 3.4 × 103 photons/s for the Athenae and 2.9 × 104 photons/s for the cSTART. For the cSTART, due to a high bunch charge of 27.5 pC, the photon flux by ISR is much greater than the operating limit with a bandwidth of 105 nm. The photon flux for the Athenae is lower than the operating limit of our scheme, ~2 × 104 photons/s, defined by the numerical simulation with the total noise and quantum efficiency of the camera. However, it can be enhanced by CSR generated by a shorter bunch with a length of 1.0 fs for a bandwidth of 50 nm and 1.04 fs for a bandwidth of 105 nm. Furthermore, from the statistical error analysis, the error of the visibility retrieval at the low intensity is smaller than 3.6% at the operating limit with a bandwidth of 105 nm. The error transfer from relative visibility retrieval error (\(\left|{{\Delta }}\gamma /\gamma \right|\)) to spatial resolution (Δσ) is calculated according to the following equation: \({{\Delta }}\sigma =\lambda L/(2\pi D\sqrt{2{{{{{{\mathrm{ln}}}}}}}\,\left|1/\gamma \right|})\times \left|{{\Delta }}\gamma /\gamma \right|\), resulting in a spatial resolution of fewer than 1 μm. It can be improved significantly by narrowing the bandwidth of the wavelength filter. The beam size is underestimated for the lower visibility region, while an overestimation is observed for the higher visibility region, it is precisely retrieved for the visibility of 0.47–0.69 since the error is relevant to the absolute visibility value as well as the photon intensity (see the Supplementary Note 1). This agrees well with analytical evaluations for suppressing systematic errors toward small beam size measurements43. Since the visibility not only depends on a beam size but also the set up in a beamline such as a slit separation, distance from the source point, and central wavelength, the slit separation and wavelength, therefore, should be defined carefully to stand the absolute visibility value within 0.4–0.7 at low intensity with the bandwidth as narrow as possible. For example, visibility of 0.69 can be achieved for a beam size of 11 μm with a wavelength of 550 nm, a distance of 1.5 m, and a slit separation of 10 mm. In addition, the monitor could achieve a high resolution with a bandwidth of the wavelength filter of up to 105 nm that increases the total intensity at the detector because the deterioration of the visibility due to the phase shift by the finite bandwidth is negligible.
Statistical errors in the absolute visibility (\(\left|{\gamma }_{12}\right|\)) determination depend on photon flux which is dominated by the bunch length, bunch charge, and energy. The required bunch length to achieve the photon flux at the detector is calculated with a beam energy of 200 MeV for Athenae and 50 MeV for cSTART, a bunch charge of 0.38 pC for Athenae and 27.5 pC for cSTART, and a repetition rate of 10 Hz. The photon flux by CSR and ISR is calculated using SPECTRA code with a bunch charge of the lower case (0.38 pC) in Athenae, and a magnetic field of 0.85 T in the bending magnet, and a slit opening of 3 × 3 mm2 including obstacles such as the double-slit and the optical wavelength filter. The photon flux is defined as the number of photons per second (ph/s) at the detector.
Image processing algorithm
The number of photons per pixel is comparable to the statistical noise, which results in a distortion of the intensity information due to a nonlinear response. The statistical noise causes dilution of the interferometry fringes, so it deteriorates the accuracy of the visibility retrieval. It highly demands a sophisticated method for rejecting the noise appositely to gauge the small beam size accurately since the imprecise discrimination of the noise by using a smooth speckle filtering technique leads to misleading of the visibility, resulting in intolerant stochastic error. We developed a robust algorithm to yield the correct visibility value by suppressing the influence of the noise using advanced filtering technique, Savitzky–Golay filter, that is achieved, in a process known as convolution, by fitting successive subsets of adjacent data points with a low-degree polynomial by the method of linear least squares. The flowchart of the algorithm is elaborated in Fig. 3.
The algorithm features a preprocessing procedure using a reference image taken at a high intensity and automatic detection of the window sizes for projection and Savitzky–Golay filter. In the preprocessing, after removing speckle noise by applying 2D median filtering to the reference image, the contour line was detected at points greater than 90% of the peak intensity, and the rotation angle was calculated by a least-square fitting using an ellipse function. The calculated angle is stored in a processing parameter and is reflected for the rotational transformation. This process enables precise correction of a rotational error that can be occurred by comatic aberration and misalignment of the camera and leads to the distortion of the visibility during the image projection. For beam experiments at plasma accelerators, the reference image can be taken by increasing the exposure time of the camera since the signal level is linearly proportional to exposure time, but the noise intensity increases by only 0.5 e−/s, resulting in an increase in the S/N ratio that improves the clearness of an image. Following the angle correction, the code detects the intensity variation in a perpendicular direction to the double-slit interferometry pattern to determine the appropriate projection window size, which is an assured step to improve the S/N ratio. The projection window was determined by the FWHM of the peak when peak intensity is greater than 10 photons, and in other cases, it was determined by the width at 90 % of peak intensity. We observed that the 1-D intensity profile obtained through the projection is still distorted by statistical noise. Two different filtering techniques, median filter, and Savitzky–Golay filter are tested (see Supplementary Note 2). The median filter, however, dilutes beam signals although this vanishes high-frequency noise well since it replaces each entry with the median of neighboring entries. Then we adopt Savitzky–Golay filter that is capable of eliminating the noise while minimizing distortion of signals. This algorithm automatically defines the cutoff frequency of the filter by twice the frequency of the signal identified by Fourier analysis. We tested the code with an artificial image generated by the Monte-Carlo method to verify the reliability and the result shows quantitative consistency with the preset values.
Experimental setup
This technique was implemented and experimentally demonstrated at the infrared (IR) beamline44 of the metrology light source (MLS) of the Physikalisch-Technische Bundesanstalt in Berlin. The MLS is a low-energy compact storage ring dedicated to metrology science in EUV, VUV, and UV and researches up to the FIR/ THz spectral range45,46. The standard operating mode of the ring typically stores electron beams with an energy of 629 meV and the beam current usually decays from 200 to 80 mA in a time interval of 6 h47,48. The IR beamline is connected to a bending magnet and equipped with two plane mirrors, two cylindrical mirrors, and one parabolic mirror to collimate the visible to IR light to the experimental stand. The schematic layout of the beamline is shown in Fig. 4.
The photon flux of synchrotron radiation at the beamline was measured experimentally using a precise photon-power detector (Si Photo-diode with reflective ND (OD2) surface coating, S130C from Thorlabs) that has a resolution of 100 pW (3.78 × 108 photons/s) with an operating range of 500 pW to 5 mW. The measured flux is 1011 photons/s at a central wavelength of 750 nm with a bandwidth of 10 nm (FWHM). Our system was installed inside an enclosure to prevent background noise by ambient light around the experimental stand. The background noise was suppressed to 0.41 % of the signal level. Since the photon intensity is reduced at the double-slit by two orders of magnitude and the polarizer by 20%, additional photon intensity retrenchment by five orders of magnitude is necessary for approaching the operating limit regime. Absorptive neutral density (ND) filters have been used to reduce the photon intensity further. Since the transmission rate of the ND filter depends on a wavelength, it is verified quantitatively at the target wavelength with a precision of 3%. Due to the manipulation of the angular distribution of synchrotron radiation by the focusing mirrors installed upstream of the beamline, direct conversion of the visibility to the beam size is not feasible. But the optical ray-transfer matrix allows the retrieval of the angular distribution of radiation from the beamline to be reinterpreted as a state at the upstream without distortion. Due to the focusing mirror, our experiments were conducted at a wavelength of 750 nm with a slit separation of 1 mm and various focal lengths and slit openings although shorter wavelength and wider slit separation are appropriate for small beam size measurements. The maximum visibility value that can be implemented in experimental control variables is 0.132.
Interpretation of experimental data
Figure 5a–d shows the resulting IBSM images measured at the weakest operational intensity for various focal lengths and slit sizes. The slit opening and the focal length of the lens modify the lateral size of the interferometry fringe and it dominates the spatial photon density, which is the most substantial parameter for the measurement at low intensity. For instance, the slit opening from 2 mm (Fig. 5c) to 10 mm (Fig. 5d) gains the photon density increase by a factor of 2.4 roughly. This can be interpreted by the Sinc term in Eq. (1), which determines the width of the interferometric pattern. The wide slit-opening also not only increases the number of photons passing through the slit but also reduces the width of the central diffraction maximum that is inversely proportional to the width of the slit, increasing the spatial density of the final image. The focal length (Fig. 5a–c) also manipulates the photon density by a magnification of the image. However, this also deteriorates the resolution of the monitor since the number of the measurement point within the period of the spatial oscillation of the interferometric intensity is limited due to the finite size of the camera pixel although these parameters allow exploiting the technique at low intensity. From all the analysis results, these results have proven that a minimum of 5 photons at the peak is required for visibility of 0.132 to reconstruct the interferometry fringes properly. It corresponds to an S/N ratio of about 4 at the peak and an S/N ratio of about 3 at the neighboring minimum. The criteria are consistent quantitatively with the numerical simulation. The IBSM diagnostics with a single-photon camera and dedicated image-processing algorithm is capable of retrieving the visibility at a photon intensity of ~2.9 × 104 photons reliably. Considering that the camera has a quantum efficiency of about 95 % in the 550–600 nm range, but decreases to about 75% at 750 nm wavelength, the practical number of photons in the image can be translated to 2.3 × 104 photons, which is close to the operating limit, 2 × 104 photons, estimated by numerical simulations. Furthermore, the operating limit in our experiment with a 10 cm focal length lens can be reduced further when a slit opening in the horizontal direction is increased to 10 mm since the photon density at the imaging plane is inversely proportional to the square of the focal length of the lens and proportional to the square root of the slit opening approximately. Apart from this, it is recommended to start experiments with as wide an opening in a perpendicular direction as possible because the number of photons that pass the slit will linearly increase by the wider opening.
Interferometry images are measured at minimum measurable intensity using a focusing lens with a focal length f of a 10 cm (2.9 × 104 photons), b 25 cm (1.8 × 105 photons), and c 50 cm (8.1 × 105 photons) with slit opening of 2 mm (horizontally) × 0.5 mm (vertically) and d a focal length of 50 cm with slit opening of 10 mm (horizontally) × 0.5 mm (vertically) (3.4 × 105 photons). e Results of the measured absolute visibility (\(\left|{\gamma }_{12}\right|\)) at various intensities. The gray line represents the beam size measured by a director source size monitor. The error bar of each data point represents a statistical error estimated by analyzing multiple image samples and one standard deviation from the mean. Taking into account a quantum efficiency of the camera of about 75 % at 750 nm wavelength, the photon flux at the lowermost intensity is about 2.3 × 104 photons per second (ph/s).
Conclusion
In this study, we have proposed and demonstrated an experimental method for measuring an absolute lateral size of low-energy and high-quality beams generated by plasma-wakefield accelerators. Due to a low average beam-current of these accelerators that results in a lack of the photon intensity by synchrotron radiation, so this does call for research and development for high spatial-resolution diagnostics that can be operated at a low photon intensity. It is inevitable towards the commissioning and continuous operation. We proposed to exploit a visible-light interferometric technique on strong CSR, which appears when the wavelength of the emitted radiation is significantly longer than the particle bunch length. In the plasma-wakefield accelerator, the sub-femtosecond short bunch property produces the CSR on a visible regime and it offers numerous gains of photon intensity compared to the ISR. This enables the implementation of the interferometric technique that can achieve a few-μm spatial resolution. Particularly, we developed such a system with the single-photon sCMOS camera and the sophisticated analysis algorithm that enables a robust measurement at an extremely low intensity. This was validated by beam experiments at the IR beamline of MLS. The substantial parameters such as the focal length of the lens and slit opening, which determine the spatial density of the photons on the image plane were also investigated at the photon intensity level of 104. The intensity is close to an S/N ratio of about 4 at the peak and about 3 at the neighboring minimum for visibility of 0.132 and it agrees well with the theoretical limit defined by the Monte-Carlo simulation. The results have proven that our technique can be used on a bunch charge of 0.38 pC with a length of about 1 fs of Athenae, and for cSTART, measurements can also be performed by ISR due to a higher bunch charge. Furthermore, this diagnostics can be operated as a direct source monitor by removing the double-slit, and the expected resolution by diffraction, which is called Abbe-limit, is about 80 μm. This leads to the operating limit being lower by two orders of magnitude, in turn, this is capable of the measurement of spatial beam distribution in Athenae with ISR. In addition, this can observe the orbit perturbation by measuring the phase variation of the interferometer fringes which is given by (2πDxΔx)/(λL), where Δx denotes the offset of the slit separation. The resolution of the phase-detection is better than π/20 that corresponds to 1.38 μm, for a slit separation of 15 mm, a wavelength of 550 nm, a distance from the source of 1.5 m, and a focal length of the focusing lens of 10 cm, which defines the number of points in the data (see the Supplementary Note 3).
Methods
Interferometry beam size monitor
An Interferometry Beam Size Monitor (IBSM) adapts Young’s double-slit interferometry techniques. When incident waves are in phase at two holes which is a case for a point-like source, minima of the interference fringe produced by a double-slit become zero because the relative phase changes along the observation plane are out of phase for half a cycle, i.e., the amplitude at the observation plane is canceled each other out completely (destructive interference) owing to the phase changes caused by the difference of traveling distance between the two waves from the two holes. However, for synchrotron radiation which has a finite spatial distribution of the source, two photons emitted from one electron travel different paths, which results in differences in the phase at the slit owing to off-centered electron beams with respect to the slit. The phase changes produce the complex degree of spatial coherence γ12 that quantifies the contrast of interferences. The intensity distribution of the interferometry fringes by a double-slit with a finite source size is given by49,50
where E1 and E2 denote the two modes of one photon emitted simultaneously from one point source, observed at \(\overrightarrow{{{{{{{{{\bf{r}}}}}}}}}_{1}}\) at a time t1 and at \(\overrightarrow{{{{{{{{{\bf{r}}}}}}}}}_{2}}\) at a time t2, respectively, and τ = t2 − t1. The complex degree of coherence for the source with a finite spatial distribution can be expressed as51,52
where νx = Δx/λL and νy = Δy/λL are the spatial frequencies, λ is the wavelength, L is the distance between the source and the slit, and f(x, y) is the two-dimensional distribution of the source point.
Monte-Carlo simulations
The Monte-Carlo method is computational algorithms that rely on repeated random sampling to obtain numerical results for a specific probability density function. This is useful for simulating systems with many coupled degrees of freedom including modeling phenomena with significant uncertainty in inputs. For the simulations in this study, the arrival position of each photon at the detector is simulated according to the diffraction of individual photons at the double slit. The Monte-Carlo technique is used to allocate an initial position to each photon following a Gaussian distribution in both horizontal and vertical directions. In the same way, each photon is randomly allocated a wavelength following a uniform distribution with a central wavelength of a filter. Based on the generated particle distribution, the artificial image was generated by counting the number of particles within the finite size of the pixel and adding the Poisson noise onto each pixel. Fifty artificial images were generated for each intensity and these were analyzed by the image processing algorithm to estimate the statistical fluctuation of the visibility retrieval (see Supplementary Note 1).
Intensity estimation of driver Laser at the detector
The laser beam is separated by the electron-transparent mirror that has a hole in the middle through. This leads to a leak of the fractional laser power to the diagnostics beamline. However, the leaked power can be mitigated by a factor of 2.1 × 103 using the mirror, by a factor of 3 × 102–9 × 103 using the double-slit, and by a factor of 108–1010 using a dual-wavelength filter. For 100 TW/Hz lasers, the number of photons by the laser beam obtained by conservative estimations yields approximately 24 photons in the detector. If it is crucial in experiments, a few notch filters can be placed in front of the slit and polarizer to suppress the laser light further. The central wavelength of the filter is typically optimized to achieve a higher photon yield at the camera that the quantum efficiency has a peak value around 500–650 nm. Even a central wavelength of 650 nm with a bandwidth of 100 nm (650 ± 50 nm) is not overlapped with the driver laser wavelength (800 nm). A notch filter can suppress the laser intensity by a factor of 105 per filter.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Veksler, V. I. Coherent principle of acceleration of charged particles. Paper presented at the CERN Symposium on High Energy Accelerators and Pion Physics, pp. 80 (1956).
Tajima, T. & Dawson, J. M. Laser electron accelerator. Phys. Rev. Lett. 43, 267 (1979).
Chen, P., Dawson, J. M., Huff, R. W. & Katsouleas, T. Acceleration of electrons by the interaction of a bunched electron beam with a plasma. Phys. Rev. Lett. 54, 693 (1985).
Everett, M. et al. Trapped electron acceleration by a laser-driven relativistic plasma wave. Nature 368, 527 (1994).
Amiranoff, F. et al. Observation of laser wakefield acceleration of electrons. Phys. Rev. Lett. 81, 995 (1998).
Leemans, W. P. et al. GeV electron beams from a centimetre-scale accelerator. Nat. Phys. 2, 696 (2006).
Blumenfeld, I. et al. Energy doubling of 42 GeV electrons in a metre-scale plasma wakefield accelerator. Nature 445, 741 (2007).
Buck, A. et al. Shock-Front injector for high-quality laser-plasma acceleration. Phys. Rev. Lett. 110, 185006 (2013).
Wang, X. et al. Quasi-monienergetic laser-plasma acceleration of electrons to 2 GeV. Nat. Commun. 4, 1988 (2013).
Leemans, W. P. et al. Multi-GeV electron beams from capillary-discharged-guided subpetawatt laser pulses in the self-trapping regime. Phys. Rev. Lett. 113, 245002 (2014).
Litos, M. et al. High efficiency acceleration of an electron beam in a plasma wakefield accelerator. Nature 515, 92 (2014).
Thaury, C. et al. Shock assisted ionization injection in laser-plasma accelerators. Sci. Rep. 5, 16310 (2015).
Corde, S. et al. High-field plasma acceleration in a high-ionization-potential gas. Nat. Commun. 7, 11898 (2016).
Ferran Pousa, A., Assmann, R., Brinkmann, R. & MartinezdelaOssa, A. External injection into a laser-driven plasma accelerator with sub-femtosecond timing jitter. J. Phys. 874, 012032 (2017).
Ferran Pousa, A. F., Martinez de la Ossa, A. & Assmann, R. Intrinsic energy spread and bunch length growth in plasma-based accelerators due to betatron motion. Sci. Rep. 9, 17690 (2019).
Ferran Pousa, A. F., Martinez de la Ossa, A., Brinkmann, R. & Assmann, R. Compact multistage plasma-based accelerator design for correlated energy spread compensation. Phys. Rev. Lett. 123, 054801 (2019).
Svystun, E. et al. Beam quality preservation studies in a laser-plasma accelerator with external injection for EuPRAXIA. Nucl. Inst. Methods A 909, 90 (2018).
Svystun, E. N. et al. Two-stage laser-driven plasma acceleration with external injection for EuPRAXIA. J. Phys. 1067, 042011 (2018).
Couperus, J. P. et al. Demonstration of a beam loaded nanocoulomb-class laser wakefield accelerator. Nat. Commun. 8, 487 (2017).
Hillenbrand, S. et al. Study of laser Wakefield accelerators as injectors for synchrotron light sources. Nucl. Inst. Methods A 740, 153 (2014).
Shalloo, R. J. et al. Automation and control of laser wakefield accelerators using Bayesian optimization. Nat. Commun. 11, 6355 (2020).
Härer, B. et al. Non-Linear Features of the cSTART Project. Paper presented at the 10th International Particle Accelerator Conference. Proc. IPAC’19, TUPGW020, Melbourne, Australia (2019).
D’Arcy, R. et al. FLASHForward: plasma wakefield accelerator science for high-average-power applications. Philos. Trans. R. Soc. A 377, 20180392 (2019).
Marchetti, B. et al. Technical Design Considerations about the SINBAD-ARES linac. Paper presented at the 7th International Particle Accelerator Conference. Proc. IPAC’16, MOPMB015, Busan, Korea (2016).
Marchetti, B., Assmann, R., Dorda, U. & Zhu, J. Conceptual and technical design aspects of accelerators for external injection in LWFA. Appl. Sci. 8, 757 (2018).
Svystun, E. N., Assmann, R., Dorda, U., Marchetti, B. & Martinez de la Ossa, A. Numerical studies on electron beam quality optimization in a laser-driven plasma accelerator with external injection at SINBAD for ATHENAe. J. Phys. 1350, 012058 (2019).
Downer, M. C., Zgadzaj, R., Debus, A., Schramm, U. & Kaluza, M. C. Diagnostics for plasma-based electron accelerators. Rev. Mod. Phys. 90, 035002 (2018).
Schröder, S. et al. High-resolution sampling of beam-driven plasma wakefields. Nat. Commun. 11, 5984 (2020).
Ye, K. R. et al. Synchrotron radiation monitor and mirror at SSRF. Paper presented at the 9th European Workshop on Beam Diagnostics and Instrumentation for Particle Accelerators. Proc. DIPAC’09, TUPD37, Basel, Switzerland (2009).
Corbett, J. et al. Interferometer beam size measurements in SPEAR3. Paper presented at the 23rd Particle Accelerator Conference. Proc. PAC’09, TH6REP033, Vancouver, BC, Canada (2009).
Ryu, J. et al. Beam-size measurements by using a synchrotron radiation interferometer. J. Korean Phy. Soc. 58, 35 (2011).
Wang, S. T. et al. Visible-light beam size monitors using synchrotron radiation at CESR. Nucl. Inst. Methods A 703, 80 (2012).
Torino, L., Iriso, U. & Mitsuhashi, T. Beam size measurements using synchrotron radiation interferometry at ALBA. Paper presented at the 3rd International Beam Instrumentation Conference. Proc. IBIC’14, TUPF23, Monterey, CA, USA (2014).
Koopmans, M. et al. Status of a double slit interferometer for transverse beam size measurements at BESSY II. Paper presented at the 8th International Particle Accelerator Conference. Proc. IPAC’17, MOPAB032, Copenhagen, Denmark, Canada (2017).
Mitsuhashi, T. Spatial coherency of the synchrotron radiation at the visible light region and its application for the electron beam profile measurement. Paper presented at the 1997 Particle Accelerator Conference. Proc. PAC’97, pp. 766, Vancouver, BC, Canada (1997).
Parc, Y. W., Kim, C., Huang, J. Y. & Ko, I. S. Reconstruction of electon beam distribution using phase-retrieval algorithm. J. Synchrotron Radiat. 18, 436 (2011).
Kim, C. et al. Two-dimensional SR Interferometer for PLS-II. J. Korean Phy. Soc. 58, 725 (2011).
Trad, G. et al. Beam size measurements using interferometry at LHC. Paper presented at the 5th International Beam Instrumentation Conference. Proc. IBIC’16, WEBL02, Barcelona, Spain (2016).
Torino, L. & Iriso, U. Transverse beam profile reconstruction using synchrotron radiation interferometry. Phys. Rev. Accel. Beams 19, 122801 (2016).
Koopmans, M. et al. Applications of the interferometric beam size monitor at BESSY II. Paper presented at the 9th International Particle Accelerator Conference. Proc. IPAC’18, WEPAK009, Vancouver, BC, Canada (2018).
Schiwietz, G., Hwang, J.-G., Jankowiak, A., Koopmans, M. & Ries, M. Bunch-resolved diagnostics for a future electron-storage ring. Nucl. Inst. Methods A 990, 164992 (2021).
Tanaka, T. & Kitamura, H. SPECTRA: a synchrotron radiation calculation code. J. Synchrotron Radiat. 8, 1221 (2001).
Naito, T. & Mitsuhashi, T. Very small beam-size measurement by a reflective synchrotron radiation interferometer. Phys. Rev. ST Accel. Beams 9, 122802 (2006).
Müller, R. et al. Planned infrared beamlines at the metrology light source of PTB. Infrared Phys. Technol. 49, 161 (2006).
Klein, R. et al. Operation of the metrology light source as a primary radiation source standard. Phys. Rev. ST Accel. Beams 11, 110701 (2008).
Beckhoff, B. et al. A quarter-century of metrology using synchrotron radiation by PTB in Berlin. Phys. Status Solidi B 246, 1415 (2009).
Feikes, J. et al. Metrology light source: the first electron storage ring optimized for generating coherent THz radiation. Phys. Rev. Spec. Top. Accel. Beams 14, 030705 (2011).
Ries, M. Nonlinear Momentum Compaction and Coherent Synchrotron Radiation at the Metrology Light Source. PhD thesis. (Humboldt University of Berlin, 2014).
Mitsuhashi, T. Beam profile and size measurement by SR interferometers. In Beam measurement. Presented at Joint US-CERN-Japan-Russia School on Particle Accelerators, Montreux and Geneva, Switzerland, May 11–20, pp. 399 (1998).
Koopmans, M. Interferometric Beam Size Monitor for BESSY II. Master dissertation. (Humboldt-Universität zu Berlin, 2017).
Mitsuhashi, T. Spatial coherency of the synchrotron radiation at the visible light region and its application for the electron beam profile measurement. Conf. Proc. C 970512, 766 (1997).
Mitsuhashi, T. Beam profile and size measurement by SR interferometers. in (ed Kurokawa, S. et al.) Beam Measurements 399–427 (World Scientific, 1999).
Acknowledgements
We wish to express their gratitude to Prof. Gregor Schiwietz in Helmholtz-Zentrum Berlin for his valuable discussion. This work was supported by the German Bundesministerium für Bildung und Forschung, Land Berlin and Athena grants by the Helmholtz Association.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
J.-G.H. conceived the proposed scheme and J.-G.H. and B.A. performed the numerical simulations. J.-G.H., K.A. and A.H. performed beam experiments at MLS. J.-G.H., K.A., B.A. and T.K. analysed the results of numerical simulations and beam experiments. All authors reviewed the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Physics thanks Nicolas Delerue and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hwang, JG., Albrecht, K., Hoehl, A. et al. Monitoring the size of low-intensity beams at plasma-wakefield accelerators using high-resolution interferometry. Commun Phys 4, 214 (2021). https://doi.org/10.1038/s42005-021-00717-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00717-x
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.