Abstract
Relativistically moving dielectric perturbations can be used to manipulate light in new and exciting ways beyond the capabilities of traditional nonlinear optics. Adiabatic interaction with the moving front modulates the wave simultaneously in both space and time, and manifests a front-induced transition in both wave vector and frequency yielding exotic effects including non-reciprocity and time-reversal. Here we introduce a technique called SLIPSTREAM, Spacetime Light-Induced Photonic STRucturEs for Advanced Manipulation, based on the creation of relativistic fronts in a semiconductor-filled planar waveguide by photoexcitation of mobile charge carriers. In this work, we demonstrate the capabilities of SLIPSTREAM for the manipulation of terahertz (THz) light pulses through relativistic front-induced transitions. In the sub-luminal front velocity regime, we generate temporally stretched THz waveforms, with a quasi-static field lasting for several picoseconds tunable with the front interaction distance. In the super-luminal regime, the carrier front outpaces the THz pulse and a time-reversal operation is performed via a front-induced intra-band transition. We anticipate our platform will be a versatile tool for future applications in the THz spectral band requiring direct and advanced control of light at the sub-cycle level.
Similar content being viewed by others
Introduction
Light in the terahertz (THz) band, already immensely important for spectroscopy and imaging applications1, has been touted as a frontier for next generation high-speed wireless communications2,3,4. As with other spectral bands, the advancement of future THz technologies will be done in lockstep with the development of new methods for controlling the spatial and temporal properties of THz light5,6,7,8,9,10,11. While significant advances have been made on controlling the spatial evolution of THz waves with metasurfaces and wavefront engineering12,13,14,15, methods for actively controlling the temporal properties of THz light on the level of the electric field cycle are typically only possible through self-induced temporal phase modulation using intense THz pulses16,17,18,19,20,21,22,23,24. Only recently an arbitrary THz pulse shaper was introduced, employing a hybrid digital wave synthesis technique using light-induced structures in a waveguide25. Such planar waveguide approaches have the benefit of being amenable to chip-scale integration26.
Alternative approaches to nonlinear optics, however, draw on the concept of time-varying linear media introduced first by Morgenthaler7,11,27. These ideas were tested in experiments involving plasma physics via the rapid ionization of gases28 or sudden carrier injection through optical excitation in semiconductors29. Temporal modulation is attractive for wavelength conversion as it does not require nonlinear media or strong field interactions. Subsequently, several studies have emerged, focused on temporally modulated photonic crystals30,31 and cavities32,33 for wavelength conversion applications. The non-adiabatic modulation of meta-atoms was recently demonstrated as a means to achieve wavelength conversion in the THz band34. In addition, sub-cycle slicing using intense optical pulses illuminating semiconductor surfaces is also capable of pulse narrowing and spectral expansion in the THz band35,36.
Simultaneous control over the wavevector and frequency of light through combined spatial and temporal modulation can produce a variety of exotic photonic operations5,37,38. These spacetime, front-induced transitions can be used to time-reverse a light pulse,6,39,40, for example, which has important applications in dispersion compensation41 and imaging through random scattering media42. THz interactions with moving fronts were first investigated in pioneering experiments using photoexcitation in a semiconductor to create an overdense, reflective plasma interaction that is counter-propagating with the incoming THz wave. Considerable spectral broadening was observed via relativistic Doppler shifts43,44,45.
Here, we introduce SLIPSTREAM, Spacetime Light-Induced Photonic STRucturEs for Advanced Manipulation, for exploring front-induced transitions in the THz band. The SLIPSTREAM technique is based on the same compact platform for spatio-temporal manipulation we have previously introduced, capable of performing a range of photonic operations including pulse steering46, mode control47, spectral shaping48, arbitrary pulse shaping25, and phase control49. As shown schematically in Fig. 1a, a parallel plate waveguide (PPWG) supporting dispersionless, low loss, TEM THz propagation is formed by coating both sides of a d = 50-μm-thick high resistivity float zone silicon (ρ > 10,000 Ω cm) slab with optically transparent and conducting indium tin oxide (sheet resistance of 1 Ω/sq). The transparency of the ITO coatings allows optical excitation of the silicon through the top plate with a near-infrared (1035 nm, 190 fs, 30 μJ) pump pulse derived from a Yb:KGW amplified femtosecond laser system (Light Conversion, PHAROS). This excitation is close to the indirect band gap of Si, with pump penetration depths exceeding 100 μm, ensuring a homogeneous excitation across the Si slab. The pump pulse has its pulse front tilted using a diffraction grating, producing a linear gradient in the pump arrival time along the waveguide propagation axis. A portion of the NIR beam is split off to a CMOS camera to record the pump intensity spatial profile. Control over the pulse front tilt of optical pump pulses is routinely used to optimize phase-matching in THz generation schemes, notably via optical rectification in lithium niobate50,51, at semiconductor surfaces52, or in biased gapped microstrip lines53,54,55. We utilize the fact that as the pump pulse front illuminates the silicon, a moving front of photoinduced carrier density is created within the PPWG. With the SLIPSTREAM platform, our work takes the next step in the continuing proliferation of THz technology by engineering the speed and travel distance of moving dielectric perturbations in a silicon-filled parallel plate waveguide, leading to two unconventional photonic operations: the temporal stretching and time-reversal of THz pulses.
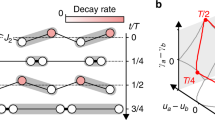
a Schematic of the SLIPSTREAM platform, generating and manipulating THz pulses using the injection of a near-infrared (NIR) pulse with a tilted intensity profile into a Si-filled parallel plate waveguide (PPWG). The velocity of the intensity front vf is set by the tilt angle relative to the THz velocity c/n, where c is the vacuum speed of light and n is the refractive index. b Symbolic construction of a THz plateau pulse by the space-time-delayed, ultrafast switching of static Schottky currents built into the top (Jtop) and bottom (Jbot) interfaces, shown in successive snapshots in time until the moving front has ended its travel at time t = T. c Measured THz transients typical of the sub-luminal, luminal and super-luminal regimes of front velocity for a maximal induced photocarrier density of approximately 5 × 1016 cm3, with d the corresponding spectra normalized to unity. e Integrated spectral power peaking for the luminal case due to synchronicity with the emission, maximizing the interaction with the moving front. Each datapoint is an average over several scans and is accompanied by the standard deviation, and arb. u. stands for arbitrary units.
Results and discussion
The photoexcitation of a moving front results in the emission of a phase-locked THz pulse within the waveguide that propagates in the TEM mode. Since no electrical bias is applied and the plates are grounded, the sole source of THz emission is due to transient currents created by built-in Schottky fields, oppositely oriented at the metal-semiconductor interfaces, upon arrival of the pump pulse at the top and bottom waveguide plates, as shown in Fig. 1b. Photoinjecting free carriers within the band bending regions at these interfaces leads to the transient currents Jtop(t, z) and Jbot(t−ζ, z) directed normal to the waveguide plates and temporally separated by the transit time of the NIR pump pulse ζ. These delayed and transient currents emit THz light in the same manner as an Auston switch, and similar to a continuous version of a segmented dc-to-ac radiation converter53,54,56,57,58,59,60,61. For an estimate of the NIR-to-THz power conversion efficiency, see the “Methods” section. Once coupled out of the PPWG, the THz emission is collected by an off-axis parabolic mirror with an effective focal length of 76.2 mm, and then detected by free-space electro-optic sampling in a 5-mm-thick (110) GaP crystal using a weak NIR detection pulse split off from the pump. Such a thick crystal is optimal for detecting the low-amplitude, low-frequency THz pulses we generate as it displays phase-matched response for frequencies below 2 THz, allowing sizeable coherent signal to build up62.
The emitted THz electric field transients, shown in Fig. 1c, depend critically on the pulse front velocity, vf, with respect to the THz TEM mode phase velocity c/nSi with refractive index nSi = 3.41863. The front velocity is continuously tunable from the sub-luminal to super-luminal regime with the femtosecond pump pulse front tilt angle. In the sub-luminal regime, vf < c/nSi, a THz plateau pulse is created with a stretch of quasi-dc electric field bookended by unipolar structure, shown in the top panel of Fig. 1c. The emitted THz waves escape the excitation front, which produces a superposition of linearly delayed single cycle pulses along the propagation axis. The result is a temporally stretched THz pulse, whose duration is tunable with front velocity and total propagation distance. Such pulses displaying quasi-static plateaus in their temporal electric field profile are new to the THz regime, but recently have been theoretically proposed64. At the luminal condition vf = c/nSi, the resultant THz pulse is of single cycle duration, as all emission points add in phase along the entire propagation axis. Tuning the front to the super-luminal regime vf = 1.5c/nSi, the pulse character remains single cycle but loses some high frequency components as the front overtakes the THz wave, and it experiences approximately homogeneous loss in the plasma, here with a plasma frequency ωp/2π ≈ 1 THz. This is verified by the Fourier amplitudes plotted in Fig. 1d, also wherein the sub-luminal data peaks at a low frequency of about 0.1 THz, reflecting its quasi-static form. The total integrated power of these pulses, normalized to the respective optical fluence used, is shown in Fig. 1e to peak at luminal velocity due to maximal interaction with the moving front. Each of these pulses were produced by similar excitations of about 1.6 ± 0.2 mm in width, with the exception of 1 mm width for the sub-luminal data in Fig. 1c. We observe no effect from any secondary emission events due to delayed, multiple reflections of the excitation pulse in the PPWG.
Stretching of the electric field cycle
In the sub-luminal regime, the duration of the THz field plateau is tunable with propagation length as shown in Fig. 2. Truncated carrier density profiles, calibrated from camera images and power measurements, are given in Fig. 2a with the subsequently measured THz pulses plotted in Fig. 2b. The positions of two sharp knife edges in the beam map directly to start tstart and stop times tend of the THz pulse, corresponding to the measured pulse arising from the leading and trailing edge of the carrier density front, respectively. Sliding either knife edge by Δz and measuring the pulse duration change Δt allows a precise calibration of the front velocity as described in the “Methods” section, which in this case yields a sub-luminal velocity of vf = 0.86c/nSi. The amplitude of the plateau follows the Gaussian profile of the NIR beam due to the linearity of field emission with the local current density.
a Carrier density profiles in the waveguide for different beam clippings of a sub-luminal front at vf = 0.86c/nSi, varying either its termination (top) or start position (bottom), where the vacuum speed of light is c and the refractive index in silicon is nSi. b Measured (solid and filled) and simulated (dashed) electric fields of the THz plateau pulses. Each curve is color-matched to an input pump profile from a, with red and blue fill indicating the positive and negative parts of the electric field, respectively.
Two-dimensional finite-difference time-domain (2D-FDTD) simulations were performed to further understand the influence of the moving front on the THz pulse waveforms. A perfectly conducting layer was chosen to bound the domain and Schottky fields were placed on the top and bottom extending into the silicon by the Debye length (about 1 μm). The dispersion of photoexcited silicon was modeled with a Drude form governed by the carrier density profiles in Fig. 2a which reach a maximum value of about 1017 cm−3 and a scattering time of τ = 0.1 ps65. The electric field of the emitted THz wave coupled to the TEM mode was extracted at a fixed position within the waveguide just outside the illuminated region, and a filter function was applied in order to approximate the experimental losses from the waveguide and detection response function66. The simulated THz pulses, shown in Fig. 2b agree well with the measured THz waveforms, qualitatively reproducing the variations in the plateau amplitudes. Residual disagreement, particularly at the negative endpoints of the pulses, can be accounted for by a thorough spatial analysis of the THz beam at the detection crystal.
Time-reversal of a THz pulse
Setting vf > c/nSi forces the emitted THz waves to interact with the moving front over the entire propagation distance, bringing about front-induced transitions. Deep in the super-luminal regime, the underdense plasma rapidly overtakes the THz wave and the pulse experiences both absorption and dispersion much the same as it would for transiting a static dispersive plasma49, as we have verified for vf = 1.5c/nSi conditions. For vf very close but still exceeding c/nSi, however, the front interacts with the THz emission for an extended interaction length without being consumed by the absorptive plasma. The wave therefore exists within the plasma skin depth, which is about 150 μm at f = 0.5 THz and that spans a single wavelength in the photoexcited silicon, supporting single cycle pulses.
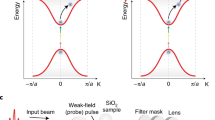
Figure 3 demonstrates the concept of a front-induced transition, which is explained in more detail in ref. 5. For dispersionless (ωpτ ≪ 1) and underdense (ωp < ω) plasmas, where hard reflections can be ignored, the photonic band structure of the photoexcited silicon is approximately linear with a phase velocity given by
The two insets of Fig. 3a show that increasing the plasma frequency from low (blue) to high (red) adds curvature to the band, flattening at low THz frequencies. Front-induced transitions on a dispersion diagram, from an initial state (ω1, β1) to a final state (ω2, β2), must obey the phase continuity relation ω1t − zfβ1 = ω2t − zfβ2 where zf = vft. The ratio of frequency change to wavenumber change is equal to the front velocity, i.e., Δω/Δβ = (ω2 − ω1)/(β2 − β1) = vf. Thus the allowed transitions are tunable with the dispersion of the perturbation via the optical excitation power controlling ωp and the pump tilt angle controlling vf. The main diagram in Fig. 3a shows the dispersion relative to unexcited silicon for three possible perturbations with increasing ωp labeled by 1, 2, and 3. Again, the dispersion of the plasma is modeled in Drude form as before but now a variable plasma frequency ωp is set by the pump fluence. In each plot, the phase continuity condition is denoted by the dashed black line, where a slightly super-luminal front velocity of vf = 1.0035c/nSi has been chosen for reasons that will be explained below.
a Plasma dispersion relation β projected onto the unexcited transverse electro-magnetic (TEM) mode wavenumber β0 (horizontal black line) for excitation conditions: (1—light blue line) ω2/β2 < vf, (2—cyan line) ω2/β2 = vf and (3—green line) ω2/β2 > vf. The dashed line is the front velocity vf = 1.0035c/nSi. The vacuum speed of light is c and the refractive index in silicon is nSi. The left inset shows that only forward intra-band scattering is possible at weak excitation (blue line), whereas the right inset shows that a time-reversal scattering event (−β1 → β2, empty dot to solid circle) becomes phase matched for highly photoexcited (red line) dispersion conditions. b Real space pictures that follow the evolution of initially-forward (pulse A) and initially-backward (pulse B) propagating THz waves for plasma conditions induced below and above critical fluence. c, d Measured THz pulses generated by a slightly super-luminal front for indicated levels of pump fluence. The single cycle pulses in c display time-reversal at t = 2.5 ps whereas a chirped pulse is shown in d to build up about 10 ps later from low-frequency waves surviving the plasma. e Amplitude spectra of only the pulses displaying time-reversal in c for all fluences explored, categorized above critical fluence (and below in the inset). f Integrated spectral power of the time-reversed THz pulses (squares) and those arising 10 ps later (circles), assuming 3% error in the measured optical power. The shading in c–e corresponds to the different plasma frequencies indicated in f, and arb. u. stands for arbitrary units.
The Schottky THz emission mechanism produces an outgoing spherical electromagnetic wave containing components traveling towards the detector (positive β) as well as those pointed backward into the plasma front (negative β). For a super-luminal front, the emission is immediately swept up by the plasma so only intra-band front-induced transitions may take place. Considering that only positive wavevectors will be detected, three scenarios are indicated in Fig. 3a, the first for which (1—blue line) ω2/β2 < vf, where transitions involving solely positive wavenumbers can occur. For high fluences (3—green line) ω2/β2 > vf, transitions from backward propagating initial states to forward propagating states within the plasma become possible. In this scenario, the backward wave undergoes a time-reversal as the spatial distribution remains unchanged but the group velocity changes sign. Higher plasma frequencies forbid intraband scattering at lower frequencies until time-reversal scattering from −β1 to +β2 takes over. Here, in the intermediate regime, the special case (2—cyan line) ω2/β2 = vf prohibits all forward initial states from undergoing transitions. The plasma frequency that satisfies this dispersion condition allows Eq. (1) to be solved for the front velocity.
Figure 3b illustrates in real space a picture of the pulse time-reversal we obtain through control over the plasma dispersion in the regime where vf is slightly super-luminal. At low fluence, i.e., scenario 1, the forward propagating THz component (pulse A) can be projected up to higher frequency states whereas its backward counterpart (pulse B) is undetected, lost to the plasma. When the front stops at the edge of the photoexcited region, the blueshifted forward THz wave is ejected. In scenario 3, the optical fluence is tuned above a critical value Fc for which the slope of the photoexcited band matches the front velocity. The additional curvature in the plasma dispersion prohibits fast forward waves of type A from undergoing intraband transitions. Instead, the highly dispersive front prevents their passage and they recede back to the plasma skin depth (pulse A\(^{\prime}\)), where they are made to co-travel with the front. Finally, in the same regime above critical fluence, the initially-backwards wave (pulse B) is able to find transitions to final states with positive β, reversing its group velocity through intra-band reflection.
Figure 3c, d together show the influence of tuning the plasma dispersion curve on the detected THz waveforms for a slightly super-luminal velocity front. For these results we utilize a PPWG composed of ITO/Si/Au layering, where 5–10 nm of Ti is used to adhere 150 nm of Au to the bottom layer. This alternative PPWG yielded identical results to the symmetric ITO/Si/ITO one with the exception of less loss due to the finite sheet resistivity of ITO. Furthermore, this PPWG served as a test of any influence from possible built-in potentials arising from the difference in work functions of the top and bottom coating materials. Varying the fluence of the NIR pump pulse, we observe in Fig. 3c single cycle THz pulses as expected, however for an intermediate fluence (scenario 2), we see a near extinction of the pulse followed by a π phase inversion at higher fluences. This extinction marks the crossover from forward intraband scattering to a time-reversal scattering event. Figure 3d highlights the development at increasing fluence of a second low-frequency THz pulse emerging roughly 10 ps later, corresponding to the type A\(^{\prime}\) pulses that have been held back in the low-frequency plasma skin before ejection.
Finally, we take a frequency-domain view of our experiment, first by analyzing the evolution of measured type B pulses as we alter their dielectric environment. Amplitude spectra obtained from numerical fast Fourier transform of these pulses are shown in Fig. 3e, revealing how the final states populate as the plasma frequency is swept through the scenarios 1, 2, and 3 described in Fig. 3a. A steep super-Gaussian filter has been applied in order to window the pulses. Each spectrum displays a high-frequency shoulder due to waveguide loss. As ωp is decreased from its highest value, the spectra acquired between scenarios 3 to 2 maintain a smooth broadband shape while reducing in amplitude, consistent with front-induced transitions occurring across the entire detection bandwidth. However, in the inset, between scenarios 2 to 1 a spectral dip suddenly appears and develops near 0.4 THz. As seen in Fig. 3a, weak excitation produces dispersion that is predominantly linear, i.e., well-approximated by Eq. (1), and we therefore expect this dip to arise from interference between co-propagating frequency states populated inside and just outside the moving plasma front, both traveling in the neighborhood of c/nSi. In Fig. 3f, we verify the distinct behavior of the pulses as the plasma frequency of the excitation is tuned through the three identified scenarios. Type A\(^{\prime}\) pulses follow a continuous decrease in integrated power, whereas as type A evolves into type B a minimum occurs at scenario 2, which marks the crossover between forward intraband scattering to time-reversing front-induced transitions followed by a resurgence and finally a true nought.
In summary, we have demonstrated that the SLIPSTREAM platform enables the interaction between THz light and relativistic moving fronts of photoinduced dielectric modulation. In the sub-luminal regime, the relativistic front generates a structured THz pulse displaying a quasi-static electric field profile via the extraction of energy from built-in Schottky fields at metal-semiconductor boundaries. The temporal profile of the electric field can be tailored by the intensity distribution of the optical photoexcitation. This capability allows, for example, applications where long, tunable THz pulses may act as an ultrafast optical bias67,68. In addition, we showed that when the front velocity is tuned just above luminal in the silicon, the fluence dependence of the dispersion of the carrier plasma is crucial in determining the front-induced transitions that may occur. We observed time-reversal of a THz pulse as the photoinduced dispersion of the dielectric perturbation was optically tuned relative to the front velocity. This work establishes our platform as a practical avenue to explore the interaction of light with moving dielectric fronts. The ability to apply localized dielectric modulation by optical means on a silicon chip has significant implications for investigating, for example, the relativistic Doppler effect44,45,69, optical horizon analogs70 and experimentally unorthodox effects associated with the motion of shock-like dielectric modulations traveling in photonic crystal landscapes71.
Methods
Waveguide device fabrication
Silicon-filled PPWGs were fabricated using high resistivity (ρ > 10, 000 Ω cm) float zone silicon wafers, double-side polished to a thickness of 50 μm. The (100)-cut silicon was cleaved to 1 square cm and the cleanliness of the cuts was verified under microscope. Two types of waveguides were fabricated, differentiated by the deposition on the bottom of either ITO with a sheet resistivity of 1 Ω/sq (coated by VacuLayer Corp.) or 150 nm of Au using a 5–10 adhesion layer of Ti. As explained in the main text, the high static conductivity of Au provides lower loss than ITO but yielded comparable results. ITO was used for the top surface to complete the parallel plate waveguide, while simultaneously providing transparency to the NIR pump beam exciting the waveguide from above.
Adiabatically tapered THz beam coupling
The top and bottom aluminum plates comprising the housing for the silicon-filled PPWG were adiabatically tapered with a 54 mm radius of curvature. This facilitated efficient coupling of the THz light generated by the moving front to free space, where it was detected by free-space electro-optic sampling. The aluminum plates were hand polished to mirror-like finish and pressed against the Si chip with four screws at the corners of the flat 21.5 mm long central region. An 8 × 8 mm2 window at the midpoint of the top plate allows optical access to the Si chip within. At the exit of the waveguide, an HDPE cylindrical lens with a radius of curvature of 76.2 mm is used to improve THz out-coupling and collimation. The beam is then focused by an off-axis parabolic mirror (Ø = 2″, f = 3″) on a (110)-oriented, 5 mm-thick GaP detection crystal for electro-optic detection.
Beam alignment and field calibration
In order to optimally orient and align the waveguide for THz pulse propagation in the TEM mode, we initially used a high-field THz source based on optical rectification in a lithium niobate prism, as in previous work49. Electric field strengths were calibrated via standard free-space electro-optic sampling72.
Spatio-temporal properties of the NIR pump
Injection of NIR pump light into the ITO-coated silicon-filled waveguide imprints a photocarrier density profile into the device along the THz propagation axis. The photoinduced front is set in motion through the application of pulse front tilt to the NIR beam using the first-order diffraction from a reflection grating (1200 lines/mm). This angularly dispersed beam is imaged into the waveguide using a f = 75 mm biconvex lens. We measure the spatial beam profile by splitting off a small portion to a CMOS camera (Thorlabs). Background subtraction is performed by recording a dark signal in the absence of the NIR pump. In order to calibrate the spatial profiles to pump fluence or photocarrier density in the silicon, the pump power is measured with a power meter (Gentec-EO) just above the waveguide.
Calibration of the front velocity
We found that the tilt angles at the waveguide position could not be accurately calculated from the measured diffraction angle and imaging conditions as a result of non-ideal imaging conditions in the confined geometry and uncertainty in the grating parameters. Instead, we used a more direct method to obtain the tilt angle from which the front velocity is easily obtained. We perform a cutback type of experiment, where a change in the distance traveled by the optical front is measured as a change in the timing of the THz pulse, as outlined in Fig. 2. Two sharp knife edges placed in the NIR beam, one before and one immediately after the grating to minimize diffraction effects, determine the start and end of the moving photoconductivity front. A change in their respective positions maps directly into a temporal step of either the leading or trailing endpoint of the THz pulse. The front velocity can then be accurately calculated simply using the relation
Power conversion efficiency
Our approach to pulse engineering via the SLIPSTREAM technique is THz source independent. Although we have utilized an inefficient THz generation mechanism built into the PPWG, we may improve the practicality of our technique through either boosting the achievable THz field strength or, alternatively, integrating external sources of intense THz pulses, such as those produced via optical rectification in LiNbO350, as employed in our prior work25,48,49. That said, in the current configuration a best-case estimate of the optical-to-THz power conversion efficiency based on the largest-amplitude luminal data from Fig. 1c puts it on the order of 10−6. To increase the total yield from a sub-luminal excitation front, in particular, one should take advantage of the linearity of the output THz field with the input optical fluence. For example, three strategies include: (i) use of a more transparent conductive oxide than ITO, maintaining the same sheet conductivity for THz confinement; (ii) enhancement of the band bending regions at the metal–semiconductor interfaces via ion implantation, increasing the built-in field; or (iii) incorporating a wider pump beam to elongate the positive cycle of the field in the time domain. In the super-luminal regime, the dispersion of the moving front must be taken into account. The fact that the framework of front-induced transitions describes linear processes facilitates the use of even weak THz sources, as shown herein.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Jepsen, P., Cooke, D. & Koch, M. Terahertz spectroscopy and imaging—modern techniques and applications. Laser Photonics Rev. 5, 124–166 (2011).
Nagatsuma, T. et al. Terahertz wireless communications based on photonics technologies. Opt. Express 21, 23736–23747 (2013).
Mittleman, D. M. Perspective: Terahertz science and technology. J. Appl. Phys. 122, 230901 (2017).
Sengupta, K., Nagatsuma, T. & Mittleman, D. M. Terahertz integrated electronic and hybrid electronic-photonic systems. Nat. Electron. 1, 622–635 (2018).
Gaafar, M., Baba, T., Eich, M. & Petrov, A. Front-induced transitions. Nat. Photonics 13, 737–748 (2019).
Gaafar, M., Holtorf, J., Eich, M. & Petrov, A. Pulse time reversal and stopping by a refractive index front. APL Photonics 5, 080801 (2020).
Biancalana, F., Amann, A., Uskov, A. & O’Reilly, E. P. Dynamics of light propagation in spatiotemporal dielectric structures. Phys. Rev. E 75, 046607 (2007).
Geltner, I., Avitzour, Y. & Suckewer, S. Picosecond pulse frequency upshifting by rapid free-carrier creation in ZnSe. Appl. Phys. Lett. 81, 226–228 (2002).
Lampe, M., Ott, E. & Walker, J. Interaction of electromagnetic waves with a moving ionization front. Phys. Fluids 21, 42–54 (1978).
Semenova, V. I. Reflection of electromagnetic waves from an ionization front. Radiophys. Quantum Electron. 10, 599–604 (1967).
Caloz, C. et al. Electromagnetic nonreciprocity. Phys. Rev. Appl. 10, 047001 (2018).
Chan, W. L. et al. A spatial light modulator for terahertz beams. Appl. Phys. Lett. 94, 213511 (2009).
Yu, N. & Capasso, F. Wavefront engineering for mid-infrared and terahertz quantum cascade lasers [Invited]. J. Opt. Soc. Am. B 27, B18–B35 (1680).
Shabanpour, J., Beyraghi, S. & Cheldavi, A. Ultrafast reprogrammable multifunctional vanadium-dioxide-assisted metasurface for dynamic THz wavefront engineering. Sci. Rep. 10, 8950 (2020).
Watts, C. M. et al. Terahertz compressive imaging with metamaterial spatial light modulators. Nat. Photonics 8, 605–609 (2014).
Ganichev, S. & Prettl, W. Intense Terahertz Excitation of Semiconductors (Oxford University Press, 2005).
Razzari, L. et al. Nonlinear ultrafast modulation of the optical absorption of intense few-cycle terahertz pulses in n-doped semiconductors. Phys. Rev. B 79, 193204 (2009).
Hoffmann, M., Brandt, N., Hwang, H., Yeh, K. & Nelson, K. Terahertz Kerr effect. Appl. Phys. Lett. 95, 231105 (2009).
Liu, M. et al. Terahertz-field-induced insulator-to-metal transition in vanadium dioxide metamaterial. Nature 487, 345–348 (2012).
Turchinovich, D., Hvam, J. M. & Hoffmann, M. C. Self-phase modulation of a single-cycle terahertz pulse by nonlinear free-carrier response in a semiconductor. Phys. Rev. B 85, 201304 (2012).
Sharma, G. et al. Carrier density dependence of the nonlinear absorption of intense THz radiation in GaAs. Opt. Express 20, 18016–18024 (2012).
Al-Naib, I. et al. Effect of local field enhancement on the nonlinear terahertz response of a silicon-based metamaterial. Phys. Rev. B 88, 195203 (2013).
Raab, J. et al. Ultrafast terahertz saturable absorbers using tailored intersubband polaritons. Nat. Commun. 11, 4290 (2020).
Hafez, H. A. et al. Terahertz nonlinear optics of graphene: from saturable absorption to high-harmonics generation. Adv. Opt. Mater. 8, 1900771 (2020).
Gingras, L. & Cooke, D. G. Direct temporal shaping of terahertz light pulses. Optica 4, 1416 (2017).
Ma, J., Karl, N. J., Bretin, S., Ducournau, G. & Mittleman, D. M. Frequency-division multiplexer and demultiplexer for terahertz wireless links. Nat. Commun. 8, 729 (2017).
Morgenthaler, F. Velocity modulation of electromagnetic waves. IRE Trans. Microw. Theory Tech. 6, 167–172 (1958).
Yablonovitch, E. Spectral broadening in the light transmitted through a rapidly growing plasma. Phys. Rev. Lett. 31, 877–879 (1973).
Nishida, A. et al. Experimental observation of frequency up-conversion by flash ionization. Appl. Phys. Lett. 101, 161118 (2012).
Tanaka, Y. et al. Dynamic control of the Q factor in a photonic crystal nanocavity. Nat. Mater. 6, 862–865 (2007).
Notomi, M. Manipulating light with strongly modulated photonic crystals. Rep. Prog. Phys. 73, 096501 (2010).
Xu, Q., Dong, P. & Lipson, M. Breaking the delay-bandwidth limit in a photonic structure. Nat. Phys. 3, 406–410 (2007).
Sato, Y. et al. Strong coupling between distant photonic nanocavities and its dynamic control. Nat. Photonics 6, 56–61 (2012).
Lee, K. et al. Linear frequency conversion via sudden merging of meta-atoms in time-variant metasurfaces. Nat. Photonics 12, 765–773 (2018).
Mayer, B. et al. Sub-cycle slicing of phase-locked and intense mid-infrared transients. N. J. Phys. 16, 063033 (2014).
Shalaby, M., Peccianti, M., Cooke, D. G., Hauri, C. P. & Morandotti, R. Temporal and spectral shaping of broadband terahertz pulses in a photoexcited semiconductor. Appl. Phys. Lett. 106, 051110 (2015).
Caloz, C. & Deck-Léger, Z. Spacetime metamaterials—part I: general concepts. IEEE Trans. Antennas Propag. 68, 1569–1582 (2020).
Caloz, C. & Deck-Léger, Z. Spacetime metamaterials—part II: theory and applications. IEEE Trans. Antennas Propag. 68, 1583–1598 (2020).
Yanik, M. & Fan, S. Time reversal of light with linear optics and modulators. Phys. Rev. Lett. 93, 173903 (2004).
Chumak, A. et al. All-linear time reversal by a dynamic artificial crystal. Nat. Commun. 1, 141 (2010).
Yariv, A., Fekete, D. & Pepper, D. M. Compensation for channel dispersion by nonlinear optical phase conjugation. Opt. Lett. 4, 52–54 (1979).
Mosk, A. P., Lagendijk, A., Lerosey, G. & Fink, M. Controlling waves in space and time for imaging and focusing in complex media. Nat. Photonics 6, 283–292 (2012).
Thomson, M. D., Tzanova, S. M. & Roskos, H. G. Terahertz frequency upconversion via relativistic doppler reflection from a photoinduced plasma front in a solid-state medium. Phys. Rev. B 87, 085203 (2013).
Meng, F., Thomson, M. D. & Roskos, H. G. Relativistic Doppler frequency upconversion of terahertz pulses reflecting from a photoinduced plasma front in silicon. Phys. Rev. B 90, 155207 (2014).
Kohno, N., Itakura, R. & Tsubouchi, M. Relativistic Doppler reflection of terahertz light from a moving plasma front in an optically pumped Si wafer. Phys. Rev. B 102, 235201 (2020).
Cooke, D. & Jepsen, P. Dynamic optically induced planar terahertz quasioptics. Appl. Phys. Lett. 94, 241118 (2009).
Gingras, L., Georgin, M. & Cooke, D. G. Optically induced mode coupling and interference in a terahertz parallel plate waveguide. Opt. Lett. 39, 1807 (2014).
Gingras, L., Blanchard, F., Georgin, M. & Cooke, D. G. Dynamic creation of a light-induced terahertz guided-wave resonator. Opt. Express 24, 2496 (2016).
Gingras, L., Cui, W., Schiff-Kearn, A. W., Ménard, J.-M. & Cooke, D. G. Active phase control of terahertz pulses using a dynamic waveguide. Opt. Express 26, 13876 (2018).
Fülöp, J. A., Pálfalvi, L., Almási, G. & Hebling, J. Design of high-energy terahertz sources based on optical rectification. Opt. Express 18, 12 (2010).
Guiramand, L., Nkeck, J. E., Ropagnol, X., Ozaki, T. & Blanchard, F. Near-optimal intense and powerful terahertz source by optical rectification in lithium niobate crystal. Preprint at https://arxiv.org/abs/2104.10804 (2021).
Bakunov, M. I., Maslov, A. V. & Bodrov, S. B. Phase-matched generation of a terahertz surface wave by a subluminous optical strip. J. Appl. Phys. 98, 033101 (2005).
Bae, J., Xian, Y. J., Yamada, S. & Ishikawa, R. Doppler frequency up conversion of electromagnetic waves in a slotline on an optically excited silicon substrate. Appl. Phys. Lett. 94, 091120 (2009).
Fukuda, T. et al. Experiments of forward THz emission from femtosecond laser created plasma with applied transverse electric field in air. Jpn. J. Appl. Phys. 59, 020902 (2020).
Islam, Q.-U., Meng, F., Thomson, M. D. & Roskos, H. G. Terahertz photoconductive waveguide emitter with excitation by a tilted optical pulse front. Opt. Express 28, 22 (2020).
Mori, W. B., Katsouleas, T., Dawson, J. M. & Lai, C. H. Conversion of dc fields in a capacitor array to radiation by a relativistic ionization front. Phys. Rev. Lett. 74, 542–545 (1995).
Higashiguchi, T. et al. Experimental observation of further frequency upshift from dc to ac radiation converter with perpendicular dc magnetic field. Phys. Rev. Lett. 85, 4542–4545 (2000).
Hashimshony, D., Zigler, A. & Padadopoulos, K. Conversion of electrostatic to electromagnetic waves by superluminous ionization fronts. Phys. Rev. Lett. 86, 2806 (2001).
Ohata, N., Yaegashi, K., Li, K., Higashiguchi, T. & Yugami, N. THz radiation from a DARC source via a laser-produced relativistic ionization front. In Proceedings on SPIE6772, 174–179 Terahertz Physics, Devices, and Systems II (International Society for Optics and Photonics, 2007).
Kostin, V. A. & Vvedenskii, N. V. Dc to ac field conversion due to leaky-wave excitation in a plasma slab behind an ionization front. N. J. Phys. 17, 033029 (2015).
Otsuka, T. P., Hommyo, T., Hyuga, Y., Yugami, N. & Kodama, R. Generation of sub-terahertz radiation using the DC-to-AC radiation converter. Jpn. J. Appl. Phys. 56, 110308 (2017).
Wu, Q. & Zhang, X. 7 terahertz broadband GaP electro-optic sensor. Appl. Phys. Lett. 70, 1784 (1997).
Grischkowsky, D., Keiding, S., van Exter, M. & Fattinger, C. Far-infrared time-domain spectroscopy with terahertz beams of dielectrics and semiconductors. J. Opt. Soc. Am. B 7, 2006–2015 (1990).
Bakunov, M. I., Maslov, A. V. & Tsarev, M. V. Optically generated terahertz pulses with strong quasistatic precursors. Phys. Rev. A 95, 063817 (2017).
Meng, F., Thomson, M. D., Sernelius, B. E., Jörger, M. & Roskos, H. G. Ultrafast dynamic conductivity and scattering rate saturation of photoexcited charge carriers in silicon investigated with a midinfrared continuum probe. Phys. Rev. B 91, 075201 (2015).
Côté, D., Sipe, J. E. & van Driel, H. M. Simple method for calculating the propagation of terahertz radiation in experimental geometries. J. Opt. Soc. Am. B 20, 1374 (2003).
Tehini, R., Hamraoui, K. & Sugny, D. Shaping of field-free molecular orientation by THz laser pulses. Phys. Rev. A 99, 033419 (2019).
Wimmer, L. et al. Terahertz control of nanotip photoemission. Nat. Phys. 10, 432 (2014).
Kurnikov, M., Novokovskaya, A., Efimenko, E. & Bakunov, M. Long propagating velocity-controlled einstein’s mirror for terahertz light conversion. Opt. Express 28, 33084 (2020).
Faccio, D. Hawking radiation. Contemp. Phys. 53, 97 (2012).
Reed, E. J., Soljačić, M. & Joannopoulos, J. D. Color of shock waves in photonic crystals. Phys. Rev. Lett. 90, 203904 (2003).
Planken, P., Nienhuys, H.-K., Bakker, H. & Wenckebach, T. Measurement and calculation of the orientation dependence of terahertz pulse detection in ZnTe. J. Opt. Soc. Am. B 18, 313–317 (2001).
Acknowledgements
The authors wish to acknowledge financial support from the Natural Sciences and Engineering Research Council of Canada (NSERC), Fonds de Recherche du Qu\(\acute{\,\text{e}\,}\)bec Nature et Technologies (FRQNT) and the Canadian Foundation for Innovation (CFI). We also gratefully acknowledge useful discussions with E. Yablonovich.
Author information
Authors and Affiliations
Contributions
D.G.C. and J.-M.M. conceived the experiment and supervised the work. A.W.S.-K. and L.G. performed the experiments. L.G. and D.G.C. designed the experimental apparatus. N.C. wrote initial simulation code and S.B. performed these simulations under supervision of K.A. The manuscript was written by A.W.S.-K. and D.G.C. with contributions from L.G., J.-M.M., S.B., and K.A.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schiff-Kearn, A.W., Gingras, L., Bernier, S. et al. Front-induced transitions control THz waves. Commun Phys 4, 162 (2021). https://doi.org/10.1038/s42005-021-00667-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00667-4
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.