Abstract
Exceptional points are a ubiquitous concept widely present in driven-dissipative coupled systems described by a non-Hermitian Hamiltonian. To date, exceptional points have been extensively examined in the systems supporting only a few optical modes, thereby leaving the observation of collective (multimode) effects outside of the scope of the study. In the present paper, we analyze the role of exceptional points in nonlinear multimode photonics. Specifically, we provide insights into the complex nonlinear dynamics arising in a continuous wave-driven pair of strongly coupled microresonators. Investigating this system, we demonstrate mechanisms of dissipative Kerr soliton formation in two fundamentally different regimes separated by a line of exceptional points. Highlighting the diversity of emergent nonlinear effects, we describe the on-demand generation of single-solitons, perfect soliton crystals and bright-dark soliton pairs on either side of exceptional points.
Similar content being viewed by others
Introduction
Symmetry is one of the main fundamental concepts in physics which underpins conservation laws, micro- and macro-properties of matter, rising of degeneracies1 and topological properties2. Breaking of symmetry in spontaneous or deterministic way is responsible for a variety of phenomena3,4,5. Systems obeying Parity-Time (\({\mathcal{P}}{\mathcal{T}}\)) symmetry have been shown to provide a possibility to treat open quantum systems described by a non-Hermitian Hamiltonian and nonetheless retrieve a real spectrum of eigenvalues6,7. Eigenvalues of \({\mathcal{P}}{\mathcal{T}}\) symmetric Hamiltonian have two typical regions on the parameters space corresponding to preserved and broken symmetry. The transient point where the eigenvalues and eigenvectors coalesce is called an exceptional point (EP)8,9.
The effect has been observed in various physical systems7,10. Due to the well-controlled laboratory conditions and a wide range of possible applications, guided optics serves as one of the primary platforms for investigating effects that emerge in \({\mathcal{P}}{\mathcal{T}}\)-symmetric systems9,11,12,13. These effects cover observation of strong non-reciprocity in banded waveguides, enhanced lasing and (classical noise limited) sensing in coupled ring resonators with loss and gain (for more examples see review article9). It has been shown that \({\mathcal{P}}{\mathcal{T}}\) symmetry can be unraveled in completely passive resonators having different loss rates after a gauge transformation9,14. Here, it is important to mention that the majority of these studies have been considering linear effects in single-mode arrangements or nonlinear ones in nonresonant systems15,16,17.
Almost in parallel, another field of study has been rapidly developing in photonics: design and fabrication of passive nonlinear coherent broadband light sources18. For this purpose, exactly the same optical platforms have been used: optical waveguides and resonators but in the opposite, strongly nonlinear regime. Nonlinear waveguides served as a sources of supercontinuum signals19,20, while micro- and macro-resonators has been used for generation of stable and coherent frequency combs21. The latter has been achieved due to the observation of localized coherent structures in passive optical micro-resonators22. These structures generated in media with χ(3) nonlinearity are called dissipative Kerr solitons (DKSs). They have been widely investigated in nonlinear photonics over the last decades21,23,24,25. The existence of DKSs relies on the balance between chromatic dispersion, Kerr-type nonlinearity, parametric gain and the intrinsic cavity losses26. DKSs are exact solutions of the damped-driven nonlinear Schrödinger equation known as Lugiato–Lefever equation (LLE)27,28. Their observation in passive macroscopic (fiber) cavities25 and (integrated) microcavity systems22,29 has spurred a vivid research effort unravelling a rich inherent dynamical behavior30,31,32,33,34,35,36. The discovery of DKSs in microresonators revolutionized the field, bringing coherent frequency combs to outside-of-laboratory applications21. Later, a pioneering theoretical proposal considering the DKS generation in the \({\mathcal{P}}{\mathcal{T}}\)-symmetric system has been presented in ref. 37.
Recently, DKSs have been discovered in a high-Q multimode photonic dimer (pair of strongly-coupled, almost identical nonlinear resonators)38. The photonic dimer has revealed a pleiad of emergent phenomena including soliton hopping, periodic appearance of commensurate and incommensurate dispersive waves (DWs), and symmetry breaking related to the discreteness of the system. Solitons have been generated in both resonators simultaneously and due to the underlying field symmetry were called gear solitons (GSs).
In this work, we investigate an all-passive photonic dimer with a hidden (passive) \({\mathcal{P}}{\mathcal{T}}\)-symmetry (further referred to as \({\mathcal{P}}{\mathcal{T}}\)-symmetry for simplicity)9 in linear and nonlinear multimode regimes. In the linear regime, we analyze conditions for the critical coupling and demonstrate that the line of EPs is a demarcation of these conditions. The EP line splits the parameter space into two parts, which we refer to as split resonance (\({\mathcal{P}}{\mathcal{T}}\) symmetric) and split dissipation (\({\mathcal{P}}{\mathcal{T}}\)-symmetry broken). In the split resonance regime, we show insights into the effects previously reported in ref. 38, using the supermode basis representation. Passing through an EP, we observe the divergence of the nonlinear interaction efficiency which hints at the enhanced sensitivity. Further, we investigate the nonlinear dynamics in the split dissipation regime which includes single-resonator DKS, dark-bright DKSs pairs, and highly-efficient perfect soliton crystals. Finally, we demonstrate switching of the soliton-generating cavity caused by the nonlinear alteration of the \({\mathcal{P}}{\mathcal{T}}\) symmetry.
Results
Exceptional point as a demarcation of the critical coupling conditions
We consider the system of two multimode resonators [Fig. 1(a)], with identical intrinsic loss rate κ0, mode spacing D1, and geometry, such that the dispersion and Kerr nonlinearity coefficient are also identical. A global offset between the resonant frequencies ωμ of their respective modes μ is introduced with the inter-resonator detuning δ. The two resonators are coupled to each other by the evanescent field with the rate Jμ, which generally depends on the mode number. Each resonator is coupled to a waveguide (through and drop ports) with the rates κex,i, i = 1, 2. Resonator 1 is pumped by a continuous wave (CW) laser at frequency ωp. Nonlinear dynamics in the photonic dimer can be described by two coupled LLEs, which in Fourier space is expressed as follows38,39:
where \({g}_{{\rm{K}}}=\frac{\hslash {\omega }_{0}^{2}c{n}_{2}}{{n}_{0}^{2}{V}_{{\rm{eff}}}}\) is the Kerr coefficient, c stands for the speed of light in vacuum, ℏ—the Planck constant, ω0—the frequency of the pumped mode, \({V}_{{\rm{eff}}}={{\mathcal{A}}}_{{\rm{eff}}}L\)—the effective mode volume (with the effective nonlinear mode-area \({{\mathcal{A}}}_{{\rm{eff}}}\) and circumference of the cavity L), n0 and n2 are linear and nonlinear refractive indexes, respectively, δμ,0 is the Kronecker delta, \({s}_{{\rm{in}}}=\sqrt{\frac{{P}_{{\rm{in}}}}{\hslash {\omega }_{0}}}\)—the input pump field amplitude, Aμ, Bμ are the field amplitudes of the modes with index μ in the first and second resonator, respectively. The variables A, B are the slowly varying intra-resonator field envelops, and \({\mathcal{F}}{[...]}_{\mu }\) denotes the μth-component of the discrete Fourier transform, which are defined in Supplementary Note 1.
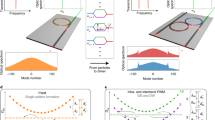
a Schematic of the two resonators. b, c Field intensity in the resonator 1 (blue) and 2 (red) as a function of the laser detuning. b Shows a typical resonance splitting (orange shading) at critical coupling for J = 10κ0, c the same for the split dissipation regime (purple shading) at critical coupling for J = 1.5κ0. d Critical coupling coefficients as a function of J for κex,2 = 0, in the split dissipation (resonances) regime above (below) the exceptional point line (dotted). The two conditions branch off at the exceptional point of J = 1/2κ0, highlighted by the star. e Real and imaginary parts of the eigenvalues σ± as a function of κex,1 for J = 1.5κ0.
Modes of each resonator with identical angular momentum are linearly coupled with the inter-resonator coupling rate Jμ. In contrast, the Kerr nonlinearity couples all the modes within each resonator via four-wave mixing (FWM) processes. The interplay between the linear coupling in the spatial dimension and the nonlinear coupling in the frequency dimension is the source of the rich dynamics of the system.
In the present section, we restrict ourselves to a linear and single mode analysis by considering only the central mode μ = 0 with gK = 0. The critical coupling conditions are of particular interest for maximizing the pump transfer to the resonators and the eigenvalue analysis of the coupled mode matrix for finding the EP conditions, which separate two conceptually different dimer states.
Critical coupling conditions
Let us analyze the condition for critical coupling. In the linear single-mode representation, Eq. (1) is simplified as follows:
In Eq. (2), we defined the external coupling mismatch Δκex = κex,1 − κex,2 and the average external coupling \({\kappa }_{{\rm{ex}}}=\frac{1}{2}({\kappa }_{{\rm{ex}},1}+{\kappa }_{{\rm{ex}},2})\). The identity matrix is denoted as I. Critical coupling is achieved when the transmission via the through port [Fig. 1(a)] vanishes, i.e., sout,1 = 0. In the case of a single resonator, critical coupling is achieved when the external coupling rate matches the loss, i.e., κex = κ040,41. For two resonators, the conditions are easily found in case of δ = 0. There are two possibilities
Equation (3) is a natural generalization of the critical coupling conditions for a single resonator that can be achieved by setting J to zero. Equation (4) satisfies the critical coupling condition at \({\omega }_{p}={\omega }_{0}\pm \sqrt{4{J}^{2}-{({\kappa }_{0}+{\kappa }_{{\rm{ex}},2})}^{2}}\). This condition requires strong coupling, i.e., \(J\, > \, \frac{1}{2}({\kappa }_{0}+{\kappa }_{{\rm{ex}},2})\). The critical coupling conditions are shown in Fig. 1(d) for κex,2 = 0. We note that the latter condition is the equivalent in the mean-field approximation to that found using coupled matrix formalism42. Typical cavity field intensities for both cases are plotted in Fig. 1(b, c) as a function laser detuning.
The first critical coupling condition given by Eq. (3) has a quadratic dependence on the inter-resonator coupling rate [Fig. 1(d)]. It leads to a broad resonance with a dip in the first resonator (blue) and a narrow resonance in the second resonator (red) at the same resonance frequency [Fig. 1(c)]. The second critical coupling condition [Eq. (4)] branches off the first one at J/κ0 = 0.5 and does not depend on the inter-resonator coupling rate. It features split resonances with identical linewidths [Fig. 1(b)].
Experimental implementation of the multimode photonic dimer demonstrated the presence of the non-vanishing inter-resonator detuning δ caused by the fabrication imperfectness. Nonetheless, the possibility to control and manipulate δ, and thereby establish control over the output solitonic spectrum, has been demonstrated and efficiently implemented by imprinting heaters directly on the photonic device38,43. Critical coupling at non-vanishing δ is possible as well. The inter-resonator detuning introduces asymmetry in the distribution of the supermodes (eigenvectors) in each resonator. Thus, the supermode confined in the first (second) resonator requires smaller (larger) κex,1 to be critically coupled. It follows that in general when δ ≠ 0 only one supermode can be critically coupled for a given value of κex,1. For more details, see Supplementary Fig. 1 and Supplementary Note 2.
The qualitative behavior of the photonic dimer can be anticipated by examining the eigenvalues of the system Eq. (2). Operating with a naturally Non-Hermitian system, we can exploit the concept of EP8 to shed light on the nature of each critical coupling conditions.
Eigenvalues and exceptional points
The eigenvalues of the matrix M defined in Eq. (2) in case of δ = 0, κex,2 = 0, and ω0 = ωp are given by
where the real (imaginary) part corresponds to resonance frequency (loss rate). The eigenvalues are shown in Fig. 1(e) as a function of κex,1 for an inter-resonator coupling J = 1.5κ0. Two different regions of split resonance and split dissipation are identified and shaded in Fig. 1 with orange and purple, respectively. For κex,1 < 6κ0, the eigenvalues have degenerate imaginary part and split real parts, associated with the split resonances as depicted in Fig. 1(b). In contrast, κex,1 > 6κ0 leads to degenerate real parts and split imaginary parts, i.e., to identical resonance frequencies but different loss rates, as can be seen in Fig. 1(c). The two regions correspond to the \({\mathcal{P}}{\mathcal{T}}\)-symmetric and \({\mathcal{P}}{\mathcal{T}}\)-symmetry broken states, respectively.
An EP is found between the two regions at κex,1 = 6κ0, where the system eigenvalues become degenerate and the two eigenvectors coalesce because of the vanishing square root in Eq. (5). EPs lie along the line defined by κex,1 = 4J, which separates the two critical coupling conditions in the (J, κex,1) plane. It is noteworthy that the two critical coupling conditions and the EP line fork at \(J=\frac{1}{2}{\kappa }_{0},\,{\kappa }_{{\rm{ex}},1}=2{\kappa }_{0}\). This particular point is highlighted by the blue star in Fig. 1(d). It is the only EP that satisfies a critical coupling condition. This point also marks the entry into the strong coupling regime (\(J\,> \, \frac{1}{2}{\kappa }_{0}\)). Above reasoning is valid when κex,2 = 0. In the general case (κex,2 ≠ 0) the line of EPs can cross the line corresponding to critical coupling conditions.
Concluding, there are two types of critical coupling conditions in the photonic dimer. These conditions are found on both sides of the EPs, such that critical coupling can be achieved in the \({\mathcal{P}}{\mathcal{T}}\)-symmetric as well as \({\mathcal{P}}{\mathcal{T}}\)-symmetry broken states. In the next sections, we examine the versatile nonlinear dynamics and dissipative Kerr soliton generation in these states.
Critically coupled resonators: split resonance (\({\mathcal{P}}{\mathcal{T}}\)-symmetric)
In the present section we discuss the case of the split resonance (\({\mathcal{P}}{\mathcal{T}}\)-symmetric). We revisit ideas presented earlier in ref. 38 by looking at the nonlinear dynamics from the supermode perspective. We demonstrate a separability of the GS dynamics from DWs living in the S supermodes. Finally, we show how this representation explains the origin of soliton hopping effect. An essential part of the investigation of the dynamics inherent to the photonic dimer and described by Eq. (1) relies on numerical simulations.
Four-wave mixing pathways between supermodes
The linear part of Eq. (1) can be diagonalized by a linear transformation on each pair of modes with index μ. We define the complex inter-resonator detuning \({\delta }_{c}=\delta -i\frac{1}{2}{{\Delta }}{\kappa }_{{\rm{ex}}}\). If the inter-resonator coupling is independent of the wavelength, the complex frequency splitting \({{\Delta }}{\omega }_{c}=\sqrt{4{J}^{2}+{\delta }_{c}^{2}}\), and the (complex) normalized inter-resonator detuning
are independent of the mode index. Therefore, the non-unitary transformation diagonalizing the linear part of Eq. (1) is given by As,μ = αAμ + βBμ, Aas,μ = βAμ − αBμ, where
Here S and AS stand for the symmetric (S) and antisymmetric (AS) mode, as they are completely symmetric (antisymmetric) at dc = 0 in the split resonance regime. Then, by defining the spatial envelope of the field in the S and AS modes As(θ) = ∑μAs,μeiμθ, Aas(θ) = ∑μAas,μeiμθ, we can express Eq. (1) in the supermode basis (see details in Supplementary Note 3 and alternative Hamiltonian formulation in ref. 38):
As one can see, the linear anti-diagonal terms are eliminated in the supermode basis, while the nonlinear terms (diagonal in the resonator basis) induce nonlinear coupling between the supermodes. In particular, we identify FWM processes between the supermodes. We note that a similar diagonalization which introduced high- and low-frequency soliton was made in the context of \({\mathcal{P}}{\mathcal{T}}\)-symmetric nonlinear couplers15.
The efficiencies of FWM pathways are associated with nonlinear coupling coefficients ti, i = 1, . . , 4, defined in Supplementary Note 3 (see Eq. S20). For example, the term \(\frac{1}{2}{t}_{3}{A}_{{\rm{as}}}^{2}{A}_{{\rm{s}}}^{* }\) in Eq. (7) signifies the annihilation of two photons in the AS supermode and the creation of two photons in the S supermode. The rate of the process is proportional to gKt3. Each FWM process can be represented by a quantum Hamiltonian term, for example
where \({\hat{a}}_{i,\mu }^{\dagger }\) (\({\hat{a}}_{i,\mu }\)) is the creation (annihilation) operator for supermode i = s, as with longitudinal mode index μ, and μ1 + μ2 = μ3 + μ4. The nine different nonlinear processes from Eq. (7) to Eq. (8) are depicted in Fig. 2(a), where they are arranged in categories corresponding to intra-band even processes, inter-band even processes and inter-band odd processes.
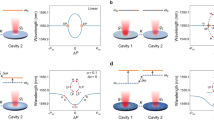
a Table of the nine possible FWM pathways represented with quantum operators and corresponding coefficients ti. b Real (solid) and imaginary (dashed) part of nonlinear coupling coefficients as a function of the normalized inter-resonator detuning d for 2 values of the external coupling mismatch Δκex in the split resonance regime (J = 20κ0). Δκex is the source of the imaginary component, which however is small compared to the real part, except for t4 around d = 0. c, d Schematic integrated dispersion profile with emphasized FWM pathways. The labelling indexes are specified in (a). Empty dashed circles denotes cold cavity mode, filled circle denotes Kerr comb mode, and color codes AS (green) or S (purple) mode family. c GS generated in the AS supermodes via conventional FWM (even intra-band processes) and the emergence of commensurate dispersive waves via odd inter-band processes. d Soliton in the AS supermodes and the generation of a soliton in the S supermodes caused by even processes.
We refer to a nonlinear process as intra-band when two annihilated and two created photons are from the same supermode family, while inter-band processes imply nonlinear mixing of photons belonging to different supermodes, inspired by the concept of Bloch bands in condensed matter Physics. The number parity of the process (even or odd) refers to the number of photons from each supermode family that is involved. We note that processes (2,4,7,9) are the counterparts of processes (1,3,6,8) for permuted supermodes index. Schemes of possible FWM pathways between the supermodes (while a solitonic state is generated in the AS supermode family) are shown in Fig. 2(c,d) These processes are distinguished by the nature of FWM: Fig. 2(c) shows odd processes (except the conventional even process #1, associated with Hamiltonian term \({\hat{a}}_{{\rm{as}},{\mu }_{1}}^{\dagger }{\hat{a}}_{{\rm{as}},{\mu }_{2}}^{\dagger }{\hat{a}}_{{\rm{as}},{\mu }_{3}}{\hat{a}}_{{\rm{as}},{\mu }_{4}}\)), while Fig. 2(d) shows even processes leading to soliton hopping.
While the index μ has been omitted in Fig. 2(a) for readability, both the mode number and the energy have to be conserved in a FWM process. We employ the concept of integrated dispersion Dint(μ) = ωμ − (ω0 + D1μ) to depict the processes which satisfy the phase matching conditions.
The real and imaginary parts of the nonlinear coupling coefficients are shown in Fig. 2(b) as a function of the normalized inter-resonator detuning \(d=\delta /\sqrt{4{J}^{2}+{\delta }^{2}}\) with solid and dashed dotted lines, respectively. The parameters are chosen in the split resonance regime with J = 20κ0. Vanishing and non-vanishing Δκex are considered, emphasizing that the imaginary parts of all the nonlinear coupling coefficients originate from the external coupling mismatch. The imaginary part, however, generally constitutes only a small fraction of the absolute value of the nonlinear coupling coefficients.
Coefficient t1 is responsible for the intra-band processes, that is, the usual FWM within the same mode family (S) or (AS). It has its lowest value equal to 0.5 at the maximum hybridization (d = 0). In contrast, coefficient t3 is maximized at d = 0 and causes inter-band and even processes. The coefficients t2 and t4 are responsible for inter-band and odd processes. Their real parts are odd with respect to d. Therefore, there are no odd FWM processes at d = 0, unless an external coupling mismatch is present. In this case, coefficient t4 has a non-vanishing absolute value.
Nonlinear dynamics and soliton generation in split resonance (\({\mathcal{P}}{\mathcal{T}}\)-symmetric) regime
The type of the critical coupling conditions corresponding to the split resonances allows for accessing dynamical states characterized by efficient generation of bright DKSs in both cavities. Emergent dynamical effects described in ref. 38 are found in this regime. In this section, we provide an additional (to the result already shown in ref. 38) and complementary description of these phenomena by representing the inter-resonator field in the hybridized supermodes basis.
Modulation instability state
We restrict ourselves to the AS supermodes pumping scheme since we did not observe dynamics different from the single resonator case when exciting the S supermode family. Figure 3(a, b) show the intracavity power evolution as a function of laser detuning in the resonator and supermode basis, respectively. It is numerically generated by exciting the system in a soft manner, i.e., adiabatically changing the laser detuning ξ = ω0 − ωp from blue to red side of the AS hybridized resonance. Initial dynamics is found to be similar to the single resonator case. We observe the formation of primary combs in the AS supermode family followed by cnoidal waves (Turing rolls). The subsequent chaotic modulation instability stage [yellow area in Fig. 3(a, b)] already demonstrates a significant difference. Namely, the average intracavity power evolution in the second resonator, which is depicted by the red line, as a function of normalized detuning ξ/Δω exhibits a local maximum inside the modulation instability area which corresponds to the efficient photon transfer to the S supermodes [violet curve in Fig. 3(b)]. At these values of detuning (ξ/Δω ≈ −1), we observe an enhancement of spectral components distinct from the modulation instability gain region. The mode number of the components correspond exactly to the distance from the pumped mode to the lower (S supermodes) parabola for a given value of the laser detuning, as described in ref. 38. This is a first signature of the interaction between the supermodes.
a Evolution of the intracavity field power Pint in resonator basis. b Intracavity field power evolution in supermode basis. c, d Spatiotemporal diagrams for the field evolution in AS and S supermodes, respectively. Parameters of numerical simulations are close to the exact critical coupling conditions: κ0/2π = 50 MHz, κex,1/2π = 100 MHz, κex,2/2π = 20 MHz, δ/2π = 4 GHz, J/2π = 4.5 GHz, the pump power was fixed to 1.2 W. DWs: dispersive waves.
Figure 3 (c, d) provide the underlying evolution of intracavity power (spatiotemporal diagram) in the supermode basis. The modulation instability region in the conventional basis does not differ for the single-particle dynamics. However, the supermode basis reveals that the transfer of photons to the S supermode family occurs after a certain detuning threshold. As follows from the spatiotemporal diagram of the AS state, it occurs in the developed AS supermodes modulation instability stage, where collision and annihilation of unstable coherent structures lead to the enhancement of wings in the optical spectrum44 and thereby populates the modes in vicinity of the symmetric resonances.
Breathing state
As in conventional single resonator systems above a threshold pump power level, the modulation instability region is followed by the breathing solitons region [violet area in Fig. 3(a, b)]. Breathing originates from the Hopf bifurcation as demonstrated for the single resonator case45. It manifests itself as a periodic oscillation of localized coherent structures (similar to solitons on a finite background, such as Kuznetsov-Ma soliton46,47—a solution of the nonlinear Schrödinger equation), which radiates DWs at every cycle of oscillation. Figure 4(a) shows the intracavity power evolution. Breathers in the photonic dimer exist in both resonators and oscillate in phase. However, the intracavity trace is found to be randomly deviating from the average because of the photon transfer to the S supermodes and, therefore, the generation of additional DWs.
a, b Evolution of the intracavity power Pint with a fixed pump laser detuning (a) in the first and second resonator (shown by blue and red lines) and (b) in the supermode basis (green and violet for AS and S mode families, respectively). c–f Nonlinear dispersion relations (c, e) for the first and second resonators (d, f) for AS and S supermode families. DW: Dispersive wave.
The periodic oscillation of a coherent structure in slow time results in the appearance of a ladder of straight and equally-spaced lines on the nonlinear dispersion relation48. The presence of such ladder has been experimentally demonstrated (see38, supplementary information) by reconstructing the comb spectrum with high resolution. Indeed, as follows from Fig. 4(c, e) the breathing frequency is given by the frequency offset between the lines. The same reasoning can be applied to the single resonator breathing states. There, it has been demonstrated experimentally that the breathing frequency linearly depends on the pump laser detuning32. Therefore, we can make a conjecture that the breathing occurs due to the photon transfer between the Kerr-shifted dispersion parabola and the first solitonic line given by the laser detuning, while the breathing frequency is the corresponding gap. In the points where the ladder crosses the AS supermodes parabola enhancement of the comb power is observed. Therefore, optical spectrum of a breather contains a set of sidebands32,49,50.
In the supermode basis [see Fig. 4(b)] it becomes evident that the breathing occurs mostly in AS supermode families. Therefore, the breathing dynamics in the AS mode family does not show significant difference from the conventional breathing found in the single resonator case as follows from the nonlinear dispersion relation [Fig. 4(d)], although it demonstrates significant differences in the resonator basis. Figure 4(f) shows the nonlinear dispersion relation for the S supermode family. The origin of the DWs which perturb the breathing state can be seen as an enhancement of the certain supermodes in the S family (μ ≈ ±70) in the places where the ladder from AS supermodes crosses the S parabola.
Soliton hopping state
The soliton hopping state recently predicted in the photonic dimer38 is characterized by a periodic energy exchange between the coupled resonators in the presence of temporally-localized coherent structures. Inter-resonator oscillations have a frequency equal to the splitting between the supermode parabolas. The average power modulation is much stronger than in the breathing state, which leads to the enhanced sideband amplitudes in the optical spectrum [see Fig. 5(b)].
a, b Intracavity field power evolution and power spectral density (PSD) at fixed laser detuning corresponding to the the soliton hopping regime, in supermode basis. c, d Nonlinear dispersion relation for AS and S supermode families, respectively. White dots show points on the nonlinear dispersion relation where the spectral components are enhanced. Arrows connect these points with the corresponding spectral components.
The spatiotemporal diagrams for the diagonalized system [see Fig. 3(c, d)] reveal an insight about the soliton hopping state. The soliton hopping range [blue area in Fig. 3(a, b)] coincides with the emergence of a localized coherent structure in the S supermodes family accompanied by a characteristic solitonic step in the average intracavity power evolution as follow from Fig. 3(b). This coherent structure is generated via the emerged FWM pathways depicted in Fig. 2(d). Soliton in AS supermode family acts in this case as a source of photons which triggers the parametric processes, thereby resonantly populating the S parabola in the vicinity of the 0th mode (i.e., with the offset − Δω) via the process #5 (\({\hat{a}}_{{\rm{as}},{\mu }_{1}}^{\dagger }{\hat{a}}_{{\rm{s}},{\mu }_{2}}^{\dagger }{\hat{a}}_{{\rm{as}},{\mu }_{3}}{\hat{a}}_{{\rm{s}},{\mu }_{4}}\)). Energy conservation is ensured by populating supermodes offset by approximately + Δω. Cascaded parametric process #2 (\({\hat{a}}_{{\rm{s}},{\mu }_{1}}^{\dagger }{\hat{a}}_{{\rm{s}},{\mu }_{2}}^{\dagger }{\hat{a}}_{{\rm{s}},{\mu }_{3}}{\hat{a}}_{{\rm{s}},{\mu }_{4}}\)) populates the neighboring S supermodes similarly to the CW-pumped single resonator. Therefore, we assume that the coherent structure generated in S supermodes is a GS (i.e., supermode dissipative Kerr soliton). Thus, the origin of the oscillatory behavior can be seen as a time periodic interference of coherent structures living in different supermodes.
Figure 5 (a) shows the dimer dynamics at fixed pump laser detuning, in the soliton hopping regime in AS and S supermodes representation. It can be obtained numerically by seeding the solitonic state in the AS supermode (see Supplementary Note 4) and further tune into the soliton hopping state. The average power exhibits small amplitude oscillations around a certain value. Periodic oscillations in slow time results into the series of sidebands (similar to Kelly-sidebands widely present in the mode-locked lasers51) in the optical spectrum as has been shown in ref. 38. Corresponding nonlinear dispersion relation shows a ladder of lines similar to the breathing state, but the spacing between them is equal to the splitting between the DWs parabolas. The origin of the double maxima spectral sidebands is well seen in the supermode basis [see Fig. 5(b)]. They appear due to the different Kerr nonlinearity-induced shift of supermodes in the presence of inter-resonator detuning. White dots indicate the point where the ladder crosses dispersive parabolas and the continuing arrows indicate the corresponding spectral components enhancement. Both nonlinear dispersion relations depicted in Fig. 5(c, d) contain a corresponding DW parabola and the hopping ladder. Since the ladder crosses parabolas at slightly different mode numbers, sidebands have two maxima.
Experimental and numerical evidences of the deterministic single soliton generation
Deterministic generation of a single soliton state in optical microresonators is essential for a turn-key dissipative Kerr soliton-based broadband frequency combs generation. Indeed, passing the chaotic modulation instability stage, soliton arrangement inside the cavity can be arbitrary which leads to a non-homogeneous spectral profile due the interference of different solitonic components. One way to control and structure the soliton arrangement inside the cavity is to introduce a background modulation which leads to the generation of perfect soliton crystals35. However, the single soliton state is, nonetheless, difficult to achieve in this configuration.
Another way to naturally fall into the single soliton state has been described in ref. 52. It has been proposed to employ a strong avoided mode crossing with higher-order modes of the resonator, which leads to an extensive cavity Cerenkov radiation29,53,54. In this case, the soliton, being a line on the nonlinear dispersion relation20,55, crosses the distorted cavity mode, which leads to effective photon transfer toward the higher-order modes56. In this way, every soliton acts as a source of DWs. Therefore, if the energy of the DWs is sufficient to perturb the solitonic states the number of solitons will decay toward unity, where the state will be stabilized.
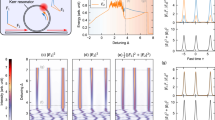
Here, we present a deterministic version of this mechanism utilizing discovered properties of the photonic dimer38. Due to the more complex dispersion landscape, the single soliton generation process does not require any additional interaction with higher-order mode, even though it is shown to be enhanced for certain supermodes due to the underlying symmetry57. Indeed, the periodic intra-resonator field enhancement due to the crossing of the S supermode parabola is found to be sufficient to trigger the process discussed in ref. 52. In order to verify this claim, we investigate both numerically and experimentally the GSs generation. Figure 6 shows the qualitative comparison of numerical and experimental phase diagrams. As follows from the numerical simulations of coupled LLEs (1), single soliton generation occurs when passing a threshold power of 0.9 W [see Fig. 6(b, c)]. A similar result follows from the experimental investigations. A schematic of the experimental setup is shown in Fig. 6(a). Single GSs are generated with an integrated Si3N4 photonic dimer driven by external cavity diode laser. The CW pump is amplified by an erbium doped fiber amplifier to achieve the power level need for the investigation of the threshold of the process. After passing a fiber polarization controller needed to guarantee that the solitons are generated in a single polarization mode family, the light is injected in the photonic dimer. The generated light is filtered by a fiber Bragg grating (FBG) and recorded with a fast oscilloscope. Figure 6(d, e) show 50 traces of the generated combs power at different values of the pump power as a function of the laser detuning from the position of the AS resonance. The central frequency of a widely tunable external cavity diode laser has been controlled by the piezo-tuning technique. Other details of the experimental measurements can be found in ref. 38, Methods section.
a Key elements of experimental setup for a single GS generation with an integrated Si3N4 photonic dimer driven by external cavity diode laser (ECDL). CW light is amplified by an erbium doped fiber amplifier (EDFA) and after passing a fiber polarization controller (FPC) is injected in the photonic dimer. The generated light is filtered by a fiber Bragg grating (FBG) and recorded with a fast oscilloscope (OSC). b–e Numerical and experimental confirmations of the single GS generation. b Simulation of average intracavity field evolution for different input powers as a function of pump laser detuning. For every value of the pump power there are ten traces superimposed. c Examples at three different powers. Single GSs are depicted by arrow. d, e Experimental confirmation obtained by piezo-tuning of the central frequency of a widely tunable ECDL over the AS resonance. For every value of the pump power there are 50 generated light traces superimposed.
Critically coupled resonators: split dissipation (\({\mathcal{P}}{\mathcal{T}}\)-broken)
Passing through an EP, which exhibits a singularity of nonlinear interactions efficiency, we enter the domain of split dissipation (\({\mathcal{P}}{\mathcal{T}}\)-symmetry broken phase), which exhibits drastically different dynamical features. We study soliton generation in this region and show that \({\mathcal{P}}{\mathcal{T}}\)-symmetry breaking leads to soliton generation in either cavities. The soliton localization can be switched by increasing the pump power and thereby flipping the broken \({\mathcal{P}}{\mathcal{T}}\)-symmetry. Four distinct dynamical states are identified, we observe among them on-demand perfect soliton crystals generation, which can be a promising alternative to the existing technology relying on the resonator’s mode interaction35.
Nonlinear coupling coefficients and their divergence at the exceptional point
The system of Eq. (1) can be diagonalized to Eq. (7) and Eq. (8) in the \({\mathcal{P}}{\mathcal{T}}\)-symmetry broken state in the same way as in the \({\mathcal{P}}{\mathcal{T}}\)-symmetric state, by applying a transformation matrix Tm such that \({T}_{{\rm{m}}}M{T}_{{\rm{m}}}^{-1}\) is diagonal [see Eq. (2)]. The diagonalization enables the computation of the nonlinear coupling coefficients describing the nonlinear interaction between the supermodes. The non-vanishing values of the nonlinear coupling coefficients are displayed in Fig. 7(c) as a function of J, where the external coupling κex,1 is varied quadratically with J to satisfy the critical coupling condition [Eq. (3)]. The nonlinear coupling coefficients are normalized by a real factor
equal to the square of the norm of Tm(1, 0)T. Indeed, the system is non-Hermitian such that Tm does not preserve the norm (the transformation is not Unitary). This means the variables ∣As,μ∣2, ∣Aas,μ∣2 are not proportional to the number of photons. The normalization allows the interpretation of tigK/N as a rate per photon.
a Schematic phase diagram represented as a function of input power and J. Four states are identified: soliton in resonator 1 (S1, blue region), soliton crystal in resonator 1 (C1, cyan region), coexistence of soliton in resonator 2 and periodic coherent structure resonator 1 (S2/C1, green region), and soliton in resonator 2 (S2, yellow region). The insets show the intracavity field intensity in the resonators 1 (blue) and 2 (red), at the parameter indicated by the gray dot. White color refers to the absence of stable solitonic state. b Intracavity power traces at different input powers for J/2π = 70 MHz. c Nonvanishing values of the nonlinear coupling coefficients and normalizing factor N presented as a function of J along the critical coupling condition. The crossing of the EP at J/κ0 = 0.5 corresponds to a singularity in coefficients t1, t2, and t4. Parameters for the simulations are κ0/2π = 50 MHz, κex,2 = 0, δ = 0, D1/2π = 180 GHz, D2/2π = 4 MHz.
The nonlinear coupling coefficients behave differently in the regime of split dissipation with d = 0 than in the regime of split resonance: t3, associated with even inter-band processes, vanishes completely, while t2, t4, (t1) become purely imaginary (real). These are related to odd inter-band (even intra-band) processes. At the EP (J/κ0 = 0.5) they diverge. The normalization corrects the divergence of t1 and t2, but not of t4, which exhibits a singularity at the EP. The constant value t1/N = 1 signifies that the rate of the intra-band FWM does not vary with J in this critical coupling condition.
Although the linear concepts of \({\mathcal{P}}{\mathcal{T}}\) symmetry are useful to understand the dynamics of the \({\mathcal{P}}{\mathcal{T}}\)-symmetry broken state, we observe that the solitonic states presented in the next section are not distributed spatially according to the supermode basis like in the \({\mathcal{P}}{\mathcal{T}}\)-symmetric regime. On the contrary, they are distributed in the resonator basis, which is diagonal with respect to nonlinearity.
Phase diagram: inter-resonator coupling vs pump power
We numerically explore the phase diagram under the condition of critical coupling in the nondegenerate dissipation regime [see Fig. 7(a)]. In Fig. 7(a, c), κex,1 is varied with J in the way that the critical coupling condition [Eq. (3)] is satisfied across the phase diagram and the dimer is in a state of broken \({\mathcal{P}}{\mathcal{T}}\)-symmetry (split dissipation). An EP is found at J = 0.5κ0 [see Fig. 1(d)].
Dynamical states in split dissipation (\({\mathcal{P}}{\mathcal{T}}\)-broken) regime
We differentiate four dynamical states in this regime: multi or single soliton in resonator 1 (S1, blue region), soliton crystal in resonator 1 (C1, cyan region), coexistence of periodic coherent structures in resonator 1 and soliton in resonator 2 (S2/C1, green region), and soliton in resonator 2 (S2, yellow region). The parameter regions enabling their generation are coloured on the phase diagram and their characteristic intracavity intensity profile are shown in the insets [see Fig. 7(a)]. White region refer to the absence of solitonic states.
At weak inter-resonator coupling (\(J\,<\,\frac{1}{2}{\kappa }_{0}\)), the system qualitatively follows the single resonator dynamics and features the S1 state, where DKSs exist in resonator 1 while resonator 2 only features their low-power projection. Increasing the inter-resonator coupling, dynamical regions corresponding to states C1, S2/C1, and eventually S2 are accessed.
The states are almost exactly partitioned in the resonator basis. For example, state S1 is confined in resonator 1 although a negligible amount (<<1%) is found in resonator 2. That is, the field amplitude distribution between the resonators does not follow the supermode distribution which is given by linear analysis. We assume that the nonlinearity changes the field distribution of the supermode, making them localized in the resonators. These supermodes are referred to as high-loss (confined in resonator 1) and low-loss (confined in resonator 2).
Parametric switching of the soliton-localization
In the range of 1.2κ0 ≲ J ≲ 1.8κ0, the four stable states can also be accessed by changing the pump power. Figure 7(b) shows the intracavity power evolution as a function of the laser detuning for pump power levels corresponding to four dynamical states in this range of J. Therefore, gradually increasing the pump power, states S2, S2/C1, C1, and S1 can be sequentially accessed.
In this process, the soliton-localization switches from resonator 2 to resonator 1. Linear analysis predicts that the resonant soliton will be confined in the low-loss supermode while the red-detuned CW background will be in the high-loss supermode [see Fig. 1(c)] as is the case for state S2 [inset of Fig. 7(a)]. However, despite the field distribution predicted by the linear analysis, the presence of nonlinearity in the system introduces a mechanism allowing for the parametric switching between the cavities.
Indeed, at low pump power, only the low-loss supermode has a quality factor sufficient for the soliton generation, resulting in state S2. At higher pump powers, both supermodes can sustain a coherent structure, leading to the coexistance of soliton and periodic coherent structure that has been observed in a limited intermediate range of parameters. Above a threshold, solitons are not generated in resonator 2. Moreover, in the C1 and S1 state, the parametric gain is able to compensate the difference of losses between the supermodes, and invert the \({\mathcal{P}}{\mathcal{T}}\) symmetry: the parametric gain (via intra-band FWM) is larger in the supermode localized in resonator 1 than in the other supermode making the state of broken \({\mathcal{P}}{\mathcal{T}}\)-symmetry flipped in comparison to the linear regime for longitudinal modes with μ ≠ 0.
We note that no specific solitonic state was found at the EP. We suppose that the Kerr shift lifts the degeneracy between the two supermodes. However, an extensive investigation of the soliton generation in the close vicinity of the EP is beyond the scope of this study.
Deterministic soliton crystal and efficient comb generation
In this section, we study the generation of state C1, which corresponds to the deterministic generation of a soliton crystal35. Figure 8 shows the numerical simulations of Eq. (1) setting the pump power to 0.2 W and J/2π = 75 MHz. Figure 8(a) shows the intracavity power in both resonators as a function of laser detuning. The incident light couples into both high- and low-loss, supermodes of the system simultaneously, such that the low-loss supermode features a chaotic regime while the high-loss supermode remains in the cnoidal wave regime [Fig. 8(c, e)]. After passing a critical detuning (~7κ0), resonator 2 leaves the chaotic regime without any coherent structures generated while cnoidal waves of resonator 1 transition into a soliton crystal state. Figure 8(b) shows that the crystal state at detuning I [Fig. 8(a)] is perfect35 with more than 100 dB of extinction over almost the full existence range.
a Intracavity power as a function of detuning. b, d Spectrum (b) and waveform (d) at detuning I. c, e Spatiotemporal diagrams for resonators 1 (c) and 2 (e). f Output power of the through port Pout, showing pump conversion above 75% into coherent comb. Pin = 0.2 W and J/2π = 75 MHz. Other parameters are identical to Fig. 7.
This state is known to exhibit a high conversion efficiency due to the high occupancy of the resonator 1 as shown in Fig. 8(b, d). Figure 8(f) shows the output power in the pump mode (μ = 0) and comb modes (μ ≠ 0). We observe that the perfect soliton crystal formation leads to a conversion efficiency higher than 75%. Also, we note that the pump is almost completely absorbed by the system, such that an effective nonlinear critical coupling is achieved. According to ref. 35, the soliton crystal is generated deterministically when the pump power is below the threshold to avoid spatiotemporal chaos under the condition that modal crossings with higher-order modes trigger background modulation. Here, we observe deterministic soliton generation in the absence of modal crossings.
Bright-dark solitons coexistence and their interaction with periodic coherent structures
We perform and analyze a simulation with J/2π = 75 MHz, Pin = 0.1W, as shown in Fig. 9 in order to generate S2/C1 state depicted by green in the phase diagram [Fig. 7(a)]. The power trace [Fig. 9(a)] shows the presence of a step in each resonator. The spectrum and temporal intensity at detuning I are shown in Fig. 9(b). A soliton exists in resonator 2, while background modulation reminiscent of C1 state are present in both resonators. The comb modes in both resonators are excited in this state, hinting at nonlinearly-induced \({\mathcal{P}}{\mathcal{T}}\)-transition that restores the \({\mathcal{P}}{\mathcal{T}}\) symmetry in the comb modes58,59. Spatiotemporal diagrams shown in Fig. 9(c, e) as a function of the laser detuning indicate that the S2/C1 state decays into a S2 state after the end of the soliton existence range in resonator 1. After transitioning to the S2 state, the field in resonator 1 acts as a source for resonator 2, resonantly supplying additional energy to the solitonic state. This results into a coexistence of a bright and dark solitons synchronously rotating in the resonators. This situation is similar to a dual fiber loop arrangement presented in ref. 60 but in the limit of equal cavities.
a Intracavity power as a function of laser detuning. b Spectrum and waveform at detuning I. c, e Spatiotemporal diagram in resonator 1 (c) and 2 (e). d, f Simulation at fixed detuning seeded with the state from I, showing the evolution of the bright-dark soliton pair interacting with periodic coherent structures in resonator 1. Pin = 0.1 W. Other parameters are identical to Fig. 8.
While the existence of a periodic coherent structure in resonator 1, bright-dark soliton pair can be generated as well. A simulation at a fixed detuning starting from the initial conditions I [Fig. 9(b)] is shown in the spatiotemporal diagrams Fig. 9(d, f). We observe that the soliton pair is bounded by the effective nonlinear potential induced by the periodic structures in the neighboring cavity. The spatiotemporal diagram depicts the possibility for the bright-dark soliton pair to tunnel from one potential unit cell to another interacting with their boundaries in an oscillatory manner. In addition to the fast oscillations, a random walk of the pair is observed at a slower timescale.
Discussion
In this article we investigate nonlinear dynamics in a driven-dissipative photonic dimer exhibiting an EP. We analyze the generation of DKSs on both sides of the EP, which acts as a demarcation of the dimer critical coupling conditions. These two regimes are the split resonance regime (with the preserved symmetry) and split dissipation regime (with broken symmetry), as found in conventional \({\mathcal{P}}{\mathcal{T}}\)-symmetric systems with gain and loss. Each regime exhibits unique nonlinear dynamics not found in the single resonator.
In the split resonance regime, which has been substantially discussed in ref. 38, we observe that dimer solitons can be generated in either supermodes, however, only the AS one exhibits non-conventional soliton dynamics related to the emerging efficient FWM pathways. The dynamics is conveniently expressed in the supermode basis, for which we developed the concepts of inter-band four-wave mixing. Supermode representation reveal that, despite the complexity of the dimer system, we are able to separate conventional single-resonator soliton dynamics from the DWs emerging in another supermode. Breathing state of the photonic dimer in the supermode basis appears to be similar to its single-resonator counterpart except for a small perturbation. In this case, the intra-resonator power of both cavities oscillates in phase. Rapid and counter-phase power oscillations (soliton hopping) are observed above a threshold pump power, originating from the generation of synchronized solitons in both supermodes. We highlight the fact that all the dynamics appearing in the split resonance regime can be well understood in the supermode representation.
The same does not apply to the regime of split dissipation. The absence of the resonance splitting implies the pumping of both supermodes simultaneously. Therefore, the most convenient representation in this case is the conventional resonator basis which exhibits the broken \({\mathcal{P}}{\mathcal{T}}\)-symmetry of the system. Satisfying the critical coupling condition, we impose different loss rates on the two resonators so resonator 1 becomes substantially overcoupled. We observe the generation of four different stable solitonic states localized in either or both resonators. In these states we observe: the synchronization of bright-dark soliton pairs (in resonators 2 and 1, respectively), the interaction of periodic coherent structures in resonator 1 with the bright-dark soliton pair, the deterministic generation of soliton crystal states with more than 75% pump conversion efficiency into the comb lines, and bright solitons in resonator 1. Thereby, the pump power enables the parametric switching of the soliton localization between resonator 1 and 2. The switching is induced by flipping the broken \({\mathcal{P}}{\mathcal{T}}\) symmetry so the lossy resonator 1 has more gain in the comb modes than resonator 2. We suspect nonlinearly-induced \({\mathcal{P}}{\mathcal{T}}\) transition to take place in the intermediate regime58,59. Moreover, we compute the nonlinear coupling coefficients between the supermodes. We normalize the divergence of two of them. One however seems to exhibit a singularity at the EP, which could demonstrate enhanced sensitivity in its vicinity61.
Concluding, we would like highlight the abundance of nonlinear dynamics occurring in the simplest element of soliton resonator lattices - photonic dimer. Despite the formal similarities with the single-mode dimer systems extensively studied in the context of non-Hermitian photonics, massively multimode nonlinear dimer exploiting another degree freedom reveals a variety of solitonic states and emerging dynamics, which cannot be covered in depth in one study. The fundamental aspects of this systems—two ideal coupled resonators—can be of interest far beyond the photonics community.
Methods
Numerical simulations
The system is modelled numerically based on Eq. (1). We employ step-adaptative Dormand-Prince Runge-Kutta method of Order 8(5,3). In the strong coupling regime, we approximate the dispersion operator by pseudo-spectral method. The coupling coefficient J is considered linear and frequency independent. The inter-resonator detuning δ is incorporated in the integrated dispersion. Seed noise is taken on the level of 10−6 photons per mode with uniformly distributed random phases.
The intracavity field is numerically reconstructed by exciting the system by adiabatically changing the central frequency of the pump ωp from blue to red side of resonances.
Numerical reconstruction of the phase diagram
We selected 14 values of pump power distributed logarithmically from 0.01 W to 1.5 W and 13 values of inter-resonator detuning distributed linearly from 0κ0 to 2.4κ0. For each set of parameters, we employ the conventional soliton generation scheme by scanning the resonance from blue to red-detuned side. The spatiotemporal and spectrum evolution diagrams in the resonator basis is used to identify the stable soliton state that is generated during the scan. Thus, for different points on the phase diagram, the value of detuning is not the same. If several stationary states are identified, we choose the first state in the soliton existence range. The phase diagram is averaged over 3 realizations and the pump laser frequency is swept at the speed \(\frac{1}{10}{\kappa }_{0}^{2}/2\pi\), corresponding to a change of frequency κ0 every 10 photon lifetimes (2π/κ0).
Experimental setup
The experimental setup used in this manuscript represents a simplified version of the experimental setups used in previous works31,38. We employ a tunable external cavity diode laser Toptica CTL operating in the optical C band (ECDL). The optical pump is amplified by an erbium-doped fiber amplifier (EDFA) and coupled to the photonic chip. Chips are fabricated with the photonic Damascene reflow process on Si3N462. The laser is tuned into the AS resonance via the piezo tuning method described in ref. 22. The generated light can be either detected at the transmission or drop waveguide ports. The pump light is reflected by a tunable FBG redirected by an optical circulator (CIRC), transmitted light impinges onto a fast photodiode (PD). The passive stability of the pump laser and fiber-chip coupling is sufficient to retain the state of the soliton during a scan.
Data availability
All data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
Code availability
Numerical codes used in this study are available from the corresponding author upon reasonable request.
References
Elliott, J. & Dawber, P. Symmetry in Physics, Volume 1 and 2 (Macmillan, 1979).
Chiu, C.-K., Teo, J. C., Schnyder, A. P. & Ryu, S. Classification of topological quantum matter with symmetries. Rev. Mod. Phys. 88, 035005 (2016).
Prigogine, I., Lefever, R., Goldbeter, A. & Herschkowitz-Kaufman, M. Symmetry breaking instabilities in biological systems. Nature 223, 913–916 (1969).
Bernstein, J. Spontaneous symmetry breaking, gauge theories, the higgs mechanism and all that. Rev. Mod. Phys. 46, 7 (1974).
Malomed, B. A. Spontaneous symmetry breaking, self-trapping, and Josephson oscillations (Springer, 2013).
Bender, C. M. & Boettcher, S. Real spectra in non-hermitian hamiltonians having \({\mathcal{P}}{\mathcal{T}}\) symmetry. Phys. Rev. Lett. 80, 5243–5246 (1998).
El-Ganainy, R. et al. Non-hermitian physics and pt symmetry. Nat. Phys. 14, 11–19 (2018).
Miri, M. A. & Alù, A. Exceptional points in optics and photonics. Science 363, eaar7709 (2019).
Özdemir, K., Rotter, S., Nori, F. & Yang, L. Parity-time symmetry and exceptional points in photonics. Nat. Mater. 18, 783–798 (2019).
Khurgin, J. B. Exceptional points in polaritonic cavities and subthreshold fabry–perot lasers. Optica 7, 1015–1023 (2020).
Rüter, C. E. et al. Observation of parity-time symmetry in optics. Nat. Phys. 6, 192–195 (2010).
Longhi, S. Parity-time symmetry meets photonics: a new twist in non-hermitian optics. EPL 120, 64001 (2017).
Feng, L., El-Ganainy, R. & Ge, L. Non-hermitian photonics based on parity-time symmetry. Nat. Photon. 11, 752–762 (2017).
Peng, B. et al. Loss-induced suppression and revival of lasing. Science 346, 328–332 (2014).
Alexeeva, N. V., Barashenkov, I. V., Sukhorukov, A. A. & Kivshar, Y. S. Optical solitons in \({\mathcal{PT}}\)-symmetric nonlinear couplers with gain and loss. Phys. Rev. A 85, 063837 (2012).
Konotop, V. V., Yang, J. & Zezyulin, D. A. Nonlinear waves in \({\mathcal{PT}}\)-symmetric systems. Rev. Mod. Phys. 88, 035002 (2016).
Suchkov, S. V. et al. Nonlinear switching and solitons in pt-symmetric photonic systems. Laser Photon. Rev. 10, 177–213 (2016).
Gaeta, A. L., Lipson, M. & Kippenberg, T. J. Photonic-chip-based frequency combs. Nat. Photon. 13, 158–169 (2019).
Dudley, J. M., Genty, G. & Coen, S. Supercontinuum generation in photonic crystal fiber. Rev. Mod. Phys. 78, 1135 (2006).
Skryabin, D. V. & Gorbach, A. V. Colloquium: looking at a soliton through the prism of optical supercontinuum. Rev. Mod. Phys. 82, 1287–1299 (2010).
Kippenberg, T. J., Gaeta, A. L., Lipson, M. & Gorodetsky, M. L. Dissipative kerr solitons in optical microresonators. Science 361, eaan8083 (2018).
Herr, T. et al. Temporal solitons in optical microresonators. Nat. Photon. 8, 145–152 (2014).
Wabnitz, S. Suppression of interactions in a phase-locked soliton optical memory. Opt. Lett. 18, 601–603 (1993).
Barashenkov, I. & Smirnov, Y. S. Existence and stability chart for the ac-driven, damped nonlinear schrödinger solitons. Phys. Rev. E 54, 5707 (1996).
Leo, F. et al. Temporal cavity solitons in one-dimensional kerr media as bits in an all-optical buffer. Nat. Photon. 4, 471 (2010).
Herr, T. et al. Mode spectrum and temporal soliton formation in optical microresonators. Phys. Rev. Lett. 113, 1–6 (2014).
Haelterman, M., Trillo, S. & Wabnitz, S. Dissipative modulation instability in a nonlinear dispersive ring cavity. Opt. Commun. 91, 401–407 (1992).
Chembo, Y. K. & Menyuk, C. R. Spatiotemporal lugiato-lefever formalism for kerr-comb generation in whispering-gallery-mode resonators. Phys. Rev. A 87, 053852 (2013).
Brasch, V. et al. Photonic chip–based optical frequency comb using soliton cherenkov radiation. Science 351, 357–360 (2016).
Jang, J. K., Erkintalo, M., Coen, S. & Murdoch, S. G. Temporal tweezing of light through the trapping and manipulation of temporal cavity solitons. Nat. Commun. 6, 1–7 (2015).
Guo, H. et al. Universal dynamics and deterministic switching of dissipative kerr solitons in optical microresonators. Nat. Phys. 13, 94–102 (2017).
Lucas, E., Karpov, M., Guo, H., Gorodetsky, M. L. & Kippenberg, T. J. Breathing dissipative solitons in optical microresonators. Nat. Commun. 8, 1–11 (2017).
Wang, Y. et al. Universal mechanism for the binding of temporal cavity solitons. Optica 4, 855–863 (2017).
Guo, H. et al. Intermode breather solitons in optical microresonators. Phys. Rev. X 7, 1–10 (2017).
Karpov, M. et al. Dynamics of soliton crystals in optical microresonators. Nat. Phys. 15, 1071–1077 (2019).
Yu, S.-P. et al. Spontaneous pulse formation in edgeless photonic crystal resonators. Nat. Photon. 15, 461–467 (2021).
Milián, C., Kartashov, Y. V., Skryabin, D. V. & Torner, L. Cavity solitons in a microring dimer with gain and loss. Opt. Lett. 43, 979–982 (2018).
Tikan, A. et al. Emergent nonlinear phenomena in a driven dissipative photonic dimer. Nat. Phys. 17, 604–610 (2021).
Hansson, T., Modotto, D. & Wabnitz, S. On the numerical simulation of Kerr frequency combs using coupled mode equations. Opt. Commun. 312, 134–136 (2014).
Yariv, A. Critical coupling and its control in optical waveguide-ring resonator systems. IEEE Photon. Technol. Lett. 14, 483–485 (2002).
Matsko, A. B. & Ilchenko, V. S. Optical resonators with whispering-gallery modes-part i: basics. IEEE J. Sel. Top. Quantum Electron. 12, 3–14 (2006).
Darmawan, S. & Chin, M. K. Critical coupling, oscillation, reflection, and transmission in optical waveguide-ring resonator systems. J. Opt. Soc. Am. B 23, 834–841 (2006).
Miller, S. A. et al. Tunable frequency combs based on dual microring resonators. Opt. Express 23, 21527–21540 (2015).
Coulibaly, S. et al. Turbulence-induced rogue waves in kerr resonators. Phys. Rev. X 9, 011054 (2019).
Leo, F., Gelens, L., Emplit, P., Haelterman, M. & Coen, S. Dynamics of one-dimensional Kerr cavity solitons. Opt. Express 21, 9180 (2013).
Kuznetsov, E. A. Solitons in a parametrically unstable plasma. DoSSR 236, 575–577 (1977).
Kibler, B. et al. Observation of kuznetsov-ma soliton dynamics in optical fibre. Sci. Rep. 2, 463 (2012).
Tusnin, A. K., Tikan, A. M. & Kippenberg, T. J. Nonlinear states and dynamics in a synthetic frequency dimension. Phys. Rev. A 102, 023518 (2020).
Milián, C., Gorbach, A. V., Taki, M., Yulin, A. V. & Skryabin, D. V. Solitons and frequency combs in silica microring resonators: Interplay of the raman and higher-order dispersion effects. Phys. Rev. A 92, 033851 (2015).
Driben, R., Yulin, A. & Efimov, A. Resonant radiation from oscillating higher order solitons. Opt. Express 23, 19112–19117 (2015).
Kelly, S. Characteristic sideband instability of periodically amplified average soliton. Electron. Lett. 28, 806–807 (1992).
Bao, C. et al. Spatial mode-interaction induced single soliton generation in microresonators. Optica 4, 1011 (2017).
Akhmediev, N. & Karlsson, M. Cherenkov radiation emitted by solitons in optical fibers. Phys. Rev. A 51, 2602 (1995).
Yang, Q.-F., Yi, X., Yang, K. Y. & Vahala, K. Spatial-mode-interaction-induced dispersive waves and their active tuning in microresonators. Optica 3, 1132–1135 (2016).
Leisman, K. P., Zhou, D., Banks, J., Kovačič, G. & Cai, D. Effective dispersion in the focusing nonlinear schrödinger equation. Phys. Rev. E 100, 022215 (2019).
Yi, X. et al. Single-mode dispersive waves and soliton microcomb dynamics. Nat. Commun. 8, 14869 (2017).
Tikan, A. et al. Symmetry protection of topological states in multimode photonic resonator chains. arXiv preprint arXiv:2011.07976 (2020).
Lumer, Y., Plotnik, Y., Rechtsman, M. C. & Segev, M. Nonlinearly induced pt transition in photonic systems. Phys. Rev. Lett. 111, 263901 (2013).
Hassan, A. U., Hodaei, H., Miri, M.-A., Khajavikhan, M. & Christodoulides, D. N. Nonlinear reversal of the \({\mathcal{PT}}\)-symmetric phase transition in a system of coupled semiconductor microring resonators. Phys. Rev. A 92, 063807 (2015).
Xue, X., Zheng, X. & Zhou, B. Super-efficient temporal solitons in mutually coupled optical cavities. Nat. Photon. 13, 616–622 (2019).
Hodaei, H. et al. Enhanced sensitivity at higher-order exceptional points. Nature 548, 187–191 (2017).
Pfeiffer, M. H. P. et al. Photonic damascene process for integrated high-q microresonator based nonlinear photonics. Optica 3, 20–25 (2016).
Acknowledgements
This publication was supported by Contract D18AC00032 (DRINQS) from the Defense Advanced Research Projects Agency (DARPA), Defense Sciences Office (DSO). This material is based upon work supported by the Air Force Office of Scientific Research under award number FA9550-19-1-0250. This work was further supported by the EU H2020 Research and Innovation Program under the Marie Skłodowska-Curie grant agreement 812818 (MICROCOMB), and by the Swiss National Science Foundation under grant agreement No. 192293. Si3N4 samples were fabricated and grown in the Center of MicroNanoTechnology (CMi) at EPFL.
Author information
Authors and Affiliations
Contributions
K.K. and A.T. developed and performed theoretical and numerical analysis with the assistance of A. Tu. and H.G. J.R., and M.C. performed experiments and data analysis with the assistance of A.T. A.T. and K.K. wrote the paper. T.J.K. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Komagata, K., Tusnin, A., Riemensberger, J. et al. Dissipative Kerr solitons in a photonic dimer on both sides of exceptional point. Commun Phys 4, 159 (2021). https://doi.org/10.1038/s42005-021-00661-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00661-w
This article is cited by
-
Parity-time symmetry enabled ultra-efficient nonlinear optical signal processing
eLight (2024)
-
Nonlinear dynamics and Kerr frequency comb formation in lattices of coupled microresonators
Communications Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.