Abstract
Nanoscale coherent imaging has emerged as an indispensable modality, allowing to surpass the resolution limit given by classical imaging optics. At the same time, attosecond science has experienced enormous progress and has revealed the ultrafast dynamics in complex materials. Combining attosecond temporal resolution of pump-probe experiments with nanometer spatial resolution would allow studying ultrafast dynamics on the smallest spatio-temporal scales but has not been demonstrated yet. To date, the large bandwidth of attosecond pulses poses a major challenge to high-resolution coherent imaging. Here, we present broadband holography-enhanced coherent imaging, which enables the combination of high-resolution coherent imaging with a large spectral bandwidth. By implementing our method at a high harmonic source, we demonstrate a spatial resolution of 34 nm in combination with a spectral bandwidth of 5.5 eV at a central photon energy of 92 eV. The method is single-shot capable and retrieves the spectrum from the measured diffraction pattern.
Similar content being viewed by others
Introduction
Coherent diffractive imaging (CDI) has been a driving force for advances in short-wavelength imaging throughout the past decade1,2,3,4. The reason for its widespread use is that CDI bypasses imaging optics, resulting in three major advantages over classical, lens-based imaging: a simple experimental configuration, no aberrations induced by imperfect optical components, and flux efficiency. While the experimental setup tends to simplify through the lens-less nature of CDI, this advantage comes together with the need for sophisticated inverse modeling, including phase retrieval techniques. In recent years, CDI has seen great progress. Experiments from the soft to the hard X-ray range have been performed at large scale facilities. The spatial resolution has been pushed to ~5 nm5 and a variety of applications have been enabled ranging from 3D imaging of integrated circuits6 or whole cells7 to chemical sensitive imaging5 of complex solid-state samples.
Lately, lens-less imaging using table-top high harmonic generation (HHG) has gained attention8, since these sources allow performing experiments on an optical table that were so far only possible at large scale facilities9,10,11,12,13,14. These sources can provide extremely broad spectra and pulses in the attosecond regime15 with a natural synchronization to the ultrashort driving laser pulses. As a result, attosecond pulses generated by HHG are intrinsically suitable for ultrafast studies by means of pump probe experiments, and have quickly evolved as a tool to answer fundamental questions in atomic16, molecular17, and solid-state physics18,19. Today, isolated attosecond pulses with µJ pulse energies are available20 and attosecond pulses at free-electron lasers are emerging as well21. An open challenge is the combination of attosecond science with nanoscale imaging, unlocking access to ultrafast phenomena at mesoscopic spatial scales. The required bandwidth leads to a shortened longitudinal coherence length, which reduces the contrast in the diffraction pattern and thus limits the spatial resolution22.
So far, several sophisticated methods for the reconstruction of samples using broadband illumination have been demonstrated. Broadband extensions23,24 to multishot techniques such as Ptychography25,26 or the combination of Fourier transform spectroscopy with lens-less imaging27 have been demonstrated but appear difficult to be implemented in a pump-probe scenario, where additional scanning of the pump-probe delay is required. In contrast, advanced phase retrieval algorithms28 or deconvolution-based monochromatization of the measured diffraction pattern29,30 demonstrated broadband CDI from a single measured diffraction pattern with µm resolution with visible light and hard X-rays. However, both approaches require precise knowledge about the spectrum of the illumination, which might not be accessible if shot-to-shot fluctuations are present. Generally, applications have so far been restricted to narrow bandwidth and temporal resolution in the few-ten femtosecond regime31,32,33.
In this work, we present broadband holography-enhanced coherent diffraction imaging. In short, multiple reference structures around the sample provide additional information about the sample and the illumination, which is encoded in the measured diffraction pattern. This allows extracting the spectrum of the illuminating light source34 as well as a monochromatized and deblurred amplitude- and phase image of the sample. The retrieved spectrum and deblurred sample can be used as input to a broadband iterative phase retrieval algorithm for further refinement of the image. The holographic input data significantly improves the reliability, convergence, speed, and image quality of the iterative phase retrieval. In a proof-of-principle experiment, using a high harmonic source centered at 92 eV, a spatial resolution of 34 nm has been achieved with a bandwidth of 5.5 eV, which corresponds to a theoretical Fourier-limited pulse duration of 380 as.
Results and discussion
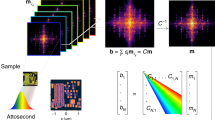
For the presented experiment we used a laser-driven, high-order harmonic (HHG) source, which generates a broadband XUV spectrum up to 100 eV and is focused on the sample (Fig. 1a). From this very broadband spectrum, a bandwidth of 5.5 eV at a central photon energy of 92 eV is selected, which corresponds to a relative bandwidth λ/Δλ of 17 and a theoretical Fourier-limited pulse duration of 380 as (Fig. 1b). A more detailed description of the XUV source and experimental geometry is given in the methods section. A resolution test chart with a diameter of 1 µm is placed in the focus of the XUV-beam and acts as a test sample. The sample is similar to a Siemens star and consists of small apertures in an otherwise absorbing material (see Fig. 1c). Thus, our test sample is non-dispersive. To provide holographic reference waves, five circular apertures with a diameter of 90 nm are placed evenly spaced around the sample on a circle with a radius of 2 µm. Adding the reference apertures enables mask-based Fourier transform holography35 (FTH). The recorded hologram is shown in Fig. 1d.
a A spatially coherent high-harmonic beam is focused on the sample using a broadband multilayer mirror (ML-mirror). From the broadband extreme ultraviolet (XUV) continuum a bandwidth of 5.5 eV is selected at a central photon energy of 92 eV. The resulting spectrum is shown in arbitrary units (a.u.) in b. The small inset shows the Fourier transform of the spectrum assuming a flat spectral phase, which yields a Fourier limited pulse duration of 380 as. c SEM (scanning electron microscope) image of the sample: a resolution-test pattern is located in the center and surrounded by five reference apertures. The scale bar in c corresponds to 2 µm and color white correspongs to a high secondary electron intensity. d Measured (intensity) hologram of the sample in log-scale. The scale bar in d corresponds to 10 µm−1 and the intensity is shown in arbitrary units (a.u.).
Broadband Fourier transform holography
In order to extract a high-resolution image of the sample, we follow a two-step approach. First, we extract an amplitude and phase image of the sample from the hologram via FTH. Thus, a simple Fourier transform of the measured hologram (Fig. 1d) yields a representation of the objects exit wave, henceforth referred to as reconstructed object, as shown in Fig. 2a–d. Since the object is surrounded by five reference pinholes, five reconstructed objects (cross-correlation of the sample with the reference), and their complex conjugates are visible. A closer look at one of the reconstructions (Fig. 2b) shows that the reconstructed object is noticeably smeared, which can be attributed to the broad-bandwidth radiation used in the experiment. A vertical and horizontal lineout along the features of the resolution test target is shown in Fig. 2d. Clearly, the smearing effect (i.e., the spatial resolution) is anisotropic. The features along the horizontal direction are resolved, while the features along the vertical direction are blurred. This behavior is explained in more detail in Supplementary Note 1. Mainly, the large distance between the reference hole and sample causes a large shift of the cross-correlation term with the wavelength. For a broadband source, this effect leads to continuous smearing along the pinhole-sample direction, whereas the smearing in the perpendicular direction is much weaker. The influence of a broadband spectrum on the sample reconstruction has been observed in previous experiments36, but was so far accounted for by a specialized sample design37,38.
a Fourier transform of the measured hologram shown in Fig. 1d. The intense autocorrelation in the center is blocked and only the five cross-correlation terms and their corresponding complex-conjugates are shown. The scale bar represents 1.5 µm. b A magnified version of the top cross-correlation. c A magnified version of a smeared cross-correlation of two reference apertures. d The vertical and horizontal lineouts indicated in b. The amplitude is given in arbitrary units (a.u.).
In order to de-smear the reconstructed object, we utilize the diverse information provided by the five pinholes. In Fig. 2a one can clearly see that each cross-correlation term is smeared in a different direction. Instead of averaging over all reconstructed objects39, we thus combine the non-smeared spatial frequencies from all cross-correlation terms to a single de-smeared image. For doing so, we cut the five reconstructed objects (see Fig. 3a) from the reconstruction and apply a Fourier transform on each of the reconstructions (Fig. 3b). In Fourier space, we apply a suitable filter on each reconstructed object. Here, five binary, hourglass-shaped masks (small insets in Fig. 3b) are used, which keep the high-resolution spatial frequency components along the axis perpendicular to the sample-pinhole direction and discard the low-resolution spatial frequency components. In essence, our method is similar to the application of Yaroslavsky-Caulfield filters40, which are used in monochromatic experiments using extended references to enhance the resolution41.
a Each cross-correlation term is transformed into Fourier space by applying an fast Fourier transform (FFT) (b), where a binary filter is applied (small inset), which preserves the high-resolution spatial frequencies. The spatial frequencies are summed and yield a high-resolution Fourier space image which is shown in c. d An enlarged smeared cross-correlation term before the broadband Fourier transform holography (FTH) method was applied and e shows the result of the broadband FTH method. The scalebar in d corresponds to 1 µm and is shared for d and e. The amplitude and intensity is given in arbitrary units (a.u.).
The remaining spatial frequency components are summed up (Fig. 3c) and finally the improved reconstruction is obtained by an inverse Fourier transform. Compared to the initial reconstruction (Fig. 3d), the resulting high-resolution reconstruction of the object (Fig. 3e) shows a significantly improved image quality. A lineout for both reconstructions is shown in Fig. 4. Features separated by a distance of 90 nm, which were previously not resolved, are now clearly distinguishable. A knife-edge test along the white line in Fig. 3d suggests a resolution of 115 nm for standard FTH, which is in good accordance with the temporal coherence limit given by the bandwidth (110 nm). In contrast, the broadband-FTH method achieves a resolution of 65 nm along the white line in Fig. 3e, which agrees well with the 60 nm limit imposed by the diameter of the reference aperture42 (~70% of the diameter). So far, we have demonstrated an improved resolution of 65 nm using broadband FTH, which beats the temporal coherence limit by a factor of 1.7. From theory this de-smearing factor can be as large as 5, more details can be found in the Supplementary Note 2.
Lineouts along the white-line in Fig. 3d (blue, standard FTH), Fig. 3e (orange, broadband FTH) and Fig. 5e (green, phase retrieval of the broadband FTH method). The achieved resolution was estimated using a knife-edge test on the standard Fourier transform holography (FTH) reconstruction and broadband FTH reconstruction. The amplitude is given in arbitrary units (a.u.).
Broadband iterative phase retrieval
In a second step, we refine the reconstructed object by an iterative phase retrieval algorithm43, which enhances the resolution and signal-to-noise ratio of the reconstruction44,45. Methods to reconstruct the phase for broadband diffraction patterns have already been developed, but require a precise measurement of the spectrum28,30. At this point we can benefit from the additional information encoded in the hologram again, namely, we can extract the spectrum from it. For this purpose, we investigated the cross-correlations of the reference apertures (see Fig. 2c), which are smeared by the source spectrum in the same way as the sample is. An average of multiple smeared cross-correlation terms is shown in Fig. 5a. The smearing can be described by a convolution of the reference aperture cross-correlation term with the spectrum used. Therefore, the spectrum can be recovered by a deconvolution procedure if the convolution kernel is known. The convolution kernel was estimated from the cross-correlation term itself assuming a circular shape of the reference aperture by averaging along the horizontal direction (Fig. 5c). In the next step the spectrum is recovered by a deconvolution of the smeared axis (Fig. 5b). The recovered spectrum is shown in Fig. 5d (blue) and agrees well with the measured spectrum (orange). In the next step, the recovered spectrum and the result of the broadband FTH method are seeded into a broadband iterative phase retrieval algorithm28. The reconstruction algorithm assumes a non-dispersive object, which is a valid assumption for our experiment. The result of the phase retrieval is shown in Fig. 5e. The lineouts of the recovered object from the iterative phase retrieval procedure, as indicated in Fig. 5e, are compared to the lineouts from the FTH method (see Fig. 3d, e) in Fig. 4. It is seen that the combined phase retrieval and broadband FTH method achieves the highest resolution. We estimate the improved resolution to be 34 nm using the 1/e criterion on the phase retrieval transfer function46 (PRTF), which is close to the Abbe-limit of 16 nm. The reconstruction is fast, since only 200 iterations were needed for the final reconstruction. A good starting point was already given by the broadband FTH reconstruction. Furthermore, the reconstruction is also particularly stable, since the quality of the reconstruction did not change with the reconstruction parameters (e.g. beta parameter). Although the diffraction pattern was recorded with a high dynamic range and sufficient oversampling, an unseeded phase retrieval failed. Note that for the employed phase retrieval, all necessary input data including the spectrum are obtained from a single measured hologram. Thus, the presented holography-enhanced coherent imaging method can be used in case of significant pulse-to-pulse fluctuations of the spectrum e.g., at unseeded free-electron-lasers or single-shot HHG experiments47. A requirement for using the presented 2-step approach is a uniformly distributed spectrum over the extend of the sample, because a single object is reconstructed for the entire spectrum. This was the case in the presented experiment.
a The average of five cross-correlations of two reference apertures each. b, c The lineouts of the averaged cross-correlation terms, which are averaged over the vertical and horizontal axis. d Spectrum obtained by deconvolving b with c, which is compared to the measured spectrum (orange). e Reconstructed object after applying a broadband, iterative phase retrieval algorithm on the measured diffraction pattern with Fig. 3e as the initial field and Fig. 5d as input spectrum. The scale bar in e corresponds to 1 µm. The amplitude and spectral intensity is given in arbitrary units (a.u.).
Discussion
In previous polychromatic lens-less imaging experiments using HHG-sources, comb-like spectra have been used27,48,49,50,51,52. Here, we have shown the combination of a broad and continuous XUV-spectrum from a HHG source with nano-scale imaging. Time-resolved pump-probe experiments are often performed near resonances where the sample is dispersive. In the future, the presented method could be combined with more advanced phase retrieval algorithms53, which allow reconstructing dispersive samples and benefit from the good initial guess provided by the broadband FTH method. This will pave the way to the observation of ultrafast transport and transfer processes of charges18,19 and spins54,55,56, which are the basis of next-generation electronics, data storage, energy conversion, and energy storage devices. Further, the presented approach is robust. First, FTH itself is stable due to the use of a monolithic mask design57,58, and at the same time offers a fast and direct reconstruction of the object. Second, a good starting point for the iterative algorithm as well as the required spectrum are extracted from a single hologram. Thus, the presented method is ideally suited for single-shot imaging using broadband table-top HHG sources and can be employed at synchrotron-radiation sources, since a broader bandwidth is tolerated and thus less spectral filtering is necessary. Moreover, the presented approach can be applied at free-electron-lasers, since our method is single-shot capable, scanning free, and tolerates fluctuations of the spectrum, pointing and power of the source. Thus, broadband holography-enhanced coherent imaging increases the usable bandwidth in FTH experiments, and promises a combination of nanoscale imaging with ultrafast experiments that require a broad bandwidth.
Conclusion
In summary, we demonstrated holography enhanced coherent diffractive imaging with a broadband high harmonic source on a non-dispersive test-sample. In a proof-of-concept experiment, a broad XUV continuum was generated. A bandwidth of 5.5 eV was selected by multilayer mirrors at a photon energy of 92 eV, which corresponds to a relative energy bandwidth of 17. Using a broadband extension to FTH a spatial resolution of 65 nm was demonstrated, which is beyond the temporal coherence limit. Moreover, it was shown that the broadband spectrum can be recovered from the measured hologram as well, which allows seeding the spectrum and the broadband FTH result to a broadband iterative phase retrieval algorithm. Combining these methods, a spatial resolution of 34 nm has been demonstrated with a bandwidth supporting pulses as short as 380 as.
Methods
Sample fabrication
A Si3N4 membrane with a thickness of 50 nm was coated with 250 nm Cu, which results in an overall transmissivity of 4.5 × 10−7 at 92 eV and acts as an absorber. The resolution test sample and reference apertures were structured by means of focused gallium ion beam milling on a FEI Helios NanoLab G3 UC. The resolution test sample and the corresponding reference apertures were written in parallel using an ion energy of 30 keV and current of 7.7 pA to achieve the high aspect ratio of the holes and bridges. After fabrication, the size of the reference apertures were measured using a transmission electron microscope yielding a diameter of 90 nm. The sample diameter was chosen to be 1 µm. The reference pinholes were placed at a radius of 2 µm equally spaced around the sample. Since the resolution imposed by the bandwidth depends on the maximal size of the sample (see Eq. 1), the reference aperture should be placed as close as possible to the object. However, certain design rules have to be followed, which are explained in more detail in Supplementary Note 3.
Experiment and data processing
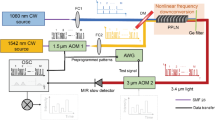
A high-power fiber laser with a central wavelength of 1 µm was compressed to a pulse duration of 7 fs with a pulse energy of 400 µJ at a repetition rate of 76 kHz, which results in an average power of 30 W. The IR-laser is focused in a gas jet with a diameter of 500 µm, where argon with a backing pressure of 0.6 bar is applied. A broadband spectrum reaching up to 100 eV is generated with a flux of 7 × 109 phot/s/eV at 92 eV. A more detailed description of the XUV-source has been recently published59. To separate the high-power IR laser beam from the XUV-beam 4 grazing incidence plates reflecting XUV radiation, and transmitting the IR beam followed by two Zr filters with a thickness of 200 nm are used. Three broadband XUV-multilayer mirrors with a peak reflectivity each of 30 % at 92 eV are used to select a bandwidth of 5.5 eV (FWHM) and to focus the beam on the holography sample. The spectrum incident on the sample (Fig. 1b) was calculated by multiplication of the measured spectrum of the HHG source, which was measured in an independent measurement using an XUV spectrometer, with the calibrated reflectivity of the three multilayer mirrors. The theoretical Fourier limit of the spectrum on the sample was calculated to be 380 as. The true XUV pulse duration was not measured but is expected to be in the femtosecond range. It was previously shown that CEP stable laser with similar parameters indeed provide isolated attosecond pulses60. Note that the laser used for this experiment is not CEP stable and therefore does not generate isolated attosecond pulses. However, it has already been shown61 that such a laser can be made CEP stable and thus also generate isolated attosecond pulses. Since a high degree of spatial coherence is required for lensless imaging experiments62, the spatial coherence was characterized with a double slit. A visibility of better than 0.9 was measured59, which justifies the assumption of a spatially coherent beam. The XUV-camera (Andor iKon-L) was placed 30 mm behind the sample, which results in a NA of 0.42 and therefore in a diffraction limit of 16 nm. During the measurements, the CCD was cooled down −50 °C. The hologram in Fig. 1d) was recorded with a total exposure time of 120 s using 2 by 2 on-chip binning. After the measurement, the hologram was corrected for the curvature on the Ewald’s sphere, which is due to the high numerical aperture63. The resolution limit Δr, imposed by the bandwidth of the source was estimated using28
where D corresponds to the largest extend of the sample (2.5 µm for a single reference aperture) and lc to the longitudinal coherence length, which was approximated by the coherence length of a Gaussian-shaped spectrum (\(l_{\rm{c}} = \sqrt {2\ln (2)} /\pi \ast \lambda ^2/{\Delta}\lambda\)) and results in a bandwidth-limited resolution of 110 nm.
Recovery of the spectrum
In order to reconstruct the spectrum, the smeared cross-correlation of two reference apertures was used (Fig. 2a). To increase the signal-to-noise ratio, we averaged over several cross-correlations. For this purpose, the smeared cross-correlation terms were isolated, rotated by an angle of 36°, 72°, 108°, and 144°, respectively and added up. The smearing along the horizontal axis can be described in a good approximation by a convolution of the monochromatic case with the spectrum. A detailed mathematical description can be found in Supplementary Note 4. Hence, the spectrum can be recovered by a deconvolution, if the convolution kernel (i.e., the monochromatic cross-correlation of two reference apertures) is known. The 1D line profile of the smeared cross-correlation term, which is shown in Fig. 5b, was extracted by calculating the mean value along the vertical axis. The next step is to estimate the convolution kernel. Since the reference aperture has a circular shape and the smearing along the vertical axis can be neglected, the vertical profile of the cross-correlation can be used as an approximation of the convolution kernel. To improve the signal-to-noise ratio, the convolution kernel, as it is shown in Fig. 5c, was approximated by the average along the horizontal axis. Finally, the spectrum was extracted by deconvolving the vertically averaged horizontal lineout (Fig. 5b) by the horizontally averaged vertical lineout (Fig. 5c). The deconvolution was calculated by using the Richardson-Lucy algorithm64,65.
Broadband, iterative phase retrieval algorithm
The broadband-FTH result was seeded as the initial field to the broadband28 version of the RAAR-algorithm in combination with the shrink-wrap algorithm66. The initial support was estimated by applying a threshold on the broadband-FTH reconstruction. Next, we ran the shrink-wrap algorithm for five iterations, where we updated the support by applying a threshold on the convolution with a Gaussian kernel. We used a threshold of 0.2 for the inner part, where the object is located and a threshold of 0.05 at the area where the pinhole is located. The different limits were used because the exposure of the reference apertures was much weaker than the exposure of the test targe area. After we obtained the support we ran the algorithm for 200 iterations using a beta parameter of 0.95 and updated the support every 20 iterations. The achieved resolution was evaluated with the PRTF (Supplementary Note 5), which results in a resolution of 34 nm.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Miao, J., Ishikawa, T., Robinson, I. K. & Murnane, M. M. Beyond crystallography: diffractive imaging using coherent X-ray light sources. Science 348, 530–535 (2015).
Chapman, H. N. & Nugent, K. A. Coherent lensless X-ray imaging. Nat. Photonics 4, 833–839 (2010).
Kaulich, B., Thibault, P., Gianoncelli, A. & Kiskinova, M. Transmission and emission x-ray microscopy: operation modes, contrast mechanisms and applications. J. Phys. Condens. Matter 23, 83002 (2011).
Pfeiffer, F. X-ray ptychography. Nat. Photonics 12, 9–17 (2018).
Shapiro, D. A. et al. Chemical composition mapping with nanometre resolution by soft X-ray microscopy. Nat. Photonics 8, 765–769 (2014).
Holler, M. et al. High-resolution non-destructive three-dimensional imaging of integrated circuits. Nature 543, 402–406 (2017).
Jiang, H. et al. Quantitative 3D imaging of whole, unstained cells by using X-ray diffraction microscopy. Proc. Natl Acad. Sci. USA 107, 11234–11239 (2010).
Rothhardt, J., Tadesse, G. K., Eschen, W. & Limpert, J. Table-top nanoscale coherent imaging with XUV light. J. Opt. 20, 113001 (2018).
Baksh, P. D. et al. Quantitative and correlative extreme ultraviolet coherent imaging of mouse hippocampal neurons at high resolution. Sci. Adv. 6, eaaz3025 (2020).
Kfir, O. et al. Nanoscale magnetic imaging using circularly polarized high-harmonic radiation. Sci. Adv. 3, eaao4641 (2017).
Tanksalvala, M. et al. Nondestructive, high-resolution, chemically specific 3D nanostructure characterization using phase-sensitive EUV imaging reflectometry. Sci. Adv. 7, 9667–9694 (2021).
Tadesse, G. K. et al. Wavelength-scale ptychographic coherent diffractive imaging using a high-order harmonic source. Sci. Rep. 9, 1–7 (2019).
Tadesse, G. K. et al. High resolution XUV Fourier transform holography on a table top. Sci. Rep. 8, 1–8 (2018).
Gardner, D. F. et al. Subwavelength coherent imaging of periodic samples using a 13.5 nm tabletop high-harmonic light source. Nat. Photonics https://doi.org/10.1038/NPHOTON.2017.33 (2017).
Li, J. et al. 53-attosecond X-ray pulses reach the carbon K-edge. Nat. Commun. 8, 1–5 (2017).
Krausz, F. & Ivanov, M. Attosecond physics. Rev. Modern Phys. https://doi.org/10.1103/RevModPhys.81.163 (2009).
Kobayashi, Y., Chang, K. F., Zeng, T., Neumark, D. M. & Leone, S. R. Direct mapping of curve-crossing dynamics in IBr by attosecond transient absorption spectroscopy. Science 364, 79–83 (2019).
Schultze, M. et al. Attosecond band-gap dynamics in silicon. Science 346, 1348–1352 (2014).
Zürch, M. et al. Direct and simultaneous observation of ultrafast electron and hole dynamics in germanium. Nat. Commun. 8, 1–11 (2017).
Takahashi, E. J., Lan, P. & Midorikawa, K. Generation of an isolated attosecond pulse with microjoule-level energy. in Optics InfoBase Conference Papers QTh5B.10 (Optical Society of America (OSA), 2012). https://doi.org/10.1364/qels.2012.qth5b.10.
Hartmann, N. et al. Attosecond time-energy structure of X-ray free-electron laser pulses. Nat. Photonics 12, 215–220 (2018).
van der Veen, F. & Pfeiffer, F. Coherent x-ray scattering. J. Phys. Condens. Matter 16, 5003–5030 (2004).
Batey, D. J., Claus, D. & Rodenburg, J. M. Information multiplexing in ptychography. Ultramicroscopy 138, 13–21 (2014).
Enders, B. et al. Ptychography with broad-bandwidth radiation. Appl. Phys. Lett. 104, 171104 (2014).
Thibault, P. et al. High-resolution scanning x-ray diffraction microscopy. Science 321, 379–382 (2008).
Maiden, A. M. & Rodenburg, J. M. An improved ptychographical phase retrieval algorithm for diffractive imaging. Ultramicroscopy 109, 1256–1262 (2009).
Witte, S., Tenner, V. T., Noom, D. W. & Eikema, K. S. Lensless diffractive imaging with ultra-broadband table-top sources: From infrared to extreme-ultraviolet wavelengths. Light Sci. Appl. 3, 163 (2014).
Abbey, B. et al. Lensless imaging using broadband X-ray sources. Nat. Photonics 5, 420–424 (2011).
Dilanian, R. A. et al. Diffractive imaging using a polychromatic high-harmonic generation soft-x-ray source. J. Appl. Phys. 106, 23110 (2009).
Huijts, J. et al. Broadband coherent diffractive imaging. Nat. Photonics https://doi.org/10.1038/s41566-020-0660-7 (2020).
Karl, R. M. et al. Full-field imaging of thermal and acoustic dynamics in an individual nanostructure using tabletop high harmonic beams. Sci. Adv. 4, eaau4295 (2018).
Ravasio, A. et al. Single-shot diffractive imaging with a table-top femtosecond soft X-ray laser-harmonics source. Phys. Rev. Lett. 103, 28104 (2009).
Wang, T. et al. Femtosecond single-shot imaging of nanoscale ferromagnetic order in Co/Pd multilayers using resonant X-ray holography. Phys. Rev. Lett. 108, 267403 (2012).
Flewett, S. & Eisebitt, S. Experimental geometry for simultaneous beam characterization and sample imaging allowing for pink beam Fourier transform holography or coherent diffractive imaging. Appl. Opt. 50, 852–858 (2011).
Eisebitt, S. et al. Lensless imaging of magnetic nanostructures by X-ray spectro-holography. Nature 432, 885–888 (2004).
Pfau, B. et al. Femtosecond pulse X-ray imaging with a large field of view. N. J. Phys. 12, 95006 (2010).
Williams, G. O. et al. Fourier transform holography with high harmonic spectra for attosecond imaging applications. Opt. Lett. 40, 3205 (2015).
Willems, F. et al. Multi-color imaging of magnetic Co/Pt heterostructures. Struct. Dyn. 4, 14301 (2017).
Schlotter, W. F. et al. Multiple reference Fourier transform holography with soft x rays. Appl. Phys. Lett. 89, 163112 (2006).
Yaroslavsky, L. P. & Caulfield, H. J. Deconvolution of multiple images of the same object. Appl. Opt. 33, 2157 (1994).
Zhu, D. et al. High-resolution X-ray lensless imaging by differential holographic encoding. Phys. Rev. Lett. 105, 43901 (2010).
Schlotter, W. F. Lensless Fourier Transform Holography with Soft x-Rays (Stanford University, 2007).
Fienup, J. R. Phase retrieval algorithms: a comparison. Appl. Opt. 21, 2758 (1982).
Eisebitt, S. et al. Scalable approach for lensless imaging at x-ray wavelengths. Appl. Phys. Lett. 84, 3373–3375 (2004).
Tenner, V. T., Eikema, K. S. E. & Witte, S. Fourier transform holography with extended references using a coherent ultra-broadband light source. Opt. Express 22, 25397 (2014).
Chapman, H. N. et al. High-resolution ab initio three-dimensional x-ray diffraction microscopy. J. Opt. Soc. Am. 23, 1179 (2006).
Gauthier, D. et al. Single-shot femtosecond x-ray holography using extended references. Phys. Rev. Lett. 105, 93901 (2010).
Chen, B. et al. Multiple wavelength diffractive imaging. Phys. Rev. A 79, 23809 (2009).
Loetgering, L. et al. Tailoring spatial entropy in extreme ultraviolet focused beams for multispectral ptychography. Optica 8, 130 (2021).
Zhang, B. et al. Ptychographic hyperspectral spectromicroscopy with an extreme ultraviolet high harmonic comb. Opt. Express 24, 18745 (2016).
Jansen, G. S. M., Rudolf, D., Freisem, L., Eikema, K. S. E. & Witte, S. Spatially resolved Fourier transform spectroscopy in the extreme ultraviolet. Optica 3, 1122 (2016).
Malm, E. et al. Singleshot polychromatic coherent diffractive imaging with a high-order harmonic source. Opt. Express 28, 394 (2020).
Malm, E., Fohtung, E. & Mikkelsen, A. Multi-wavelength phase retrieval for coherent diffractive imaging. Opt. Lett. 46, 13 (2021).
Siegrist, F. et al. Light-wave dynamic control of magnetism. Nature 571, 240–244 (2019).
Hofherr, M. et al. Ultrafast optically induced spin transfer in ferromagnetic alloys. Sci. Adv. 6, eaay8717 (2020).
Dewhurst, J. K., Elliott, P., Shallcross, S., Gross, E. K. U. & Sharma, S. Laser-induced intersite spin transfer. Nano Lett. 18, 1842–1848 (2018).
Geilhufe, J. et al. Monolithic focused reference beam X-ray holography. Nat. Commun. 5, 1–6 (2014).
Büttner, F. et al. Dynamics and inertia of skyrmionic spin structures. Nat. Phys. 11, 225–228 (2015).
Klas, R., Eschen, W., Kirsche, A., Rothhardt, J. & Limpert, J. Generation of coherent broadband high photon flux continua in the XUV with a sub-two-cycle fiber laser. Opt. Express 28, 6188 (2020).
Krebs, M. et al. Towards isolated attosecond pulses at megahertz repetition rates. Nat. Photonics 7, 555–559 (2013).
Shestaev, E. et al. High-power ytterbium-doped fiber laser delivering few-cycle, carrier-envelope phase-stable 100 µJ pulses at 100 kHz. Opt. Lett. 45, 97 (2020).
Ge, X. et al. Impact of wave front and coherence optimization in coherent diffractive imaging. Opt. Express 21, 11441 (2013).
Sandberg, R. L. et al. High numerical aperture tabletop soft x-ray diffraction microscopy with 70-nm resolution. Proc. Natl Acad. Sci. USA 105, 24–27 (2008).
Richardson, W. H. Bayesian-based iterative method of image restoration. J. Opt. Soc. Am. 62, 55 (1972).
Lucy, L. B. An iterative technique for the rectification of observed distributions. Astron. J. 79, 745 (1974).
Marchesini, S. et al. X-ray image reconstruction from a diffraction pattern alone. Phys. Rev. B 68, 140101 (2003).
Acknowledgements
We thank L. Loetgering for the fruitful discussions and for commenting on our manuscript. This work was supported by the Federal State of Thuringia (2017 FGR 0076), the European Social Fund (ESF), the Thüringer Aufbaubank (TAB) for funding the junior research group HOROS (FKZ: 2017 FGR 0076), the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programm (grant agreement No [835306], SALT) and the Fraunhofer Cluster of Excellence Advanced Photon Sources. Further, this work was partially funded by the Center of Advanced Systems Understanding (CASUS) which is financed by Germany’s Federal Ministry of Education and Research (BMBF) and by the Saxon Ministry for Science, Culture and Tourism (SMWK).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
W.E., S.W., C.L., R.K., and J.R. performed the imaging experiments. W.E., S.W., and J.R. analyzed the data. M.S. fabricated the sample and acquired the electron microscope image. S.Y. fabricated the broadband XUV mirrors. W.E., S.W., and H.M. implemented the broadband, iterative phase retrieval algorithm and M.B., T.P., J.L., and J.R. initiated the project and designed parts of the experiment. All authors contributed to writing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Eschen, W., Wang, S., Liu, C. et al. Towards attosecond imaging at the nanoscale using broadband holography-assisted coherent imaging in the extreme ultraviolet. Commun Phys 4, 154 (2021). https://doi.org/10.1038/s42005-021-00658-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00658-5
This article is cited by
-
Progress on table-top isolated attosecond light sources
Nature Photonics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.