Abstract
Topological phases of matter offer exciting possibilities to realize lossless charge and spin information transport on ultrafast time scales. However, this requires detailed knowledge of their nonequilibrium properties. Here, we employ time-, spin- and angle-resolved photoemission to investigate the ultrafast response of the Sb(111) spin-polarized surface state to femtosecond-laser excitation. The surface state exhibits a giant mass enhancement which is observed as a kink structure in its energy-momentum dispersion above the Fermi level. The kink structure, originating from the direct coupling of the surface state to the bulk continuum, is characterized by an abrupt change in the group velocity by ~70%, in agreement with our GW-based band structure calculations. Our observation of this connectivity in the transiently occupied band structure enables the unambiguous experimental verification of the topological nature of the surface state. The influence of bulk-surface coupling is further confirmed by our measurements of the electron dynamics, which show that bulk and surface states behave as a single thermalizing electronic population with distinct contributions from low-k electron-electron and high-k electron-phonon scatterings. These findings are important for future applications of topological semimetals and their excitations in ultrafast spintronics.
Similar content being viewed by others
Introduction
Understanding the elementary scattering processes which govern the ultrafast response of topological states of matter to femtosecond-laser excitation is crucial for applications in ultrafast spintronics and opto-spintronics1,2,3,4. This often requires the experimental determination of the electronic band dispersion of excited states above the Fermi level (EF), simultaneously facilitating for a more complete understanding of a system’s topological order5.
A prominent example are three-dimensional \({{\mathbb{Z}}}_{2}\) topological insulators (3D TIs)6,7,8, which possess an inverted band structure arising from a high spin–orbit interaction9, and hence a metallic surface hosting topologically protected surface states10,11 that could be used as channels in which to drive and coherently control pure spin currents and spin-polarized electrical currents on ultrafast time scales12,13,14,15,16.
To date, the experimental verification of these topologically nontrivial states has been possible either through the enumeration of an odd number of Fermi surface contours, contributed by the state of interest, around time-reversal invariant momenta17,18, or by the direct observation of their Dirac-like dispersion with a unique helical spin texture17,18,19,20,21,22. Both are hallmarks of a nontrivial topological invariant, ν0 = 1, distinguishing strong topological materials from topologically weak or trivial materials (ν0 = 0)23,24,25.
The fundamental principle of bulk-boundary correspondence is responsible for the enforced existence of a spin-polarized surface state bridging the bulk band gap of a 3D TI26. The surface and bulk electronic structures are therefore fundamentally coupled9,26,27. Already, the influence of this type of bulk-surface coupling on the electronic and transport properties of TIs was investigated for prototypical systems such as Sb2Te3, Bi2Te3, and Bi2Se327,28,29,30,31,32. For Sb2Te3, it was shown how it leads to relatively small changes in the linear band dispersion of the surface state near its connectivity points with the bulk valence bands below EF27. Such an unexpectedly weak bulk-surface coupling was also confirmed in magnetotransport experiments33, and by the observation that the connectivity between bulk and surface bands is mediated by bulk-derived surface resonances exhibiting a reversed spin texture with respect to that of the topological surface state in Bi2Te334 and Bi2Se335. This scenario was further confirmed by measurements of the electron dynamics, which revealed a highly decoupled surface and bulk state dynamics following ultrafast optical excitation35.
For metals such as Au5,36,37,38 and semimetals such as Bi39,40,41,42 and Sb18,43,44,45, however, due to the absence of a global band gap or to the presence of a very small relative band gap, the identification of topological states and their coupling to the bulk proved to be more complex. Au metal is widely accepted as a conventional spin–orbit material with ν0 = 0, consistent with the even number of concentric Fermi contours formed by the spin sub-bands of the Rashba-split surface state enclosing the \(\overline{{{\Gamma }}}\) point on the (111) surface36,37,38. Recently, however, the Au(111) surface state was identified as \({{\mathbb{Z}}}_{2}\) topologically nontrivial based on its connectivity to the bulk bands far above EF and on the parity analysis of the band structure5. In a similar context, the connectivity of the Rashba-split surface state of Ir(111) to bulk bands below EF was discussed in terms of topological properties46. In contrast, Bi was predicted to be a topologically trivial system (ν0 = 0) which can undergo a topological phase transition to a \({{\mathbb{Z}}}_{2}\) TI47 via the application of strain, or into a topological crystalline insulator phase48. Strikingly, however, based on a detailed experimental analysis of the electronic band structure, Bi was also suggested to be topologically nontrivial with ν0 = 141,49.
The semimetal Sb, on the other hand, is regarded as the parent compound underlying the microscopic origin of topological order in the Bi1−xSbx TI class17,18,39. The similarity between the electronic structures of elemental Sb with the prototypical TI Bi0.9Sb0.1 has prompted the suggestion that Sb itself can be described by ν0 = 1, and that its surface supports a Berry’s phase18. Indeed, several previous direct measurements of the (111) surface band dispersion confirm the presence of a surface state with a chiral, momentum-locked spin texture18,43,50,51,52. However, efforts towards a rigorous demonstration of the nontrivial nature of the surface state have been hindered both due to the presence of bulk pockets at EF45, and due to the fact that the connection of the surface state to the bulk continuum between time-reversal invariant momenta occurs above EF. Therefore, direct observation of the relevant surface-bulk connectivity, crucial for the final verification of topological character, remains out of reach for experimental techniques probing only the occupied ground state electronic structure such as conventional angle-resolved photoemission (ARPES). The question on the band connectivity of Sb is also directly related to how bulk-surface coupling influences the dispersion of the surface state, and whether it is consistent with decoupled bulk and surface electron dynamics as previously suggested for strong \({{\mathbb{Z}}}_{2}\) TIs35.
To investigate these issues, we experimentally follow, by means of time-resolved ARPES (tr-ARPES) in combination with spin resolution, the energy-momentum dispersion of the Sb(111) surface state beyond EF, as well as its connectivity to bulk states. Our main finding is a kink structure in the band dispersion of the surface state which causes a giant mass enhancement due to coupling to the bulk continuum above EF. Our observation of this band connectivity above EF allows to unambiguously verify the topological character of the surface state. The experimental results are supported by quasiparticle self-consistent GW (QSGW) calculations. The strong bulk-surface coupling is also revealed by our measurements of the electron dynamics, which show that the excited states behave as a single thermalizing electron population due to a dominant contribution from interband electron–electron scatterings. These findings are critically important for the implementation of advanced functionalities in future spintronics based on topological semimetals.
Results and discussion
Transient band structure and kink above Fermi level
We performed tr-ARPES experiments on Sb(111) single crystals using pump and probe femtosecond (fs) laser pulses of 1.5 and 6 eV photon energy under the experimental geometry shown in Fig. 1a (see Methods for details). The high-quality of the cleaved surface was confirmed by low-energy electron diffraction, as seen in Fig. 1b.
a The infrared (IR) pump (1.5 eV) and ultraviolet (UV) probe (6 eV) fs pulses impinge the sample under an angle of 45∘. The electron emission and light incidence planes are orthogonal to each other, and fixed with respect to the laboratory reference frame. The detection plane (spanning over an angle of 2θ) was oriented along the \(\overline{{{\Gamma }}}\)-\(\overline{\,\text{K}\,}\) or \(\overline{{{\Gamma }}}\)-\(\overline{\,\text{M}\,}\) direction by an azimuthal (α) rotation of the sample around the z axis. b Low-energy electron diffraction image (incident electron energy of 98.6 eV) of clean Sb(111), with the surface Brillouin zone shown as solid purple lines.
The energy-momentum band dispersion of Sb(111) measured by tr-ARPES along the \(\overline{\,\text{M}\,}\)-\(\overline{{{\Gamma }}}\)-\(\overline{\,\text{K}\,}\) direction at a time delay Δt = 300 fs following optical excitation by the pump pulse is shown in Fig. 2a. Above EF, the unoccupied part of the band structure is transiently populated with excited electrons and can be observed directly. One can identify the dispersion of the spin-polarized surface-state bands, as well as bulk states and bulk-derived surface resonances both below and above EF (denoted as SS, BS, and SR, respectively). Here, and in general due to the surface sensitive nature of photoemission (even with the slightly enhanced bulk sensitivity at probe photon energies of 6 eV)53, surface-related bands appear as more-intense narrower features, while less-intense broad features correspond to pure bulk states. The assignment of bulk and surface character to the states in Fig. 2 is further supported by our band structure calculations, which will be discussed in the next section, and consistent with previous theoretical works54,55.
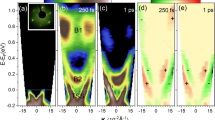
a Energy-momentum dispersion of Sb(111) along the \(\overline{\,\text{M}\,}\)-\(\overline{{{\Gamma }}}\)-\(\overline{\,\text{K}\,}\) direction measured by time- and angle-resolved photoemission (tr-ARPES) at a time delay Δt = 300 fs after optical excitation. Photoemission intensity is given in arbitrary units (arb. u.). Surface-state bands, bulk-derived surface resonances and pure bulk states are denoted as SS, SR, and BS, respectively. To increase the visibility of higher-energy states, the spectra have been normalized by a Fermi function with kBT ≈ 175 meV. b Zoom-in on the region of mass enhancement along the \(\overline{\,\text{M}\,}\)-\(\overline{{{\Gamma }}}\) direction. Extracted band positions are shown in red. Dashed black lines are linear fits to the band positions either side of the bulk-surface connectivity point, with corresponding group velocities indicated. c, d Spin-resolved tr-ARPES energy distribution curves (blue/red circles for spin up/down respectively) and spin polarizations (pol., black open circles) corresponding to c the in-plane chiral (Sy) and d out-of-plane (Sz) spin components, taken at the momentum position indicated in a and at a time delay of Δt = 300 fs. The spectra are displayed on a logarithmic scale to increase visibility above EF. The insets reproduce the data on a linear scale. Peaks are labeled according to the corresponding band features. Schematic illustrations which based on the measured band structure depict two possible scenarios where the bulk connectivity of surface states is consistent with (e) a topologically trivial (topological invariant ν0 = 0) and (f) a topologically nontrivial (ν0 = 1) system. Red/blue colors denote opposite spin states.
Along the \(\overline{{{\Gamma }}}\)-\(\overline{\,\text{K}\,}\) direction, one can clearly identify the top of the bulk valence band below EF (k∥,y = 0.12 Å, E − EF = −0.2 eV), and the bottom of the bulk conduction band above EF closer to the \(\overline{{{\Gamma }}}\) point (k∥,y = 0.075 Å, E − EF = 0.1 eV). The two V-shaped surface-state bands, which possess an opposite spin texture18,51,52, exhibit a distinct dispersion along this direction. The inner V-shaped surface band crosses EF and merges with bulk conduction band states above EF, while the outer V-shaped surface band bends back before reaching EF and merges with bulk valence band states below EF. The observed band connectivity along \(\overline{{{\Gamma }}}\)-\(\overline{\,\text{K}\,}\), in fact, resembles that characterizing 3D TIs8. However, it should be emphasized that, for the semimetal Sb, a direct observation of similar bulk-surface connectivity above EF in between the time-reversal invariant momentum points \(\overline{{{\Gamma }}}\) and \(\overline{{\rm{M}}}\) is mandatory to verify the topological character of the surface state.
Along the \(\overline{{{\Gamma }}}\)-\(\overline{\,\text{M}\,}\) direction, as seen in Fig. 2a, both the local bulk conduction band minimum near \(\overline{{{\Gamma }}}\), and the bulk valence band top are above EF. The outer V-shaped surface band crosses EF and, in a similar way as for the \(\overline{{{\Gamma }}}\)-\(\overline{\,\text{K}\,}\) direction, it bends back at k∥,x = −0.2 Å to couple to the bulk valence band exhibiting hole-like behavior. The inner V-shaped surface band, on the other hand, crosses EF and merges with bulk conduction band states above EF (k∥,x = 0.08 Å, E − EF = 0.1 eV). This behavior clearly excludes the scenario in which (i) there is a turn back in the dispersion of the inner V-shaped surface band without connectivity to bulk conduction band states above EF, followed by (ii) its subsequent re-appearance below EF as one of the surface resonances18,45 only connecting to the valence band continuum at larger ∣k∣ and closer to \(\overline{{\rm{M}}}\) point. The observed connectivity, in turn, unambiguously demonstrates both the expected partner-switching behavior of a topologically nontrivial system with ν0 = 18, and that the inner V-shaped surface-state band encloses the \(\overline{{{\Gamma }}}\) point an odd number of times up to the wave vector of the bulk connectivity point above EF, which has never been measured before.
Looking in more detail at the previously unobserved connectivity region between surface state and bulk conduction band above EF, the most striking observation in Fig. 2a is the appearance of a kink structure in the band dispersion of the surface state as it approaches the connectivity point along the \(\overline{{{\Gamma }}}\)-\(\overline{\,\text{M}\,}\) direction. A zoom-in of this region, presented in Fig. 2b, demonstrates how the kink is very pronounced, evidencing a significant enhancement of the effective mass. A careful extraction of the photoemission peaks along with linear fits of the band dispersion (red symbols and dashed lines in Fig. 2b, respectively) reveals that the kink structure is characterized by a significant drop of about 70% in the group velocity of the surface state, which changes from 4.67 to 1.45 eVÅ.
Using the definition of the transport mass56, one can extract the corresponding increase of effective mass to the drop in group velocity of this region of the band dispersion. In this way we derive that, due to the kink structure, the effective mass of the surface band increases by a factor of 4, from ~0.1 to ~0.4 me, where me denotes the free-electron mass. Such a large surface mass enhancement near the connectivity point with pure bulk states pinpoints strong bulk-surface coupling as the underlying mechanism responsible for the appearance of the kink structure.
The data in Fig. 2a also demonstrate how, due to the interaction with the bulk continuum, the surface bands preferentially follow the dispersion of the border of the bulk band gap. For the outer V-shaped surface band along both the \(\overline{{{\Gamma }}}\)-\(\overline{\,\text{M}\,}\) and \(\overline{{{\Gamma }}}\)-\(\overline{\,\text{K}\,}\) directions, it is thus difficult to extract or visualize a kink structure because the band exhibits hole-like behavior and the band top is flat. Similarly, along the \(\overline{{{\Gamma }}}\)-\(\overline{\,\text{K}\,}\) direction, the absence of a clear kink structure above EF is related to the fact that the inner V-shaped surface state energetically favors a linear dispersion near the border of the kz-projected bulk manifold closest to the \(\overline{{{\Gamma }}}\) point57.
Our present finding of a strong bulk-surface coupling in the semimetal Sb differs from the situation in prototypical 3D TIs, where the coupling was reported to be weak due to the presence of surface resonances with high degree of spin polarization inhibiting the interaction with pure bulk states27,35. In this respect, it is important to note that along the \(\overline{{{\Gamma }}}\)-\(\overline{\,\text{M}\,}\) direction in Fig. 2a, we observe bulk-derived surface-resonance states in the immediate vicinity of the kink structure above EF. Our spin-resolved tr-ARPES measurements taken along \(\overline{{{\Gamma }}}\)-\(\overline{\,\text{M}\,}\) at k∥,x = –0.11 Å and Δt = 300 fs in Fig. 2c, d, however, in contrast to the case of 3D TIs, reveal that the bulk-derived surface resonance in Sb is neither spin split nor spin-polarized. We do note that along \(\overline{{{\Gamma }}}\)-\(\overline{\,\text{K}\,}\), the surface resonance is also visible but with much lower intensity, probably due to photoemission matrix-element effects. The inner and outer V-shaped surface bands, on the other hand, exhibit a clear spin polarization which, in agreement with previous findings18,51,52, reach values of ~60% for the in-plane chiral (Fig. 2c) and of ~15% for the out-of-plane (Fig. 2d) spin components. This observed spin texture is consistent with a Berry’s phase18. Note, however, that without a direct observation of the bulk-surface connectivity above EF, the measurement of the spin texture alone cannot be taken as an exclusive proof of the topological character of the Sb surface state. A prominent example in this context is the helical spin texture observed for topologically trivial surface states near the quantum critical point of a phase transition between a trivial and a topological insulator58.
In Fig. 2e, f, we show a schematic representation of two possible scenarios where the hybridization between surface and bulk states can be differently affected by surface-resonance states. For instance, the interaction between parallel spins (Fig. 2e) could lead to spin-dependent avoided crossings or even a breakdown of the bulk-surface connectivity, which for a system with an even number of band inversions in the bulk, can result in a weak topological or topologically trivial phase (ν0 = 0). In contrast, a strong coupling to the bulk continuum is possible (Fig. 2f) when the surface resonances are spin-degenerate, which for a system with an odd number of band inversions in the bulk, can result in a kink structure and a topologically nontrivial phase (ν0 = 1) in agreement with our experimental findings.
Ab initio calculations and comparison to experiment
To further verify this scenario and especially to understand whether the kink structure is a property of the ground state, we performed QSGW-based calculations (see Methods) of the Sb(111) band structure as shown in Fig. 3. In Fig. 3a, b, the continuum bulk-energy bands are represented by gray-shaded regions, while the colored lines correspond to the discrete bands of a 100-bilayer slab. Here, the color coding represents the localization of the wave function of each state on the topmost bilayer. In Fig. 3c, d, we show the calculated spin polarization of the bands corresponding to the results in Fig. 3a, b, respectively. The red/blue color representation highlights the magnitude and direction of the chiral spin component perpendicular to electron momentum, with the other spin components negligible. Overall, around the \(\overline{{{\Gamma }}}\) point the calculation shows qualitatively good agreement with the experimental results of Fig. 2 concerning the dispersion of the bulk bands both below and above EF. The calculated bulk band dispersion near the \(\overline{{\rm{M}}}\) point is also consistent with previous ARPES measurements accessing only occupied states18. Equally important, the calculated surface-state spin sub-bands exhibit the partner-switching behavior of a topological system with ν0 = 1 and strong bulk-surface coupling (see Fig. 2f). In Fig. 3, we can also identify bulk-derived surface resonances with different degree of surface localization and negligible spin polarization in agreement with the experimental results.
a Calculated band structure of Sb(111) obtained with a tight-binding model based on quasiparticle self-consistent GW calculations (see Methods) along the full \(\overline{\,\text{M}\,}\)-\(\overline{{{\Gamma }}}\)-\(\overline{\,\text{K}\,}\) direction. The continuum of bulk states is displayed as a gray background, and lines show the discrete bands of a 100-bilayer slab. The degree of surface localization on the topmost bilayer is indicated by the band coloring. SS, SR, and BS denote surface-state bands, bulk-derived surface resonances and pure bulk states, respectively. b Zoom-in on the region of the kink structure seen in a along the \(\overline{\,\text{M}\,}\)-\(\overline{{{\Gamma }}}\) direction. c, d Calculation of the spin polarization of the bands corresponding to the results shown in a and b, respectively. The magnitude and direction of the chiral spin component (Schiral) is represented by the red/blue color scale. Equivalent band structure calculations with orbital projection onto the px, py, and pz orbitals for e, f and g respectively.
A closer view of the connectivity region between surface and bulk conduction band states is shown in the calculation of Fig. 3b. Similar to the tr-ARPES measurements of Fig. 2b, the surface state exhibits a kink structure in the calculated band dispersion near the connectivity point to the bulk continuum. The kink structure, which up to date has not been reproduced in previous calculations of the Sb band structure solely based on conventional density-functional theory (DFT), is characterized by a change in the calculated group velocity of the surface band from ~2.8 to 1.2 eVÅ. These values represent a drop in the group velocity of 57%, in good agreement with the experimental value. This behavior is equivalent to a large increase in the effective mass of the surface band from ~0.1 to ~ 0.3 me as it crosses the connectivity point. The overall change corresponds to a surface mass enhancement by a factor of 3 which is qualitatively consistent with the one derived from the experimental band dispersion of Fig. 2b. The abrupt change in the surface band dispersion near the bulk connectivity point underlines direct hybridization between surface and pure bulk states as the origin of the kink structure. The negligible spin polarization of surface-resonance states in Fig. 3d is also consistent with this picture. The observed mass enhancement, to the best of our knowledge, exceeds by far the one found in any other prototypical TI up to date27. The strong bulk-surface coupling is also evident in Fig. 3a, b from the decrease seen in the localization of the surface bands caused by the interaction with pure bulk states. In Fig. 3a, it can also be seen that when the bulk band gap is very large (small) the surface states are strongly (weakly) localized on the surface. More in detail, our analysis of the orbital character of the surface state around the bulk connectivity point, shown in Fig. 3e–g, reveals an abrupt change in the relative contribution of py and pz orbitals due to hybridization with pure bulk states.
The QSGW approach is known as a powerful method which substantially improves the description of the electronic band structure with respect to conventional DFT calculations47,59. For instance, band structure calculations within the local-density approximation (LDA) suffer from an underestimation of non-inverted band gaps such as the one at \(\overline{{\rm{M}}}\) point. In this case, the LDA band gap of 0.07 eV increases to 0.27 eV when QSGW is applied. On the contrary, inverted band gaps, such as the one at \(\overline{{{\Gamma }}}\), tend to be overestimated by LDA47,59. In the present case, the band gap decreases from 0.59 eV in LDA to 0.53 in QSGW enabling the connectivity of the surface state to the bulk continuum much closer to the \(\overline{{{\Gamma }}}\) point. This behavior is consistent with our parity analysis within both LDA and QSGW which shows the presence of a band inversion at the Γ point of the bulk Brillouin zone, whereas the band gaps at the three L points projecting onto \(\overline{{\rm{M}}}\) are non-inverted. Thus, the semimetal Sb is characterized by an odd number of band inversions in the bulk, giving rise to a nontrivial \({{\mathbb{Z}}}_{2}\) invariant. This situation is in contrast to the case of Bi, in which the band gap at Γ is inverted, but the gaps at the three L points are inverted too, resulting in inverted gaps at four time-reversal invariant momenta, and therefore to a topologically trivial value of the \({{\mathbb{Z}}}_{2}\) invariant47.
Ultrafast response to optical excitation
To further verify the crucial role of strong bulk-surface coupling for the appearance of the kink structure, we investigated the ultrafast temporal evolution of the transient electron populations within different states following optical excitation by the pump pulse. These type of measurements also provide insight into the elementary scattering processes underlying thermalization of carriers, and whether the coupling influences the relevant scattering channels of ultrafast charge and energy transfer between different states. In Fig. 4a–d, we show several tr-ARPES dispersions at selected time delays following optical excitation. One can see that after ~2.4 ps, high-energy excited states have completely decayed, and that relaxation of excited electrons along \(\overline{{{\Gamma }}}\)-\(\overline{\,\text{M}\,}\) and \(\overline{{{\Gamma }}}\)-\(\overline{\,\text{K}\,}\) directions proceeds according to similar dynamics. This behavior can also be recognized in Fig. 4e, f, where we show momentum-resolved intensities extracted at different energies above EF as a function of pump-probe delay for surface and bulk states (Fig. 4e), as well as for surface-resonance states (Fig. 4f).
a–d Energy-momentum dispersions along the \(\overline{\,\text{M}\,}\)-\(\overline{{{\Gamma }}}\)-\(\overline{\,\text{K}\,}\) direction measured by time- and angle-resolved photoemission at selected time delays following optical excitation. To increase the visibility of higher-energy states, the spectra have been normalized by a Fermi function with kBT ≈ 175 meV. Photoemission intensity is given in arbitrary units (arb. u.). e, f Time evolution of the momentum-resolved intensities at various energies above EF, as indicated by horizontal dashed lines in a–d. Surface-state bands, surface resonances and pure bulk states are denoted as SS, SR, and BS, respectively. g Momentum-integrated dispersion as a function of time delay, Δt. Note the logarithmic color scale. h Electronic temperature (blue circles) extracted from fits of the image in g to Fermi–Dirac distributions. Changes in the transient chemical potential are negligible. The error bars (±one standard deviation) are a metric for the deviation from a new equilibrium state of the excited electron population within the experimental resolutions. The blue solid line is a fit to an exponential decay convolved with a Gaussian profile to account for the time resolution, δt, as measured from the pump-probe cross correlation (inset). i Fits (red lines) of energy-distribution curves (black lines) to a Fermi–Dirac (F–D) distribution at selected time delays.
The faster relaxation of excited electrons at higher energy seems consistent with the expected energy dependence of the relaxation times of a single thermalizing electronic population of surface and bulk states. In particular, one can see that excited electrons within surface and bulk states decay with similar relaxation rates, behaving as dynamically locked electron populations, which evidences the signatures of the coupling between the different states. From Fig. 4 we also derive that the overall dynamics of bulk and surface bands can be described approximately by a global Fermi–Dirac distribution with a single transient electronic temperature reaching a maximum value of Te ≈ 2100 K at the onset of the excitation. This is shown in Fig. 4g, h, where a momentum-integrated spectrum (Fig. 4g) is fit to a Fermi–Dirac distribution from which the temporal evolution of the electronic temperature is derived (Fig. 4h). The error bars in Fig. 4h are largest at early delay times where a Fermi–Dirac distribution is less appropriate, i.e. when the electronic population is far out-of-equilibrium. This is shown explicitly in Fig. 4i, where fits to Fermi–Dirac distributions are shown for selected delay times. Therefore, whilst interband thermalization proceeds on a time scale of about 0.9 ps which is longer than the laser excitation (inset of Fig. 4h), as in some simple metallic systems where nonthermal effects are important60,61,62, the dynamics of surface and bulk carriers do still proceed on similar time scales due to strong bulk-surface coupling. This is also supported by the fact that this initial process occurs on a time scale corresponding to that in which the electronic distribution relaxes from high energies to energies slightly above the energy of the kink structure (Fig. 4c), pinpointing the crucial role of electronic hybridization in the process of interband thermalization. These findings taken together therefore suggest that, owing to strong bulk-surface coupling, the interband electron scattering processes between bulk and surface states are predominantly responsible for the synchronous progression towards a thermalized state.
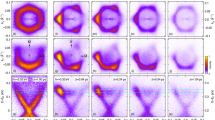
In Fig. 5, we analyse this behavior in more detail by comparing the tr-ARPES intensities integrated within small energy-momentum windows distributed throughout the dispersion of different states (Fig. 5a). The fact that the temporal evolution of the photoemission intensity at fixed energy is independent of the nature of the excited states pinpoints the importance of bulk-surface coupling in the process of interband thermalization (Fig. 5b). The symmetric tr-ARPES intensity distribution of the surface bands upon rotation of the electron spin by 180 degrees at opposite wave vectors (Fig. 5c), or by 90 degrees at orthogonal wave vectors (Fig. 5d), indicates that the spin texture of the surface state plays a minor role in the electron dynamics. It is understood that spin selection rules do not influence the probability of interband transitions between spin-degenerate bulk states and spin-polarized surface states which will always be allowed under all possible scattering angles. The crucial role of bulk-assisted interband scattering is further supported by the synchronous evolution of the transient electron populations when compared to that of excited bulk states (Fig. 5e). As a result, surface and bulk states behave as a single thermalizing electron population exhibiting a universal energy dependence in the relaxation times which is independent of electron spin (Fig. 5f) and momentum (Fig. 5g). This situation is in stark contrast to the case of prototypical TIs where it has been shown that as a consequence of the complex spin texture of surface resonances hindering the coupling to the bulk continuum27,35, surface and bulk states behave as two independently thermalizing electron populations relaxing on different time scales35. In this regard, we expect the dynamics of excited states in the semimetal Sb, as observed here, to be unusual in the context of systems where spin–orbit interaction is important, especially in topological systems where surface states and resonances are in most cases strongly spin-polarized22,27,34,35,58.
a Time- and angle-resolved photoemission (tr-ARPES) dispersion at a time delay Δt = 300 fs. The energy-momentum windows from which the data shown in b–g were extracted are shown as an overlay. Surface-state bands, bulk-derived surface resonances and pure bulk states are denoted as SS, SR, and BS, respectively. High-symmetry directions [purple (green) coloring for \(\overline{\,\text{M}\,}\)-\(\overline{{{\Gamma }}}\) (\(\overline{{{\Gamma }}}\)-\(\overline{\,\text{K}\,}\))], energies and band features are indicated in all panels. b Tr-ARPES intensities as a function of delay time for different states at energy E6. c Similar traces for the inner branch of the surface state extracted at +k∥,x (blue) and −k∥,x (red) wave vectors. Tr-ARPES intensities of the inner branch of the surface state (d) and bulk state (e) along different momentum directions. Traces in b–e are fit to an exponential decay convolved with a Gaussian profile to account for the time resolution. Decay times represented according to spin character of the states (f) or the momentum direction (g). Vertical error bars correspond to ± one standard deviation. Each error bar along the energy axis indicates the size of the integrated energy window from which the decay time has been obtained. Dashed line in black (orange) is a fit to a model including (not including) nonthermal effects. Note that the orange dashed line corresponds to the prediction of a two-temperature (2T) model.
Elementary scattering mechanisms of ultrafast charge and energy transfer
More in detail, we derive that the energy dependence of the relaxation times can be well described as \({\tau }^{-1}={\tau }_{0}^{-1}+\alpha {(E-{E}_{{\rm{F}}})}^{\beta }\) (represented as a black dashed line in Fig. 5f, g). Here, τ0 is an effective time constant containing the contributions from electron–phonon scattering as well as electron transport, and the second term is related to the contribution from electron–electron scattering61. The parameter α is the characteristic electron–electron scattering constant which depends on the averaged electron–electron scattering probability, and therefore on the electron–electron interaction strength61,62.
Although somewhat oversimplified, Fig. 5f, g demonstrate that this model, with fitting parameters of τ0 = 2550 ± 80 fs, α = 0.025 ± 0.003 fs−1 eV−2 and β = 1.82 ± 0.05, is in good agreement to the data. Our observation that the energy dependence of τ behaves with β close to the predicted value of 2 highlights the significance of nonthermal contributions to the electron dynamics, specifically the role of electron–electron scatterings61,62. This is also supported by the fact that the characteristic electron–electron scattering constant α that we obtain is not far from that predicted for simple metallic systems when nonthermal effects are taken into account61, which is in principle expected as Sb lies in the metallic regime of the Bi1−xSbx series18.
To further verify the role of nonthermal contributions to the electron dynamics, we also display as a dashed orange line in Fig. 5f, g the relaxation times obtained based on a two-temperature model63 according to which electron–phonon scatterings are the only mechanism responsible for the relaxation of the electronic population. Nonthermal effects, or in other words, the important contribution of electron–electron interactions to the relaxation61,62 are completely neglected in this model. Instead, thermalization of the electronic population is assumed to be much faster than the laser excitation, or instantaneous, which is clearly not the case here (see e.g. Fig. 4i). Despite the limited applicability of this assumption, the result of Fig. 4h is fit with an electron temperature distinct from the lattice temperature, and the energy-dependence of the relaxation times derived solely based on Fermi–Dirac statistics and by completely neglecting the important influence of nonthermal effects to the relaxation (dashed orange line).
Let us now compare the experimental results along with the initial model, which explicitly accounts for electron–electron scatterings, to the results of the two-temperature model. From Fig. 5f, g, it is evident that the relaxation dynamics from high energies down to energies of ≈0.15 eV proceeds according to faster electron–electron scattering processes. Therefore, in this energy region, electron–electron scatterings are the main driving mechanism for the relaxation of the electronic population. In the low-energy region, on the other hand, we observe that the relaxation times exceed the two-temperature model prediction down to EF.
Using the experimentally determined electron–phonon coupling constant λ = 0.2243, one can determine an electron–phonon scattering time of ≈29 fs. This, in conjunction with ℏωD = 13 meV, where ωD is the Debye frequency64, provides an estimate of \(\tilde{\tau }\ \approx \) 1780 fs for an electron to lose 0.8 eV (corresponding to a high-energy excited state in Fig. 5) by assuming a linear dependence of the relaxation rate. This time scale is consistent with the two-temperature model prediction near EF of ~1800 fs. We note that an additional contribution from e.g. electron transport would act to further decrease the relaxation times at low energy, and therefore cannot account for this underestimation of the relaxation times in the low-energy region. Instead, nonthermal effects are responsible for the slower low-energy relaxation times. Following the arguments presented in a recent theoretical work62, in the limit 0.05 < γep/βee < 2 the time in which excited electrons lose their energy can be well approximated as \(\tau ^{\ast }\approx {2.5\cdot \gamma _{\mathrm{ep}}^{-0.75}}{\beta}_{\mathrm{ee}}^{-0.25}\). Here βee is the relaxation rate for 0.5 eV excitations, representing the strength of the electron–electron interactions. The electron–phonon interaction strength, \({\gamma }_{{\rm{ep}}}{\approx} {\tilde{\tau }}^{-1}\), is determined from the relaxation rates near EF predicted by the two-temperature model62. For our present case, we derive γep/βee ≈ 0.1 yielding βee/(0.5 eV)2 = 0.025 fs−1 eV−2 and τ* = 2475 fs. These estimations are in excellent agreement to the fitting parameters obtained within the initial model for the values of the characteristic electron–electron scattering constant, α, and τ0, respectively (black dashed line in Fig. 5f, g).
Pathways for ultrafast charge and energy transfer
Figure 6 shows a schematic representation of the most relevant channels of ultrafast charge and energy transfer between different states based on our experimental findings. After laser excitation, electrons and holes start thermalizing via interband transitions between bulk and surface states caused by electron–electron and electron–phonon scattering processes, with predominance of electron–electron scatterings the higher the energy of the excited electron. Note that these transitions can also be driven between bulk valence and conduction band states. Higher-energy excited states within the bulk conduction band continuum relax through electron–electron scatterings into lower-energy states, and the overall transfer of charge and energy during this process requires low-k transfers. Similarly, electron–electron scatterings lead to a continuous exchange of charge and energy between surface and bulk valence band states, with the difference that this process requires large-k transfers. It is understood that transitions between states of opposite spin are strictly forbidden, and that relaxation of an electron via electron–electron scattering is accompanied by the excitation of a second electron under the conservation of spin, energy, and momentum. Therefore, interband transitions between bulk and surface states are allowed under all possible scattering angles.
Interband transitions between bulk and surface states due to electron–electron (e–e) and electron–phonon (e–ph) scatterings are highlighted, with distinct contributions from low-k and high-k transfers, as well as energy dissipation into the lattice. Blue and red colors emphasize different branches of the surface state with opposite spin (SS±). Bulk conduction and bulk valence band states are denoted as BCB and BVB, respectively.
The relaxation process via electron–electron scatterings proceeds through energy redistribution between high-energy and lower-energy states. Due to energy conservation, the relaxation of highly excited electrons via electron–electron scatterings results in secondary electron excitations at lower energies. In consequence, as the process of interband thermalization progresses, the number of excited electrons increases by about a factor of two in every thermalization step61. This cascade process results in an excess population at low energies, thereby increasing the number of existing electrons emitting phonons, and affecting the relaxation rates also at low energies60,62, where transiently occupied bulk valence band states do also act as scatterers.
As the Fermi level is approached, electron–electron scatterings are still required to continuously re-establish a thermal equilibrium in every relaxation step of the excess population at low energies, and the efficiency of this process depends on the relative electron–electron and electron–phonon interaction strengths. For sufficiently weak electron–electron interactions, as in the case of Sb, nonthermal effects in this energy region are not negligible, resulting from the fact that, on average, each electron–phonon scattering event sets-in before a thermal state can be completely re-established. As many more electron–phonon scattering events are required to relax the excess population, leading to more phonons being emitted, the overall electron–phonon energy relaxation process in the vicinity of EF is bottlenecked. While electron–phonon scatterings have less strict selection rules, they are still constrained by spin selection. Although the total change in energy achievable is small due to the small energy of the phonons, at longer time delays the energy of the electronic system is released into the lattice through electron–phonon scatterings, which govern the slower relaxation of the excited electron population in the immediate vicinity of EF.
Our findings taken altogether provide evidence of the crucial role of bulk-surface coupling as a ground state property which is not only responsible for the observed mass enhancement, but also for the ultrafast response of excited states in a topological semimetal to fs-laser excitation. The underlying interactions offer a versatile platform to tune essential material properties. Control over the coupling strength can be expected when driving the system into a bulk-insulating or two-dimensional regime across a topological phase transition via intentional doping or quantization, thereby paving the way for a systematic tuning of the mass enhancement and the relevant time scales of ultrafast charge and energy transfer. These properties are key ingredients playing a central role in the generation and manipulation of lossless spin-polarized currents for efficient information processing on ultrafast time scales, which is highly relevant for spintronic applications. In future studies, it would be interesting to explore the influence of intense fs-laser fields on the coupling strength and the possibility of generating and transiently modifying hybrid photon–electron states. Our results are also important for other topological systems such as Weyl semimetals, where depending on the coupling strength, laser-driven surface currents originating from topological Fermi arcs and transient bulk currents originating from tilted Dirac cones could be independently manipulated on ultrafast time scales.
Conclusion
To summarize, we have investigated the previously unmeasured connectivity of the Sb(111) surface state to the bulk continuum above EF by means of tr-ARPES in combination with spin resolution. We have provided a clear observation of this connectivity in the transiently occupied band structure between time-reversal invariant momenta, enabling the unambiguous verification of the topological character of the surface state. Our main finding has been a kink structure in the energy-momentum dispersion of the surface state above EF that is consistent with a giant mass enhancement originating from strong bulk-surface coupling. We have performed self-consistent QSGW band structure calculations and found good agreement with the experimental results. The strong bulk-surface coupling was also confirmed by our measurements of the electron dynamics, which revealed that excited states behave as a single thermalizing electronic population due to distinct contributions from interband transitions via electron–electron and electron–phonon scatterings. These findings have important implications in designing future strategies to exploit optical control of transient spin currents from topological semimetals in ultrafast spintronics.
Methods
Photoemission experiments
We carried out tr-ARPES experiments using linearly polarized 1.5 eV pump and 6 eV probe femtosecond (fs) laser pulses incident on the sample under an angle of 45 degrees. The high-quality Sb(111) single crystals were cleaved in situ at room temperature. The pump-probe time delay Δt was varied using an optical delay stage. The time resolution was ~200 fs, and the pump fluence ~100 μJ/cm2. The pulses were generated with a Ti: Sapphire fs oscillator coupled to an ultrafast amplifier laser system (RegA, Coherent) operated at 150 kHz. Photoelectrons were detected with a Scienta R4000 analyzer at the RGBL-2 station in Helmholtz-Zentrum Berlin, and the base pressure of the setup was ~1 × 10−10 mbar. The angular and energy resolutions of the tr-ARPES measurements were 0.1∘ and 20 meV, respectively. To combine spin resolution with tr-ARPES, we used a Mott-type spin polarimeter operated at 25 kV and capable of detecting both in-plane and out-of-plane components of the spin polarization. Resolutions of spin-resolved tr-ARPES measurements were 0.75∘ (angular) and 80 meV (energy).
Quasiparticle self-consistent GW calculations
The ab initio calculations were carried out with the DFT code fleur (www.flapw.de) and the GW code spex65, based on the all-electron full-potential linearized augmented-plane-wave (FLAPW) formalism. For the DFT calculation that serves as a starting point for the quasiparticle self-consistent QSGW calculation47,66, we used the LDA, an angular momentum cutoff of \({l}_{\max }\)= 10 in the muffin-tin spheres and a plane-wave cutoff of 4.0 bohr−1 in the interstitial region. Angular and linear momentum cutoffs of l = 5 and 2.9 bohr−1 were employed to construct the mixed product basis for the dielectric matrix and the screened interaction67. A 8 × 8 × 8 k-point mesh was used to sample the Brillouin zone. To compute the Green and polarization functions, 500 bands were used. Spin–orbit coupling was included self-consistently47,68. For the surface calculation, a tight-binding Hamiltonian based on Wannier functions69 was constructed from the QSGW calculation of the bulk59.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The FLEUR code is available at http://www.flapw.de. The SPEX code (http://www.flapw.de/spex) is available from the authors upon request.
References
Žutić, I., Fabian, J. & Sarma, S. D. Spintronics: fundamentals and applications. Rev. Mod. Phys. 76, 323–410 (2004).
Pesin, D. & MacDonald, A. H. Spintronics and pseudospintronics in graphene and topological insulators. Nat. Mater. 11, 409–416 (2012).
Manchon, A. A new moment for Berry. Nat. Phys. 10, 340–341 (2014).
Carva, K. Ultrafast spintronics: Give it a whirl. Nat. Phys. 10, 552–553 (2014).
Yan, B. et al. Topological states on the gold surface. Nat. Commun. 6, 10167 (2015).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Moore, J. E. The birth of topological insulators. Nature 464, 194–198 (2010).
Fu, L., Kane, C. L. & Mele, E. J. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007).
Zhang, H. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438–442 (2009a).
Fu, L. Hexagonal warping effects in the surface states of the topological insulator Bi2Te3. Phys. Rev. Lett. 103, 266801 (2009).
Roushan, P. et al. Topological surface states protected from backscattering by chiral spin texture. Nature 460, 1106–1109 (2009).
McIver, J. W., Hsieh, D., Steinberg, H., Jarillo-Herrero, P. & Gedik, N. Control over topological insulator photocurrents with light polarization. Nat. Nanotechnol. 7, 96–100 (2012).
Kastl, C., Karnetzky, C., Karl, H. & Holleitner, A. W. Ultrafast helicity control of surface currents in topological insulators with near-unity fidelity. Nat. Commun. 6, 6617 (2015).
Wang, Y. H., Steinberg, H., Jarillo-Herrero, P. & Gedik, N. Observation of Floquet-Bloch States on the Surface of a Topological Insulator. Science 342, 453 (2013).
Mahmood, F. et al. Selective scattering between Floquet-Bloch and Volkov states in a topological insulator. Nat. Phys. 12, 306–310 (2016).
Luo, L. et al. Ultrafast manipulation of topologically enhanced surface transport driven by mid-infrared and terahertz pulses in Bi2Se3. Nat. Commun. 10, 607 (2019).
Hsieh, D. et al. A topological Dirac insulator in a quantum spin Hall phase. Nature 452, 970–974 (2008).
Hsieh, D. et al. Observation of unconventional quantum spin textures in topological insulators. Science 323, 919 (2009a).
Hsieh, D. et al. A tunable topological insulator in the spin helical Dirac transport regime. Nature 460, 1101–1105 (2009b).
Xia, Y. et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nat. Phys. 5, 398–402 (2009).
Souma, S. et al. Direct measurement of the out-of-plane spin texture in the Dirac-cone surface state of a topological insulator. Phys. Rev. Lett. 106, 216803 (2011).
Sánchez-Barriga, J. et al. Photoemission of Bi2Se3 with circularly polarized light: probe of spin polarization or means for spin manipulation? Phys. Rev. X 4, 011046 (2014).
Moore, J. E. & Balents, L. Topological invariants of time-reversal-invariant band structures. Phys. Rev. B 75, 121306 (2007).
Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
Roy, R. Z2 classification of quantum spin Hall systems: an approach using time-reversal invariance. Phys. Rev. B 79, 195321 (2009).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Seibel, C. et al. Connection of a topological surface state with the bulk continuum in Sb2Te3(0001). Phys. Rev. Lett. 114, 066802 (2015).
Steinberg, H., Laloë, J.-B., Fatemi, V., Moodera, J. S. & Jarillo-Herrero, P. Electrically tunable surface-to-bulk coherent coupling in topological insulator thin films. Phys. Rev. B 84, 233101 (2011).
Saha, K. & Garate, I. Theory of bulk-surface coupling in topological insulator films. Phys. Rev. B 90, 245418 (2014).
Singh, S. et al. Linear magnetoresistance and surface to bulk coupling in topological insulator thin films. J. Phys. Condens. Matter 29, 505601 (2017).
Velkov, H., Bremm, G. N., Micklitz, T. & Schwiete, G. Transport in topological insulators with bulk-surface coupling: Interference corrections and conductance fluctuations. Phys. Rev. B 98, 165408 (2018).
Yang, X. et al. Light control of surface-bulk coupling by terahertz vibrational coherence in a topological insulator. npj Quantum Mater. 5, 13 (2020).
Takagaki, Y., Giussani, A., Perumal, K., Calarco, R. & Friedland, K.-J. Robust topological surface states in Sb2Te3 layers as seen from the weak antilocalization effect. Phys. Rev. B 86, 125137 (2012).
Sánchez-Barriga, J. et al. Subpicosecond spin dynamics of excited states in the topological insulator Bi2Te3. Phys. Rev. B 95, 125405 (2017).
Cacho, C. et al. Momentum-resolved spin dynamics of bulk and surface excited states in the topological insulator Bi2Se3. Phys. Rev. Lett. 114, 097401 (2015).
LaShell, S., McDougall, B. A. & Jensen, E. Spin splitting of an Au(111) surface state band observed with angle resolved photoelectron spectroscopy. Phys. Rev. Lett. 77, 3419–3422 (1996).
Wissing, S. N. P. et al. Rashba-type spin splitting at Au(111) beyond the Fermi level: the other part of the story. N. J. Phys. 15, 105001 (2013).
Hoesch, M. et al. Spin structure of the Shockley surface state on Au(111). Phys. Rev. B 69, 241401 (2004).
Fu, L. & Kane, C. L. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007).
Li, L. et al. Phase Transitions of Dirac Electrons in Bismuth. Science 321, 547 (2008).
Ohtsubo, Y. et al. Non-trivial surface-band dispersion on Bi(111). N. J. Phys. 15, 033041 (2013).
Nayak, A. K. et al. Resolving the topological classification of bismuth with topological defects. Sci. Adv. 5, eaax6996 (2019).
Sugawara, K. et al. Fermi surface and anisotropic spin-orbit coupling of Sb(111) studied by angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 96, 046411 (2006).
Seo, J. et al. Transmission of topological surface states through surface barriers. Nature 466, 343–346 (2010).
Bianchi, M. et al. Surface states on a topologically nontrivial semimetal: the case of Sb(110). Phys. Rev. B 85, 155431 (2012).
Varykhalov, A. et al. Ir(111) Surface State with Giant Rashba Splitting Persists under Graphene in Air. Phys. Rev. Lett. 108, 066804 (2012).
Aguilera, I., Friedrich, C. & Blügel, S. Electronic phase transitions of bismuth under strain from relativistic self-consistent GW calculations. Phys. Rev. B 91, 125129 (2015).
Munoz, F. et al. Topological crystalline insulator in a new Bi semiconducting phase. Sci. Rep. 6, 21790 (2016).
Ito, S. et al. Proving nontrivial topology of pure bismuth by quantum confinement. Phys. Rev. Lett. 117, 236402 (2016).
Bian, G., Miller, T. & Chiang, T.-C. Passage from spin-polarized surface states to unpolarized quantum well states in topologically nontrivial Sb films. Phys. Rev. Lett. 107, 036802 (2011).
Kadono, T. et al. Direct evidence of spin-polarized band structure of Sb(111) surface. Appl. Phys. Lett. 93, 252107 (2008).
Hsieh, D. et al. Direct observation of spin-polarized surface states in the parent compound of a topological insulator using spin- and angle-resolved photoemission spectroscopy in a Mott-polarimetry mode. N. J. Phys. 12, 125001 (2010).
Hüfner, S. Very High Resolution Photoelectron Spectroscopy (Springer-Verlag, 2007). https://doi.org/10.1007/3-540-68133-7.
Chang, T.-R. et al. Band Topology of Bismuth Quantum Films. Crystals 9, 510 (2019).
Campi, D., Bernasconi, M. & Benedek, G. Phonons and electron-phonon interaction at the Sb(111) surface. Phys. Rev. B 86, 075446 (2012).
Whalley, L. D., Frost, J. M., Morgan, B. J. & Walsh, A. Impact of nonparabolic electronic band structure on the optical and transport properties of photovoltaic materials. Phys. Rev. B 99, 085207 (2019).
Zhang, H.-J. et al. Electronic structures and surface states of the topological insulator Bi1−xSbx. Phys. Rev. B 80, 085307 (2009b).
Sánchez-Barriga, J. et al. Anomalous behavior of the electronic structure of (Bi1−xInx)2Se3 across the quantum phase transition from topological to trivial insulator. Phys. Rev. B 98, 235110 (2018).
Aguilera, I., Friedrich, C. & Blügel, S. Many-body corrected tight-binding Hamiltonians for an accurate quasiparticle description of topological insulators of the Bi2Se3 family. Phys. Rev. B 100, 155147 (2019).
Groeneveld, R. H. M., Sprik, R. & Lagendijk, A. Effect of a nonthermal electron distribution on the electron-phonon energy relaxation process in noble metals. Phys. Rev. B 45, 5079–5082 (1992).
Groeneveld, R. H. M., Sprik, R. & Lagendijk, A. Femtosecond spectroscopy of electron-electron and electron-phonon energy relaxation in Ag and Au. Phys. Rev. B 51, 11433–11445 (1995).
Wilson, R. B. & Coh, S. Parametric dependence of hot electron relaxation timescales on electron-electron and electron-phonon interaction strengths. Commun. Phys. 3, 179 (2020).
Allen, P. B. Theory of thermal relaxation of electrons in metals. Phys. Rev. Lett. 59, 1460–1463 (1987).
Tamtögl, A., Mayrhofer-Reinhartshuber, M., Kraus, P. & Ernst, W. E. Surface Debye temperature and vibrational dynamics of Antimony(111) from helium atom scattering measurements. Surf. Sci. 617, 225–228 (2013).
Friedrich, C., Blügel, S. & Schindlmayr, A. Efficient implementation of the GW approximation within the all-electron FLAPW method. Phys. Rev. B 81, 125102 (2010).
Faleev, S. V., van Schilfgaarde, M. & Kotani, T. All-electron self-consistent GW approximation: application to Si, MnO, and NiO. Phys. Rev. Lett. 93, 126406 (2004).
Kotani, T. & van Schilfgaarde, M. All-electron GW approximation with the mixed basis expansion based on the full-potential LMTO method. Solid State Commun. 121, 461–465 (2002).
Aguilera, I., Friedrich, C. & Blügel, S. Spin-orbit coupling in quasiparticle studies of topological insulators. Phys. Rev. B 88, 165136 (2013).
Mostofi, A. A. et al. wannier90: a tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 178, 685 (2008).
Acknowledgements
O.J.C. and J.S.-B. are thankful to M. Battiato for fruitful discussions. Financial support from the Impuls- und Vernetzungsfonds der Helmholtz-Gemeinschaft under grant No. HRSF-0067 (Helmholtz-Russia Joint Research Group) and from the Russian Science Foundation (RSF) under Grant No. 19-42-06303 are gratefully acknowledged. We acknowledge the computing time granted through JARA on the supercomputer JURECA at Forschungszentrum Jülich.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
O.J.C., F.F., and J.S.-B. performed spin- and time-resolved photoemission experiments. I.A. performed band structure calculations. A.S.F., A.M.I., S.I.B., and L.V.Y. performed surface preparation and preliminary characterization. O.J.C. and J.S.-B. performed data analysis and prepared the Figures. J.S.-B. and O.J.C. wrote the manuscript with input from all co-authors. J.S.-B. was responsible for the conception and coordination of this work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Clark, O.J., Freyse, F., Aguilera, I. et al. Observation of a giant mass enhancement in the ultrafast electron dynamics of a topological semimetal. Commun Phys 4, 165 (2021). https://doi.org/10.1038/s42005-021-00657-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00657-6
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.