Abstract
A growing leaf is a prototypical active solid, as its active units, the cells, locally deform during the out-of-equilibrium process of growth. During this local growth, leaves increase their area by orders of magnitude, yet maintain a proper shape, usually flat. How this is achieved in the lack of a central control, is unknown. Here we measure the in-plane growth tensor of Tobacco leaves and study the statistics of growth-rate, isotropy and directionality. We show that growth strongly fluctuates in time and position, and include multiple shrinkage events. We identify the characteristic scales of the fluctuations. We show that the area-growth distribution is broad and non-Gaussian, and use multiscale statistical methods to show how growth homogenizes at larger/longer scales. In contrast, we show that growth isotropy does not homogenize in time. Mechanical analysis shows that with such growth statistics, a leaf can stay flat only if the fluctuations are regulated/correlated.
Similar content being viewed by others
Introduction
Out of equilibrium active solids are prevalent in nature and include bio-mechanical systems under development and physiology such as animal epithelium1,2 and plant tissues3,4,5. In recent years synthetic active solids are designed and studied as well6,7,8,9. The role of activity in such systems calls for an extension of existing theories, which were developed to describe passive solids10,11,12. Such theories should account for the local, intrinsic injection of energy and describe the emergent stabilities, or instabilities, dynamic patterns, and properties in such active-elastic materials. For comparison, in the case of fluids, classical theory has been successfully amended to account for the local activity of the particles, also due to extensive experimental research that uncovered basic microscopic mechanisms in different natural and synthetic active systems13. In the case of solids, such experimental data is sparse. A prominent example of such a system is a growing plant leaf, which in short time scales behaves as a thin elastic sheet, but in long time scales, where growth becomes relevant, involves multiple mechanical and biochemical active processes14,15. Detailed measurements of growing plant leaves can, thus, provide important input for the development of a continuum theory for active-elastic sheets.
Plant cells, unlike many animal cells, do not migrate nor change neighbors during development. The cells are surrounded by rigid cell walls that are cemented to each other and create a permanent matrix. In-plant lateral organs, such as leaves and petals, cell division is stopped at the early stages of development and most of the increase in volume occurs via cell expansion (typical 10–100 fold increase in volume and up to a cell diameter of 10–100 microns). The main force that drives cell expansion is the turgor pressure—the osmotic pressure between the exterior and the interior of the cell. This pressure is of order 0.1–1 MPa4 and can be varied via changes in ions concentration in the cell and water exchange between cells. The shape and size of the pressurized cells are stabilized by the high stiffness of their cell walls. These viscoelastic walls are made of polymer networks and cell expansion is thought to involve slow yielding of the cell wall to the internal pressure16 and deposition of new material from within the cell. Based on this mechanical view of the process, one would expect leaf growth to be smooth and isotropic, as in the swelling of a balloon. In such a scenario, growth regulation is expected to be active in large length scales, balancing long-wavelength inhomogeneity in growth.
However, measurements show that leaf growth is neither uniform, smooth or isotropic. Highly anisotropic cell expansions were measured17 as well as large variations in expansion levels in different regions of the leaf18,19. Moreover, recent measurements and models indicate that the growth field is heterogenous also at small scales, as neighboring cells can undergo extremely different expansion levels20,21,22,23. These observations show that the process is governed locally, at the cellular scale, yet so far there was no systematic study of the growth heterogeneity and its statistical properties.
Importantly, growth that is not correlated between cells or tissue parts is likely to achieve a geometrical incompatibility, leading to the buildup of internal stresses24,25 and potentially morphological distortion of the organ26. Therefore, we assume cell growth must be regulated in order to generate a precise shape of an organ, whether flat or spatially complex. Different genetic and molecular networks in plants are known to participate in growth regulation17,27,28,29,30, but recently, feedback mechanisms between stress and growth were proposed to be involved as well, in order to achieve desired shapes. Such feedbacks are being studied in animals, mainly in Drosophila embryo development, as means to homogenize growth and keep a growing object flat or self-similar, or as a source of instability and creation of complex shapes4,31,32,33,34,35,36. In plants, it has been shown that a directional stress on leaves and primordia (leaf “embryo”) could affect the orientation of growth to correlate with the stress4,37,38,39. Currently, it is still not known if and how chemical and mechanical fields are coordinated in a way that leads to the proper growth of leaves.
In this work, we measure the surface growth of Tobacco (Nicotiana tabacum) leaves in high spatial and temporal resolutions for the duration of days. We find that a leaf growth involves large and sharp growth variations at short time and length scales, while at large scales in time and space the field appears smooth and well represented by its means. We study the statistics of the relevant quantities- the growth rate, anisotropy, and directionality. The results reveal several facts about leaf growth, including the abundance of local shrinkage events in the tissue, the typical time and length scales of the area-growth heterogeneity, the homogenization of the area-growth field in time and space but accumulation of anisotropy in time, and the qualitative difference between growth during day and night. These observations suggest that leaf growth should be seen as a multiscale phenomenon (similar in that sense to turbulence), and that in order to understand the process and its regulation, one needs to account for its small-scale variations, and not only its spatial/temporal/many leaves average. In the discussion, we bring preliminary ideas regarding the implications of our results to growth regulation models.
Results
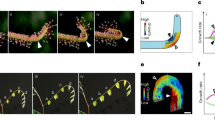
We built an experimental system to measure the local lateral growth tensor of the top surface of leaves growing free of external constraints. The system includes a profilometer, which provides the surface topography z(x, y) in high resolution over the entire leaf. In addition, the system includes a camera, which captures small features on the tissue that act as tracers for the growth measurements. The calculations of growth fields were obtained from the combination of periodic profilometer scans and optical images, taken at 15 min intervals (Fig. 1a–c, Supplementary Note 1, and “Methods” section).
a A pot with a living plant is placed on the x–y stage of a profilometer. The stage and the lighting conditioned are controlled by a preset program, by which the leaf is automatically scanned (red line marks scanning beam) and then optically imaged, in constant time intervals for days. The camera is set at 200 cm distance from the leaf plane, in order to minimize optical artifacts due to vertical growth (Supplementary Note 1). b A typical leaf topography z(x,y) of a Tobacco wild-type leaf (after smoothing) as obtained by the profilometer. Scale bar: 1 mm. c An optical image of the leaf in b, after deleting the low spatial frequency data (black). the small-scale features (white) are used as tracers in the growth calculation algorithm. d An example of an area-growth field, (AG), measured within the time interval \(\Delta t = 15\,{\mathrm{min}}\). Spatial resolution: 250 × 250 micron. e A histogram of all area-growth values, during 90 intervals of \(\Delta t = 15\,{\mathrm{min}}\) during 2 days of measurement (∼70,000 growth events). The most probable value is ∼1% (dashed line). A Gaussian distribution with the same mean and std is depicted in a solid red line. f–h Principal growth measurements, taken from the same leaf area (marked with a rectangle in d) with different time intervals (indicated, all during light-time). At each point, the maximal and minimal growth vectors are depicted: The lines are oriented along the principal directions and their lengths indicate the relevant growth values (scaled by the same arbitrary factor in all panels). Blue lines represent positive growth, red lines represent shrinkage. Scale bar: 0.5 mm. More samples of such data, in Supplementary Fig. 3.
Using Particle Image Velocimetry (PIV) algorithm over sequential images, we obtain the 2D displacement field in the xy plane. Then, we project this 2D vector field onto the relevant topographic scans from the profilometer, obtaining the 3D grids before and after the growth. By summing over the history of the displacement field, we move from Eulerian to Lagrangian coordinates (a grid that evolves with the leaf surface). Then, we calculate a local growth tensor, G(u, v) (Supplementary Note 3) whose eigen vectors and values are denoted \(\hat v_1,\hat v_2,\lambda _1,\lambda _2\). These encode the maximal and minimal growth orientations and magnitudes, as well as the local area-growth rate \({AG}\left( {t,\Delta t} \right) = \sqrt {\lambda _1\lambda _2} - 1\). We also define the anisotropy \({AI} = \frac{{\lambda _1}}{{\lambda _2}}\) (where \(\lambda _1\, > \, \lambda _2\)) and the main growth angle, ϕ, to be the angle between the maximal growth direction and the leaf main vein. These definitions allow complete decoupling of area growth from the anisotropy. more details in methods and Supplementary Note 3.
A Tobacco (Nicotiana tabacum) plant is placed in its pot on the moving stage of the measuring system, under controlled “short-day” conditions (8 h of light per day, details in Supplementary Note 1). Leaf 6 in the order of growth was measured every 15 min for 2 days, in which the leaf total area was tripled (28–89 mm2). The leaf grew flat and its area increased by ∼4% every hour (not shown). The increase in leaf surface area (Supplementary Note 2) reflects the average local growth rate.
Plotting the local area-growth field across the leaf, AG(u, v), during a specific 15 min interval in a resolution of 250 μm (∼10 cells) (Fig. 1d), we find it has vast and large local variations. Surprisingly, although the leaf grew overall during that time interval (i.e., its surface area increased) many spots shrank (blue areas in Fig. 1d). Plotting the histogram of the local surface growth during 90 intervals of 15 min each (Fig. 1e) shows a significant part of the distribution consists of negative values of AG. The histogram is broad—its std is much larger than its mean. It is non-Gaussian (i.e., not a distribution of a random, non-correlated variable), as it has long tails that are slightly skewed. Looking at the growth along the principal directions (Fig. 1f) reveals fluctuations in the level of anisotropy, while the principal directions themselves fluctuate in space as well. There may be some effect of the leaf’s vein network on to the growth orientation (maximal growth aligns with the vein), but it is only along the large veins and it is statistically negligible in our analysis (Supplementary Note 4).
Once realizing the “noisy” nature of the growth field measured at small scales, we turn to study its statistical properties. We start by increasing the time intervals Δt over which growth is calculated. In Fig. 1g, h, we present examples of such growth fields calculated on images separated by 1 and 3 h. In addition to the trivial increase in the amount of growth with Δt, the growth fields appear smoother. While local shrinkage events (red lines) are common during 15 min of growth, they completely disappear at larger time intervals, leading to an apparent smooth growth field. Looking at the total distribution of such AG fields vs Δt (Fig. 2a, inset), we see that as Δt increases, the centers of the histograms shift to larger positive values and the distribution broadens (see also Fig. 2b). However, the ratio between the spatial mean and the standard deviation (std) of the distributions decreases with Δt, (Fig. 2b, inset), reflecting the fact that the growth field becomes smoother (more spatially homogenous) when measured over longer time intervals. The shape of the histograms is not Gaussian (Fig. 2a), having stretched exponential tails. Its higher moments, however, are constant in Δt (skewness\(\cong 1\), kurtosis \(\cong 5\)). Finally, our measurements indicate that the growth field during night time is more heterogeneous than the growth during day time (Fig. 2b, inset), which is due to both lower mean and higher std of AG (not shown).
a Histograms of all area-growth (AG) values taken during 48 h (more than 70k data points), with space resolution \({{\Delta }}x = 250\,{\mu}{\mathrm{m}}\) and different time intervals Δt (indicated in the figure). All histograms are normalized to integrate to 1 (i.e., are treated as probability density functions), shifted to have zero mean, and normalized to have the same std. The dashed line is a Gaussian distribution with the same mean and std. Inset: the same histograms before equalizing the mean and std. b The mean (solid line) and std (dashed line) of the histograms in a, as functions of Δt. Error bars are the standard deviation of the measurements. Inset: the ratio \(\frac{{{\mathrm{std}}}}{{{\mathrm{mean}}}}\) for measurements that were taken during day time (solid line, 64k data points) and during night time (dashed line, 26k data points). c Histograms of all AG values taken during 48 h with \(\Delta t = 15\,{\mathrm{min}}\) and different Δx (indicated in the figure). The histograms are normalized to have the same area and zero mean. The dashed line is a Gaussian distribution with the same mean and std. d The mean (solid line) and std (dashed line) of the histograms in c, as functions of Δx. Error bars are the standard deviation of the measurements, sometimes smaller than the symbol.
Next, we study the spatial properties of the growth fields. We coarse-grain the growth field in the spatial scale (by decreasing the spatial resolution of the displacement field measurement). The growth grid step, Δx is increased from 16 pixels (240 μm) gradually to 560 pixels (1.44 mm) (Fig. 2c). As expected, the mean of the distribution is not affected by the coarse graining, but the standard deviation decreases (Fig. 2d), i.e., the growth measured with lower spatial resolution seem much smoother. In that sense, measurements of low spatial and temporal resolution may give the erroneous impression that leaf growth is a smooth process, a “balloon-like” expansion, at all scales.
The large variations in the measured growth field are highly relevant to the question of growth regulation. If the local temporal AG was a random variable chosen repeatedly and independently from some distribution (such as Fig. 1e), one would expect a buildup of large internal stresses within the leaf tissue (details in Supplementary Note 4) and possibly its distortion into a 3D configuration via buckling instabilities. The fact that such distortions are not observed indicates that some regulation does occur at a relatively small time and length scales, and should be manifested in spatial/temporal correlations.
The spatial correlation function of the AG provides information about the spatial scales of regulation. To calculate that, we choose a set of 50 random points on the leaf, and take series of mean AG values at distance d from them. In Fig. 3a, we plot the auto-correlation on these series. Four selected results, obtained for both day and night, are shown. All four correlation functions decay to zero over a finite distance. As expected, the measured decorrelation length increases with coarse graining in time. A distinct result is a big difference between growth during day and night. The decorrelation length at night is significantly shorter than the ones measured for growth during day time (∼1 vs. ∼5 mm). Anti-correlation was measured for night growth during the shortest measured intervals (15 min).
a Spatial correlation between area-growth (AG) values as a function of the distance between them, d. Different line styles and colors represent different time samples (see legend). Measurements were taken as the leaf grew from 6 to 13 mm in length. Dotted lines are linear extrapolations of the data from 0 to 1 mm. b Mean Fourier transform in time over 1200 signals \({AG}(t)\), taken during light-time intervals of 1 day (8 h). ω is the temporal frequency. The signal \({AG}(t)\) is taken in Lagrangian coordinates. The plot does not include the long, dominant, time scale of 24 h (Supplementary Fig. 2).
Next, we attempt to identify a typical time scale that governs the fluctuations in the area-growth fields. We measure growth in Δt = 15 min time intervals over long duration of time (8 h, during light-time). The measurements are converted to Lagrangian coordinates and AG(t) is evaluated in grid points that are continuously drifted with growth (i.e., 1200 locations in the growing leaf are measured for the entire 8 h). For each such Lagrangian grid point, we perform Fourier transform of the signal AG(t) with Δt = 15 min. We then average the absolute value of the result over all grid points, obtaining \({AG}\left( \omega \right)\). The spectrum is broad, indicating a multiscale process, but a clear peak in \({AG}\left( \omega \right)\) is seen at \(\omega = 0.14\left[ {{\mathrm{min}}^{ - 1}} \right]\) (Fig. 3b), which indicates a dominant time scale of ∼45 min. Therefore, the growth rate in a typical fixed location on a leaf fluctuates with a characteristic time scale.
We now switch our interest to the directional properties of the tensorial growth field. The distributions of maximal and minimal growth values for \(\Delta t = 15\,{\mathrm{min}}\) are presented in Fig. 4a. The histograms of the local anisotropy \({AI} = \frac{{\lambda _1}}{{\lambda _2}}\) (that is the growth eccentricity) show an increase in its mean value as a function of Δt (Fig. 4b, c) and not a decay, as expected if the local orientation was not correlated in time (Fig. 4c). The standard deviation of the anisotropy grows as well (Fig. 4c). We conclude that there is an accumulation of anisotropy, which means that on average growth has a locally preferred direction. Finally, we plot a histogram of the growth angle, ϕ (the angle between maximal growth and the leaf main vein) (Fig. 4d). The histogram shows that indeed during the day the preferred orientation of the local maximal growth is perpendicular to the main vein, while during the night there is no preferred directionality of growth.
a A histogram of the maximal and minimal directional growths \(\left( {\lambda _1,\lambda _2} \right)\) for the minimal time interval \(\Delta t = 15\,{\mathrm{min}}\) and space interval \({{\Delta }}x = 250\,{\mu}{\mathrm{m}}\) during light-time. b Histograms of the anisotropy distributions for \({{\Delta }}x = 250\,{\mu}{\mathrm{m}}\) and different \(\Delta t\) (indicated in the figure) during light-time. c The means of the histograms in b, error bars are the standard deviation of the measurements. d A histogram of growth directions (angle between maximal growth direction and the leaf’s main vein) for \({{\Delta }}x = 250\,{\mu}{\mathrm{m}}\) and \(\Delta t = 15\,{\mathrm{min}}\), during the day (green squares) and the night (cyan circles).
Discussion
Our measurements suggest, to the best of our knowledge, a new view on growth processes in leaves. The growth is not a smooth process in time and space, as could be concluded from low-resolution measurements, or from data that is averaged over many leaves. Instead, growth is a multiscale field with large and sharp variations at small scales that homogenize at larger scales. As such, we analyze the growth fields using statistical tools commonly applied in stochastic dynamics of fluids and active matter.
Among our major findings is the abundance of local tissue shrinkage during growth. Though the surface area of large sections of a leaf increases monotonically (in a typical rate of ∼4%/h), the growth in small regions, of ∼100 cells, oscillates between swelling and shrinking. These oscillations are characterized by a typical time scale of ∼45 min (which may be related to stomata opening40,41 or to growth bursts known as nutation processes42,43) and are correlated over short distances of order millimeters. The higher the measurement resolution in time and space, the larger are the measured growth variations. It is plausible that further increasing the resolution (to a single cell level) would reveal even rougher fields. Decreasing resolution, to 1 h or a few mm, the measurements smoothen, and the ratio of std to mean saturates to a low value (∼0.5, Fig. 2b, d). Note, that the homogenization process, of reaching this saturation, happens at a speed of ±2% area in 1 h (see Fig. 2b, inset) while the average speed of growth itself is ∼4%area/h. Therefore, there is no scale separation, and we cannot distinguish between the growth and the process of homogenization. Finally, though the direction of growth varies as well, it must be correlated in time as the mean anisotropy is increasing with Δt.
One immediately notes that these observations are relevant to the question of growth regulation. If growth was a random process, i.e., growth parameters \(\left( {\lambda _1,\lambda _2,\phi } \right)\) were chosen randomly from our measured distribution at each grid point independently and repeatedly, with no spatial/temporal correlations, we estimate a typical stress developing within 15 min on a flat unit area of 250 × 250 microns to be in the order of ∼0.5 Mpa (Supplementary Note 6). Using the distribution of growth in 2 h, the stress estimation on the same unit area would exceed 1 MPa. Such stress would have led to significant buckling of the surface and distortion of the leaf24,26,44,45. In reality, the leaf grows flat, which indicates that some mechanism regulates growth over small time and length scales. The non-gaussian growth distribution (Figs. 1e and 2a, c), the correlation time and length scales, and the increasing anisotropy (Fig. 4c) also indicate that indeed, though rough in time and space, the growth field is not entirely random, i.e., include some spatial/temporal correlations.
Currently, we see two options to understand the multiscale phenomena we observe in the growth of flat leaves. One is that the dynamics is entirely deterministic. Multiple nonlinear chemical and mechanical fields are involved (e.g., pressure fields and cell–cell channel opening, residual stresses, hormone diffusion and transport, cell wall softening and deposition of new matter) and possibly feedback loops between them, which make growing leaves a complex active system, with the resulting dynamic growth patterns that we see. The other option is that there are sources of randomness in the system that constantly create biological “noise” (e.g., light-induced stomata opening, thermally driven hormonal production or opening of cell–cell channels, etc), however, these must constantly be corrected, possibly via the mentioned stabilizing mechano-chemical feedback.
Further experimentation can shed light on these processes. Specifically, high-resolution measurements of chemical and mechanical fields in the relevant time and length scales we found, can reveal the source of the variations. Then, one should look for mechano-chemical interactions in the system that may be the source of the local smoothing/homogenization of growth. Examples of such interactions are known from flat-growing animal epithelia (drosophila wing disc46), e.g., stiffening under tension, growth direction alignment with tension, enhanced growth rate under tension and reduced rate under compression.
The different growth modes, we found during the day vs. night may provide another clue on growth regulation and homogenization: We showed that the growth during the day is more homogenous than at night, the correlation lengths during the day are larger than at night, and that the direction of growth is oriented roughly perpendicularly to the main vein at day, but lack of global orientation at night. It is possible that most of the active growth takes place during the day, and the accumulated internal stresses are released during the night.
Lastly: though we observed qualitatively similar results in measurements of many Tobacco and Arabidopsis leaves, measurements in other species are needed in order to determine how general our observations are. In addition, the stochastic approach should be implemented on measurements at the cellular scale. Finally, studies of mathematical and physical nature are needed in order to better understand the relation between the growth governing rules, its resulting statistics, mechanics of the leaf, and its final global shape.
Methods
Data acquisition
Our experimental system is designed to measure the local lateral growth tensor of the top surface of leaves growing free of external constraints. The system includes a profilometer (MiniconScan 3000) which provides the surface topography z(x, y) in high resolution (50 μm in x–y, 5 μm in z) over the entire leaf (typically 3 × 3 cm). The calculations of growth fields were obtained from the combination of periodic profilometer scans and optical images, taken at 15 min intervals (Fig. 1a–c and Supplementary Note 1).
Data processing
Using image processing and PIV, we obtain the displacement field \(\vec d(u,v)\) between images on a flat square grid (u, v) of resolution 250 μm × 250 μm (~10 by 10 cells).
We project the 2D grids of sequential measurements, onto the relevant topographical scans, obtaining the 3D grids before and after the growth \(u\left( {x,y,z,t} \right),v\left( {x,y,z,t} \right)\). Using these Lagrangian coordinates, that evolve with the leaf surface, we calculate the local growth tensor, G(u, v). We define the growth tensor in a way the allows complete decoupling between the area-growth rate and its anisotropy (Supplementary Note 3). For each Lagrangian grid point, we calculate the ratio between the surface geometrical metrics in time t1 and t2. The result is a locally defined rank-two tensor whose eigen vectors represent the directions of maximal and minimal growth. The maximal and minimal local elongations between t1 and t2 are \(\sqrt {\lambda _1} - 1,\sqrt {\lambda _2} - 1\), respectively, where \(\lambda _1,\lambda _2\) are the eigen values of \(G(u,v)\). The local area growth is \({AG} = \sqrt {\lambda _1\lambda _2} - 1\) (The normalized change in area of a surface element at t1 and t2). The estimated measurement error in AG is ∼0.2% (Supplementary Note 5). Growth rates, are obtained by dividing the growth values by \(\Delta t = t_2 - t_1\). We define the anisotropy to be \({AI} = \frac{{\lambda _1}}{{\lambda _2}}\) where \(\lambda _1\, > \, \lambda _2\). We define the main growth angle, ϕ, to be the angle between the maximal growth direction and the leaf main vein. For a full description of the local growth, any three independent scalar parameters are sufficient, e.g., \(\left( {\lambda _1,\lambda _2,\phi } \right)\).
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
All data used in this work are available from the corresponding author upon request.
Code availability
All codes used in this work are available from the corresponding author upon request.
References
Guillot, C. & Lecuit, T. Mechanics of epithelial tissue homeostasis and morphogenesis. Science 340, 1185–1189 (2013).
Blanchard, G. B., Étienne, J. & Gorfinkiel, N. From pulsatile apicomedial contractility to effective epithelial mechanics. Curr. Opin. Genet. Dev. 51, 78–87 (2018).
Hong, L. et al. Heterogeneity and robustness in plant morphogenesis: from cells to organs. Annu. Rev. Plant Biol. 69, 469–495 (2018).
Mirabet, V., Das, P., Boudaoud, A. & Hamant, O. The role of mechanical forces in plant morphogenesis. Annu. Rev. Plant Biol. 62, 365–385 (2011).
Smithers, E. T., Luo, J. & Dyson, R. J. Mathematical principles and models of plant growth mechanics: From cell wall dynamics to tissue morphogenesis. J. Exp. Bot. 70, 3587–3599 (2019).
Levin, I., Deegan, R. & Sharon, E. Self-Oscillating Membranes: Chemomechanical Sheets Show Autonomous Periodic Shape Transformation. Phys. Rev. Lett. 125, 178001 (2020).
Chen, Y. Y., Huang, G. L. & Sun, C. T. Band Gap Control in an Active Elastic Metamaterial With Negative Capacitance Piezoelectric Shunting (2014).
Scheibner, C. et al. Odd elasticity. Nat. Phys. 16, 475–480 (2020).
Nash, L. M. et al. Topological mechanics of gyroscopic metamaterials. Proc. Natl Acad. Sci. USA 112, 14495–14500 (2015).
Hawkins, R. J. & Liverpool, T. B. Stress reorganization and response in active solids. Phys. Rev. Lett. 113, 028102 (2014).
Zemel, A., Bischofs, I. B. & Safran, S. A. Active elasticity of gels with contractile cells. Phys. Rev. Lett. 97, 128103 (2006).
Maitra, A. & Ramaswamy, S. Oriented active solids. Phys. Rev. Lett. 123, 238001 (2019).
Marchetti, M. C. et al. Hydrodynamics of soft active matter. Rev. Mod. Phys. 85, 1143–1189 (2013).
Efroni, I., Eshed, Y. & Lifschitz, E. Morphogenesis of simple and compound leaves: a critical review. Plant Cell 22, 1019–1032 (2010).
Pantin, F., Simonneau, T. & Muller, B. Coming of leaf age: control of growth by hydraulics and metabolics during leaf ontogeny. N. Phytol. 196, 349–366 (2012).
Lockhart, J. A. An analysis of irreversible plant cell elongation. J. Theor. Biol. 8, 264–275 (1965).
Sauret-Güeto, S., Schiessl, K., Bangham, A., Sablowski, R. & Coen, E. JAGGED controls Arabidopsis petal growth and shape by interacting with a divergent polarity field. PLoS Biol. 11, e1001550 (2013).
Wiese, A., Christ, M. M., Virnich, O., Schurr, U. & Walter, A. Spatio-temporal leaf growth patterns of Arabidopsis thaliana and evidence for sugar control of the diel leaf growth cycle. N. Phytol. 174, 752–761 (2007).
Remmler, L. & Rolland-Lagan, A.-G. Computational method for quantifying growth patterns at the adaxial leaf surface in three dimensions. Plant Physiol. 159, 27–39 (2012).
Fruleux, A. & Boudaoud, A. Modulation of tissue growth heterogeneity by responses to mechanical stress. Proc. Natl Acad. Sci. USA 116, 1940–1945 (2019).
Hong, L. et al. Variable cell growth yields reproducible organ development through spatiotemporal averaging. Dev. Cell 38, 15–32 (2016).
Elsner, J., Michalski, M. & Kwiatkowska, D. Spatiotemporal variation of leaf epidermal cell growth: a quantitative analysis of Arabidopsis thaliana wild-type and triple cyclinD3 mutant plants. Ann. Bot. 109, 897–910 (2012).
Sampathkumar, A. et al. Primary wall cellulose synthase regulates shoot apical meristem mechanics and growth. Development 146, dev179036 (2019).
Wang, C.-C. In Mechanics of Generalized Continua 247–250 (Springer, 1968).
Efrati, E., Sharon, E. & Kupferman, R. Elastic theory of unconstrained non-Euclidean plates. J. Mech. Phys. Solids 57, 762–775 (2009).
Goriely, A. & Ben Amar, M. Differential growth and instability in elastic shells. Phys. Rev. Lett. 94, 198103 (2005).
Kazama, T., Ichihashi, Y., Murata, S. & Tsukaya, H. The mechanism of cell cycle arrest front progression explained by a KLUH/CYP78A5-dependent mobile growth factor in developing leaves of Arabidopsis thaliana. Plant Cell Physiol. 51, 1046–1054 (2010).
Palatnik, J. F. et al. Control of leaf morphogenesis by microRNAs. Nature 425, 257–263 (2003).
Burko, Y. & Ori, N. The tomato leaf as a model system for organogenesis. Methods Mol. Biol. 959, 1–19 (2013).
Ha, C. M., Jun, J. H. & Fletcher, J. C. Control of Arabidopsis leaf morphogenesis through regulation of the YABBY and KNOX families of transcription factors. Genetics 186, 197–206 (2010).
Labouesse, M. & Farge, E. Mechanotransduction in development. Curr. Top. Dev. Biol. 95, 243–265 (2011).
Chiou, K. K., Hufnagel, L. & Shraiman, B. I. Mechanical stress inference for two dimensional cell arrays. PLoS Comput. Biol. 8, e1002512 (2012).
Schluck, T., Nienhaus, U., Aegerter-Wilmsen, T. & Aegerter, C. M. Mechanical control of organ size in the development of the Drosophila wing disc. PLoS ONE 8, e76171 (2013).
Irvine, K. D. & Shraiman, B. I. Mechanical control of growth: ideas, facts and challenges. Development 144, 4238–4248 (2017).
Chiou, K. K., Hufnagel, L. & Shraiman, B. I. Mechanical stress inference for two dimensional cell arrays. PLoS Comput. Biol. 8, e1002512 (2012).
LeGoff, L. & Lecuit, T. Mechanical forces and growth in animal tissues. Cold Spring Harb. Perspect. Biol. 8, a019232 (2016).
Hamant, O. et al. Developmental patterning by mechanical signals in Arabidopsis. Science 322, 1650–1655 (2008).
Bar-Sinai, Y. et al. Mechanical stress induces remodeling of vascular networks in growing leaves. PLoS Comput. Biol. 12, e1004819 (2016).
Sahaf, M. & Sharon, E. The rheology of a growing leaf: stress-induced changes in the mechanical properties of leaves. J. Exp. Bot. 67, 5509–5515 (2016).
Purwar, P. & Lee, J. In-situ real-time field imaging and monitoring of leaf stomata by high-resolution portable microscope. Preprint at bioRxiv https://doi.org/10.1101/677450 (2019).
Lawson, T. & Blatt, M. R. Stomatal size, speed, and responsiveness impact on photosynthesis and water use efficiency. Plant Physiol. 164, 1556–1570 (2014).
Stolarz, M. Circumnutation as a visible plant action and reaction physiological, cellular and molecular basis for circumnutations. Plant Signal. Behav. 4, 380–387 (2009).
Mugnai, S., Azzarello, E., Masi, E., Pandolfi, C. & Mancuso, S. In Rhythms in Plants: Dynamic Responses in a Dynamic Environment (eds. Mancuso, S. & Shabala, S.) 19–34 (Springer International Publishing, 2015).
Efrati, E., Sharon, E. & Kupferman, R. Buckling transition and boundary layer in non-Euclidean plates. Phys. Rev. E 80, 016602 (2009).
Ventsel, E., Krauthammer, T. & Carrera, E. Thin plates and shells: theory, analysis, and applications. Appl. Mech. Rev. 55, B72–B73 (2002).
Khalilgharibi, N. et al. Stress relaxation in epithelial monolayers is controlled by the actomyosin cortex. Nat. Phys. 15, 839–847 (2019).
Acknowledgements
We thank Prof. Naomi Ori for providing the plants and the advice for their growth; Oded Ben David for his help with the experimental setup, and Hillel Aharoni for useful theoretical discussions.
Author information
Authors and Affiliations
Contributions
Designed the research: S.A. and E.S. Performed the experiments and analyzed the data: S.A. Wrote the random growth theoretical models: M.M. Wrote the manuscript: S.A., M.M., and E.S.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Armon, S., Moshe, M. & Sharon, E. The multiscale nature of leaf growth fields. Commun Phys 4, 122 (2021). https://doi.org/10.1038/s42005-021-00626-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00626-z
This article is cited by
-
An optimized pipeline for live imaging whole Arabidopsis leaves at cellular resolution
Plant Methods (2023)
-
Proliferating active matter
Nature Reviews Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.