Abstract
An accelerating photodetector is predicted to see photons in the electromagnetic vacuum. However, the extreme accelerations required have prevented the direct experimental verification of this quantum vacuum effect. In this work, we consider many accelerating photodetectors that are contained within an electromagnetic cavity. We show that the resulting photon production from the cavity vacuum can be collectively enhanced such as to be measurable. The combined cavity-photodetectors system maps onto a parametrically driven Dicke-type model; when the detector number exceeds a certain critical value, the vacuum photon production undergoes a phase transition from a normal phase to an enhanced superradiant-like, inverted lasing phase. Such a model may be realized as a mechanical membrane with a dense concentration of optically active defects undergoing gigahertz flexural motion within a superconducting microwave cavity. We provide estimates suggesting that recent related experimental devices are close to demonstrating this inverted, vacuum photon lasing phase.
Similar content being viewed by others
Introduction
One of the most striking consequences of the interplay between relativity and the uncertainty principle is the predicted detection of real photons from the quantum electromagnetic field vacuum by non-inertial, accelerating photodetectors. For the special case of a photodetector with uniform, linear acceleration a in Minkowski vacuum, the Unruh effect predicts that the detected photons are furthermore in a thermal state with temperature T = ℏa/(2πckB)1,2,3,4,5. However, to measure for example a 1 K thermal photon temperature, a uniform detector acceleration a = 2.47 × 1020 m s−2 is required, which seems impossibly high for any current or planned tabletop experiments.
Given the difficulty in achieving uniform photodetector accelerations of sufficient magnitude and duration, certain experimental approaches have instead considered electrons that are accelerated nonuniformly by intense electromagnetic fields such that the trajectories are confined to a finite spatial volume. In particular, Bell and Leinass6 interpreted the observed spin depolarization of electron(s) undergoing uniform circular motion in a storage ring in terms of effective heating by vacuum fluctuations (see also refs. 7,8). And Schützhold et al.9 showed that oscillating electrons emit both classical (Larmor) and quantum radiation, with the latter corresponding to the accelerating electrons converting quantum vacuum fluctuations into entangled photon pairs.
Motivated by the goal to enhance the detection of photons from vacuum, a proposal by Scully et al.10 locates an accelerating photodetector atom within an electromagnetic cavity; the idealized, perfectly conducting walls of the enclosing cavity effectively modify the spacetime geometry from Minkowki space to a finite volume for the electromagnetic vacuum2. This finite confining cavity volume then necessitates a non-uniform, i.e., oscillatory acceleration, similar to the accelerating electron proposal of ref. 9; the photodetector atom is envisaged for example as attached to a piezoelectrically driven, vibrating cantilever structure. Another recent relevant proposal11 considers a rapidly rotating, initially excited atom in a cavity, such that the atom’s spontaneous emission is enhanced when the sum of the rotation and atom splitting frequencies resonantly matches a cavity mode frequency.
In these investigations, the electrons and atom photodetectors accelerate nonuniformly (in either direction or magnitude) and in contrast to the Unruh effect as conventionally defined3,4,5, the predicted photon spectrum is not expressible as a thermal distribution with temperature given solely in terms of the acceleration and fundamental constants12,13. Nevertheless, the effects of entangled photon pair production and photon detection from vacuum are still direct consequences of the non-inertial motion of electrons and atoms.
In recent work14,15, we proposed close analogs of the vacuum, oscillatory photodetection effect that involve coplanar, i.e., two-dimensional (2D) superconducting microwave cavity circuit systems16. The photodetector is modelled alternatively as a harmonic oscillator14 and as a qubit15 that capacitively couple to the 2D cavity via a mechanically oscillating film bulk acoustic resonator (FBAR)17; by increasing the FBAR capacitor plate area, a strong detector-cavity coupling can be achieved. Furthermore, when the FBAR mechanical frequency matches the sum of the cavity mode and detector ground-first excited energy level splitting, the photon production rate from cavity vacuum is resonantly enhanced10 so as to be detectable. The use of an FBAR introduces an actual mechanical acceleration, in contrast to previous circuit-based analogs where the accelerating photodetector is mimicked by an electromagnetically induced, time changing detector coupling18,19.
However, a feasible way to demonstrate "genuine" oscillatory acceleration detection and production of photons from vacuum, where the photodetectors are accelerating within a three-dimensional (3D) electromagnetic cavity (as opposed to the above 2D analogues) is still lacking. Despite the resonant gain resulting from placing an accelerating atom inside a cavity10,11, currently achievable cavity quality factors, atom-cavity coupling strengths, and mechanical oscillation acceleration magnitudes are insufficient for attaining measurable photon production from vacuum for a single accelerating detector.
In this paper, we describe a way to realize acceleration photodetection from vacuum with a scheme that involves “many” oscillating photodetectors contained within a microwave cavity (Fig. 1). Such a scheme may be realized by exploiting optically active defects that are embedded within a vibrating membrane structure, such that the defects effectively function as accelerating photodetectors. As one concrete example, we consider a gigahertz (GHz) vibrating diamond membrane containing nitrogen vacancy (NV) color centre defects20. We shall take advantage of a Dicke superradiance-like21,22,23,24, vacuum amplification effect due to the collective motion of the many accelerating photodetectors. While the possibility has been mentioned before to coherently enhance photon production from vacuum using many accelerating electrons9 or detectors25,26, no such investigations have been carried out previously to the best of our knowledge. (Note, however, the proposal of ref. 27 to amplify and hence detect cavity photons produced via the dynamical Casimir effect for an accelerating cavity mirror through their superradiant-enhanced interaction with a cloud of optically pumped atoms).
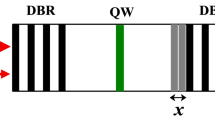
A two-dimensional membrane (shown in crossection) located at x = Lx/2, midway between cavity wall (mirror) boundaries at x = 0, Lx, undergoes flexural vibrations normal to its surface in the x-coordinate direction, resulting in the oscillatory acceleration of pointlike, two level system (TLS) photodetectors embedded within the membrane. An accelerating TLS can undergo a transition to its excited state level, with the accompanying emission of a photon into the cavity mode vacuum. A possible implementation might utilize a diamond membrane with nitrogen vacancy (NV) defect centres20,23,24 furnishing the TLSs, where the flexural vibrations of the membrane are induced for example by piezoactuators (not shown).
Results
Cavity-N accelerating detectors model
We first introduce our model for a cavity field interacting with N ≫ 1 accelerating two level system (TLS) photodetectors and show how the model maps by approximation onto a simpler, parametrically driven Dicke-type Hamiltonian28,29. Referring to Fig. 1, the N TLS detectors are assumed to be embedded within a two-dimensional membrane material system undergoing driven, small amplitude GHz flexural vibrations in the x-coordinate direction (i.e., displacements normal to the static, equilibrium membrane y–z surface), hence imparting acceleratory motion to the TLSs’ centres of mass; the GHz membrane flexural motion may be actuated via piezoelectric transducers, for example. The membrane is enclosed by a microwave cavity ‘box’ with volume V = LxLyLz and box dimensions Li ~ few cm. The cavity dimension in the flexural motion (x coordinate) direction is denoted as Lx, and the membrane is assumed to be located at the cavity midway point x = Lx/2. We consider the following starting model action for the combined cavity field-N detector system:
where the detectors, classically modelled by internal, one-dimensional anharmonic oscillator coordinates Qi, i = 1, …N, are linearly coupled to a 3 + 1 dimensional massless scalar field denoted as \({{\Phi }}(t,\overrightarrow{r})\) that models the electromagnetic field within the cavity. Equation (1) generalizes the starting action of ref. 30 to include more than one detector, as well as assumed weakly anharmonic oscillator potential energy terms \(g{Q}_{i}^{4}/4!\). The latter allows the detectors’ internal degrees of freedom to be truncated to TLSs under parametric resonance conditions; while the harmonic oscillator detector model is beneficial for analytical calculations30, it is somewhat artificial since no detector is purely harmonic, and in particular results in an unphysical parametric instability beyond a critical field-detector(s) coupling14. The detectors are assumed to have identical centre of mass rest frame internal harmonic oscillator frequency ωd0, anharmonic coupling g, and coupling strength λ0 between each detector’s internal degree of freedom and the cavity field. Possible, direct interaction terms between the detectors are not considered in our model; as we show later below, coherent enhancements in the photon production from vacuum can occur as a consequence of the detectors coupling via the cavity field, provided the average spacing between neighbouring detectors is much smaller than the resonant cavity field mode wavelength.
With the membrane undergoing driven flexural oscillations at some frequency Ωm, the centre of mass of the ith detector follows the worldline \({z}_{i}^{\mu }(t)=(t,{L}_{x}/2+A\cos \left({{{\Omega }}}_{{\rm{m}}}t+{\phi }_{i}\right),{y}_{i},{z}_{i})\), where A is the detector’s centre of mass acceleration amplitude and ϕi its phase. The phase ϕi accounts for the fact that the membrane’s GHz flexural mode wavelength ( ~ few μm) is much smaller than the extent of the detector distribution ( ≳ few mm), so that individual oscillating detectors may be out of phase with respect to each other depending on their relative separation in the y–z plane. The ith detector’s proper time is denoted by τi, and its transverse centre of mass coordinates are assumed to satisfy yi ~ Ly/2 and zi ~ Lz/2. The latter condition allows the simplifying approximation that the transversely distributed detectors couple equally to the resonant cavity mode. Note that we adopt the Minkowski metric sign convention ημν = diag(−1, 1, 1, 1).
The action (1) yields the following model Hamiltonian for the cavity-TLS detectors system in the rest frame of the cavity as derived in Supplementary Note 1:
where we assume a single mode approximation for the cavity field with mode frequency ωc = ckc, \({k}_{{\rm{c}}}=\sqrt{{(2\pi /{L}_{x})}^{2}+{(\pi /{L}_{y})}^{2}+{(\pi /{L}_{z})}^{2}}\), and we truncate the anharmonic oscillator detector state space to that spanned by the ground and first excited energy eigenstates with transition frequency \({\tilde{\omega }}_{{\rm{d}}}\) and with TLS-cavity mode coupling \(\tilde{\lambda }\) defined in Supplementary Note 1. Here, we consider the (nx, ny, nz) = (2, 1, 1) cavity mode, which has a node at Lx/2 (see Fig. 1) resulting in a first order dependence on oscillation amplitude A in the interaction term of Hamiltonian (2); if we were to instead use the (nx, ny, nz) = (1, 1, 1) mode, the coupling would involve a cosine instead of a sine term and hence would be much smaller at second order in A. The cavity single mode approximation and detector two level truncation are justified under the condition of parametric resonance between the driven, flexural membrane frequency Ωm and the (renormalized) detector and cavity mode frequencies (see later below). Hamiltonian (2) accounts for relativistic time dilation for the accelerating TLSs through the presence of the reciprocal Lorentz factors \(d{\tau }_{i}/dt=\sqrt{1-{\xi }^{2}{\sin }^{2}\left({{{\Omega }}}_{{\rm{m}}}t+{\phi }_{i}\right)}\), where ξ = ΩmA/c, and may be thought of as a relativistic, parametrically driven Dicke model28,29.
With for example an achievable membrane flexural, microwave scale frequency Ωm ~ 2π × 10 GHz and oscillation amplitude A ~ 10−10 m, we have ξ = ΩmA/c ~ 10−8 and hence the time dilation factors can be safely neglected for potential laboratory realizations. The sinusoidal interaction term can then be well-approximated as \(\sin \left[{k}_{{\rm{c}}}A\cos \left({{{\Omega }}}_{{\rm{m}}}t+{\phi }_{i}\right)\right]\approx {k}_{{\rm{c}}}A\cos \left({{{\Omega }}}_{{\rm{m}}}t+{\phi }_{i}\right)={\omega }_{{\rm{c}}}A/c\cos \left({{{\Omega }}}_{{\rm{m}}}t+{\phi }_{i}\right)\), and with ωc ~ Ωm under conditions of resonance, we see that the individual TLS detector-cavity coupling \(\tilde{\lambda }\) is effectively reduced by the maximum TLS velocity-to-speed of light ratio vm/c ≪ 1.
Nevertheless, from a theoretical standpoint it is still interesting to allow also for relativistic TLS accelerations in exploring photon production when starting initially with the TLSs in their ground states and the cavity in its vacuum state. As we show just below, even under conditions of extreme relativistic TLS motion, Hamiltonian can be mapped onto a much simpler, time-independent Hamiltonian (2) through a type of renormalized, rotating wave approximation (RWA), provided the TLS-cavity coupling \(\tilde{\lambda }\) is sufficiently small (see Supplementary Note 1 for the details of the mapping).
In particular, setting the phases ϕi = 0, we can describe the collection of N TLSs as a single N + 1-level system viewed as a large pseudospin vector of length j = N/2, with the collective spin operators given by \({J}^{z}\equiv \mathop{\sum }\nolimits_{i = 1}^{N}{\sigma }_{i}^{z}/2\) and \({J}^{\pm }\equiv \mathop{\sum }\nolimits_{i = 1}^{N}{\sigma }_{i}^{\pm }\). Expanding the time-dependent terms in Eq. (2) and keeping only terms up to second harmonics in Ωm, the TLS transition frequency is renormalized as \({\omega }_{{\rm{d}}}={\tilde{\omega }}_{{\rm{d}}}{D}_{0}\) and there is an additive frequency modulation \({\tilde{\omega }}_{{\rm{d}}}{D}_{2}\cos (2{{{\Omega }}}_{{\rm{m}}}t)\), where D0 and D2 are ξ-dependent constants (defined in Supplementary Note 1). Imposing the resonance condition Ωm = ωc + ωd, we then transform the frequency renormalized, modulated Hamiltonian to the rotating frame via the unitary operator \({U}_{{\rm{RF}}}(t)=\exp \left(i{\omega }_{{\rm{c}}}{a}^{\dagger }at+i{J}^{z}\left[{\omega }_{{\rm{d}}}t+{\tilde{\omega }}_{{\rm{d}}}{D}_{2}\sin (2{{{\Omega }}}_{{\rm{m}}}t)/2{{{\Omega }}}_{{\rm{m}}}\right]\right)\). Applying the rotating wave approximation (RWA), we finally have that the relativistic, driven Dicke type Hamiltonian (2) can be replaced by the following much simpler approximate Hamiltonian:
where the coupling constant is \(\lambda =\frac{1}{2}\tilde{\lambda }{C}_{1}\left[{J}_{0}\left({\tilde{\omega }}_{{\rm{d}}}{D}_{2}/2{{{\Omega }}}_{{\rm{m}}}\right)-{J}_{1}\left({\tilde{\omega }}_{{\rm{d}}}{D}_{2}/2{{{\Omega }}}_{{\rm{m}}}\right)\right]\), with C1 a ξ, Ωm-dependent constant (defined in Supplementary Note 1), and J0(z), J1(z) are Bessel functions of the first kind (not to be confused with the spin operators J±).
An actual microwave cavity will be lossy, while TLSs in their excited state will relax through photon and phonon emission, with the latter decay channel a consequence of the TLSs embedded within an elastic membrane. For the possible realization considered below, the dominant TLS relaxation channel is through phonon emission23,24, and since as mentioned above the phonon wavelength is much smaller than the extent of the TLS distribution, we model the TLSs as coupled to approximately independent environments. We assume that the cavity-TLSs system dynamics can be described by the following Lindblad master equation:
where γc and γd are the cavity and individual TLS energy damping rates, respectively, and the Lindblad superoperator is defined as \({{\mathcal{L}}}_{A}[\rho ]\equiv A\rho {A}^{\dagger }-\frac{1}{2}{A}^{\dagger }A\rho -\frac{1}{2}\rho {A}^{\dagger }A\). Here, we suppose that the environment temperature is small compared to the frequencies of the cavity mode and TLSs (i.e., kBT/ℏ ≪ ωc, ωd), and also that each TLS has approximately the same damping rate; for the possible realization with microwave cavity and detector frequencies of a few GHz, it suffices to work at dilution fridge temperatures of a few tens of mK or below in order to be in this low-temperature regime.
Analysis of the model
The single cavity mode approximation in Hamiltonian (2) is justified provided the approximate resonance condition Ωm ≈ ωc + ωd is satisfied14. This resonance condition also justifies the RWA Hamiltonian (3), provided ∣λ∣ ≪ ωc, ωd. The advantage to working with the much simpler Hamiltonian (3) is that the Lindblad master Eq. (4) can be solved numerically for up to 20 or so TLSs, while for the full, relativistic time-dependent Hamiltonian (2), numerically solving the Lindblad equation is only possible for less than around 10 TLSs before the computational run times become excessively long. It is noteworthy in this respect that using the approximate Hamiltonian (3) in the master equation provides an accurate description of the average photon number dynamics even for relativistic TLS centre of mass motions with ξ = ΩmA/c ≲ 1 (see Supplementary Fig. 1). Furthermore, for the assumed independent TLS damping, the average photon number dynamics is relatively insensitive to the phase ϕi-dependencies of the TLSs’ motions, justifying setting ϕi = 0 above (see Supplementary Fig. 1). From now on, we will use Hamiltonian (3) in the master equation (4).
One analyical approach to solving the above master equation (but with independent damping replaced by collective damping29–see below) begins with the Holstein–Primakoff (H–P) transformation \({J}^{+}={b}^{\dagger }\sqrt{2j-{b}^{\dagger }b}\), \({J}^{-}=\sqrt{2j-{b}^{\dagger }b}b\), which maps the collective spin operators J± to the bosonic creation and annihilation operators b†, b31. In the large j = N/2 limit, the collective spin of the N TLSs is approximated as a single harmonic oscillator, with Hamiltonian (3) mapped to \(\hslash \sqrt{N}\lambda ({a}^{\dagger }{b}^{\dagger }+ab)\). This coincides with the RWA Hamiltonian that was used in ref. 14 to describe the oscillatory acceleration for a system comprising a photodetector coupled to a cavity electromagnetic field in the single mode approximation, with the detector’s internal degrees of freedom modeled as a harmonic oscillator, and the detector’s centre of mass oscillating at a frequency Ωm that matches the sum of the cavity frequency and detector internal frequency. This system describes a nondegenerate parametric amplification process, with cavity-detector photon pairs produced from the vacuum via mechanical pumping. Including cavity and detector damping and solving analytically the corresponding master equation for the above bosonic Hamiltonian, the average cavity photon number in the long time limit is 〈a†a〉 = 4γdNλ2/[(γc + γd)(γcγd − 4Nλ2)]. Note that the system exhibits a parametric instability when the effective coupling strength \(\sqrt{N}\lambda \) exceeds the value \(\sqrt{{\gamma }_{{\rm{c}}}{\gamma }_{{\rm{d}}}}/2\). While such an instability indicates a breakdown of the above H–P derived approximation method, it does point to the existence of an enhanced vacuum photon production phase for N > Ncrit = γcγd/(4λ2) in the original cavity-TLSs model dynamics given by Eqs. (2)–(4), where there is no such instability32. In the following analysis, we will continue to use the definition Ncrit = γcγd/(4λ2) also for the independent damping master Eq. (4); as we show in Supplementary Note 2, a cumulant expansion analysis of this equation establishes that Ncrit delineates different phases of photon production.
In Fig. 2a, we show for some example, illustrative parameters corresponding to Ncrit = 1, the dynamical behavior of the average scaled cavity photon number 〈a†a〉/N starting from the cavity mode vacuum and with all the TLSs initially in their ground states at time t = 0. The solid line plots are obtained by numerically solving33 the Lindblad master (equation) (4) with the RWA Hamiltonian (3); the utilized numerical method exploits the permutation symmetry of the density operator34, which reduces the size of the Hilbert space required for the TLSs and increases the accessible value of N up to around 20, depending on the parameter choices. The dashed line plots are obtained by solving approximate equations for the non-vanishing first- and second-order moments derived from the master Eq. (4). We find dramatically improved accuracy as compared with usual cumulant expansion approximation methods32,35,36, even for relatively small N, by instead setting certain fourth-order instead of third-order cumulants to zero (see Supplementary Fig. 1). In particular, with each of the TLSs giving an identical contribution to the moment equations, we can replace \({\sigma }_{i}^{z}\), \({\sigma }_{i}^{\pm }{\sigma }_{j}^{z}\) (i ≠ j) with \({\sigma }_{1}^{z}\), \({\sigma }_{2}^{\pm }{\sigma }_{1}^{z}\), respectively. Furthermore, utilizing the identity \({\sigma }_{1}^{z}=2{\sigma }_{1}^{+}{\sigma }_{1}^{-}-1\) and approximating that the fourth cumulants vanish, we obtain for example the following non-vanishing third moment approximation (see Supplementary Equation S21): \(\langle {a}^{\dagger }{\sigma }_{2}^{+}{\sigma }_{1}^{z}\rangle =\langle {a}^{\dagger }{\sigma }_{2}^{+}\rangle \langle {\sigma }_{1}^{z}\rangle +2\langle {a}^{\dagger }{\sigma }_{1}^{+}\rangle \langle {\sigma }_{1}^{-}{\sigma }_{2}^{+}\rangle\). Note that the latter approximation contains an additional term involving products of second moments as compared with the usually employed, third cumulant vanishing approximation32,35,36.
a Evolution of the scaled cavity average photon number: 〈a†a〉/N; solid lines are the numerical solutions and dashed lines are the cumulant expansion approximation. b Evolution of 〈a†a〉/N (green solid line), Fano factor (purple dotted line), as well as the entanglement (logarithmic negativity \({E}_{{\mathcal{N}}}\)–orange dashed line) for the N = 15 case. c Wigner function snapshots at approximate time instants indicated by vertical dashed lines appearing in Fig. 2b. The parameters are γc = γd = 0.02 and λ = 0.01 (in units ωc = 1), corresponding to Ncrit = 1.
The purpose for using the above cumulant expansion approximation is that the photon production from cavity vacuum can be investigated for N ⋙ 1, relevant for possible realizations, while the numerical Lindblad solutions for smaller N are useful for validating the cumulant approximation, as well as giving a more complete picture of the quantum dynamics.
As N increases above Ncrit, a burst peak of cavity photon production from vacuum appears in Fig. 2a that progressively grows in magnitude, narrows, and shifts to earlier times. Furthermore, the long time limit steady-state average photon number grows in magnitude. These features qualitatively resemble those of Dicke superradiance21,22, although in the latter process the TLSs are initially prepared in their excited state and the cavity in the ground state. (Note that ref. 37 considers the effect on superradiance of N = 6 uniformly accelerating, initially excited photodetectors, which is different from the collective enhancement effect for photon detection from vacuum considered here).
In order to get a better idea of the cavity mode-TLSs state, in Fig. 2b we show for N = 15 the time dependence of the logarithmic negativity measure of entanglement \({E}_{{\mathcal{N}}}\)38 between the cavity mode and TLS ensemble and also the cavity mode state Fano factor \((\langle {({a}^{\dagger }a)}^{2}\rangle -{\langle {a}^{\dagger }a\rangle }^{2})/\langle {a}^{\dagger }a\rangle \) in comparison with the average scaled cavity photon number. The entanglement grows and reaches a maximum roughly when the Fano factor is a maximum, while the entanglement is relatively small, although non-zero, in the long-time limit. This non-zero entanglement growth from vacuum indicates that the cavity photon production and TLS excitation are correlated. Such entanglement probes are essential in potential future experiments in order to distinguish correlated vacuum photon production and TLS excitation from possible radiative heating effects (for which the entanglement between the cavity mode and TLSs vanishes). The Fano factor gives partial information about the cavity mode state, in particular the photon number variance, and complements the information provided by the cavity mode Wigner function snapshots shown in Fig. 2c; these latter snapshots correspond to the instants when the Fano factor reaches its peak, subsequent trough, and long-time limit steady state. The photon production from a vacuum burst corresponds to the cavity mode Wigner function rapidly first spreading out and then forming a ring with width close to that of a coherent state (characterized by Fano factor = 1), and eventually settling into a thicker ring in the steady state due to environmental diffusion (with Fano factor > 1). The Fano factor and Wigner function plots help to characterize, for example, how close the cavity mode state is to an effective thermal state (i.e., having a centred, Gaussian Wigner function with Fano factor > 1); in contrast to the usual Unruh effect involving a uniformly accelerating detector, we see from Fig. 2c that the vacuum generated, cavity photon state with its ring-like Wigner function in the long-time limit is clearly non-thermal. This is not surprising given that the TLSs’ motion is non-uniform, i.e., oscillatory.
Possible implementation
In order to get a more quantitative sense of the average cavity photon number dynamics scaling dependence on TLS number N, as well as model possible experimental set-ups, we must go to the large Ncrit limit where it is not feasible to numerically solve the master Eq. (4). As an alternative, we can apply the approximate first- and second-order moment equations (see Supplementary Equation S22) that should become increasingly accurate in the large N limit, provided N is not too close to Ncrit35,36, and which can be straightforwardly solved numerically for arbitrarily large N since the number of coupled moment equations is fixed and small.
We will assume in part the parameters of the 3D microwave cavity-coupled nitrogen vacancy (NV) centre defect scheme of refs. 23,24, which observed signatures of Dicke superradiance21,22. In particular, we consider a coupling strength \(\tilde{\lambda }=2\pi \times 0.07\ {\rm{Hz}}\), corresponding to an NV defect coupling via its magnetic moment to the magnetic field component of the considered cavity electromagnetic vacuum mode with frequency ωc = 2π × 3.2 GHz24. Assuming a diamond membrane flexural oscillation amplitude A = 10−10 m, the nonrelativistic coupling strength is \(\lambda =\tilde{\lambda }{\omega }_{{\rm{c}}}A/(2c)\approx 1.5\times 1{0}^{-9}\ {{\rm{s}}}^{-1}\). For the NV defects, the dominant relaxation process is through spin-phonon interactions with rate γd ≈ 2 × 10−4 s−124. On the other hand, assuming a realizable, superconducting microwave cavity quality factor Qc = 10639, we have γc = ωc/Qc ≈ 2 × 104 s−1. With these numbers, we have \({N}_{{\rm{crit}}}={\gamma }_{{\rm{c}}}{\gamma }_{{\rm{d}}}/{\left(2\lambda \right)}^{2}\approx 4\times 1{0}^{17}\); the number N of microwave field-coupled defects in the experiment of ref. 24 is in the range (0.36−1.5) × 1016, not far below this Ncrit value.
Figure 3a gives the first burst peak maximum and the long time limit steady-state rescaled cavity photon number 〈a†a〉/N dependencies on N/Ncrit. We observe clear evidence of a phase transition, with the slope of average photon number dependence on N changing sharply as N moves through Ncrit. In particular, in the long time steady state, we obtain the following approximate analytical expressions well below and above Ncrit, respectively (see Supplementary Equation S24): \(\langle {a}^{\dagger }a\rangle =\frac{N}{{N}_{{\rm{crit}}}}\frac{{\gamma }_{{\rm{d}}}}{{\gamma }_{{\rm{c}}}+{\gamma }_{{\rm{d}}}}\approx 2\times 1{0}^{-26}N \lll 1\) for N ≪ Ncrit, and 〈a†a〉 = Nγd/(2γc) ≈ 5 × 10−9N ⋙ 1 for N ≫ Ncrit; we can clearly see that the average cavity photon number generated from vacuum is negligible below and non-negligible above Ncrit. While these steady-state average photon numbers scale linearly with N, from Fig. 3b we see that in contrast the first burst peak scales as Nα with α ≈ 2 for N > Ncrit (i.e., quadratically with N to a good approximation); the peak average photon number rapidly grows in magnitude relative to the steady-state value with increasing N above Ncrit. In Fig. 3c, we see that the delay td in the appearance of this first burst peak starting from the initial cavity vacuum state becomes shorter as N increases, with the inverse delay \({t}_{{\rm{d}}}^{-1}\) scaling linearly with N.
a Scaled cavity photon number 〈a†a〉/N versus N/Ncrit at the instant of the first vacuum photon production burst peak (blue dots) and in the long time limit steady state (green triangles). b First peak value of 〈a†a〉/N versus N/Ncrit for N ≫ Ncrit. c First peak inverse delay time 1/td versus N/Ncrit for N ≫ Ncrit. Assumed parameters are γc ≈ 2 × 104s−1, γd ≈ 2 × 10−4s−1, and Ncrit ≈ 4 × 1017.
While these observed scaling dependencies for the first burst peak of photon production from vacuum coincide with those for Dicke superradiant bursts24, they are not properly a superradiant phase however32,36,40. In order to understand better the nature of this enhanced vacuum photon production phase, it is informative to apply the unitary transformation \(U=\exp (i\pi {J}^{x}/2)\) to the master Eq. (4); the RWA Hamiltonian (3) then transforms to the Tavis–Cummings Hamiltonian H = ℏλ(a†J− + aJ+), which involves co-rotating terms only, while the Lindblad operators \({{\mathcal{L}}}_{{\sigma }_{i}^{-}}[\rho ]\) are transformed to \({{\mathcal{L}}}_{{\sigma }_{i}^{+}}[\rho ]\), with each TLS initial ground state transformed to its corresponding excited state. The cavity-oscillatory TLSs system is thus unitarily equivalent to a Tavis–Cummings model with an incoherent pump. While the latter model does not exhibit a Dicke superradiant transition, which requires the presence of both co-rotating and counter-rotating terms of the Hamiltonian, it nevertheless exhibits a so-called "inverted lasing" (or "counterlasing") transition32,36,40. For this reason, the transition to enhanced acceleration detection from vacuum may be thought of as a transition from a normal, incoherent phase below Ncrit to a coherent inverted lasing phase above Ncrit.
Discussion
The challenge of any experimental scheme is to exceed the threshold for coherent photon production from vacuum (equivalently the inverted lasing threshold32,36,40), which in terms of the TLS number N is given by the condition \(N\;> \;{N}_{{\rm{crit}}}={\gamma }_{{\rm{c}}}{\gamma }_{{\rm{d}}}/{\left(2\lambda \right)}^{2}\). In order to reduce the size of Ncrit, we require microwave cavities with large quality factors, TLSs with small damping rates, and large TLS-photon coupling strengths λ. One way to enhance λ is to reduce the microwave cavity volume, for example by utilizing 2D coplanar microwave cavities41,42,43. However, this creates challenges for locating a sufficiently large number of TLSs within the microwave cavity region. On the other hand, while achievable λ couplings for 3D microwave cavities are a few orders of magnitude smaller than what is possible for 2D coplanar cavities, correspondingly much greater numbers of TLSs can be located within the 3D microwave cavity region, furnished by defects within a flexurally vibrating membrane. The above mentioned NV centre scheme for probing Dicke superradiance23,24 is a promising direction, although larger cavity quality factors are required, as well as larger surface area diamond membranes that can be actuated into GHz frequency flexural motion.
While we have focused in the present investigation on a microwave cavity-GHz oscillating membrane defect scheme, it is worth considering other possible schemes as well that effectively incorporate many accelerating photodetector/emitter degrees of freedom. In particular, it would be interesting to revisit the oscillating electron–photon pair production scheme of ref. 9, but instead consider many electrons accelerating in a strong, periodic electromagnetic field. Under conditions where the dominant wavelength of emitted photon pairs is large compared to the average electron separation, we might expect a superradiant-like coherent enhancement of the pair production rate. Alternatively, we might consider a cloud of atoms (i.e., quantum dipoles)44, although the challenge to impart sufficient acceleration magnitude to the cloud’s centre of mass would need to be addressed. Furthermore, electron–electron and dipole–dipole interactions would likely need to be taken into account; such interactions might result in quantum synchronization44, where small initial differences in the individual electron/dipole acceleration magnitudes and phases do not influence the resulting coherent emission of radiation starting from the vacuum state. Finally, with the long-sought goal to demonstrate the original Unruh effect, it would be interesting to investigate possible collective enhancements of photodetection from vacuum for a dense cloud of detectors accelerating uniformly over a sufficiently long time interval in Minkowski vacuum, such that the detected photon spectrum is thermal to a good approximation.
In conclusion, we have proposed a way to demonstrate photon production from vacuum as a consequence of genuinely accelerating photodetectors. Our scheme involves a membrane with a dense cloud of embedded NV defects (equivalently TLS photodetectors) undergoing driven, transverse flexural vibrations within a microwave cavity, and modelled as a driven Dicke-type Hamiltonian. Under the condition of resonance, where the TLS’s centre of mass acceleration frequency matches the sum of the cavity mode and internal TLS’s transition frequency, the system Hamiltonian considerably simplifies via the RWA, thus allowing for an accurate analytical solution using a cumulant expansion approach. When the number N of TLS defects exceeds a critical value Ncrit, the system undergoes a transition to an inverted lasing phase, signalled by a ‘burst’ peak in the average cavity photon number that scales as N2, yielding significantly enhanced, collective photon production from vacuum.
While the primary motivation for the present investigation concerns the interplay between the fundamental physics of relativistic quantum field vacuum and many body quantum dynamics, the possibility to realize entangled many TLS (i.e., qubit)-microwave photon states, purely by mechanically driving a membrane structure initially in a cavity vacuum, may also find broader relevance and application in quantum information science and technology.
Data availability
The codes and generated data that were used to produce the figures in this paper are available by request from the corresponding author.
References
Unruh, W. G. Notes on black-hole evaporation. Phys. Rev. D 14, 870–892 (1976).
DeWitt, B. S. General Relativity: An Einstein Centenary Survey (eds. Hawking, S.W. & Israel, W.) (Cambridge Univ. Press, 1980).
Crispino, L. C. B., Higuchi, A. & Matsas, G. E. A. The unruh effect and its applications. Rev. Mod. Phys. 80, 787–838 (2008).
Fulling, S. A. & Matsas, G. E. Unruh effect. Scholarpedia 9, 31789 (2014).
Ben-Benjamin, J. S. et al. Unruh acceleration radiation revisited. Int. J. Mod. Phys. A 34, 1941005 (2019).
Bell, J. S. & Leinaas, J. The unruh effect and quantum fluctuations of electrons in storage rings. Nucl. Phys. B 284, 488–508 (1987).
Unruh, W. Acceleration radiation for orbiting electrons. Phys. Rep. 307, 163–171 (1998).
Biermann, S. et al. Unruh and analogue unruh temperatures for circular motion in 3 + 1 and 2 + 1 dimensions. Phys. Rev. D 102, 085006 (2020).
Schützhold, R., Schaller, G. & Habs, D. Tabletop creation of entangled multi-kev photon pairs and the unruh effect. Phys. Rev. Lett. 100, 091301 (2008).
Scully, M. O., Kocharovsky, V. V., Belyanin, A., Fry, E. & Capasso, F. Enhancing acceleration radiation from ground-state atoms via cavity quantum electrodynamics. Phys. Rev. Lett. 91, 243004 (2003).
Lochan, K., Ulbricht, H., Vinante, A. & Goyal, S. K. Detecting acceleration-enhanced vacuum fluctuations with atoms inside a cavity. Phys. Rev. Lett. 125, 241301 (2020).
Hu, B. L. & Roura, A. Comment on “enhancing acceleration radiation from ground-state atoms via cavity quantum electrodynamics”. Phys. Rev. Lett. 93, 129301 (2004).
Doukas, J., Lin, S.-Y., Hu, B. L. & Mann, R. B. Unruh effect under non-equilibrium conditions: oscillatory motion of an unruh-dewitt detector. J. High Energy Phys. 2013, 119 (2013).
Wang, H., Blencowe, M. P., Wilson, C. M. & Rimberg, A. J. Mechanically generating entangled photons from the vacuum: a microwave circuit-acoustic resonator analog of the oscillatory unruh effect. Phys. Rev. A 99, 053833 (2019).
Blencowe, M. P. & Wang, H. Analogue gravity on a superconducting chip. Phil. Trans. R. Soc. A 378, 20190224 (2020).
Nation, P. D., Johansson, J. R., Blencowe, M. P. & Nori, F. Colloquium: stimulating uncertainty: amplifying the quantum vacuum with superconducting circuits. Rev. Mod. Phys. 84, 1–24 (2012).
Sanz, M., Wieczorek, W., Gröblacher, S. & Solano, E. Electro-mechanical casimir effect. Quantum 2, 91 (2018).
Felicetti, S. et al. Relativistic motion with superconducting qubits. Phys. Rev. B 92, 064501 (2015).
García-Álvarez, L., Felicetti, S., Rico, E., Solano, E. & Sabín, C. Entanglement of superconducting qubits via acceleration radiation. Sci. Rep. 7, 1–7 (2017).
Piracha, A. H. et al. Scalable fabrication of high-quality, ultra-thin single crystal diamond membrane windows. Nanoscale 8, 6860–6865 (2016).
Dicke, R. H. Coherence in spontaneous radiation processes. Phys. Rev. 93, 99 (1954).
Gross, M. & Haroche, S. Superradiance: an essay on the theory of collective spontaneous emission. Phys. Rep. 93, 301–396 (1982).
Angerer, A. et al. Collective strong coupling with homogeneous rabi frequencies using a 3d lumped element microwave resonator. Appl. Phys. Lett. 109, 033508 (2016).
Angerer, A. et al. Superradiant emission from colour centres in diamond. Nat. Phys. 14, 1168–1172 (2018).
del Rey, M., Porras, D. & Martín-Martínez, E. Simulating accelerated atoms coupled to a quantum field. Phys. Rev. A 85, 022511 (2012).
del Rey, M. Quantum detectors and vacuum correlations in space and time: theoretical results and simulation proposals. Ph.D. thesis, Universidad Complutense de Madrid (2015).
Kim, W.-J., Brownell, J. H. & Onofrio, R. Detectability of dissipative motion in quantum vacuum via superradiance. Phys. Rev. Lett. 96, 200402 (2006).
Bastidas, V. M., Emary, C., Regler, B. & Brandes, T. Nonequilibrium quantum phase transitions in the dicke model. Phys. Rev. Lett. 108, 043003 (2012).
Chitra, R. & Zilberberg, O. Dynamical many-body phases of the parametrically driven, dissipative dicke model. Phys. Rev. A 92, 023815 (2015).
Lin, S.-Y. & Hu, B. L. Accelerated detector-quantum field correlations: from vacuum fluctuations to radiation flux. Phys. Rev. D 73, 124018 (2006).
Holstein, T. & Primakoff, H. Field dependence of the intrinsic domain magnetization of a ferromagnet. Phys. Rev. 58, 1098 (1940).
Kirton, P., Roses, M. M., Keeling, J. & Dalla Torre, E. G. Introduction to the dicke model: from equilibrium to nonequilibrium, and vice versa. Adv. Quantum Technol. 2, 1800043 (2019).
Johansson, J. R., Johansson, G., Wilson, C. M., Delsing, P. & Nori, F. Nonclassical microwave radiation from the dynamical casimir effect. Phys. Rev. A 87, 043804 (2013).
Shammah, N., Ahmed, S., Lambert, N., De Liberato, S. & Nori, F. Open quantum systems with local and collective incoherent processes: efficient numerical simulations using permutational invariance. Phys. Rev. A 98, 063815 (2018).
Kirton, P. & Keeling, J. Suppressing and restoring the dicke superradiance transition by dephasing and decay. Phys. Rev. Lett. 118, 123602 (2017).
Kirton, P. & Keeling, J. Superradiant and lasing states in driven-dissipative dicke models. New J. Phys. 20, 015009 (2018).
Richter, B., Terças, H., Omar, Y. & de Vega, I. Collective dynamics of accelerated atoms. Phys. Rev. A 96, 053612 (2017).
Vidal, G. & Werner, R. F. Computable measure of entanglement. Phys. Rev. A 65, 032314 (2002).
Stammeier, M., Garcia, S. & Wallraff, A. Applying electric and magnetic field bias in a 3d superconducting waveguide cavity with high quality factor. Quantum Sci. Technol. 3, 045007 (2018).
Shchadilova, Y., Roses, M. M., Dalla Torre, E. G., Lukin, M. D. & Demler, E. Fermionic formalism for driven-dissipative multilevel systems. Phys. Rev. A 101, 013817 (2020).
Devoret, M., Girvin, S. & Schoelkopf, R. Circuit-qed: how strong can the coupling between a josephson junction atom and a transmission line resonator be? Ann. Phys. 16, 767–779 (2007).
Probst, S. et al. Inductive-detection electron-spin resonance spectroscopy with 65 spins/hz sensitivity. Appl. Phys. Lett. 111, 202604 (2017).
Ranjan, V. et al. Electron spin resonance spectroscopy with femtoliter detection volume. Appl. Phys. Lett. 116, 184002 (2020).
Zhu, B. et al. Synchronization of interacting quantum dipoles. New J. Phys. 17, 083063 (2015).
Acknowledgements
We thank A.D. Armour, W.F. Braasch, S.-Y. Lin, O.B. Wright, N. Shammah, A.R.H. Smith, and J. Yang for very helpful discussions. This work was supported by the NSF under grant nos. DMR-1507383 and PHY-2011382.
Author information
Authors and Affiliations
Contributions
H.W. and M.B. jointly conceived the idea for the project. H.W. performed the analytical and numerical calculations, and plotted the figures. H.W. and M.B. both contributed to the interpretation of the calculations and jointly wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, H., Blencowe, M. Coherently amplifying photon production from vacuum with a dense cloud of accelerating photodetectors. Commun Phys 4, 128 (2021). https://doi.org/10.1038/s42005-021-00622-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00622-3
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.