Abstract
Studying the collective excitations in charge neutral graphene (CNG) has recently attracted a great interest because of unusual mechanisms of the charge carrier dynamics. The latter can play a crucial role for formation of recently observed in twisted bilayer CNG graphene plasmon polaritons (GPPs) associated with the interband transitions between the flat electronic bands. Besides, GPPs in CNG can be a tool providing insights into various quantum phenomena in CNG via optical experiments. However, the properties of interband GPPs in CNG are not known, even in the simplest configurations. Here, we show that magnetically-biased single-layer CNG can support interband GPPs of both transverse magnetic and transverse electric polarizations (particularly, at zero temperature). GPPs exist inside the absorption bands originating from the electronic transitions between Landau levels and are tunable by the magnetic field. We place our study into the context of potential near-field and far-field optical experiments.
Similar content being viewed by others
Introduction
Graphene plasmon polaritons (GPPs)—electromagnetic fields coupled to oscillating Dirac charge carriers in graphene—exhibit nanoscale field confinement allowing for an active control of their wavelength via gating, and are thus highly interesting for nanophotonics and optoelectronics1. To support GPPs, graphene needs to host a sufficient amount of free charge carriers, which can be achieved by doping (chemical or via gating)2,3, thermal fluctuations4,5 or optical pumping6. In doped graphene, currently considered as a standard platform for exploring GPPs, the energies of GPPs (and thus frequencies at which they can be excited) are limited by the Fermi energy, EF, which can reach a few tenths of an electronvolt. There is a strong desire to extend GPP spectral range exploiting additional ways to tune GPPs at higher energies7. One way to tune GPPs in doped graphene is to apply a static magnetic field, resulting in so called graphene magnetoplasmons8,9,10. However, the performance of the magnetoplasmons in doped graphene is still limited by the high electron scattering rates and the need of high magnetic fields (typically, several Tesla).
Recently, it has been realized that in certain conditions charge neutral graphene (CNG) could become an alternative to doped graphene for GPP applications, since CNG possesses specific optical properties. For instance, being exposed to reasonably low magnetic fields, CNG manifests the colossal magneto-optical activity in the mid-infrared and terahertz frequency ranges11. Besides, as reported in12, CNG shows the giant intrinsic photoresponse due to the small electron-electron scattering rates. Interestingly, collective effects in twisted bilayer CNG can enable the formation of GPP associated with the interband transitions13,14 between the flat electronic bands that appear at the magic angle. Intriguingly, these interband GPP can be closely related with the superconducting states appearing in periodically strained single-layer CNG15 and magic angle twisted bilayer graphene16,17,18. Up to now, although having a high interest for superconducting states formation and increasing of operational frequencies for graphene-based plasmonic devices, GPPs in CNG have been barely explored.
Here, motivated by the recent experimental data11, we show that a single-layer CNG biased by external static magnetic field, or, simply, magnetized CNG (MCNG), can support interband GPPs of both transverse magnetic (TM) and transverse electric (TE) polarizations in both infrared and terahertz (THz) frequency range. To the best of our knowledge, GPPs in MCNG are the unique case of low-frequency interband plasmons. Importantly, their wavelength and energy can be controlled by an external magnetic field, while their figure of merit (the ratio between GPP propagation length and GPP wavelength) and lifetime are comparable with those of the low-loss phonon/exciton polaritons recently discovered in van der Waals (vdW) crystal slabs19,20. Besides, the interband TE GPPs have two orders of magnitude larger confinement of the electromagnetic fields than TE intraband GPPs21,22,23. A much better confinement of the fields in the interband TE GPPs favors their excitation via Bragg resonances in a graphene grating, as we demonstrate in our calculations. On the other hand, we show that TM GPPs can be very efficiently excited either via Fabry–Perot resonances in an array of graphene ribbons (in the far-field experiments) or by means of near-field microscopy (in the near-filed experiments).
Results and discussion
The origin of interband GPPs in MCNG and their properties
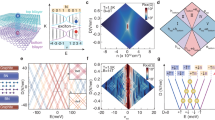
Recall that conventional GPPs in doped graphene arise from intraband electronic transitions (ones between two states within the same band, either the conduction band or valence band, see Fig. 1a), and can be described within the classical Drude model of the conductivity24,25,26,27,28. From this point of view conventional GPPs are similar to the well-known surface plasmon polaritons in noble metals. In contrast, in MCNG intraband transitions are Pauli-blocked, e.g., being not possible, but interband transitions are allowed both between Landau levels (LLs) of opposite sign and the ones involving the zero-th LL (see Fig. 1d). At that, levels with negative sign belong to the valence band, the levels with positive sign belong to the conduction band, and the zeroth level belongs to both of them.
a Schematics for propagating graphehe plasmon-polaritons (GPP) and optical transitions between the valence band and the conduction band in the doped non-magnetized graphene. The electron filling is shown by the dark gray color. b Real and imaginary parts of the normalized conductivity of doped non-magnetized graphene (shown in units of the fine structure constant α0 = 1/137) as a function of frequency, v. The frequency bands where Im[α] > 0 and Im[α] < 0 are highlighted by white and blue horizontal stripes, respectively. c Dispersion relations for GPPs in doped non-magnetized graphene calculated at zero temperature, T, at Fermi energy EF = 0.1 eV and relaxation time τ = 1 ps. d Schematics for propagating GPP and schematics of optical transitions between the valence band and the conduction band in magnetized CNG. The electron filling is shown by the dark gray color. Landau levels are shown by blue and red lines in the Dirac cones. e Real and imaginary parts of the normalized conductivity of magnetized CNG as a function of frequency, v. The frequency bands where Im[α] > 0 and Im[α] < 0 are highlighted by white and blue horizontal stripes, respectively. f Dispersion relations for GPPs in magnetized CNG calculated at T = 0oK, τ = 1 ps and applied magnetic field B = 1.3 T.
Even in the undoped system, electrons in the LL can couple to the time-periodic electromagnetic field and build up an oscillating charge density characteristic of a GPP (note that similar collective oscillations occur in doped graphene in magnetic field10). Thus, interband GPPs in MCNG result from Landau Level quantization and, contrary to conventional intraband GPPs, have no classical counterpart.
The properties of GPPs in MCNG (their wavelength, lifetime, etc.) are fully determined by the magneto-optical conductivity of MCNG, \(\hat \sigma\). Although in general \(\hat \sigma\) of a magnetized graphene is a tensor, in case of MCNG at zero temperature, \(\hat \sigma\) diagonalizes so that, σxx = σyy = σ. This happens due to the symmetry of the LL transitions −n → n − 1 and −n + 1 → n (n is number of LL) which contribute equally but with opposite sign to the non-diagonal conductivity11. Thus, similarly to non-magnetized doped graphene the magneto-optical conductivity of MCNG at zero temperature is characterized by a scalar σ which can be calculated within the linear-response approximation29.
Throughout the paper we consider CNG and neglect any possible deviations from the charge neutrality point, (which could be caused, for example, by the presence of the electron-hole puddles in the graphene sample30). However, as we show in Supplementary Note 1 (Supplementary Fig. 1), interband GPPs can exist even in doped graphene, provided that the doping is low enough to avoid Pauli blocking of the LL transitions. Specifically, the Fermi energy, EF, has to be smaller than one half of the LL transition energy, \(E_c\left( {\sqrt {\left| {n - 1} \right|} + \sqrt {\left| n \right|} } \right)\), where \(E_c\left( B \right) = \sqrt {2e\hbar v_F^2B}\) is cyclotron energy, vF is Fermi velocity and B is the magnetic field. For example, even assuming EF = Ec/2 = 24 meV (the concentration of the charge carriers of 3.1 × 1010 cm−2), Supplementary Fig. 1 shows that, at B = 1.3 T, the dispersion relation of TM GPP in doped graphene remains virtually undistinguishable from that in MCNG. TE GPPs are more sensitive to doping. However, rising the doping up to 3.1 × 1010 cm−2 their dispersion relation at 11.3 THz shifts only by Δk/kpl ≈ 0.007, where kpl is wavevector of GPP in MCNG. For simplicity, we restrict our analysis of the GPPs dispersion relation to the case of a free standing MCNG. Nevertheless, later on, in order to mimic realistic near-field and far-field experiments, we consider MCNG encapsulated between thin hBN slabs. Encapsulated graphene samples are commonly used in the optical experiments, as they show record-high mobilities of charge-carriers, and thus the highest GPPs lifetimes31. In addition, through the whole paper we will limit ourselves to CNG at zero temperature, T = 0oK. It is worth noticing that (as we show in Supplementary Fig. 2 in Supplementary Note 1) the dispersion relation of TM GPPs in MCNG undergoes negligible changes with an increase of temperature up to 100 °K. Even at room temperature (T = 300°K) the dispersion relation of TM GPPs only shows a slight frequency shift of the order of 0.5 THz, with an otherwise unaltered shape of the dispersion curve. TE GPPs are more sensitive to temperature (at T = 300 °K, B = 1.3 T and frequency 11.24 THz the dispersion relation shifts by \(\frac{{{\Delta}k}}{{k_{pl}}} \approx 0.01\)), but they are still observable at T = 300 °K. For definiteness and unless explicitly stated, in all calculations we will consider a relaxation time of charge carriers τ = 1 ps. Note that this relaxation time depends on the joint density of states of LLs and is thus not directly related to the one for direct current transport. The value of τ used in the paper provides absorption spectra linewidths comparable to those reported in measurements in hBN-encapsulated MCNG11. Other values used in the paper are: Fermi velocity υF = 1.15 × 106 ms−1 and external magnetic field B = 1.3 T (Ec = 48 meV) (reachable with neodymium magnets).
In Fig. 1b and 1e we show the real and imaginary parts of the dimensionless conductivity, α = 2πσ/c, as a function of frequency,v, for non-magnetized doped graphene (with EF = 0.1 eV taken for reference) and MCNG, respectively. Both Re(α) and Im(α) of MCNG behave in a markedly different manner compared to those of the non-magnetized doped graphene. Namely, in MCNG Re(α) has a series of pronounced peaks. These peaks correspond to the interband LL transitions, |n − 1| → |n| and |n| → |n−1|, occurring at the discrete frequencies \(\nu _n = E_c\left( {\sqrt {\left| {n - 1} \right|} + \sqrt {\left| n \right|} } \right)/h\) and mark the GPP bands.
The polarization of the GPP mode in each of the bands is determined by the sign of lm(α). Indeed, when the graphene conductivity is a scalar, the dispersion relation of TM GPP reads26,32: 1/qz + α = 0, correspondingly, where \(q_z = \sqrt {1 - q_{pl}^2}\)and \(q_{pl} = k_{pl}/k_0\)are the dimensionless out-of-plane and in-plane GPP wavevector components, respectively, with k0 = 2πv/c being the wavenumber in vacuum. For TE GPPs the dispersion relation satisfies qz + α = 0. The condition that the plasmon fields must decay away from the graphene layers imply that TE plasmons only exist for negative Im(α), while the existence of TM plasmons require lm(α) > 0. In MCNG, Im(α) changes its sign from negative to positive at frequencies vn. On the other hand, at the frequencies \(\tilde \nu _n \approx \sqrt {\left( {\nu _n - \nu _{n + 1}} \right)^2 - \nu _{n + 1}\nu _n}\) (which are in-between of vn and vn+1) Im[α] changes its sign from positive to negative. Therefore, TM GPPs exist in the frequency intervals \(\nu _n\, <\, \nu\, <\, \tilde \nu _n\) (shown by white regions in Fig. 1b,e). Oppositely, in the frequency intervals 0 < v < vn and \(\tilde \nu _n\, <\, \nu\, <\, \nu _n\) (shown by blue areas in Fig. 1b, e) Im[α] < 0, so that TE GPPs can be supported.
In Fig. 1c, f we illustrate the dispersion curves for the GPPs in non-magnetized doped graphene (with EF = 0.1 eV) and MCNG, respectively. In each case, the dispersion of TM (TE) GPPs is shown by the blue (red) curves. We see that GPPs in MCNG and in non-magnetized doped graphene behave very differently. Namely, while in the non-magnetized doped graphene both TM and TE intraband GPPs exist in two continuous frequency intervals, in case of MCNG, the dispersion of the interband GPPs is split into a set of narrow frequency bands with the energy band width \(h{\Delta}\nu \approx E_c\) for the first TM and TE bands. The band widths increase with the magnetic field and decrease with band index, n.
At the high-frequency border of the GPPs frequency bands, the dispersion curves of both TM and TE modes present a back-bending toward \(q_{pl} = k_{pl}/k_0 = 0\), taking place due to the losses in graphene (given by Re(α)). Although the losses in MCNG inevitably limit the propagation of the GPPs, their figure of merit—defined as the ratio between GPP propagation length, Lpl, and the GPP wavelength, λpl, \({\mathrm{FOM}} = L_{pl}/\lambda _{pl}\)—can be comparably large.
Indeed, in case of TM GPP in MCNG, for small values of α, we can approximate \({\lambda}_{pl} = \lambda {\mathrm{Im}}(\alpha )\) and \(L_{pl} = \frac{{\lambda {\mathrm{Im}}(\alpha )^2}}{{2\pi {\mathrm{Re}}(\alpha )}}\) so that \({\mathrm{FOM}} = {\mathrm{Im}}(\alpha )/2\pi {\mathrm{Re}}(\alpha ).\) The condition \(Im(\alpha )\gg Re(\alpha )\), providing high FOM, is fulfilled at the frequencies in the middle of each TM band. Inside each band FOM grows proportionally to both the relaxation time and the magnetic field as \(\propto \left( {\tilde \nu _n\left( B \right) - \nu _n\left( B \right)} \right)\tau\), where both \(\tilde \nu _n\left( B \right)\) and vn(B) are proportional to \(\sqrt B\). For the realistic parameters considered in Fig. 1f, the FOM of TM GPP in the first frequency band reaches ~3.5 (see Supplementary Fig. 4a in Supplementary Note 2). Thus, FOMs of TM GPPs in MCNG can be of the same order of magnitude as FOM of phonon polariton in h-BN33. This result is not intuitive since GPPs present completely different loss channels compared to phonon polaritons (electron-electron and electron-phonon scattering versus phonon phonon scattering, respectively), but it may be very useful as, in contrary to the case of phonon polaritons, GPPs in MCNG are tunable.
To better illustrate the strong confinement of TM GPPs in MCNG in Fig. 2a we show the spatial distribution of the vertical electric field generated by a vertical electrical dipole positioned at z = 60 nm above the graphene, assuming the applied magnetic field of 1.3 T, and v = 12 THz (λ0 = 25 μm). The fringes of the opposite polarities propagating away from the dipole region clearly indicate the polaritonic wavelength (λpl = 4.3 μm) being much smaller than the free-space wavelength, λ0 = 25 μm, indicated by the horizontal black arrow (the corresponding frequency, v = 12 THz, is marked by the black point in the red dispersion curve and by the horizontal dashed line in Fig. 2c).
a Electric field snapshot for the TM GPP in magnetized CNG, at B = 1.3 T. b Propagation length and wavelength of the TM GPP in magnetized CNG as a function of the magnetic field. c Dispersion relation for TM GPP in magnetized CNG calculated for different magnetic fields. d Real part of the z-component of the electric field, calculated for both B = 1.3 T and B = 1 T (with wavelengths λp1 = 4.3 μm and λp2 = 0.97 μm, respectively). In all panels the frequency v = 12 THz (λ0 = 25 μm).
The properties of TM GPP in MCNGs strongly depend on the applied magnetic field. In Fig. 2d we plot the real part of the z-component of electric field of TM GPP, excited by the dipole, as a function of the distance along graphene, x, at two different values of the magnetic field: B = 1.3 T and B = 1 T. These field profiles illustrate that TM GPP wavelength increases with B (λpl is almost five times larger for B = 1.3 T than for B = 1 T), the latter tendency of λpl(B) being further confirmed by the red curve in Fig. 2b. The explicit dependence λpl(B) can be estimated from the dispersion relation, shown in Fig. 2c for several values of the magnetic field within the first band. Away from the band-bending, the GPP wavelength can be written as (see Supplementary Note 3)
with \(W_n = \frac{{\sigma _{uni}}}{\pi }\frac{{E_c^2}}{{h^2\nu _n}}\) being the spectral weight11 and \(\sigma _{uni} = \frac{{e^2}}{{4\hbar }}\) the universal optical conductivity, thus non-linearly scaling with B.
Apart from the importance of FOM for applications requiring propagating polaritons, it can be also important that polaritons have large lifetimes. The latter can be calculated as \(\tau _{life} = L_{pl}/v_{gr}\), where vgf is the group velocity, given by \(v_{gr} = 2\pi d\nu /dk_{pl}\). From Eq. (1) we can obtain \(v_{gr} \approx W_n/\sqrt {W_nk_{pl} + \pi ^2\nu _n^2}\). Thus, at a frequency 12 THz and for a magnetic field B = 1.3 T, for which Lpl ≈ 2 μm (see Fig. 2c), kpl ≈ 1.5 μm−1 (see Fig. 2d), and vgr = 106 m/s, we can estimate τlife ≈ 2 ps. This value is comparable with that of long-lived phonon/exciton polaritons in vdW crystal slabs and 2D layered materials19,20,33.
In strong contrast to the TM modes, the TE GPP in MCNG are far less confined, as shown by the magnetic field snapshot in Fig. 3a (where we use a vertical magnetic dipole source positioned at z = 5 μm above the graphene at the frequency of v = 11.2 THz). The excitation of TE GPP in MCNG is confirmed by the diffraction shadow34 seen in Fig. 3a. It appears because of the destructive interference of the excited TE GPP in MCNG and the dipole radiation. This is due to the comparable wavelengths of free-scape radiation and TE GPPs. At a sufficient distance from the source the TE plasmon is clearly distinguishable from the free-space fields. For a more quantitative analysis of the TE plasmons launched by the dipole, in Fig. 3d we plot the field profile along graphene for two values of the magnetic field: B = 1.3 T (red curve) and B = 1.4 T (blue curve). For comparison, the field launched by the dipole in free-space without graphene (with the wavelength λ0 = 26.77 μm) is also shown by the black curve. According to the field profiles, the difference between λ0 and the wavelength of TE GPP in MCNG does not exceed 2%. Besides, we see that, in contrast to TM modes, the wavelength of TE GPP in MCNG depends on the applied magnetic fields, see Fig. 3b (red curve). Nevertheless, as the plasmons propagate away from the source, the phase shift between the field profiles for different magnetic fields becomes considerable (see the shift between the red and green field profiles in Fig. 3b). The propagation length of TE GPP in MCNG is also much more sensitive to the magnetic field than their wavelength, as shown in Fig. 3b (in Fig. 3d the red field profile clearly decays much quicker than the green one). The latter can be explained by the vertical shift of the dispersion curves of the TE plasmons with the increase of the magnetic field, and thus the back-bending region (where the absorption is increased), see Fig. 3c. The sensitivity of both the phase shift and the propagation length to the magnetic field can be potentially used for the applications of TE GPPs, particularly in interferometers.
a Snapshot of the vertical component of the magnetic field of a TE GPP in magnetized CNG, at B = 1.3 T. b Propagation length and wavelength of the TM GPP in magnetized CNG as a function of the magnetic field. c Dispersion relation for TE GPP in magnetized CNGs, calculated for different magnetic fields. d Real part of the z-component of magnetic field calculated for both B = 1.3 T and B = 1.4 T (the corresponding GPP wavelengths are λpl = 26.32 μm and λpl = 26.66 μm, respectively). For comparison, the free-space wave oscillation (with wavelength λ0) is shown by the black curve. In all panels the frequency v = 11.2 THz (λ0 = 26.77 μm).
TE GPPs in MCNG are much more confined to the graphene sheet than conventional TE GPPs. The strongest confinement takes place close to the back-bending of the dispersion curve with the value ~1/qpl(max) where qpl(max) is the maximum momentum (see Supplementary Note 3), \(q_{pl} = q_{pl}^{({\mathrm{max}})} \approx 1 + \frac{1}{2}\left[ {\frac{{W_n\tau }}{c}} \right]^2\), reached at the frequencies \(\nu ^{\left( {{\mathrm{max}}} \right)} \approx \nu _n - 2/\left( {3\pi \tau } \right)\). At the maximal momentum the confinement is two orders of magnitude smaller than in non-magnetized doped graphene16,17,18. At lower frequencies TE GPP dispersion curve asymptotically tends to the light line, qpl = 1 and thus becomes undistinguishable from the dispersion of the free-space waves.
GPPs in MCNGs can be potentially observed experimentally using either near-field microscopy of non-structured MCNG or far-field transmission/reflection spectroscopy of periodically patterned MCNG. The near-field microscopy, however, is more appropriate for TM GPP in MCNG, since the tip of the near-field microscope typically presents a vertically polarized dipole source, thus better matching with the TM polarized excitations. In the next sections we mimic both near-field and far-field experiments.
Prospects for potential spectral near-field experiments for the characterization of TM GPPs in MCNG
Scattering-type near-field optical microscopy (s-SNOM) utilizes a tip of an atomic force microscope (AFM), which is illuminated with an external infrared laser35,36. The laser beam is focused at the apex of the tip, providing the necessary momentum to launch GPPs in graphene, as illustrated in Fig. 4(a). GPPs emanate from the tip and upon reaching the sample edge, they are reflected back. As the tip is scanned toward the edge, the back-scattered signal is collected in the detector as a function of the tip position2,3. By using a broad-band light source, the near-field light scans can be represented as a function of frequency6. By Fourier transforming the interferogram as a function of frequency, the dispersion relation of GPPs can be retrieved.
a Illustration of the simulation model: the atomic force microscope tip is approximated by a vertical electric dipole with a constant dipole moment. The dipole is located 55 nm above the charge neutral graphene encapsulated into hBN (the thicknesses of the top and bottom layers are 5 nm and 10 nm, respectively). b Near-field image |Ez(x,v)| simulated for magnetic field B = 1.3 T. The field Ez is taken below the dipole, 10 nm above the graphene sheet. c Fourier transform of |Ez(x,v)|. The bright feature matches v(2qpl) what reflects the fact that the graphene plasmon-polariton between being excited, reflected and gathered by the tip travelling the distance 2x.
In our numerical model we represent the illuminated AFM tip by a vertical dipole source. As has been shown in37, the absolute value of the vertical component of electric field taken at some distance below the dipole, |Ez|, can reproduce qualitatively the signal scattered by tip. Therefore, when modeling, we calculate |Ez| below the dipole, as a function of the dipole position (x) and frequency (v), composing a near-field hyperspectral image, |Ez(x,v)|.
An example of the near-field hyperspectral image of the single layer of MCNG encapsulated between two flakes of hBN (the thicknesses of the top and bottom hBN layers are 5 nm and 10 nm, respectively) is shown in Fig. 4b. For simplicity, in these simulations we consider a free standing hBN-encapsulated CNG. Nevertheless, in Supplementary Note 4 we show (see Supplementary Fig. 5) that a 10 nm thick hBN film is enough to make the influence of a substrate negligible. We perform simulations at the frequencies of the first frequency band of TM GPP in MCNG: 11.5–22.35 THz.
In Fig. 4b we clearly observe several bright fringes representing the alternating NF minima and maxima. They appear due to the interference between the GPP launched by the dipole and GPP reflected by the edge. The fringe spacing (the distance between neighboring NF minima or maxima) taken far from the edge equals approximately to the half of the GPP wavelength, λpl/2. As v increases the fringes become thinner and their inter-spacing decreases. The latter decrease is consistent with the dependence \(\lambda _{pl} \propto \left( {\nu ^2 - \nu _n^2} \right)^{ - 1}\), see Eq. (1), where for the first band vn = v1 = 11.5THz. Besides, the amplitude of the fringes decays with the increase of v, which can be attributed to the increase of MCNG losses (i.e., growth of Re(α)) particularly, when approaching the limiting frequency, \({\tilde {\nu}} _1 = 22.35\) THz.
In Fig. 4c we plot the Fourier transform of the near-field hyperspectral image represented in Fig. 4b. The bright maximum seen in the color plot perfectly matches the GPP dispersion curve (the dashed green curve), assuming that the momenta of the GPPs are doubled, 2qpl(v). The latter is consistent with the λpl/2 distance between the interference fringes in Fig. 4b. With our analysis we conclude that the GPPs in hBN-encapsulated MCNG should be observable in s-SNOM experiments for realistic parameters of graphene, even at moderate external magnetic fields.
Prospects for far-field spectroscopy experiments
For the coupling with GPPs from the far-field, the graphene can be structured into ribbons38,39,40,41. Such structuring allows one to avoid the momentum mismatch between the GPPs and free-space waves. Depending upon the parameters of the grating, the excited GPPs present either “quantized” Fabry–Perot modes inside the ribbons, or Bragg-resonances manifesting themselves a dip/peak in the transmission/reflection spectrum. In our simulations for the excitation of both TM and TE GPP in MCNGs we consider a periodic array of micro-ribbons made in either free-standing or hBN-encapsulated graphene, as illustrated in Fig. 5a.
a Schematics of the structure. A MCNG ribbon array with the ribbon period L and ribbon width W is encapsulated in the hBN layer shown by blue color. The red arrow shows schematically the direction of an incident plane wave. The thick blue and black arrows correspond to the electric field vector and wavevector of the incident plane wave. b Absorption spectra, A(v), of TM polarized light incident onto hBN-encapsulated (solid curves) and free-standing (dashed curves) MCNG ribbon arrays with different ribbon widths, W. The thickness of both top and bottom hBN layers is 10 nm The bottom panel shows the dispersion relation of TM GPP in MCNGs. c The same as in (b), but for TE polarized light. The inset in the upper panel shows a zoom of the resonance region. The periods of the ribbon arrays are L = 0.22 μm and L = 28 μm for the TM and TE polarizations, respectively. In both cases, the magnetic field is B = 1.3 T.
In Fig. 5b we show the absorption spectra, A(v), of the ribbon arrays (of different ribbon widths, W, and a fixed period, L = 0.22 μm) illuminated by a normally-incident monochromatic plane wave. The latter is polarized along the x-direction, thus matching with the polarization of TM GPPs. The solid and dashed curves in Fig. 5b correspond to the absorption by the hBN-encapsulated and free-standing MCNG ribbon arrays, respectively. In continuous MCNG (solid black curve in Fig. 5b), the absorption spectra present only one maximum, matching with the interband transition frequency v1 = 11.5 THz. In contrast, the absorption spectrum of the MCNG ribbon array, (both for hBN-encapsulated and free-standing graphene), has a set of resonant maxima. For instance, at W = 3L/4 the absorption spectra (solid blue curve) has one strong resonance at 12.5 THz and set of much weaker ones at higher frequencies. With decreasing W, the resonances blueshift away from v1 dropping in their magnitudes. Similarly to doped graphene ribbon arrays, the emergence of the absorption maxima can be explained by Fabry–Perot resonances in a single ribbon, forming while the GPPs reflect back and forth from the ribbon edges. In the resonance, the GPP refractive index, \(q_{pl} = \frac{{\lambda _0}}{{\lambda _{pl}}}\), should satisfy42
where m is an even number. Note that the modes with the odd integers have antisymmetric distribution of the vertical electric field with respect to the ribbon axis and do not couple to normally-incident waves. For all W, the absorption resonances in the spectrum of hBN-encapsulated graphene ribbon array appear at lower frequencies compared to the ones in the free-standing array. This can be explained by the stronger confinement of GPPs in encapsulated graphene than in the free-standing one. The strong confinement of TM GPPs makes them excellent candidates for sensing the environment43. In fact, changes in the environment can be detected via the resulting frequency shifts of the plasmonic resonances in the far-field spectrum. The absorption resonances are corroborated by the dispersion curves in the bottom panel of Fig. 5b (GPPs in the encapsulated graphene have larger momenta). The vertical dotted lines connecting the absorption maxima (Fig. 5b, top panel) with the GPP dispersion curves (Fig. 5b, bottom panel) mark the frequency positions of the peaks. The frequencies of the peaks match well with the ones given by the simple Fabry–Perot 0th-order resonances in Eq.(2). Substituting Eq.(1) in Eq.(2) we can find that the resonance frequencies are proportional to \(\sqrt {B/W}\), which means that they are tunable by both magnetic field and the ribbon width (see Supplementary Note 5).
To resonantly excite the TE GPPs, we now illuminate the hBN-encapsulated graphene ribbon arrays by a normally-incident monochromatic plane wave with electric field pointing along the y direction. Due to much smaller momenta of TE GPPs, the array period must be more than two orders of magnitude larger than the one considered for excitation of TM plasmons. In Fig. 5c we present A(v), as before, for different W and for the period L = 28 μm (see analogous simulations for smaller relaxation times in Supplementary Note 6). Each color curve demonstrates two strong resonant maxima. The broader resonances are related to the absorption maximum at the interband transition frequency. Indeed, the position of the broader peaks coincides with the resonance in the continuous MCNG (black curve). The appearance of the second (narrow) peak in each curve is very different from the resonance in the case of the TM polarization. First, the narrow peak appears at lower frequency compared to the interband transition. This is clearly related to the spectral region of the TE GPPs (located below the interband transition, as shown in the bottom panel of Fig. 5c). Second, the frequencies of the narrow resonance are almost independent upon the ribbon width. The inset in Fig. 5c showing the zoomed-in frequency region of the narrow resonances demonstrates the minor changes in the magnitude of the peak with change of W. The minor sensitivity of the frequency position of the narrow resonance to the ribbon width is related to a different nature of the resonance. Because the momentum of the TE GPPs is very close to the light line, they can easily leak out of the ribbon while reflecting from the edges, and therefore cannot build the Fabry–Perot resonances in individual ribbons. Instead, the TE GPPs in the grating constitute the Bloch modes and lead to the “collective” Bragg resonances. In this case the resonance condition for the TE GPP refractive index is linked to the grating’s period, L, (rather than to the ribbon width): \(q_{pl} \approx \sin \theta + m\frac{\lambda }{L},\) where m = ±1,… is the diffraction order and θ is the angle of incidence (the dependence of the TE Bragg resonances upon both angle of incidence and frequency is illustrated in more detail in the Supplementary Note 7).
Due to the weak confinement, TE GPPs are less sensitive to the dielectric environment of graphene. Indeed, in the inset of Fig. 5c the absorption spectra by the free-standing array (dashed curves) increase in their amplitudes and slightly shift from those by the hBN-encapsulated ribbon array (solid curves).
We thus demonstrate that MCNG micro-ribbon arrays are a powerful system for controlling the coupling between light and both TM and TE GPP modes. This enables enhancement and tailoring of THz absorption by changing ribbon width and period or applied magnetic fields (in Supplementary Note 5 we also illustrate the tunability of the absorption spectra of the MCNG ribbon arrays by a slight variation of the applied magnetic field).
Conclusion
Summarizing, our work demonstrates that a single-layer CNG biased by an external magnetic field supports magnetically-tunable interband GPPs of both TM and TE polarizations. Some differences between interband GPPs in MCNG and conventional plasmon in doped graphene are worth stressing. From the fundamental side, GPPs in MCNG are rooted in LL quantization and have no classical counterpart, while conventional plasmons can be described by a classical Drude-like response. Figures of merit and lifetimes of GPPs in MCNG are comparable to those of phonon/exciton polaritons in vdW materials. For example, for the applied magnetic field B = 1.3 T the maximal figure of merit and lifetime of TM GPP in the first frequency band reaches ~3.5 and 2-3 ps, respectively, thus being similar to the corresponding values for phonon polaritons in hBN33. However, in difference to phonon polaritons, which are supported by polar slabs within very narrow Reststrahlen bands (determined by the lattice parameters and thus being hardly tunable), the equally narrow frequency bands of interband GPP in MCNG are easily tunable by the applied magnetic field. Notably, the interband TE GPPs in MCNG are two orders of magnitude more confined than TE GPPs in doped graphene, favoring their excitation and potential use in applications.
We have simulated realistic experimental set-ups (both near-field optical microscopy and far-field spectroscopy), which demonstrate that GPP in MCN are detectable with currently available techniques. Importantly, our calculations show that rather low values of magnetic fields (B < 2 T) are already suitable for the observations.
From a different perspective, we believe that our analysis of plasmons in a single-layer magnetized CN graphene can be a tool providing insights into various intriguing quantum phenomena in CNG via optical experiments12,13,15. We foresee that the intriguing phenomena recently discovered in the single-layer CN graphene, as for instance the giant intrinsic photoresponse12, colossal magneto-optical activity11 and markedly reduced electronic noise44, combined with the ability to support GPPs, make magnetized CN graphene promising for a graphene-based magnetically controllable nanoplasmonic and optoelectronic devices, such as gas sensors or bio-sensors44,45,46 or magnetically tunable plasmon-assistant photodetectors47, among other.
Methods
First principle numerical simulation
Full wave electromagnetic simulations were performed using the COMSOL software based on finite-element methods in frequency domain. The graphene layer was modeled as a surface current, implemented in the boundary conditions. In order to achieve convergence, the mesh element size in the vicinity of graphene was much smaller than the plasmon wavelength.
Simulation of NF experiment
In the simulation, the tip was modeled by a vertical point dipole source (polarized along z-axis). We assume that the vertical component of the field below the dipole, Ez, approximates the scattered signal in a s-SNOM experiment28. We thus simulated the near-field profiles by recording the calculated Ez as a function of the dipole position, x (due to the translational symmetry of the problem along the y-axis, Ez does not depend upon y), and dipole frequency. The NF value of Ez is taken 5 nm above the top hBN interface. The dispersion diagram of GPP in MCNG is obtained from the real-space Fourier transform of these NF values taken in space–frequency domain (x, w).
Data availability
The data supporting the findings of this study are included in the main text and in the Supplementary Information files, and are also available from the corresponding authors upon reasonable request.
References
Gonçalves, P. A. D. and Peres, N. M. R. An introduction to graphene plasmonics, (World Scientific Publishing Co. Pte. Ltd., 2016).
Fei, Z. et al. Gate-tuning of graphene plasmons revealed by infrared nano-imaging. Nature 487, 82–85 (2012).
Chen, J. et al. Optical nano-imaging of gate-tunable graphene plasmons. Nature 487, 77–81 (2012).
Vafek, O. Thermoplasma polariton within scaling theory of single-layer graphene. Phys. Rev. Lett. 97, 266406 (2006).
Alonso-González, P. et al. Acoustic terahertz graphene plasmons revealed by photocurrent nanoscopy. Nat. Nanotech. 12, 31–35 (2017).
Ni, G. et al. Ultrafast optical switching of infrared plasmon polaritons in high-mobility graphene. Nat. Photon. 10, 244–247 (2016).
Bezares, F. J. et al. Intrinsic Plasmon–Phonon Interactions in Highly Doped Graphene: A Near-Field Imaging Study. Nano Lett. 17, 5908–5913 (2017).
Yan, H. et al. Infrared spectroscopy of tunable Dirac terahertz magneto-plasmons in graphene. Nano Lett. 12, 3766–3771 (2012).
Crassee et al. Intrinsic terahertz plasmons and magnetoplasmons in large scale monolayer graphene. Nano Lett. 12, 2470–2474 (2012).
Ferreira, A., Peres, N. M. R. & Castro Neto, A. H. Confined magneto-optical waves in graphene. Phys. Rev. B 85, 205426 (2012).
Nedoliuk, I. O., Hu, S., Geim, A. K. & Kuzmenko, A. B. Colossal infrared and terahertz magneto-optical activity in a two-dimensional Dirac material. Nat. Nanotechnol. 14, 756–761 (2019).
Ma, Q. et al. Giant intrinsic photoresponse in pristine graphene. Nat. Nanotech. 14, 145–150 (2019).
Sharma, G. et al. Superconductivity from collective excitations in magic-angle twisted bilayer graphene. Physical Review Research 2, 022040 (2020).
Hesp, N. et al. Collective excitations in twisted bilayer graphene close to the magic angle. Preprint at https://arxiv.org/abs/1910.07893 (2019).
Peltonen, T. & Heikkilä, T. Flat-band superconductivity in periodically strained graphene: mean-field and Berezinskii–Kosterlitz–Thouless transition. Journal of Physics: Condensed Matter 32, 365603 (2020).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Yankowitz, M. et al. Tuning superconductivity in twisted bilayer graphene. Science 363, 1059 (2019).
Lu, X. et al. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 574, 653–657 (2019).
Dai, S. et al. Tunable Phonon Polaritons in Atomically Thin van der Waals Crystals of Boron Nitride. Science 343, 1125–1129, https://doi.org/10.1126/science.1246833 (2014).
Ma, W. et al. In-plane anisotropic and ultra-low-loss polaritons in a natural van der Waals crystal. Nature 562, 557–562 (2018).
Mikhailov, S. A. & Ziegler, K. New electromagnetic mode in graphene. Phys. Rev. Lett. 99, 016803 (2007).
Jablan, M., Buljan, H. & Soljacic, M. Transverse electric plasmons in bilayer graphene. Opt. Express 19, 11236–41 (2011).
Pellegrino, F. M. D., Angilella, G. G. N. & Pucci, R. Linear response correlation functions in strained graphene. Phys. Rev. B 84, 195407 (2011).
Hanson, G. W. J. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. Appl. Phys. 103, 064302 (2008).
Jablan, M., Buljan, H. & Soljacic, M. Plasmonics in graphene at infrared frequencies. Phys. Rev. B 80, 245435 (2009).
Falkovsky, L. A. Optical properties of graphene and IV–VI semiconductors. Phys. Uspekhi 51, 887–897 (2008).
Hwang, E. H. & Das Sarma, S. Dielectric function, screening, and plasmons in two-dimensional graphene. Phys. Rev. B 75, 205418 (2007).
Wunsch, B., Stauber, T., Sols, F. & Guinea, F. Dynamical polarization of graphene at finite doping. N. J. Phys. 8, 318–318 (2006).
Gusynin, V. P., Sharapov, S. G. & Carbotte, J. P. Magneto-optical conductivity in graphene. J. Phys. Condens. Matter 19, 026222 (2007).
Katsnelson, M. I., Novoselov, K. S. & Geim, A. K. Chiral tunnelling and the Klein paradox in graphene. Nat. Phys. 2, 620–625 (2006).
Woessner, A. et al. Highly confined low-loss plasmons in graphene–boron nitride heterostructures. Nat. Mater. 14, 421–425 (2015).
Nikitin, A. Y. World Scientific Handbook of Metamaterials and Plasmonics. World Sci. Ser. Nanosci. Nanotechnol. 4, 307–338 (2017).
Yoxall, E. et al. Direct observation of ultraslow hyperbolic polariton propagation with negative phase velocity. Nat. Photon 9, 674–678 (2015).
Nikitin, A. Y., Rodrigo, S. G., García-Vidal, F. J. & Martín-Moreno, L. In the diffraction shadow: Norton waves versus surface plasmon polaritons in the optical region. N. J. Phys. 11, 123020 (2009).
Ocelic, N., Huber, A. & Hillenbrand, R. Pseudoheterodyne detection for background-free near-field spectroscopy. Appl. Phys. Lett. 89, 101124 (2006).
Yang, H. U. et al. A cryogenic scattering-type scanning near-field optical microscope. Rev. Sci. Instrum. 84, 023701 (2013).
Nikitin, A. Y. et al. Real-space mapping of tailored sheet and edge plasmons in graphene nanoresonators. Nat. Photon 10, 239–243 (2016).
Ju, L. et al. Graphene plasmonics for tunable terahertz metamaterials. Nat. Nanotechnol. 6, 630–634 (2011).
Yan, H. et al. Damping pathways of mid-infrared plasmons in graphene nanostructures. Nat. Photonics 7, 394–399 (2013).
Nikitin, A. Y., Guinea, F., Garcia-Vidal, F. J. & Martin-Moreno, L. Surface plasmon enhanced absorption and suppressed transmission in periodic arrays of graphene ribbons. Phys. Rev. B 85, 081405 (2012).
García de Abajo, F. J. Graphene plasmonics: challenges and opportunities. ACS Photonics 1, 135–152 (2014).
Nikitin, A. Y. Low, Tony, Martin-Moreno. Luis Phys. Rev. B 90, 041407 (2014).
Vasić, B., Isić, G. & Gajić, R. Localized surface plasmon resonances in graphene ribbon arrays for sensing of dielectric environment at infrared frequencies. J. Appl. Phys. 113, 013110 (2013).
Fu, W. et al. Biosensing near the neutrality point of graphene. Sci. Adv. 3, e1701247 (2017).
Kanti, P. R., Badhulika, S., Saucedo, N. M. & Mulchandani, A. Graphene nanomesh as highly sensitive chemiresistor gas sensor. Anal. Chem. 84, 8171–8178 (2012).
Salehi-Khojin, A. et al. Polycrystalline Graphene Ribbons as Chemiresistors. Adv. Mater. 24, 53–57 (2012).
Koppens, F. et al. Photodetectors based on graphene, other two-dimensional materials and hybrid systems. Nat. Nanotech. 9, 780–793 (2014).
Acknowledgements
We acknowledge funding from Spain’s MINECO under Grant No. MAT2017-88358-C3 and funding from the European Union Seventh Framework Programme under grant agreement no. 881603 Graphene Flagship for Core 3 . L.M.M. acknowledge Aragon Government through project Q-MAD. A.Y.N. acknowledges the Basque Department of Education (grant numbers PIBA-2020-1-0014). The research for A.B.K. was supported by the Swiss National Science Foundation.
Author information
Authors and Affiliations
Contributions
A.B.K., A.Y.N. and L.M.M. conceived the work. T.M.S., A.Y.N. and L.M.M. performed numerical and analytical calculations. T.M.S. and A.Y.N. wrote the paper with the input from all co-authors. J.M.P. contributed to the interpretation of the results. All the authors contributed to the discussion of the results.
Corresponding authors
Ethics declarations
Competing interests
The author(s) declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Slipchenko, T.M., Poumirol, JM., Kuzmenko, A.B. et al. Interband plasmon polaritons in magnetized charge-neutral graphene. Commun Phys 4, 110 (2021). https://doi.org/10.1038/s42005-021-00607-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00607-2
This article is cited by
-
Infrared nano-imaging of Dirac magnetoexcitons in graphene
Nature Nanotechnology (2023)
-
Manipulating polaritons at the extreme scale in van der Waals materials
Nature Reviews Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.