Abstract
Optical frequency comb technology has been the cornerstone for scientific breakthroughs in precision metrology. In particular, the unique phase-coherent link between microwave and optical frequencies solves the long-standing puzzle of precision optical frequency synthesis. While the current bulk mode-locked laser frequency comb has had great success in extending the scientific frontier, its use in real-world applications beyond the laboratory setting remains an unsolved challenge due to the relatively large size, weight and power consumption. Recently microresonator-based frequency combs have emerged as a candidate solution with chip-scale implementation and scalability. The wider-system precision control and stabilization approaches for frequency microcombs, however, requires external nonlinear processes and multiple peripherals which constrain their application space. Here we demonstrate an internal phase-stabilized frequency microcomb that does not require nonlinear second-third harmonic generation nor optical external frequency references. We demonstrate that the optical frequency can be stabilized by control of two internally accessible parameters: an intrinsic comb offset ξ and the comb spacing frep. Both parameters are phase-locked to microwave references, with phase noise residuals of 55 and 20 mrad respectively, and the resulting comb-to-comb optical frequency uncertainty is 80 mHz or less. Out-of-loop measurements confirm good coherence and stability across the comb, with measured optical frequency instability of 2 × 10−11 at 20-second gate time. Our measurements are supported by analytical theory including the cavity-induced modulation instability. We further describe an application of our technique in the generation of low noise microwaves and demonstrate noise suppression of the repetition rate below the microwave stabilization limit achieved.
Similar content being viewed by others
Introduction
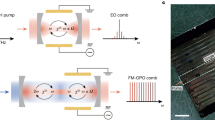
Phase-stabilized optical frequency combs (OFCs), with the multitude of coherent and stable spectral lines, bridges the research frontiers in ultrastable laser physics and ultrafast optical science.1,2,3,4,5,6 Phase stabilization requires two-dimensional feedback control on the comb’s intrinsic two degrees of freedom, the comb spacing and one of the comb line optical frequencies. While the comb spacing can be readily measured with a high-speed photodetector, assessment of the comb line optical frequency fluctuations often requires non-trivial and/or nonlinear processes. One approach is to compare the OFC against an external optical reference, and previous phase stabilization of Kerr frequency comb has been predominantly demonstrated with schemes based on this approach.7,8 The requirement of an external optical reference, however, limits the achievable compactness of Kerr frequency comb and impairs its integration of chip-based photonics with electronics. Another approach is to devise a nonlinear optical interferometry which reveals the optical frequency instability through the so-called carrier-envelope-offset frequency fceo, an internal OFC property resulting from the difference in the phase and group velocities.9 Knowledge of frep and fceo fully determines the optical frequencies of a mode-locked laser-based OFC, and phase locking them to stable microwave references ensures the intricate stability of the optical frequency synthesizer. Figure 1a shows the schematic of a state-of-the-art f–2f nonlinear interferometer widely adopted to measure the fceo.10 First, the output pulse from a mode-locked laser is spectrally broadened in a highly nonlinear photonic crystal fiber such that its optical spectrum spans more than an octave. Then the octave-level spectrum is separated into two parts: the lower-frequency end undergoes second-harmonic generation in a nonlinear crystal while the higher-frequency end only experiences free-propagation. Finally, the two beams are put together in both transverse and longitudinal coordinates for them to interfere on a photodetector and generate a beat note at fceo. For the nonlinear processes to work properly, spectral broadening, in particular, few-cycle pulses with peak powers in the 10-kW level are required.6
a Schematic of the current f–2f nonlinear interferometry to measure fceo. By comparing the higher-frequency comb segment and the second-harmonic of the lower-frequency segment, a beat note at fceo with sufficient signal-to-noise-ratio (SNR) is generated on a photodetector (PD). This often requires comb spectral broadening in a highly nonlinear fiber and/or a broad octave-level comb span. b The unique generation mechanism of frequency microcombs provides an alternative full-stabilization route that does not require external nonlinear processes. Modulation instability and four-wave mixing then generates the initial comb lines with Δ spacing, and subsequently secondary lines with frep spacing. Often, Δ is not an integer multiple of frep. The frequency microcomb therefore has an offset frequency ξ innately. As elaborated later, ξ resembles fceo in directly gauging the optical frequency instability. c Example frequency microcomb spectrum showing subcombs around primary lines yet to fully merge. d Primary comb lines are formed with a spacing (Δ) of 1.1 nm and then generate overlapping subcombs. e Electrical spectrum measures two distinct beat notes of frep = 17.9 GHz and ξ = 523.35 MHz, confirming the presence of a unique ξ (f) and (g) Free-running change in frep and ξ at different spectral regions are measured to be the same within error bars of ≈2 kHz and ≈200 kHz, respectively. At wavelengths where the beat notes have SNR higher than 10 dB (100 kHz RBW), 10 measurements are taken to determine the mean values of the comb spacing and offset frequencies. Measurement error bar is the peak-to-peak deviation from 10 measurements.
While the microresonator-based OFC, or Kerr frequency microcomb, is approaching the performance of mode-locked laser-based OFC in many aspects,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35 its output pulse duration and peak power are still lower by orders of magnitude. Application of f–2f and 2f–3f nonlinear interferometer technique to the Kerr frequency comb is thus challenging and power demanding. The pulse duration can potentially be improved by finer dispersion engineering, but the peak power is fundamentally limited by the bandwidth-efficiency product36 and the large comb spacing. On the other hand, the 10 to 100 GHz comb spacing of Kerr frequency comb is considered an advantageous feature for applications like coherent Raman spectroscopy,37 optical arbitrary waveform generation,38 high bandwidth telecommunication,39,40 and astrospectrograph calibration.41,42,43 In a recent pioneering demonstration of self-referenced Kerr frequency comb where f–2f nonlinear interferometer technique is adopted,27,44 a hybrid approach was utilized with two interlocking combs, a THz spacing comb with dispersive waves at f and 2f is used to calculate fceo while a second relatively closely spaced comb is simultaneously generated to measure frep. This approach is successful; however, the experimental setup includes several components including lasers at different wavelengths, frequency shifters, and a thulium amplifier. In addition, in recent years there have been several experiments attempting to facilitate stabilization and reduce the size, weight, and power (SWaP) impact of peripherals via more compact control,45 electro-optic modulation of large spacing combs,46 and micromachined atomic cells.47,48
In this work, we attempt to extend current stabilization techniques using the unique generation mechanism of Kerr frequency microcombs. We demonstrate comb stabilization using only internal degrees of freedom in a single resonator with no external nonlinear processes and achieve an Allan deviation (AD) of 2 × 10−11 at a 20-s gate time for the stabilized comb lines. After the stabilization of frep, we show that ξ resembles fceo in gauging the optical frequency instability without the need of an external optical reference. ξ is specifically sensitive to the fluctuation in pump frequency, which is at the same time the 0th comb line frequency. Phase locking of frep and ξ to low-noise microwave oscillators thus guarantees the optical frequency stability of the microcomb. This method has potential for chip-scale integration, while circumventing the need for a large number of peripherals, thereby preserving the key SWaP advantage of frequency microcombs.
Results and discussion
Kerr frequency comb formation in the microresonator is illustrated in Fig. 1b. The intracavity power is gradually increased by decreasing the frequency of an initially blue-detuned pump. As coupled cavity power crosses a threshold, modulation instability (MI) gain dominates over cavity loss forming primary comb lines via degenerate four-wave mixing (FWM). The frequency difference between the primary lines (Δ) is determined by dispersion, pump power and mode interaction. In general, however, Δ need not be an integer multiple of the cavity repetition rate frep. Thus, on the formation of subcombs with secondary comb lines spaced by frep, around the primary lines, the generated comb exhibits an intrinsic offset frequency ξ, that may be directly detected by a photodetector.13,14,15,16 While in general the comb state can be complex with multiple offset beats or chaotic (see Supplementary Note I), with detuning and pump power control it is possible to generate just a single set of primary lines (unique Δ) and therefore a microcomb with a well-defined ξ uniquely. Figure 1c shows the optical spectrum of such a comb in the C-band, the particular phase-locked breather state generated necessitates a modulated comb spectrum since we do not have full merging of the subcombs. Figure 1d zooms in to a 3 nm bandwidth showing the spacing Δ and the merging of subcombs. In Fig. 1e, we see the resultant RF beat notes at ξ = 523.35 MHz and frep = 17.9 GHz, as detected by a high-speed photodetector. We further confirm the existence of only one primary comb family and the uniformity of frep and ξ across the Kerr frequency comb by measuring the beat notes at different spectral segments with a tunable 0.22-nm bandpass filter, in Fig. 1f and g, respectively. The breather state generated is stable and exists across a range of powers and detuning. In our specific instance, we see a stable breather over a detuning span of over GHz and with a power tolerance of ≈1 dB. In addition to being of use in locking, such phase-locked breather Kerr combs have also recently come under some scrutiny for their rich cavity dynamics.49
Experimental characterization of microcomb full stabilization
Figure 2a depicts the frequency microcomb setup for stabilization.50 Detailed descriptions of the chip fabrication and measurement setup are included in the “Method” and Supplementary Notes II and III, respectively. The Si3N4 microresonator is fabricated with CMOS-compatible processes and the spiral design ensures that the relatively large resonator fits into a tight field-of-view to avoid additional cavity losses introduced by photomask stitching and discretization errors. The resonator has a quality factor Q of 1.2 million intrinsically in the transverse-electric mode polarization, with near-critical coupling for a 600,000 loaded Q. The waveguide width of 2 μm (725 nm height) allows for significant mode overlap between the fundamental and first-order TE modes, and thereby the resonator exhibits periodic mode-interaction spaced by 4 nm. Free-space to chip coupling is implemented by a 600 µm long adiabatic coupler which allows, with our coupling free-space lens, a total chip coupling loss not more than 5.5 dB. In order to suppress environmental temperature fluctuations from the microcomb, the resonator chip is placed on a thermoelectric cooler for thermal control and placed in a box with two layers of thermal foam insulation. We note that the box is not entirely sealed, which gives little convective currents within the box or between the external environment and the box, leading to some temperature fluctuations. The entire setup including the optics is then placed in an acrylic chamber. Acoustic noise is dampened by placing the enclosed setup on a sorbothane sheet and then placing it on an active optical table. The comb spacing of 17.9 GHz is directly measurable by sending the output to a high-speed photodetector. The comb spacing is then phase locked and stabilized to a microwave oscillator by controlling the pump power through a fiber electro-optic modulator (primary loop) and either the gain of the erbium-doped fiber amplifier (slow loop marked in yellow) or temperature of the chip mount (slow loop marked in green). Quality of the frep stabilization is detailed in Supplementary Note III.
a Frequency microcomb setup for stabilization. Here EOM, Electro-optic modulator; EDFA, Erbium-doped fiber amplifier. For ξ and frep stabilization, an EOM controls the pump power and the ECDL diode current controls the pump laser frequency, through two phase-locked loops. We also note that, in place of the EOM, a polarization rotator with a PBS can also serve for intensity modulation. To increase the locking duration, we implemented slow control of the ECDL PZT (red dashed line) and the EDFA gain (yellow dashed path). The slow feedback to the EDFA gain may also alternatively be replaced by sending the feedback signal to the temperature controller on the chip holder (which controls device temperature) instead (green dashed path). This reduces loop dynamic range but also mitigates the effects of ambient temperature drift. The stability of the locked microcomb is interrogated out-of-loop by beating with an independently stabilized fiber frequency comb. b Frequency domain illustration of the demonstrated full-stabilization technique. Here the offset frequency, ξ, is linked with the primary comb line spacing, Δ, by the constitutive relation \(\xi = \Delta - \left| {\frac{\Delta }{{f_{{\mathrm{rep}}}}}} \right|f_{{\mathrm{rep}}}\). Furthermore, \(\Delta = \frac{1}{{\sqrt {\pi c\left| {\beta _2} \right|} }}\sqrt {\eta \left( {n_{\mathrm{g}}f_{\mathrm{p}} - N\frac{{n_{\mathrm{g}}^2}}{{n_0}}f_{{\mathrm{rep}}} - \frac{{\gamma cP_{{\mathrm{int}}}}}{\pi }} \right)} \) where β2 is the group velocity dispersion (GVD), \(\eta = \frac{{\beta _2}}{{\left| {\beta _2} \right|}}\) is the sign of the GVD, ng is the group index, no is the refractive index, N is the longitudinal mode number, c is the speed of light in vacuum, γ is the nonlinear coefficient, and Pint is the intracavity pump power. c Subsequent to frep stabilization, the offset frequency shows strong linear correlation with pump wavelength (blue circles) with a slope of about 4.5 MHz per picometer shift of pump. The simulated slope (plotted in orange) also shows good agreement with measured data. d Measured offset frequency as a function of applied pump power, after frep stabilization. The pump power is stepwise changed by a total of 3.4% via the EFDA gain. The offset frequency remains constant within the error bar, verifying that frep stabilization effectively eliminates the intracavity pump power fluctuation. For (c) and (d), 10 measurements are taken to determine the mean value, and the error bars are defined as the peak-to-peak deviations from the 10 measurements. Here the pump frequency is not yet stabilized, resulting in the error bars in the offset frequency measurements.
Of note, the free-running offset frequency ξ is much noisier than the comb spacing frep due to the additional multiplier in the constitutive equation that is proportional to the spacing between the primary comb lines and pump (Δ) divided by the repetition rate (the brackets in Eq. (1) correspond to the floor operation):
To this end, frep stabilization loop is always engaged before measurements on the offset frequency is conducted. Comparison between free-running and post-frep stabilization ξ is included in Supplementary Note III. As the offset frequency is localized to the spectral region where secondary comb lines overlap, a 0.22 nm optical bandpass filter is used to select the overlapped comb lines around 1553.5 nm for detection. The beat note is thus improved to 50 dB above the noise floor with a resolution bandwidth (RBW) of 10 kHz, sufficient for a reliable feedback stabilization (more than 45 dB with 10 kHz RBW). The offset frequency is divided by 15 before it is phase locked and stabilized to a microwave synthesizer. The pre-scaling reduces the phase fluctuation, while preserving the instability of the oscillator frequency, and thus it makes the ξ phase-locked loop more robust against noise. The high-bandwidth feedback on ξ is achieved by direct current modulation of the external cavity diode laser (ECDL), and the slow feedback is done through piezoelectric transducer control of the ECDL. We heterodyne beat our Kerr frequency comb with a stabilized fiber frequency comb (FFC) to measure out-of-loop stability. All microwave oscillators and frequency counters are commonly referenced to a rubidium-disciplined crystal oscillator with a 5 × 10−12 frequency instability at 1 s integration time.
Kerr frequency comb generation mechanism can be described by the nonlinear Schrӧdinger equation and the cavity boundary condition:51,52,53
where En(z,t) is the electric field envelope function at the nth cavity round-trip, z is the propagation, t is the retarded time, α is cavity round-trip loss, β2 is the group velocity dispersion (GVD), γ is the nonlinear coefficient, T is transmission coefficient of the coupler, and φ0 is the phase accumulated in a round-trip. Here the microresonator is assumed to be critically coupled, for simplicity. Under the mean-field approximation and the good cavity limit, the primary comb spacing, which depends on the optimal frequency where modulation instability gain reaches its maximum, can be solved as (Supplementary Note IV):
where \(\eta = \frac{{\beta _2}}{{\left| {\beta _2} \right|}}\) is the sign of the GVD, ng is the group index, no is the refractive index, N is the longitudinal mode number, c is the speed of light in vacuum, fp is the pump frequency, and Pint is the intracavity pump power. This picture of comb formation is illustrated in the schematic Fig. 2b.
Equations (1) and (4) explicitly show the dependence of ξ on fp, frep, and Pint. In the high-Q Si3N4 microresonator, Pint is resonantly enhanced to be as high as 30 W and it is the dominant heat source to change the cavity temperature and subsequently the comb spacing.29 For instance, a pump power variation of 0.12% results in a microcomb line-to-line frequency spacing of 1.6 × 10−5 fluctuation, corresponding to a large cavity temperature fluctuation of 1 K. While frep is directly dependent on cavity temperature and Pint,54 we note that frep is only indirectly dependent on fp. This indirect dependence is eventually attributable to a change in Pint since a change in detuning changes the power coupled to the cavity.
Theoretically this can be understood by noting that the usual way fp directly contributes to changes in frep is via Raman self-frequency shift,54 however since our comb is not a soliton, this effect is negligible. Thus, we expect the frep stabilization will effectively eliminate the Pint fluctuation. Under this assumption, the offset frequency is reduced to just a function of pump frequency once the comb spacing is stabilized. Control of frep and ξ is thus equivalent to the regulation of frep and fceo in full stabilization of the Kerr frequency comb. Figure 2c plots the measured and simulated offset frequency as a function of pump wavelength after the frep stabilization (The simulated slope in Fig. 2c is described in detail in Supplementary Note IV). We observe that the offset frequency scales linearly with the pump wavelength at a slope of 4.5 MHz per picometer shift of pump (corresponding to a sensitivity of 3.7 × 10−2). In addition, in Fig. 2d, we introduce an out-of-loop perturbation to pump power after frep stabilization, but observe no change in the breather tone. If the frep lock had not entirely eliminated the introduced power change, the Pint dependence of Δ (and hence ξ) would have caused a change in the breather frequency. The measurements therefore validate the assumption that frep stabilization effectively eliminates the intracavity pump power fluctuation and reduces the dependence of ξ to just a function of pump frequency. Mode hybridization in the current multi-mode Si3N4 microresonator leads to abrupt increase of local GVD and results in the pinning of primary comb lines.55,56 The effect reduces the slope, i.e. sensitivity, of offset frequency in gauging the pump frequency fluctuation (Eq. 4). Nevertheless, the sensitivity is already more than two orders of magnitude larger than the optical frequency division ratio, \(\partial f_{{\mathrm{rep}}}/\partial f_{{\mathrm{opt}}}\sim 10^{ - 4}\), where fopt is the optical frequency of any the generated comb lines. Thus the fluctuations of the Kerr frequency comb lines \(\delta f_{{\mathrm{opt}}} = \frac{1}{{\partial f_{rep}/\partial f_{{\mathrm{opt}}}}}\delta f_{{\mathrm{rep}}} + \frac{1}{{\partial \xi /\partial f_{{\mathrm{opt}}}}}\delta \xi \) (\(\delta \)ξ is under constant frep) are thus bounded by the residual error and the local oscillator of the frep stabilization loop (Supplementary Note III), when both frep and ξ are stabilized. We must note here that although the coefficient of the \(\delta \xi \) term is relatively small, if ξ is not locked at all then the pump is still free to drift (in this situation dξ will be orders of magnitude larger than dfrep) and fopt is no longer stable.
Characterization of the proposed stabilization technique
Figure 3a, b shows the quality of the ξ stabilization (after frep stabilization is engaged). To minimize the crosstalk between the two phase-locked loops, here the proportional-integral corner frequency is set lower than that of the frep stabilization loop. On the other hand, a second integrator at 500 Hz is included to better suppress low-frequency noise. Compared to the unstabilized beat note, the stabilized ξ shows a clear resolution limited coherent spike (Fig. 3a). The noise oscillation at 205 kHz is the remaining crosstalk derived from the corresponding noise peak in the frep stabilization loop (Supplementary Note III). Figure 3b. plots the single-sideband phase noise of the reference oscillator as well as the residual error of our feedback loop from 1 Hz to 1 MHz. While the low-frequency noise is well suppressed to below the reference, excessive phase noise above 2 kHz from carrier is observed. The root mean square phase error integrated from 6 Hz to 600 kHz is 55 mrad. To verify the uniformity of the offset frequencies, ξ are measured at two distinct spectral regions other than 1553.5 nm where the beat note is used for stabilization. The selected spectral segments (marked red in Fig. 3c) are representative as each ξ is generated from the overlap of different groups of secondary comb lines. Counter results and the corresponding histogram analysis are summarized in Fig. 3d, e. The mean values at 1544.72 nm and 1547.86 nm are 523349999.84 Hz and 523349999.92 Hz, respectively, while the beat note at 1553.5 nm is stabilized to 523350000 Hz. Offset frequencies at different spectral regions are identical within a sub-Hz error, confirming the uniformity of ξ across the Kerr frequency comb. Phase locking of frep and ξ to low-noise microwave oscillators is complete and it should guarantee the optical frequency stability of the Kerr frequency comb.
a Electrical spectrum of the stabilized beat note of ξ with a resolution bandwidth (RBW) of 10 Hz. To minimize the crosstalk between the two phase-locked loops, here the proportional-integral corner frequency is set lower than that of the frep loop. Furthermore, a second integrator at 500 Hz and a differentiator at 100 kHz are included to better suppress low-frequency noise and improve the loop stability, respectively. b Single-sideband (SSB) phase noise of the reference 523.35 MHz local oscillator and the residual loop error, showing excess phase noise of the stabilized ξ above 2 kHz from carrier. c To verify the uniformity of the offset frequencies, ξ are measured at two other spectral regions (marked in red; 1544.72 nm and 1547.86 nm) beside the 1553.5 nm region where the beat note is stabilized to 523350000 Hz in the phase-locked loop. The selected spectral segments are representative as each ξ is generated from the overlap of different groups of secondary comb lines. (d) and (e) Counter results and the corresponding histogram analysis (insets). The mean value at 1544.72 nm is 523349999.84 Hz, the standard deviation over 160 measurements is 600 mHz, and the interquartile range is 50 mHz. The mean value at 1547.86 nm is 523349999.92 Hz, the standard deviation over 160 measurements is 390 mHz, and the interquartile range is 40 mHz.
Out-of-loop assessment of the stabilized Kerr frequency comb
We interrogated the locked microcomb by beating with an external stabilized FFC, and counting the beat frequencies with a 10-digit, Λ-type frequency counter. The FFC is independently stabilized with the f–2f interferometer technique (Supplementary Note V). In Fig. 4a an external perturbation is artificially introduced by disconnecting the slow feedback to the laser piezo control and instead using the piezo to induce a periodic 20 MHz frequency fluctuation. The inset shows clear suppression of the external perturbation (>20 dB) when both phase locked loops are engaged. In Fig. 4b we plot the Allan deviations (ADs) of the comb lines under two different locking schemes. When slow feedback is provided to the EDFA and there is no ambient temperature stabilization (yellow path in Fig. 2a), a 5 × 10−11/\(\sqrt \tau \) (at 1 s) frequency instability is observed, close to the 17.9 GHz reference oscillator. No apparent difference is observed between the ADs of the two comb lines 43 nm apart, indicating a good coherence transfer across the Kerr frequency comb. For longer gate times, the ADs show a characteristic linear dependence on the gate time that can be attributed to the uncompensated ambient temperature drift. For instance, considering the current chip holder has a long-term temperature stability of less than 10 mK which is limited by the resolution of the temperature sensor, a pump power proportional change of 1.2 × 10−5 is needed to keep the intracavity temperature and consequently the frep constant. Such pump power variation in turn results in a change of 13 kHz in the pump frequency (\(\Delta f_{\mathrm{p}} = \frac{{\gamma c}}{{\pi n_{\mathrm{g}}}}\Delta P_{{\mathrm{int}}}\) from Eq. (4)). The frequency instability is gauged to be in the range of 7 × 10−11 when compared to optical carrier of ≈188 THz, in agreement with the asymptotic behavior of the measured AD. We can however partially compensate this ambient temperature drift via improved double-walled packaging along with slow feedback to a TEC on the chip holder that directly controls chip temperature (green path in Fig. 2a). After implementing these improvements we achieve an improved Allan deviation of 2 × 10−11 at 20-s gate time, and decreased the slope of AD increase from τ to τ0.23, marked as the blue line in Fig. 4b.
a Optical beat frequency between the pump and the stabilized fiber frequency comb (FFC). With both the frep and ξ phase-locked loops engaged, the artificially introduced pump frequency perturbation (red curve) is suppressed and the optical beat frequency remains constant (black curve). The inset plots the corresponding power spectral densities, showing a more than 20 dB pump frequency noise suppression by the stabilization loops. b Free-running comb Allan Deviation (AD) is plotted with black hexagons. The orange and brown circles plot the AD of the pump and ith comb line, respectively, when stabilized with slow feedback to the preamp (yellow path in Fig. 2a). No apparent difference is observed between the ADs of the two comb lines 43 nm apart, indicating a good coherence transfer across the microcomb. Our measured values are close to the local oscillator AD (gray pentagons) used to stabilize frep. For longer gate times, ADs show a characteristic linear dependence on the gate time, attributed to the uncompensated ambient temperature drift. To mitigate this, improved environmental isolation and partial compensation of ambient temperature drift (via green path in Fig. 2a) are implemented and AD of stabilized pump with is plotted in blue squares. The AD is improved to 2 × 10−11 at 20-s gate time, and slope of AD increase is reduced from τ to τ0.23. The shaded region on the right marks the point where slow thermal drift degrades the lock performance. c The setup schematic to generate low-noise microwaves. The pump laser is directly locked to an optical reference, in this case, a fully stabilized FFC referenced to an ultrastable cavity. Subsequently the offset ξ is also locked via feedback to pump power (through the action of the polarization rotator and PBS). The above-mentioned loops indirectly lock frep due to suppression of both pump frequency noise and power fluctuations. Slow feedback is sent to the temperature of the chip mount via a TEC to partially suppress ambient thermal drift. d frep is plotted in the black bars and ξ is plotted in blue. Both frep and ξ are strongly correlated with pump power, with measured correlation greater than 0.997. The absolute and frequency sensitivity to pump power are, respectively, ≈15 and ≈6,700 times larger for ξ than frep. e Locking of both ξ and pump frequency allows for suppression of frep noise (also see Supplementary Note VII). Here, the phase noise of the locked ξ (at 40 MHz) is plotted in black and the measured frep, after engaging both feedback loops (and carried down to 40 MHz), is plotted in blue. We observe a 62 dB suppression of noise at high offset frequencies matching well with our expectations, in the unshaded region to the right; however, at lightly shaded region in the center uncompensated 1/f2 thermal noise (plotted in the dashed red line) begins to dominate and eventually surpasses the locked signal in the shaded region on the left. We can mitigate the effect of this thermal noise via better environmental isolation or passive cavity temperature feedback.
The unique stabilization technique thus implemented can be used to stabilize the absolute frequency of each comb line in the Kerr frequency comb without the need of an octave-level comb spectrum and any external nonlinear process. We also confirm the universality of this method by finding comb states with unique ξ across multiple rings with widely varying frep and waveguide geometries (detailed in Supplementary Note VI). However, this method does not allow us to determine the precise optical frequency of each line without calibration via an optical reference. Despite this apparent limitation, the method described here can be used to extend the functionality of frequency combs to various applications while preserving a low SWaP as external nonlinear processes are not required for comb stabilization. We briefly describe one such application and lay out a path for its achievement.
Generation of low-noise microwaves
As another application of the correlation between fp, pump power, frep and ξ, we propose the generation of low-noise microwaves by stabilizing the pump frequency and ξ. The following method may also be applied to full-stabilization of combs with frep too large to directly measure. In prior literature low-noise microwave generation via optical frequency division57,58 has been accomplished with broad octave-level combs that allow for internal detection of fceo via f–2f interferometry and atomic transition or external cavity reference that may be used to stabilize a single comb line.59,60,61,62,63 The comb frep instability would then be suppressed by a factor close to the optical frequency division ratio (≈104) when compared to the optical reference instability. We can however remove the requirement for the detection of fceo and hence for the comb spectrum to be across an octave in frequency if we instead use a modified method based on the stabilization of ξ described previously.64
To generate low-noise microwaves, we propose locking the pump to a stable optical reference and then locking the frequency ξ to a microwave LO, it can be shown that doing so stabilizes the frep. This is because ξ depends on both pump frequency and pump power and upon stabilizing the pump frequency to an optical reference, pump power is the sole factor determining the stability of both ξ and frep which are now directly correlated. Figure 4c shows the setup schematic for stabilization. The device is pumped with a high power EDFA and a comb state measured to have a unique offset ξ at 40 MHz frequency with over 50 dB SNR (at an RBW of 100 kHz) is generated. The pump is then locked to a fully-stabilized fiber frequency comb referenced to an ultrastable cavity. The offset ξ is locked via feedback to a polarization rotator. Together with the PBS placed after the EDFA, this can modulate the input power to the device. To adjust the chip mount and resonator temperature, we feedback with slow bandwidth to the TEC. This partially suppresses ambient thermal drift and increases lock dynamic range. We confirm the strong linear correlation between pump power, frep and ξ in Fig. 4d. We observe that for a 3% change in pump power, corresponding to a 200 kHz change in frep, there is a 3 MHz change in ξ. This implies that the frequency sensitivity of ξ to pump power fluctuations ≈15 times higher, and (due to the large difference in the carrier frequencies) the frequency sensitivity of ξ to pump power is ≈6700 times higher than that of frep. Locking ξ may thus suppress phase noise in frep, beyond what would be achieved by directly locking frep to a microwave reference. When frep is divided down (in the limit of no residual noise) to the carrier frequency of ξ, this would correspond to a phase noise suppression of 64.7 dB. frep before and after ξ lock is recorded on the ESA and plotted in Supplementary note VII, confirming that locking ξ suppresses frep noise. In Fig. 4e we plot the phase noise of both the locked ξ and frep (divided down to 40 MHz), we see that at high offset frequencies the noise is suppressed by over 60 dB as per our expectations, however there is still uncompensated f-2 thermal noise due to the coupled ambient temperature fluctuations, that our loops cannot remove. This noise can however be further reduced by suppressing ξ’s phase noise parameters, and increasing the thermal isolation or implementing passive temperature stabilization techniques such as an auxiliary laser34
Conclusion
Utilizing only internally accessible comb-parameters such as frep and offset frequency ξ, we have demonstrated an approach to fully stabilize comb line frequencies of appropriately generated comb states. The existence of microcombs with only one set of primary comb lines, critical for the new stabilization method, is a consistent property of these nonlinear microresonators and have been found in devices across multiple chipsets with very different dispersion, Q and frep. The sensitivity for our device is measured as 3.7 × 10−2, already more than two orders of magnitude larger than the optical frequency division ratio, and it can be improved by novel microresonator designs to suppress the mode hybridization.63 Furthermore, having both frep and ξ phase-locked to low-noise microwave oscillators concurrently enables the frequency microcomb optical stability. Simulation results of the correlation between ξ and pump frequency, needed for a successful lock, are also in good agreement with the experiment. We further show the frequency microcomb has frequency instability of 2 × 10−11 at 20-s gate time, bounded by the external microwave reference. For gate times longer than 20 s, AD increases due to the uncompensated ambient temperature drift. Such long-term drift can be improved by a better thermal shield or a more effective temperature control.65 We have also discussed an avenue in which this method might prove useful, namely in the generation of low-noise microwaves, and we have also demonstrated a proof-of-principle experiment showing this. We believe our method could find use in a range of applications that require stable chip-scale OFCs due to its advantages of low SWaP and potentially reduced need for optical peripherals.
Methods
Si3N4 microresonator fabrication
First a 3 μm thick oxide layer is deposited via plasma-enhanced chemical vapor deposition (PECVD) on p-type 8” silicon wafers to serve as the under-cladding oxide. Then low-pressure chemical vapor deposition (LPCVD) is used to deposit a 725 nm silicon nitride for the spiral resonators, with a gas mixture of SiH2Cl2 and NH3. The resulting silicon nitride layer is patterned by optimized 248 nm deep-ultraviolet lithography and etched down to the buried oxide layer via optimized reactive ion dry etching. The sidewall is observed to have an etch verticality of 85°. Next the silicon nitride spiral resonators are over-cladded with a 3 μm thick oxide layer and annealed at 1200 °C. The refractive index of the silicon nitride film is measured with an ellipsometric spectroscopy from 500 nm to 1700 nm. The fitted Sellmeier equation assuming a single absorption resonance in the ultraviolet, \(n\left( \lambda \right) = \sqrt {1 + \frac{{\left( {2.90665 \pm 0.00192} \right)\lambda ^2}}{{\lambda ^2 - \left( {145.05007 \pm 1.03964} \right)^2}}} \), is imported into the COMSOL Multiphysics for the waveguide dispersion simulation, which includes both the material dispersion and the geometric dispersion.
Stabilization setup and out-of-loop analysis
The PI2D control servos we use for feedback in both frep and ξ phase-locked loops have a full bandwidth of 10 MHz and can be set to have two PI corners, to effectively suppress low-frequency noise, in addition to a PD corner to increase the loop stability. To ensure minimal crosstalk between the loops, the PI corners are set at very different frequencies. For the frep stabilization, the PI corner for the first integrator is set to 200 kHz while the second integrator is switched off. For the ξ stabilization, the PI corners are set to 500 Hz and 50 kHz to achieve higher suppression for low-frequency noise. In addition, the PD corners are set to 200 kHz and 100 kHz, respectively, with a differential gain of 10 dB. The derivative control is important in our system to make the feedback loop more stable and achieve optimal noise suppression. Due to alignment drift in the optics, the mean level of the servo output keeps increasing until the lock is lost in a few minutes. To increase the operation time, we also include in each loop a slow feedback where the feedback error signal is generated by integrating the servo output for 1 s. The control units of the slow feedback loops are the EDFA gain and the piezoelectric transducer (PZT), which have larger dynamic ranges than the EOM and the diode current. For out-of-loop analysis, the beat frequency between the Kerr frequency comb and the fiber laser frequency comb is counted with a 10-digit, Λ-type frequency counter and the Allan deviation is estimated using the equation \(\sigma _{\mathrm{A}}\left( \tau \right) = \sqrt {\frac{1}{N}\mathop {\sum}\nolimits_{i = 1}^{i = N} {\frac{{\left( {\bar y_{{\mathrm{i}} + 1} - \bar y_{\mathrm{i}}} \right)^2}}{2}} } \), where τ, \(\bar y_{\mathrm{i}}\), and \(N = {\mathrm{min}}\left\{ {20,\left[ {\frac{{200}}{\tau }} \right]} \right\}\) are the gate times, the fractional frequencies, and the number of samples, respectively. The grating-based filter critically removes the unwanted reference fiber laser frequency comb teeth such that clean heterodyne beat notes with more than 30 dB signal to noise ratio (measured with a 100 kHz RBW), sufficient for reliable counting measurements, can be routinely obtained.
Data availability
The datasets generated during and/or analyzed during the study are available from the corresponding authors on reasonable request.
Code availability
The code used in the analysis of the datasets is available from the corresponding authors on reasonable request.
References
Udem, T., Holzwarth, R. & Hänsch, T. W. Optical frequency metrology. Nature 416, 233 (2002).
Diddams, S. A., Bergquist, J. C., Jefferts, S. R. & Oates, C. W. Standards of time and frequency at the outset of the 21st century. Science 306, 1318 (2004).
Piglosiewicz, B. et al. Carrier-envelope phase effects on the strong-field photoemission of electrons from metallic nanostructures. Nat. Photon. 8, 37 (2014).
Krausz, F. & Stockman, M. I. Attosecond metrology: from electron capture to future signal processing. Nat. Photon. 8, 205 (2014).
Diddams, S. A. et al. Direct link between microwave and optical frequencies with a 300 THz femtosecond laser comb. Phys. Rev. Lett. 84, 5102 (2000).
Wirth, A. et al. Synthesized light transients. Science 334, 195 (2011).
Del’Haye, P., Arcizet, O., Schliesser, A., Holzwarth, R. & Kippenberg, T. J. Full stabilization of a microresonator-based optical frequency comb. Phys. Rev. Lett. 101, 053903 (2008).
Lim, J. et al. Stabilized chip-scale Kerr frequency comb via a high-Q reference photonic microresonator. Opt. Lett. 41, 3706 (2016).
Jones, D. J. et al. Carrier-envelope phase control of femtosecond mode-locked lasers and direct optical frequency synthesis. Science 288, 635 (2000).
Ye, J. & Cundiff, S. T. Femtosecond Optical Frequency Comb Technology (Springer, 2005).
Del’Haye, P. et al. Optical frequency comb generation from a monolithic microresonator. Nature 450, 1214 (2007).
Yang, J. et al. Coherent satellites in multispectral regenerative frequency microcombs. Nat. Comm. Phys. 3, 27 (2020).
Herr, T. et al. Universal formation dynamics and noise of Kerr-frequency combs in microresonators. Nat. Photon. 6, 480 (2012).
Papp, S. B., Del’Haye, P. & Diddams, S. A. Parametric seeding of a microresonator optical frequency comb. Opt. Express 21, 17615 (2013).
Del’Haye, P., Papp, S. B. & Diddams, S. A. Hybrid electro-optically modulated microcombs. Phys. Rev. Lett. 109, 263901 (2012).
Del’Haye, P., Beha, K., Papp, S. B. & Diddams, S. A. Self-injection locking and phase locked states in microresonator based optical frequency combs. Phys. Rev. Lett. 112, 043905 (2014).
Moss, D. J., Morandotti, R., Gaeta, A. L. & Lipson, M. New CMOS-compatible platforms based on silicon nitride and Hydex for nonlinear optics. Nat. Photon. 7, 597 (2013).
Saha, K. et al. Modelocking and femtosecond pulse generation in chip-based frequency combs. Opt. Express 21, 1335 (2013).
Papp, S. B. et al. Microresonator frequency comb optical clock. Optica 1, 10 (2014).
Herr, T. et al. Temporal solitons in optical microresonators. Nat. Photon. 8, 145 (2014).
Huang, S.-W. et al. Mode-locked ultrashort pulse generation from on-chip normal dispersion microresonators. Phys. Rev. Lett. 114, 053901 (2015).
Huang, S.-W. et al. Quasi-phase-matched multispectral Kerr frequency comb. Opt. Lett. 42, 2110 (2017).
Jang, Y.-S. et al. Nanometric precision distance metrology via hybrid spectrally resolved and homodyne interferometry in a single soliton frequency microcomb. Phys. Rev. Lett. 126, 023903 (2021).
Li, Y. et al. Real-time transition dynamics and stability of chip-scale dispersion-managed frequency microcombs. Light Sci. Appl. 9, 52 (2020).
Xue, X. et al. Mode-locked dark pulse Kerr combs in normal-dispersion microresonators. Nat. Photon. 9, 594 (2015).
Huang, S.-W. et al. A low-phase-noise 18 GHz Kerr frequency microcomb phase-locked over 65 THz. Sci. Rep. 5, 13355 (2015).
Spencer, D. T. et al. An optical-frequency synthesizer using integrated photonics. Nature 557, 81 (2018).
Brasch, V. et al. Photonic chip–based optical frequency comb using soliton Cherenkov radiation. Science 351, 357 (2016).
Huang, S.-W. et al. A broadband chip-scale optical frequency synthesizer at 2.7 × 10−16 relative uncertainty. Sci. Adv. 2, e1501489 (2016).
Brasch, V., Lucas, E., Jost, J. D., Geiselmann, M. & Kippenberg, T. J. Self-referenced photonic chip soliton Kerr frequency comb. Light.: Sci. Appl. 6, 16202 (2017).
Zhang, M. et al. Broadband electro-optic frequency comb generation in a lithium niobate microring resonator. Nature 568, 373 (2019).
Li, Q. et al. Stably accessing octave-spanning microresonator frequency combs in the soliton regime. Optica 4, 193–203 (2017).
Stern, B., Ji, X., Okawachi, Y., Gaeta, A. L. & Lipson, M. Battery-operated integrated frequency comb generator. Nature 562, 401 (2018).
H. Zhou, H. et al. Soliton bursts and deterministic dissipative Kerr soliton generation in auxiliary-assisted microcavities. Light: Sci. Appl. 8, 50 (2019).
Yao, B. C. et al. Gate-tunable frequency combs in graphene-nitride microresonators. Nature 558, 410 (2018).
Bao, C. et al. Nonlinear conversion efficiency in Kerr frequency comb generation. Opt. Lett. 39, 6126 (2014).
Ideguchi, T. et al. Coherent Raman spectro-imaging with laser frequency combs. Nature 502, 355 (2013).
Cundiff, S. T. & Weiner, A. M. Optical arbitrary waveform generation. Nat. Photon. 4, 760 (2010).
Palomo, P. M. et al. Microresonator-based solitons for massively parallel coherent optical communications. Nature 546, 274 (2017).
Geng, Y. et al. Terabit optical OFDM superchannel transmission via coherent carriers of a hybrid chip-scale soliton frequency comb. Opt. Lett. 43, 2406 (2018).
Li, C.-H. et al. A laser frequency comb that enables radial velocity measurements with a precision of 1 cm s−1. Nature 452, 610 (2008).
Obrzud, E. et al. A microphotonic astrocomb. Nat. Photon. 13, 31 (2019).
Suh, M.-G. et al. Searching for exoplanets using a microresonator astrocomb. Nat. Photon. 13, 25 (2019).
Briles, T. C. et al. Interlocking Kerr-microresonator frequency combs for microwave to optical synthesis. Opt. Lett. 43, 2933 (2018).
Kuse, N., Briles, T. C., Papp, S. B. & Fermann, M. E. Control of Kerr-microresonator optical frequency comb by a dual-parallel Mach-Zehnder interferometer. Opt. Express 27, 3873 (2019).
Drake, T. E. et al. Terahertz-rate Kerr-microresonator optical clockwork. Phys. Rev. X 9, 031023 (2019).
Hummon, M. T. et al. Photonic chip for laser stabilization to an atomic vapor with 10−11 instability. Optica 5, 443–449 (2018).
Stern, L. et al. Direct Kerr frequency comb atomic spectroscopy and stabilization. Sci. Adv. 6, 9 (2020).
Coillet, A. et al. On the transition to secondary Kerr combs in whispering-gallery mode resonators. Opt. Lett. 44, 3078 (2019).
Kumar, A. et al. Internally phase stabilized Kerr frequency comb. In Conference on Lasers and Electro-Optics (CLEO), San Jose, CA (IEEE, 2017).
Coen, S. & Haelterman, M. Modulational instability induced by cavity boundary conditions in a normally dispersive optical fiber. Phys. Rev. Lett. 79, 4139 (1997).
Lugiato, L., Prati, F. & Brambilla, M. Nonlinear Optical Systems 342–370 (Cambridge University Press, 2015).
Hansson, T. & Wabnitz, S. Dynamics of microresonator frequency comb generation: models and stability. Nanophotonics 5, 231 (2016).
Stone, J. R. et al. Thermal and nonlinear dissipative-soliton dynamics in Kerr-microresonator frequency combs. Phys. Rev. Lett. 121, 063902 (2018).
Liu, Y. et al. Investigation of mode coupling in normal-dispersion silicon nitride microresonators for Kerr frequency comb generation. Optica 1, 137 (2014).
Huang, S.-W. et al. Smooth and flat phase-locked Kerr frequency comb generation by higher order mode suppression. Sci. Rep. 6, 26255 (2016).
Chembo, Y. K. Kerr optical frequency combs: theory, applications and perspectives. Nanophotonics 5(2), 214 (2016).
Pasquazi, A. et al. Micro-combs: a novel generation of optical sources. Phys. Rep. 729, 1 (2018).
Alnis, J. et al. Thermal-noise-limited crystalline whispering-gallery-mode resonator for laser stabilization. Phys. Rev. A 84, 011804(R) (2011).
Fortier, T. M. et al. Generation of ultrastable microwaves via optical frequency division. Nat. Photon. 5, 425 (2011).
Millo, J. et al. Ultralow noise microwave generation with fiber-based optical frequency comb and application to atomic fountain clock. Appl. Phys. Lett. 94, 141105 (2009).
Bartels, A. et al. Femtosecond laser based synthesis of ultrastable microwave signals from optical frequency references. Opt. Lett. 30, 667 (2005).
McFerran, J. J. et al. Low noise synthesis of microwave signals from an optical source. Electron. Lett. 41, 36 (2005).
Vinod, A. K. et al. Optical clocks via breather stabilization in chip-scale frequency combs. In Conference on Lasers and Electro-Optics (CLEO), San Jose, CA (IEEE, 2019).
Moille, G. et al. Kerr-microresonator soliton frequency combs at cryogenic temperatures. Phys. Rev. Appl. 12, 034057 (2019).
Acknowledgements
The authors acknowledge discussions with Futai Hu, Jinkang Lim, Roberto Diener, Robert Lutwak, Abirami Sivananthan, Wenting Wang and James F. McMillan. We acknowledge funding support from the DARPA (HR0011-15-2-0014), ONR (N00014-16-1-2094), and the AFOSR Young Investigator Award (FA9550-15-1-0081). This manuscript is dedicated to Professor Tatsuo Itoh for his kind guidance and in his memory.
Author information
Authors and Affiliations
Contributions
S.W.H. designed the experiment and A.K. conducted the experiment. S.W.H. and J.Y. designed the microresonator. M.Y. and D.-L.K. performed the device nanofabrication. S.W.H. and A.K. analyzed the data. S.W.H., A.K., and C.W.W. contributed to writing and revision of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vinod, A.K., Huang, SW., Yang, J. et al. Frequency microcomb stabilization via dual-microwave control. Commun Phys 4, 81 (2021). https://doi.org/10.1038/s42005-021-00573-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00573-9
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.