Abstract
Brain temperature is an important yet understudied medical parameter, and increased brain temperature after injury is associated with worse patient outcomes. The scarcity of methods for measuring brain temperature non-invasively motivates the need for computational models enabling predictions when clinical measurements are challenging. Here, we develop a biophysical model based on the first principles of energy and mass conservation that uses data from magnetic resonance imaging of individual brain tissue and vessel structure to facilitate personalized brain temperature predictions. We compare model-predicted 3D thermal distributions with experimental temperature measured using whole brain magnetic resonance-based thermometry. We find brain thermometry maps predicted by the model capture unique spatial variations for each subject, which are in agreement with experimentally-measured temperatures. As medicine becomes more personalized, this foundational study provides a framework to develop an individualized approach for brain temperature predictions.
Similar content being viewed by others
Introduction
Brain temperature is a key parameter for brain health, function, and recovery after injury1,2,3. Homeostasis is maintained by heat generated from the high metabolic demand of the brain, followed by heat dissipation into cooler circulating arterial blood3,4,5,6,7. Disruptions in metabolism or blood flow due to injury or disease can lead to a hemodynamic imbalance which may result in both local and global changes in brain temperature. Numerous reports have demonstrated the importance of brain thermoregulation after head injury, stroke, and cardiac arrest, where increased brain temperatures are associated with worse patient outcomes2,8. For example, increases as small as 1 °C have been observed to correlate positively with tissue damage induced by ischemia and mortality after traumatic brain injury (TBI)1,9,10,11,12. Further support for the crucial role of brain temperature is the observation that systemic cooling, or therapeutic hypothermia, can mitigate brain damage and aid in recovery after stroke, cardiac arrest, and brain injury2,9,13,14,15.
Despite its demonstrated importance in both health and disease, brain temperature is largely uncharacterized due to the absence of non-invasive brain thermometry methods that are routinely implemented in the clinical setting. Body temperature is the most common surrogate for fever management after injury or for monitoring thermal therapies15,16,17. While brain and body temperatures are highly correlated in healthy mammals, implanted temperature probes have confirmed brain temperature is higher than body temperature due to distinct regulatory mechanisms10,18,19,20,21,22. Decoupling of brain and body temperatures has been reported after stroke and injury, and our group previously observed significant brain–body temperature differences after induced ischemic stroke in a non-human primate model that were not observed pre-ischemia23. In neurosurgery patients, dissociation of brain and body temperatures was a strong predictor of poor prognosis and death11. Furthermore, our previous research identified a potential thermal biomarker, the brain thermal response. We observed spatially localized regions of cerebrovascular impairment and thermal response, suggesting that temperature differences across the brain are important6. As brain temperature may be a key biomarker after neuronal or cerebrovascular injury, and body temperature is often an inadequate surrogate, methods for improved brain thermometry are needed.
Multiple experimental approaches to brain thermometry have been developed using temperature-sensitive magnetic resonance (MR) parameters including magnetization transfer24,25, diffusion26, proton density27, T1 and T2 relaxation times25,27,28, and proton resonance frequency (PRF)29,30,31,32. Among these methods, PRF-based MR thermometry has been reported to be a promising non-invasive method for in vivo temperature mapping30,32,33,34. PRF-based measurements can be achieved using either phase-difference mapping or chemical shift thermometry using magnetic resonance spectroscopy (MRS). Although phase-difference mapping has been successfully used in clinical applications to monitor thermal ablation35,36, phase-based methods provide relative estimates of temperature changes rather than absolute temperatures. Chemical shift thermometry facilitates absolute temperature measurements using the chemical shift difference between water (temperature-sensitive PRF) and a temperature-insensitive reference compound such as N-acetylaspartate (NAA). Most studies of chemical shift thermometry rely on single-voxel MRS or multi-voxel chemical shift imaging, but recent advances have demonstrated whole-brain thermometry using echo planar spectroscopic imaging (EPSI)37,38.
While these MR thermometry methods are promising, direct validation in healthy volunteers is not feasible and most methods have not been integrated into clinical practice. To address the clear need for an expanded understanding of brain thermoregulation, particularly after injury, biophysical models have been developed to understand drivers of local variations in brain temperature and close the gap between empirical observations and underlying heat transfer mechanisms. Recent work has made important improvements in achieving higher fidelity thermal modeling for predictions of spatially resolved temperature39,40,41,42. The Pennes’ bioheat equation41 and discrete vasculature model (DiVa)42 both incorporate MR-based measurements of vasculature and non-simplified anatomy in an attempt to capture the directional flow and counter-current effects. Despite significant progress towards realistic models that capture brain anatomy and vasculature39, adherence to first principles of fluid and thermal energy transport that ensure local energy conservation is still lacking in brain temperature predictions. As hemodynamics are at the crux of thermal response, a high-fidelity multiscale model that adheres to basic conservation laws is a requirement for any model to have predictive value. Previous work has proposed bioheat models derived from the first principles43. However, these models are not used in practice due to their high computational load and lack of experimentally supported arguments to justify the use of complex phenomenological closure laws, particularly at the microstructure level which is beyond the resolution of experimental methods. Instead, simpler empirical models (e.g., Pennes’ model) are used to interpret experimental results even though these models lack generality and are deficient in establishing the fundamental understanding of key heat transfer mechanisms responsible for brain temperature. Furthermore, no approaches have been developed that account for individual variations in metabolism, vessel structure, and blood flow, which can vary widely, resulting in brain temperature predictions that are of generic value and are not subject-specific. Given that both MR thermometry and implanted probes suggest temperature may vary within brain regions and across subjects, a biophysical model that can predict this variability would be of immediate utility.
Here, we develop a biophysical model of brain temperature that features a low number of free parameters and generate subject-specific brain temperature predictions using individual MR data as inputs for the model. The model is derived from first principles, i.e., by imposing mass and energy conservation locally and using standard linear constitutive equations. We account for subject-specific variability using MR-derived tissue and vessel structures acquired from each subject to enable personalized brain temperature maps. Our biophysical model is compared to measures obtained with non-invasive whole-brain MR thermometry which show strong agreement with the predicted values. This proof-of-concept study suggests that brain temperature distribution may vary between individuals and motivates future studies to further characterize these differences.
Results
Theoretical approach
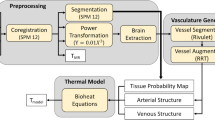
Building upon the framework of the vascular porous (VaPor) model, we report a rigorous biophysical model to predict brain temperature that follows the first principles of mass and energy conservation. To construct the model equations, we define three heat transfer domains including arteries, veins, and tissue, and three modes of energy transfer including conduction, convection, and advection. The transfer of energy between domains is shown in Fig. 1. Our theoretical approach that incorporates individual subject data while still maintaining the first principles of the underlying physics includes the following key steps:
-
i.
Construct individual arterial, venous, and tissue structure maps for each subject from MR angiography (MRA), MR venography (MRV), and structural imaging, respectively.
-
ii.
Augment the MR-derived vasculature, consisting of the major arteries and veins, with additional vessel segments using a rapidly exploring random tree (RRT) algorithm44.
-
iii.
Determine flow rates for each vessel segment using quasi-steady-state mass conservation based on the total blood supplied to the brain.
-
iv.
Determine 3D flow rates through tissue from the hydrodynamic resistance of each porous voxel and inter-domain blood flow rates (arteries to tissues or tissues to veins), imposing local mass conservation.
-
v.
Using probability-weighted imaging to determine gray matter and white matter densities on a voxel-wise basis, calculate local metabolic rates to represent the distributed heat generation sources.
-
vi.
Formulate a set of steady-state governing equations for each simulation domain (arteries, tissues, and veins; “Methods” section, Eqs. 1–3) based on local energy conservation and solve for the 3D temperature distribution in interacting domains. Similar to the DiVa approach42, each domain is coupled via thermal exchange represented by local convective heat transfer coefficients and inter-domain advection terms associated with blood mass exchange between domains.
Metabolically generated thermal energy is transported between the tissues, arteries, and veins by three heat transfer modes: conduction, advection (transport of thermal energy by a moving fluid), and convection (heat transfer from a flowing fluid to a wall resulting from combined effects of local conduction and advection represented by the local heat transfer coefficient). Energy and mass are conserved within each domain locally and globally across the whole brain and described by a system of equations (see “Methods” section). Red arrows represent the direction of blood flow and subsequent advection. Blue arrows represent conductive heat transfer from higher to lower temperature regions. Purple arrows that cross a vessel segment and intersected voxel represent the presence of convective heat transfer. The shaded (or darker) vessel segment or tissue voxel represents a higher temperature than the unshaded (or brighter) vessel segment or tissue voxel.
The mathematical equations that govern the blood flow and brain temperature evolution derived from the conservation of energy, along with the boundary conditions and property inputs, are described in the “Methods” with more detailed derivations, assumptions, and descriptions in the Supplementary Methods.
Subject-specific MR-derived brain structures
Tissue probability maps and segmented vessel structures were derived from MR images acquired from each subject and used as input data into our biophysical model. Representative axial T1-weighted MR images and MR-derived arterial and vessel structures are shown in Fig. 2. As expected, unique gray matter and white matter distributions are observed (yellow dashed ovals) along with distinct arterial and venous architecture (black dashed ovals). Tissue structure was used to determine local metabolic rates. Similarly, geometries of vessels are used to model regional cerebral blood flow (CBF) across the brain. As MRA and MRV are unable to detect smaller vessels such as arterioles and venules, this baseline vessel architecture was then augmented using a stochastic procedure.
a–c Tissue structure for each subject was acquired from T1-weighted magnetic resonance (MR) images. Yellow ovals highlight unique gray and white matter distribution patterns for each subject. d–f Arterial (red) and venous (blue) structures were generated from segmented MR angiography and venography data, respectively. Black ovals highlight the unique arterial and venous morphology in the posterior region of each subject. Scale bar is 50 mm and all images are on the same scale. The arteriovenous structure is on the same scale as the corresponding T1-weighted MR image.
Effect of vessel augmentation on cerebral vasculature
MR-derived arterial and venous vessel structures (Fig. 2) were augmented using the RRT algorithm44. Increasing the number of RRT iterations (incrementally from 5000 to 500,000) resulted in decreased mean length and diameter of terminal vessels as well as mean CBF (Fig. 3 and Supplementary Table 1). As the same number of RRT iterations were applied to generate additional arterial and venous nodes, the mean length and length range of terminal arterial and venous segments were similar (Supplementary Table 1). The maximum length was fixed at 3 mm for newly generated vessel segments, consistent with MR-derived terminal arterial segments (i.e., no augmentation applied) which had a maximum value of ~3 mm. After 500,000 RRT iterations, the median and 95th percentile diameter of terminal arterial segments were 51.2 and 147.8 µm, respectively, indicating that most terminal arterial segments had a diameter <150 µm. Diameters of terminal venous segments were approximately twice the size of terminal arterial segments (Supplementary Table 1). Mean distances between each terminal arterial segment to the nearest terminal venous segment were also calculated as a surrogate measure of blood transport distance through tissue. After 500,000 RRT iterations, the median distance was 667.0 and 1025.6 µm in gray and white matter, respectively (Supplementary Tables 2 and 3). The median blood transport distance throughout the whole brain was 683.9 µm, similar to the distance in gray matter. A shorter blood transport distance in gray matter suggests a higher density of terminal segments, which we observed. Quantitatively, the mean number of terminal arterial and venous segments across all subjects was higher in gray matter (361,654 and 361,195, respectively) compared to white matter (31,551 and 31,557, respectively). This was also consistent with higher mean CBF values in gray matter compared to white matter.
a Increasing the number of RRT iterations resulted in reduced and more realistic CBF values. Maximum CBF after 5000, 20,000, 100,000, and 500,000 RRT iterations (indicated at the top of each column) was 3901.3, 1326.4, 506.9, and 270.4 mL 100 g−1 min−1, respectively. CBF color bar ranges from 0 to 140 mL 100 g−1 min−1. b Changes in CBF distribution due to increased RRT iterations subsequently affects model-predicted brain temperature. More uniform temperatures were observed after more RRT iterations. The temperature color bar ranges from 36.5 to 38.0 °C. The scale bar is 50 mm and all the images are on the same scale.
The effect of varying the number of RRT iterations on brain temperature and CBF is shown in Fig. 3. CBF into a tissue voxel is determined by the terminal arterial segments. For RRT iterations ≤20,000, arterial terminations are sparse and limited to peripheral gray matter regions, resulting in unrealistically high CBF in gray matter (\(\gg\)140 mL 100 g−1 min−1). As the total blood flow rate supplied to the brain over time was constant, calculated as the voxel-wise sum of blood flow rate in each tissue voxel (10.2, 12.2, and 12.1 g s−1 for the three subjects), \(\le\)20,000 iterations resulted in underestimated CBF and overestimated temperatures in white matter regions. Increasing the number of RRT iterations resulted in blood supply from terminal arterial segments to tissue voxels that was distributed more realistically throughout both gray and white matter. Quantitatively, the mean CBF in gray and white matter regions after 500,000 RRT iterations was 83.5 mL 100 g−1 min−1 and 21.3 mL 100 g−1 min−1, respectively (Supplementary Tables 2 and 3). All subsequent analyses used 500,000 RRT iterations to generate vasculature for brain temperature predictions.
Effect of tissue voxel size on brain temperature calculations
To determine the effect of voxel size on brain temperature analysis, three tissue voxel sizes were compared: 1.3 × 1.3 × 1.0 mm3, 2.6 × 2.6 × 2.0 mm3, and 5.2 × 5.2 × 4.0 mm3. While higher resolution tissue voxels could, in theory, improve predictive accuracy, there is a tradeoff between resolution and computational time. The baseline voxel size was set to 2.6 × 2.6 × 2.0 mm3 to match the length scale of the terminal arterial segments derived from MRA. Temperature maps were also generated using a refined voxel size (1.3 × 1.3 × 1.0 mm3), to match the T1-weighted MR image resolution after registration and resampling, and a coarsened voxel size (5.2 × 5.2 × 4.0 mm3) (Supplementary Fig. 1). The coarsened voxel size resulted in a temperature map with a root mean square deviation of 0.07 °C when compared to the temperature map generated using baseline resolution. Upon visual inspection, local temperature differences varied between the temperature maps, indicating that brain temperature predictions are sensitive to tissue voxel size. When comparing the temperature maps generated using the refined voxel size and the baseline voxel size, the root mean square deviation was 0.05 °C. Most of the differences were observed at the boundary between gray matter and fat regions. However, the spatial temperature variations across the brain were substantially similar, suggesting that a voxel size equal to or less than the maximum length scale of the vessel segments (3 mm) may be adequate.
Subject-specific brain temperature predictions
The primary outcome of this study was the generation of subject-specific metabolic heat, CBF, and brain temperature maps for three human subjects (Figs. 4 and 5), predicted with our fully conserved biophysical model using individual inputs of tissue and vessel structure. Distinct spatial patterns and local temperature values were observed for each subject. This was consistent with the expected variation due to unique tissue and vessel structure across individuals (Fig. 2) owing to the individual metabolic heat and CBF maps, respectively. Metabolic heat generation is higher in gray matter than in white matter, represented in our model with different metabolic rates (16,700 and 4,175 W m−3 for gray and white matter, respectively45,46,47) (Fig. 4a). Similarly, cerebral vasculature is highly varied across subjects. Locations of vessel terminations and branch points are key factors in modeling blood flow and subsequent heat dissipation. As shown in Fig. 4b, unique distributions of vessel terminations result in distinct, subject-specific distributions of voxel-wise blood flow in the tissue. Comparison of our subject-specific model prediction with non-subject-specific predictions using generic brain atlases (the current state-of-the-art) are shown in Fig. 5. Qualitatively, local variations in predicted temperature values exist between subjects. Further differences exist when comparing subject-specific temperature maps to the generic non-subject-specific temperature map which is unable to predict localized temperature differences due to individual anatomy.
a Metabolic heat was calculated voxel-wise from the gray and white matter probability of each tissue voxel using rates of 16,700 W m−3 for pure gray matter voxels and 4175 W m−3 for pure white matter voxels. Color bar ranges from 0 to 16,700 W m−3. b CBF maps were computed from magnetic resonance-derived and rapidly exploring random tree-augmented vasculature. Color bar ranges from 0 to 140 mL 100 g−1 min−1. c Model-predicted brain temperature maps for each subject. Unique, subject-specific patterns in metabolic heat, CBF, and brain temperature were observed. Temperature color bar ranges from 36.5 to 38.0 °C. The scale bar is 50 mm and all the images are on the same scale.
The generic model-predicted temperature map used non-subject-specific atlas-based input data. For each subject, model-predicted temperature maps were generated using subject-specific magnetic resonance input data. While all model-predicted maps show higher temperatures in white matter compared to gray matter, temperatures varied spatially between individual subjects. The temperature color bar ranges from 36.5 to 38.0 °C. Scale bars are 50 mm and all the images from subject-specific data are on the same scale.
Comparison of model-predicted and MR-measured brain temperatures
Model-predicted temperatures were compared with measured whole-brain temperatures acquired with MR chemical shift thermometry (Supplementary Table 4 and Fig. 6). Both predicted and MR-measured whole-brain temperatures were higher than axillary body temperatures for all subjects. Mean model-predicted temperatures were \(\le\)0.5 °C higher than the core body temperature for all subjects. Absolute differences within the experimental threshold of |0.8 °C| (see “Methods” section) are shown in Fig. 6. Agreement within this threshold was observed for most voxels, with the exception of frontal lobe regions that are attributed, in part, to a lack of experimental data acquisition in these regions (Supplementary Fig. 2). Voxel-wise temperature distributions of MR-measured and model-predicted data from the three subjects were compared using histograms (Supplementary Fig. 3). Mean values fall within similar temperature ranges for all subjects. Model-predicted temperatures follow a narrower distribution due to the absence of errors associated with measurements, follow the same trend over the entire temperature range, and fall entirely within the range of MR-measured temperature distributions without significant bias. Mean differences between MR-measured brain and core body temperatures were 0.5, 0.1, and 0.1 °C for subjects 1, 2, and 3, respectively (Supplementary Table 4). At the voxel-wise level, differences between MR-measured and model-predicted brain temperatures for the same subjects had 95% confidence intervals of [−0.86 °C, 0.70 °C], [−0.75 °C, 0.71 °C], and [−0.86 °C, 0.58 °C], respectively.
Blue voxels indicate differences between MR-measured and model-predicted brain temperatures within the threshold of |0.8 °C| (see “Methods” section) for the same axial slices shown in Fig. 5. MR thermometry was acquired across most of the brain, with the exception of portions of the frontal lobe. MR acquisition volumes are shown in Supplementary Fig. 2. The scale bar is 50 mm and all the images are on the same scale.
Discussion
Whole-brain temperature maps for individual patients are largely absent in the clinical setting given the lack of both high-fidelity models and robust MR thermometry methods amenable for clinical use. Our initial findings suggest that while mean brain temperatures are similar between individuals, spatial temperature variations exist due to unique tissue structure and vasculature, motivating the development of methods that can both measure and predict spatial variations in brain temperature. Previous studies with implanted probes have demonstrated the deep brain is warmer than the periphery and thermal asymmetries exist in the healthy brain3,18. Neuronal damage in response to temperature changes after the injury is brain region specific1,48, empirically supporting the presence of intracerebral temperature differences. Local variations are even more critical after injury and during thermal therapies where regional changes in perfusion drive stroke risk, tissue damage, and therapeutic response49,50.
Our modeling approach ensures mass and energy conservation and therefore can be expected to reliably yield results that can serve as a proxy for the true temperature when supplied with accurate model inputs. Combined with individual experimental input data including vasculature and gray and white matter distribution from each subject, we demonstrate it is possible to make reasonable predictions of local brain temperature that are consistent with MR-measured values. The governing thermal equations in our model (Eqs. 1–3) build upon the previously reported VaPor model39 but establish a revised formulation in which local energy conservation is satisfied rigorously. In prior work, terms representing advective heat transfer in the energy equations for all three domains were simplified by applying a form of the continuity equation that is incorrect when inter-domain blood flow occurs. Furthermore, inter-domain advection was not coupled with temperature in the domain where blood flow originates, resulting in a violation of energy conservation. By ensuring full mass and energy conservation within and between domains, a locally conservative model for predicting brain temperature was implemented. This was further complemented by individual structural data from each subject to enable localized temperature predictions, as the cerebral temperature is determined by local metabolic heat generation in tissue and heat dissipation through blood circulation. Both factors are determined by individual tissue and vessel structures which, not surprisingly, are unique for each individual. Adherence to mass and energy conservation principles, combined with individual anatomy, are both required to generate realistic and personalized predictions.
A key aspect of model development was to determine the appropriate number of RRT iterations to generate physiologically reasonable vasculature and CBF distribution. To distribute blood flow throughout the whole brain, RRT was conducted to generate fine arterial and venous structures. Increasing the number of RRT iterations produces more vessel branches or segments and, to maintain mass conservation, results in smaller vessel diameters and shorter terminal vessel segments. In determining a reasonable number of RRT iterations, terminal arterial segment diameters, CBF, and mean blood transport distance were used as metrics to ensure appropriate blood flow and subsequent oxygen delivery to the tissue. While distribution of terminal vessel segment lengths was similar, diameters differed between terminal arteries and veins as these are dependent on CBF rates in vessel segments as well as the vessel tree structure (e.g., branch points). After 500,000 RRT iterations, the 95th percentile diameter of terminal arterial and venous segments was <150 and <400 µm, respectively. Lemons et al. reported that arterial segments with a diameter <100 µm and venous segments with a diameter <400 µm are in local thermal equilibrium with their surroundings, supporting the treatment of blood flow through arterioles and venules as flow through porous media with the blood locally at the same temperature as adjacent tissue51. This is consistent with the vascular porous treatment of brain tissue, as the entire length of terminal arteries can supply blood to the surrounding tissue and capillary continuum. Additionally, 500,000 RRT iterations produced CBF rates most similar to previously reported values for gray matter (80 mL 100 g−1 min−1), white matter (20 mL 100 g−1 min−1), and the whole brain (50–65 mL 100 g−1 min−1)47,52, while \(\le\)20,000 iterations resulted in extremely high CBF (\(\gg\)140 mL 100 g−1 min−1) in some voxels. The final parameter used to optimize the number of RRT iterations was the blood transport distance, calculated as the mean distance between terminal arterial segments to the nearest point along a terminal venous segment. The median blood transport distance for all arterioles was <800 µm after 500,000 RRT iterations. Previous work using arteriolar and venular tree structures generated from 3D confocal laser microscopy images of human brain sections reported minimum point-to-point distances between arterioles and venules ranging from ~150 to 800 µm53. While the true capillary distance cannot be calculated from our model as the capillary mesh is incorporated within the tissue as a single domain, the length scale of blood transport is consistent with previous reports.
Comparison of brain temperature maps produced using different tissue voxel sizes revealed that a voxel size smaller or equal to the maximum vessel length produced consistent temperature maps. A larger voxel size resulted in multiple terminal arterial or venous segments in each voxel, leading to an underestimation of the thermal variation due to a more coarse CBF distribution. These results suggest the tissue voxel size in our model is optimally determined by the vascular characteristics, particularly the length of terminal vessel segments. Additionally, as computation time increased non-linearly with the number of both RRT iterations (5000 iterations: ~30 s, 500,000 iterations: >1.5 h) and voxel size (for 5000 RRT iterations, baseline voxel size: ~30 s, refined voxel size: >1 h), optimized simulations must consider both physiological and computational constraints.
While a gold standard for non-invasive absolute thermometry does not exist, chemical shift thermometry has been shown to approximate absolute temperature30,34,37. Here, we observed similar voxel-wise temperature values between model-predicted and MR-measured brain temperatures, suggesting that local temperature differences predicted in the model are consistent with those measured with MR thermometry. Mean MR-measured brain temperatures for each subject varied. Both model-predicted and MR-measured brain temperatures were higher yet similar to core body temperature for all subjects. Mean differences between MR-measured and core body temperatures ranged from 0.1 to 0.5 °C, consistent with prior studies that reported mean MR-measured brain and body temperature differences between 0.1 to 0.8 °C54 as well as numerous reports that brain is higher than body temperature in healthy mammals10,18,19,20,21,22. Future work will determine if similar differences between model-predicted brain and core body temperatures are observed after injury or disease.
While we have demonstrated the ability to implement a fully conserved thermodynamic model using MR-derived tissue and vessel structure, future work aims to incorporate several enhancements. The capillary network was treated as a homogeneously distributed, mesh-like structure that is represented via void space in porous media as previously reported55,56,57. The network is inherently connected between hemispheres, yet most thermal exchange is limited due to the presence of cerebrospinal fluid. While some exchange between hemispheres may be expected, particularly for voxels in the corpus callosum, thalamus, and anterior and posterior commissures, thermal exchange is unlikely along the falx cerebri (dura). In our model, voxels that comprise the dura may have a small degree of heat transfer, and further refinement of heat exchange particularly near the hemispheric boundaries is needed. The current model considers only the steady state and does not capture the dynamics of blood flow or transient changes in metabolic heat generation, for example, in response to injury. Modeling the transient response is an immediate next step. Experimentally, whole-brain thermometry is facilitated by an EPSI sequence that is subject to artifacts, highly sensitive to inhomogeneity of the magnetic field, and often not feasible in patients. Differences in MR-measured and model-predicted temperatures are largely attributed to limitations in experimental thermometry (e.g., magnetic field inhomogeneity near the sinuses). While MR thermometry is inherently limited by spectral resolution and signal-to-noise ratio of the peaks of interest (i.e., water and NAA), further advances in MR hardware, magnetic field shimming, and sequence design will continue to facilitate whole-brain chemical shift thermometry. Improved accuracy and resolution of MR thermometry will enable effective assessment and refinement of the model, including determination of the role of any errors introduced via simplifying assumptions and rigorous characterization of the impact of uncertainty in input parameters. Finally, while these initial studies support the ability of our thermal model to better capture individual temperature differences measured with MR thermometry when compared to a generic, non-subject-specific model of the brain, a larger study with more subjects will facilitate a more comprehensive evaluation.
The important role of temperature after injury to the brain is undisputed, however, the underlying mechanisms that relate higher temperatures to tissue damage are less clear. As patient care becomes more personalized, biophysical models that facilitate individual predictions at the subject level may have broad applications in prognosis, treatment stratification, and patient monitoring. Particularly for thermal therapies implemented after injury or illness that are often not optimized and have variable success rates, a personalized approach to temperature management may facilitate improved outcomes for these emerging interventions. Our first principles biophysical model accounts for heterogeneity between individuals and represents the first step in a personalized approach to brain temperature predictions, motivating further characterization of the thermal response in the healthy and injured brain.
Methods
First principles biophysical model of brain temperature
The biophysical model used to predict brain temperature considers energy transfer in three domains: arteries, tissues, and veins. Tissues and capillaries are assumed to be in thermal equilibrium, so these are treated as a single domain with the same temperature (tissue and blood in tissue). Tissue structure is treated as a porous medium as previously reported, allowing blood to flow across tissue regions, which are discretized into voxels39. Heat is transferred between domains via three modes: conduction, advection, and convection. Equations 1–3 are used to calculate temperatures by imposing energy conservation for each domain, capturing the contribution of each energy transfer mode within arteries, tissue, and veins, respectively. These equations are derived using control volume analysis applied to (1) blood vessels for Eqs. 1 and 3, for which discretization is node-based and control volumes are defined as the nearest half of all segments meeting at the node, and (2) brain voxels for Eq. 2.
The thermal energy equation for the arterial blood vessels is
Here, T is temperature, subscripts 1 and 2 indicate arteries and tissue, respectively, and an overbar indicates an appropriately defined average value. The first summation is over all surfaces of the arterial control volume segment through which blood flows: Ac denotes the cross sectional area, \(K_{\mathrm{b}}\) is the thermal conductivity of blood, \(\rho _{\mathrm{b}}\) is its density, and \(c_{\mathrm{b}}\) is its constant pressure specific heat. The projection of the local blood temperature gradient on the outward unit normal of the local differential area element is \(\partial T_i/\partial n\), and similarly the projection of the local blood velocity on the outward unit normal of the local differential area element is \(U_{1n}\). The terms in this summation capture the net effects of energy transport into and out of the segment by conduction and by advection of energy via flow within the segment. The second summation is over all arterial segments in the control volume, and the integration is over each of their lengths La: \(\dot M_{1 \to 2}^\prime\) is the mass flow rate of blood leaving an arterial blood vessel per unit length, \(h\) is the local heat transfer coefficient, and pa is the local wetted perimeter of the arterial segment a. The terms in the second summation capture the net effects of energy transport into and out of the segments by convection and by advection of energy via flow leaving the arterioles and entering the tissue.
The thermal energy equation for the tissue and blood in tissue is
where subscript 3, for the venous domain, has been introduced. The first integral is over the control volume (voxel) surface where \(K\) is the local thermal conductivity. The terms in this integral capture the effects of conduction and advective flow into and out of the voxel across its boundaries to other voxels. The second integral is over the voxel volume where \(\dot Q_{{\mathrm{met}}}\) is the local volumetric rate of heat generation by metabolism. The summations are over all arterial and venous segments and the prefactors, \(\emptyset _{k,i}\), denote the fraction of the overall length of segment k (where k = a for arterial segments and k = v for venous segments) that is in voxel i, i.e., \(\mathop {\sum}\nolimits_i {\emptyset _{k,i}} = 1\). \(\dot M_{2 \to 3}^\prime\) is the mass flow rate of blood entering a venous blood vessel per unit length, and pv is the wetted perimeter of a venous segment v. These summations mirror those in Eqs. 1 and 3 ensuring energy transport by convection and advection between phases is conserved.
Finally, the thermal energy equation for the venous blood vessels is
The first summation is over all surfaces of the venous control volume segment through which blood flows. The second summation is over all of the venous segments in the control volume and the integration is over each of their lengths, Lv. \(\dot M_{2 \to 3}^\prime\) is the mass flow rate of blood entering a venous blood vessel per unit length.
The brain was modeled in the steady-state and both heat generation by metabolism and flow rates were assumed to be constant over time. The formulation, Eqs. 1–3, requires boundary and inlet conditions. The thermal boundary condition is location dependent and is a Dirichlet condition of applied uniform scalp temperature (33.5 °C) except at the base where a zero heat flux (adiabatic) boundary condition was applied. The inlet blood temperature at the right and left internal carotid arteries and basilar artery was set to 37 °C. Flow in blood vessels and tissue was calculated by adopting the VaPor model approach. Briefly, the overall mass flow rate of blood into and out of the brain is specified and split into 3 inlets (40%/40%/20%) and 2 outlets (50%/50%). Flow within the tissue is treated as flow in a porous medium and velocity boundary conditions of no-penetration (zero normal velocity) and no tangential stress (free slip) are used. Blood flow to and from a tissue occurs uniformly in blood vessel terminating segments according to their relative length and serves as sink and source terms for a discretized porous blood flow model which imposes mass continuity onto the flow of blood in the tissue to obtain a blood flow velocity field. Flow rates in the vessels are based on mass conservation (using the terminal segment flow rates) and are used to estimate vessel diameters39.
Our model relied upon previously reported biophysical formulations. However, two key changes were implemented to ensure an intrinsic adherence to local energy conservation. First, advection in the blood vessel domains is treated conservatively in Eqs. 1 and 3, rather than the previously used simplification in which a discretized form of \({\mathbf{U}}_i \cdot \nabla T_i\) was applied39, introducing errors in terminal segments where there is a transfer of mass from one domain to another. Second, the VaPor model accounted for energy transport via inter-domain advection as affecting only flow-receiving domains (capillaries or veins) and described it as being proportional to the temperature difference between the domains, i.e., \(c_{\mathrm{b}}\dot M_{i \to j}(\bar T_j - \bar T_i)\). In actuality, inter-domain blood flow advects energy to and from all domains with an energy transfer that is proportional to the temperature of the domain (not the temperature difference) in which the blood originates. The description of this energy transfer should be mirrored between domains as it is in Eqs. 1–3 to ensure overall energy conservation.
MR data acquisition
The Emory University Institutional Review Board approved the study and written informed consent was obtained from all subjects prior to the MR scan. Non-contrast MR data were collected from 3 healthy subjects (1 male and 2 females; ages 36, 28, and 26 years old) on a 3T whole-body MR scanner (PrismaFIT, Siemens Healthcare) using a 32-channel phased receive array head coil. To generate tissue probability maps, T1-weighted images were acquired using the magnetization-prepared rapid gradient echo (MPRAGE) sequence (repetition time (TR)/inversion time (TI)/echo time (TE) = 2300/900/3.39 ms, flip angle = 9°, field of view (FOV) = 256 × 256 mm2, matrix size = 192 × 192, 160 slices, slice thickness = 1 mm). To generate arterial structures, MRA was collected using a 3D time-of-flight (TOF) sequence (TR/TE = 22/3.86 ms; flip angle = 15°, FOV = 200 × 200 mm2, matrix size = 256 × 256, slice thickness = 0.62 mm). To generate venous structures, MRV was collected using a 2D TOF sequence (TR/TE = 18/3.79 ms, flip angle = 60°, FOV = 220 × 220 mm2, matrix size = 256 × 256, slice thickness = 3.0 mm). EPSI was acquired for MR chemical shift thermometry (TR1/TR2/TE = 1551/511/17.6 ms, flip angle = 71°, FOV = 280 × 280 mm2, and interpolated resolution = 64 × 64 × 32). Axillary temperature was monitored continuously throughout the MR scan using a fiber optic temperature sensor (OTG-MPK5, Opsens) placed underneath the right arm.
MR inputs and parameters for the model
MR data acquired from each subject were used as inputs into the model to generate subject-specific brain temperature maps. All MR images, including MRA, MRV, and EPSI, were registered to the T1-weighted structural image for each subject and resampled to a final resolution of 1.3 × 1.3 × 1.0 mm3 (T1-weighted image resolution). T1-weighted structural images were segmented into six domains (gray matter, white matter, cerebrospinal fluid, soft tissue, skull, and background) using SPM 12 (www.fil.ion.ucl.ac.uk/spm)58 and MATLAB (R2019b, MathWorks). Subject-specific tissue probability maps were utilized to determine the thermal conductivity \(K\), density \(\rho\), specific heat capacity \(c\), and the average volumetric metabolic heat generation rate \(\dot Q_{{\mathrm{met}}}\) of each tissue voxel using volume-based averaging. A voxel size sensitivity analysis was conducted to determine the effect of varying the voxel resolution on brain temperature. Starting with a baseline voxel size of 2.6 × 2.6 × 2.0 mm3 to match the length scale of the largest terminal vessel segment (prior to augmentation with RRT), a coarsened voxel size of 5.2 × 5.2 × 4.0 mm3 and a refined voxel size of 1.3 × 1.3 × 1.0 mm3 were compared. The resolution of the final temperature maps was matched to the larger of the two voxel sizes for comparison. To facilitate quantitative comparisons, the root mean square deviation between resolution matched temperature maps was calculated voxel-wise.
For arterial and venous segmentation, MRA and MRV images were reconstructed into 3D maximal intensity projection (MIP) images. Based on the 3D MIP images, arteries and veins were segmented using the semi-automatic neuron morphing tool, neuTube 1.059 to quantify vessel diameters, identify locations of nodes (i.e., the terminal point of a vessel segment), and identify the index of the previous node (i.e., starting point of a vessel segment). Due to a limited amount of fine vessel structure that is captured in non-contrast MRA and MRV, individual vessel structures for each subject were augmented using the RRT algorithm44. RRT generates a branch to the nearest point from the previous tree using weights based on the ideal CBF map. The ideal CBF map is defined by a gray/white matter distribution percentage: \({\mathrm{CBF}}\left( v \right) = 80 \ast {\mathrm{Prob}}_{{\mathrm{GM}}}\left( v \right) + 20 \ast {\mathrm{Prob}}_{{\mathrm{WM}}}\left( v \right)\), where \(v\) is the voxel index, \({\mathrm{Prob}}_{{\mathrm{GM}}}\left( v \right) + {\mathrm{Prob}}_{{\mathrm{WM}}}\left( v \right) = 1\), and in units of mL 100 g−1 min−1. The RRT algorithm results in a CBF map that is distributed across the voxels in the tissue domain. After new vessel segments were generated using RRT (5000, 10,000, 20,000, 50,000, 100,000, 200,000, and 500,000 iterations), geometric characteristics including vessel length, vessel diameter, and the mean distance between terminal segments were computed. The length of a segment was calculated as the distance between two nodes, and the diameter as the mean diameter of the two nodes. The maximum vessel length was set to 3 mm and the minimum vessel diameter was set to 10 μm during vessel generation by RRT. The mean distance between the arterial and venous terminal segments, used as a surrogate for blood transport distance via the capillaries, was calculated by averaging the distance between 10 equidistant points on each terminal arterial segment to the closest terminal venous segment. The mean distance along the full length of the terminal arterial segments (rather than the terminal point of the vessel) was used to represent that, in our model, blood is delivered to tissue along the entire segment length.
The MR-derived and RRT-generated vasculature were then used to calculate the inter-domain blood flow (\(\dot M_{1 \to 2},\dot M_{2 \to 3}\)). From the total blood flow rate, \(\dot F_{{\mathrm{tot}}}\) (calculated as the sum of ideal CBF across all tissue voxels), inter-domain blood flow from terminal arterial segments (\(\dot M_{1 \to 2}\)) and into terminal venous segments (\(\dot M_{2 \to 3}\)) is assumed to be proportional to the length of the terminal segments. For example, if the length of terminal arterial segment \(a_i\) is \(L_{a_i}\), blood flow from the arterial segment to a voxel is \(\dot M_{1 \to 2}\left( {a_i} \right) = \dot F_{{\mathrm{tot}}}L_{a_i}/\mathop {\sum }\limits_j L_{a_j}\) where the summation is over all terminal arterial segments. Likewise, if the length of the terminal venous segment \(v_i\) is \(L_{v_i}\), blood flow from the arterial segment to a voxel is \(\dot M_{2 \to 3}\left( {v_i} \right) = \dot F_{{\mathrm{tot}}}L_{v_i}/\mathop {\sum }\limits_j L_{v_j}\). Model-derived CBF was defined as \(\dot M_{1 \to 2}\), which represents the blood supply from arteries to tissue (or the capillary network). If a voxel did not intersect with any terminal arterial segments, the voxel was considered to have zero CBF. Model details and derivation are provided as Supplementary Methods.
A generic (non-subject-specific) model, similar to previous reports39, was generated using the same method as described above except tissue and vessel structures were defined from the following sources: brain tissue structures from the default tissue probability map template (International Consortium for Brain Mapping 152) in SPM 1258, arterial structure from subject BG001 in the BraVa database (http://cng.gmu.edu/brava)60, and venous structure acquired from a single subject as previously reported (https://github.com/sblowers/VaPor/tree/master/Vessels)39. Inlet blood temperature was set to 37 °C.
Proton resonance frequency chemical shift thermometry
Whole-brain temperature maps were generated from EPSI data using the metabolite imaging and data analysis system (MIDAS) software (http://mrir.med.miami.edu:8000/midas/)61. Voxel-wise temperature was calculated using the chemical shift difference between water and NAA (\(\delta _{{\mathrm{water}}} - \delta _{{\mathrm{NAA}}}\)) with Eq. 437,62:
Temperature, \(T\), is calculated in units of °C and chemical shift values for water \(\left( {\delta _{{\mathrm{water}}}} \right)\) and NAA \(\left( {\delta _{{\mathrm{NAA}}}} \right)\) are in parts per million. The temperature equation, as previously described62, was derived from a linear calibration using a temperature-controlled brain phantom and EPSI acquisition for MR thermometry. As gray and white matter have different magnetic susceptibility, a correction was applied based on the gray/white matter fraction as previously reported37. Quality control criteria for spectra included in the final temperature map were metabolite linewidth (<13 Hz), water linewidth (<12 Hz), Cramer–Rao lower bounds of water (<2%), and frequency shift of the metabolites or water peaks (<20 Hz). Whole-brain MR temperature maps were registered to T1-weighted image space as described above to facilitate voxel-wise comparisons between model-predicted and MR-measured brain temperatures. A Gaussian filter (standard deviation σ = 1) was applied to the final MR-measured brain temperature maps for visualization. Core body temperature, used for comparison with brain temperature, was calculated by adding 1.1 °C to the mean axillary temperature measured at three-time points during the EPSI MR thermometry scan, based on previously reported differences between rectal and axillary temperatures in healthy adults63. MR-measured and model-predicted temperatures are reported as the mean ± standard deviation of all voxels. For quantitative validation of model-predicted temperatures, voxel-wise absolute differences between MR-measured and model-predicted temperatures were calculated. A within-threshold map for each subject was generated from the whole-brain absolute difference map for voxels with absolute differences ≤0.8 °C (Fig. 6). The threshold was set to 0.8 °C based on previous phantom studies by our group34.
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
Raw MR data are available from the corresponding author on reasonable request.
Code availability
Computational code may be available upon request, subject to any restrictions due to intellectual property protection.
References
Busto, R. et al. Small differences in intraischemic brain temperature critically determine the extent of ischemic neuronal injury. J. Cereb. Blood Flow. Metab. 7, 729–738 (1987).
Soukup, J. et al. The importance of brain temperature in patients after severe head injury: relationship to intracranial pressure, cerebral perfusion pressure, cerebral blood flow, and outcome. J. Neurotrauma 19, 559–571 (2002).
Wang, H. et al. Brain temperature and its fundamental properties: a review for clinical neuroscientists. Front. Neurosci. 8, 307–313 (2014).
Yablonskii, D. A., Ackerman, J. J. & Raichle, M. E. Coupling between changes in human brain temperature and oxidative metabolism during prolonged visual stimulation. Proc. Natl Acad. Sci. USA 97, 7603–7608 (2000).
Sukstanskii, A. & Yablonskiy, D. An analytical model of temperature regulation in human head. J. Therm. Biol. 29, 583–587 (2004).
Fleischer, C. C. et al. The brain thermal response as a potential neuroimaging biomarker of cerebrovascular impairment. Am. J. Neuroradiol. 38, 2044–2051 (2017).
Hayward, J. & Baker, M. Role of cerebral arterial blood in the regulation of brain temperature in the monkey. Am. J. Physiol. 215, 389–403 (1968).
Mrozek, S., Vardon, F. & Geeraerts, T. Brain temperature: physiology and pathophysiology after brain injury. Anesthesiol. Res. Pract. 2012, 989487 (2012).
Clifton, G. L. et al. Marked protection by moderate hypothermia after experimental traumatic brain injury. J. Cereb. Blood Flow. Metab. 11, 114–121 (1991).
Jiang, J. Y. et al. Relationship between body and brain temperature in traumatically brain-injured rodents. J. Neurosurg. 74, 492–496 (1991).
Fountas, K. et al. Disassociation between intracranial and systemic temperatures as an early sign of brain death. J. Neurosurg. Anesthesiol. 15, 87–89 (2003).
Childs, C. Human brain temperature: regulation, measurement and relationship with cerebral trauma: part 1. Br. J. Neurosurg. 22, 486–496 (2008).
Ginsberg, M., Sternau, L., Globus, M., Dietrich, W. D. & Busto, R. Therapeutic modulation of brain temperature: relevance to ischemic brain injury. Cerebrovasc. Brain Metab. Rev. 4, 189–225 (1992).
Wolff, B., Machill, K., Schumacher, D., Schulzki, I. & Werner, D. Early achievement of mild therapeutic hypothermia and the neurologic outcome after cardiac arrest. Int. J. Cardiol. 133, 223–228 (2009).
Hypothermia after Cardiac Arrest Study Group. Mild therapeutic hypothermia to improve the neurologic outcome after cardiac arrest. N. Engl. J. Med. 346, 549–556 (2002).
Robinson, J. L., Seal, R. F., Spady, D. W. & Joffres, M. R. Comparison of esophageal, rectal, axillary, bladder, tympanic, and pulmonary artery temperatures in children. J. Pediatr. 133, 553–556 (1998).
Lefrant, J.-Y. et al. Temperature measurement in intensive care patients: comparison of urinary bladder, oesophageal, rectal, axillary, and inguinal methods versus pulmonary artery core method. Intensive Care Med. 29, 414–418 (2003).
Mellergård, P. Intracerebral temperature in neurosurgical patients: intracerebral temperature gradients and relationships to consciousness level. Surg. Neurol. 43, 91–95 (1995).
Smith, C. M. et al. Brain-systemic temperature gradient is temperature-dependent in children with severe traumatic brain injury (TBI). Pediatr. Crit. Care Med. 12, 449–454 (2011).
Henker, R. A., Brown, S. D. & Marion, D. W. Comparison of brain temperature with bladder and rectal temperatures in adults with severe head injury. Neurosurgery 42, 1071–1075 (1998).
Karaszewski, B. et al. Relationships between brain and body temperature, clinical and imaging outcomes after ischemic stroke. J. Cereb. Blood Flow. Metab. 33, 1083–1089 (2013).
Mcilvoy, L. Comparison of brain temperature to core temperature: a review of the literature. J. Neurosci. Nurs. 36, 23–31 (2004).
Dehkharghani, S., Fleischer, C. C., Qiu, D., Yepes, M. & Tong, F. Cerebral temperature dysregulation: MR thermographic monitoring in a nonhuman primate study of acute ischemic stroke. Am. J. Neuroradiol. 38, 712–720 (2017).
Graham, S. J., Stanisz, G. J., Kecojevic, A., Bronskill, M. J. & Henkelman, R. M. Analysis of changes in MR properties of tissues after heat treatment. Magn. Reson. Med. 42, 1061–1071 (1999).
Graham, S. J., Bronskill, M. J. & Henkelman, R. M. Time and temperature dependence of MR parameters during thermal coagulation of ex vivo rabbit muscle. Magn. Reson. Med. 39, 198–203 (1998).
Bleier, A. R. et al. Real‐time magnetic resonance imaging of laser heat deposition in tissue. Magn. Reson. Med. 21, 132–137 (1991).
Gultekin, D. H. & Gore, J. C. Temperature dependence of nuclear magnetization and relaxation. J. Magn. Reson. 172, 133–141 (2005).
Parker, D. L. Applications of NMR imaging in hyperthermia: an evaluation of the potential for localized tissue heating and noninvasive temperature monitoring. IEEE Trans. Biomed. Eng. 31, 161–167 (1984).
Poorter, J. D. et al. Noninvasive MRI thermometry with the proton resonance frequency (PRF) method: in vivo results in human muscle. Magn. Reson. Med. 33, 74–81 (1995).
Kuroda, K. & Non-invasive, M. R. thermography using the water proton chemical shift. Int. J. Hyperth. 21, 547–560 (2005).
Rieke, V. & Butts Pauly, K. MR thermometry. J. Magn. Reson. Imaging 27, 376–390 (2008).
Corbett, R., Laptook, A. & Weatherall, P. Noninvasive measurements of human brain temperature using volume-localized proton magnetic resonance spectroscopy. J. Cereb. Blood Flow. Metab. 17, 363–369 (1997).
Cady, E. B., Penrice, J. & Robertson, N. J. Improved reproducibility of MRS regional brain thermometry by ‘amplitude‐weighted combination’. NMR Biomed. 24, 865–872 (2011).
Dehkharghani, S. et al. Proton resonance frequency chemical shift thermometry: experimental design and validation toward high-resolution noninvasive temperature monitoring and in vivo experience in a nonhuman primate model of acute ischemic stroke. Am. J. Neuroradiol. 36, 1128–1135 (2015).
Coakley, F. V. et al. Pelvic applications of MR-guided high intensity focused ultrasound. Abdom. Imaging 38, 1120–1129 (2013).
Schwarzmaier, H. J. et al. MR‐guided laser irradiation of recurrent glioblastomas. J. Magn. Reson. Imaging 22, 799–803 (2005).
Maudsley, A. A., Goryawala, M. Z. & Sheriff, S. Effects of tissue susceptibility on brain temperature mapping. NeuroImage 146, 1093–1101 (2017).
Zhang, Y. et al. Reproducibility of whole-brain temperature mapping and metabolite quantification using proton magnetic resonance spectroscopy. NMR Biomed. 33, e4313 (2020).
Blowers, S. et al. How does blood regulate cerebral temperatures during hypothermia? Sci. Rep. 8, 1–10 (2018).
Bhowmik, A., Singh, R., Repaka, R. & Mishra, S. C. Conventional and newly developed bioheat transport models in vascularized tissues: a review. J. Therm. Biol. 38, 107–125 (2013).
Pennes, H. H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1, 93–122 (1948).
Kotte, A. et al. A description of discrete vessel segments in thermal modelling of tissues. Phys. Med. Biol. 41, 865–884 (1996).
Shrivastava, D. Theory and Applications of Heat Transfer in Humans (2018).
LaValle, S. M. & Kuffner, J. J. Jr, Randomized kinodynamic planning. Int. J. Robot. Res. 20, 378–400 (2001).
Diao, C., Zhu, L. & Wang, H. Cooling and rewarming for brain ischemia or injury: theoretical analysis. Ann. Biomed. Eng. 31, 346–353 (2003).
Werner, J. & Buse, M. Temperature profiles with respect to inhomogeneity and geometry of the human body. J. Appl. Physiol. 65, 1110–1118 (1988).
Hall, J. E. Guyton and Hall Textbook of Medical Physiology 13 edn (2010).
Minamisawa, H., Nordström, C.-H., Smith, M.-L. & Siesjö, B. K. The influence of mild body and brain hypothermia on ischemic brain damage. J. Cereb. Blood Flow. Metab. 10, 365–374 (1990).
Lee, J. et al. MR perfusion lesions after TIA or minor stroke are associated with new infarction at 7 days. Neurology 88, 2254–2259 (2017).
Nam, K.-W. et al. Regional arterial spin labeling perfusion defect is associated with early ischemic recurrence in patients with a transient ischemic attack. Stroke 51, 186–192 (2020).
Lemons, D., Chien, S., Crawshaw, L., Weinbaum, S. & Jiji, L. Significance of vessel size and type in vascular heat transfer. Am. J. Physiol. Regul. Integr. Comp. Physiol. 253, R128–R135 (1987).
Vavilala, M. S., Lee, L. A. & Lam, A. M. Cerebral blood flow and vascular physiology. Anesthesiol. Clin. North Am. 20, 247–264 (2002).
Peyrounette, M., Davit, Y., Quintard, M. & Lorthois, S. Multiscale modelling of blood flow in cerebral microcirculation: Details at capillary scale control accuracy at the level of the cortex. PLoS ONE 13, e0189474 (2018).
Childs, C., Hiltunen, Y., Vidyasagar, R. & Kauppinen, R. A. Determination of regional brain temperature using proton magnetic resonance spectroscopy to assess brain–body temperature differences in healthy human subjects. Magn. Reson. Med. 57, 59–66 (2007).
Nakayama, A. & Kuwahara, F. A general bioheat transfer model based on the theory of porous media. Int. J. Heat. Mass Transf. 51, 3190–3199 (2008).
Khaled, A.-R. & Vafai, K. The role of porous media in modeling flow and heat transfer in biological tissues. Int. J. Heat. Mass Transf. 46, 4989–5003 (2003).
Majchrzak, E. & Turchan, Ł. Numerical analysis of tissue heating using the bioheat transfer porous model. Comp. Assist. Mech. Eng. Sci. 20, 123–131 (2017).
Ashburner, J. & Friston, K. J. Unified segmentation. NeuroImage 26, 839–851 (2005).
Feng, L., Zhao, T. & Kim, J. neuTube 1.0: a new design for efficient neuron reconstruction software based on the SWC format. Eneuro 2, e0049–0014 (2015).
Wright, S. N. et al. Digital reconstruction and morphometric analysis of human brain arterial vasculature from magnetic resonance angiography. NeuroImage 82, 170–181 (2013).
Maudsley, A. A. et al. Comprehensive processing, display and analysis for in vivo MR spectroscopic imaging. NMR Biomed. 19, 492–503 (2006).
Prakash, K. N. et al. Echo planar spectroscopic imaging based temperature calibration at 7T and 3T for whole brain temperature measurement in rodents and humans. Proc. Int. Soc. Magn. Reson. Med 22, 2871 (2014).
Geneva, I. I., Cuzzo, B., Fazili, T. & Javaid, W. Normal body temperature: a systematic review. Open Forum Infect. Dis. 6, ofz032 (2019).
Acknowledgements
MR data acquisition was supported by the Emory University Center for Systems Imaging Core. The Woodruff Professorship and Rae S. & Frank H. Neely Chair funds provided partial salary support for PAK. This research was supported in part by the Emory University Department of Radiology & Imaging Sciences.
Author information
Authors and Affiliations
Contributions
C.C.F., A.G.F., P.A.K., B.B.R., J.W.A., and F.N. designed the research; D.S., P.A.K., A.G.F., and C.C.F. performed the research; D.S. and P.A.K. analyzed the data, and D.S. and C.C.F. wrote the paper. All authors reviewed the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
F.N. serves as an expert witness. The remaining authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sung, D., Kottke, P.A., Risk, B.B. et al. Personalized predictions and non-invasive imaging of human brain temperature. Commun Phys 4, 68 (2021). https://doi.org/10.1038/s42005-021-00571-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00571-x
This article is cited by
-
Lanthanide luminescence nanothermometer with working wavelength beyond 1500 nm for cerebrovascular temperature imaging in vivo
Nature Communications (2024)
-
Comparisons of healthy human brain temperature predicted from biophysical modeling and measured with whole brain MR thermometry
Scientific Reports (2022)
-
An Optoelectronic thermometer based on microscale infrared-to-visible conversion devices
Light: Science & Applications (2022)
-
A Method of Microwave Radiothermometry in Studies of Circadian Rhythms of Brain Temperature
Bulletin of Experimental Biology and Medicine (2022)
-
Demographic reporting across a decade of neuroimaging: a systematic review
Brain Imaging and Behavior (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.