Abstract
Atmospheric gas discharge is very likely to constrict into filaments and diffuse plasma formation is inefficient in most cases. Developing cost-efficient atmospheric diffuse plasma devices represents a significant challenge for high performance in biomedical decontamination and material processing. Here, we propose an alternative roadmap to produce a diffuse argon plasma jet by expanding and quenching the existing filamentary discharge at the initial or middle stage of streamer development. Possible mechanisms are summarized. With the gas flow velocity comparable to the ion drift one, enhancing ambipolar diffusion near the edge of the positive-streamer channel promotes the radial diffusion of newly-produced electrons, realizing the radial expansion of channel. Weakening electric field in front of the streamer head through head expansion and field offset, prevents the further development of streamer, leading to a positive-pseudo-streamer discharge. Reducing electric field in front of the negative-streamer head through ion compensation, impedes the initial growth of streamer, resulting in a negative pulseless glow discharge. The positive-pseudo-streamer and negative pulseless glow discharges function together to form the diffuse plasma jet.
Similar content being viewed by others
Introduction
Recently, nonequilibrium atmospheric-pressure plasmas have received increasing attention due to their various potential applications, such as biomedical decontamination, material processing, thin film deposition, chemical analysis, and nanoscience1,2,3,4,5. Atmospheric-pressure plasma jets (APPJs) are becoming a competitive plasma device, because they deliver abundant active species from the confined space to the open air, which can be used to directly treat objects without the limitation on the shape and size6,7,8,9,10,11. The APPJs are generally produced by dielectric-barrier discharges (DBDs) because of the simple electrode configuration and low power consumption. To avoid damaging samples due to the Joule heat, many research efforts are devoted to achieving a diffuse Townsend or glow-like DBD, rather than a filamentary one. Plasma diffusion and plasma stability are particularly important in generation and application of the APPJs. To meet the requirements, expensive helium is frequently used as feeding gas, where a streamer-like diffuse discharge is guided by a dielectric tube12,13,14,15,16,17. When using available low-cost argon at atmospheric pressure, the discharge channel is very likely to constrict into filament, where this filamentary discharge is dominated by positive and negative streamers18,19,20,21. This harmful factor remains a major obstacle in effectively and efficiently utilizing plasmas. To prevent the discharge constrict, some additives, including hydrogen, acetone, and ammonia, were usually added to the argon flow to form diffuse plasma by slowing down the ionization rate22,23,24,25. Our previous work showed that a diffuse plasma could be transformed from a filamentary discharge by expanding the preexisting filaments10. But the low transformation efficiency largely reduces the plasma chemical activity. In addition, other methods, such as fast rising time of pulse voltage, dielectric-barrier with shallow traps, and preheated feeding gas also make it possible to realize atmospheric diffuse discharge26,27,28,29,30. Almost all the methods mentioned above are based on the well-known streamer coupling model, where multiple streamers develop simultaneously and couple into a large discharge channel under a relatively low electric field25,31. Although this model contributes much to understanding and producing diffuse discharges, the adverse behavior of likely-formed-filament DBDs at atmospheric pressure still largely restrains the popularization and application of plasma devices. Thus, an untraditional roadmap is in urgent need for realizing diffuse DBDs at atmospheric pressure.
In this paper, in contrast to the streamer coupling model, an alternative train of thought is demonstrated to generate a stable and diffuse plasma by expanding and quenching the existing filamentary discharge at the initial or middle stage of the streamer development. Based on this guideline, a promising method is proposed to produce diffuse APPJs by a combination of pseudo-streamer discharge and pulseless glow discharge in the positive and negative alternations of applied voltage, respectively. This combination process is realized by technically controlling the gas flow in a large gap DBD, which is equipped with a thin quartz tube in a linear field. This work provides us another route to understand and explore the diffuse discharge formation.
Results
Electrical and optical emission characteristics
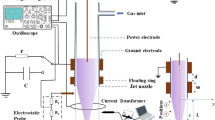
Figure 1a shows the experiment was performed in a cylindrical DBD system. The feeding gas argon (99.999%) flows into a thin quartz tube from the upper inlet (indicating by the blue arrow), ejects out of the tube from the nozzle, and rushes toward the ground electrode (GE). When the applied voltage increases to a certain value, there occurs the gas breakdown between the high-voltage electrode (HVE) and GE. The plasma jet pattern (filament or diffusion) is controlled by adjusting the gas flow. Figure 1b shows the electrostatic field pattern associated with the cylindrical DBD, which was calculated by solving the Laplacian equation in an axisymmetric cylindrical coordinate (r–z). The geometry configuration and material properties in the numerical simulation are the same as those in the experiment. The relative permittivity of quartz tube is set as 3.7. We modeled the field distribution by imposing a potential of 11 kV between the two electrodes without discharge. The potential value approximately equals the amplitude of the sinusoidal alternating high voltage applied in the experiment. It is clearly seen that the electric field between the electrodes is parallel with the tube axis and the discharge occurs in a linear field (rather than a cross-field), in which the charged particles drift along or against the gas flow. The distribution of electric field along the quartz tube axis is shown in Fig. 1c. It is found that the electric field presents a small rise near the HVE and reaches its maximum of 8.8 kV cm−1 at z = −22 mm. After a sharp drop and a slow decrease through the quartz tube, the electric field arrives at the minimum of 1.3 kV cm−1 at the nozzle (z = 0). Following a fluctuation due to the rapid permittivity variation on the nozzle end face, the electric field decreases slowly and reaches its local minimum at z = 4 mm in the open air. Finally, the field increases again and reaches its local maximum of 4.5 kV cm−1 at the GE.
a Schematic diagram of the experimental setup. The gas flow is indicated by the blue arrow. The plasma jet extends along the z-axis. HVE, GE, PMT, and ICCD mean the high-voltage electrode, ground electrode, photomultiplier tube, and intensified charge-coupled device, respectively. b The electrostatic field pattern of the cylindrical dielectric-barrier discharge (DBD), modeled by imposing a potential 11 kV between the electrodes. The relative permittivity of quartz tube is set as 3.7. c The distribution of electric field along the central axis of the quartz tube. The blue circles are the simulation data of electric field. The position of HVE and GE is marked by the red arrow. The shaded region is introduced in order to focus the attention on the area, where a plasma jet could be produced.
Figure 2 shows the typical waveforms of displacement current, discharge current (subtracting the displacement component from the total current), and integrated light emission from the plasma jet, along with the applied voltage (peak voltage 11.6 kV) under different gas flowrates. When the flowrate is set at 0.5 l min−1, it follows from the discharge current waveform in Fig. 2a that several current pulses are irregularly presented in both the positive and negative alternations, with the maximum current peak about 250 mA. An approximately symmetric temporal evolution of discharge current appears in the whole cycle, despite of the asymmetric electrode configuration. Examining the light emission indicates that the plasma jet emits light at each current pulse. As seen from Fig. 2b, with the flowrate increasing to 1.1 l min−1, both the discharge current and light emission exhibit similar temporal evolutions as the case at 0.5 l min−1, except that the maximum current peak increases to about 330 mA. In the two cases, the current pulse width ranges from 150 to 350 ns and the time interval of current pulses remains in the range of 6–12 μs, which is qualified as the typical characteristic of microdischarge consisting of many discharge filaments in the gas gap32. The displacement current is much smaller than the discharge current. For clear observation, the displacement component is enlarged by ten times in Fig. 2a, b. With the applied voltage unvaried, the displacement current has the same temporal evolution at 0.5 l min−1 and 1.1 l min−1.
a Typical waveforms of applied voltage (gray solid line), discharge current (dark blue solid line), displacement current (light blue solid line), and integrated light emission (light red solid line) with the gas flowrate fixed at 0.5 l min−1. The displacement component is enlarged by ten times. b Same as a, but with the gas flowrate fixed at 1.1 l min−1. c Typical waveforms of applied voltage (gray solid line), discharge current (dark blue solid line), displacement current (light blue solid line), and integrated light emission (red solid line) with the gas flowrate fixed at 2.2 l min−1. d Same as c, but with the gas flowrate fixed at 7.8 l min−1 and the light emission indicated by the light red solid line. e The enlarged view of the applied voltage (gray solid line) and light emission (red solid line) marked in the gray shadow in the positive alternation at 2.2 l min−1 in c. f The enlarged view of the applied voltage (gray solid line) and light emission (red solid line) marked in the orange shadow in the negative alternation at 2.2 l min−1 in c. The shaded regions are introduced in order to focus the attention on the difference of light emission in the negative alternation from that in the positive alternation.
When the flowrate increases to 2.2 l min−1, a great change occurs in the temporal evolution of discharge current, as shown in Fig. 2c. A remarkable feature is that the current pulses only appear in the positive alternation and no pulses are observed in the negative one. The maximum current peak sharply drops to around 30 mA. It is worthy of notice that almost no current components could be distinguished in the negative alternation even though a room was made during the current signal acquisition, which is probably attributed to the detection capacity limitation of the instruments employed in our experiment. But to our surprise, the light emission from the plasma jet could be detected not only in the positive but also in the negative alternation. In the negative alternation, the temporal evolution of light emission follows a ripple-shape, rather than a sharp pulse. To compare the light emissions recorded in the positive and negative alternations clearly, their temporal evolutions marked in the gray and orange shadows are enlarged and shown in Fig. 2e, f, respectively. Although the emission intensity in the negative alternation is much smaller than that in the positive one, its duration occupies a quarter of the cycle (~30 μs) and far exceeds the typical width of light emission pulse (~230 ns). The discharge current changes greatly in comparison with the cases at 0.5 l min−1 and 1.1 l min−1, but the displacement current does not change at all and exhibits the same waveform as shown in Fig. 2a, b.
The waveforms of discharge current and light emission for the discharge at 7.8 l min−1 were shown in Fig. 2d. It is found that in comparison with the case at 2.2 l min−1, the peak current in the positive alternation rises to some extent and its maximum nearly increases to 50 mA. Contrastingly, the current pulse is clearly observed once again in the negative alternation and its peak current is comparable to most of the counterparts in the positive alternation. The discharge current waveform indicates that the discharge assumes a typical characteristic of microdischarge. This characteristic is also verified by the light emission examination, where the light emission is observed at each current pulse in the positive and negative alternations, with its pulse width <350 ns. With increasing the gas flowrate, a great change is observed in the discharge current and light emission, but the displacement current remains unvaried all throughout.
The morphology of plasma jet were examined under three different gas flowrates, with the results shown in Fig. 3. Figure 3a shows several typical physical appearances of the plasma jet produced at 0.5 l min−1. The images were captured by a digital camera with the exposure time of 10 ms. It is found that the 41 mm long gas gap is occupied by many discharge filaments. To go further into the filaments, a fast intensified charge-coupled device (ICCD) camera was employed to clarify the discharge details. The gate width was 4 μs and the detailed capture strategy can be found in the “Methods” section. For observing the plasma patterns more clearly, the tube profile without discharge is exhibited in Fig. 3d. Figure 3d also shows the images of filaments generated in four random current pulses for both the positive and negative alternations. Significantly, for each current pulse, only one filament is produced in the thin quartz tube.
a Typical images of the plasma jet acquired by a digital camera with the gas flowrate fixed at 0.5 l min−1 at four different moments. The plasma jet extends along the z-axis, with its length of 18 mm. The exposure time is 10 ms. b Same as a, but with the gas flowrate fixed at 2.2 l min−1 at four different moments. c Same as a, but with the gas flowrate fixed at 7.8 l min−1 at four different moments. d Typical images of the plasma jet captured by a fast intensified charge-coupled device (ICCD) camera with the gas flowrate fixed at 0.5 l min−1 at four random current pulses for both the positive alternation (PA) and negative alternation (NA), as well as the tube profile without discharge. Images in PA and NA are separated by the red dashed line. The gate width is 4 μs. e Same as d, but with the gas flowrate fixed at 2.2 l min−1 at six random current pulses for both PA and NA. f Same as d, but with the gas flowrate fixed at 7.8 l min−1 at four random current pulses for both PA and NA. g Plots (purple solid circle) of the plasma jet length as a function of the gas flowrate. Within the flowrate range from 2.2 to 7.8 l min−1, the plots show an average of five experimental measurements, and the measurement uncertainty (one standard deviation) is indicated by the error bars and is estimated to be 5–7%. The shaded regions are introduced in order to focus the attention on the variation of discharge mode with the gas flowrate, i.e., gray shadow for the filamentary discharge, green shadow for the diffuse discharge, orange shadow for the mixing mode of filamentary and diffuse discharge, and red shadow for the discharge interruption. h Spatial distributions of light intensity of discharge along the transverse direction at the distance of 1 mm away from the nozzle for the gas flowrates of 0.5 l min−1 (black dotted line), 2.2 l min−1 (red solid line), and 7.8 l min−1 (blue dashed line). The origin is set at the center of the quartz tube.
Figure 3b shows the plasma jet generated at the gas flowrate of 2.2 l min−1. It is obviously observed that the discharge transforms from the filamentary regime into the diffuse mode and the visible region of the plasma jet extends downstream only about 8 mm away from the nozzle. The stability of the diffuse plasma was verified by monitoring of the plasma jet continuously working for several hours without mode transition. To further identify the diffuse feature of the plasma jet, ICCD images were taken with the gate width of 4 μs (much less than the duration of light emission in the negative alternation), with the results shown in Fig. 3e. It is seen that even for the random narrow current pulses in the positive alternation, the quartz tube is filled with diffuse plasma, rather than the filament. This feature is quite different from the traditional filamentary DBDs, where the random narrow current pulse is always accompanied by the luminous filaments32.
With the gas flowrate further increasing, the length of the diffuse plasma jet grows, as shown in Fig. 3g. When approaching 5.1 l min−1, the length increases to around 9.5 mm and the diffuse plasma jet starts to become unstable, where the diffuse plasma is mixed with sparse filaments and these filaments extend toward the GE. The number of filaments grows with increasing the flowrate. Meanwhile, the diffuse plasma gives place to the filaments and gradually fades away. The length of the diffuse plasma jet reaches its maximum of 12 mm at 6.8 l min−1. When the flowrate reaches up to 7.8 l min−1, a great number of filaments bridge the gas gap, and the discharge thoroughly turns back to a filamentary one. The filamentary discharge cannot be sustained with the gas flowrate increasing beyond 12.3 l min−1. Figure 3c exhibits the filamentary discharge with the flowrate of 7.8 l min−1 at four different moments. The ICCD images in Fig. 3f further indicate that this filament can be observed in both the positive and negative alternations of applied voltage.
To clarify the difference of the discharge profiles at the three gas flowrates, the spatial distributions of light intensity of these discharges in the transverse direction at the distance of 1 mm away from the nozzle are comparatively shown in Fig. 3h. Here, the intensity curves (normalized to their respective maximum) were calculated from one of the plasma jet digital photographs shown in Fig. 3a–c, respectively. It follows that a similar spatial distribution of light intensity exists in the filamentary discharges at 0.5 and 7.8 l min−1, where three intensity peaks are observed obviously. But for the diffuse discharge at 2.2 l min−1, the light intensity approximately presents a ladder-shaped profile along the transverse direction.
Proposing mechanisms of the diffuse plasma formation
The waveform of discharge current in the positive alternation suggests that the discharge is operated in the positive-streamer regime33. Recent simulations showed that the electric field at the streamer head is much higher than that in the streamer channel and the average field across the whole streamer channel is nearly equal to the external electric field34,35. For simplicity of calculation, the average field \(\overline E \) approximately takes the value of 2.7 kV cm−1, i.e., the field breakdown threshold in atmospheric pure argon36. Assuming the electron mobility μe = 3.9 × 102 cm2 v−1 s−1 and the ion mobility μI = 1.9 cm2 v−1 s−1 37, the electron drift velocity \(v_{\mathrm{e}}\) and the ion drift velocity \(v_{\mathrm{i}}\) in the streamer channel are estimated to be 1.1 × 106 cm s−1 and 5.1 × 103 cm s−1, respectively. Our previous work indicated that the gas temperature in the streamer channel was as high as 780 K and much higher than the room temperature21. Several collisions of particles in discharge, largely depending on the gas temperature and electron energy, eliminate the initial oriented velocity of charged particles36. Thus, the influence of gas flow on the electron and ion drift velocity in the streamer channel is negligible. In our case, the filaments are confined in the thin quartz tube, which prevents the filaments from being distorted largely and makes the electrons and ions drift along the quartz tube axis as far as possible.
It is generally accepted that the formation and evolution of filaments in DBDs could be influenced by the residual charged particles coming from the last discharge32. According to the relationship between the current I and electron density, the peak electron density is expressed as \(n_{{\mathrm{ep}}} = I/{\uppi}r^2ev_{\mathrm{e}}\), where e is the unit charge and r is the filament radius. With the peak current about 300 mA and the diameter of filaments around 0.02 cm (determined by comparing the filament images with the tube profile in Fig. 3d), the peak electron density in the streamer channel is estimated to be 5.43 × 1015 cm−3. For argon discharge, the recombination coefficient β is about 1 × 10−7 cm3 s−1 36. The electron density ne(t) after the discharge termination can be derived from the differential equation \(\partial n_{\mathrm{e}}(t)/\partial t = - \beta n_{\mathrm{e}}(t)^2\), and we obtain
With the driving frequency of 8.9 kHz, the residual electron density just before the next half-cycle discharge is determined to be 1.78 × 1011 cm−3. These residual charged particles, especially the positive ions, do not stay still, but drift along with the gas flow, leading to the destroy of memory effect38. This is the main reason for the formation of irregular filaments at 0.5 and 1.1 l min−1. The happening of filamentary discharge suggests that the residual charged particles, acting as seeding electrons, do not reach the minimum pre-ionization level required for the streamer coupling to form a diffuse plasma.
It is likely that more feeding gas could be ionized with increasing the gas flow, where more seeding electrons are provided for the formation of diffuse plasma through the streamer coupling in the next half-cycle discharge. For easier comparison, we assume that the discharge occurs uniformly along the cross-section of the tube for both the filamentary and diffuse modes. With the peak current of 300 mA in the filamentary discharge and 30 mA in the diffuse discharge, the peak electron density during the discharge is, respectively, estimated to be 2.17 × 1014 and 2.17 × 1013 cm−3 for the two cases. Based on Eq. (1), the residual electron density just before the next half-cycle discharge is calculated as 1.78 × 1011 cm−3 for the filamentary mode and 1.77 × 1011 cm−3 for the diffuse mode. It is found that the increase of gas flow does not enhance the seeding electron density but reduces it a little in our case. This means that the formation of diffuse plasma jet at the higher gas flowrate of 2.2 l min−1 does not result from the improvement of pre-ionization level.
Here, maintaining gas flow in a limited flowrate range from 2.2 to 5.1 l min−1 allows for the discharge transition from filamentary to diffuse mode, which suggests that the root cause of the diffuse discharge formation should be sought from the gas flow itself. At the small gas flowrates of 0.5 and 1.1 l min−1, the velocities of the residual charged particles due to the gas flow velocity \(v_{\mathrm{g}}\) are, respectively, estimated to be 1.1 × 103 and 2.3 × 103 cm s−1, which are much less than the drift velocities of electrons and ions newly produced in the streamer channel. Since the drag force due to the gas flow is only valid for macroscopic objects39, the effect of gas flow on the residual electrons is not considered. These remnants have almost no effect on the filament evolvement. But as the gas flowrate increases to the range of 2.2 to 5.1 l min−1, the corresponding velocity of residual charged particles varies from 4.4 × 103 to 1.1 × 104 cm s−1. This value is much smaller than the electron drift velocity, but comparable to the ion drift one, i.e., about 0.9–2.1 times of the ion drift velocity (5.1 × 103 cm s−1). When these residual ions move with the comparable velocity in the same direction as the ions newly produced in the streamer channel, the residual and newly produced ions almost could not be distinguished from each other. Then, the residual ions, the newly produced ions, and the newly produced electrons in the streamer channel compose a subsystem, in which the residual and newly produced ions could form a unified whole and influence the motion of newly produced electrons in the same manner40. The number density of ions substantially increases near the edge of the streamer channel in the subsystem, due to the assistance of the residual ions. Based on the diffusion-recombination theory41,42, the ambipolar diffusion is considered as the major factor that withstands the filament formation. The ambipolar diffusion coefficient can be derived as42:
Here, De is the free diffusion coefficient of electrons, ne is the number density of electrons newly produced in the streamer channel, and \(\mu _{{\mathrm{i1}}}\) and \(\mu _{{\mathrm{i2}}}\) are mobilities of atomic and molecular argon ions, respectively. Recent simulations also showed that the number density of molecular argon ions \([{\mathrm{Ar}}_2^ + ]\) is much more than that of the atomic argon ions \([{\mathrm{Ar}}^ + ]\) in atmospheric argon discharges43,44,45. Thus, Eq. (2) is modified as:
where \(\left[ {{\mathrm{Ar}}_2^ + } \right]_{{\mathrm{ch}}}\) represents the number density of molecular argon ions newly produced in the streamer channel and \(\left[ {{\mathrm{Ar}}_2^ + } \right]_{{\mathrm{res}}}\) means the number density of residual ions in the gas gap. Since the movement of residual electrons is quite different from the newly produced electrons in the streamer channel, the residual electrons are not taken into account in this subsystem. In the channel, the discharge is electrically neutral and \(\left[ {{\mathrm{Ar}}_2^ + } \right]_{{\mathrm{ch}}}\) approximately equals \(n_{\mathrm{e}}\). Thus, Eq. (3) is simplified as:
Figure 4a shows the temporal evolutions of residual electron density under the conditions of three different initial peak electron densities, i.e., 1.0 × 1013, 1.0 × 1014, and 1.0 × 1015 cm−3. The residual electron densities decrease rapidly with the time, and they nearly tend to be the same value of 1.8 × 1011 cm−3 before the next half-cycle discharge (labeled with a white star), although the initial peak electron densities vary over two orders of magnitude. No significant influence of the initial peak electron density on the residual one is observed in the discharge. Considering the electric neutrality of plasma, the number density of residual ions \(\left[ {{\mathrm{Ar}}_2^ + } \right]_{{\mathrm{res}}}\) safely takes the value of 1.8 × 1011 cm−3. It follows from Eq. (4) that the ambipolar diffusion coefficient increases with decreasing the number density of newly produced electrons. This variation trend is clearly illustrated in Fig. 4b. It was reported that for the microdischarge, most of the charged particles are concentrated in the radial center of the channel and the charge density rapidly drops along the radial direction46,47. The number density of newly produced electrons will decline to the level of the residual ions density (\(\sim 10^{11}{\mathrm{ cm}}^{ - 3}\)) or less near the edge of the channel, where the ambipolar diffuse coefficient is increased by several or even a dozen times, as highlighted in the yellow rectangle region. The enhancement of ambipolar diffusion allows more newly produced electrons to diffuse along the radial direction by the electrostatic force, leading to the expansion of the streamer channel. As a conclusion, it is very likely that when the velocity of residual ions is comparable to that of newly produced ions in the streamer channel, the residual and newly produced ions could form a unified whole and together influence the motion of newly produced electrons through ambipolar diffusion, guiding these electrons to run out of the streamer channel by electrostatic force and finally resulting in the channel expansion.
a Plots of the residual electron density as a function of the time under three different initial peak electron densities, i.e., 1.0 × 1013 cm−3 (blue solid triangle), 1.0 × 1014 cm−3 (red solid circle), and 1.0 × 10 cm−3 (black solid square). \(n_{{\mathrm{ep}}}\) represents the initial peak electron density. The label (white star) shows a typical point, where the residual electron density approximately decays to be the same value 1.8 × 1011 cm−3 within a short period of time (54.5 μs, indicated by the magenta vertical line segment) under the three different initial peak electron densities. b Variation of the ambipolar diffusion coefficient (purple solid diamond) with the number density of newly produced electrons in the streamer channel. μe, μi, De, and Da are the electron mobility, ion mobility, free diffusion coefficient of electrons, and ambipolar diffusion coefficient, respectively. The label (white star) denotes a typical point, where the growth multiple of ambipolar diffusion coefficient increases to 15 with the electron density on the level of 1010 cm−3 near the edge of the streamer channel. The shaded region is introduced in order to focus the attention on the considerable growth of the ambipolar diffuse coefficient near the edge of the streamer channel.
As we know, for the nonequilibrium plasma, the ambipolar diffusion coefficient is generally expressed as36:
Comparing Eqs. (4) and (5) indicates that the equivalent electron diffusion coefficient in our case can be given below:
At a distance \(x = v_{\mathrm{e}}t\) from the point where electrons start, the electron group has spread in the transverse direction to a radius36:
Substituting Eq. (6) into Eq. (7), we obtain:
Here, t takes the value of 230 ns. At room temperature, De equals \(6.3 \times 10^5/p[{\mathrm{torr}}]\,{\mathrm{cm}}^{\mathrm{2}}\,{\mathrm{s}}^{ - 1}\)36. When the growth multiple of the ambipolar diffusion coefficient \(\eta = 1 + \left[ {{\mathrm{Ar}}_2^ + } \right]_{{\mathrm{res}}}/n_{\mathrm{e}} \approx 15\) (labeled with a white star in Fig. 4b), the radius \(r{\prime}\sim {\mathrm{0}}{\mathrm{.5}}\,{\mathrm{mm}}\). This approximate calculation suggests that the streamer channel could be effectively expanded under the impact of the ambipolar diffusion, finally leading to the formation of diffuse plasma observed in the positive alternation.
As is known to us, a streamer is born from an avalanche when the electric field Estr induced from the space charge in the streamer head reaches a value on the order of the external electric field E0. The corresponding approximate equality is expressed as36:
where \(\varepsilon _0\) is the permittivity of vacuum, α is the first Townsend ionization rate, and \(R_0\) is the characteristic radius of space charge in the streamer head. Due to the electrostatic force between electrons and ions in the ambipolar diffuse, the radial diffusion of newly produced electrons inevitably enlarges the transverse size of the streamer head, which increases the characteristic radius of space charge and reduces the number density of space charge (newly produced ions) in the streamer head. The induced electric field is modified as:
where \(R_0^\prime \) is the effective characteristic radius of space charge in the streamer head after the streamer channel expansion. Equation (10) suggests that the ambipolar diffusion decreases the induced electric field in front of the positive-streamer head. Additionally, in this subsystem, the residual ions located in front of the positive-streamer head produce an electric field Eres:
where \(Q_ + \) is the equivalent charge of the residual ions and \(R_1\) is the characteristic radius of residual ions in front of the streamer head. Since the number density of residual ions is much less than that of newly produced ions in the streamer channel or head, the field Eres of the residual ions is smaller than the field induced by the streamer head. In the region very close to the streamer head, Eres is opposite to the direction of Estr. Thus, the resulting electric field (not including the external field) there is given below:
It follows from Eq. (12) that the electric field induced by the streamer head is partly offset by that of the residual ions. Under the combined effects of the expansion of the streamer head transverse radius due to the ambipolar diffusion and the offset of the electric field by residual ions, the induced electric field in front of the streamer head is reduced below the level of the external field. These possible behaviors restrain the initiation of secondary avalanches to some extent and subsequently impede further development of the streamer. As a result, the positive streamer comes to a premature end in its development path and only quite a small charged particles or current flows through the long gas gap, which here is defined as the positive-pseudo-streamer discharge. Figure 5a schematically illustrates the radial expansion process of the streamer channel due to the ambipolar diffusion and the abortion procedure of positive streamer because of the electric field reduction.
a The evolution of the positive streamer in the positive alternation. b The evolution of the negative streamer in the negative alternation. The vector vg means the gas flow velocity, the vector vi denotes the drift velocity of newly produced ions in the streamer channel, the vector E indicates the electric field.
In the negative alternation, the residual ions move with the comparable velocity but opposite to the drift direction of the ions newly produced in the streamer channel, and they could not affect the filaments through ambipolar diffusion. But these residual ions could compensate for the loss of newly produced ones that drift from the negative-streamer head to the streamer channel. This possible behavior prevents the separation of positive and negative charges in the avalanche or streamer head to a certain degree, leading to the reduction of space charge. Thus, the electric field induced from the space charge in the avalanche or streamer head is modified as:
It is found from Eq. (13) that the electric field decreases in front of the avalanche or streamer head. Since no negative streamer is formed and no corresponding current pulses appear, this field fails to reach the level of the external field. The initiation of secondary avalanches is largely prevented in the initial stage of the streamer development. The influence of residual ions on the negative streamer is also schematically depicted in Fig. 5b. Instead, another kind of discharge mode comes into being.
Figure 3e also shows the ICCD images of the discharge occurring in this case. A diffuse plasma can be produced even in the absence of current pulses. It was reported that a negative pulseless glow could exist in the point-to-plane DBD powered by a sinusoidal alternating high voltage33, where this glow followed the Trichel pulse and came before the spark breakdown. The pulseless glow discharge was characterized by a relatively low amplitude of currents (0.1–1 mA) and a fan shaped luminous diffuse region, which lasted several or even tens of microseconds (about a quarter of the cycle). Examination of the discharge current, light emission, and images of the diffuse plasma jet, and comparison with the negative pulseless glow behavior in the point-to-plane DBD, bring a confirmation of the negative pulseless glow existence in the negative alternation in the large gas gap cylindrical DBD.
Analyzing the pulse discharge in the positive alternation and the pulseless discharge in the negative alternation reveals that the diffuse plasma jet could be generated by a combination of the positive-pseudo-streamer discharge and the negative pulseless glow discharge through technical control of the gas flow, without any additive or auxiliary facility.
Nonequilibrium and chemical activity
To verify the nonequilibrium of the diffuse plasma jet generated at 2.2 l min−1, the rotational temperature (Trot) and vibrational temperature (Tvib) were, respectively, examined along the plasma jet by fitting the experimental spectral bands of \({\mathrm{OH}}({\mathrm{A}}{\,}^2{\Sigma}^ + \to {\mathrm{X}}{\,}^2{\Pi},{\Delta}\nu = 0)\) and \({\mathrm{N}}_2({\mathrm{C}}{\,}^3{\Pi}_\mu \to {\mathrm{B}}{\,}^3{\Pi}_{\mathrm{g}},\,{\Delta}\nu = - 2)\). As seen from Fig. 6a, the rotational temperature, approximately considered as the gas temperature, follows the value of 310 K at the nozzle, then slowly increases with increasing the jet length, and finally reaches 340 K at the jet end. This means that the gas temperature is very close to the room temperature and the plasma jet is beneficial to treating samples susceptible to high temperature. In most cases, the rotational temperature decreases along the plasma jet due to the cooling by the ambient air. But in our case, the increasing temperature along the jet is observed, which is mainly ascribed to the enhanced collisions among the particles with the electric field increased in whole from the nozzle to the GE. As for the vibrational temperature, it takes the value of 1980 K at the nozzle, but decreases along the plasma jet, and reaches its minimum 1810 K at the position z = 4 mm. Subsequently, this temperature increases rapidly and reaches its maximum 2900 K at the jet end. The distribution profile of vibrational temperature is very consistent with that of the electrostatic field in the open air, where the field reaches its local minimum at z = 4 mm. The variation of vibrational temperature along the plasma jet results from the change of electron energy that is gained from the electric field from the nozzle to the GE. Comparing the rotational and vibrational temperatures indicates that the plasma jet is in the nonequilibrium condition, which contributes much to the enhancement of plasma chemistry.
a The distributions of the rotational temperature (Trot) and vibrational temperature (\(T_{{\mathrm{vib}}}\)) along the plasma jet (z-axis). The red solid square shows the case of rotational temperature, while the blue solid inverted triangle indicates the case of vibrational temperature. The plots show an average of five experimental measurements, and the measurement uncertainty (one standard deviation) is indicated by the error bars and is estimated to be 5–9% for the rotational temperature and 2–4% for the vibrational temperature. b The distributions of the OES of active species along the plasma jet (or z-axis). The black solid square shows the case of excited hydroxyl radical (OH), the red solid circle indicates the case of excited nitrogen molecule (N2), and the blue solid triangle represents the case of excited argon atom (Ar). The plots show an average of five experimental measurements and the measurement uncertainty (one standard deviation) is estimated to be 7–9%. Since the error bars are too small to be shown distinctly, especially in the range of larger plasma jet length, they are not displayed. The shaded region is introduced in order to focus the attention on the plasma jet area at the gas flowrate of 2.2 l min−1.
To clarify the spatial distributions of active species in the plasma, the optical emission spectra of excited hydroxyl radical (OH, 309.7 nm), excited nitrogen molecule (N2, 337.1 nm), and excited argon atom (Ar, 763.7 nm) were examined along the plasma jet. It follows from Fig. 6b that the emission intensities of both OH and Ar decrease sharply with increasing the jet length, and drop to zero at z = 10 mm. The reduction of Ar emission intensity mostly results from the decrease of Ar concentration along the plasma jet. In contrast to the Ar and OH optical emissions, the N2 emission intensity firstly grows along the plasma jet because of the increasing concentration of N2 along the jet, then reaches its maximum at z = 8 mm, and finally exhibits a slow drop to zero at the GE.
As we know, vapor has a significantly smaller mole fraction than nitrogen in ambient air. But close to the nozzle, the OH optical emission originated from the vapor is much stronger than that of N2, and even overwhelms the Ar optical emission. It is likely that the impurity vapor in the feeding gas argon makes a great contribution to the OH optical emission therein. Since the emission intensity of OH presents a descending tendency along the plasma jet and acts similarly as the feeding gas concentration, the optical emission from the \({\mathrm{OH}}({\mathrm{A}}{\,}^2{\Sigma}^ + \to X{\,}^2{\Pi})\) transition in the plasma jet area is dominated by the vapor in the argon, instead of that in the ambient air. Considering the increase in both the nitrogen concentration and the electric field toward the GE, the reduction of N2 emission intensity in the region z > 8 mm shows that the excited \({\mathrm{N}}_{\mathrm{2}}\,{\mathrm{(C}}\,{\,}^{\mathrm{3}}{\mathrm{{\Pi}}}_{\upmu}{\mathrm{)}}\) molecule is mainly generated from the energy transfer from the excited and metastable argon atoms, instead of the direct impact of electron on the ground state or metastable nitrogen.
Discussion
In this work, we successfully fabricated an atmospheric diffuse argon plasma jet in a large gas gap cylindrical DBD equipped with a thin quartz tube. The formation of diffuse plasma is based on the guideline of expanding and quenching the existing filamentary discharge at the initial or middle stage of the streamer development. We discuss the possible mechanisms of diffuse plasma formation as follows.
The thin quartz tube employed here lets only one filament produced in a current pulse, and makes the electrons and ions drift along or against the gas flow as far as possible. When maintaining the gas flow velocity (or the velocity of residual ions) at the level of drift velocity of ions newly produced in the streamer channel, the residual ions are capable to indirectly influence the movement of newly produced electrons and the development of streamer. As for the positive-pseudo-streamer discharge in the positive alternation, the residual and newly produced ions could form a unified whole and dominate the motion of newly produced electrons through ambipolar diffusion. Substantial enhancement of the ambipolar diffusion near the edge of the streamer channel promotes more newly produced electrons to diffuse along the radial direction, and then realizes the radial expansion of streamer channel. In addition, expanding the streamer head transverse radius through the ambipolar diffusion and offsetting the electric field by the residual ions reduce the induced electric field in front of the streamer head, and then quench the streamer in its development path. Finally, a positive-pseudo-streamer discharge is presented in front of us.
With respect to the negative pulseless glow discharge in the negative alternation, the loss of newly produced ions in the negative-streamer head is compensated with the residual ones, which prevents the separation of positive and negative charges in the avalanche or streamer head and decreases the space charge there. The electric field is reduced in front of the streamer head, and the negative streamer is aborted accordingly. The discharge finally transforms into a negative pulseless glow mode. It is the positive-pseudo-streamer discharge and the negative pulseless glow discharge function together to promote the formation of the diffuse plasma jet, where no any additives or auxiliary facilities are required.
The train of thought proposed to generate diffuse plasma is essentially different from the existing streamer coupling theory. Our work sets about understanding and exploring the diffuse discharge formation from another point of view. The possible mechanisms behind the diffuse plasma formation could be further proved by capturing the time-resolved images of a single current pulse with a streak camera. Additionally, since the evolutions of avalanche and streamer become very complex in flowing gas with residual charged particles, efforts should focus on coupling the preionized stream field and the ambipolar diffusion into the streamer fluid model scientifically. A complete streamer simulation model could help us gain insight into the transition process of discharge from filamentary to diffuse mode. In terms of application, the stable and diffuse feature, low-cost and simply constructed superiority, low-temperature nature, and enhanced plasma chemical activity allow this device to be used as a promising source for biomedical and materials processing.
Methods
Experimental setup
Figure 1a shows the schematic diagram of the experimental setup. A piece of copper foil with the length of 8 mm, serving as the HVE, is closely attached on the outer surface of the thin quartz tube with the inner diameter of 1 mm and the outer diameter of 2.2 mm. The spacing between the HVE and the quartz tube nozzle is 23 mm. A circle aluminum plate with the diameter of 10 mm is used as the GE, which is mounted downstream of the tube and 18 mm away from the tube nozzle. The normal direction of the plate coincides with the axial line of the quartz tube. The DBD is powered by a HV alternating current transformer (Nanjing Suman Electronics CTP-2000K) with the maximum peak voltage of 30 kV and the driving frequency ranging from 5 to 20 kHz. Here, the peak voltage is fixed at 11.6 kV and the driving frequency is set at 8.9 kHz. The feeding gas argon (99.999%) flows into the quartz tube from the upper inlet (indicating by the blue arrow), ejects out of the tube from the nozzle, and rushes toward the GE. With the applied voltage increasing to a certain value, gas breakdown occurs between the HVE and the GE. A plasma jet is produced in the open air and its pattern (filament or diffusion) is controlled by adjusting the gas flow.
Experimental measurement
The applied voltage was measured by a HV probe (Tektronix P6015A) and the discharge current was examined by a current probe (Tektronix TCP312A). It is noted that the displacement current was measured under the condition that no feeding gas argon was provided and no plasma was formed in the gas gap with the external voltage applied48,49. The integrated light emission from the plasma jet was detected by a homemade photomultiplier tube (PMTH-S1-CR131) operated in the wavelength range from 185 to 900 nm. All the three sets of data (voltage, current, and light emission) were simultaneously recorded by using a digital oscilloscope (Tektronix 3054C). The plasma jet images were caught by using either a digital camera (Nikon D5200) or a fast ICCD camera (DH340T-25F-03) as required. When using the ICCD camera, the threshold voltage was set at 0.5 V. The time delay was set at 15 μs for snapping the positive-alternation discharge and 68 μs for catching the negative-alternation discharge. All the images were acquired in a single shot. The light intensity of discharge was calculated from the plasma jet images by using the software ImageJ, rather than Abel inversion, because the plasma jet possesses a profile without rigorously axial symmetry in most cases. Two spectrometers with different resolution were employed to detect the emission spectra from the plasma jet. One spectrometer (AvaSpec-ULS2048-USB2), which has a moderate resolution of 0.6 nm in the wavelength range from 200 to 1000 nm, was employed to identify various active species in the plasma jet. The other spectrometer (AvaSpec-ULS2048-3-USB2), which possesses a high resolution of 0.05 nm in the wavelength range from 200 to 416 nm and 0.3 nm in the wavelength range from 415 to 940 nm, was used to determine the rotational and vibrational temperatures of the plasma jet. The fiber probe was arranged perpendicular to the plasma jet, with a spacing of 1.0 cm.
ICCD image capture strategy
To go further into the discharge process, an ICCD camera was employed to catch the details of discharge occurring in a short period of time. Here, examining the time-resolved images of discharge cannot be implemented because the current pulse appears randomly. However, the pattern of single pulse discharge can be acquired by setting the gate width of the ICCD camera reasonably. From the electric diagnosis of pulse discharge presented in Fig. 2a, b, d, e, it follows that the time interval between two adjacent current pulses is greater than 6 μs. This suggests that the image will not be superimposed by the discharge patterns originated from different current pulses, with the gate width less than 6 μs. As for the pulseless discharge in the negative alternation, the light emission shown in Fig. 2f has a long duration of about 30 μs, which occupies a quarter of the cycle and far exceeds the typical width of light emission pulse (~230 ns) in the positive alternation. To improve the success rate of catching the patterns of plasma jet as far as possible, the gate width of the ICCD camera was set at 4 μs for both the positive-alternation discharge and the negative-alternation discharge.
Data availability
The data that support the finding of this study are available from the corresponding author on reasonable request.
References
Nie, Q. Y., Cao, Z., Ren, C. S., Wang, D. Z. & Kong, M. G. A two-dimensional cold atmospheric plasma jet array for uniform treatment of large-area surfaces for plasma medicine. N. J. Phys. 11, 115015 (2009).
Massines, F., Sarra, B. C., Fanelli, F., Naudé, N. & Gherardi, N. Atmospheric pressure low temperature direct plasma technology: status and challenges for thin film deposition. Plasma Process. Polym. 9, 1041–1073 (2012).
Lu, X. et al. Reactive species in non-equilibrium atmospheric-pressure plasmas: Generation, transport, and biological effects. Phys. Rep. 630, 1–84 (2016).
Zhang, B., Fang, Z., Liu, F., Zhou, R. & Zhou, R. Comparison of characteristics and downstream uniformity of linear-field and cross-field atmospheric pressure plasma jet array in He. Phys. Plasmas 25, 063506 (2018).
Tang, J. et al. A highly efficient magnetically confined ion source for real time on-line monitoring of trace compounds in ambient air. Chem. Commun. 54, 12962–12965 (2018).
Shao, T. et al. Surface modification of polymethyl-methacrylate using atmospheric pressure argon plasma jets to improve surface flashover performance in vacuum. IEEE Trans. Dielectr. Electr. Insul. 22, 1747–1754 (2015).
Li, X. et al. Performance of a large-scale barrier discharge plume improved by an upstream auxiliary barrier discharge. Appl. Phys. Lett. 109, 204102 (2016).
Xia, W. J. et al. The effect of ethanol gas impurity on the discharge mode and discharge products of argon plasma jet at atmospheric pressure. Plasma Sources Sci. Technol. 27, 055001 (2018).
Jiang, W., Tang, J., Wang, Y., Zhao, W. & Duan, Y. A low-power magnetic-field-assisted plasma jet generated by dielectric-barrier discharge enhanced direct-current glow discharge at atmospheric pressure. Appl. Phys. Lett. 104, 013505 (2014).
Li, J. et al. A diffuse plasma jet generated from the preexisting discharge filament at atmospheric pressure. J. Appl. Phys. 122, 013301 (2017).
Li, J. et al. A highly cost-efficient large-scale uniform laminar plasma jet array enhanced by V–I characteristic modulation in a non-self-sustained atmospheric discharge. Adv. Sci. 7, 1902616 (2020).
Walsh, J. L., Shi, J. J. & Kong, M. G. Contrasting characteristics of pulsed and sinusoidal cold atmospheric plasma jets. Appl. Phys. Lett. 88, 171501 (2006).
Laroussi, M. & Akan, T. Arc-free atmospheric pressure cold plasma jets: a review. Plasma Process. Polym. 4, 777–788 (2007).
Winter, J., Brandenburg, R. & Weltmann, K. Atmospheric pressure plasma jets: an overview of devices and new directions. Plasma Sources Sci. Technol. 24, 064001 (2015).
Liu, X. Y., Pei, X. K., Lu, X. P. & Liu, D. W. Numerical and experimental study on a pulsed-dc plasma jet. Plasma Sources Sci. Technol. 23, 035007 (2014).
Hofmans, M. et al. Characterization of a kHz atmospheric pressure plasma jet: comparison of discharge propagation parameters in experiments and simulations without target. Plasma Sources Sci. Technol. 29, 034003 (2020).
Lietz, A. M., Barnat, E. V., Foster, J. E. & Kushner, M. J. Ionization wave propagation in a He plasma jet in a controlled gas environment. J. Appl. Phys. 128, 083301 (2020).
Ebert, U. & Sentman, D. D. Streamers, sprites, leaders, lightning: from micro-to macroscales. J. Phys. D Appl. Phys. 41, 230301 (2008).
Becker, M. M., Hoder, T., Brandenburg, R. & Loffhagen, D. Analysis of microdischarges in asymmetric dielectric barrier discharges in argon. J. Phys. D: Appl. Phys. 46, 355203 (2013).
Shirafuji, T., Kitagawa, T., Wakai, T. & Tachibana, K. Observation of self-organized filaments in a dielectric barrier discharge of Ar gas. Appl. Phys. Lett. 83, 2309–2311 (2003).
Li, J. et al. A filamentary plasma jet generated by argon dielectric-barrier discharge in ambient air. IEEE Trans. Plasma Sci. 47, 3134–3140 (2019).
Kloc, P., Wagner, H. E., Trunec, D., Navratil, Z. & Fedoseev, G. An investigation of dielectric barrier discharge in Ar and Ar/NH3 mixture using cross-correlation spectroscopy. J. Phys. D Appl. Phys. 43, 345205 (2010).
Urabe, K., Yamada, K. & Sakai, O. Discharge-mode transition in jet-type dielectric barrier discharge using argon/acetone gas flow ignited by small helium plasma jet. Jpn. J. Appl. Phys., Part 1 50, 116002 (2011).
Hofmann, S., Sobota, A. & Bruggeman, P. Transitions between and control of guided and branching streamers in dc nanosecond pulsed excited plasma jets. IEEE Trans. Plasma Sci. 40, 2888–2899 (2012).
Wu, S., Lu, X., Zou, D. & Pan, Y. Effects of H2 on Ar plasma jet: from filamentary to diffuse discharge mode. J. Appl. Phys. 114, 043301 (2013).
Starikovskaia, S., Anikin, N., Pancheshnyi, S., Zatsepin, D. & Starikovskii, A. Pulsed breakdown at high overvoltage: development, propagation and energy branching. Plasma Sources Sci. Technol. 10, 344–355 (2001).
Wu, S., Xu, H., Lu, X. & Pan, Y. Effect of pulse rising time of pulse dc voltage on atmospheric pressure non-equilibrium plasma. Plasma Process. Polym. 10, 136–140 (2013).
Liu, Z. et al. A large-area diffuse air discharge plasma excited by nanosecond pulse under a double hexagon needle-array electrode. Spectrochim. Acta Part A Mol. Biomol. Spectr. 121, 698–703 (2014).
Li, M., Li, C., Zhan, H., Xu, J. & Wang, X. Effect of surface charge trapping on dielectric barrier discharge. Appl. Phys. Lett. 92, 031503 (2008).
Qi, F. et al. Uniform atmospheric pressure plasmas in a 7 mm air gap. Appl. Phys. Lett. 115, 194101 (2019).
Palmer, J. A physical model on the initiation of atmospheric-pressure glow discharges. Appl. Phys. Lett. 25, 138–140 (1974).
Fridman, A., Chirokov, A. & Gutsol, A. Non-thermal atmospheric pressure discharges. J. Phys. D Appl. Phys. 38, R1–R24 (2005).
Petit, M., Goldman, A. & Goldman, M. Glow currents in a point-to-plane dielectric barrier discharge in the context of the chemical reactivity control. J. Phys. D Appl. Phys. 35, 2969–2977 (2002).
Babaeva, N. Y. & Naidis, G. V. Two-dimensional modelling of positive streamer dynamics in non-uniform electric fields in air. J. Phys. D Appl. Phys. 29, 2423–2431 (1996).
Naidis, G. V. Simulation of streamers propagating along helium jets in ambient air: Polarity-induced effects. Appl. Phys. Lett. 98, 141501 (2011).
Raizer, Y. P. Gas Discharge Physics 2nd edn (Springer, 1991).
Richards, A. D., Thompson, B. E. & Sawin, H. Continuum modeling of argon radio frequency glow discharges. Appl. Phys. Lett. 50, 492–494 (1987).
Fan, Z., Qi, H., Liu, Y., Yan, H. & Ren, C. Effects of airflow on the distribution of filaments in atmospheric AC dielectric barrier discharge. Phys. Plasmas 23, 123520 (2016).
White, F. M. Fluid Mechanics 4th edn (WCB/McGraw-Hill, 1999).
Mortimer, R. G. Physical Chemistry 3rd edn (Elsevier Academic Press, 2008).
Tang, J. et al. Observation and interpretation of energy efficient, diffuse direct current glow discharge at atmospheric pressure. Appl. Phys. Lett. 107, 083505 (2015).
Dyatko, N. et al. Experimental and theoretical study of the transition between diffuse and contracted forms of the glow discharge in argon. J. Phys. D Appl. Phys. 41, 055204 (2008).
Farouk, T., Farouk, B., Staack, D., Gutsol, A. & Fridman, A. Simulation of dc atmospheric pressure argon micro glow-discharge. Plasma Sources Sci. Technol. 15, 676–688 (2006).
Balcon, N., Hagelaar, G. J. M. & Boeuf, J. P. Numerical model of an argon atmospheric pressure RF discharge. IEEE T. Plasma Sci. 36, 2782–2787 (2008).
Zhu, S. et al. Influence of longitudinal argon flow on DC glow discharge at atmospheric pressure. Jpn. J. Appl. Phys. 55, 056202 (2016).
Babaeva, N. Y. & Naidis, G. V. Dynamics of positive and negative streamers in air in weak uniform electric fields. IEEE T. Plasma Sci. 25, 375–379 (1997).
Yurgelenas, Y. V. & Wagner, H. A computational model of a barrier discharge in air at atmospheric pressure: the role of residual surface charges in microdischarge formation. J. Phys. D Appl. Phys. 39, 4031–4043 (2006).
Lu, X., Jiang, Z., Xiong, Q., Tang, Z. & Pan, Y. A single electrode room-temperature plasma jet device for biomedical applications. Appl. Phys. Lett. 92, 151504 (2008).
Li, X. et al. Morphology transition from diffuse to diffuse-and-filamentary for an argon plume with varying sinusoidal frequency or voltage amplitude. Plasma Sources Sci. Technol. 29, 065015 (2020).
Acknowledgements
The authors acknowledge financial support from the National Natural Science Foundation of China (Grant No. 51877210), the Natural Science Foundation of Shaanxi Province (Grant No. 2020JM-309), the Natural Science Basic Research Program of Shaanxi (Grant No. 2019JCW-03), the Key Deployment Research Program of XIOPM (Grant No. S19-020-III), the Major Science and Technology Infrastructure Pre-research Program of the CAS (Grant No. J20-021-III), the Open Research Fund of Key Laboratory of Spectral Imaging Technology of the CAS (Grant No. LSIT201807G), and the China Scholarship Council (CSC).
Author information
Authors and Affiliations
Contributions
J.T. initiated the idea of the study. J.T. and Y.W. supervised the project. J.L., B.L., and B.X. conducted the measurements and analyzed the data. J.W. and S.R. carried out the numerical simulations. J.T., J.L., and B.L. wrote the manuscript. Y.W., T.Z., W.Z., and Y.D. contributed to result discussion and manuscript revision.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, J., Lei, B., Wang, J. et al. Atmospheric diffuse plasma jet formation from positive-pseudo-streamer and negative pulseless glow discharges. Commun Phys 4, 64 (2021). https://doi.org/10.1038/s42005-021-00566-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00566-8
This article is cited by
-
Holistic analysis of a gliding arc discharge using 3D tomography and single-shot fluorescence lifetime imaging
Communications Engineering (2024)
-
Quantification of surface charging memory effect in ionization wave dynamics
Scientific Reports (2022)
-
Contrasting time-resolved characteristics of laser-induced plasma spatially confined by conical cavities with different bottom diameters
Applied Physics B (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.