Abstract
In non-magnetic materials the combination of inversion symmetry breaking (ISB) and spin-orbit coupling (SOC) determines the spin polarization of the band structure. However, a local spin polarization can also arise in centrosymmetric crystals containing ISB subunits. This is namely the case for the nodal-line semimetal ZrSiTe where, by combining spin- and angle-resolved photoelectron spectroscopy with ab initio band structure calculations, we reveal a complex spin polarization. In the bulk, the valence and conduction bands exhibit opposite spin orientations in two spatially separated two-dimensional ZrTe sectors within the unit cell, yielding no net polarization. We also observe spin-polarized surface states that are well separated in energy and momentum from the bulk bands. A layer-by-layer analysis of the spin polarization allows us to unveil the complex evolution of the signal in the bulk states near the surface, thus bringing the intertwined nature of surface and bulk effects to the fore.
Similar content being viewed by others
Introduction
In the absence of a magnetic field, the spin degeneracy of the band structure is preserved in the bulk of materials that exhibit inversion symmetry. It is therefore generally assumed that a finite spin polarization can only arise in non-centrosymmetric (NC) materials. A typical example is that of III–V semiconductors with the zinc-blend structure, where spin–orbit coupling (SOC) determines the momentum-dependent spin splitting of the light-hole and heavy-hole bands (j = 3/2), the Dresselhaus effect1. If the NC crystal contains polar atomic sites2, the Rashba effect3 adds an additional source of spin–orbit splitting, with a characteristic helical spin texture4. The Rashba term is also responsible for the spin polarization observed at surfaces5,6 and heterostructures7 that exhibit a structural inversion asymmetry (SIA).
While breaking the inversion symmetry is necessary for the appearance of a net polarization, a recent theory8,9 predicted a so far overlooked source of spin polarization in centrosymmetric (CS) materials containing spatially separated structural subunits that break space inversion. In this case a local and momentum-resolved spin polarization develops, even if the material remains globally nonpolarized. The conditions for the emergence of such “hidden” spin polarization are then determined by the local point group at the atomic sites, rather than by the space group of the crystal. One can distinguish two possible situations, illustrated in Fig. 1. If the NC site has no electric dipole moment, as for a tetrahedral site, the system exhibits the Dresselhaus effect and a local spin polarization. If the local dipole moment is nonzero, as for a pyramidal site, the Dresselhaus and the Rashba effects are simultaneously present. They were dubbed, respectively, D-2 and R-2 in refs. 8,9 to distinguish them from the usual—D-1 and R-1—cases of NC crystals. The resulting k-resolved local spin polarization may play a role in the mechanism behind the large nonsaturating magnetoresistance observed in Dirac semimetals10,11,12, as recently proposed for WTe213. Both in R-2 and D-2, however, the contributions from all sites add to zero, which hampers the direct detection of the local polarization by spatially averaging probes. Spin-resolved and angle-resolved photoelectron spectroscopy (spARPES) is a laterally averaging probe, but its signal decays exponentially with the distance of the probed region from the surface, according to the photoelectron mean free path. The very short (λ ~ 5−10 Å) probing depth can then be exploited to gain local sensitivity. In layered materials where a k-resolved local spin polarization appears, this alternates in successive planes parallel to the surface. As a result, the contribution from the two (even- and odd-) families of planes to the spARPES signal can be remarkably different. For a typical interplane distance d = 5 Å and a 10 Å lattice parameter, their ratio is (Iodd/Ieven) ≃ 1.7−2.7 for λ = 5−10 Å. Final state effects and possible interference terms in the photoemission process can modify these values14,15, but a net spin signal is still expected. Indeed, spARPES measurements have revealed spin-polarized bands in WSe216 and in the superconductors Bi221217,18 and LaO0.55F0.45BiS219. Theory and conventional ARPES experiments have reached similar conclusions for BaNiS220 and MoS221. Those results have established the concept of hidden spin polarization in CS materials, but questions about the relative importance of the local site asymmetry vs. the surface SIA in determining the bulk polarization remain open.
a Examples of non-polar (blue) and polar (green) sites with inversion asymmetry. The red arrow indicates a local dipole moment. b Point groups of the site occupied by the blue atom in a. c Resulting type of spin polarization8.
Here we address the spin–orbit splitting of the electronic states and the spin texture in the nodal-line semimetal ZrSiTe22,23. The crystal structure of ZrSiTe is CS, but contains polar sites with a local electric dipole field (Fig. 2). Therefore, one expects the D-2 and R-2 effects to impose a spin polarization on its bands. Our spARPES data and fully relativistic ab initio bulk calculations confirm that the Dirac quasiparticles are spin-polarized. ZrSiTe also exhibits surface states that are well separated in energy and momentum from the bulk bands24, and we find that these surface states are also spin polarized. Slab calculations and a layer-by-layer analysis unveil the complex evolution of the spin signal of the bulk states near the surface. This observation suggests that the interference between wave functions forming the bulk continuum with their reflection from the surface barrier might influence the bulk spin polarization, as previously discussed for the cases of Bi25 and noble metals26,27.
a The unit cell. Green, blue, and bronze balls represent the Zr, Si, and Te atoms, respectively. b Side view of the unit cell, highlighting the ZrTe sectors (I and III) and the Si plane (II). Red triangles picture the orientation of the ZrTe4 square pyramids. c Artist’s view of the valence (VB) and conduction (CB) bands, without spin–orbit coupling (SOC). The crossing constitutes the nodal-line. d SOC opens a gap along the nodal line.
Results
Crystal and electronic structure
ZrSiTe is a layered material. It crystallizes in the tetragonal non-symmorphic space group P4/nmm (no. 129), with lattice parameters a = 3.692 Å and c = 9.499 Å28. The structure is obtained by stacking (Te−Zr−Si−Zr−Te) quintuple layers along the c-axis (Fig. 2a). Each unit cell contains two ZrTe bilayers built from ZrTe4 square pyramids, indicated by I and III in Fig. 2b. Inversion symmetry is broken within the bilayers, and each pyramid carries a local electric dipole perpendicular to the layer. The two ZrTe sectors, ~5 Å apart, are separated by a planar Si square-lattice, which coincides with a glide plane for the structure. Owing to the large c/a ratio—the largest in the ZrSiX series (X = S, Se, Te)—and to the presence of the Si interlayer, the interaction between the ZrTe bilayers is weak. This is a favorable condition for the appearance of a sizeable local polarization, as discussed in ref. 9. Adjacent quintuple layers are weakly coupled through a van der Waals gap, so that the crystals are easily mechanically exfoliated to expose a Te-terminated (001) surface.
Compounds of the ZrSiX family have recently been in the limelight, following suggestions that they would realize the topological nodal-line semimetal phase22,23,24,29,30,31. Figure 2c, d shows a cartoon of the low-energy band structure. In the absence of SOC the linearly dispersing valence band (VB) and conduction band (CB) would cross each other at the Fermi level (EF) forming a nodal line, i.e. a line of Dirac points in momentum space32. SOC lifts the degeneracy of the nodal line throughout the Brillouin zone (BZ) and opens a hybridization gap between VB and CB. Owing to the local breaking of inversion symmetry, and under the action of SOC, the bands can acquire a local hidden spin polarization, as we show in the next section.
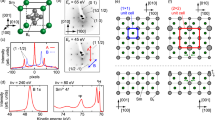
ARPES data and band structure calculations of Fig. 3 illustrate the prominent features of the electronic structure of ZrSiTe. The ARPES measurements were performed with s (blue color scale) and p (brown color scale) linearly polarized light at a photon energy of 107 eV, corresponding to a perpendicular wave vector kz~π/c. The complex experimental Fermi surface follows the periodicity of the square (001)-projected surface BZ in Fig. 3a, b. It consists of two concentric diamond-like contours centered at \(\overline{{{\Gamma }}}\), with additional smaller features around the \(\overline{{\rm{X}}}\) points. A comparison with the calculated (001)-projected spectral weight at the Fermi level in Fig. 3c assigns the former to the residual nodal-line bulk states and the latter to surface states (labeled SS), in agreement with the literature22,24,29. E vs. k ARPES intensity maps are shown in Fig. 3d for the \(\bar{{\rm{M}}}\bar{\Gamma }\bar{{\rm{M}}}\) and in Fig. 3e for the \(\bar{{\rm{X}}}\bar{\Gamma }\bar{{\rm{X}}}\) high-symmetry directions, with overlaid calculated bulk (red lines) and surface (green lines) bands. ARPES matrix elements are quite strong and parts of the band structure have appreciable intensity only with one polarization, as a consequence of the different orbital character of the bands. First principles33 and simple tight binding calculations34 assign the negative effective mass VB to predominantly Si px + py orbitals and the positive effective mass CB to Zr \({d}_{{x}^{2}-{y}^{2}}\) orbitals. VB and CB intersect above EF along \(\bar{{\rm{M}}}\bar{\Gamma }\bar{{\rm{M}}}\) and below EF along \(\bar{{\rm{X}}}\bar{\Gamma }\bar{{\rm{X}}}\), which indicates that the nodal line disperses in energy. The surface state SS is visible in the projected bulk gap along \(\bar{{\rm{M}}}\bar{{\rm{X}}}\bar{{\rm{M}}}\) in Fig. 3f. Theory predicts a small energy spin splitting for this band, which is later confirmed in the next sections of the manuscript.
a The bulk Brillouin zone and its projection on the (001) surface. b The Fermi surface at wave vector kz~π/c, measured by angle-resolved photoemission spectroscopy using 107 eV s-polarized light. The black square is the surface Brillouin zone. The dashed line indicates the cut where the data of Fig. 4 have been acquired. c Calculated Fermi surface obtained by integration over all kz values and projected over the (001) surface. d–f Experimental band dispersion along the \(\bar{{\rm{M}}}\bar{\Gamma }\bar{{\rm{M}}}\), \(\bar{{\rm{X}}}\bar{\Gamma }\bar{{\rm{X}}}\), and \(\bar{{\rm{M}}}\bar{{\rm{X}}}\bar{{\rm{M}}}\) high-symmetry directions. Brown (blue) color scales correspond to p−(s−) polarization. The results of a 9-layers slab calculation including spin–orbit coupling are overlayed on the experimental data as red (green) lines are bulk (surface) states. Photoemission intensities are illustrated by the color gradient shown next to each panel.
Bulk states: hidden spin polarization
We now address the spin polarization of the bulk bands that form the nodal line. Let us first consider an unrealistic limit where the valence and the CB were perfectly confined within the Si plane and, respectively, within the ZrTe layers. In this case one would expect a large local spin polarization in the CB from the polar Zr sites and no polarization at all in the VB from the CS Si sites. In reality the VB and CB hybridize, but retain a largely two-dimensional character, which is confirmed by their weak dispersion along the c axis (see Supplementary Note 1) and by independent quantum oscillations experiments35. Therefore, their overlap remains small. As a result, the local polarization of the CB decreases from the ideally confined situation36, but at the same time the VB acquires a spin polarization. The partial delocalization of the hybrid bands satisfies both the criteria of wave function’s segregation and overlap with polar sites, the key ingredients for the occurrence of a hidden spin polarization9.
The hidden spin polarization is confirmed by bulk calculations. To assess the spatially resolved spin structure of the VB and CB, we project the spin expectation value on the top and bottom (I and III) ZrTe sectors and on the intermediate (II) Si sector, with a methodology described in details in the Supplementary Discussion. For each sector we plot in Fig. 4a–c the x component of the spin polarization (Px), and in Fig. 4d–f the y component (Py), along a cut at ky = 0.53 (π/a) and for kz = π/c in the bulk BZ, indicated by the black dashed line of Fig. 3b. Additional results for different values of kz are discussed in the Supplementary Discussion. In the ZrTe sector we observe a sizeable polarization, both above and below EF. Px and Py have opposite sign in the top and bottom sectors, while the polarization is essentially zero in the intermediate Si plane. Furthermore, Px is symmetric with respect to kx = 0, while Py is antisymmetric, consistent with the helical Rashba R-2 texture. As expected by the presence of polar atomic sites, the D-2 term alone could not reproduce the observed spin texture. A quantitative assessment of the relative strength of the two contributions would require measuring the spin texture over the whole BZ and a theoretical analysis, e.g. by a k ⋅ p model, as recently done to analyze the spin texture of the surface alloy Bi/PbAg237, which is beyond the scope of the present work.
Calculated bulk band structure along the dashed line of Fig. 3b. We compare calculations in a–f the bulk and g–l for a slab composed by 9 unit cells. In the former case, the results correspond to the wave vector kz = π/c, while the latter refer to the innermost unit cell of the slab. In both cases, we project the calculations on the different sector, the top and bottom ZrTe sectors are indicated by filled wedges, while a filled rectangle denotes the intermediated Si plane. The color of the lines encodes in a–c, g–i the Px component and in d–f, j–l the Py component of the local spin polarization. The values of the spin polarization are mapped using a color gradient for both the bulk (on the left) and for the slab (on the right) calculations.
Bulk calculations alone cannot elucidate the role of the surface SIA in the formation of the spin polarization. To this end we have also performed a fully relativistic ab initio calculation on a 9-unit cells slab. Before assessing the effect of the surface SIA, we compare the calculations of the projected spin polarization in the bulk and in the slab. The results are shown in Fig. 4g–l, for the same cut at ky = 0.53 (π/a), and projected on the innermost unit cell of the slab. We can see a fairly good agreement between bulk and slab calculations. We ascribe the somewhat smaller values obtained from the slab calculations to a reduced segregation of the wave function in the different sectors (see Supplementary Discussion for further details).
We have measured by spARPES the spin polarization of the CB at three wave vectors connected by reflections about high-symmetry planes: A = (−0.13, 0.53)(π/a), B = (0.13, 0.53)(π/a), and C = (0.13,−0.53)(π/a). The light was p-polarized, and the photon energy hν = 48.5 eV was chosen near the minimum of the photoelectron mean free path to enhance the depth selectivity, as previously discussed. A sketch of the experimental setup is given in the Supplementary Note 2. We stress here that during the experiment the sample position was fixed, and different regions of the BZ were accessed by means of an electrostatic deflection lens.
The spin-averaged ARPES intensity map of Fig. 5a, also collected at ky = 0.53 (π/a), is well reproduced by the calculated bands of Fig. 4. Figure 5b–d shows spARPES results for the x spin component, and Fig. 5e–g displays the corresponding spin polarization Px, measured at A and B along the red lines of Fig. 5a and at C, respectively. The data show a clear spin signal within ~0.6 eV of EF, corresponding to the CB. The polarization Px extracted from the spectra has the same sign at A and B, but opposite sign at C. Finally, the polarization Py is very weak and of opposite sign at A and B (see Supplementary Note 3), as predicted by the calculations in Fig. 4d–f.
a Angle-resolved photoemission spectroscopy (ARPES) intensity map measured along the dashed line of Fig. 3b for a photon energy equal to 48.5 eV. b–d Spin-resolved ARPES spectra for the x spin component measured at wave vectors A = (−0.13,0.53)(π/a), B = (0.13,0.53)(π/a) (red lines in panel a), and C = (0.13,−0.53) (π/a). e–g Spin polarization Px measured at wave vectors A, B and C, respectively. The error bars in panels b–g represent the statistical error as described in the “Methods” section.
These results are consistent with the theoretical predictions. A fully quantitative comparison would require to evaluate possible final state effects and interference effects from different unit cells14,15, and is beyond the scope of the present paper. Nevertheless, the consistency between theory and experiment already provides sufficient evidence for the existence of a hidden spin polarization in the bulk states of a CS nodal-line semimetal. This leaves open questions about the possible influence of the surface SIA on the bulk polarization. This point is addressed in the following.
Surface states: net spin polarization
We now focus on the SS that linearly disperses across EF around the \(\overline{{\rm{X}}}\) point22,24,29. Theory has predicted the existence of topologically protected SSs (TSS) in gapless nodal-line semimetals32, and indeed there is evidence for TSS in TlTaSe238, PbTaSe239, and ZrB240. For the ZrSiX family, despite some suggestions24,41, the topological nature of the SSs has not been established, and their origin is probably different. The non-symmorphic space group requires the bulk states to be fourfold degenerate along the \(\overline{{\rm{X}}}\) \(\overline{{\rm{M}}}\) line at the BZ boundary, but the surface breaks translational symmetry and removes all non-symmorphic symmetries. This lifts the degeneracy and leaves a SS state “floating” on top of the bulk bands24. Under the influence of the SIA and SOC the Rashba effect can then split the SS and induce a spin polarization. This is confirmed by our results.
Figure 6a displays the band structure calculated for the slab geometry near the \(\overline{{\rm{X}}}\) point, with the “floating” SS in the gap between the VB and the CB, from which it is split off. The splitting of the SS predicted by theory is now resolved in the ARPES constant-energy map of Fig. 6b, which covers a portion of the experimental Fermi surface. The spin-resolved calculation of Fig. 6c captures all features of the E vs. k intensity map of Fig. 6d measured along the dashed line near and parallel to \(\bar{{\rm{M}}}\bar{{\rm{X}}}\bar{{\rm{M}}}\), including the small splitting of the SS and the bottom of the CB at the \(\overline{{\rm{X}}}\) point. The calculated spin polarization Py, in the direction perpendicular to \(\bar{{\rm{M}}}\bar{{\rm{X}}}\bar{{\rm{M}}}\), is encoded in the color of the symbols. It has odd parity with respect to \(\overline{{\rm{X}}}\), while the small Px component is even (see Supplementary Note 4). This finding is in good agreement with a recent study of the spin polarization in the surface state of HfSiS42, where it is shown that the Dresselhaus and the Rashba terms similarly contribute to form an unique unidirectional spin texture.
a Calculated band structure with spin–orbit coupling along high-symmetry directions near the X point. b Portion of the Fermi surface measured by angle-resolved photoemission spectroscopy (ARPES) near the \(\overline{{\rm{X}}}\) point. c Calculated dispersion along \(\bar{{\rm{M}}}\bar{{\rm{X}}}\bar{{\rm{M}}}\), showing the “floating” surface states. The color of the symbols encodes the Py spin polarization, whose intensity is indicated by the blue-white-red color scale. d ARPES dispersion measured along the dashed line in panel b. e Spin-resolved ARPES spectra for the y spin component measured at positions 1–7 in panel d. In the experiment the photon energy corresponds to 48.5 eV. The error bars in panel e represent the statistical error as described in the “Methods” section.
We have probed by spARPES the spin polarization of the SS at various kx values, indicated by dotted lines (1–7) in Fig. 6d, symmetrically located with respect to the kx = 0 plane. The experimental data are presented in Fig. 6e for the spin projection along ky. The spin-resolved spectra indicate the presence of two components with opposite spin, separated by ~50 meV, corresponding to the spin-split partners of the SS, which cannot be fully resolved owing to the experimental broadening. The sign of Py is opposite at the (1) and (7) extremes, where the inner subband has already crossed EF. Between these extremes the two peaks overlap, but it is still possible to recognize that their relative position is reversed on opposite sides of kx = 0, consistent with the calculation. By contrast, the spectra for the kx spin projection are essentially identical on both sides, and the polarization Px is small (see Fig. S4d). In summary, both theory and experiment confirm that the SS is split into spin-polarized bands due to the action of the surface SIA. In the following section we will discuss how this term can also influence the spin polarization of the bulk states.
Discussion
The results of the previous sections demonstrate that both the bulk and the surface states of ZrSiTe are spin polarized. The surface SIA is the origin of the polarization of the SS. Bulk calculations predict that the interaction with the polar ZrTe sites will induce a combined hidden R-2 and D-2 polarization in the bulk states. The wave functions of the bulk states however experience the presence of the surface, and one cannot exclude an influence of the surface SIA also on the bulk polarization. To address this question we performed a detailed layer-by-layer analysis of the slab calculations. We select three representative states from SS and from the bulk valence band (BS). They are indicated by a circle and, respectively, a square and a triangle on the band dispersion of Fig. 7a, corresponding to the same path investigated in Figs. 4 and 5. For these states we then plot in Fig. 7b–d the calculated local probability density ∣Ψ(z)∣2 within each quintuple layer of the 9-layers slab. We also encode in the color of the symbols the local polarization Px(z).
a Calculated band structure along the dashed line of Fig. 3b, plotted for positive wave vectors kx. b Probability density (logarithmic scale) calculated within each quintuple layer of a 9-unit cells slab and plotted as a function of the z axis, for the surface state indicated by a circle in panel a. The color of the symbols encodes the local spin polarization Px, whose magnitude is indicated by the blue-white-red color scale. Dashed lines separate different unit cells. c and d Same as in panel b for the bulk states indicated by a square and a triangle in panel a.
For the SS, Fig. 7b, ∣ΨSS(z)∣2 decreases by three orders of magnitude within three layers of the surface. The spin polarization is already strongly reduced in the second layer, and disappears in the deeper layers. Therefore, we attribute the polarization to the rapid variation of the surface potential as described by the surface Rashba–Bychkov effect. The situation is more complex in the bulk continuum. Depending on the state considered, ∣ΨBS(z)∣2 is partially reduced (Fig. 7c) or approximately constant at the surface (Fig. 7d), but the surface SIA has nonetheless a sizable effect on the spin polarization. Even when the spin polarization in the innermost layers alternates between opposite ZrTe sectors, as expected for the hidden spin polarization, the surface layers behave differently. In Fig. 7c, the polarization over a surface region of ~20 Å shows no alternation and a net polarization is thus established. For the state displayed in Fig. 7d, no clear signature of a spin oscillation between the sectors is observed. This suggests that the influence of the surface on the spin polarization dominates over the bulk effect. A possible explanation for this observation is the interference between the incident Bloch wave and the wave reflected at the surface. It results in a spin density with energy and spatial dependence26, as previously observed in Bi25 and in Au27.
In comparing the values of the spin polarization of the surface and bulk states, one should be aware that final states effects may affect the ARPES measurement, therefore we refrain from drawing quantitative conclusions, which we leave for a future investigation. From the point of view of the calculations, we notice that, in the slab model, the value of the spin polarization for both the BS and the SS is small, and the latter is comparably larger than the former. This difference results from the asymmetry of the wave functions43,44, but also reflects the relative intensities of the surface electric field and the local field at the bulk polar sites. This is explicitly assessed in Fig. 8, in order to compare their relative importance. Figure 8a displays the layer dependence of the electrons potential energy within the first two unit cells below the surface, and of the z component of the electric field (Fig. 8b). As expected from the structure, a local dipole is formed within each ZrTe sector with an average value of ∣Ez∣ = 0.7 V/Å as computed over the shaded area, a value that is large but two times smaller than the one predicted for BaNiS220. In order to evaluate the electric field induced by the SIA, Fig. 8c shows the difference between Ez calculated in the first (black line) and second (red line) unit cell of the slab with respect to the result of the bulk calculations. We clearly see that the behavior in the second unit cell is already an excellent approximation of the bulk, whereas in the first unit cell the difference becomes sizeable only above the topmost Te atoms. This shows that the SIA is responsible for an electric field with a peak value of 3 V/Å. Although the electric field is confined in a shallow region of ~1 Å, it might still influence the bulk continuum by introducing a spin-dependent dephasing in the formation of the stationary states.
a Electrons potential energy calculated for the two top-most unit cells of the slab as a function of the z-axis, orthogonal to the sample surface. b Corresponding electric field, Ez, represented by arrows. The shaded areas in sectors I and III indicate where the average value of 0.7 V/Å is computed. c Difference between Ez calculated in the first (black line) and second (red line) unit cell of the slab with respect to the result of the bulk calculations and plotted as a function of the z axis. The surface contribution of Ez is localized in a shallow region of ~1 Å, close to the sample surface.
In summary, spARPES data and first-principles calculations of the electronic structure show that the layered nodal-line semimetal ZrSiTe hosts spin-polarized bulk and surface states. Our bulk calculations confirm that CS materials can develop a local hidden spin polarization in the presence of polar sites. Our extensive analysis of the slab calculations illustrate the possible role of the surface SIA in contributing to a net spin polarization in the bulk state at the surface, which is accessible to spARPES.
Finally, the ZrTe sectors are an example of a high-mobility 2D electron system with sizeable SOC, and can be considered an experimental realization of an intrinsic spin Hall semimetal45. Their integration on a suitable insulating substrate, such as SrTiO333, would thus potentially produce an efficient spin-Hall filter of interest for spintronic devices.
Methods
Sample growth and angle-resolved photoemission spectroscopy measurements
High-quality single crystals of ZrSiTe grown by vapor transport were mechanically exfoliated in situ under ultra-high vacuum conditions (base pressure in low 10−10 mbar). All the photoemission spectra have been taken using hemispherical VG-SCIENTA electron analyzers operating in deflection mode at the 7.0.2 MAESTRO beamline, ALS, Berkeley (US), at the APE beamline, ELETTRA, Trieste (IT), and at the ASPHERE III endstation of beamline P04 at PETRA III. In the latter setup, the sample temperature was kept at ~30 K, and the bulk band periodicity was investigated with circularly polarized light in the energy range between 420 and 500 eV, with energy and angular resolution of 50–100 meV and 0.07 Å−1, respectively. The other ARPES data have been acquired at 80 K, and we used 107 eV photon energy with variable polarization for the data taken at ALS and 48.5 eV with p-polarization at APE. The energy and momentum resolution was better than 20 meV and 0.01 Å−1 for the ARPES spectra.
Spin and angle-resolved photoemission spectroscopy measurements
The spin-resolved photoemission spectra were measured at APE using a VLEED-based spin detector. Energy distribution curves (EDCs) of the spin-polarized photoelectron intensity (I) were measured after magnetizing the detectors along different directions and orientations, using coils. The spectra were renormalized to the same acquisition time and corrected for possible differences in the detectors’ efficiency (of the order of few %) for opposite magnetizations. For a specific wave vector, we have used the two detectors to acquire Ii along three orthogonal directions in the reference system of the electron analyzer. These quantities have been combined in order to obtain the electron spin components in the reference system of the crystal surface, and the spin polarization according to
where S = 0.3 is the value of the Sherman function previously determined by measuring the spin polarization of the Shockley surface states of Au(111). \({I}_{i}^{+}\) and \({I}_{i}^{-}\) are the spin-polarized photoelectron intensities for the target magnetized (+) or (−) along the i axis. From Pi we retrieve the relative populations of spin up and down electrons in the material’s band structure \({S}_{i}^{\uparrow /\downarrow }\), according to \({S}_{i}^{\uparrow /\downarrow }=(1\pm {P}_{i})\frac{{I}_{i}^{+}+{I}_{i}^{-}}{2}\). The uncertainty \(\delta {I}_{i}^{+/-}\) associated to the measured photoelectron intensities \({I}_{i}^{+/-}\) is estimated assuming a Gaussian statistics, and it is equal to \(\sqrt{{I}_{i}^{+/-}}\). The uncertainty over the spin polarization Pi is \(\delta {P}_{i}={P}_{i}\cdot \sqrt{\frac{{(\delta {I}_{i}^{+})}^{2}+{(\delta {I}_{i}^{-})}^{2}}{{({I}_{i}^{+}+{I}_{i}^{-})}^{2}}+\frac{{(\delta {I}_{i}^{+})}^{2}+{(\delta {I}_{i}^{-})}^{2}}{{({I}_{i}^{+}-{I}_{i}^{-})}^{2}}}\). Finally, the uncertainty over \({S}_{i}^{\uparrow /\downarrow }\) is \(\delta {S}_{i}^{\uparrow /\downarrow }={S}_{i}^{\uparrow /\downarrow }\cdot \sqrt{\frac{{(\delta {P}_{i})}^{2}}{{(1\pm {P}_{i})}^{2}}+\frac{{(\delta {I}_{i}^{+})}^{2}+{(\delta {I}_{i}^{-})}^{2}}{{({I}_{i}^{+}+{I}_{i}^{-})}^{2}}}\). These quantities are indicated by the error bars in the figures of this manuscript and of the Supplemental Information. The energy and momentum resolution was better then 100 meV and 0.05 Å−1 for the spin-resolved ARPES spectra.
Ab initio calculations
The electronic structure of both bulk and slab models were obtained within density functional theory using the plane-wave pseudopotentials method as implemented in the Quantum Espresso package46. We used fully relativistic optimized norm-conserving vanderbilt pseudopotentials (ONCVPSP)47 obtained from the sg15 database48. The exchange and correlation were treated within the Perdew–Burke–Ernzerhof (PBE) approximation49. The energy cut-off of the plane-wave was set to 80 Ry, and we used a 8 × 8 × 3 and a 12 × 12 × 1 Monkhorst–Pack grid for the bulk and slab calculations, respectively. In order to compute the spin expectation value projected on atomic sites, we projected the eigenstates onto orthogonalized atomic wavefunctions using the projwfc.x code of the Quantum Espresso package. Subsequently, in the case of non-collinear calculations, we rotated the basis set from the total angular-momentum basis set to the atomic and spin angular momentum50,51,52. For the slab calculations we used a tetragonal unit cell where the ZrSiTe unit cells were arranged along the [001] direction leaving a 23 Å vacuum region between slabs. The weight of the spectral function in the (001) surface was computed with the surface Green’s function of a semi-infinite system using the method described by A. Umerski53. To compute the bulk Green’s function we used the Hamiltonian in the basis of maximally localized Wannier functions obtained with the Wannier90 code54. The maximally localized Wannier functions were obtained by projecting the Bloch bands into the d orbitals of Zr, p orbitals of Te and the s and p orbitals of Si.
Data availability
Source data are available for this paper in ref. 55. Additional data used to support the findings of this work are available, upon reasonable request, from the corresponding authors.
References
Dresselhaus, G. Spin–orbit coupling effects in zinc blende structures. Phys. Rev. 100, 580–586 (1955).
Tilley, R. Crystals and Crystal Structures 67–79 (Wiley, 2006).
Bychkov, Y. A. & Rashba, E. I. Properties of a 2D electron gas with lifted spectral degeneracy. Pis’ma Zh. Eksp. Teor. Fiz. 39, 66–69 (1984).
Ishizaka, K. et al. Giant Rashba-type spin splitting in bulk BiTeI. Nat. Mater. 10, 521–526 (2011).
LaShell, S., McDougall, B. A. & Jensen, E. Spin splitting of an Au(111) surface state band observed with angle resolved photoelectron spectroscopy. Phys. Rev. Lett. 77, 3419–3422 (1996).
Reinert, F., Nicolay, G., Schmidt, S., Ehm, D. & Hüfner, S. Direct measurements of the L-gap surface states on the (111) face of noble metals by photoelectron spectroscopy. Phys. Rev. B 63, 115415 (2001).
Luo, J., Munekata, H., Fang, F. F. & Stiles, P. J. Effects of inversion asymmetry on electron energy band structures in GaSb/InAs/GaSb quantum wells. Phys. Rev. B 41, 7685–7693 (1990).
Zhang, X. et al. Hidden spin polarization in inversion-symmetric bulk crystals. Nat. Phys. 10, 387–393 (2014).
Yuan, L. et al. Uncovering and tailoring hidden Rashba spin–orbit splitting in centrosymmetric crystal. Nat. Commun. 10, 906 (2019).
Chiu, Y.-C. et al. Origin of the butterfly magnetoresistance in a Dirac nodal-line system. Phys. Rev. B 100, 125112 (2019).
Schoenemann, R. et al. Fermi surface of the Weyl type-II metallic candidate. Phys. Rev. B 96, 121108(R) (2017).
Liang, T. et al. Ultrahigh mobility and giant magnetoresistance in the Dirac semimetal Cd3As2. Nat. Mater. 14, 280–284 (2014).
Jiang, J. et al. Signature of strong spin–orbital coupling in the large nonsaturating magnetoresistance material WTe2. Phys. Rev. Lett. 115, 166601 (2015).
Zhu, Z.-H. et al. Layer-by-layer entangled spin–orbital texture of the topological surface state in Bi2Se3. Phys. Rev. Lett. 110, 216401 (2013).
Xie, Z. et al. Orbital-selective spin texture and its manipulation in a topological insulator. Nat. Commun. 5, 3382 (2014).
Riley, J. M. et al. Direct observation of spin-polarized bulk bands in an inversion-symmetric semiconductor. Nat. Phys. 10, 835–839 (2014).
Gotlieb, K. et al. Revealing hidden spin-momentum locking in a high-temperature cuprate superconductor. Science 362, 1271–1275 (2018).
Fanciulli, M., Muff, S., Weber, A. P. & Dil, H. J. Spin polarization in photoemission from the cuprate superconductor Bi2Sr2CaCu2O8+δ. Phys. Rev. B 95, 245125 (2017).
Wu, S.-L. et al. Direct evidence of hidden local spin polarization in a centrosymmetric superconductor LaO0.55F0.45BiS2. Nat. Commun. 8, 1919 (2017).
Santos-Cottin, D. et al. Rashba coupling amplification by a staggered crystal field. Nat. Commun. 7, 11258 (2016).
Razzoli, E. et al. Selective probing of hidden spin-polarized states in inversion-symmetric bulk MoS2. Phys. Rev. Lett. 118, 086402 (2017).
Topp, A. et al. Non-symmorphic band degeneracy at the Fermi level in ZrSiTe. New J. Phys. 18, 125014 (2016).
Topp, A. et al. The effect of spin-orbit coupling on nonsymmorphic square-net compounds. J. Phys. Chem. Solids 128, 296–300 (2017).
Topp, A. et al. Surface floating 2D bands in layered nonsymmorphic semimetals: ZrSiS and related compounds. Phys. Rev. X 7, 041073 (2017).
Kimura, A. et al. Strong Rashba-type spin polarization of the photocurrent from bulk continuum states: experiment and theory for Bi(111). Phys. Rev. Lett. 105, 076804 (2010).
Krasovskii, E. E. & Chulkov, E. V. Rashba polarization of bulk continuum states. Phys. Rev. B 83, 155401 (2011).
Wissing, S. N. P. et al. Rashba-type spin splitting at Au(111) beyond the Fermi level: the other part of the story. New J. Phys. 15, 105001 (2013).
Bensch, W. & Durichen, P. Structure of the layer compound ZrSiTe. Acta Crystallogr. C50, 346–348 (1994). 1-3.
Schoop, L. M. et al. Dirac cone protected by non-symmorphic symmetry and three-dimensional Dirac line node in ZrSiS. Nat. Commun. 7, 11696 (2016).
Chen, C. et al. Dirac line nodes and effect of spin–orbit coupling in the nonsymmorphic critical semimetals MSiS(M=Hf,Zr). Phys. Rev. B 95, 125126 (2017).
Hosen, M. M. et al. Tunability of the topological nodal-line semimetal phase in ZrSiX-type materials (X = S, Se, Te). Phys. Rev. B 95, 161101(R) (2017).
Burkov, A. A., Hook, M. D. & Balents, L. Topological nodal semimetals. Phys. Rev. B 84, 235126 (2011).
Xu, Q. et al. Two-dimensional oxide topological insulator with iron-pnictide superconductor LiFeAs structure. Phys. Rev. B 92, 205310 (2015).
Rudenko, A. N., Stepanov, E. A., Lichtenstein, A. I. & Katsnelson, M. I. Excitonic instability and pseudogap formation in nodal line semimetal ZrSiS. Phys. Rev. Lett. 120, 216401 (2018).
Hu, J. et al. Evidence of topological nodal-line fermions in ZrSiSe and ZrSiTe. Phys. Rev. Lett. 117, 016602 (2016).
Li, P. & Appelbaum, I. Illuminating spin-polarized Bloch wave-function projection from degenerate bands in decomposable centrosymmetric lattices. Phys. Rev. B 97, 125434 (2018).
Nechaev, I. A. & Krasovskii, E. E. Spin polarization by first-principles relativistic k ⋅ p theory: application to the surface alloys PbAg2 and BiAg2. Phys. Rev. B 100, 115432 (2019).
Bian, G. et al. Drumhead surface states and topological nodal-line fermions in TlTaSe2. Phys. Rev. B 93, 121113(R) (2016).
Bian, G. et al. Topological nodal-line fermions in spin-orbit metal PbTaSe2. Nat. Commun. 7, 10556 (2016).
Lou, R. et al. Experimental observation of bulk nodal lines and electronic surface states in ZrB2. npj Quantum Mater. 3, 43 (2018).
Hosen, M. M. et al. Observation of gapless Dirac surface states in ZrGeTe. Phys. Rev. B 97, 121103(R) (2018).
Wang, X. et al. Disentangling orbital and spin textures of surface-derived states in non-symmorphic semimetal HfSiS. Phys. Rev. B 100, 205140 (2019).
Park, S. R. & Kim, C. Microscopic mechanism for the Rashba spin-band splitting: perspective from formation of local orbital angular momentum. J. Electron Spectrosc. Relat. Phenomena 201, 6–17 (2015).
Bihlmayer, G. et al. The Rashba-effect at metallic surfaces. Surf. Sci. 600, 3888 (2006).
Sinova, J. et al. Universal intrinsic spin Hall effect. Phys. Rev. Lett. 92, 126603 (2004).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys.: Condens. Matter 21, 395502 (2009).
Hamann, D. R. Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B 88, 085117 (2013).
Scherpelz, P., Govoni, M., Hamada, I. & Galli, G. Implementation and validation of fully relativistic GW calculations: spin–orbit coupling in molecules, nanocrystals, and solids. J. Chem. Theory Comput. 12, 3523 (2016).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Kleinman, L. Relativistic norm-conserving pseudopotential. Phys. Rev. B 21, 2630 (1980).
Theurich, G. & Hill, N. A. Self-consistent treatment of spin-orbit coupling in solids using relativistic fully separable ab initio pseudopotentials. Phys. Rev. B 64, 073106 (2001).
Corso, A. D. & Conte, A. M. Spin–orbit coupling with ultrasoft pseudopotentials: application to Au and Pt. Phys. Rev. B 71, 115106 (2005).
Umerski, A. Closed-form solutions to surface Green’s functions. Phys. Rev. B 55, 5266 (1997).
Mostofi, A. A. et al. An updated version of wannier90: a tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 185, 2309 (2014).
Gatti, G. et al. Data for “Hidden bulk and surface effects in the spin polarization of the nodal-line semimetal ZrSiTe”, Materials Cloud Archive 2021. https://doi.org/10.24435/materialscloud:pp-qe (2021).
Acknowledgements
We acknowledge financial support by the Swiss National Science Foundation (SNSF), in particular M.F. acknowledges the SNFN support through grant P2ELP2_181877. D.G.-M. and O.V.Y. acknowledge the support by the NCCR Marvel. All first-principles calculations were performed at the Swiss National Supercomputing Centre (CSCS) under the project s1008. This work has been partly performed in the framework of the nanoscience foundry and fine analysis (NFFA-MIUR Italy Progetti Internazionali) facility. We thank DESY (Hamburg, Germany), a member of the Helmholtz Association HGF, for the provision of experimental facilities. Parts of this research were carried out at PETRA III. Funding for the photoemission spectroscopy instrument at beamline P04 (Contracts 05KS7FK2, 05K10FK1, 05K12FK1, and 05K13FK1 with Kiel University; 05KS7WW1 and 05K10WW2 with Würzburg University) by the Federal Ministry of Education and Research (BMBF) is gratefully acknowledged.
Author information
Authors and Affiliations
Contributions
G.G. and A.C. conceived the experiment. G.G., A.C., S.R., M.F., M.Z., performed the ARPES experiments with the assistance of M.K., K.R., C.J., A.B., E.R., I.V., J.F. G.G., A.C., S.R., M.F., M.Z., carried out the spin-resolved ARPES experiment with the assistance of I.V. and J.F. D.G.-M. and O.V.Y. performed the ab initio calculations. H.B. and A.M. grew the high-quality single crystals. G.G. wrote the manuscript and coordinated the project under the supervision of A.C. and M.G. All authors discussed the data and actively contributed to the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gatti, G., Gosálbez-Martínez, D., Roth, S. et al. Hidden bulk and surface effects in the spin polarization of the nodal-line semimetal ZrSiTe. Commun Phys 4, 54 (2021). https://doi.org/10.1038/s42005-021-00555-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00555-x
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.