Abstract
Until very recently, super-resolution localization and tracking of fluorescent particles used camera-based wide-field imaging with uniform illumination. Then it was demonstrated that structured illuminations encode additional localization information in images. The first demonstration of this uses scanning and hence suffers from limited throughput. This limitation was mitigated by fusing camera-based localization with wide-field structured illumination. Current implementations, however, use effectively only half the localization information that they encode in images. Here we demonstrate how all of this information may be exploited by careful calibration of the structured illumination. Our approach achieves maximal resolution for given structured illumination, has a simple data analysis, and applies to any structured illumination in principle. We demonstrate this with an only slightly modified wide-field microscope. Our protocol should boost the emerging field of high-precision localization with structured illumination.
Similar content being viewed by others
Introduction
Fluorescently labeled molecules and particles are localized and tracked with super-resolution throughout the nano- and biosciences. The structure and processes of life at the nanoscale are probed with these tools1,2,3,4. The spatio-temporal resolution of these techniques improves with improving microscopy modalities5, fluorescent probes6, and cameras7. But resolution also improves with improving localization methods1,8 and image analyses9. In a recent such improvement, MINFLUX8 vastly improved the “photon economy”10 of localization by utilizing a doughnut-shaped illumination structure for localization, albeit with low throughput due to its scanning implementation. A new class of localization methods (ROSE11, SIMPLE12, SIMFLUX13), sometimes referred to as modulation-enhanced localization microscopy (MELM14) methods, avoid the bottleneck of scanning by combining the use of wide-field structured illumination with camera-based imaging. While current implementations compare favorably to conventional methods, they, unfortunately, use only half the localization information encoded by their structured illuminations in actual measurements, as detailed below.
In camera-based (wide-field) localization microscopy, any structure in the illumination of the sample is unintended but predominantly varies slowly across the image15,16,17,18. Regardless, fluorescent point-emitters image as diffraction-limited spots9,19 (Fig. 1a, Supplementary Note 1). The location of the emitter is determined with high precision by fitting a theoretical model of the point-spread function (PSF) to the spot9 (Fig. 1a, Supplementary Note 1–3). Such PSF-fitting is used extensively to track molecules and particles with nanometer resolution19 and is leveraged by various super-resolution methods (e.g., PALM20, STORM21 and DNA PAINT22) to overcome the diffraction limit.
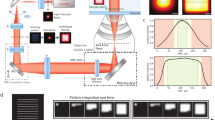
a In conventional camera-based localization microscopy, the illumination is spatially constant (green line). Thus, all fluorescent point-source (purple stars) are illuminated with the same intensity. Consequently, the diffraction-limited images (spots) of identical sources (orange bars) are equally intense on average. If those spots are non-overlapping, the position of each point-source can be determined by fitting its spot with a model point-spread function (PSF) (black solid lines, Methods). b Under structured illumination (Exposure 1, green line), the average number of photons, N1, in the diffraction-limited spot of each point-source (Image 1, orange bars) depends on the position of the source relative to the illumination. If the structured illumination is phase-shifted (Exposure 2, green line), the average number of photons, N2, in the diffraction-limited spot of each point-source changes (compare Image 1 to Image 2, orange bars). Regardless of intensity, the position of a point-source thus imaged twice is determined by fitting a model-PSF that has the position coordinate among its fitted parameters (black solid lines). Since we know the structure of the illumination from calibration and the distance, L, it was translated (Methods), the relative number of photons N1,2/(N1 + N2) in the two spots from a point-source reveal its position modulo L (Methods). c The resulting effective photon number of an optimized MELM method (Neffective in Eq. 1), is the sum of the effective photon numbers for PSF-fitting and camera-based MINFLUX, assuming identical total exposure time (Methods, Supplementary Fig. 1). Note that the values for Neffective correspond to the values realized in our 2D C-MELM experiment below (Supplementary Fig. 1, Supplementary Note 7–8).
Since the spot registers a finite number of photons, N, the position coordinates of the emitter can be determined only with limited precision. The variance of estimates for a position coordinate x is
where σ is a constant length that is specific to the experiment and proportional to the wavelength of the emitted light, while i quantifies the localization information per photon achieved with a given image analysis. It is not always possible to reduce this variance by increasing N: The value of N may be limited by, for example, a desired temporal resolution (frame rate), and/or photobleaching of the emitter, and/or phototoxicity to the sample. Instead of increasing N, one may maximize i and thereby increase the effective photon number, Neffective. While other methods exist15,23, it is well established that maximum likelihood estimation (MLE) with a correct model of the PSF is one optimal method to this end9,10,24,25. It achieves the minimal possible variance allowed theoretically by the so-called Cramér-Rao lower bound (CRLB26), by using all localization information present in a spot9,10,24,25. Thus, it is impossible to do better than that for a given image.
MINFLUX8,27, on the other hand, localizes and tracks fluorescent particles with up to 22-fold improvement of Neffective compared to that of optimal fitting of PSFs8. This is achieved by comparing the particle’s total intensity from exposures to different doughnut-shaped illumination structures. This allows ultra-fast tracking of individual particles, but the scanning implementation limits throughput severely.
For localization purposes, the bottleneck in throughput can be mitigated by use of wide-field structured illumination, which amounts to camera-based MINFLUX (Supplementary Note 4–6). Conceptually, for each of two orthogonal directions in the image plane, it works as follows: The sample is illuminated with a spatially periodic intensity and imaged with a camera through a microscope (Fig. 1b). An isolated point source images as a diffraction-limited spot. The intensity of each such spot depends on where its point-source is located in the structured illumination (Fig. 1b). After a translation (phase shift) of the illumination, each spot appears at its unchanged position in a new image, but typically with different intensity (Fig. 1b). If the position-dependent intensity of both illuminations is known, the relative intensity of a spot in its two images determines the position of its source, modulo the period of the structured illumination. SIMPLE12 is a recent protocol to this end. It determined the relative intensities with masks.
The relative intensities are, however, optimally determined by fitting a theoretical PSF to the spots recorded under different illuminations (Fig. 1b, Methods). Such fits determine both the intensities and, simultaneously and directly, the position of each point-source. This extra position-information resolves the ambiguity caused by the periodicity of the structured illumination. It also improves position-estimates because the total intensity and the source coordinates are statistically independent aspects of a spot.
ROSE11 and SIMFLUX13 are recent implementations of such a hybrid approach. ROSE generates the structured illumination with electro-optical modulators and cycles repeatedly between phase-shifts during the recording of a “frame”, where a “frame” is the set of images recorded of one sample with differently phase-shifted illumination structures. Each image in a “frame” is recorded in a separate area of the camera by changing the emission path in synchrony with the phase-shift. SIMFLUX, on the other hand, records each image in a “frame” in a single exposure. Its structured illumination is generated and shifted with a set of piezo-mounted gratings. Both methods calibrate the structured illumination using the sample itself. This requires a dense sample, a complicated data-processing pipeline, and illumination structures that are purely harmonic with no excess spatial variation due, e.g., to imperfect optics. Thus, for sparse samples and/or in the presence of excess variation in the structured illumination, this strategy may fail. Even if it does not fail, however, its calibrating-while-localizing uses information for calibration that could have improved localization. A better “photon economy”10 uses all photons from point-sources to be localized for localization and calibrates the structured illumination before it is used, with other, less precious sources.
Additionally, and importantly, while ROSE11 and SIMFLUX13 do realize ~2–3-fold improvements on Neffective relative to conventional localization applied to the same data, this is only half the improvement possible with these methods. Specifically, the CRLB for SIMFLUX allows a ~5-fold improvement, but only ~2.3-fold improvement was realized in actual measurements (additional improvements were achieved during brief measurements lasting less than one second)13. The CRLB for ROSE allows ~6-fold improvement, but only a ~3-fold improvement was realized11. In both cases, residual drift in the system was invoked to explain these shortcomings.
Below, we demonstrate that the CRLB can be realized in actual measurements with a pre-calibrated structured illumination: We extract all structured illumination-encoded localization information from images. Specifically, for each emitter we fit its theoretical PSF to its image simultaneously in every illumination employed, using MLE and a model of the structured illumination which was already calibrated locally and independently. This vastly simplifies the data analysis by reducing it to just a single fit of a model to recorded images. The resulting method, C-MELM (Calibrated Modulation Enhanced Localization Microscopy), localizes point-sources in camera-acquired images with maximal Neffective, the maximal value allowed by the CRLB for the experiment (Fig. 1c). This maximal Neffective is the sum of values for Neffective from each of a MELM method’s constituent camera-based localization methods (Fig. 1c, Supplementary Fig. 1, Supplementary Note 7–8) since these provide statistically independent information. With C-MELM, we thus localize single molecules with an Neffective of ~4.4, amounting to an increase in localization precision by a factor of ~2.1. This compares favorably to previous camera-based MELM implementations. Finally, C-MELM also localizes point-sources with theoretically maximal precision if the structured illuminations are distinctly non-harmonic, we show.
Results
Experimental implementation and calibration of C-MELM
For experimental demonstration, we used a commercial epi-fluorescence microscope with a modified excitation light path (Fig. 2a, Methods, Supplementary Fig. 2). Specifically, we used a collimated laser beam to image a digital micromirror device (DMD) through the objective using two-beam interference28 (Methods). This served as illumination of the sample12,29. We configured the mirrors to create lines12,29 with a duty ratio of 3/9 (Fig. 2b, Methods). We translated (i.e. phase shifted) the structured illumination as needed by using our control of the positions of the lines from the DMD. This simple setup provided optimized, consistent, and controllable structured illumination of the sample.
a Experimental setup consisting of a commercial wide-field epi-fluorescence microscope with a modified excitation path (Methods): The excitation light (green) is reflected off the DMD before it is relayed by a telescope, undergoes diffraction through the objective and results in structured illumination in the sample plane. See Supplementary Fig. 2 for details. b Subset of the DMD array configured in a periodic series of “on” and “off”-mirrors. c, d Example characterization of the structured illumination using a single 46-nm fluorescent bead (Methods). c We translated a fluorescent bead relatively to the structured illumination generated with the DMD configuration in b and recorded the number of photons in its resulting diffraction-limited spots (top row) for each position (blue dots) during 50-ms exposures. For each position of the bead, this was repeated for a total of three phases of the structured illumination (colored dots). A harmonic function with parameters obtained by a fit to data (colored curves, Methods, Supplementary Note 3) describes the data perfectly and thus characterizes the structured illumination. For each position, the total intensities were normalized by the total photon number observed in the three diffraction-limited spots recorded at that position. Error bars represent standard error of the calculated relative photon number. d Experimental bead images (top row) obtained at a single stage position (gray area in c) under illumination from three different phases as in c. All three images are fitted with a point-spread function model (bottom row) for a point-source under assumption that its position is identical in the three images (Methods, Supplementary Note 3). This enables accurate estimation of total intensity also in dim images (e.g., for Phase 2). The effective pixel size was 107 nm.
The local intensity of the illumination is required input to C-MELM. We therefore characterized the illumination by translating bright 46-nm fluorescent beads across the stationary structured illumination (Fig. 2c, d, Methods). We repeated this characterization for all three phases of the structured illumination that we would use (Fig. 2c, d) and along both coordinate axes (Supplementary Fig. 3), to check that the profile of the structured illumination is conserved under its translations (phase shifts). We repeated these checks and analyses for multiple beads distributed randomly in the field of view (FOV), in order to account for smooth excess spatial variations in the structured illumination caused by the optics15,16,17,18. For practical application, we interpolated between the nearest five such characterizations of the structured illumination in order to determine the illumination at a given position in the FOV (Methods, Supplementary Note 10). We found the structured illumination resulting from this illumination scheme to be harmonic with a period of ~230 nm and a contrast of up to ~0.9 (Fig. 2c), Importantly, however, our calibration assumes neither that the structured illumination is harmonic nor that it is free from excess spatial variation15,16,17,18. By abstaining from assumptions, it (i) eliminates a potential source of error present in ROSE, SIMPLE and SIMFLUX, which all assume such ideal conditions (ii) ensures that C-MELM estimates may be calculated directly with a single MLE fit to images with no need for subsequent iterative refinement of particle positions and/or structured illumination parameters, and (iii) ensures that C-MELM also works with other microscopy modalities and sources of structured illumination (see below).
C-MELM localizes single molecules with maximal precision
To demonstrate C-MELM’s performance, we imaged single Atto-590-labeled Streptavidin molecules immobilized on a coverslip as a time-lapse recorded movie (Methods). Each “frame” in this movie consists of six images of the sample, one for each of three phase-shifted illumination structures along each of two orthogonal coordinate axes (Fig. 3a, Methods). For each isolated single molecule, we obtained the C-MELM estimate of its position by assuming that its six diffraction-limited images (“spots”) in a “frame” could be modeled with six 2D Gaussians produced by a common point-source at a single position, but with intensities that were constrained by the calibrated structured illumination (Methods, Supplementary Note 7). The theoretical images resulting from this fitted model agree with the experimental data (Fig. 3a), which indicates that our 2D-Gaussian approximation to the PSF (Methods) is accurate.
a Single Atto590-labeled Streptavidin molecules were subjected to six 50-ms exposures of structured illumination: three phases of, respectively, y-periodic (ϕy) and x-periodic illumination (ϕx). Each molecule thus produced six diffraction-limited images (top row), which constitute one measurement. The molecule’s position and six spot intensities were estimated by a simultaneous maximum likelihood estimation fit of six model point-spread functions (PSFs) with shared point-source location, in which we constrained the relative intensities in spots as expected from the illumination structures (bottom row, Methods). For display, each image was averaged over ten frames for noise-reduction, but all position estimates obtained below were done on individual frames. The effective pixel size was 107 nm. b 310 positions of the molecule in a obtained, respectively, by PSF-fitting (blue) and C-MELM (orange). The estimates are centered on their respective mean values. Position estimates for each coordinate and localization method are normally distributed yielding a localization precision as given by the s.d. in the legend. c Histograms of all position estimates for PSF-fitting (blue) and C-MELM (orange) centered on their mean values and in units of their theoretically predicted s.d. calculated from the Cramér-Rao lower bound (CRLB). Agreement with a standard normal distribution with unit variance (black curve) demonstrates that localization in each case is optimal. d Sample variances of x- (crosses) and y-coordinates (circles) of positions obtained, respectively, with PSF-fitting (blue) and the C-MELM (orange) for 14 isolated single molecules in the field of view in units of their respective theoretical variance (calculated from the CRLB). The data fluctuate around 1, which is expected when estimates achieve the theoretical limit for performance, the CRLB. Error bars indicate the s.d. of the sample variance.
For comparison with state-of-the-art fitting of PSFs to images recorded with uniform illumination, we used the set of six exposures as input to ensure that the total number of photons was identical between the localization methods (Supplementary Note 3). We localized each molecule multiple times with both methods. Typically, we obtained ~300 position estimates for each localization method from which we calculated the localization precision as the s.d. of the positions (Fig. 3b). For the example molecule shown in Fig. 3a, b, we found that C-MELM more than doubled the localization precision: it yielded an Neffective of ~4.4. Note that both localization methods achieved their optimal performance with the available photons, since their position estimates scattered as standard normal distributions when rescaled by their theoretical s.d. calculated from the CRLB (Fig. 3c, Supplementary Fig. 4, Supplementary Note 8).
We repeated this analysis for 14 well-isolated molecules in the FOV of the time-lapse movie. For each molecule, we thus calculated the sample variance of position estimates obtained using, respectively, C-MELM and state-of-the-art fitting of PSFs to images (effectively) recorded with uniform illumination. The localization variances obtained from the molecules agree with their theoretically predicted values (Fig. 3d), which demonstrates that C-MELM makes optimal use of the information content in both of its constituent camera-based localization methods: it achieves the theoretical limit for performance, its CRLB. This shows that C-MELM is consistently superior to PSF-fitting by a factor of ~4.4 on Neffective, which is a significant improvement relative to the experimentally realized values of previous camera-based MELM methods.
C-MELM localizes particles with maximal precision under non-harmonic illumination
In order to demonstrate that C-MELM does not require harmonic illumination structures in order to localize with theoretically optimal precision, we modified our excitation light path in an alternative manner (Supplementary Fig. 5). Most notably, instead, we used three-beam interference for generation of the structured illumination28 (Methods). For this setup, we used a 1/8 duty ratio on the DMD, which optimized the period/contrast relationship in this case. The realized structured illumination was distinctly non-harmonic but perfectly described by a single, simple theoretical model with phase-shifts (Methods, Supplementary Figs. 6 and 7 and Supplementary Note 9). For characterization of the resulting structured illumination, we used 51-nm fluorescent beads (Methods).
For demonstration, we imaged another set of 51-nm fluorescent beads as a time-lapse recorded movie (Fig. 4a, Methods). Due to the non-harmonic structure of the structured illumination, we used four phases to ensure that C-MELM’s performance is independent of the particle’s position relative to the structured illumination (Supplementary Fig. 8). For analysis, we used a set of eight 2D Gaussians produced by a common point-source at a single position, but with intensities that were constrained by the calibrated structured illumination in Fig. 4c, d (Methods, Supplementary Note 7, Supplementary Fig. 9). Also, in this case, the theoretical images resulting from this fitted model agree with the experimental data (Fig. 4b), which indicates that our 2D-Gaussian approximation to the PSF is accurate also for fluorescent beads9.
a Camera-based microscopy image of a sample containing multiple isolated fluorescent 51-nm beads (Methods). Effective pixel width, 107 nm. A bead used as example for demonstration in subsequent panels is indicated (red circle). b The sample in a was subjected to eight 50-ms exposures of structured illumination (Methods): four phases of x-periodic illumination (ϕx) and four phases of y-periodic illumination (ϕy). This resulted in eight recordings of diffraction-limited spots (top row) from the same bead, which constitute one measurement. The fluorescent bead’s position and eight intensities were estimated by a simultaneous maximum likelihood estimation fit of eight model point-spread functions with shared point-source location, in which we constrained the relative intensities in spots as expected from the illumination structures (bottom row, Methods). c, d Relative photon numbers expected from the characterization of four phases of structured illumination (solid lines with various colors, Methods, Supplementary Note 9, Supplementary Fig. 9) along the x- (c) and y-axes (d), respectively. The bead’s approximate position is indicated (dashed lines). e, f Sample variance of position estimates, for x- (e) and y-coordinates (f), for all 40 isolated particles in the field of view in a for C-MELM (orange) and conventional camera-based localization (blue). Error bars represent the s.d. of the sample variance. The information-theoretical lower bound (Cramér-Rao lower bound (CRLB), Supplementary Note 8) for the variance is indicated for both methods (solid lines). C-MELM achieves its lower bound and is uniformly the superior method as it has the smaller variance, corresponding to an Neffective larger by a factor ~1.7 (Eq. 1).
We repeated this analysis for all 40 well-isolated beads in the FOV of the time-lapse movie (Fig. 4a). For each bead, we thus calculated the sample variance of position estimates obtained using, respectively, C-MELM and state-of-the-art fitting of PSFs to images recorded with uniform illumination (Fig. 4e, f). The total photon number obtained from beads varied due to spatial variations in the excitation laser intensity and variations in the size of beads. Regardless, C-MELM is consistently superior to PSF-fitting by a factor of ~1.7 on Neffective, thus nearly doubling the photon efficiency. Since this structured illumination has a poorer period/contrast relationship than the harmonic structured illumination realized above, each of C-MELM’s constituent camera-based localization methods here contribute substantially to the resulting photon efficiency, and C-MELM makes optimal use of both: it achieves the theoretical limit for performance, its CRLB (Fig. 4e, f, Methods, Supplementary Note 8). Consequently, no other unbiased estimator can do better with this structured illumination.
The duration of recording of each calibration and test movie was around three minutes during which fluorescent particles were imaged for four seconds at each position (Methods). We observed negligible sample and focal drift, and thus no correction for drift was required. The presence of significant sample and/or focal drift would have prevented C-MELM from achieving its CRLB, which assumes no drift. The time between recordings of data for calibration and measurement typically was a couple of hours and included a change of experimental sample in the case of single-molecule imaging. During such time periods, we observed a slight drift of the structured illumination, which gave rise to a bias for the C-MELM position estimates. We corrected our estimates for this bias (Methods). Note, however, that the drift of the structured illumination had negligible effect on the precision of C-MELM position estimates (Figs. 3 and 4). This demonstrates the stability and feasibility of C-MELM in practical settings.
Finally, we extended our results using computer-simulated data to confirm C-MELM’s ability to localize particles with accuracy and maximal precision according to the CRLB over a range of experimentally relevant total photon numbers (Supplementary Fig. 10).
Discussion
The attainable resolution in a structured illumination-enhanced localization experiment depends crucially on the total number of source photons (Supplementary Fig. 10), on the background, and on the contrast and period of the structured illumination (Supplementary Note 11 and Supplementary Fig. 11). In our single-molecule experiments, our structured illumination yielded a contrast of ~0.9 and a period of ~230 nm, which is comparable to the illumination structures used in ROSE and SIMFLUX. We, however, were able to extract all the localization information encoded in photons by the structured illumination. Doing this, we have experimentally realized the full potential of camera-based MELM methods and have in practice achieved a factor of ~4.4 on Neffective, which corresponds to an improvement by a factor of ~2.1 on the localization precision.
Additionally, we employed C-MELM with a structured illumination, which was distinctly non-harmonic. This shows that C-MELM does not rely on a specific structured illumination, as long as it can be characterized and modeled. With this non-harmonic illumination structure, we obtained an Neffective of ~1.7, which is the optimal improvement possible for a contrast of ~0.75 and a period of ~400 nm.
Thus, C-MELM makes optimal use of the resources in a given experiment, we have shown. Furthermore, C-MELM is readily applicable to other experiments that use wide-field structured illumination to enhance localization (e.g., SIMPLE, ROSE, SIMFLUX), since it only relies on a rigorous analysis in conjunction with a locally-calibrated model for the structured illumination but not on a specific structured illumination. Thus, all the benefits of C-MELM may be realized with both previous and future implementations of localization microscopy with any source of structured illumination5,30,31,32,33. The resulting gain in photon efficiency may be utilized to achieve better spatial resolution, or faster imaging, or both. In the context of various single-molecule super-resolution modalities (e.g., PALM20, STORM21, and DNA PAINT22), our calibrated illumination structures provide yet another advantage: They may be used to verify the presence/absence of blinking and/or bleaching of a molecule of interest or of any influential nearby molecules. To do this, one takes advantage of the fact that the different intensities from a molecule measured under different exposures are coupled in a known manner for given position of the molecule. Consequently, they may be used to indicate absence of blinking in a measurement or, alternatively, to flag it for individual analysis or rejection. This permits realization of all the benefits of our protocol also in the context of super-resolution imaging, even in the presence of complex blinking dynamics.
It is a common misconception that the PSF in experiments similar to ours is an Airy function with its characteristic diffraction rings. Rather, the PSF has an intense central peak, like the Airy function, but no diffraction rings, only tails that decrease slowly, approximately with the distance to the center of the PSF cubed, starting with a “shoulder” to the peak9. The central peak and its “shoulder” is described well by a 2D-Gaussian standing on a constant “background”9 (Supplementary Note 1, Methods). This “background” adds to any actual fluorescent background in images, but depends on the incident illumination, since it is part of the PSF. Consequently, source photons contribute to it in a manner that is proportional to the structured illumination at the position of the point-source. This effectively allows for extraction of structured illumination-encoded information from an additional ~20 per cent of photons9, when localizing emitters in images with sufficiently low actual background (Supplementary Note 7). When this is possible, it constitutes another improvement relative to ROSE and SIMFLUX.
That PSF is the result of an isotropic superposition of light emitted by an isotropic superposition of fluorophores that essentially are dipole emitters. This isotropic superposition may be the result of a single fluorophore that is free to rotate and does so sufficiently fast relative to the lifetime of its excited state that any dependence on the polarization of the excitation light field is lost. Alternatively, a collection of randomly oriented fluorophores in a fluorescent bead under isotropic illumination will result in the same PSF. A fluorescent bead imaged under total internal reflection fluorescence (TIRF) conditions has a similar PSF9.
On the other hand, the emission dipole moment of a single fluorophore may be fixed in orientation due to steric hindrances, electrostatic interactions, or deliberately with two linkers9,24,25,34,35,36,37. Such circumstances affect C-MELM analysis as well as conventional PSF fitting. If the fluorophore is fixed during the recording of each “frame”, an appropriate PSF for this purpose must be used for accurate localization9,24,25,38. That PSF should also be used in C-MELM analysis, for localization and because its use guarantees an accurate quantification of the spot intensity. The fact that the spot’s intensity depends on the orientation of the excitation dipole moment relative to the excitation field does not influence C-MELM, since this analysis depends only on relative intensities. If, instead, the fluorophore is fixed in orientation only during the recording of each image in a “frame”, the influence of excitation light field must also be accounted for. This also applies in the case where the fluorophore is partially free to rotate. If the fluorophore reorients between discrete states within an exposure time, C-MELM analysis seems challenging.
We note, finally, that our method is applicable in principle also to other experiments in which the PSF may be radically different, e.g., in the presence of significant aberrations39,40,41 and/or in 3D imaging39,40,41,42,43, provided that the PSF is known or can be modeled sufficiently well.
Conclusion
In conclusion, we have demonstrated that C-MELM optimally exploits the localization information in images obtained in experiments using wide-field structured illumination to enhance localization microscopy. Its ease-of-use and compatibility with existing and future implementations of this paradigm should ensure that all localization information is put to maximal use.
Methods
Sample preparation
In our first experiment, red-fluorescent polymer nanoparticles with ø = 46 nm (Invitrogen, FluoroSphere carboxylated) were used as light emitters for calibration of the structured illumination. Their maximum excitation and emission wavelengths were 580 nm and 605 nm, respectively. The stock solution of nanoparticles was diluted 104 times in MiliQ and sonicated for at least 30 min. A fixed amount was diluted further 10 times in 99% ethanol for a final dilution of 105. A high-precision coverslip (Marienfeld cat no. 0107052) was cleaned with UV/ozone for 60 min before use. To deposit nanoparticles on the coverslip, the coverslip was incubated with 5 μL of the nanoparticle solution and dried at 50 °C for 1 h in an oven. Subsequently, the coverslip was mounted on a microscope slide with 10 μL of 1xTE. Slides were sealed with epoxy glue and imaged right away.
For the secondary experimental setup, green-fluorescent polymer microspheres with ø = 51 nm (Duke Scientific Corporation cat no G50) were used as light emitters. Their maximum excitation and emission wavelengths were 468 nm and 508 nm, respectively. The stock solution of microspheres was diluted 104 times in PBS and sonicated for at least 30 min. To deposit microspheres on the coverslip, the coverslip was incubated with 10 μL of the microsphere solution for 1 min on a glass slide to spread the microspheres evenly across the surface. The coverslip was briefly dipped in PBS and then in Milli-Q water, before it was dried under a nitrogen flow. Subsequently, the coverslip was mounted on a microscope slide with 8 μL of Mowiol solution and left overnight to harden.
Single-molecule samples were obtained by grafting Streptavidin labeled with Atto-590 onto a BSA/BSA-biotin layer. 10 µg/mL BSA was mixed with 1 µg/mL BSA-biotin complex in a 10:1 ratio. 100 µL was added to UV/ozone cleaned coverslips for 20 min and washed in 1xTE for 2 min. Next, 100 µL of 1 µg/mL Streptavidin labeled with Atto-590 was added to the coverslip and left covered for 10 min before washed in 1xTE for 2 min. The coverslip was mounted with degassed 1xTE, sealed with nail polish, and imaged right away.
Microscope
Fluorescence imaging was performed with a Nikon Eclipse Ti2-U inverted microscope with a 100x oil objective (Nikon Plan Apochromat Lambda 100x/1.45). The microscope was modified for structured illumination (see below, Fig. 2, Supplementary Figs. 2 and 5). A dichroic mirror (AHF, quad band F73-478) allowed us to use the objective in both excitation and emission pathways. Prior to recording, the emission of the sample was guided through an emission filter (AHF, quad band cat no. F72-866) and a 1.5x magnifying tube lens. The microscope was placed on an optical table. A motorized XY-stage was used to localize the emitters, while an XY-piezo stage (MCL, NanoH) was used for high-precision positioning during imaging. Focus was adjusted manually and inspected using the average spatial s.d. of spots in an image, to ensure that images were well-focused.
Generation of structured illumination using a digital micromirror device (DMD)
A 561-nm laser (Cobolt, 06-DLP 561 nm) was used as excitation light source. The light was expanded with 2 lenses (Thorlabs; f = 30 mm and f = 200 mm, respectively). Two mirrors (Thorlabs, BBE02) guided the expanded light onto a digital micromirror device (DMD, Texas Instruments Lightcrafter 9000). The DMD consists of an array of micrometer-sized square mirrors that can be either “on” (reflection to sample) or “off” (reflection away from sample). The angle between the incident light and the DMD was ~24 degrees, such that the most intense first diffraction order of the “on”-position mirrors was normal to the DMD plane. At this angle, and for the chosen wavelength, the blaze-grating angle condition was satisfied and ensured that i) the main diffraction angle is intense and ii) the two first diffraction orders created by the lines on the DMD are of equal intensity29,44. This light was sent through a telescope (Thorlabs, f = 300 mm) and collimated by a third (projection) lens (Edmund optics, f = 300 mm). The two lenses of the telescope, the projection lens, and the objective were all positioned in 4 f configurations, such that i) the DMD was imaged in the sample plane and ii) the back focal plane of the objective is conjugated with the focal plane of the telescope. Following Reymond et al.12, we utilize this plane to, first, control the polarization of light by introducing a linear polarizer and a quarter wave plate oriented at 45 degrees relative to the linear polarizer to create circularly polarized light. Secondly, the zeroth order diffraction beam was filtered out by insertion of a home-made spatial mask. The polarization of the first diffraction-order beams, used to create the line pattern on the sample, was controlled by a home-made segmented polarizer, as depicted in Supplementary Figure 2. Because the blaze-grating condition is satisfied, it was not necessary to adjust the intensity of the two first-diffraction spots independently29. Finally, a second dichroic mirror is placed perpendicularly to the dichroic mirror inserted in the microscope, to compensate for polarization changes induced by the original dichroic mirror45.
The DMD was used to create line patterns consisting of 3 row/column of mirrors in the “on”-position, followed by 6 rows/columns in the “off”-position (Fig. 2). This was repeated periodically across the face of the DMD. The mirror configuration of the DMD was controlled using BitMap Picture (BMP) files. The files were loaded into the software DLP LightCrafter 6500 & 9000 version 4.0.0 and displayed on the DMD. The intensity of the illumination through the objective was ~2 W/cm2.
For the secondary setup a 473-nm laser (Cobolt, 06-MLD 473 nm) was used as excitation source. The microscope setup described above was utilized also for this experiment, except that the excitation path bypassed the all optical components between the DMD and the microscope (the second telescope, linear polarizer, quarter-wave plate and the segmented polarizer). This resulted in a structured illumination created by three-beam interference28.
The intensity was reduced from 100 mW to 30 mW using neutral density filters and the polarization was made circular using a linear polarizer combined with a quarter wave plate oriented at 45 degrees relative to the linear polarizer. The DMD pattern for this setup was 1 mirror “on” and 7 mirrors “off”. The intensity of the illumination through the objective varied from 4.6 W/cm2 to 6.9 W/cm2.
EMCCD camera
For imaging of fluorescent emitters, we used a highly sensitive EMCCD camera (Evolve 512, Photometrics). For all imaging, we used a field-of-view of 512 × 512 square pixels of 16 μm width. The combined magnification of the microscope (objective and tube lenses) resulted in an effective pixel width of 107 nm. Throughout measurements, the EM gain was set to 500, which corresponded to a signal-to-photon conversion factor of 72. The constant offset added to all pixel output values before readout was 505. The camera’s pixel rows were aligned to the horizontal lines of the DMD. We corrected all theoretical variances by a factor of two9,46, due to excess noise originating in the electron multiplication process.
Characterization of structured illumination
Since the beads are small (ø = 46-51 nm) relatively to the period of the illumination (~230 nm, respectively, 400 nm), the excitation intensity experienced by each bead is proportional to the intensity of the structured illumination at the bead’s position. Specifically, even for the largest particles in the reported size distribution, the pattern contrast is sampled with ~96% accuracy, assuming uniform dye distribution in the volume of each bead (Supplementary Fig. 12). Consequently, the integrated intensity in each bead’s spot can be used as a direct estimate of the local illumination intensity (Fig. 2c, d). Using this, we measured the intensity of the illumination as a function of position by translating the beads in steps across the structured illumination and imaging them between steps (Fig. 2c). Specifically, the beads were translated through 31 positions with a step length of ~71 nm along a diagonal line. At each position, we ten times imaged six/eight patterns: three/four phases of the structured illumination for each of two orthogonal directions in the image plane. Each phase shift was three/two mirror units on the DMD, i.e., a third/quarter period of the structured illumination (Fig. 2 and Supplementary Fig. 6). Each pattern was displayed on the DMD for 49 ms, which resulted in a time-lapse of 50 ms between images. For each position, each bead in the sample thus was imaged as 60 diffraction-limited spots in as many images. For analysis, we selected spots that were sufficiently isolated from each other as fiducials. The varying intensity of each spot as a function of the phase of the structured illumination allowed us to characterize the intensity profile of the experimentally realized structured illumination. In order to determine intensities, we applied a joint MLE-fit of six/eight 2D-Gaussian model-PSFs (see below) to each set of six/eight images (Supplementary Note 3). We fitted using the fact that the position-coordinates of the source and the width of its PSF were the same under all six/eight illuminations. Only the number of photons, N, and background, b, could differ between the six/eight illuminations (Fig. 2). For each pattern of structured illumination, we averaged the number of photons estimated for each particle in this manner over the ten repetitions and used that average to characterize the pattern (Fig. 2). We either modeled the pattern as a harmonic function (two-beam interference) or as a series of top-hat functions describing the lines of illumination, convolved with a Gaussian PSF describing diffraction by the objective47 (three-beam interference, Supplementary Note 9, Supplementary Fig. 7). This described data accurately (Fig. 2, Supplementary Figs. 3 and 6). The relevant parameters were obtained by weighted least-squares fitting of the model to data.
C-MELM measurements
The six/eight illumination patterns characterized above were used for C-MELM measurements. Each C-MELM measurement consisted of six/eight images in which the sample was exposed to three/four phases of the structured illumination for each of two orthogonal directions in the image plane, with an exposure time of ~49 ms per image. In order to determine the position of an isolated point-source with C-MELM, first the position was crudely determined. When we used a densely populated sample as basis for characterization, a single characterization measurement was sufficient in terms of reasonable FOV-coverage. In that case, the five fiducials nearest to the determined position were selected in order to describe the local values of the structured illuminations as functions of phase and, by interpolation between fiducials, as function of position (Supplementary Fig. 13, Supplementary Note 10). In cases where the sample used for characterization was sparse, we used multiple FOVs to ensure sufficient coverage. In such cases, the same interpolation was carried out to determine the shape of the structured illumination, but its phase was estimated based on the variation of intensities of the emitter to be localized as a function of the phase-shifted illumination structures.
Then, a joint MLE fit of six/eight 2D-Gaussians model PSFs (see below) was used to analyze the six/eight diffraction-limited spots produced by each fluorescent source to be localized. Again, we assumed identical positions and PSF widths in all spots from any given source. For a given source, however, the six/eight intensities recorded with the six/eight different illuminations were assumed related as the illuminations at the position of the source—this is the end to which we characterized the illuminations. This protocol simultaneously uses the positional information encoded in the intensity of a spot by the structured illumination and encoded in the position of the spot by any illumination (Supplementary Note 7). We repeated the C-MELM measurement and analysis for all chosen, well-isolated emitters in the sample that showed reasonable photostability.
Any drift of the structured illumination between characterization and measurement can lead to bias in the C-MELM estimate, due to discrepancies between characterized structured illumination position and actual structured illumination position at the time of measurement. To correct for this potential bias, we utilized the fact that positions of particles in the sample obtained with camera-based localization alone are unbiased. In the measurements in which the prior characterization was based on a single FOV of a densely populated sample, we determined the common bias for all investigated spot and corrected for it. Alternatively, in measurements where the characterization was based on several FOVs, the bias is already adjusted for by the determination of the phase of the structured illumination based on the emitter to be localized, as described above.
PSF model for image-based localization and C-MELM analysis
Throughout, we used a 2D-Gaussian-plus-a-constant as theoretical model-PSF. As described by Mortensen et al.9, this provides an accurate approximation to the actual PSF. We used MLE to fit this PSF to images recorded with uniform illumination (or any illumination, without using its structure). This localizes fluorescent point-sources optimally9. See Supplementary Notes 1–3 for details.
Simulations
For Monte Carlo simulations of experiments (Supplementary Figs. 1 and 10), we assumed Poisson statistics for the number of photons recorded in each pixel. Simulated experiments were analyzed identically to our experimental data using C-MELM and PSF-fitting (see above). Note that variances calculated using such simulations should be corrected by a factor of two, to account for excess noise in the EM process of an EMCCD camera, if one wishes to compare to experiments obtained using an EMCCD camera. Parameters used in the simulations are given in the relevant figures.
Data availability
All data that support the findings of this study are available from the corresponding author upon request.
Code availability
Source code for simulations and C-MELM analysis are available from the corresponding author upon request.
References
Deschout, H. et al. Precisely and accurately localizing single emitters in fluorescence microscopy. Nat. Methods 11, 253–266 (2014).
Shashkova, S. & Leake, M. C. Single-molecule fluorescence microscopy review: shedding new light on old problems. Biosci. Rep. 37, 1–19 (2017).
Elf, J. & Barkefors, I. Single-molecule kinetics in living cells. Annu. Rev. Biochem. 88, 635–659 (2019).
Von Diezmann, A., Shechtman, Y. & Moerner, W. E. Three-dimensional localization of single molecules for super-resolution imaging and single-particle tracking. Chem. Rev. 117, 7244–7275 (2017).
Chen, B. C. et al. Lattice light-sheet microscopy: imaging molecules to embryos at high spatiotemporal resolution. Science 346, 1257998 (2014).
Grimm, J. B. et al. A general method to fine-tune fluorophores for live-cell and in vivo imaging. Nat. Methods 14, 987–994 (2017).
Huang, F. et al. Video-rate nanoscopy using sCMOS camera-specific single-molecule localization algorithms. Nat. Methods 10, 653–658 (2013).
Balzarotti, F. et al. Nanometer resolution imaging and tracking of fluorescent molecules with minimal photon fluxes. Science 355, 606–612 (2017).
Mortensen, K. I., Churchman, L. S., Spudich, J. A. & Flyvbjerg, H. Optimized localization analysis for single-molecule tracking and super-resolution microscopy. Nat. Methods 7, 377–381 (2010).
Larson, D. R. The economy of photons. Nat. Methods 7, 357–359 (2010).
Gu, L. et al. Molecular resolution imaging by repetitive optical selective exposure. Nat. Methods 16, 1114–1118 (2019).
Reymond, L. et al. SIMPLE: Structured illumination based point localization estimator with enhanced precision. Opt. Express 27, 24578 (2019).
Cnossen, J. et al. Localization microscopy at doubled precision with patterned illumination. Nat. Methods 17, 59–63 (2020).
Reymond, L., Huser, T., Ruprecht, V. & Wieser, S. Modulation-enhanced localization microscopy (meLM). J. Phys. Photonics 2, 041001 (2020).
Copeland, C. R. et al. Subnanometer localization accuracy in widefield optical microscopy. Light Sci. Appl. 7, 31 (2018).
Kask, P., Palo, K., Hinnah, C. & Pommerencke, T. Flat field correction for high-throughput imaging of fluorescent samples. J. Microsc. 263, 328–340 (2016).
Douglass, K. M., Sieben, C., Archetti, A., Lambert, A. & Manley, S. Super-resolution imaging of multiple cells by optimized flat-field epi-illumination. Nat. Photonics 10, 705–708 (2016).
Khaw, I. et al. Flat-field illumination for quantitative fluorescence imaging. Opt. Express 26, 15276 (2018).
Yildiz, A. et al. Myosin V walks hand-over-hand: single fluorophore imaging with 1.5-nm localization. Science 300, 2061–2065 (2003).
Betzig, E. et al. Imaging intracellular fluorescent proteins at nanometer resolution. Science 313, 1642–1645 (2006).
Rust, M. J., Bates, M. & Zhuang, X. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM). Nat. Methods 3, 793–795 (2006).
Schnitzbauer, J., Strauss, M. T., Schlichthaerle, T., Schueder, F. & Jungmann, R. Super-resolution microscopy with DNA-PAINT. Nat. Protoc. 12, 1198–1228 (2017).
Parthasarathy, R. Rapid, accurate particle tracking by calculation of radial symmetry centers. Nat. Methods 9, 724–726 (2012).
Mortensen, K. I., Sung, J., Flyvbjerg, H. & Spudich, J. A. Optimized measurements of separations and angles between intra-molecular fluorescent markers. Nat. Commun. 6, 1–9 (2015).
Mortensen, K. I., Sung, J., Spudich, J. A. & Flyvbjerg, H. How to measure separations and angles between intramolecular fluorescent markers. Methods Enzymol. 581, 147–185 (2016).
Rao, C. R. Linear Statistical Inference and its Applications. (Wiley, 1973).
Eilers, Y., Ta, H., Gwosch, K. C., Balzarotti, F. & Hell, S. W. MINFLUX monitors rapid molecular jumps with superior spatiotemporal resolution. Proc. Natl Acad. Sci. USA 115, 6117–6122 (2018).
Heintzmann, R. & Huser, T. Super-resolution structured illumination microscopy. Chem. Rev. 117, 13890–13908 (2017).
Li, M., Li, Y., Liu, W., Zhanghao, K. & Xi, P. Structured illumination microscopy using digital micro-mirror device and coherent light source. Appl. Phys. Lett. 116, 233702 (2020).
Gustafsson, M. G. L. Surpassing the lateral resolution limit by a factor of two using structured illumination microscopy. J. Microsc. 198, 82–87 (2000).
Frohn, J. T., Knapp, H. F. & Stemmer, A. True optical resolution beyond the Rayleigh limit achieved by standing wave illumination. Proc. Natl Acad. Sci. USA 97, 7232–7236 (2000).
Shao, L., Kner, P., Rego, E. H. & Gustafsson, M. G. L. Super-resolution 3D microscopy of live whole cells using structured illumination. Nat. Methods 8, 1044–1048 (2011).
Fiolka, R., Shao, L., Hesper Rego, E., Davidson, M. W. & Gustafsson, M. G. L. Time-lapse two-color 3D imaging of live cells with doubled resolution using structured illumination. Proc. Natl Acad. Sci. USA 109, 5311–5315 (2012).
Toprak, E. et al. Defocused orientation and position imaging (DOPI) of myosin V. Proc. Natl Acad. Sci. USA 103, 6495–6499 (2006).
Backer, A. S., Backlund, M. P., Lew, M. D. & Moerner, W. E. Single-molecule orientation measurements with a quadrated pupil. Opt. Lett. 38, 1521–1523 (2013).
Aguet, F., Geissbühler, S., Märki, I., Lasser, T. & Unser, M. Steerable filters for orientation estimation and localization of fluorescent dipoles. Opt. Express 17, 6829–6848 (2009).
Backlund, M. P. et al. Simultaneous, accurate measurement of the 3D position and orientation of single molecules. Proc. Natl Acad. Sci. USA 109, 19087–19092 (2012).
Enderlein, J., Toprak, E. & Selvin, P. R. Polarization effect on position accuracy of fluorophore localization. Opt. Express 14, 8111 (2006).
Babcock, H. P. & Zhuang, X. Analyzing single molecule localization microscopy data using cubic splines. Sci. Rep. 7, 1–8 (2017).
Li, Y. et al. Real-time 3D single-molecule localization using experimental point spread functions. Nat. Methods 15, 367–369 (2018).
Xu, F. et al. Three-dimensional nanoscopy of whole cells and tissues with in situ point spread function retrieval. Nat. Methods 17, 531–540 (2020).
Pavani, S. R. P. et al. Three-dimensional, single-molecule fluorescence imaging beyond the diffraction limit by using a double-helix point spread function. Proc. Natl Acad. Sci. USA 106, 2995–2999 (2009).
Kirshner, H., Aguet, F., Sage, D. & Unser, M. 3-D PSF fitting for fluorescence microscopy: Implementation and localization application. J. Microsc. 249, 13–25 (2013).
Sandmeyer, A. et al. DMD-based super-resolution structured illumination microscopy visualizes live cell dynamics at high speed and low cost. 1–32 https://doi.org/10.1101/797670 (2019).
Zhanghao, K. et al. Super-resolution imaging of fluorescent dipoles via polarized structured illumination microscopy. Nat. Commun. 10, 4694 (2019).
Mortensen, K. I. & Flyvbjerg, H. ‘Calibration-on-the-spot’: How to calibrate an EMCCD camera from its images. Sci. Rep. 6, 28680 (2016).
Fry, G. A. Square-wave gratings convoluted with a Gaussian spread function. J. Opt. Soc. Am. 58, 1415–1416 (1968).
Acknowledgements
This work was funded by the Novo Nordisk Foundation Challenge Programme (NNF16OC0022166). We thank A. Kristensen for generously sharing microscopy components with us.
Author information
Authors and Affiliations
Contributions
H.F. and K.I.M. conceived the idea. M.S., R.M. and K.I.M. designed research. A.C.H. and R.M. built the experimental setup and performed experiments. M.S. and K.I.M. developed the theory. M.S. analyzed the data. K.I.M. supervised the data analysis. M.S. wrote the initial manuscript draft. Everybody discussed results and contributed to and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schmidt, M., Hundahl, A.C., Flyvbjerg, H. et al. Camera-based localization microscopy optimized with calibrated structured illumination. Commun Phys 4, 41 (2021). https://doi.org/10.1038/s42005-021-00546-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00546-y
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.