Abstract
Superconductivity induced by a magnetic field near metamagnetism is a striking manifestation of magnetically-mediated superconducting pairing. After being observed in itinerant ferromagnets, this phenomenon was recently reported in the orthorhombic paramagnet UTe2. Here we explore the phase diagram of UTe2 under two magnetic-field directions: the hard magnetization axis b, and a direction titled by ≃25-30° from b in the (b,c) plane. Zero-resistivity measurements confirm that superconductivity is established beyond the metamagnetic field Hm in the tilted-field direction. While superconductivity is locked exactly at fields either smaller (for H | | b), or larger (for H tilted by ≃27° from b to c), than Hm, the variations of the Fermi-liquid coefficient in the electrical resistivity and of the residual resistivity are similar for the two field directions. The resemblance of the normal states for the two field directions puts constraints for theoretical models of superconductivity and implies that some subtle ingredients must be in play.
Similar content being viewed by others
Introduction
Unconventional superconductivity is observed in an ever-growing number of correlated-electron systems1, ranging from heavy-fermion2,3, high-temperature cuprate4, iron-based pnictide and chalcogenide5, to the newly discovered nickelate6 and graphene-superlattice7 families. New unusual superconducting phases continue to be discovered, such as those reported during the last two decades in the ferromagnets UGe2, URhGe, and UCoGe8,9,10 with orthorhombic crystal structures. Instead of antiferromagnetic fluctuations, which are suspected to be the glue for superconductivity and to lead to a singlet order parameter in most heavy-fermion superconductors3, ferromagnetic fluctuations were proposed to drive the pairing mechanism of these ferromagnets, where the strong exchange field suggests that a spin-triplet superconducting order parameter with equal-spin pairing may be realized11. Nuclear-magnetic-resonance (NMR) experiments brought microscopic support for such triplet state and they further highlighted the role of magnetic fluctuations12,13. In these three systems, a magnetic field also leads to a re-entrance or reinforcement of superconductivity, and magnetic-field-induced ferromagnetic fluctuations are suspected to directly control the pairing strength, which can be qualitatively understood as the enhancement of a strong-coupling superconducting parameter λ with field11. A S-shape in the temperature dependence of the superconducting critical field Hc2 was observed in UGe2 under pressure with a magnetic field along the easy magnetization axis a14. Re-entrance or reinforcement of superconductivity occurs in the isostructural ferromagnets URhGe and UCoGe under a magnetic field applied along their hard-magnetic axis b15,16. In URhGe, field-induced superconductivity coincides with a metamagnetic transition at µ0Hm = 12 T, where enhanced magnetic fluctuations17,18 accompany a sudden rotation of the magnetic moments (from the initial easy direction c to the direction b)15. In this system, a Fermi-surface instability is observed at Hm, beyond which a polarized paramagnetic (PPM) regime is established19,20,21. In UCoGe, the situation is more subtle, since a metamagnetic transition occurs at a field µ0Hm ≃ 50 T much higher than that of ≃15 T at which the reinforcement of superconductivity is observed22.
Recently, superconductivity was found to develop in the paramagnetic heavy-fermion material UTe2 at temperatures below Tsc = 1.6 K23,24. This system crystallizes in an orthorhombic crystal structure with space group Immm (#71, \(D_{2h}^{25}\)) and is characterized by an anisotropic magnetic susceptibility [see Fig. 1(a)]. No sign of long-range magnetic order has been found down to the lowest temperatures (25 mK)25. For a magnetic field applied along the easy magnetic axis a, a large low-temperature magnetic susceptibility and a scaling plot of magnetization data were interpreted as the indication for a nearby ferromagnetic instability23. Following the observation of a large anisotropic upper critical field, which exceeds the normal paramagnetic limitation for all field directions23,24 and of a tiny change in the NMR Knight shift through Tsc26, a spin-triplet nature of superconductivity has been proposed23. The possibility of chiral spin-triplet superconductivity was suggested from scanning tunneling microscopy27 and Kerr-effect experiments28. However, while magnetic fluctuations were observed by NMR29 and muon-spin relaxation measurements25, evidence supporting their ferromagnetic nature is still lacking. Furthermore, the presence of antiferromagnetic fluctuations has been reported by inelastic neutron scattering30.
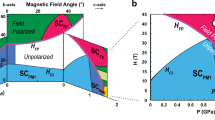
a Temperature-dependence of the inversed magnetic susceptibility 1/χ of UTe2 in magnetic fields H applied along the three main crystallographic directions a, b, and c. Inset: Temperature-dependence of the magnetic susceptibility χ for H||a, b, and c, in a log-log scale. b Low-temperature magnetic-field versus angle phase diagram of UTe2, in fields applied along variable directions from b to a (angle ϕ) and from b to c (angle θ). Two low-temperature paramagnetic regimes and identified: correlated paramagnetism (CPM) and polarized paramagnetism (PPM). SC1 is the low-field superconducting phase, and SC2 and SC-PPM are the superconducting phases induced by magnetic fields H||b and H tilted by 27 ± 5° from b in the (b, c) plane, respectively. Hc,2 is the critical superconducting field and Hm is the metamagnetic field. Data from by Ran et al.33 and Knebel et al.37 were plotted in this Figure.
In UTe2 at temperatures T < TCEP ≃ 7 K, a magnetic field applied along the hard-magnetic axis b induces a first-order metamagnetic transition at µ0Hm ≈ 35 T, which separates a low-field correlated paramagnetic (CPM) regime from a high-field PPM regime31,32,33. It is accompanied by sudden jumps ΔM ≈ 0.3–0.6 μB/U in the magnetization31,33 and Δρ ≈ 100 μΩ cm in the residual resistivity32, and by a large enhancement of the effective mass at Hm31,32,34. An empirical and almost universal relation 1 T ↔ 1 K between Hm and the temperature Tχmax ≈ 35 K at the maximum in the magnetic susceptibility35 is observed, as for a large number of heavy-fermion paramagnets36. It indicates that the CPM regime delimited by Hm and Tχmax is, within a first approximation, controlled by a single energy scale. For H || b, superconductivity is reinforced above 15 T and it abruptly disappears in the PPM regime above Hm33,37. Calorimetric studies showed the appearance of a second superconducting phase, labeled by SC2, under pressure in zero magnetic field38. A boundary between SC2 and the ambient-pressure and low-field superconducting phase SC1 was observed from tunnel-diode-oscillator measurements under pressure and magnetic field H || b39. The extrapolation of this boundary for p → 0 suggests that the superconducting phase SC2 induced under pressure and the superconducting region induced by a magnetic field H || b could be the same phase. In the following, we will label SC1 and SC2 the respective low-field and high-field superconducting regions for H || b. However, to date there is no definitive experimental evidence of a magnetic-field-induced transition between SC1 and SC2 at ambient pressure. An alternative picture without phase transition between SC1 and SC2 cannot be excluded, since the upturn of Hc2 could result from a tight balance between the orbital limitation and the increase of the coupling λ with field37. We further note that, at ambient pressure and zero magnetic field, a single superconducting transition was identified in23,24,40 but two separated superconducting transitions were reported in28,41.
Figure 1(b) presents a combination of low-temperature magnetic-field versus field-angle phase diagrams of UTe2 obtained by Ran et al.33 and Knebel et al.37 It summarizes the effect of magnetic fields applied in the (a, b) and (b, c) planes. A key property is that Hm is minimum for H || b. It strongly increases when the field is tilted from b towards the easy magnetic axis a, and exceeds the maximum applied field (60 T) for ϕ = (b, a) > 20°. The increase of Hm is softer when the field is tilted from b towards c, where it could be followed up to angles θ = (b, c) ≈ 50°. At small angles ϕ and θ, the field-reinforcement of superconductivity rapidly disappears. For the three field-directions a, b, and c, the low-temperature critical fields µ0Hc2,a ≈ 6 T, µ0Hc2,c ≈ 10 T, and µ0Hc2,b ≈ 15–20 T (i.e., the extrapolated value of µ0Hc2,b ignoring the field-reinforcement below 300 mK) delimiting the low-field superconducting phase SC1 are inversely-correlated with the low-temperature magnetic susceptibilities χa > χc > χb (see Fig. 1 and refs. 23,31,35). A similar inverse relation between the magnetic anisotropy and the anisotropy of Hc2 was observed in many other heavy-fermion superconductors, such as URu2Si242,43, CeCoIn544,45, UCoGe and URhGe11,46. Spectacularly, a second field-induced superconducting phase was reported in UTe2 for a field tilted from b towards c by an angle 20 < θ < 40°33. This phase, labeled here as SC-PPM, was observed only in the PPM regime, in fields higher than µ0Hm ≃ 40–45 T and up to more than 60 T33.
In the present work, we focus on a study by electrical resistivity of the superconducting phases SC2 and SC-PPM induced in UTe2 at ambient pressure, under a magnetic field applied either along b, or tilted by an angle θ ≃ 27 ± 5° from b towards c. In the initial report of the SC-PPM phase, the electrical resistivity was not exactly zero, likely due to a phase issue in the pulsed-field measurement and to deviations from isothermal measurements resulting from the use of fastly varying pulsed magnetic fields33. The almost isothermal conditions of our experiments using long-duration (rise = 70 ms, fall = 300 ms) magnetic-field pulses allow studying temperature-dependent effects in a high magnetic field. Our results show zero resistance in the SC-PPM phase, confirming its superconducting nature. We extract the full magnetic-field-temperature phase diagrams of UTe2 for H || b and H tilted by θ ≃ 27° from b to c. From a Fermi-liquid analysis we also determine the field-dependence of the residual resistivity ρ0 and estimate the variation of the effective mass m*47. These quantities show striking similarities for the two field-directions in contrast with the very different superconducting phase diagrams. In the discussion, elements resulting from experiments are summarized and confronted to the theoretical challenge to understand the nature of the field-induced superconducting phases in UTe2.
Results
Low-temperature and high-magnetic-field electrical resistivity
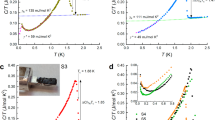
The magnetic-field variation of the electrical resistivity ρ of UTe2 single crystals, measured with a current injected along the a-direction, is presented in Fig. 2. Data obtained for the two magnetic field directions, H || b and H tilted by θ = 27 ± 5° from b in the (b, c) plane are shown in Fig. 2(a–b) and Fig. 2(c–d), respectively, for a large range of temperatures varying from 200 mK to 80 K. A comparison of field-upsweep and downsweep data (see Supplementary Note 1 and Supplementary Figs. 1–6) shows almost no heating of the samples by eddy currents in the low-temperature data, which were obtained in long-duration pulsed magnetic fields. At temperatures from T = 2.2 K to TCEP ≈ 5–6 K, at which a critical end-point is observed in the data, and under magnetic fields H || b (Fig. 2(a)) and H tilted by θ = 27 ± 5° (Fig. 2(c)), similar and sharp first-order step-like increases of ρ are observed at µ0Hm, which equals 34 and 45 T for the two field directions, respectively. For both directions, when the temperature is increased above TCEP, the sharp anomaly at Hm changes into a broad maximum, at a field also labeled Hm, which vanishes at temperatures higher than 30 K.
Figure 2(b) shows that, for H || b, field-induced superconductivity develops just below Hm, with an onset at a maximal temperature of 1.2 K and a zero-resistivity reached below the maximal superconducting temperature TSC ≃ 1 K. In spite of a non-zero-resistivity due to small out-of-phase contamination of the signal, this new set of data confirms, in magnetic fields extended up to 60 T, the two recent reports of field-reinforcement of superconductivity in UTe2 for H || b33,37. For H tilted by θ = 27 ± 5° from b in the (b, c) plane, Fig. 2(d) shows a zero-resistivity regime in fields higher than Hm. These data support the presence of a field-induced superconducting phase SC-PPM above Hm33. After an onset at a maximal temperature of 2 K, zero-resistivity is reached below the maximal superconducting temperature TSC ≃ 1.5 K, which is higher than the superconducting temperature reported for the field-induced phase for H || b. The magnetic field at which the zero-resistivity superconducting phase SC-PPM develops is locked to the value µ0Hm ≃ 45 T observed for T > TSC. Inside the CPM regime, the onset of the phase SC-PPM at ≃43 T precedes the zero-resistivity-state reached beyond Hm. We also confirm that the low-field superconducting phase SC1 is well-separated from the field-induced phase SC-PPM. At the lowest temperature, the phase SC1 vanishes at a moderate critical field of ≃10 T (see Fig. 1b).
Temperature-magnetic field phase diagrams and quantum critical fluctuations
Figure 3(a) presents the magnetic-field-temperature phase diagram extracted here for UTe2 in a field H || b, in agreement with ref. 37. Although the field-induced transition between SC1 and SC2 was not observed so far at ambient pressure, the phase diagram suggests that two different superconducting regimes exist with a transition or crossover at ≃15 T. The transition temperature TSC of SC2 is maximal at a magnetic field just below µ0Hm = 34 T. SC2 is presumably driven by the magnetic fluctuations induced on approaching the metamagnetic transition. These fluctuations also control the enhancement of the Sommerfeld coefficient γ in the heat capacity36 and of the coefficient A of the Fermi-liquid T2 term of the electrical resistivity32. We confirm here that SC2 is strictly bounded by Hm, at which the magnetization was found to suddenly increase and above which a PPM regime is reached31,33.
a Magnetic-field-temperature phase diagram of UTe2 in a magnetic field H||b. b Magnetic-field-temperature phase diagram of UTe2 in a magnetic field H tilted by 27 ± 5° from b in the (b, c) plane. Two low-temperature paramagnetic regimes and identified: correlated paramagnetism (CPM) and polarized paramagnetism (PPM). SC1 is the low-field superconducting phase, and SC2 and SC-PPM are the superconducting phases induced by magnetic fields H||b and H tilted by 27 ± 5° from b in the (b, c) plane, respectively. TSC is the critical superconducting temperature, Tχmax is the temperature at the maximum of the magnetic susceptibility, and Hm is the metamagnetic field. For the superconducting phases, colored points indicate the temperature at which zero-resistivity is reached and gray points indicate the temperature at the onset of the downwards deviation of the resistivity. CEP indicates the critical end-point of the first-order metamagnetic transition.
Figure 3(b) presents the magnetic field - temperature phase diagram extracted here for UTe2 in a field H tilted by θ = 27 ± 5° from b in the (b, c) plane. While the low-field superconducting phase SC1 vanishes at a critical field µ0Hc2 ≃ 10 T, µ0Hm reaches 45 T at low temperature for this field direction. When the temperature is increased, the behavior is similar to that reported for H||b: Hm loses its first-order character at the temperature TCEP ≈ 5–6 K. It transforms into a crossover at higher temperatures and finally disappears above 20–30 K. In agreement with the previously-published data33, the superconducting phase SC-PPM is only observed in fields higher than Hm, and up to a superconducting critical field higher than 60 T at low temperature. A maximal field-induced superconducting temperature TSC ≈ 1.5 K appears at a field close to Hm, emphasizing a direct link with the metamagnetic transition.
In many heavy-fermion magnets, a maximum of the effective mass is observed in the vicinity of a magnetic instability. It is commonly understood as resulting from the critical quantum magnetic fluctuations, coupled or not with a Fermi-surface instability48. Within a Fermi-liquid description, the electrical resistivity can be fitted by ρ(Τ) = ρ0 + AT2, and the A coefficient varies as the square of the effective mass m*. A Fermi-liquid picture is generally valid within first approximation, and deviations from the empirical law A ∝ m*2 can result from additional electronic effects, such as changes in carrier scattering, Fermi-surface and band structure, field-induced cyclotron motion of the carriers, etc. (see for instance this work49). In heavy-fermion systems, m* is mainly controlled by magnetic fluctuations related with the proximity of quantum magnetic instabilities. In several compounds, a non-Fermi-liquid deviation from this law is observed near quantum magnetic instabilities50. In other compounds, as CeRu2Si251, CeRh2Si252, and URhGe20, a T2 law in ρ(T) was observed down the lowest accessible temperatures at the pressure and/or magnetic-field instabilities. Recently, Fermi-liquid behaviors, including T2 laws in the electrical resistivity, were reported at the quantum instabilities of UTe2 under pressure38 and magnetic field H || b31,32,34. In continuity with these studies, fits to the electrical-resistivity data of UTe2 were done here for all fields investigated in the temperature windows 1.5 ≤ T ≤ 4.2 K for H || b, and 2.2 ≤ T ≤ 4.2 K for H tilted by θ = 27 ± 5° from b to c (see Supplementary Note 1 and Supplementary Fig. 7). As shown in Fig. 4(a–b), we find almost similar field-variations of A and ρ0 at Hm for the two field directions: while A increases by a factor ≃6 and passes through a maximum, ρ0 undergoes a sharp step-like enhancement, jumping from 15 to 80 µΩ.cm. The field-variation of A reported here for H || b, in good agreement with a previous report32, indicates a sharp and strong enhancement of the magnetic fluctuations at Hm. For H || b, a qualitatively similar enhancement of m* at Hm was found by applying a Maxwell relation to magnetization data31 and by direct heat-capacity measurements34.
a Magnetic-field variation of the quadratic coefficient A and b residual resistivity ρ0 extracted from Fermi-liquid fits to the electrical resistivity of UTe2 in a magnetic field H||b and in a magnetic field H tilted by 27 ± 5° from b in the (b,c) plane. Plots of c A and d ρ0 versus H/Hm for the two field-directions. Data are presented for both field-upsweeps and downsweeps. Details about the Fermi-liquid fits are given in Supplementary Note 1 and Supplementary Fig. 7.
Small differences between the two field-directions are visible from plots of A and ρ0 versus H/Hm [Fig. 4(c) and 4(d)]. While the variation of A through Hm is almost symmetric for H || b, it is slightly asymmetric for H tilted by θ = 27 ± 5° from b. For the tilted-field direction, A(H) is steeper for H < Hm and more gradual for H > Hm. As well, the decrease of ρ0 beyond Hm is more marked for H tilted by θ = 27 ± 5° from b. Beyond these small differences, the main result here is the robust finding that the variations of A and ρ0 are similar for the two field directions. New high-field experiments on a unique sample, using a rotation probe, are now needed for a complete angular study of the Fermi-liquid behavior.
Discussion
The ultimate goal would be to provide a full microscopic description of the different superconducting phases and their pairing mechanisms in UTe2. We are still far from this objective, but the experimental data presented here, in complement to those from ref. 33, offer a broad set of constraints for theories. The role of magnetic fluctuations for superconductivity is indicated by the maximum critical temperature of the reentrant phases observed very near to Hm for both field directions. A striking feature of the phase diagrams presented in Fig. 3(a–b) is that the superconducting phases SC2 for H || b and SC-PPM in a field H tilted by θ = 27 ± 5° from b towards c are bounded by the metamagnetic field Hm, with a substantial difference that the phase SC2 is pinned inside the CPM regime and it does not survive in the PPM regime while, inversely, the phase SC-PPM is pinned inside the PPM regime and does not develop in the CPM regime. A natural explanation would be that the pairing mechanism changes drastically on crossing the first-order line Hm, at which one would expect a difference in the nature of the critical magnetic fluctuations in the CPM and PPM regimes. This difference would change substantially for the two field-directions H || b and H tilted by 27° from b.
A rough estimation of the field-dependence of the pairing strength can be obtained from the Fermi-liquid analysis done above. A maximum of the quadratic coefficient A at Hm indicates an increase of the effective mass m*, presumably controlled by critical magnetic fluctuations. In the case of URhGe, A is maximum at Hm17, where critical magnetic fluctuations were evidenced by NMR18. A similar symmetrical enhancement of A is observed in many heavy-fermion systems at Hm, where drastic changes of magnetic fluctuations and Fermi surfaces were found53,54. In URhGe under pressure55, or in a magnetic field tilted away from b18, Hm increases and the maxima of Tsc and of the magnetic fluctuations remain glued to Hm. This suggests that field-reentrant superconductivity is induced by enhanced critical magnetic fluctuations at Hm. In a simple picture, the superconducting pairing strength λ increases as the effective mass m* in the proximity of Hm56,57. In UTe2, the fact that the enhancement of A is almost symmetric around Hm is puzzling with respect to the abrupt suppression of superconductivity for H || b, and its abrupt appearance for H tilted by θ = 27 ± 5° from b towards c. The abrupt disappearance/appearance of superconductivity at Hm could also result from a sudden change of the Fermi-surface. A Fermi-surface reconstruction is compatible with the large and sudden variation of the residual resistivity ρ0 at Hm for the two field directions, but also with the sign changes in the thermo-electric power and Hall coefficient at Hm for H || b58. However, our results raise a serious hurdle to both these pictures since the field-driven enhancement of A is very similar for H || b and H tilted by θ = 27 ± 5° from b to c. If it is an intrinsic property, the asymmetry in the field-variation of A for H tilted by 27° could suggest that the magnetic fluctuations are slightly more intense above Hm for this field direction. However, this effect would be too small to explain the differences between the phases SC2 and SC-PPM. The magnetization jumps at Hm are also very similar for H || b and H tilted by 27°33. Extra ingredients are, thus, needed to describe the field and angle domains of stability of these two field-induced superconducting phases.
Figure 5(a–c) presents views of the crystal structure of UTe2 where the magnetic uranium ions can be seen to form a ladder structure59. We highlight the family of reticular (and cleaving) planes of Miller indices (0 1 1), which contain sets of ladders having the smallest inter-ladder U–U distance (d3 = 4.89 Å). Interestingly, the direction n normal to these planes coincides, within the experimental uncertainty, with the field-direction along which the phase SC-PPM develops33. It lies in the (b, c) plane and has an angle θ = 23.7° with b. Figure 5(d) presents a view of the Brillouin zone. It emphasizes that the direction n in real space is equivalent to the direction k = (0 1 1) in reciprocal space. Although the connection with the pairing mechanism remains unclear, this coincidence may not be accidental and may constitute a possible line of approach for future theories. Indeed, the field-induced superconducting phases SC2 and SC-PPM may be sensitive to fine details of the Fermi-surface topology, in relation with high-symmetry directions. Further experimental studies, with a more accurate positioning of the samples (within misorientations Δθ, Δϕ < 1°), are now needed to test the robustness of the coincidence observed here.
a Elementary unit cell and identification of the four smallest U-U distances, b projection of the lattice structure in the (b, c) plane, c crystal structure extended to several unit cells emphasizing the network of two-leg ladders, and d Brillouin zone of UTe2. The vector n normal to a family of reticular (and cleaving) planes of Miller indices (0 1 1), with an angle θ = (b, n) = 23.7°, is indicated. These reticular planes are characteristic of the ladder structure. In reciprocal space, the corresponding wavevector k = (0 1 1), expressed in relative lattice units, is perpendicular to two planes of the Brillouin zone boundary.
In relation with the ladder structure, magnetic frustration has been invoked as a possible origin of the paramagnetic ground state in UTe2 at zero-field and ambient pressure, and a competition between ferromagnetic and antiferromagnetic configurations has been discussed59,60. Electronic-structure calculations pointed out that the ground state is sensitive to the Coulomb repulsion, and that the ferromagnetic and antiferromagnetic configurations are energetically-close59. The respective roles of ferromagnetic and antiferromagnetic fluctuations in UTe2 may, thus, be important for the superconducting phases. While UTe2 was first proposed to be nearly ferromagnetic23, the nature of the pressure-induced magnetic phase, initially reported in38, was not determined so far. Several studies suggested that UTe2 is not a simple nearly-ferromagnet and may be close to an antiferromagnetic instability41,61, which is supported by the observation of antiferromagnetic fluctuations30. At ambient pressure, the absence of metamagnetism in a magnetic field up to 55 T applied along the easy magnetic axis a31,32 indicates that UTe2 is at least not a conventional Ising paramagnet close to a ferromagnetic instability, unlike UGe2 under pressure62 and UCoAl at ambient pressure63. The negative Curie-Weiss temperatures extracted from the high-temperature magnetic susceptibility, for the three directions H || a, b, and c [see Fig. 1(a)], indicate antiferromagnetic exchange interactions (see also ref. 35). A broad maximum at the temperature Tχmax = 35 K in the magnetic susceptibility for H || b is also compatible with the onset of antiferromagnetic fluctuations, as observed in several heavy-fermion paramagnets36. Low-temperature downward deviations of the magnetic susceptibility for H || a,c (in comparison with its high-temperature behavior) are observed in the log-log plot shown in Inset of Fig. 1(a). These deviations confirm the formation of a heavy-fermion state below 50 K, which may coincide with the onset of antiferromagnetic fluctuations, possibly those observed by inelastic neutron scattering30. Interestingly, the high-temperature magnetic susceptibility for H || a varies as 1/T0.75 over more than one decade, from 20 to 300 K. However, further investigations are needed to understand this power-law behavior. Magnetic anisotropy, which drives the preferential direction of the magnetic fluctuations, is also suspected to play a significant role for superconductivity. The inverse relationship between the low-field magnetic anisotropy and the critical fields of the phase SC1 was emphasized in the introduction. The evolution of the magnetic anisotropy in a high magnetic field may also play a role for the stabilization of the field-induced superconducting phases.
The different superconducting regimes may correspond to different order parameters, with different sensitivities to a magnetic field. It has been generally assumed that all the superconducting phases in UTe2 have a triplet order parameter, mainly because of high values of the superconducting upper critical field, a small decrease of the NMR Knight shift below Tsc26 and a supposed proximity to ferromagnetism23,24,59,64. However, this still needs confirmation especially if, as pointed out above, antiferromagnetic fluctuations may play a much larger role than initially thought. The disappearance of superconducting phase SC2 as the PPM regime is entered for H || b could be related to the loss of magnetic fluctuations characteristic of the CPM regime. Thereafter, for H tilted by θ = 27 ± 5° from b to c, the phase SC-PPM could be a natural candidate for triplet superconductivity with no paramagnetic limitation. However, two questions remain: why this phase appears only for such a specific angular range, possibly in relation with the previous symmetry considerations, and especially why this phase does not develop in fields smaller than Hm? Interestingly, other superconducting phases develop in UTe2 under pressure combined with a magnetic field applied along the easy axis a61, and the resulting isobar magnetic-field-temperature phase diagrams have similar features than that reported for another compound with multiple superconducting phases, UPt3 at ambient pressure65.
A full understanding of the magnetic fluctuations and their feedback on the superconducting pairing undoubtedly requires the knowledge of the Fermi-surface and electronic structure of UTe2. As mentioned above, calculated Fermi surfaces strongly depend on the Coulomb repulsion U: for large values of U, two-dimensional Fermi surfaces along c similar to that of ThTe2 and corresponding to a localized f-electrons limit have been expected59,60,66. For quasi one-dimensional67 or quasi two-dimensional68,69 Fermi surfaces, Ginzburg-Landau theories, which neglect the role of magnetic fluctuations, also predict that the orbital limit could be suppressed for particular field directions. However, while angle-resolved-photo-emission-spectroscopy revealed a light low-dimensional band, they also showed the presence of a heavy three-dimensional band centered around the point Z of reciprocal space70. The observation of low-dimensional features in the bulk properties (for instance strongly-anisotropic electrical resistivity) are now needed to support a low-dimensional Fermi-surface model of superconductivity for UTe2.
Rich-phase diagrams were obtained for UTe2 under different field directions and pressures. Although the measurements presented here and in other works33,37,38,39,41,61,71 start to bring a clear picture of the complex phase diagram of UTe2, which includes multiple superconducting and magnetic phases, we are still far from a deep understanding of its electronic properties. A target is now to perform microscopic studies to identify the nature of the magnetic fluctuations and their change through Hm. In relation with these magnetic fluctuations, a challenge will be to identify the nearby long-range-ordered magnetic phases. The objective to characterize the Fermi-surface in the different phases is also emphasized. Beyond the need for solid experimental findings, theoretical developments are needed to describe the superconducting pairing mechanism(s) and order parameter(s). This is a stiff challenge, but the rare flurry of stunning phenomena observed in UTe2 fully justifies such forthcoming efforts.
Methods
Samples
Single crystals of UTe2 were prepared by the chemical vapor transport method with iodine as transport agent. Their structure and orientation was checked by single-crystal X-ray diffraction. A sharp bulk transition at Tsc = 1.6 K was indicated from specific heat measurements, while zero-resistivity at temperatures below Tsc was confirmed by zero-field AC resistivity measurements. Samples #5, #6, and #7, whose electrical-resistivity data are presented here, have similar residual-resistivity ratios ρ(300 K)/ρ(2 K) ≃ 25 to those of samples #1, #2, and #3 studied previously32,37, indicating similar sample qualities.
Pulsed-field experiments
Electrical-resistivity measurements were performed at the Laboratoire National des Champs Magnétiques Intenses (LNCMI) in Toulouse under long-duration pulsed magnetic fields, either up to 68 T (30 ms raise and 100 ms fall) and combined with an 4He cryostat offering temperatures down to 1.4 K, or up to 58 T (55 ms rise and 300 ms fall) and combined by a home-developed dilution fridge made of a non-metallic mixing chamber offering temperatures down to 100 mK. A standard four-probe method with currents I || a, at a frequency of 20–70 kHz, and a digital lock-in detection were used. Resistivity data were normalized so that the maximal value, at a temperature of ≈65 K and at zero-field, reaches 450 µΩ.cm (a different normalization lead to a maximum of 650 µΩ.cm in a previous work32). Normalization was made following absolute resistivity measurements on samples whose geometrical shape was known. The measurements in different field directions were done on different samples, and we cannot exclude that the small differences, as those seen in the variations of A and ρ0 extracted from a T2 law, have an extrinsic origin (they could result from a limit of reproducibility in our measurements). Concerning the tilted-field direction, the choice for an angle θ ≃ 27° was made following the initial study made by Ran et al.33, where electrical-resistivity measurements indicated that the phase SC-PPM is centered at a tilt angle θ ≃ 23.7°, while tunnel-diode-oscillator measurements showed that it is centered around θ ≃ 33°.
Data availability
The data that support the findings of this study are available from the corresponding author on reasonable request.
References
Stewart, G. R. Unconventional superconductivity. Adv. Phys. 66, 75–196 (2017).
Flouquet, J. On the heavy-fermion road. Prog. Low. Temp. Phys. 15, 139–281 (2005).
Pfleiderer, C. Superconducting phases of f-electron compounds. Rev. Mod. Phys. 81, 1551 (2009).
Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. J. Nat. 518, 179 (2015).
Johnston, D. C. The puzzle of high temperature superconductivity in layered iron pnictides and chalcogenides. Adv. Phys. 59, 803 (2010).
Li, D. et al. Superconductivity in an infinite-layer nickelate. Nature 572, 624 (2019).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43 (2018).
Saxena, S. et al. Superconductivity on the border of itinerant-electron ferromagnetism in UGe2. Nature 406, 587 (2000).
Aoki, D. et al. Coexistence of superconductivity and ferromagnetism in URhGe. Nature 413, 613 (2001).
Huy, N. T. et al. Superconductivity on the border of weak itinerant ferromagnetism in UCoGe. Phys. Rev. Lett. 99, 067006 (2007).
Aoki, D., Ishida, K. & Flouquet, J. Review of U-based ferromagnetic superconductors: comparison between UGe2, URhGe, and UCoGe. J. Phys. Soc. Jpn. 88, 022001 (2019).
Hattori, T. et al. Relationship between ferromagnetic criticality and the enhancement of superconductivity induced by transverse magnetic fields in UCoGe. J. Phys. Soc. Jpn. 83, 073708 (2014).
Manago, M. et al. Spin-triplet superconductivity in the paramagnetic UCoGe under pressure studied by 59Co NMR. Phys. Rev. B 100, 035203 (2019).
Sheikin, I. et al. Anisotropy and pressure dependence of the upper critical field of the ferromagnetic superconductor UGe2. Phys. Rev. B 64, 220503(R) (2001).
Lévy, F., Sheikin, I., Grenier, B. & Huxley, A. D. Magnetic field-induced superconductivity in the ferromagnet URhGe. Science 309, 1343 (2005).
Aoki, D. et al. Extremely large and anisotropic upper critical field and the ferromagnetic instability in UCoGe. J. Phys. Soc. Jpn. 78, 113709 (2009).
Miyake, A., Aoki, D. & Flouquet, J. Field Re-entrant superconductivity induced by the enhancement of effective mass in URhGe. J. Phys. Soc. Jpn. 77, 094709 (2008).
Tokunaga, Y. et al. Reentrant superconductivity driven by quantum tricritical fluctuations in URhGe: evidence from 59Co NMR in URh0.9Co0.1Ge. Phys. Rev. Lett. 114, 216401 (2015).
Yelland, E. A., Barraclough, J. M., Wang, W., Kamenev, K. V. & Huxley, A. D. High-field superconductivity at an electronic topological transition in URhGe. Nat. Phys. 7, 890 (2011).
Gourgout, A. et al. Collapse of ferromagnetism and fermi surface instability near reentrant superconductivity of URhGe. Phys. Rev. Lett. 117, 046401 (2016).
Sherkunov, Y., Chubukov, A. V. & Betouras, J. J. Effects of lifshitz transitions in ferromagnetic superconductors: the case of URhGe. Phys. Rev. Lett. 121, 097001 (2018).
Knafo, W. et al. High-field moment polarization in the ferromagnetic superconductor UCoGe. Phys. Rev. B 86, 184416 (2012).
Ran, S. et al. Nearly ferromagnetic spin-triplet superconductivity. Science 365, 684 (2019).
Aoki, D. et al. Unconventional Superconductivity in Heavy Fermion UTe2. J. Phys. Soc. Jpn. 88, 043702 (2019).
Sundar, S. et al. Coexistence of ferromagnetic fluctuations and superconductivity in the actinide superconductor UTe2. Phys. Rev. B 100, 140502(R) (2019).
Nakamine, G. et al. Superconducting properties of heavy fermion UTe2 revealed by 125Te-nuclear magnetic resonance. J. Phys. Soc. Jpn. 88, 113703 (2019).
Jiao, L. et al. Chiral superconductivity in heavy-fermion metal UTe2. Nature 579, 523 (2020).
Hayes, I. M., et al. Weyl superconductivity in UTe2, Preprint at arXiv:2002.02539.
Tokunaga, Y. et al. 125Te-NMR study on a single crystal of heavy fermion superconductor UTe2. J. Phys. Soc. Jpn. 88, 073701 (2019).
Duan, C. et al. Incommensurate spin fluctuations in the spin-triplet superconductor candidate UTe2. Phys. Rev. Lett. 125, 237003 (2020).
Miyake, A. et al. Metamagnetic transition in heavy fermion superconductor UTe2. J. Phys. Soc. Jpn. 88, 063706 (2019).
Knafo, W. et al. Magnetic-field-induced phenomena in the paramagnetic superconductor UTe2. J. Phys. Soc. Jpn. 88, 063705 (2019).
Ran, S. et al. Extreme magnetic field-boosted superconductivity. Nat. Phys. 15, 1250–1254 (2019).
Imajo, S. et al. Thermodynamic investigation of metamagnetism in pulsed high magnetic fields on heavy fermion superconductor UTe2. J. Phys. Soc. Jpn. 88, 083705 (2019).
Ikeda, S. et al. Single crystal growth and magnetic properties of UTe2. J. Phys. Soc. Jpn. 75(Suppl), 116 (2006).
Aoki, D., Knafo, W. & Sheikin, I. Heavy fermions in a high magnetic field. C. R. Phys. 14, 53 (2013).
Knebel, G. et al. Field-reentrant superconductivity close to a metamagnetic transition in the heavy-fermion superconductor UTe2. J. Phys. Soc. Jpn. 88, 063707 (2019).
Braithwaite, D. et al. Multiple superconducting phases in a nearly ferromagnetic system. Commun. Phys. 2, 147 (2019).
Lin, W.-C. et al. Tuning magnetic confinement of spin-triplet superconductivity, npj Quantum. NPJ Quant. Mater. 5, 68 (2020).
Cairns, L. P., Stevens, C. R., O’Neill, C. D. & Huxley, A. Composition dependence of the superconducting properties of UTe2. J. Phys.: Condens. Matter 32, 415602 (2020).
Thomas, S. M. et al. Evidence for a pressure-induced antiferromagnetic quantum critical point in intermediate valence UTe2. Sci. Adv. 6, eabc8709 (2020).
Palstra, T. T. et al. Superconducting and magnetic transitions in the heavy-fermion system URu2Si2. Phys. Rev. Lett. 55, 2727 (1985).
Bastien, G. et al. Fermi-surface selective determination of the g-factor anisotropy in URu2Si2. Phys. Rev. B 99, 165138 (2019).
Petrovic, C. et al. Heavy-fermion superconductivity in CeCoIn5 at 2.3 K. J. Phys.: Condens. Matter 13, L337–L342 (2001).
Howald, L., Knebel, G., Aoki, D., Lapertot, G. & Brison, J.-P. The upper critical field of CeCoIn5. N. J. Phys. 13, 113039 (2011).
Braithwaite, D. et al. Dimensionality driven enhancement of ferromagnetic superconductivity in URhGe. Phys. Rev. Lett. 120, 037001 (2018).
Kadowaki, K. & Woods, S. B. Universal relationship of the resistivity and specific heat in heavy-Fermion compounds. Solid State Commun. 58, 507 (1986).
von Löhneysen, H., Rosch, A., Vojta, M. & Wölfle, P. Fermi-liquid instabilities at magnetic quantum phase transitions. Rev. Mod. Phys. 79, 1015–1075 (2007).
Moriya, T. & Ueda, K. Spin fluctuations and high temperature superconductivity. Adv. Phys. 49, 555–606 (2000).
Stewart, G. R. Non-Fermi-liquid behavior in d-and f-electron metals. Rev. Mod. Phys. 73, 797–855 (2001).
Daou, R., Bergemann, C. & Julian, S. R. Continuous evolution of the fermi surface of CeRu2Si2 across the metamagnetic transition. Phys. Rev. Lett. 96, 026401 (2006).
Knafo, W. et al. Three-dimensional critical phase diagram of the Ising antiferromagnet CeRh2Si2 under intense magnetic field and pressure. Phys. Rev. B 95, 014411 (2017).
Raymond, S. et al. Magnetic instabilities in CeRu2Si2 compounds. Phys. B 259-261, 48 (1999).
Flouquet, J., Haen, P., Raymond, S., Aoki, D. & Knebel, G. Itinerant metamagnetism of CeRu2Si2: bringing out the dead. Comparison with the new Sr3Ru2O7 case. Phys. B Condens. Matter 319, 251 (2002).
Miyake, A., Aoki, D. & Flouquet, J. Pressure evolution of the ferromagnetic and field re-entrant superconductivity in URhGe. J. Phys. Soc. Jpn. 78, 063703 (2009).
Eliashberg, G. Interactions between electrons and lattice vibrations in a superconductor. Sov. Phys. JETP-USSR 11, 696–702 (1960).
Bulaevskii, L. N., Dolgov, O. V. & Ptitsyn, M. O. Properties of strong-coupled superconductors. Phys. Rev. B 38, 11290–11295 (1988).
Niu, Q. et al. Evidence of fermi surface reconstruction at the metamagnetic transition of the strongly correlated superconductor UTe2. Phys. Rev. Res. 2, 033179 (2020).
Xu, Y., Sheng, Y. & Yang, Y.-f. Quasi-two-dimensional fermi surfaces and unitary spin-triplet pairing in the heavy fermion superconductor UTe2. Phys. Rev. Lett. 123, 217002 (2019).
Ishizuka, J., Sumita, S., Daido, A. & Yanase, Y. Insulator-metal transition and topological superconductivity in UTe2 from a first-principles calculation. Phys. Rev. Lett. 123, 217001 (2019).
Aoki, D. et al. Multiple superconducting phases and unusual enhancement of the upper critical field in UTe2. J. Phys. Soc. Jpn. 89, 053705 (2020).
Taufour, V., Aoki, D., Knebel, G. & Flouquet, J. Tricritical point and wing structure in the itinerant ferromagnet UGe2. Phys. Rev. Lett. 105, 217201 (2010).
Aoki, D. et al. Ferromagnetic quantum critical endpoint in UCoAl. J. Phys. Soc. Jpn. 80, 094711 (2011).
Metz, T. et al. Point-node gap structure of the spin-triplet superconductor UTe2. Phys. Rev. B 100, 220504(R) (2019).
Hasselbach, K., Taillefer, L. & Flouquet, J. Critical point in the superconducting phase diagram of UPt3. Phys. Rev. Lett. 63, 93 (1989).
Harima, H. How to obtain fermi surfaces of UTe2. JPS Conf. Proc. 29, 011006 (2020).
Lebed, A. G. & Sepper, O. Quantum limit in a magnetic field for triplet superconductivity in a quasi-one-dimensional conductor. Phys. Rev. B 90, 024510 (2014).
Mineev, V. Reentrant superconductivity in UTe2. JETP Lett. 111, 715–719 (2020).
Lebed, A. G. Restoration of superconductivity in high magnetic fields in UTe2. Mod. Phys. Lett. B 34, 2030007 (2020).
Miao, L. et al. Low energy band structure and symmetries of UTe2 from Angle-resolved Photoemission Spectroscopy. Phys. Rev. Lett. 124, 076401 (2020).
Knebel, G. et al. Anisotropy of the upper critical field in the heavy-fermion superconductor UTe2 under pressure. J. Phys. Soc. Jpn. 89, 053707 (2020).
Acknowledgements
We acknowledge A. Miyake, J. Béard, F. Hardy, J.-P. Brison, K. Ishida, Y. Tokunaga, Y. Yanase, and H. Harima for useful discussions. This work at the LNCMI was supported by the “Programme Investissements d’Avenir” under the project ANR-11-IDEX-0002- 02 (reference ANR-10-LABX-0037-NEXT). We acknowledge the financial support of the Cross-Disciplinary Program on Instrumentation and Detection of CEA, the French Alternative Energies and Atomic Energy Commission, and KAKENHI (JP15H05882, JP15H05884, JP15K21732, JP16H04006, JP15H05745, JP19H00646).
Author information
Authors and Affiliations
Contributions
Samples were grown by G.L. in close collaboration with D.A. They were characterized in zero and low fields by G.L., M.V., D.B., and G.K. Samples measured in pulsed fields were prepared by M.V. Experiments in pulsed magnetic field were performed by W.K., M.N., and A.Z. Data were analyzed by W.K. The paper was written by W.K. and D.B., with contributions from all of the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Knafo, W., Nardone, M., Vališka, M. et al. Comparison of two superconducting phases induced by a magnetic field in UTe2. Commun Phys 4, 40 (2021). https://doi.org/10.1038/s42005-021-00545-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00545-z
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.