Abstract
A unified fundamental understanding of interfacial thermal transport is missing due to the complicated nature of interfaces. Because of the difficulty to grow high-quality interfaces and lack of materials characterization, the experimentally measured thermal boundary conductance (TBC) in the literature are usually not the same as the ideally modelled interfaces. This work provides a systematic study of TBC across the highest-quality (atomically sharp, harmonic-matched, and ultraclean) epitaxial (111) Al||(0001) sapphire interfaces to date. The comparison of measured high TBC with theoretical models shows that elastic phonon transport dominates the interfacial thermal transport and other mechanisms play negligible roles. This is confirmed by a nearly constant transmission coefficient by scaling the TBC with the Al heat capacity and sapphire heat capacity with phonon frequency lower than 10 THz. Finally, the findings in this work will impact applications such as electronics thermal management, thermoelectric energy conversion, and battery safety.
Similar content being viewed by others
Introduction
Thermal transport across interfaces at macroscopic length-scales is described by the interfacial form of Fourier’s law: thermal boundary conductance (TBC, G) defines a finite temperature drop (ΔT) for a given heat flux (Q) across an interface (G = Q/ΔT). This temperature drop was first observed across a copper and liquid helium interface at extremely low temperatures by Kapitza in 19411,2. Experimental studies of interfacial thermal transport did not move to higher temperatures until late 1970s when a transient hot-strip method was developed3. After that, several more measurements on solid–solid interfaces were reported in 1980s and 1990s with the modifications of the hot-strip method and the development of the picosecond transient thermoreflectance technique4,5,6,7,8. When time-domain thermoreflectance (TDTR) was developed, the experimental research on interfacial heat transport started to attract great attention9,10,11,12,13,14,15. Different factors, such as interfacial bonding15,16,17, interfacial mixing18,19, pressure11,14, surface chemistry20,21, crystalline orientation22,23, roughness13, and interfacial disorder24,25, were found to affect TBC, which highlights the complicated nature of interfacial thermal transport.
To explain the experimental results, theories of interfacial thermal conductance have been developed since the 1950s, such as the acoustic mismatch model (AMM) and the diffuse mismatch model (DMM)4,5,26. More recently, other theoretical tools were used to calculate TBC, for instance, equilibrium/non-equilibrium molecular dynamics (MD)27,28, interface conductance modal analysis (ICMA)29, wave packet method30, atomistic Green’s function (AGF)31,32, and non-equilibrium Landauer approach33. Due to the complicated nature of interfaces, most of the theoretical calculations cannot capture the detailed features of the interface. It still remains an open question whether the modeled interfaces are the same as the measured ones in most previous works due to the lack of detailed simultaneous material and thermal characterization of the interfaces34. This is especially true for metal–non-metal interfaces because of the complicated interfacial structures and multiple carrier transport mechanisms near the interfaces. Metal growth on non-metal substrates, usually by sputtering or evaporation, suffers from problems like chemical reaction or interfacial mixing with substrates during deposition processes, the inclusion of an oxide or contaminating layers at the interface, polycrystalline metal films with a mixture of different orientations, or poor adhesion with substrates18,24,35,36. These result in the growth of metal–non-metal interfaces to deviate from the ideal interface often assumed in theoretical modeling, so direct comparison between theoretical and experimental results limits our ability to draw accurate conclusions37,38.
In addition, interfacial thermal transport can involve multiple fundamental transport mechanisms, including elastic and inelastic phonon transport across the interface, and electron–phonon coupling in the metal and across the interface39,40,41,42. The relative contributions of these mechanisms to TBC remain unclear and are still an open question39,43. For instance, theoretical calculations show electrons on the metal side can pass some energy directly to phonons on the non-metal side, whereas experiments show that a 400-fold change in electronic density for otherwise similar metals on the metal side does not impact TBC significantly6,12,42,43. Some efforts have been made to study high-quality epitaxial interfaces9,34,44. Costescu et al.9 reported the TBC of epi-grown TiN on MgO and Al2O3 substrates by reactive magnetron sputtering, but no interfacial characterizations were performed to check the quality of the grown interfaces. Some other works used Si as the grown substrates while the chemically active nature of Si hinders obtaining ultraclean and atomically sharp interfaces with any air exposure or if the vacuum is not high enough34,44. Furthermore, Ye et al.34 deposited metals on Si substrates first, and then annealed the samples to induce reaction growth of metal silicide, which is difficult to control the sharpness and atomic diffusion near the interfaces. However, very few computational methods can take interface non-idealities into consideration45,46.
In this work, we fill the gap by epitaxially growing (111) Al on (0001) ultraclean sapphire substrates by molecular beam epitaxy (MBE). The Al–sapphire system is particularly suitable for benchmarking because MBE enables single atomic layer control during the sample growth, the sapphire substrates are atomically smooth and easily cleaned by baking at high temperatures in ultrahigh vacuum (UHV) conditions, ensuring no surface oxidation during baking and no reaction with Al during growth43. The Al–sapphire interfaces in this work are the highest-quality interfaces to date for studying metal–non-metal interfacial thermal transport. Simultaneous structural characterizations are performed with a transmission electron microscope (TEM) and X-ray diffraction (XRD). The calculated TBC by AGF and non-equilibrium Landauer approaches are compared with experimental data over a temperature range of 80–480 K. The phonon and electron transport mechanisms across interfaces and their contributions to TBC are discussed. Our work advances the field by providing a systematic study of high-quality interface growth, detailed materials characterizations showing ultraclean interfacial structure and perfect crystal orientations, accurate thermal measurements from three different groups, and newly developed theoretical models.
Results
Interface structure characterizations
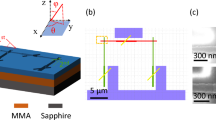
Two samples (Sub100 and Sub200) were studied in the round robin analysis in this work. The substrate temperature for Al growth was kept at 373 K for sample Sub100 and at 473 K for Sub200, whereas all the other growth conditions remained the same. More details about MBE sample growth can be found in the Methods section. A key step is that the sapphire was cleaned through a high temperature annealing step in UHV prior to the epitaxial deposition of the Al in-situ by MBE. Figure 1a shows the XRD patterns of samples Sub100 (the peaks observed for Sub200 are the same as observed for Sub100). The results show that the Al films are effectively single crystalline with the presence of twins. A standard 2θ:ω scan shows only reflections from Al (111) planes [(111) and (222) reflections] and the sapphire (0001) planes [(0006) and (000 12) reflections]. As shown in Fig. 1b, Phi scans of the Al (220) and the sapphire (1123) demonstrate that the epitaxial alignment is Al [112] || Al2O3 [1120], which fits with ±Al [110] || Al2O3 [1010]. Twinning is observed through the phi scans (there are peaks every 60°), showing that the layers include a Σ3 twin-related boundaries (180° rotation around the surface (111)). The peak width (FWHM) for the sapphire (1123) reflections is <0.1°. The Al (220) reflection FWHM is about 0.43°; while this is larger than the substrate peak widths, but still small enough to preclude high angle grain boundaries. Figure 1c shows an AFM image of the smooth Al surface and the RMS roughness for a 5 µm × 5 µm area are 0.125 nm for Sub200. Additional AFM image can be found in Supplementary Fig. 2. Figure 1d shows a cross-section high-resolution TEM (HRTEM) image of the Al–sapphire interface. The orientations of the Al and sapphire are cross-plane [111] Al||[0001] Al2O3 and in-plane [110] Al||[1010] Al2O3. These orientations are selected because of the relatively small lattice mismatch (4%) and similar crystalline structure, as shown in Supplementary Fig. 1. We see a sharp, distinct, and well-matched Al–sapphire boundary with evidence of only a sub-nm interfacial re-arrangement47. Electron back-scattered diffraction measurements (EBSD) (in Supplementary Fig. 3) confirm the film is completely (111) oriented with the Σ3 twin boundaries and the non-twinned regions extend as much as several tens of microns. More characterization in the Supplementary Fig. 4 also shows that the Al films have no strain. We note that these dimensions are more indicative of a high-quality crystalline film than those had been previously obtained for low temperature Al grown on sapphire48. These characteristics support the contention that the Al–sapphire interface is an ideal interface, which could be compared with modeling results directly.
a X-ray diffraction (XRD) patterns of Sub100 on a log scale. b Phi scans (220) Al and (1123) Al2O3. c Atomic force microscopy (AFM) images of Al surface. The length scale bar on the image is 1.0 Root-mean-square (RMS) roughness for a 5 µm × 5 µm area are 0.125 nm for Sub200. The color represents surface roughness shown by the color bar (−1 to 1 nm). d High-resolution transmission electron microscopy (HRTEM) cross-section image of Al–sapphire interface: cross-plane [111] Al ||[0001] Al2O3 and in-plane [110] Al ||[1010] Al2O3. We see a sharp and distinct Al–sapphire interface. The length scale bar is 5 nm.
Phonon transport across Al–sapphire interfaces
Figure 2a shows the phonon density of state (DOS) of Al and sapphire calculated with density-functional theory (DFT). The maximum phonon frequency of sapphire (about 25 THz) is much higher than that of Al (about 10 THz). If only considering elastic phonon scattering, phonons with frequencies between 10 and 25 THz in sapphire do not contribute to TBC. The thermal resistance circuit of thermal transport across Al–sapphire interface is shown in Fig. 2b. Electrons dominate thermal transport in metals, whereas phonons dominate in non-metals. For thermal transport across metal–non-metal interfaces, thermal energy carried by electrons in the metals is forced to be transferred to phonons in metals first because there are no free electrons in the non-metal side. Then phonons in the metals transfer energy across the interface to phonons in non-metals through elastic and inelastic processes. Near the Al–sapphire interface, we assume that the boundary condition for electron transport is adiabatic, whereas phonons in the Al side can transmit through the interface to the sapphire side11,12,41. Electrons usually transfer energy to electrons much more easily than to phonons. When applying a temperature difference across the interface, electrons in Al cannot transfer thermal energy to free electrons in the sapphire as there are no free electrons in sapphire. The thermal energy of the electrons are forced to transfer to phonons in Al. The temperature of electrons in the Al are different from the temperature of phonons in the Al near the interface, known as the two-temperature model. The temperature difference between the near-interface electrons and phonons in the Al side is a strong local non-equilibrium, which corresponds to an electron–phonon coupling thermal resistance in Al. Phonons in the Al side transfer energy to phonons in the sapphire side through elastic and inelastic channels. In addition, some theoretical calculations show electrons in the metal side could directly pass energy to phonons in the non-metal side, whereas some other calculations and experimental data show that this cross-interface electron–phonon coupling does not contribute to TBC significantly6,12,39,42,49. We add this possible heat transfer channel in Fig. 2b as well.
a Phonon density of states (DOS) of Al and sapphire. b Thermal circuit of Al–sapphire interfaces. c Comparison of temperature-dependent Al–sapphire TBC of samples Sub100 and Sub200 with measured TBC values in the literature: Hopkins I22, Stoner6, and Hopkins II50. d Comparison of measured Al–sapphire TBC with theoretical values calculated by AGF and non-equilibrium Landauer approach. The error bars are calculated by a Monte Carlo method.
The measured TBC of Al–sapphire interfaces are shown in Fig. 2c, and literature values are included as comparison. The TBC values were measured and consistent results were obtained among different university groups in the round robin. The measured TBC of Sub100 is the same as that of Sub200, indicating the substrate temperature during growth does not affect either the thermal properties or the structure of Al–sapphire interfaces. The measured TBC in this work is larger than all the other Al–sapphire TBC values in the literature6,22,50. This may be a result of the impact of the interface non-idealities of Al–sapphire grown by other methods on TBC. This may also give us new insight into the temperature dependence of the TBC of Al–sapphire interfaces and requires additional analysis of imperfect interfaces that can exist when grown by other methods. For instance, the measured TBC reaches a plateau above room temperature, which has a different trend from the measured values in the literature50 in which the increased TBC with increasing temperature at high temperatures was attributed to inelastic phonon scattering. Many factors, such as crystalline orientations, roughness, and interfacial disorder or contamination, jointly affect TBC of Al–sapphire interfaces. This highlights the importance of a benchmarking study on TBC of ideal interfaces, which cannot only be used to validate theoretical thermal models across perfect interfaces, but also act as a reference when studying how other factors impact TBC.
As shown in Fig. 2d, thermal modeling results are compared with experimental TBC values. The relative percent derivations of the measured TBC and calculated TBC are included in the Supplementary Fig. 5. Intrinsic Landauer TBC is calculated with a non-equilibrium Landauer approach where typical Landauer formula with DMM are used with further temperature corrections, which address the non-equilibrium effect of phonon transport near the interfaces. Intrinsic Landauer TBC assumes incident phonons have the same modal equivalent equilibrium temperature. More details about the non-equilibrium Landauer approach can be found in the Methods section and ref. 33. The small difference in AGF results between our result and ref. 51 should be attributed to different force constants. Here we used DFT calculation to generate force constants while ref. 51 generated the force constants via empirical lattice dynamics calculations. Both non-equilibrium Landauer approach and AGF account for quantum effect of phonon transport at the interfaces, whereas they do not include inelastic contribution to TBC in the calculation. At low temperatures, TBC increases with temperature because of the increasing phonon population involved interfacial thermal transport. When temperatures go above the Debye temperature of Al (428 K), the TBC reaches a plateau because the phonons in the Al side are fully excited52.
As shown in Fig. 2b, several thermal transport mechanisms are involved in interfacial heat transport. The good agreement between experimental data and theoretical values calculated by AGF and non-equilibrium Landauer approaches suggests that elastic phonon transport across the interface is dominant. All the other thermal transport mechanisms are negligible. AGF and non-equilibrium Landauer approach only consider elastic process. The electron–phonon coupling thermal resistance in Al is not large as well due to the large electron–phonon coupling constant of Al. We will discuss the role of each heat transfer mechanism below.
First, electron–phonon coupling in the Al side could result in a thermal resistance in series with the interfacial phonon–phonon thermal resistance41. The thermal resistance can be estimated as \(1/\sqrt {\kappa _{\mathrm{p}}G_{{\mathrm{ep}}}}\)41. Here, κp and Gep are the lattice thermal conductivity and electron–phonon coupling constant of Al. The electron–phonon energy transfer coefficient (Gep) is independent of temperature41,53,54 and its value at room temperature is 5.38 × 1017 W m−3 K−152. κp of Al at room temperature is 11 W m−1 K−1 based on first-principle calculations52,55. We also noticed that some other measurements showed temperature dependence of electron–phonon coupling constant in Cu before but here we consider that of Al as temperature independent56. The thermal resistance derived from electron–phonon coupling in Al is 0.4 m2 K GW−1, 13.6% of the measured overall thermal resistance across Al–sapphire interfaces. First-principle calculations showed that the Al phonon thermal conductivity decreases with increasing temperature in this temperature range52,55. As the temperature decreases, the lattice thermal conductivity increases, leading to a reduced electron–phonon coupling thermal resistance. The phonon–phonon TBC decreases with temperature, leading to a larger phonon–phonon thermal resistance. As a result, the effect of the electron–phonon coupling thermal resistance on overall TBC would become smaller at low temperatures. However, for temperatures comparable or higher than the Debye temperature of Al (428 K), the lattice thermal conductivity Al decreases slightly with increasing temperature52. The effect of electron–phonon coupling thermal resistance in the metal side could increase slightly, but we did not observe clear TBC change due to the effect of this mechanism in our experimental results.
In terms of cross-interface electron–phonon coupling for Al–sapphire interface, we tend to believe that it does not contribute to TBC significantly because the measured TBC is so close to the elastic phonon–phonon TBC for the whole-temperature range, especially for low temperatures where inelastic phonon contribution and electron–phonon coupling thermal resistance in the metal are not important. This cross-interface electron–phonon coupling is an additional thermal channel across the interface, which could increase TBC. However, the modeled TBC by AGF and non-equilibrium Landauer approach are slightly larger than the measured TBC at low temperatures. Furthermore, a recent theoretical work shows that this cross-interface coupling effect for Si–Cu interface contribute slightly to the overall TBC49. Other previous experimental measurements also show that cross-interface electron–phonon coupling is not important for interfacial thermal conductance6,12 even though some calculations show the opposite42,57,58.
Below, we will discuss temperature dependence of inelastic processes on TBC. Temperature affects phonon transport in three aspects: phonon energy distribution, phonon population, and phonon scattering. Increased temperature leads to the shifts of phonon energy distribution to higher energy, increased phonon population, and stronger anharmonicity because of atoms displacing further away from their equilibrium positions. All these changes of phonons with increased temperature result in stronger inelastic phonon scattering so the inelastic processes are strongly temperature-dependent. The scattering rates of anharmonic three-phonon scattering and four-phonon scattering in bulk solids are strongly temperature-dependent (proportional to temperature and temperature square, respectively)59,60. It is generally considered that inelastic processes have negligible contributions to thermal transport at low temperatures38,61. When low-energy phonons are excited on both sides of the interface, elastic processes contribute to thermal transport across the interface dominantly and the temperature dependence of the conductance tracks the temperature dependence of the total heat capacity from the material with lower Debye temperature (A) and/or the phonon heat capacity from the other-side material (B) within the same phonon frequency range. This is the case of our Al–sapphire interfaces.
When temperature increases to be higher than the Debye temperature of A, the contribution of elastic processes to TBC gradually reaches a plateau because the phonons in A are fully excited. The high-energy phonons excited in the B are not involved in the interfacial thermal transport via elastic processes because there are no corresponding phonons with the same energy in A. That’s why we observed a nearly constant Al–sapphire TBC above the Debye temperature of Al (428 K). Inelastic processes happen at high temperatures when a high-energy phonon in B breaks into multiple low-energy phonons, which have the same energy as the phonons in A62,63,64. This opens an additional channel for interfacial thermal transport and increase the TBC at high temperatures39,62,64. An increased TBC with increasing temperature instead of a constant TBC is observed at high temperatures if inelastic processes have important roles12,34,38,39,50. Apparently, we did not observe an increased TBC with increasing temperature at high temperatures for the Al–sapphire interfaces. Thus, inelastic processes have negligible contributions to the Al–sapphire TBC.
As shown in Fig. 2b, electron–phonon coupling in Al adds additional thermal resistance and reduces the overall TBC, whereas inelastic phonon contribution provides an additional thermal channel, which increases TBC. The inelastic phonon processes and the electron–phonon coupling thermal resistance in Al at high temperatures thus may counteract with each other. This contradicts the case of metal–diamond interfaces, where inelastic contribution to TBC is so large that the measured TBC is greatly higher than the radiation limit (the maximum TBC only considering elastic contribution)12,40. It may result from the high phonon DOS mismatch of metal and diamond. But it should be noted that the conclusion about metal–diamond interfaces needs to be revisited because of the unknown interfacial structure of these interfaces. In addition, researchers reported measured or calculated TBC of several other epi-interfaces, such as silicon–metal silicide interfaces and AlN/GaN interfaces, and they showed inelastic contributions are important34,39,65. So we think the contributions of inelastic processes should highly depend on materials and interface qualities.
Phonon transmission across Al–sapphire interfaces
For a single phonon mode traveling across an interface, the heat flux equals the phonon energy times the phonon velocity and transmission coefficient. If the temperature difference across the interface is small, TBC contributed by this phonon mode is the product of its heat capacity, phonon velocity, and transmission coefficient. Here, an average value of the product of phonon velocity (v) and transmission coefficient (τ) of all the phonon modes can be obtained by dividing TBC with volumetric heat capacity (Cv), namely, 〈ντ〉/3 = TBC/Cν. Here, the factor of 3 in the formula is derived from three directions and 〈 〉 means the average over all the phonon modes. As shown in Fig. 3a, very surprisingly, 〈ντ〉/3 is almost a constant over the whole-temperature range except the two lowest temperature points when we scale TBC with the Al heat capacity and sapphire heat capacity with phonon frequency lower than the max phonon frequency of Al (~10 THz). The corresponding data from non-equilibrium Landauer and AGF are also included as comparison. The relative derivations can be found in Supplementary Fig. 5. Phonon velocity is very weakly dependent on temperature. As a result, the average transmission coefficient is almost a constant for different temperatures. This validates theoretical modeling methods such as the AGF and the non-equilibrium Landauer approaches where transmission coefficient is considered to be independent of temperature for each phonon mode. This strongly supports that TBC is determined by the phonon population on the Al side and phonon contribution dominates interfacial thermal transport across Al–sapphire interfaces. The heat capacity-like TBC hints that phonons with frequency higher than the Al max phonon frequency (10–25 THz) does not contribute much to TBC. The high frequency phonons cannot transmit across interface through elastic processes and cannot contribute to TBC, which confirms that inelastic phonon contribution to TBC is negligible in interfacial thermal conductance of Al–sapphire interfaces.
a Thermal boundary conductance (TBC) scaled with volumetric heat capacity of Al and sapphire with phonon frequency <10 THz for samples Sub100 and Sub200. The lines are thermal boundary conductance (TBC) from the non-equilibrium Landauer approach and atomistic Green’s function (AGF) for comparison. The relative derivations are shown in Supplementary Fig. 5. b Temperature dependence of measured sapphire thermal conductivity. The “Cahill” data are from ref. 66 and the “Monchamp” data are from ref. 67 The error bars are calculated by a Monte Carlo method.
The temperature dependence of the measured sapphire thermal conductivity is shown in Fig. 3b. For Sub100 and Sub200, TDTR measurements are more sensitive to cross-plane direction so the measured thermal conductivity is perpendicular to the c-plane. The measured room temperature value is 32.5 W m−1 K−1, very close to the room temperature value (33 W m−1 K−1) in the ref. 67 as shown in the inset of Fig. 3b. The thermal conductivity of sapphire is weakly anisotropic for parallel or perpendicular to the c-plane. Sapphire with a crystal orientation parallel to the c-plane has a slightly larger thermal conductivity (35 W m−1 K−1 at room temperature). Reference66 did not include crystal orientation information in the paper but its measured value is very close to the measured thermal conductivity of sapphire with a crystal orientation parallel to the c-plane in ref. 67, as shown in the inset of Fig. 3b. Therefore, we speculate that the crystal orientation is parallel to the c-plane. Our temperature-dependent measured sapphire thermal conductivity matches well with the values in ref. 66 and we attribute the small difference to the weak anisotropy.
Discussion
This work provided a systematical benchmark study of interfacial thermal conductance across well-controlled epitaxial (111) Al||(0001) sapphire interfaces with simultaneous structural and thermal characterizations. The measured high TBC is compared than the other Al–sapphire TBC reported in the literature. The analysis of the result presented in this work relied greatly on the concurrent materials and thermal characterization. By having ultraclean epitaxially grown Al–sapphire interfaces, we determined that atomistic Green’s function (AGF) and a non-equilibrium Landauer approaches were sufficient for predicting the TBC of Al–sapphire interfaces. The results show that elastic phonon scattering dominates interfacial thermal conductance of Al–sapphire interfaces. Inelastic phonon scattering, electron–phonon coupling within the metal and across interface have negligible roles. The estimated electron–phonon coupling thermal resistance within Al is about 13.6% of the overall thermal resistance but we did not observe clear TBC change due to this effect. The temperature independence of Al–sapphire TBC at high temperatures suggests that the effect of inelastic phonon scattering is negligible, especially at high temperatures. By scaling TBC with the Al heat capacity and sapphire heat capacity with phonon frequency lower than the Al max phonon frequency, a nearly constant transmission coefficient is observed, indicating the phonon population in the Al side determines the Al–sapphire TBC. This nearly constant transmission coefficient validates the assumptions in AGF and non-equilibrium Landauer calculations. This demonstrates a method for characterizing the interfacial thermal conductance across metal–non-metal interfaces. It has enabled a quantitative study of TBC to validate theoretical models, and acts as a benchmark when studying how other quantities impact TBC.
Methods
Sample preparation
In this study, ~80 nm Al was deposited on high temperature annealed sapphire substrates in a Riber 32 MBE system. A multi-step annealing approach was used in order to achieve highly ordered terrace-and-step structure over the surface of sapphire substrates. High temperature annealing reduces surface energy of the sapphire substrates and forms a terrace-and-step structure, which acts as nucleation sites for subsequent deposition of Al. 2-inch diameter sapphire wafers were introduced into the front zone of Minibrute furnace and heated under nitrogen environment at 1273 K for 5 min. Subsequently, the wafers were moved into the center zone and heated under nitrogen environment at 1384 K for 15 min. The sapphire wafers were then annealed at 1384 K for 1 h under ultra-zero grade air environment followed by 5 h of heating under the same environment at 1448 K. Finally, the sapphire wafers were cooled down naturally under nitrogen. Tantalum was deposited on the backside of annealed sapphire wafers using a Unifilm DC sputterer to facilitate uniform heating during MBE growth. The backside metallized wafers were diced into 1 cm × 1 cm substrates. These high temperature annealed sapphire substrates were cleaned in a piranha solution of sulfuric and hydrogen peroxide (3:1) at 423 K for 10 to 20 min. These substrates were then loaded into a load lock chamber of the MBE and were thermally cleaned under vacuum at 473 K for 10 min. The substrates were then transferred into main chamber of the MBE and outgassed at 1073 K for 10 min. 80 nm of Al was then deposited on the sapphire substrates from a conventional Veeco effusion cell. Streaky reflection high-energy electron diffraction (RHEED) patterns were observed, which implies high surface smoothness. The substrate temperature for Al deposition was kept at 373 K for sample Sub100 and at 473 K for Sub200. Atomic force microscopy (AFM) characterization showed highly smooth Al layers. The top Al layer RMS surface roughness for Sub200 was 0.125 and 0.288 nm for Sub100 for 5 µm × 5 µm images.
TEM
Plan view and cross-section TEM samples have been prepared with a FEI Nova 600 dual-beam focused ion beam system to characterize the Al layer and sapphire substrate. HRTEM cross-section images were taken at the Al/sapphire interface with a FEI Titan S/TEM operating at 300 keV.
XRD
A Bruker JV D1 high-resolution X-ray diffractometer using Cu kα radiation with incident beam conditioning that includes an incident beam parallel beam optical element was employed for pole figures and Φ-scans. The (220) Al reflection Φ scan was measured along with the sapphire (1123) reflection. ω:2Θ scans used an additional incident beam monochromating optic (Si (220) two reflection channel cut crystal) of the deposited film on the substrate and were taken to determine which Al orientations were present. The Al lattice parameter was also determined using a high-resolution mode with both incident and scattered Si (220) channel cut crystal optics. The Φ scans and the ω:2Θ scans were taken using 0.003–0.05° step sizes.
EBSD
EBSD images were produced using an FEI Quanta 3D FEG Dual Beam (SEM/FIB) system with an HKL EBSD attachment. The data was obtained with HKL fast acquisition software. Typical step sizes were ~2 μm over areas of 250 μm × 250 μm.
TDTR
TDTR is an optical pump-probe method for thermal characterization of both bulk and nanostructured materials10. A layer of Al is usually coated on the sample surface as transducer. The thickness of Al is measured by picosecond acoustic technique (83 nm for Sub100 and 86 nm for Sub200). A modulated pump beam heats the sample surface, whereas a delayed probe beam detects the temperature variation of the sample surface via thermoreflectance. The signals picked up by a photodetector and a lock-in amplifier are fitted with an analytical heat conduction solution to infer unknown parameters. The modulation frequency and objective used in this work are 3.6 MHz and ×10 objective with pump and probe beam diameters of 19 and 13.3 μm, respectively. More detail about TDTR can be found in literature68,69. The TBC are measured by three TDTR systems in Georgia Institute of Technology, University of Virginia, and University of Notre Dame. The error bars of TDTR measurements are calculated with a Monte Carlo method by considering all the possible error sources70. The error bars of beam size measurements by a beam profiler are ±0.5 μm. The error bars of Al and sapphire heat capacity are ±2%. The error bars of Al thickness and Al thermal conductivity are ±3.5 and ±10%, respectively.
Non-equilibrium Landauer approach
The Landauer approach is a widely used method to predict TBC, and the general form of the Landauer formula is from the particle description of phonons and the TBC is calculated from net heat flux and temperature drop across the interface. In previous studies of non-equilibrium effect at the interface, it is pointed out that the phonons are in strong non-equilibrium because of the difference in modal transmission coefficients and reservoir temperatures, and this non-equilibrium effect should be considered in Landauer formula. With the recently developed non-equilibrium Landauer approach that can capture the non-equilibrium effect, the theoretical predictions agree much better with experimental results. We have applied the non-equilibrium Landauer approach to our aluminum–sapphire interface to predict the TBC. In our calculation, the phonon properties of both Al and Al2O3 are obtained from ab initio calculations within the framework of DFT, as implemented in the Vienna Ab initio Simulation Package (VASP), and the second-order force constants are obtained from Phonopy71. More details about DFT calculation can be found in the Supplementary Information (Calculation details about non-equilibrium Landauer approach).
AGF
AGF is a widely used method to calculate the transmission and related thermal properties of a system. More detailed introduction could be found in literature31. With the harmonic assumption, only the second-order force constants are needed for Green’s function calculation. Here, the second-order DFT force constants of the leads and the interface are separately obtained from the frozen-phonon method72 using QUANTUM ESPRESSO73 and Phonopy71. We used projector augmented-wave method74 of Perdew, Burke and Ernzerhof75 (Al.pbe-n-kjpaw_psl.1.0.0.UPF and O.pbe-n-kjpaw_psl.1.0.0.UPF for the two types of elements). The cut-off energy of the interface is 100 Ryd and the k-points mesh is 4 × 4 × 2 for the 2 × 2 × 1 supercell. For the aluminum lead, the cut-off energy is 50 Ryd, and the k-points mesh is 4 × 4 × 3 for the 3 × 3× 3 supercell. Although for the sapphire lead, the cut-off energy is 80 Ryd, and the k-points mesh is 4 × 4 × 2 for the 3 × 3 × 2 supercell. To represent the infinitely large transverse direction, the transverse k-points mesh is 20 × 20 in the Brillouin zone to ensure the convergence. In the experiment, Al is oriented to [111] direction to match the lattice constants of sapphire. To calculate the thermal conductivity along [111] direction of aluminum and [0001] direction of sapphire, we convert Al unit cell from rock-salt structure to hexagonal structure while keeping the space group unaltered. The lattice constants in the transverse direction is 4.9485 Å and the lattice constants in the out-of-direction are 6.7990 and 13.1172 Å for Al and sapphire, respectively. We want to highlight that we used force constants of Al/sapphire interface directly obtained from DFT calculation instead of the common simplified practice of using force constants of one material and only changing masses for the other. More details are included in the Supplementary Information (AGF in the Supplementary Methods).
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Kapitza, P. The study of heat transfer in helium II. J. Phys. 4, 181 (1941).
Pollack, G. L. Kapitza resistance. Rev. Mod. Phys. 41, 48 (1969).
Gustafsson, S. E., Karawacki, E. & Khan, M. N. Transient hot-strip method for simultaneously measuring thermal conductivity and thermal diffusivity of solids and fluids. J. Phys. D Appl. Phys. 12, 1411 (1979).
Swartz, E. & Pohl, R. Thermal resistance at interfaces. Appl. Phys. Lett. 51, 2200–2202 (1987).
Swartz, E. T. & Pohl, R. O. Thermal boundary resistance. Rev. Mod. Phys. 61, 605 (1989).
Stoner, R. & Maris, H. Kapitza conductance and heat flow between solids at temperatures from 50 to 300 K. Phys. Rev. B 48, 16373 (1993).
Paddock, C. A. & Eesley, G. L. Transient thermoreflectance from thin metal films. J. Appl. Phys. 60, 285–290 (1986).
Stoner, R., Maris, H., Anthony, T. & Banholzer, W. Measurements of the Kapitza conductance between diamond and several metals. Phys. Rev. Lett. 68, 1563 (1992).
Costescu, R. M., Wall, M. A. & Cahill, D. G. Thermal conductance of epitaxial interfaces. Phys. Rev. B 67, 054302 (2003).
Cahill, D. G. Analysis of heat flow in layered structures for time-domain thermoreflectance. Rev. Sci. Instrum. 75, 5119–5122 (2004).
Hohensee, G. T., Wilson, R. & Cahill, D. G. Thermal conductance of metal–diamond interfaces at high pressure. Nat. Commun. 6, 6578 (2015).
Lyeo, H.-K. & Cahill, D. G. Thermal conductance of interfaces between highly dissimilar materials. Phys. Rev. B 73, 144301 (2006).
Hopkins, P. E., Duda, J. C., Petz, C. W. & Floro, J. A. Controlling thermal conductance through quantum dot roughening at interfaces. Phys. Rev. B 84, 035438 (2011).
Hsieh, W.-P., Lyons, A. S., Pop, E., Keblinski, P. & Cahill, D. G. Pressure tuning of the thermal conductance of weak interfaces. Phys. Rev. B 84, 184107 (2011).
Losego, M. D., Grady, M. E., Sottos, N. R., Cahill, D. G. & Braun, P. V. Effects of chemical bonding on heat transport across interfaces. Nat. Mater. 11, 502–506 (2012).
Oh, D. W., Kim, S., Rogers, J. A., Cahill, D. G. & Sinha, S. Interfacial thermal conductance of transfer-printed metal films. Adv. Mater. 23, 5028–5033 (2011).
Cheng, Z. et al. Thermal conductance across β-Ga2O3-diamond van der Waals heterogeneous interfaces. APL Mater. 7, 031118 (2019).
Monachon, C. & Weber, L. Thermal boundary conductance between refractory metal carbides and diamond. Acta Mater. 73, 337–346 (2014).
Hopkins, P. E., Norris, P. M., Stevens, R. J., Beechem, T. E. & Graham, S. Influence of interfacial mixing on thermal boundary conductance across a chromium/silicon interface. J. Heat. Transf. 130, 062402 (2008).
Collins, K. C., Chen, S. & Chen, G. Effects of surface chemistry on thermal conductance at aluminum–diamond interfaces. Appl. Phys. Lett. 97, 083102 (2010).
Monachon, C. & Weber, L. Influence of diamond surface termination on thermal boundary conductance between Al and diamond. J. Appl. Phys. 113, 183504 (2013).
Hopkins, P. E. et al. Influence of anisotropy on thermal boundary conductance at solid interfaces. Phys. Rev. B 84, 125408 (2011).
Monachon, C. & Weber, L. Effect of diamond surface orientation on the thermal boundary conductance between diamond and aluminum. Diam. Relat. Mater. 39, 8–13 (2013).
Hopkins, P. E. et al. Reduction in thermal boundary conductance due to proton implantation in silicon and sapphire. Appl. Phys. Lett. 98, 231901 (2011).
Cheng, Z. et al. Tunable thermal energy transport across diamond membranes and diamond-Si interfaces by nanoscale graphoepitaxy. ACS Appl. Mater. Inter. 11, 18517–18527 (2019).
Landauer, R. Spatial variation of currents and fields due to localized scatterers in metallic conduction. IBM J. Res. Dev. 1, 223–231 (1957).
Stevens, R. J., Zhigilei, L. V. & Norris, P. M. Effects of temperature and disorder on thermal boundary conductance at solid–solid interfaces: nonequilibrium molecular dynamics simulations. Int. J. Heat. Mass Transf. 50, 3977–3989 (2007).
Caddeo, C. et al. Thermal boundary resistance from transient nanocalorimetry: a multiscale modeling approach. Phys. Rev. B 95, 085306 (2017).
Gordiz, K. & Henry, A. A formalism for calculating the modal contributions to thermal interface conductance. N. J. Phys. 17, 103002 (2015).
Schelling, P., Phillpot, S. & Keblinski, P. Phonon wave-packet dynamics at semiconductor interfaces by molecular-dynamics simulation. Appl. Phys. Lett. 80, 2484–2486 (2002).
Mingo, N. & Yang, L. Phonon transport in nanowires coated with an amorphous material: an atomistic Green’s function approach. Phys. Rev. B 68, 245406 (2003).
Tian, Z., Esfarjani, K. & Chen, G. Enhancing phonon transmission across a Si/Ge interface by atomic roughness: First-principles study with the Green’s function method. Phys. Rev. B 86, 235304 (2012).
Shi, J., Yang, X., Fisher, T. S. & Ruan, X. Dressed intrinsic thermal boundary conductance and radiation across interfaces a nonequilibrium Landauer approach. Preprint at https://arxiv.org/abs/1812.07910 (2018).
Ye, N. et al. Thermal transport across metal silicide-silicon interfaces: an experimental comparison between epitaxial and nonepitaxial interfaces. Phys. Rev. B 95, 085430 (2017).
Saha, D. et al. Impact of metal adhesion layer diffusion on thermal interface conductance. Phys. Rev. B 99, 115418 (2019).
Aller, H., Yu, X., Gellman, A. J., Malen, J. A. & McGaughey, A. J. 17th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm) 567–571 (IEEE, 2018).
Hopkins, P. E. Thermal transport across solid interfaces with nanoscale imperfections: effects of roughness, disorder, dislocations, and bonding on thermal boundary conductance. Hindawi Publ. Corp. 2013, 682586 (2013).
Gaskins, J. T. et al. Thermal boundary conductance across heteroepitaxial ZnO/GaN interfaces: assessment of the phonon gas model. Nano Lett. 18, 7469–7477 (2018).
Sadasivam, S. et al. Thermal transport across metal silicide-silicon interfaces: first-principles calculations and Green’s function transport simulations. Phys. Rev. B 95, 085310 (2017).
Huberman, M. & Overhauser, A. Electronic Kapitza conductance at a diamond-Pb interface. Phys. Rev. B 50, 2865 (1994).
Majumdar, A. & Reddy, P. Role of electron–phonon coupling in thermal conductance of metal–nonmetal interfaces. Appl. Phys. Lett. 84, 4768–4770 (2004).
Mahan, G. Kapitza thermal resistance between a metal and a nonmetal. Phys. Rev. B 79, 075408 (2009).
Monachon, C., Weber, L. & Dames, C. Thermal boundary conductance: a materials science perspective. Annu. Rev. Mater. Res. 46, 433–463 (2016).
Hanisch, A., Krenzer, B., Pelka, T., Möllenbeck, S. & Horn-von Hoegen, M. Thermal response of epitaxial thin Bi films on Si (001) upon femtosecond laser excitation studied by ultrafast electron diffraction. Phys. Rev. B 77, 125410 (2008).
van Roekeghem, A., Vermeersch, B., Carrete, J. & Mingo, N. Thermal resistance of Ga N/Al N graded interfaces. Phys. Rev. Appl 11, 034036 (2019).
Liang, Z. & Keblinski, P. Finite-size effects on molecular dynamics interfacial thermal-resistance predictions. Phys. Rev. B 90, 075411 (2014).
Siegel, D. J., Hector, L. G. Jr & Adams, J. B. Adhesion, atomic structure, and bonding at the Al (111)/α−Al2O3 (0001) interface: a first principles study. Phys. Rev. B 65, 085415 (2002).
Dehm, G., Inkson, B. J. & Wagner, T. Growth and microstructural stability of epitaxial Al films on (0001) α-Al2O3 substrates. Acta Mater. 50, 5021–5032 (2002).
Lu, Z., Wang, Y. & Ruan, X. Metal/dielectric thermal interfacial transport considering cross-interface electron-phonon coupling: theory, two-temperature molecular dynamics, and thermal circuit. Phys. Rev. B 93, 064302 (2016).
Hopkins, P. E., Salaway, R., Stevens, R. & Norris, P. Temperature-dependent thermal boundary conductance at Al/Al2O3 and Pt/Al2O3 interfaces. Int. J. Thermophys. 28, 947–957 (2007).
Muraleedharan, M. G. et al. Thermal interface conductance between aluminum and aluminum oxide: A rigorous test of atomistic level theories. Preprint at https://arxiv.org/abs/1807.06631 (2018).
Jain, A. & McGaughey, A. J. Thermal transport by phonons and electrons in aluminum, silver, and gold from first principles. Phys. Rev. B 93, 081206 (2016).
Schoenlein, R., Lin, W., Fujimoto, J. & Eesley, G. Femtosecond studies of nonequilibrium electronic processes in metals. Phys. Rev. Lett. 58, 1680 (1987).
Hodak, J., Martini, I. & Hartland, G. V. Ultrafast study of electron–phonon coupling in colloidal gold particles. Chem. Phys. Lett. 284, 135–141 (1998).
Shouhang Li, Z. T., Xinyu, Z., & Bao, H. Thermal conductivity and Lorenz ratio of metals at intermediate temperature: a first-principles analysis. Preprint at https://arxiv.org/abs/2004.08843 (2020).
Wang, W. & Cahill, D. G. Limits to thermal transport in nanoscale metal bilayers due to weak electron-phonon coupling in Au and Cu. Phys. Rev. Lett. 109, 175503 (2012).
Lombard, J., Detcheverry, F. & Merabia, S. Influence of the electron–phonon interfacial conductance on the thermal transport at metal/dielectric interfaces. J. Phys. Condens. Matter 27, 015007 (2014).
Lu, T., Zhou, J., Nakayama, T., Yang, R. & Li, B. Interfacial thermal conductance across metal-insulator/semiconductor interfaces due to surface states. Phys. Rev. B 93, 085433 (2016).
Feng, T., Lindsay, L. & Ruan, X. Four-phonon scattering significantly reduces intrinsic thermal conductivity of solids. Phys. Rev. B 96, 161201 (2017).
Yang, X. et al. Observation of strong higher-order lattice anharmonicity in Raman and infrared spectra. Phys. Rev. B 101, 161202 (2020).
Giri, A. & Hopkins, P. E. A review of experimental and computational advances in thermal boundary conductance and nanoscale thermal transport across solid interfaces. Adv. Func. Mater. 30, 1903857 (2019).
Hopkins, P. E., Norris, P. M. & Stevens, R. J. Influence of inelastic scattering at metal-dielectric interfaces. J. Heat. Transf. 130, 022401 (2008).
Hopkins, P. E. Multiple phonon processes contributing to inelastic scattering during thermal boundary conductance at solid interfaces. J. Appl. Phys. 106, 013528 (2009).
Hopkins, P. E., Duda, J. C. & Norris, P. M. Anharmonic phonon interactions at interfaces and contributions to thermal boundary conductance. J. Heat. Transf. 133, 6 (2011).
Polanco, C. A. & Lindsay, L. Phonon thermal conductance across GaN-AlN interfaces from first principles. Phys. Rev. B 99, 075202 (2019).
Cahill, D. G., Lee, S.-M. & Selinder, T. I. Thermal conductivity of κ-Al2O3 and α-Al2O3 wear-resistant coatings. J. Appl. Phys. 83, 5783–5786 (1998).
Monchamp, R. R. Preparation and properties of crystalline laser oxide materials. J. Solid State Chem. 12, 201–206 (1975).
Jiang, P., Qian, X. & Yang, R. Tutorial: time-domain thermoreflectance (TDTR) for thermal property characterization of bulk and thin film materials. J. Appl. Phys. 124, 161103 (2018).
Schmidt, A. J. Pump-probe thermoreflectance. Annu. Rev. Heat. Transf. 16, 159–181 (2013).
Bougher, T. L. et al. Thermal boundary resistance in GaN films measured by time domain thermoreflectance with robust Monte Carlo uncertainty estimation. Nano. Micro. Thermophys. Eng. 20, 22–32 (2016).
Togo, A. & Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 108, 1–5 (2015).
Tian, Z. et al. Phonon conduction in PbSe, PbTe, and PbTe 1− x Se x from first-principles calculations. Phys. Rev. B 85, 184303 (2012).
Espresso, Q. a modular and open-source software project for quantum simulations of materials/P. Giannozzi [et al.]. J. Phys. Condens. Matter 21, 395502 (2009).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Acknowledgements
We would like to acknowledge the financial support from Office of Naval Research MURI Grant No. N00014-18-1-2429. Z.T. and R.H. would like to acknowledge the support by Office of Naval Research under ONR Award Number N00014-18-1-2724 and the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation Grant Number ACI-1053575.
Author information
Authors and Affiliations
Contributions
Z.C., Y.K., R.L., E.L., L.Y., T.L., and P.H. performed the thermal measurements. H.A., E.C., C.M., Z.E., and A.D. grew the samples. R.H. and Z.T. did the AGF calculation and J.S. did the Landauer calculation. M.L., Y.W., T.B., and M.G. performed TEM, XRD, and EBSD measurements. Z.C. wrote the manuscript with inputs from all authors. S.G. supervised this work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interest.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cheng, Z., Koh, Y.R., Ahmad, H. et al. Thermal conductance across harmonic-matched epitaxial Al-sapphire heterointerfaces. Commun Phys 3, 115 (2020). https://doi.org/10.1038/s42005-020-0383-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-0383-6
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.