Abstract
Recent theoretical and experimental work suggests a frictionless-frictional transition with increasing inter-particle pressure explains the extreme solid-like response of discontinuous shear thickening suspensions. However, analysis of macroscopic discontinuous shear thickening flow in geometries other than the standard rheometry tools remain scarce. Here we use a Hele-Shaw cell geometry to visualise gas-driven invasion patterns in discontinuous shear thickening cornstarch suspensions. We plot quantitative results from pattern analysis in a volume fraction-pressure phase diagram and explain them in context of rheological measurements. We observe three distinct pattern morphologies: viscous fingering, dendritic fracturing, and system-wide fracturing, which correspond to the same packing fraction ranges as weak shear thickening, discontinuous shear thickening, and shear-jammed regimes.
Similar content being viewed by others
Introduction
Granular suspensions exhibit a wide variety of complex non-Newtonian flow behaviours. Micro-scale grain–grain and grain–fluid interactions can, under different circumstances, manifest as yield stresses, shear thinning, shear thickening, thixotropy, or jamming1,2,3,4,5,6. Shear thickening fluids display increasing viscosity with applied shear rate or stress. The most dramatic form is discontinuous shear thickening (DST), where the viscosity increases orders of magnitude and the material behaviour goes from liquid-like to solid-like.
In nature, oil sediments, crystal-bearing magma, muds, and clays have all been shown to display shear thickening behaviour7,8,9. In industry, DST behaviour is often undesirable as it can damage equipment during processing of granular suspensions, such as concrete, silica suspensions, cornstarch mixtures, and latex suspensions10,11,12. Recently, DST has been explored as a useful property to be engineered into composite materials for applications in shock absorption, such as soft body armour, or into smart fluids with tunable rheologies12,13,14. However, the application of DST in industrial processes is held back by an incomplete understanding of the fundamental mechanisms that govern the shear thickening behaviour15,16.
Cornstarch mixed with water provides a readily available classic example of a granular suspension that exhibits DST behaviour. In fact, it can become so resistant to motion that a person can run across the surface of the “fluid”17. Note that this behaviour is reversible: the suspension begins to relax and flow again after the stress is removed. Cornstarch in other interstitial fluids can have no DST response18 but cornstarch suspensions in water have been routinely used for experiments designed to study the DST phenomenon. Experiments have advanced our understanding through detailed rheological studies17,19,20,21,22, careful characterisation of impact generated shear-jamming (SJ) fronts23,24,25,26,27,28,29,30,31,32, and benchmarking of DST models33,34,35,36.
One proposed microscopic origin of the DST transition in dense suspensions is that the particles have a repulsive force that can be overcome by an imposed stress to cause frictional contact between particles and thus drastically increase the viscosity of the suspension20,37,38,39. Modern theories have followed this line and have reproduced DST behaviour in rheological flow curves and modelled behaviour33,35,36,40,41,42,43,44. As a result, recent experiments have examined the frictional properties of dense particle suspensions. It has been shown that cornstarch suspensions in water are frictionless with a low confining pressure45. It has also been shown that cornstarch particles have a frictional profile that transitions from low to high friction with a normal stress that matches the critical stress (σc) at which shear thickening occurs18,46. However, theoretical and experimental analysis of macroscopic DST behaviour and flows in confined geometries other than the classic rheometry tools remain scarce47.
An alternative flow geometry is represented by the Hele-Shaw cell. Originally designed to study fluid streamlines in laminar flow48, the Hele-Shaw cell has since the 1950s been used to study hydrodynamic instabilities, most notably viscous fingering (VF), where the interface between a less viscous fluid invading a more viscous defending fluid develops undulations that grow into finger-like invasion patterns49,50,51. VF has been studied in different types of complex rheologies52, including shear thinning53,54,55, shear thickening56, yield stress57, gels58, viscoelastic fluids8,9,59,60,61,62,63,64,65, and saturated granular media66,67,68.
Similarly to DST suspensions, it has been known since the 1960s that viscoelastic fluids can transition from a liquid-like state to a solid-like state8. Here the transition is a result of the timescale of the interaction (shear rate) instead of the abrupt response of stress-induced friction found in DST systems. Two regimes of Hele-Shaw invasion patterns in viscoelastic fluids, typically suspended polymer networks, have been observed: VF at low injection rates and fracture-like patterns above a threshold injection rate where the material starts to behave like an elastic solid52,61,64,69.
A rich literature has developed around invasion patterns in Hele-Shaw cell experiments with settled granular media, describing the variety of pattern morphologies observed and the parameters that control the transitions between them68,70,71,72,73,74,75,76. These multiphase Hele-Shaw cell invasion experiments are dominated by the ever-present frictional contacts between grains. The only exception is for high enough injection rate to fluidise and lubricate the granular material, producing liquid-like behaviour and VF-like invasion patterns66,68,74. Otherwise, as long as the granular medium is packed below the random close packing limit (above which the grains cannot mobilise and capillary invasion is observed), the invaded saturated granular media exhibits frictional behaviour as the invading secondary fluid forms either frictional fingers at low filling fraction or “fracture” patterns through intermittent growth in a dense, deformable granular packing66,67,68,77.
Note that the invasion phenomenon referred to as “fracturing” throughout this and similar works (narrow channels formed within a granular material by an invading fluid) is distinct from conventional fracturing of elastic and cohesive materials (separation of a previously continuous solid phase due to tensile stress). Instead, the fracture-like shape of the invasion pattern is a result of pressure and surface tension forces acting on the fracture interface, frictional forces acting between grains, and frictional forces acting between grains and the confining boundaries66,68,74,77.
Here we study the displacement by pressurised air of a shear-thickening cornstarch suspension confined in a Hele-Shaw cell. We find three distinct flow patterns: VF, dendritic fracturing (DFr), and large-scale fracturing (Fr). The packing fraction ranges at which these three patterns are manifested correspond to the packing fractions at which, respectively, continuous shear thickening (CST), DST, and SJ typically are observed33,35,36,40,41,42,43.
Results
Rheology
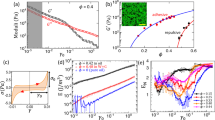
Figure 1 presents rheological measurements made with the sample concentrations used in this work. Figure 1a shows the measured flow curves: shear stress σ as a function of shear rate \(\dot{\gamma }\) for different volume fractions ϕ = 0.23–0.56. Figure 1b shows the suspension viscosity \(\eta =\sigma /\dot{\gamma }\) plotted against \(\dot{\gamma }\), illustrating an increasing degree of shear thickening with increasing ϕ as well as the shear thinning that is initially observed for all of the suspensions. The flow curves do not reveal a sharp transition from CST to DST to SJ between the different concentrations, and the choice of criteria to identify the regimes based on the flow curves alone is not inherently obvious.
a Shear stress σ as a function of shear rate \(\dot{\gamma }\) for various volume fractions ϕ. α is the exponent of the power law fit, with α > 2 indicating discontinuous shear thickening. b Suspension viscosity η plotted against \(\dot{\gamma }\) showing discontinuous shear thickening for ϕ = ≥0.45. Rheometry data obtained in stress-controlled mode. The average standard deviation from measurements of three samples per curve is 10% of the plotted value and smaller than the marker size.
One method to differentiate the varieties of shear thickening is to fit a power law to the thickening regime of the flow curve, \(\sigma \propto {\dot{\gamma }}^{\alpha }\), and use the exponent α as a measure of shear thickening. Following ref. 15, here we define shear thickening regimes based on steady state flow curves obtained from rheology with Newtonian flow α = 1, CST α > 1, DST α > 2, and SJ α tends to infinity. Thus we observe DST for the curves of ϕ ≥ 0.45, where a sharp order-of-magnitude increase in suspension viscosity is observed. DST flow curves up to and including ϕ = 0.50 are observed to level off at a plateau representing a higher effective viscosity dominated by frictional contacts33. The volume fraction of ϕ = 0.53 had an α that tended to infinity and the flow curve did not recover an upper viscosity branch, instead the rheometer began to regress its shear rate indicating an SJ state25,33. The highest volume fraction measured, ϕ = 0.56, always remained as a thick paste and we were unable to fill this material into the Hele-Shaw cell for experimentation. For reference, the unstressed, frictionless, critical jamming volume fraction of cornstarch is estimated as ϕc ≈ 0.5625,29. Overall, the measured rheometry is consistent with results in previous work by other authors17,21,25,33.
Hele-Shaw flow and pattern formation
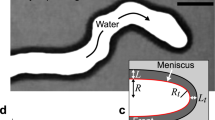
Cornstarch particles, with an average diameter of 16.1 μm, see Fig. 2a, were suspended in water at varying concentrations from ϕ = 0.23 ± 0.01 to 0.53 ± 0.01. The suspension was confined in a transparent radial Hele-Shaw cell with a 0.2-mm gap height and a 10-cm radius, see Fig. 2b. Pressurised air was then released into the suspension from a central inlet in the cell while a high-speed camera filmed from below. The air pressure ranged from P = 0.10 ± 0.02 to 10.00 ± 0.02 bar. During the experiment, the pressurised air pushes the cornstarch suspension aside as it invades into the cell gap. This suspension displacement forms an observed radial pattern, see Fig. 2c, and the experiment ends once the pressurised air reaches the edge of the cell and is released to atmosphere. We have identified three distinct pattern morphologies in our experiments: VF, DFr, and Fr as displayed in the screenshots in Fig. 3a–c, respectively. It is useful to represent the volume fraction in terms of how far the system is from the unstressed critical jamming volume fraction Δϕ = ϕc − ϕ36. Figure 4 shows measured pattern characteristics plotted against Δϕ: (a) average branch/finger width w, (b) average spatial frequency of branches/fingers D, and (c) branch/finger tip velocity vtip.
a Size distribution of the cornstarch particles. b Side-view schematic of the Hele-Shaw cell. c Example of cornstarch suspension invaded by pressurised air inside the cell (volume fraction and pressure are ϕ = 0.23 and P = 0.1 bar, respectively). The 2-cm-wide pink annulus represents the area analysed for each experiment.
Three subsequent screenshots for: a viscous fingering (VF): volume fraction ϕ = 0.34 (filling fraction difference Δϕ = 0.22), air invasion pressure P = 0.5 bar with images at 0.015, 0.045, and 0.090 s after air is released. b Dendritic fracturing (DFr): ϕ = 0.47 (Δϕ = 0.09), P = 5 bar at 0.005, 0.015, and 0.020 s. c Large fracture (Fr): ϕ = 0.53 (Δϕ = 0.03, P = 1 bar at 0.270, 0.720, and 1.020 s. Image diameters correspond to the Hele-Shaw cell diameter (20 cm).
Measures are shown as a function of the filling fraction difference Δϕ (corresponding volume fraction ϕ values in brackets) and at different pressures P. a The average width of branches w. b The average spatial frequency of branches D (the inverse of the average separation distance between branches). c Branch speed is determined by the fastest branch tip speed in an experiment vtip. w distinguishes whether the morphology is fingering (larger width) or fracturing. D is inversely proportional to the separation distance between neighbouring branches and distinguishes whether the fracturing is dendritic (high branch frequency) or system wide (low branch frequency). vtip increases for higher imposed pressures and for more dilute suspensions (lower effective viscosity). Note that there is no step change in the tip velocity at the transition between fingering and fracturing. Error bars are calculated from the standard deviation of measurements from multiple branches.
VF, with smooth curvature at the finger tips, is seen for all concentrations at low pressure (0.1 bar, see Supplementary Movie 1) and at all pressures for dilute suspensions (Δϕ > 0.11, see Fig. 3a). DFr at intermediate Δϕ (Δϕ = 0.06–0.11, see e.g. Fig. 3b and Supplementary Movie 2) are distinct from VF by having pointed branch tips, offshoots that can be perpendicular to the parent branch, and significantly narrower branch widths averaging w = 0.1 cm (Fig. 4a). The narrow DFr branches grow by frequent tip-splitting, giving rise to spatially dense fracture networks (high D, see Fig. 4b). The DFr network spreads radially outwards from the injection point.
The DFr mode displays an interesting dynamic whereby the suspension is momentarily forced into a DST solid-like state and moments later relaxes back to a fluid state after the passage of the invasion front (see Supplementary Movie 3). Figure 5a–c shows a time series of close-up images where the suspension of Δϕ = 0.06 (ϕ = 0.50) is invaded by air of P = 0.3 bar from the lower left hand corner. The suspension is sheared by the oncoming invasion front into a DST state that subsequently fractures into thin, jagged branches. After the pressurised front has passed, the shear stress on the suspension decreases and the suspension relaxes back to a liquid state. Surface tension then acts to smooth the interface and widen the branches, though it still retains a structure that is unlike VF with offshoots that are perpendicular to the main branch. Figure 5d illustrates the evolution of the average fracture width for one branch in a series of 0.5-cm-wide radial bands that shows the fractures continue to widen, at a slower rate after their initial formation, as surface tension acts on the interface after the front has passed. Relaxation behaviour on the scale of seconds in dense cornstarch suspensions has been reported on previously and linked with the time taken for local particles in contact to flow away from each other22,24.
Example of dendritic fracturing at the filling fraction difference Δϕ = 0.06 (volume fraction ϕ = 0.50) and pressure P = 0.3 bar, which straddles the viscous fingering–dendritic fracturing regime transition. a–c shows close-up of dendritic fracturing at 0.2, 0.5, and 0.8 s after the air is released, respectively, where the invading fracture front temporarily forces the suspension into a discontinuous shear thickening state with narrow “pointed” fracture branches, which then relax back to a liquid state with widening “rounded” branches after the front has passed. d The evolution of the average fracture width for one branch that shows the fractures continue to widen after the front has passed. Error band (±0.01 cm) determined by maximum resolution of pixels during analysis of fracture width.
The densest suspension (Δϕ = 0.03, see e.g. Fig. 3c and Supplementary Movie 4) displays a very different fracturing pattern. Here the suspension in the entire cell appears to jam up under the stress as the air invades in long, uninterrupted branches that span the radius of the cell. While also having a narrow branch width (w < 0.2 cm), the large fracture mode (Fr) is distinguished from the DFr by having a much lower spatial fracture frequency D (Fig. 4b).
There is no abrupt change in the tip velocity as the pattern transitions from fingering to fracturing. The general trend (Fig. 4c) is simply increased velocity for higher imposed pressures and for more dilute suspensions (with lower effective viscosity).
Summarising, the branch width w distinguishes whether the morphology is fingering (large width) or fracturing (narrow width). The branch spatial frequency D distinguishes whether the fracturing is dendritic (high branch frequency) or system wide (low branch frequency).
Discussion
The behaviour of the quantities we used to characterise the different observed patterns can be displayed as a phase diagram as a function of air pressure P versus filling fraction difference Δϕ. In particular, we show these diagrams in a log–log scale for the branch width w (Fig. 6a), branch frequency D (Fig. 6b), and tip velocity vtip (Fig. 6c). Data have been normalised by the maximum value they assume within the analysed interval (as presented in Fig. 4). The system’s behaviour can thus be summarised in a unique phase diagram by combining the measurements for these three quantities into a three-dimensional red–green–blue colour space interpolated between a total of the 40 experiments spanning the P–Δϕ space (Fig. 6d). Superposing patterns from selected experiments, it is revealed that they are thus grouped by the measured characteristics: large fractures (Fr) for the densest suspensions in a green hue, DFr for intermediate Δϕ and P > 0.5 bar in yellow–orange, and VF in blue–pink–purple hues corresponding to dilute suspensions and low imposed air pressure.
Each plot has the same axes and are in a logarithmic scale, with the invasion pressure P against the filling fraction difference Δϕ. a The experimental data for branch width w normalised within a blue colour space. b The experimental data for the branch frequency D normalised within a red colour space. c The experimental data for the branch speed vtip normalised within a green colour space. d Samples of patterns formed at varying P and Δϕ. Volume fractions are reported in brackets below the corresponding values of Δϕ. The sample patterns presented are to scale, the diameter of their image equivalent to Hele-Shaw cell diameter of 20 cm. Background plot of d represents the combined normalised experimental data from a to c in a three-dimensional RGB colour space. Similar pattern morphologies correspond to similar colours. Three phases are noted, fracturing (Fr), dendritic fracturing (DFr), and viscous fingering (VF).
Many proposals have been made to explain the intriguing DST phenomenon. However, recent theoretical works33,35,36,40,43, simulations41,42,78, and experiments20,25,26,45,46,79,80 have converged on the explanation that DST in dense suspensions is caused by inter-particle repulsion that subdues frictional contacts35. The repulsive force between particles prevents particle contact at low stresses, but at a critical higher stress, σc inter-particle pressure overcomes the repulsion allowing frictional contacts to be made and thus greatly increasing the viscosity of the system. The increase in viscosity is sudden because the repulsive force prevents a more gradual breakdown of lubrication films29,81. Thus the rheology is split between frictionless and frictional regimes. The two regimes have a different volume fraction at which the rheology diverges due to jamming, the frictional regime ϕj being less than the frictionless ϕc. This also explains why neither emulsions nor attractive colloids shear thicken. Emulsions are always lubricated and do not experience a frictional state, whereas attractive colloids are always frictional and do not experience a lubricated state.
Given this explanation, models suggest that three responses can be observed, depending on ϕ, when a suspension transitions from the frictionless regime to the frictional above σc: CST, DST, and SJ. DST occurs in the frictional regime when the suspension can locally elastically sustain an applied stress41. This is only possible for a minimum volume fraction ϕ > ϕDST, where the volume fraction of particles in frictional contact is high enough for solid-like behaviour to dominate the response of the suspension (in rheology, see Fig. 1 for ϕDST ≈ 0.45). Below ϕDST, CST is observed with liquid-like behaviour. Above ϕj (in rheology, see Fig. 1 for ϕj ≈ 0.53) but below ϕc, the system shear-jams. It no longer permits homogeneous flow at σc because it is above the jamming volume fraction for the frictional regime, instead flows will be inhomogeneous. For example, particle migration and fracturing have been observed as inhomogeneous flows during rheology33,82. Above ϕc, there is no frictionless state to transition from, the system is jammed no matter the stress, i.e. it is now a system with a yield stress, see ϕ = 0.56 in Fig. 183.
Mari et al.42 suggested that a difference between the DST (ϕDST < ϕ < ϕj) and SJ (ϕj < ϕ < ϕc) phases has been observed in stress drop experiments82,84,85. For the DST phase, the solid-like frictional state would relax quickly after the stress is relieved as the whole network is not engaged, whereas for the SJ phase the stress does not completely relax from the suspension as some of it is stored elastically in the jammed contact network. We observe this dynamic between our DFr, which readily relaxes (see Fig. 5), and Fr, which holds its form for longer than the experiment.
Rheological steady-state experiments estimate solid-like behaviour to occur at a critical stress of σc, which is of the order of 1 Pa as can be seen for our rheology in Fig. 1. However, the Hele-Shaw cell experiments performed here show a transition at Pc ≈ 0.5 bar (5 × 104 Pa). How the critical limit found in these Hele-Shaw cell experiments relates to the shear stress response in other systems is yet to be determined.
Fracture-like patterns are also observed in invasion experiments using settled granular materials, typically glass beads, within Hele-Shaw cells. The narrow branch patterns are described as a solid-like fracturing process because the invading fluid has to overcome the frictional mechanical forces that resist granular rearrangement to form them66,68,72,77. The fracture growth pushes grains ahead of it and to either side, creating a local compacted front beyond which the packing is unperturbed. In other words, the fracture growth mobilises grains locally, not globally. This locality can be seen in our experiments for the DFr phase where the branches relax once the stress front has passed rather than being maintained at a distance. A transition from wide to narrow VF and then to fracturing has also been observed with increasing ϕ in settled granular systems68,74. Similarly to fracturing observed in these dense settled granular systems, both the DFr and Fr phases observed here in the dense suspended cornstarch systems have offshoot branches that can be perpendicular to the parent branch, which is not observed in VF in either of the settled or suspended systems.
Comparing fracturing in settled dense granular systems with the suspended dense cornstarch systems here, it appears that a common theme is how particle friction is critical for mixtures to fracture. It is particle friction that provides the necessary resistance in the defending mixture to support the narrow patterns where a mixture that is not dominated by friction would display widening viscous fingers. What is most interesting when comparing the two systems is the response to pressure. The dense settled granular systems have two critical injection pressures: one below which the defending fluid and grains do not move but above which they fracture and another higher critical pressure above which the system flows as viscous fingers to the open boundary66. The dense suspended cornstarch system has a somewhat inverted response with one critical injection pressure below which it always flows to the open boundary and above which it fractures. For both systems, these transitions are determined by the frictional relationship between particles. As the settled grains are resting in contact, friction is always present. It dominates the system whether particles are moving or not until the injection pressure is high enough that it can suspend and lubricate the particles out of contact and then liquid-like behaviour is observed. In contrast, at low pressures the cornstarch particles are dominated by lubrication forces and only once the invasion pressure is high enough to elicit shear thickening is solid-like frictional behaviour observed as fracturing.
We put forward the following interpretation: the VF patterns are a signature of liquid-like behaviour in the suspension. In the context of the measured rheology and theoretical models, this liquid-like behaviour occurs at low pressure or when the suspension is dilute enough that only weak (continuous) shear thickening can be obtained regardless of imposed pressure. Our results are in agreement with the central hypothesis put forward by several authors33,35,40,41,42,43, that DST is a signature of a frictionless to frictional transition. This is in particular revealed by the fact that the VF mode, i.e. liquid-like behaviour, was observed for even the highest concentrations as long as the imposed pressure was below a critical stress Pc ≈ 0.5 bar.
We propose that the fracturing mode is a signature of solid-like behaviour, which in turn is a consequence of frictional inter-particle contact, as similarly observed in other multi-phase granular systems66,68,77. This mode is associated with the order-of-magnitude increase in stress for a small increase in shear rate, i.e. DST, as evident in the measured flow curves. For the DFr mode, the suspension is locally brought into the frictional DST state around the invasion front, but the suspension relaxes back to its liquid state as the stress reduces once the front has passed by.
Theoretical models feature a distinct transition from DST to SJ corresponding to the point at which the initial ϕ for the quiescent frictionless suspension is above that of the maximum ϕj for frictional particles. This theoretical result can be associated with our measured rheology: it occurs for ϕ ≳ 0.53 when the flow curve no longer levels off at a well-defined upper viscosity branch. We suggest that this dynamic is evident in the Hele-Shaw experiments for similar values of ϕ where the stress imposed by the invading air causes a large fraction of the suspension contained in the cell to seize up in a solid-like state, resulting in large, system-spanning fractures.
In summary, here we have reported on the first use of a Hele-Shaw cell geometry to visualise invasion patterns in shear thickening and DST cornstarch suspensions in water. Air was released at a controlled pressure into suspensions with varying concentration of cornstarch and the resultant invasion patterns were captured with a high-speed camera. Results from image analysis led to a delineation between three distinct pattern morphologies: VF, DFr marked by dense frequently branching fractures, and Fr marked by sparse minimally branching fractures. These results were plotted in a P–Δϕ phase diagram and discussed in context of rheological measurements, current DST theory, and similar patterns observed in other dense granular media.
We found that the striking invasion patterns revealed by the flow geometry of the Hele-Shaw cell correspond to the packing fraction ranges of the three different rheological responses of cornstarch suspensions. VF was observed during conditions that did not correspond to DST or SJ (i.e. CST in dilute suspension and P < Pc for all suspensions). DFr was observed during conditions that correspond to DST behaviour but not SJ (P > Pc for dense suspensions of ϕ < ϕj). Fr was observed during conditions that correspond to SJ (P > Pc for ϕ > ϕj).
In addition, a DST relaxation phenomenon is reported in the DFr regime. The advancing local stress front caused by the invading air moves through the suspension initially as fractures. However, once the front has passed, the local stress is lowered and the fractures “relax” into fingers while the front continues to fracture ahead. This indicates that the DFr regime is categorised by a local DST response, rather than a global one as the SJ regime does.
Future experimental work involving Hele-Shaw cell set-ups can explore how varying the cell gap height can change the shear stress experienced by the suspension relative to the imposed invasion pressure. There is also the ongoing discussion regarding the pressure differences recorded for solid-like behaviour in DST suspensions between the rheology and impact-experiment literature. In addition, recent advancements in modelling dense DST suspensions based on frictionless–frictional theory have allowed complex mechanical responses of cornstarch suspensions to be simulated35. The simple geometry and distinct visual results presented here could be useful as a case study to validate simulations.
Methods
Experiment and analysis
The two controlled variables for experiments were the volume fraction of the cornstarch in suspension, ranging from ϕ = 0.23 ± 0.01 to 0.53 ± 0.01, and the imposed air pressure, ranging from P = 0.10 ± 0.02 to 10.00 ± 0.02 bar. The cornstarch was weighed out and mixed with deionised water to form the desired volume fraction ϕ according to the following ratio:
where mcs is the measured mass of cornstarch; ρcs is the density of cornstarch (1.6 ± 0.05 × 103 kg m−3 20,28,46); mw and ρw are the mass and density of deionised water, respectively; λ is the pore space in cornstarch that can absorb water when fully submerged (λ ≈ 0.3[ 29,86); and β is the pore space in cornstarch that has absorbed water in natural room humidity (β ≈ 0.13 27,86,87,88). The variance that results from differing humidities between days that experiments were conducted on is minimal, a change of approximately ±1% of the sample mass26,29. However, to reduce the impact of this daily variation, before weighing and mixing the cornstarch it was first prepared in a vacuum chamber for 45 min to remove ambient moisture from the sample. This process was found to remove ≈20 ± 5% giving β = 0.10 ± 0.01, which was used for all calculations.
The prepared sample was stored in a sealed container to avoid evaporation before it was used. The experiment was run within minutes of the mixture being poured into the cell to avoid settling, which takes place over several hours even without a density-matched liquid20. The particles of cornstarch were measured with a Mastersizer to have an average diameter of 16.1 μm (Fig. 2a).
The experiments were conducted in a Hele-Shaw cell made of transparent 4-cm-thick acrylic plates (Fig. 2b). The cornstarch suspension was confined in a 0.02-cm gap underneath a removable upper circular plate with a 10-cm radius. The cell was held together by clamps and had a completely open boundary at its perimeter. Pressurised air entered the cell through a central 0.5-cm diameter inlet. Air was pre-pressurised in a 3.5 L metal cylinder to the desired pressure and then released with a valve into the inlet to begin the experiment.
Invasion patterns were filmed from below with a high-speed camera (Photron Fastcam 1024-PCI) with a resolution of 1024 × 1024 pixel2 and a frame rate of 1000 fps. Pattern characterisation was performed on selected frames where the most advanced finger (or fracture branch) had reached to within 1 cm of the open boundary. Thresholding and de-speckling produced the binary images presented here. Morphology measurements were applied to a 2-cm-wide annulus with inner radius 4 cm as illustrated in Fig. 2c. Finger (branch) width w and separation distance between them d was measured with intersecting 1-pixel-wide rings and averaged within the annular region of interest. The spatial frequency of fingers (branches) was defined as D = (w + d)−1. A characteristic finger (branch) tip velocity vtip was estimated by measuring the time taken from when the air first entered the cell until the first branch reached the 10-cm radius boundary of the cell.
Rheology
Rheological tests were performed with a Bohlin Gemini HR Nano Rheometer on cornstarch suspensions prepared in the same fashion as for the Hele-Shaw experiments. A parallel plate geometry with 40 and 20 mm diameter plates with a gap size of 0.4 and 0.8 mm were used for 0.23 ≤ ϕ ≤0.41 and 0.45 ≤ ϕ ≤ 0.56, respectively. A lower height was used for the dilute suspensions to reduce secondary flows21,89. The rheology was measured in stress control mode, with shear rate the dependent variable responding to step-wise increases in imposed stress. A delay time of 5 s was set for the rheometer to adjust between measurements and a measurement window of 5 s was used. Note that, throughout this work, flow curves will be plotted in the conventional way with shear rate on the x-axis, even though a stress-controlled experiment is used and the shear rate is the independent variable.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Hu, Y. T., Boltenhagen, P., Matthys, E. & Pine, D. J. Shear thickening in low-concentration solutions of wormlike micelles. II. Slip, fracture, and stability of the shear-induced phase. J. Rheol. 42, 1209–1226 (1998).
Cates, M. E., Haw, M. D. & Holmes, C. B. Dilatancy, jamming, and the physics of granulation. J. Phys. Condens. Matter 17, S2517–S2531 (2005).
Stickel, J. J. & Powell, R. L. Fluid mechanics and rheology of dense suspensions. Annu. Rev. Fluid Mech. 37, 129–149 (2005).
Smith, M., Besseling, R., Cates, M. & Bertola, V. Dilatancy in the flow and fracture of stretched colloidal suspensions. Nat. Commun. 1, 114 (2010).
Denn, M. M. & Morris, J. F. Rheology of non-Brownian suspensions. Annu. Rev. Chem. Biomol. Eng. 5, 203–228 (2014).
Dagois-Bohy, S., Hormozi, S., Guazzelli, É. & Pouliquen, O. Rheology of dense suspensions of non-colloidal spheres in yield-stress fluids. J. Fluid Mech. 776, R2 (2015).
Sumita, I. & Manga, M. Suspension rheology under oscillatory shear and its geophysical implications. Earth Planet. Sci. Lett. 269, 468–477 (2008).
Hutton, J. F. Fracture of liquids in shear. Nature 203, 177–177 (1964).
Ligoure, C. & Mora, S. Fractures in complex fluids: the case of transient networks. Rheol. Acta 52, 91–114 (2013).
Barnes, H. A. Shear-thickening dilatancy in suspensions of nonaggregating solid particles dispersed in newtonian liquids. J. Rheol. 33, 329–366 (1989).
Feys, D., Verhoeven, R. & Schutter, G. D. Fresh self compacting concrete, a shear thickening material. Cem. Concr. Res. 38, 920–929 (2008).
Wagner, N. J. & Brady, J. F. Shear thickening in colloidal dispersions. Phys. Today 62, 27–32 (2009).
Lin, N. Y., Ness, C., Cates, M. E., Sun, J. & Cohen, I. Tunable shear thickening in suspensions. Proc. Natl Acad. Sci. USA 113, 10774–10778 (2016).
Lee, Y. S., Wetzel, E. D. & Wagner, N. J. The ballistic impact characteristics of Kevlar woven fabrics impregnated with a colloidal shear thickening fluid. J. Mater. Sci. 38, 2825–2833 (2003).
Brown, E. & Jaeger, H. M. Shear thickening in concentrated suspensions: phenomenology, mechanisms and relations to jamming. Rep. Prog. Phys. 77, 046602 (2014).
Royer, J. R., Blair, D. L. & Hudson, S. D. Rheological signature of frictional interactions in shear thickening suspensions. Phys. Rev. Lett. 116, 188301 (2016).
Crawford, N. C. et al. Shear thickening of corn starch suspensions: does concentration matter? J. Colloid Interface Sci. 396, 83–89 (2013).
Gálvez, L. O., de Beer, S., van der Meer, D. & Pons, A. Dramatic effect of fluid chemistry on cornstarch suspensions: linking particle interactions to macroscopic rheology. Phys. Rev. E 95, 030602(R) (2017).
Brown, E. & Jaeger, H. M. Dynamic jamming point for shear thickening suspensions. Phys. Rev. Lett. 103, 086001 (2009).
Brown, E. & Jaeger, H. M. The role of dilation and confining stresses in shear thickening of dense suspensions. J. Rheol. 56, 875–923 (2012).
Fall, A., Bertrand, F., Ovarlez, G. & Bonn, D. Shear thickening of cornstarch suspensions. J. Rheol. 56, 575–591 (2012).
Maharjan, R. & Brown, E. Giant deviation of a relaxation time from generalized newtonian theory in discontinuous shear thickening suspensions. Phys. Rev. Fluids 2, 123301 (2017).
Jerome, J. J. S., Vandenberghe, N. & Forterre, Y. Unifying impacts in granular matter from quicksand to cornstarch. Phys. Rev. Lett. 117, 098003 (2016).
Maharjan, R., Mukhopadhyay, S., Allen, B., Storz, T. & Brown, E. Constitutive relation for the system-spanning dynamically jammed region in response to impact of cornstarch and water suspensions. Phys. Rev. E 97, 052602 (2018).
Fall, A., Lemaître, A. & Ovarlez, G. Discontinuous shear thickening in cornstarch suspensions. EPJ Web Conf. 140, 09001 (2017).
Han, E., Peters, I. R. & Jaeger, H. M. High-speed ultrasound imaging in dense suspensions reveals impact-activated solidification due to dynamic shear jamming. Nat. Commun. 7, 12243 (2016).
Han, E., Wyart, M., Peters, I. R. & Jaeger, H. M. Shear fronts in shear-thickening suspensions. Phys. Rev. Fluids 3, 073301 (2018).
Peters, I. R. & Jaeger, H. M. Quasi-2d dynamic jamming in cornstarch suspensions: visualization and force measurements. Soft Matter 10, 6564–6570 (2014).
Peters, I. R., Majumdar, S. & Jaeger, H. M. Direct observation of dynamic shear jamming in dense suspensions. Nature 532, 214–217 (2016).
Waitukaitis, S. R. & Jaeger, H. M. Impact-activated solidification of dense suspensions via dynamic jamming fronts. Nature 487, 205–209 (2012).
Roché, M., Myftiu, E., Johnston, M. C., Kim, P. & Stone, H. A. Dynamic fracture of nonglassy suspensions. Phys. Rev. Lett. 110, 148304 (2013).
Allen, B., Sokol, B., Mukhopadhyay, S., Maharjan, R. & Brown, E. System-spanning dynamically jammed region in response to impact of cornstarch and water suspensions. Phys. Rev. E 97, 052603 (2018).
Hermes, M. et al. Unsteady flow and particle migration in dense, non-Brownian suspensions. J. Rheol. 60, 905–916 (2016).
Ozgen, O., Kallmann, M. & Brown, E. An SPH model to simulate the dynamic behavior of shear thickening fluids. Comput. Anim. Virtual Worlds 30, e1870 (2019).
Baumgarten, A. S. & Kamrin, K. A general constitutive model for dense, fine-particle suspensions validated in many geometries. Proc. Natl Acad. Sci. USA 116, 20828–20836 (2019).
Sivadasan, V., Lorenz, E., Hoekstra, A. G. & Bonn, D. Shear thickening of dense suspensions: the role of friction. Phys. Fluids 31, 103103 (2019).
Lootens, D., Damme, H. V. & Hébraud, P. Giant stress fluctuations at the jamming transition. Phys. Rev. Lett. 90, 178301 (2003).
Lootens, D., van Damme, H., Hémar, Y. & Hébraud, P. Dilatant flow of concentrated suspensions of rough particles. Phys. Rev. Lett. 95, 268302 (2005).
Hoffman, R. Discontinuous and dilatant viscosity behavior in concentrated suspensions. II. theory and experimental tests. J. Colloid Interface Sci. 46, 491–506 (1974).
Trulsson, M., Andreotti, B. & Claudin, P. Transition from the viscous to inertial regime in dense suspensions. Phys. Rev. Lett. 109, 118305 (2012).
Seto, R., Mari, R., Morris, J. F. & Denn, M. M. Discontinuous shear thickening of frictional hard-sphere suspensions. Phys. Rev. Lett. 111, 218301 (2013).
Mari, R., Seto, R., Morris, J. F. & Denn, M. M. Shear thickening, frictionless and frictional rheologies in non-Brownian suspensions. J. Rheol. 58, 1693–1724 (2014).
Wyart, M. & Cates, M. Discontinuous shear thickening without inertia in dense non-Brownian suspensions. Phys. Rev. Lett. 112, 098302 (2014).
Guy, B. M. et al. Testing the Wyart–Cates model for non-Brownian shear thickening using bidisperse suspensions. Soft Matter 16, 229–237 (2020).
Clavaud, C., Bérut, A., Metzger, B. & Forterre, Y. Revealing the frictional transition in shear-thickening suspensions. Proc. Natl Acad. Sci. USA 114, 5147–5152 (2017).
Comtet, J. et al. Pairwise frictional profile between particles determines discontinuous shear thickening transition in non-colloidal suspensions. Nat. Commun. 8, 15633 (2017).
Vázquez-Quesada, A., Wagner, N. J. & Ellero, M. Planar channel flow of a discontinuous shear-thickening model fluid: theory and simulation. Phys. Fluids 29, 103104 (2017).
Hele-Shaw, H. S. The flow of water. Nature 58, 34–36 (1898).
Saffman, P. G. & Taylor, G. I. The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 245, 312–329 (1958).
Saffman, P. G. Viscous fingering in Hele-Shaw cells. J. Fluid Mech. 173, 73 (1986).
Li, S., Lowengrub, J. S., Fontana, J. & Palffy-Muhoray, P. Control of viscous fingering patterns in a radial Hele-Shaw cell. Phys. Rev. Lett. 102, 174501 (2009).
McCloud, K. & Maher, J. Experimental perturbations to Saffman-Taylor flow. Phys. Rep. 260, 139–185 (1995).
Bonn, D., Kellay, H., Bräunlich, M., Amar, M. & Meunier, J. Viscous fingering in complex fluids. Phys. A Stat. Mech. Appl. 220, 60–73 (1995).
Lindner, A., Bonn, D., Poiré, E. C., Amar, M. B. & Meunier, J. Viscous fingering in non-Newtonian fluids. J. Fluid Mech. 469, 237–256 (2002).
White, A. R. & Ward, T. Constant pressure gas-driven displacement of a shear-thinning liquid in a partially filled radial Hele-Shaw cell: thin films, bursting and instability. J. Non-Newton. Fluid Mech. 206, 18–28 (2014).
Kagei, N., Kanie, D. & Kawaguchi, M. Viscous fingering in shear thickening silica suspensions. Phys. Fluids 17, 054103 (2005).
Lindner, A., Coussot, P. & Bonn, D. Viscous fingering in a yield stress fluid. Phys. Rev. Lett. 85, 314–317 (2000).
Foyart, G., Ramos, L., Mora, S. & Ligoure, C. The fingering to fracturing transition in a transient gel. Soft Matter 9, 7775 (2013).
Berret, J.-F. & Séréro, Y. Evidence of shear-induced fluid fracture in telechelic polymer networks. Phys. Rev. Lett. 87, 048303 (2001).
Skrzeszewska, P. J. et al. Fracture and self-healing in a well-defined self-assembled polymer network. Macromolecules 43, 3542–3548 (2010).
Zhao, H. & Maher, J. V. Associating-polymer effects in a Hele-Shaw experiment. Phys. Rev. E 47, 4278–4283 (1993).
Ignés-Mullol, J., Zhao, H. & Maher, J. V. Velocity fluctuations of fracturelike disruptions of associating polymer solutions. Phys. Rev. E 51, 1338–1343 (1995).
Vlad, D. H., Ignes-Mullol, J. & Maher, J. V. Velocity-jump instabilities in Hele-Shaw flow of associating polymer solutions. Phys. Rev. E 60, 4423–4430 (1999).
Mora, S. & Manna, M. Saffman-Taylor instability of viscoelastic fluids: from viscous fingering to elastic fractures. Phys. Rev. E 81, 026305 (2010).
Mulla, Y., Oliveri, G., Overvelde, J. T. & Koenderink, G. H. Crack initiation in viscoelastic materials. Phys. Rev. Lett. 120, 268002 (2018).
Campbell, J. M., Ozturk, D. & Sandnes, B. Gas-driven fracturing of saturated granular media. Phys. Rev. Appl. 8, 064029 (2017).
Cavanagh, A. J. & Haszeldine, R. S. The sleipner storage site: capillary flow modeling of a layered CO2 plume requires fractured shale barriers within the utsira formation. Int. J. Greenh. Gas. Control 21, 101–112 (2014).
Sandnes, B., Flekkøy, E., Knudsen, H., Måløy, K. & See, H. Patterns and flow in frictional fluid dynamics. Nat. Commun. 2, 288 (2011).
Lemaire, E., Levitz, P., Daccord, G. & Damme, H. V. From viscous fingering to viscoelastic fracturing in colloidal fluids. Phys. Rev. Lett. 67, 2009–2012 (1991).
Oppenheimer, J., Rust, A. C., Cashman, K. V. & Sandnes, B. Gas migration regimes and outgassing in particle-rich suspensions. Front. Phys. 3, 60 (2015).
Sandnes, B., Flekkøy, E. G. & Måløy, K. J. Stick slip displacement of confined granular mixtures: bubble expansion. Eur. Phys. J. Spec. Top. 204, 19–25 (2012).
Holtzman, R., Szulczewski, M. L. & Juanes, R. Capillary fracturing in granular media. Phys. Rev. Lett. 108, 264504 (2012).
Chevalier, C., Lindner, A. & Clément, E. Destabilization of a Saffman-Taylor fingerlike pattern in a granular suspension. Phys. Rev. Lett. 99, 174501 (2007).
Chevalier, C., Lindner, A., Leroux, M. & Clément, E. Morphodynamics during air injection into a confined granular suspension. J. Non-Newton. Fluid Mech. 158, 63–72 (2009).
Varas, G., Géminard, J.-C. & Vidal, V. Air invasion in a granular layer immersed in a fluid: morphology and dynamics. Granul. Matter 15, 801–810 (2013).
Varas, G., Ramos, G., Géminard, J.-C. & Vidal, V. Flow and fracture in water-saturated, unconstrained granular beds. Front. Phys. 3, 44 (2015).
Ozturk, D. & Sandnes, B. A study of three-phase fracturing in granular media using high-speed imaging. J. Porous Media 22, 987–1000 (2019).
Singh, A., Mari, R., Denn, M. M. & Morris, J. F. A constitutive model for simple shear of dense frictional suspensions. J. Rheol. 62, 457–468 (2018).
Maranzano, B. J. & Wagner, N. J. The effects of particle size on reversible shear thickening of concentrated colloidal dispersions. J. Chem. Phys. 114, 10514–10527 (2001).
Guy, B., Hermes, M. & Poon, W. Towards a unified description of the rheology of hard-particle suspensions. Phys. Rev. Lett. 115, 088304 (2015).
Melrose, J. R. & Ball, R. C. The pathological behaviour of sheared hard spheres with hydrodynamic interactions. Europhys. Lett. (EPL) 32, 535–540 (1995).
Dhar, S., Chattopadhyay, S. & Majumdar, S. Signature of jamming under steady shear in dense particulate suspensions. J. Phys. Condens. Matter 32, 124002 (2019).
Liu, A. J. & Nagel, S. R. Jamming is not just cool any more. Nature 396, 21–22 (1998).
O’Brien, V. T. & Mackay, M. E. Stress components and shear thickening of concentrated hard sphere suspensions. Langmuir 16, 7931–7938 (2000).
Larsen, R. J., Kim, J.-W., Zukoski, C. F. & Weitz, D. A. Elasticity of dilatant particle suspensions during flow. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 81, 011502 (2010).
Han, E., Ha, N. V. & Jaeger, H. M. Measuring the porosity and compressibility of liquid-suspended porous particles using ultrasound. Soft Matter 13, 3506–3513 (2017).
Whistler, R. L., Bemiller, J. N. & Paschall, E. F. Starch: Chemistry and Technology (Academic, 1984).
Sair, L. & Fetzer, W. R. Water sorption by starches. Ind. Eng. Chem. 36, 205–208 (1944).
Ewoldt, R. H., Johnston, M. T. & Caretta, L. M. in Complex Fluids in Biological Systems 207–241 (Springer, New York, 2014).
Acknowledgements
We thank Paul Williams for help with the particle size measurements and Marco Ellero for discussions. This work was supported in part by the Engineering and Physical Sciences Research Council (EP/S034587/1) and Ser Cymru National Research Network in Advanced Engineering and Materials (NRN141).
Author information
Authors and Affiliations
Contributions
D.O. contributed to the experiment design, performed all experiments, analysed all results, and was the main author of the paper. M.L.M. performed the rheological experiments and assisted in writing the paper. B.S. contributed to the experiment design and assisted in writing the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ozturk, D., Morgan, M.L. & Sandnes, B. Flow-to-fracture transition and pattern formation in a discontinuous shear thickening fluid. Commun Phys 3, 119 (2020). https://doi.org/10.1038/s42005-020-0382-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-0382-7
This article is cited by
-
Rheology of a crowd: from faster-is-slower to shear thickening
Communications Physics (2024)
-
Characterization and identification of gas invasion patterns in magnesium lithium phyllosilicate suspensions
Rheologica Acta (2024)
-
Shear-thickening of dense bidispersed suspensions
Meccanica (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.